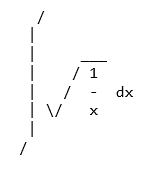SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.
В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.
Вот где применяется SymPy:
- Многочлены
- Математический анализ
- Дискретная математика
- Матрицы
- Геометрия
- Построение графиков
- Физика
- Статистика
- Комбинаторика
Для работы SymPy требуется одна важная библиотека под названием mpmath. Она используется для вещественной и комплексной арифметики с числами с плавающей точкой произвольной точности. Однако pip установит ее автоматически при загрузке самой SymPy:
pip install sympyТакие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:
>>> import sympy
>>> sympy.__version__
'1.6.2'
Исходный код можно найти на GitHub.
Символьные вычисления в SymPy
Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.
Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:
import math
print(math.sqrt(25), math.sqrt(7))
Вывод следующий:
5.0 2.6457513110645907Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:
import sympy
print(sympy.sqrt(7))
Вот каким будет вывод этого кода: sqrt(7).
Это можно упростить и показать результат выражения символически таким вот образом:
>>> import math
>>> print(math.sqrt(12))
3.4641016151377544
>>> import sympy
>>> print(sympy.sqrt(12))
2*sqrt(3)
В случае с модулем math вернется число, а вот в SymPy — формула.
Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:
from sympy import *
x = Symbol('x')
expr = integrate(x**x, x)
expr
Если выполнить эту команду в IDLE, то получится следующий результат:
Integral(x**x,x)А в Jupyter:

Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.
В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.
Числа
Основной модуль в SymPy включает класс Number, представляющий атомарные числа. У него есть пара подклассов: Float и Rational. В Rational также входит Integer.
Класс Float
Float представляет числа с плавающей точкой произвольной точности:
>>> from sympy import Float
>>> Float(6.32)
6.32
SymPy может конвертировать целое число или строку в число с плавающей точкой:
При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:
>>> Float('1.33E5')
133000.0
Представить число дробью можно с помощью объекта класса Rational, где знаменатель — не 0:
Если число с плавающей точкой передать в конструктор Rational(), то он вернет дробь:

Для упрощения можно указать ограничение знаменателя:
Rational(0.2).limit_denominator(100)
Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.
Если же в конструктор передать строку, то вернется рациональное число произвольной точности:
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:
>>> a=Rational(3, 5)
>>> print(a)
3/5
>>> print("числитель:{}, знаменатель:{}".format(a.p, a.q))
числитель:3, знаменатель:5
Класс Integer
Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:
>>> Integer(10)
10
>>> Integer(3.4)
3
>>> Integer(2/7)
0
Также есть класс RealNumber, который является алиасом для Float. В SymPy есть классы-одиночки Zero и One, доступные через S.Zero и S.One соответственно.
Другие числовые объекты-одиночки — Half, NaN, Infinity и ImaginaryUnit.
>>> from sympy import S
>>> print(S.Half)
1/2
>>> print(S.NaN)
nan
Бесконечность представлена в виде объекта-символа oo или как S.Infinity:

ImaginaryUnit можно импортировать как символ I, а получить к нему доступ — через S.ImaginaryUnit.
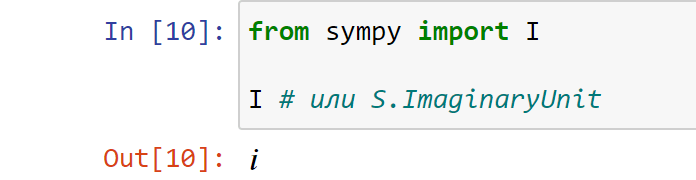
Символы
Symbol — самый важный класс в библиотеке SymPy. Как уже упоминалось ранее, символьные вычисления выполняются с помощью символов. И переменные SymPy являются объектами класса Symbol.
Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.
>>> from sympy import Symbol
>>> x = Symbol('x')
>>> y = Symbol('y')
>>> expr = x**2 + y**2
>>> expr
Код выше является эквивалентом этого выражения:
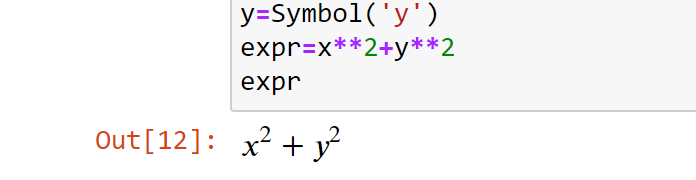
Символ может включать больше одной буквы:
from sympy import Symbol
s = Symbol('side')
s**3
Также в SymPy есть функция Symbols(), с помощью которой можно определить несколько символов за раз. Строка содержит названия переменных, разделенные запятыми или пробелами.
from sympy import symbols
x, y, z = symbols("x, y, z")
В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:
from sympy.abc import x, z
Однако C, O, S, I, N, E и Q являются заранее определенными символами. Также символы с более чем одной буквы не определены в abc. Для них нужно использовать объект Symbol. Модуль abs определяет специальные имена, которые могут обнаружить определения в пространстве имен SymPy по умолчанию. сlash1 содержит однобуквенные символы, а clash2 — целые слова.
>>> from sympy.abc import _clash1, _clash2
>>> _clash1
{'C': C,'O': O,'Q': Q,'N': N,'I': I,'E': E,'S': S}
>>> _clash2
{'beta': beta,'zeta': zeta,'gamma': gamma,'pi': pi}
Индексированные символы (последовательность слов с цифрами) можно определить с помощью синтаксиса, напоминающего функцию range(). Диапазоны обозначаются двоеточием. Тип диапазона определяется символом справа от двоеточия. Если это цифра, то все смежные цифры слева воспринимаются как неотрицательное начальное значение.
Смежные цифры справа берутся на 1 больше конечного значения.
>>> from sympy import symbols
>>> symbols('a:5')
(a0,a1,a2,a3,a4)
>>> symbols('mark(1:4)')
(mark1,mark2,mark3)
Подстановка параметров
Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.
>>> from sympy.abc import x, a
>>> expr = sin(x) * sin(x) + cos(x) * cos(x)
>>> expr
Этот код даст вывод, эквивалентный такому выражению.
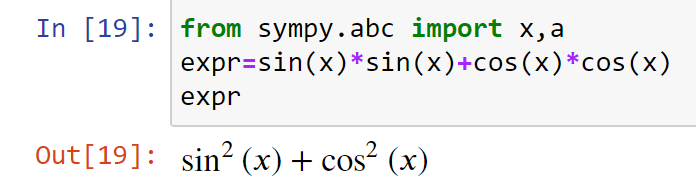
А кодом expr.subs(x,a) мы получим туже формулу, но с a вместо x.
Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5:
>>> from sympy.abc import x
>>> from sympy import sin, pi
>>> expr = sin(x)
>>> expr1 = expr.subs(x, pi)
>>> expr1
0
Также функция используется для замены подвыражения другим подвыражением. В следующем примере b заменяется на a+b.
>>> from sympy.abc import a, b
>>> expr = (a + b)**2
>>> expr1 = expr.subs(b, a + b)
>>> expr1
Это дает такой вывод:
Функция simplify()
Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:
>>> expr = "x**2 + 3*x + 2"
>>> expr1 = sympify(expr)
>>> expr1.subs(x, 2)
12
Любой объект Python можно конвертировать в объект SymPy. Однако учитывая то, что при преобразовании используется функция eval(), не стоит использовать некорректные выражения, иначе возникнет ошибка SimplifyError.
>>> sympify("x***2")
...
SympifyError: Sympify of expression 'could not parse 'x***2'' failed, because of exception being raised:
SyntaxError: invalid syntax (<string>, line 1)
Функция simplify() принимает следующий аргумент: strict=False. Если установить True, то преобразованы будут только те типы, для которых определено явное преобразование. В противном случае также возникнет ошибка SimplifyError. Если же поставить False, то арифметические выражения и операторы будут конвертированы в их эквиваленты SumPy без вычисления выражения.
Функция evalf()
Функция вычисляет данное числовое выражение с точностью до 100 цифр после плавающей точки. Она также принимает параметр subs, как объект словаря с числовыми значениями для символов. Например такое выражение:
from sympy.abc import r
expr = pi * r**2
expr
Даст такой результат: ??2
Вычислим выражение с помощью evalf() и заменим r на 5:
>>> expr.evalf(subs={r: 5})
78.5398163397448
По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:
>>> expr = a / b
>>> expr.evalf(20, subs={a: 100, b: 3})
33.333333333333333333
Функция lambdify()
Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.
>>> expr =1 / sin(x)
>>> f = lambdify(x, expr)
>>> f(3.14)
627.8831939138764
У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:
>>> expr = a**2 + b**2
>>> f = lambdify([a, b], expr)
>>> f(2, 3)
13
Но чтобы использовать numpy в качестве основной библиотеки, ее нужно передать в качестве аргумента функции lambdify().
f = lambdify([a, b], expr, "numpy")
В этой функции использовались два массива numpy: a и b. В случае с ними выполнение гораздо быстрее:
>>> import numpy
>>> l1 = numpy.arange(1, 6)
>>> l2 = numpy.arange(6, 11)
>>> f(l1, l2)
array([ 37, 53, 73, 97, 125], dtype=int32)
Логические выражения
Булевы функции расположены в модуле sympy.basic.booleanarg. Их можно создать и с помощью стандартных операторов Python: & (And), | (Or), ~ (Not), а также >> и <<. Булевы выражения наследуются от класса Basic.
BooleanTrue.
Эта функция является эквивалентом True из Python. Она возвращает объект-одиночку, доступ к которому можно получить и с помощью S.true.
>>> from sympy import *
>>> x = sympify(true)
>>> x, S.true
(True, True)
BooleanFalse.
А эта функция является эквивалентом False. Ее можно достать с помощью S.False.
>>> from sympy import *
>>> x = sympify(false)
>>> x, S.false
(False,False)
And.
Функция логического AND оценивает два аргумента и возвращает False, если хотя бы один из них является False. Эта функция заменяет оператор &.
>>> from sympy import *
>>> from sympy.logic.boolalg import And
>>> x, y = symbols('x y')
>>> x = True
>>> y = True
>>> And(x, y), x & y
Or.
Оценивает два выражения и возвращает True, если хотя бы одно из них является True. Это же поведение можно получить с помощью оператора |.
>>> from sympy import *
>>> from sympy.logic.boolalg import Or
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Or(x, x|y)
Not.
Результат этой функции — отрицание булево аргумента. True, если аргумент является False, и False в противном случае. В Python за это отвечает оператор ~. Пример:
>>> from sympy import *
>>> from sympy.logic.boolalg import Or,And,Not
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Not(x), Not(y)
(False, True)
Xor.
Логический XOR (исключающий OR) возвращает True, если нечетное количество аргументов равняется True, а остальные — False. False же вернется в том случае, если четное количество аргументов True, а остальные — False. То же поведение работает в случае оператора ^.
>>> from sympy import *
>>> from sympy.logic.boolalg import Xor
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Xor(x, y)
True
В предыдущем примере один(нечетное число) аргумент является True, поэтому Xor вернет True. Если же количество истинных аргументов будет четным, результатом будет False, как показано дальше.
Nand.
Выполняет логическую операцию NAND. Оценивает аргументы и возвращает True, если хотя бы один из них равен False, и False — если они истинные.
>>> from sympy.logic.boolalg import Nand
>>> a, b, c = (True, False, True)
>>> Nand(a, c), Nand(a, b)
(False, True)
Nor.
Выполняет логическую операцию NOR. Оценивает аргументы и возвращает False, если один из них True, или же True, если все — False.
>>> from sympy.logic.boolalg import Nor
>>> a, b = False, True
>>> Nor(a), Nor(a, b)
(True, False)
Хотя SymPy и предлагает операторы ^ для Xor, ~ для Not, | для Or и & для And ради удобства, в Python они используются в качестве побитовых. Поэтому если операнды будут целыми числами, результаты будут отличаться.
Equivalent.
Эта функция возвращает отношение эквивалентности. Equivalent(A, B) будет равно True тогда и только тогда, когда A и B оба будут True или False. Функция вернет True, если все аргументы являются логически эквивалентными. В противном случае — False.
>>> from sympy.logic.boolalg import Equivalent
>>> a, b = True, False
>>> Equivalent(a, b), Equivalent(a, True)
( False, True)
Запросы
Модуль assumptions в SymPy включает инструменты для получения информации о выражениях. Для этого используется функция ask().
Следующие свойства предоставляют полезную информацию о выражении:
sympy.assumptions.ask(выражение)
algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.
complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.
composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.
even, oddask() возвращает True, если x находится в множестве четных и нечетных чисел соответственно.
imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.
integer
Это свойство, возвращаемое Q.integer(x), будет истинным только в том случае, если x принадлежит множеству четных чисел.
rational, irrationalQ.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.
positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.
zero, nonzero
Предикат для проверки того, является ли число нулем или нет.
>>> from sympy import *
>>> x = Symbol('x')
>>> x = 10
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask(Q.complex(100))
(True, True)
>>> x, y = symbols("x y")
>>> x, y = 5, 10
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(True, None)
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(True, True, False, False)
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)
Функции упрощения
SymPy умеет упрощать математические выражения. Для этого есть множество функций. Основная называется simplify(), и ее основная задача — представить выражение в максимально простом виде.
simplify
Это функция объявлена в модуле sympy.simplify. Она пытается применить методы интеллектуальной эвристики, чтобы сделать входящее выражение «проще». Следующий код упрощает такое выражение: sin^2(x)+cos^2(x)
>>> x = Symbol('x')
>>> expr = sin(x)**2 + cos(x)**2
>>> simplify(expr)
1
expand
Одна из самых распространенных функций упрощения в SymPy. Она используется для разложения полиномиальных выражений. Например:
>>> a, b = symbols('a b')
>>> expand((a+b)**2)
А тут вывод следующий: ?2+2??+?2.
Вывод: ?2−?2.
Функция expand() делает выражение больше, а не меньше. Обычно это так и работает, но часто получается так, что выражение становится меньше после использования функции:
>>> expand((x + 1)*(x - 2) - (x - 1)*x)
-2
factor
Эта функция берет многочлен и раскладывает его на неприводимые множители по рациональным числам.
>>> x, y, z = symbols('x y z')
>>> expr = (x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor(expr)
Вывод: ?(?+2?)2.
Функция factor() — это противоположность expand(). Каждый делитель, возвращаемый factor(), будет несокращаемым. Функция factor_list() предоставляет более структурированный вывод:
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor_list(expr)
(1, [(z, 1), (x + 2*y, 2)])
collect
Эта функция собирает дополнительные члены выражения относительно списка выражений с точностью до степеней с рациональными показателями.
>>> expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
>>> expr
Вывод: ?3−?2?+2?2+??+?−3.
Результат работы collect():
>>> expr = y**2*x + 4*x*y*z + 4*y**2*z + y**3 + 2*x*y
>>> collect(expr, y)
Вывод: ?3+?2(?+4?)+?(4??+2?).
cancel
Эта функция берет любую рациональную функцию и приводит ее в каноническую форму p/q, где p и q — это разложенные полиномы без общих множителей. Старшие коэффициенты p и q не имеют знаменателей, то есть, являются целыми числами.
>>> expr1=x**2+2*x+1
>>> expr2=x+1
>>> cancel(expr1/expr2)
x + 1
Еще несколько примеров:
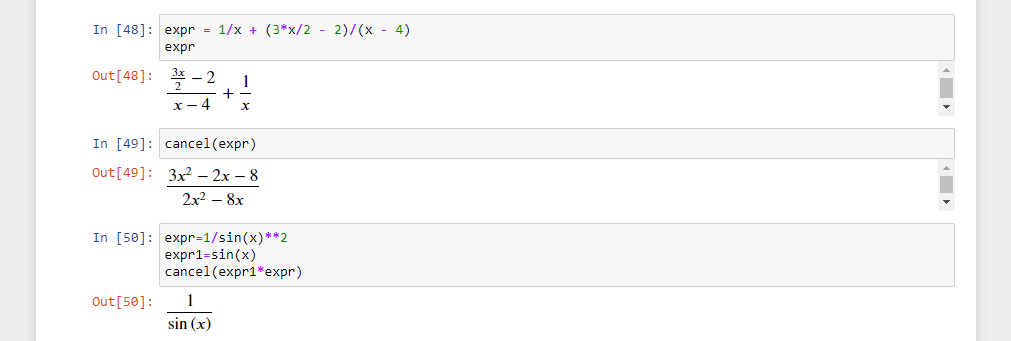
trigsimp
Эта функция используется для упрощения тригонометрических тождеств. Стоит отметить, что традиционные названия обратных тригонометрических функций добавляются в название функции в начале. Например, обратный косинус или арккосинус называется acos():
>>> from sympy import trigsimp, sin, cos
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2
>>> trigsimp(expr)
2
Функция trigsimp использует эвристику для применения наиболее подходящего тригонометрического тождества.
powersimp
Эта функция сокращает выражения, объединяя степени с аналогичными основаниями и значениями степеней.
>>> expr = x**y*x**z*y**z
>>> expr
Вывод: ??????.
Можно сделать так, чтоб powsimp() объединяла только основания или степени, указав combine='base' или combine='exp'. По умолчанию это значение равно combine='all'. Также можно задать параметр force. Если он будет равен True, то основания объединятся без проверок.
>>> powsimp(expr, combine='base', force=True)
Вывод: ??(??)?.
combsimp
Комбинаторные выражения, включающие факториал и биномы, можно упростить с помощью функции combsimp(). В SymPy есть функция factorial().
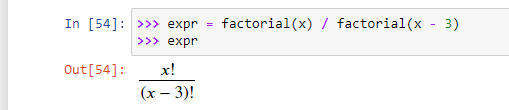
Для упрощения предыдущего комбинаторного выражения эта функция используется следующим образом.
>>> combsimp(expr)
?(?−2)(?−1)
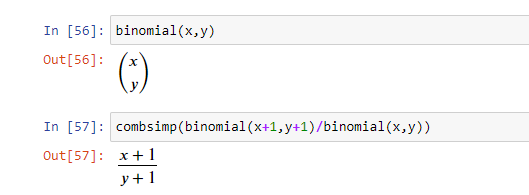
binomial(x, y) — это количество способов, какими можно выбрать элементы y из множества элементов x. Его же можно записать и как xCy.
logcombine
Эта функция принимает логарифмы и объединяет их с помощью следующих правил:
log(x) + log(y) == log(x*y)— оба положительные.a*log(x) == log(x**a)если x является положительным и вещественным.
>>> logcombine(a*log(x) + log(y) - log(z))
?log(?)+log(?)−log(?)
Если здесь задать значение параметра force равным True, то указанные выше предположения будут считаться выполненными, если нет предположений о величине.
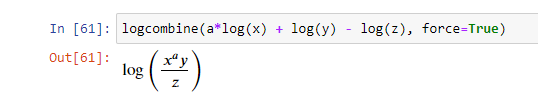
Производные
Производная функции — это ее скорость изменения относительно одной из переменных. Это эквивалентно нахождению наклона касательной к функции в точке. Найти дифференцирование математических выражений в форме переменных можно с помощью функции diff() из SymPy.
>>> from sympy import diff, sin, exp
>>> from sympy.abc import x, y
>>> expr = x*sin(x*x) + 1
>>> expr
Вывод: ?sin(?2)+1.
Чтобы получить несколько производных, нужно передать переменную столько раз, сколько нужно выполнить дифференцирование. Или же можно просто указать это количество с помощью числа.
Также можно вызвать метод diff() выражения. Он работает по аналогии с функцией.
>>> expr = x*sin(x*x) + 1
>>> expr.diff(x)
Вывод: 2?2cos(?2)+sin(?2).
Неоцененная производная создается с помощью класса Derivative. У него такой же синтаксис, как и функции diff(). Для оценки же достаточно использовать метод doit.

Интеграция
SymPy включает и модуль интегралов. В нем есть методы для вычисления определенных и неопределенных интегралов выражений. Метод integrate() используется для вычисления обоих интегралов. Для вычисления неопределенного или примитивного интеграла просто передайте переменную после выражения.
Для вычисления определенного интеграла, передайте аргументы следующим образом:
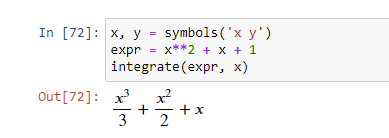
Пример определенного интеграла:
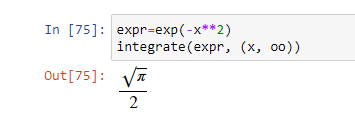
С помощью объекта Integral можно создать неоцененный интеграл. Он оценивается с помощью метода doit().
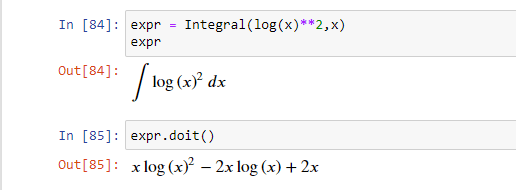
Трансформации интегралов
SymPy поддерживает разные виды трансформаций интегралов:
- laplace_tranfsorm.
- fourier_transform.
- sine_tranfsorm.
- cosine_transform.
- hankel_transform.
Эти функции определены в модуле sympy.integrals.transforms. Следующие примеры вычисляют преобразования Фурье и Лапласа соответственно:

>>> from sympy.integrals import laplace_transform
>>> from sympy.abc import t, s, a
>>> laplace_transform(t**a, t, s)
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)
Матрицы
В математике матрица — это двумерный массив чисел, символов или выражений. Теория манипуляций матрицами связана с выполнением арифметических операций над матричными объектами при соблюдении определенных правил.
Линейная трансформация — одно из важнейших применений матрицы. Она часто используется в разных научных областях, особенно связанных с физикой. В SymPy есть модуль matrices, который работает с матрицами. В нем есть класс Matrix для представления матрицы.
Примечание: для выполнения кода в этом разделе нужно сперва импортировать модуль matrices следующим образом.
>>> from sympy.matrices import Matrix
>>> m=Matrix([[1, 2, 3], [2, 3, 1]])
>>> m
⎡1 2 3⎤
⎣2 3 1⎦
Матрица — это изменяемый объект. Также в модуле есть класс ImmutableMatrix для получения неизменяемой матрицы.
Базовое взаимодействие
Свойство shape возвращает размер матрицы.
Методы row() и col() возвращают колонку или строку соответствующего числа.
>>> m.row(0)
[1 2 3]
>>> m.col(1)
⎡2⎤
⎣3⎦
Оператор slice из Python можно использовать для получения одного или большего количества элементов строки или колонки.
У класса Matrix также есть методы row_del() и col_del(), которые удаляют указанные строку/колонку из выбранной матрицы.
>>> m.row(1)[1:3]
[3, 1]
>>> m.col_del(1)
>>> m
⎡1 3⎤
⎣2 1⎦
По аналогии row_insert() и col_insert() добавляют строки и колонки в обозначенные индексы:
>>> m1 = Matrix([[10, 30]])
>>> m = m.row_insert(0, m1)
>>> m
⎡10 30⎤
⎢ 1 3 ⎥
⎣ 2 1 ⎦
Арифметические операции
Привычные операторы +, — и * используются для сложения, умножения и деления.
>>> M1 = Matrix([[3, 0], [1, 6]])
>>> M2 = Matrix([[4, 5], [6, 4]])
>>> M1 + M2
⎡7 5 ⎤
⎣7 10 ⎦
Умножение матрицы возможно лишь в том случае, если количество колонок первой матрицы соответствует количеству колонок второй. Результат будет иметь такое же количество строк, как у первой матрицы и столько же колонок, сколько есть во второй.
Для вычисления определителя матрицы используется метод det(). Определитель — это скалярное значение, которое может быть вычислено из элементов квадратной матрицы.
>>> M = Matrix([[4, 5], [6, 4]])
>>> M.det()
-14
Конструкторы матрицы
SymPy предоставляет множество специальных типов классов матриц. Например, Identity, матрица из единиц, нолей и так далее. Эти классы называются eye, zeroes и ones соответственно. Identity — это квадратная матрица, элементы которой по диагонали равны 1, а остальные — 0.
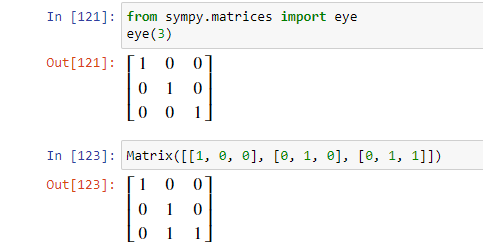
В матрице diag элементы по диагонали инициализируются в соответствии с предоставленными аргументами.
>>> from sympy.matrices import diag
>>> diag(1, 3)
⎡1 0 ⎤
⎣0 3 ⎦
Все элементы в матрице zero инициализируются как нули.
>>> from sympy.matrices import zeros
>>> zeros(2, 3)
⎡0 0 0⎤
⎣0 0 0⎦
По аналогии в матрице ones элементы равны 1:
>>> from sympy.matrices import zeros
>>> ones(2, 3)
⎡1 1 1⎤
⎣1 1 1⎦
Класс Function
В пакете SymPy есть класс Function, определенный в модуле sympy.core.function. Это базовый класс для всех математических функций, а также конструктор для неопределенных классов.
Следующие категории функций наследуются от класса Function:
- Функции для комплексных чисел
- Тригонометрические функции
- Функции целого числа
- Комбинаторные функции
- Другие функции
Функции комплексных чисел
Набор этих функций определен в модуле sympy.functions.elementary.complexes.
re — Эта функция возвращает реальную часть выражения:
>>> from sympy import *
>>> re(5+3*I)
5
>>> re(I)
0
im — Возвращает мнимую часть выражения:
>>> im(5+3*I)
3
>>> im(I)
1
sign — Эта функция возвращает сложный знак выражения..
Для реального выражения знак будет:
- 1, если выражение положительное,
- 0, если выражение равно нулю,
- -1, если выражение отрицательное.
Если выражение мнимое, то знаки следующие:
- l, если выражение положительное,
- -l, если выражение отрицательное.
>>> sign(1.55), sign(-1), sign(S.Zero)
(1,-1,0)
>>> sign (-3*I), sign(I*2)
(-I, I)
Функция abs возвращает абсолютное значение комплексного числа. Оно определяется как расстояние между основанием (0, 0) и точкой на комплексной плоскости. Эта функция является расширением встроенной функции abs() и принимает символьные значения.
Например, Abs(2+3*I), вернет √13.
conjugate — Функция возвращает сопряжение комплексного числа. Для поиска меняется знак мнимой части.
>>> conjugate(4+7*I)
4−7?
Тригонометрические функции
В SymPy есть определения всех тригонометрических соотношений: синуса, косинуса, тангенса и так далее. Также есть обратные аналоги: asin, acos, atan и так далее. Функции вычисляют соответствующее значение данного угла в радианах.
>>> sin(pi/2), cos(pi/4), tan(pi/6)
(1, sqrt(2)/2, sqrt(3)/3)
>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)
(pi/2, pi/4, pi/6)
Функции целого числа
Набор функций для работы с целым числом.
Одномерная функция ceiling, возвращающая самое маленькое целое число, которое не меньше аргумента. В случае с комплексными числами округление до большего целого для целой и мнимой части происходит отдельно.
>>> ceiling(pi), ceiling(Rational(20, 3)), ceiling(2.6+3.3*I)
(4, 7, 3 + 4*I)
floor — Возвращает самое большое число, которое не больше аргумента. В случае с комплексными числами округление до меньшего целого для целой и мнимой части происходит отдельно.
>>> floor(pi), floor(Rational(100, 6)), floor(6.3-5.9*I)
(3, 16, 6 - 6*I)
frac — Функция представляет долю x.
>>> frac(3.99), frac(10)
(0.990000000000000, 0)
Комбинаторные функции
Комбинаторика — это раздел математики, в котором рассматриваются выбор, расположение и работа в конечной и дискретной системах.
factorial — Факториал очень важен в комбинаторике. Он обозначает число способов, которыми могут быть представлены объекты.
Кватернион
В математика числовая система кватернион расширяет комплексные числа. Каждый объект включает 4 скалярные переменные и 4 измерения: одно реальное и три мнимых.
Кватернион можно представить в виде следующего уравнения: q = a + bi + cj + dk, где a, b, c и d — это реальные числа, а i, j и k — квартенионные единицы, так что i2 == j2 == k2 = ijk.
Класс Quaternion расположен в модуле sympy.algebras.quaternion.
>>> from sympy.algebras.quaternion import Quaternion
>>> q = Quaternion(2, 3, 1, 4)
>>> q
2+3?+1?+4?
Кватернионы используются как в чистой, так и в прикладной математике, а также в компьютерной графике, компьютерном зрении и так далее.

add()
Этот метод класса Quaternion позволяет сложить два объекта класса:
>>> q1=Quaternion(1,2,4)
>>> q2=Quaternion(4,1)
>>> q1.add(q2)
5+3?+4?+0?
Также возможно добавить число или символ к объекту Quaternion.
>>> q1+2
3+2?+4?+0?
>>> q1+x
(?+1)+2?+4?+0?
mul()
Этот метод выполняет умножение двух кватернионов.
>>> q1 = Quaternion(1, 2)
>>> q2 = Quaternion(2, 4, 1)
>>> q1.mul(q2)
(−6)+8?+1?+2?
inverse()
Возвращает обратный кватернион.
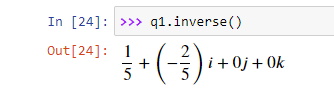
pow()
Возвращает степень кватерниона.
>>> q1.pow(2)
(−3)+4?+0?+0?
exp()
Вычисляет экспоненту кватерниона.
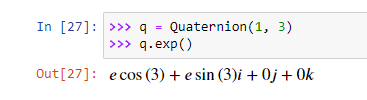
Уравнения
Поскольку символы = и == определены как символ присваивания и равенства в Python, их нельзя использовать для создания символьных уравнений. Для этого в SymPy есть функция Eq().
>>> x, y = symbols('x y')
>>> Eq(x, y)
?=?
Поскольку x=y возможно только в случае x-y=0, уравнение выше можно записать как:
Модуль solver из SymPy предлагает функцию solveset():
solveset(equation,variable,domain)Параметр domain по умолчанию равен S.Complexes. С помощью функции solveset() можно решить алгебраическое уравнение.
>>> solveset(Eq(x**2-9, 0), x)
{−3,3}
>>> solveset(Eq(x**2-3*x, -2), x)
{1,2}
Линейное уравнение
Для решения линейных уравнений нужно использовать функцию linsolve().
Например, уравнения могут быть такими:
- x-y=4
- x+1=1
Функция linsolve() также может решать линейные уравнения в матричной форме:
>>> a, b = symbols('a b')
>>> a = Matrix([[1, -1], [1, 1]])
>>> b = Matrix([4, 1])
>>> linsolve([a, b], y)
Вывод будет тот же.
Нелинейное уравнение
Для таких уравнений используется функция nonlinsolve(). Пример такого уравнения:
>>> a, b = symbols('a b')
>>> nonlinsolve([a**2 + a, a - b], [a, b])
{(−1, −1),(0, 0)}
Дифференциальное уравнение
Для начала создайте функцию, передав cls=Function в функцию symbols. Для решения дифференциальных уравнений используйте dsolve.
>>> x = ymbol('x')
>>> f = symbols('f', cls=Function)
>>> f(x)
?(?)
Здесь f(x) — это невычисленная функция. Ее производная:
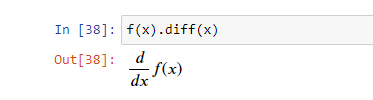
Сначала создается объект Eq, соответствующий следующему дифференциальному уравнению.
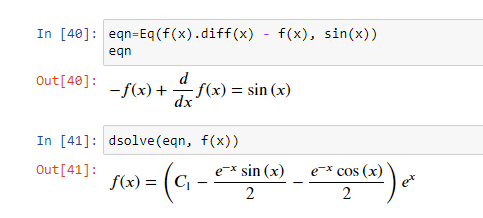
Графики
SymPy использует библиотеку matplotlib в качестве бэкенда для рендеринга двухмерных и трехмерных графиков математических функций. Убедитесь, что на вашем устройстве установлена matplotlib. Если нет, установите с помощью следующей команды.
pip install matplotlib
Функции для работы с графиками можно найти в модуле sympy.plotting:
plot— двухмерные линейные графики.plot3d— трехмерные линейные графики.plot_parametric— двухмерные параметрические графики.plot3d_parametric— трехмерные параметрические графики.
Функция plot() возвращает экземпляр класса Plot. Сам график может включать одно или несколько выражений SymPy. По умолчанию в качестве бэкенда используется matplotlib, но вместе нее можно взять texplot, pyglet или API Google Charts.
plot(expr,range,kwargs)
где expr — это любое валидное выражение SymPy. Если не сказано другое, то по умолчанию значение range равно (-10, 10).
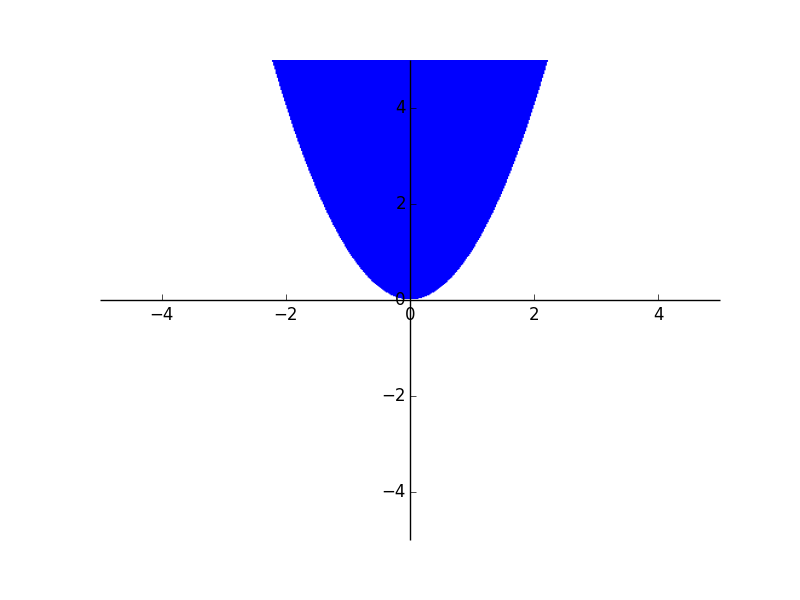
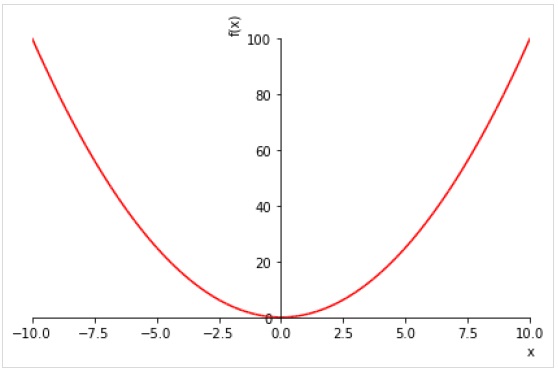
Следующий график показывает квадрат для каждого значения в диапазоне от -10 до 10.
>>> from sympy.plotting import plot
>>> from sympy import *
>>> x = Symbol('x')
>>> plot(x**2, line_color='red')
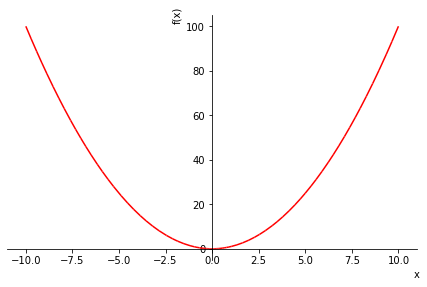
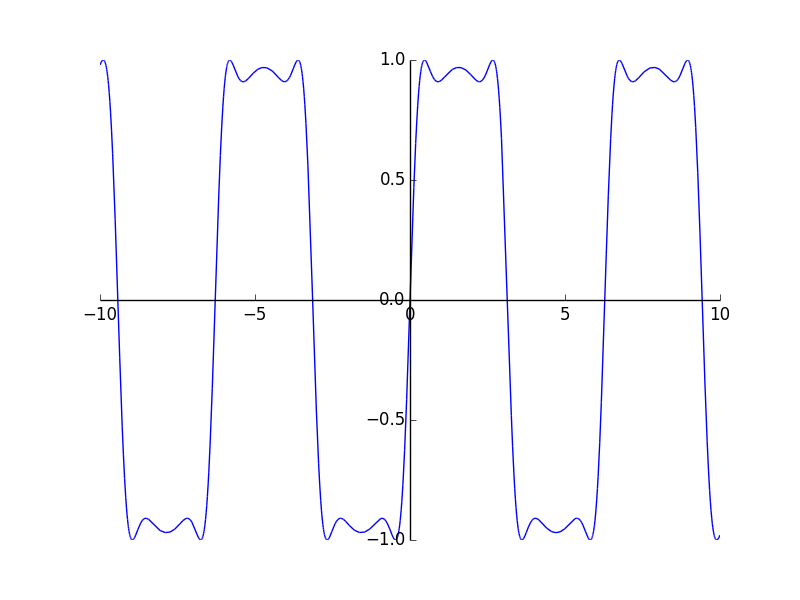
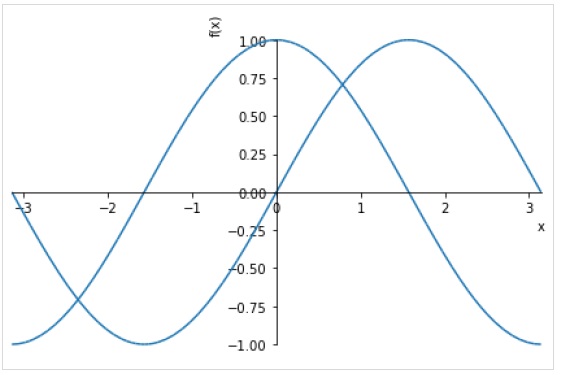
Чтобы нарисовать несколько графиков для одного диапазона, перед кортежем нужно указать несколько выражений.
>>> plot(sin(x), cos(x), (x, -pi, pi))
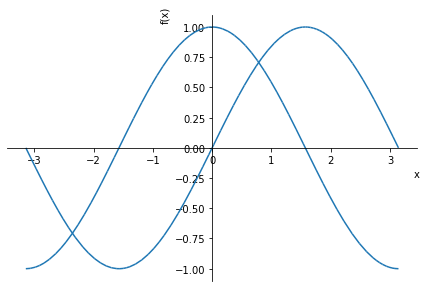
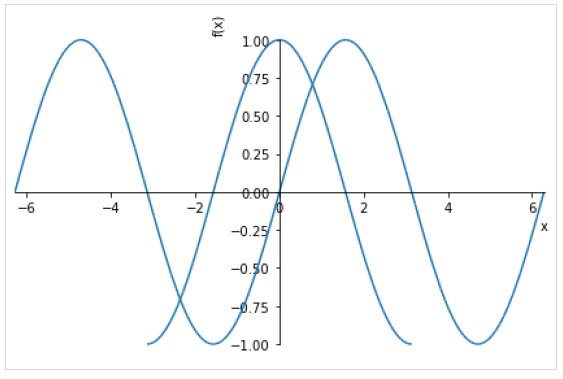
Также для каждого выражения можно задать отдельный диапазон.
plot((expr1,range1),(expr2,range2))
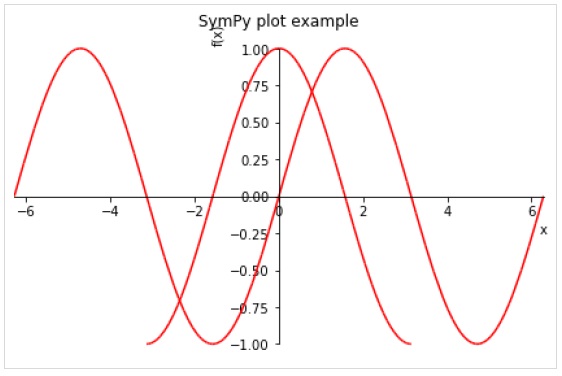
Также в функции plot() можно использовать следующие необязательные аргументы-ключевые слова.
line_color— определяет цвет линии графика.title— название графика.xlabel— метка для оси X.ylabel— метка для оси Y.
>>> plot((sin(x), (x,-pi,pi)), line_color='red', title='Пример графика SymPy')
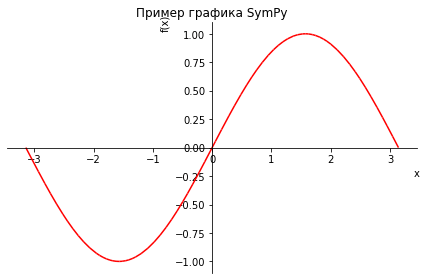
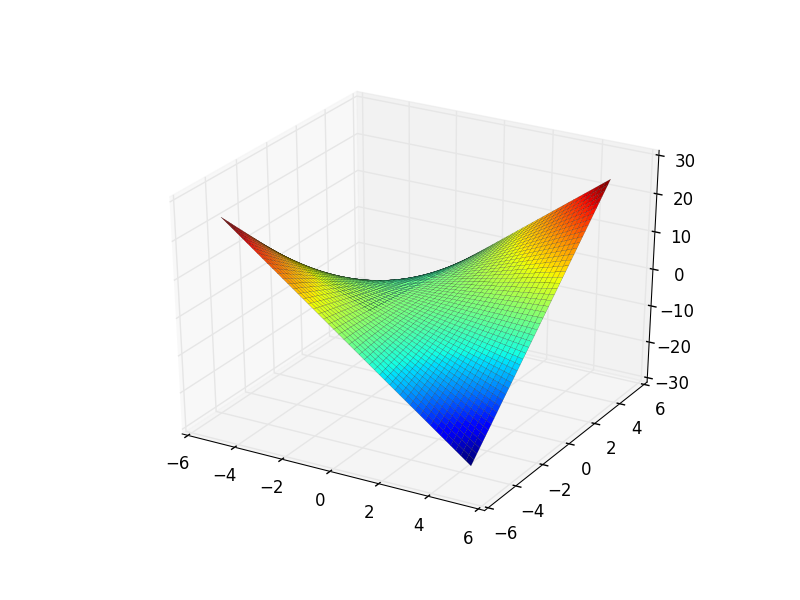
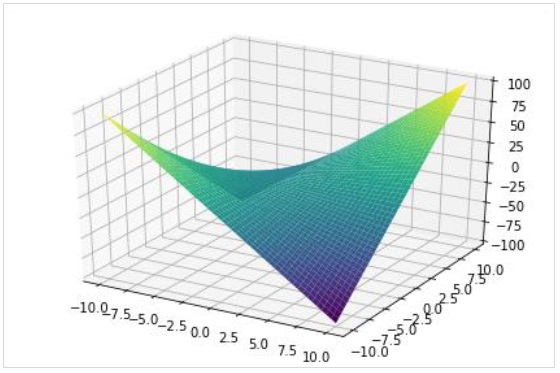
Функция plot3d() рендерит трехмерный график.
>>> from sympy.plotting import plot3d
>>> x, y = symbols('x y')
>>> plot3d(x*y, (x, -10, 10), (y, -10, 10))
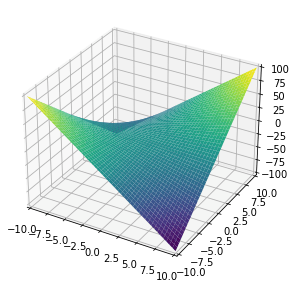
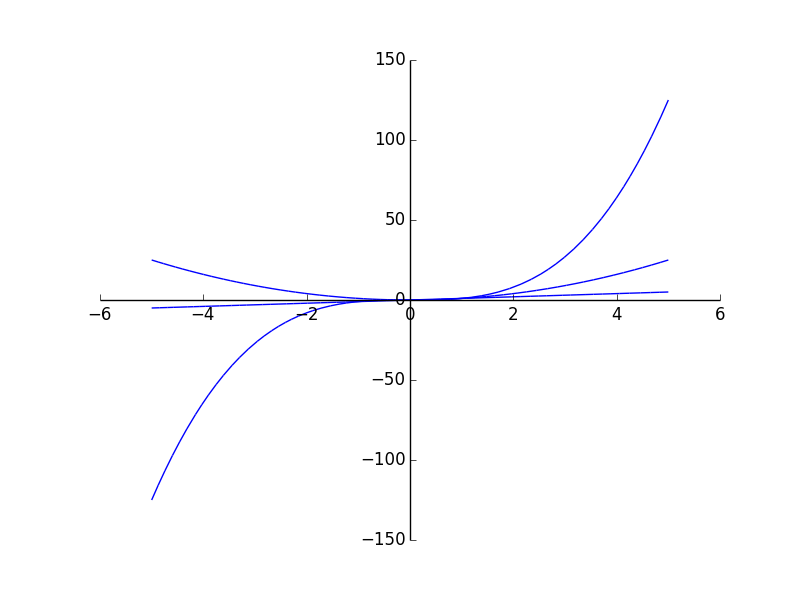
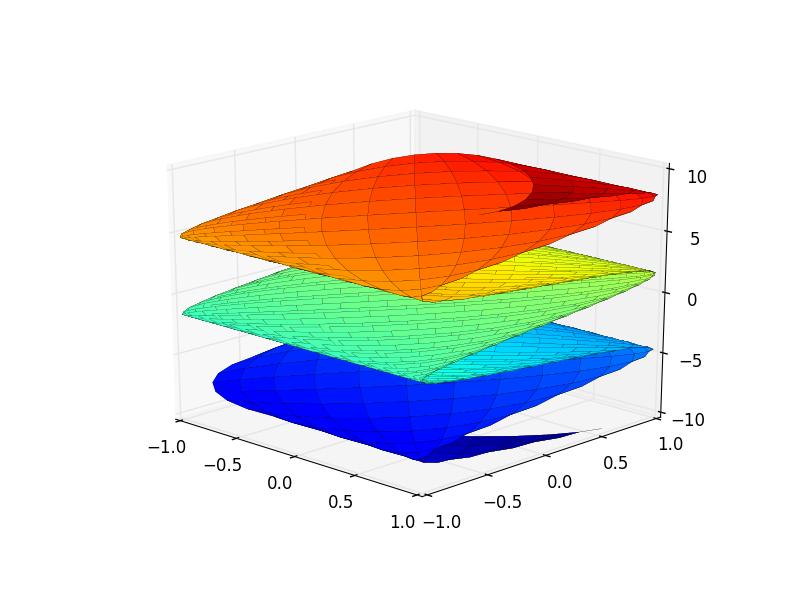
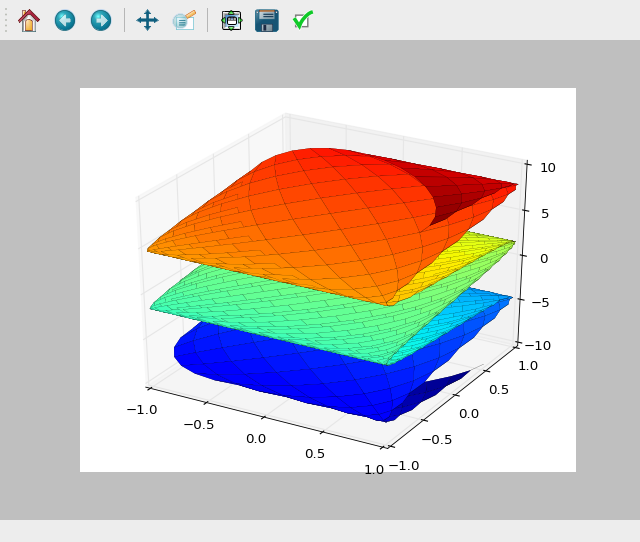
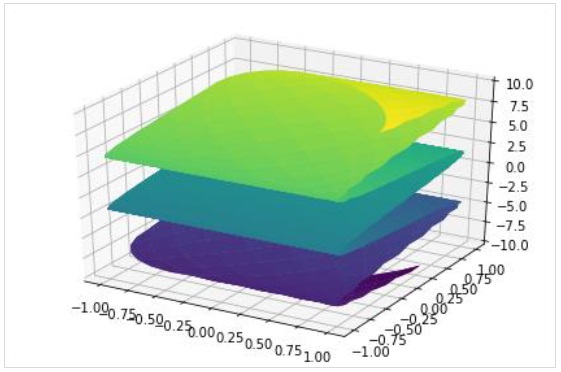
По аналогии с двухмерным трехмерный график может включать несколько графиков для отдельных диапазонов:
>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))
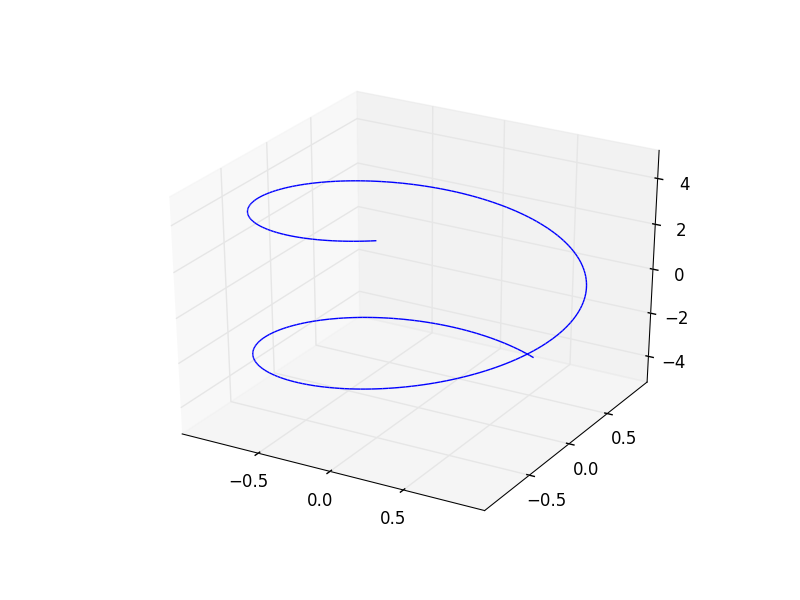
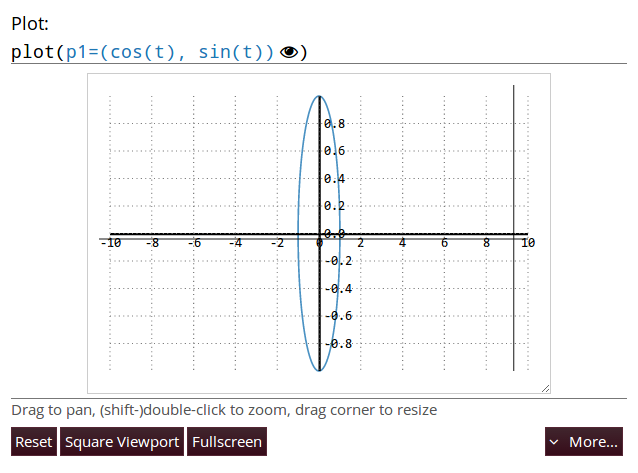
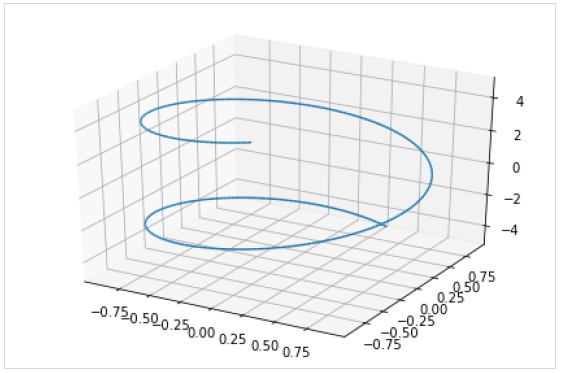
Функция plot3d_parametric_line() рендерит трехмерный линейный параметрический график:
>>> from sympy.plotting import plot3d_parametric_line
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))
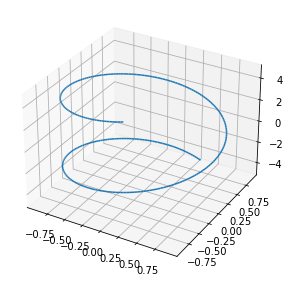
Чтобы нарисовать параметрический объемный график, используйте plot3d_parametric_surface().
Сущности
Модуль geometry в SymPy позволяет создавать двухмерные сущности, такие как линия, круг и так далее. Информацию о них можно получить через проверку коллинеарности или поиск пересечения.
Point
Класс point представляет точку Евклидового пространства. Следующие примеры проверяют коллинеарность точек:
>>> from sympy.geometry import Point
>>> from sympy import *
>>> x = Point(0, 0)
>>> y = Point(2, 2)
>>> z = Point(4, 4)
>>> Point.is_collinear(x, y, z)
True
>>> a = Point(2, 3)
>>> Point.is_collinear(x, a)
False
>>> x.distance(y)
2√2
Метод distance() класса Point вычисляет расстояние между двумя точками.
Line
Сущность Line можно получить из двух объектов Point. Метод intersection() возвращает точку пересечения двух линий.
>>> from sympy.geometry import Point, Line
>>> p1, p2 = Point(0, 5), Point(5, 0)
>>> l1 = Line(p1,p2)
>>> l2 = Line(Point(0, 0), Point(5, 5))
>>> l1.intersection(l2)
[Point2D(5/2, 5/2)]
>>> l1.intersection(Line(Point(0,0), Point(2,2)))
[Point2D(5/2, 5/2)]
>>> x, y = symbols('x y')
>>> p = Point(x, y)
>>> p.distance(Point(0, 0))
Вывод: √?2+?2
Triangle
Эта функция создает сущность Triangle из трех точек.
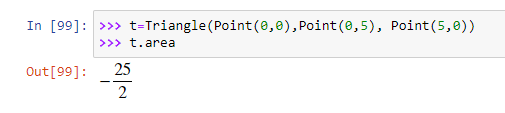
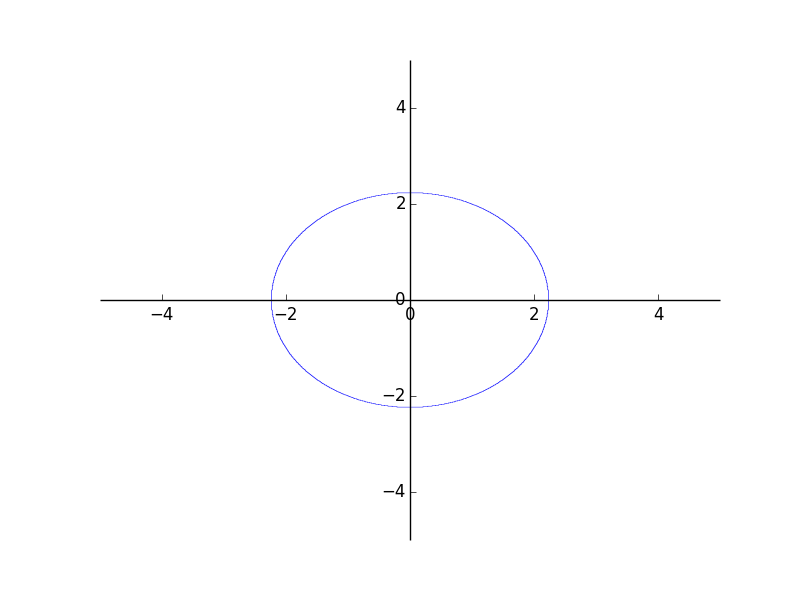
Ellipse
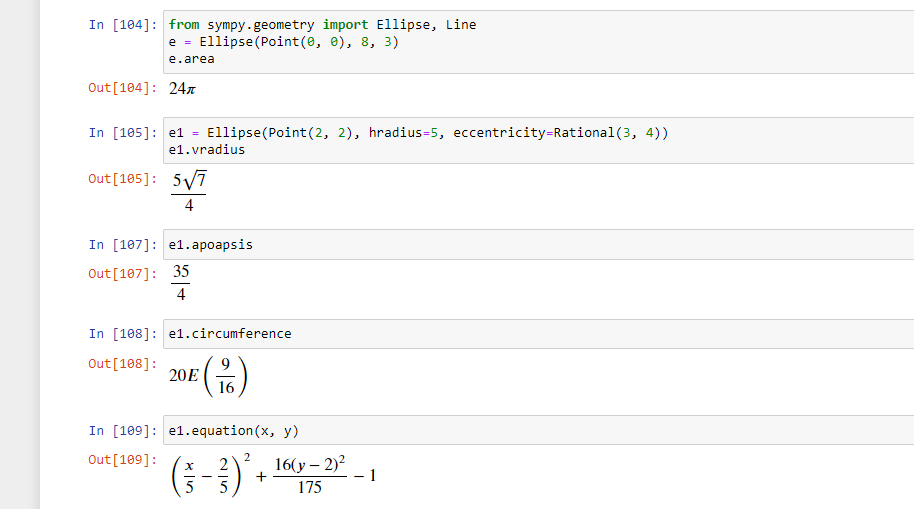
Эллиптическая геометрическая сущность создается с помощью объекта Point, который указывает на центр, а также горизонтальный и вертикальный радиусы.
ellipse(center,hradius,vradius)
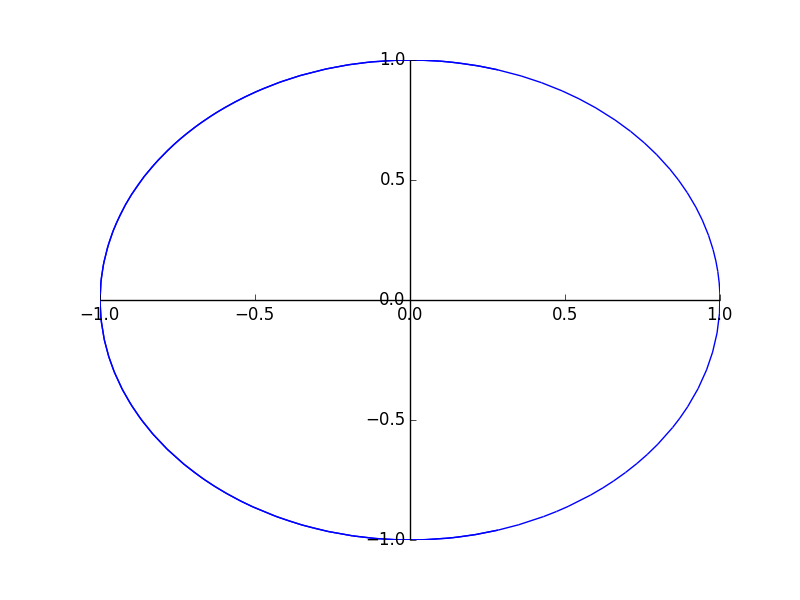
>>> from sympy.geometry import Ellipse, Line
>>> e = Ellipse(Point(0, 0), 8, 3)
>>> e.area
24?
- vradius может быть получен косвенно с помощью параметра eccentricity.
apoapsis— это наибольшее расстояние между фокусом и контуром.- метод
equationэллипса возвращает уравнение эллипса.
Множества
В математике множество — это четко определенный набор объектов, которые могут быть числами, буквами алфавита или даже другими множествами. Set — это также один из встроенных типов в Python. В SymPy же есть модуль sets. В нем можно найти разные типы множеств и операции поиска пересекающихся элементов, объединения и так далее.
Set — это базовый класс для любого типа множества в Python. Но стоит отметить, что в SymPy он отличается от того, что есть в Python. Класс interval представляет реальные интервалы, а граничное свойство возвращает объект FiniteSet.
>>> from sympy import Interval
>>> s = Interval(1, 10).boundary
>>> type(s)
sympy.sets.sets.FiniteSet
FiniteSet — это коллекция дискретных чисел. Ее можно получить из любой последовательности, будь то список или строка.
>>> from sympy import FiniteSet
>>> FiniteSet(range(5))
{{0,1,…,4}}
>>> numbers = [1, 3, 5, 2, 8]
>>> FiniteSet(*numbers)
{1,2,3,5,8}
>>> s = "HelloWorld"
>>> FiniteSet(*s)
{?,?,?,?,?,?,?}
По аналогии со встроенным множеством, Set из SymPy также является коллекцией уникальных объектов.
ConditionSet — это множество элементов, удовлетворяющих заданному условию.
Union — составное множество. Оно включает все элементы из двух множеств. Если же какие-то повторяются, то в результирующем множестве будет только одна копия.
>>> from sympy import Union
>>> l1 = [3, 7]
>>> l2 = [9, 7, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> Union(a, b)
{1,3,7,9}
Intersection же включает только те элементы, которые есть в обоих множествах.
>>> from sympy import Intersection
>>> Intersection(a, b)
{7}
ProductSet представляет декартово произведение элементов из обоих множеств.
>>> from sympy import ProductSet
>>> l1 = [1, 2]
>>> l2 = [2, 3]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> set(ProductSet(a, b))
{(1, 2), (1, 3), (2, 2), (2, 3)}
Complement(a, b) исключает те элементы, которых нет в b.
>>> from sympy import Complement
>>> l1 = [3, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> Complement(a, b), Complement(b, a)
(FiniteSet(1), FiniteSet(2))
SymmetricDifference хранит только необщие элементы обоих множеств.
>>> from sympy import SymmetricDifference
>>> l1 = [3, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> SymmetricDifference(a, b)
{1,2}
Вывод в консоль
В SymPy есть несколько инструментов для вывода. Вот некоторые из них:
- str,
- srepr,
- ASCII pretty printer,
- Unicode pretty printer,
- LaTeX,
- MathML,
- Dot.
Объекты SymPy также можно отправить как ввод в другие языки программирования, такие как C, Fortran, JavaScript, Theano.
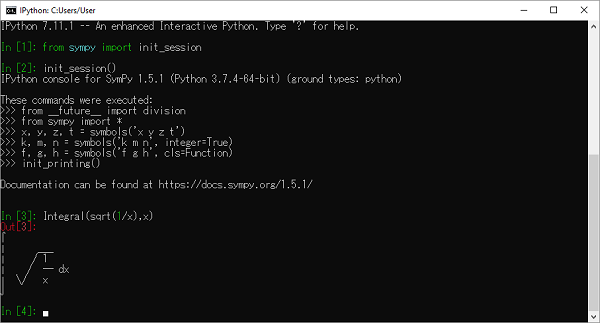
SymPy использует символы Юникод для рендеринга вывода. Если вы используете консоль Python для работы с SymPy, то лучше всего применять функцию init_session().
>>> from sympy import init_session
>>> init_session()
Python console for SymPy 1.6.2 (Python 3.8.5-64-bit) (ground types: python)
...
Выполним эти команды:
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()
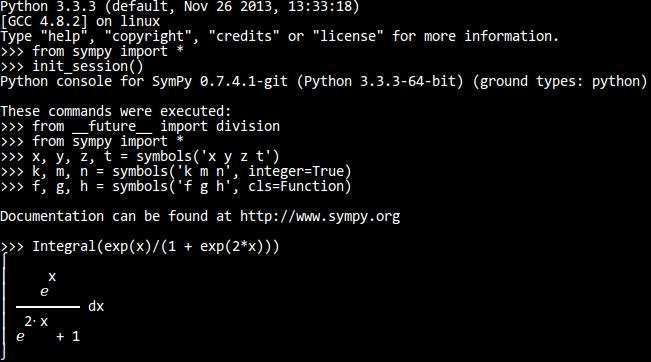
>>> Integral(sqrt(1/x), x)
⌠
⎮ ___
⎮ ╱ 1
⎮ ╱ ─ dx
⎮ ╲╱ x
⌡
Если нет LaTeX, но есть matplotlib, то последняя будет использоваться в качестве движка рендеринга. Если и matplotlib нет, то применяется Unicode pretty printer. Однако Jupyter notebook использует MathJax для рендеринга LaTeX.
В терминале, который не поддерживает Unicode, используется ASCII pretty printer (как в выводе из примера).
Для ASCII printer есть функция pprinter() с параметром use_unicode=False.
>>> pprint(Integral(sqrt(1/x), x), use_unicode=False)
/
|
| ___
| / 1
| / - dx
| \/ x
|
/Также доступ к Unicode printer можно получить из pprint() и pretty(). Если терминал поддерживает Unicode, то он используется автоматически. Если поддержку определить не удалось, то можно передать use_unicode=True, чтобы принудительно использовать Unicode.
Для получения LaTeX-формата используйте функцию latex().
>>> print(latex(Integral(sqrt(1/x), x)))
\int \sqrt{\frac{1}{x}}\, dx
Также доступен printer mathml. Для него есть функция pint_mathml().
>>> from sympy.printing.mathml import print_mathml
>>> print_mathml(Integral(sqrt(1/x),x))
<apply>
<int/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<root/>
<apply>
<power/>
<ci>x</ci>
<cn>-1</cn>
</apply>
</apply>
</apply>
>>> mathml(Integral(sqrt(1/x),x))
<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn
>-1</cn></apply></apply></apply>- Что такое SymPy?
- Зачем использовать SymPy?
- Установка SymPy
- Символы SymPy
- Функции SymPy+—
- 1. Функция sympify()
- 2. функция eval()
- 3. Функция Lambdify()
- Особенности+—
- 1. Основные возможности
- 2. Исчисление
- 3. Многочлены
- 4. Комбинаторика
- 5. Дискретная математика
- Приложения+—
- 1. Строительный калькулятор
- 2. Системы компьютерной алгебры
- 3. Исчисление
- Что еще вы можете сделать с SymPy?
- Заключение
От математики никуда не деться, будь вы студентом университета или работаете в области науки о данных.
Можно даже утверждать, что наука о данных — это разновидность прикладной математики/статистики. NumPy, SciPy, научное обучение, и TensorFlow — это лишь некоторые из библиотек Python, которые имеют дело с математикой количественно.
Однако есть только один конкурент, явно работающий с математическими символами: SymPy.
Давайте узнаем все о SymPy.
Что такое СимПи?
SymPy — это библиотека символьной математики Python. Он стремится стать полнофункциональной системой компьютерной алгебры (CAS), сохраняя при этом максимально простой код, чтобы он был понятным и легко расширяемым.
Он полностью написан на Python. Он прост в использовании, так как полагается только на mpmath, чистую библиотеку Python для произвольных арифметических операций с плавающей запятой.
Как библиотека, она была создана с упором на удобство использования. Расширяемость имеет решающее значение при разработке интерфейса прикладных программ (API).
В результате он не пытается улучшить язык Python. Цель состоит в том, чтобы пользователи могли использовать его вместе с другими Библиотеки Python в своем рабочем процессе, будь то в интерактивной среде или в качестве запрограммированного компонента более крупной системы.
SymPy, как библиотека, не имеет встроенного графического интерфейс пользователя (графический интерфейс). Библиотека это:
- Бесплатен как в отношении речи, так и в отношении пива, поскольку распространяется под лицензией BSD.
- На основе Python: он полностью разработан на Python и использует Python в качестве своего языка.
- Легкий, потому что он полагается только на mpmath, чистый Библиотека Python для произвольной арифметики с плавающей запятой, что делает его простым в использовании.
- Может быть включен в другие программы и изменен с помощью пользовательских функций в дополнение к использованию в качестве интерактивного инструмента.
Зачем использовать SymPy?
Sage, система компьютерной алгебры, также использует Python в качестве языка программирования. Sage, с другой стороны, огромен и требует загрузки более гигабайта. Преимущество в том, что он легкий.
Помимо того, что он компактен, он не имеет других зависимостей, кроме Python, что позволяет использовать его практически везде.
Кроме того, цели Sage и SymPy не совпадают. Sage стремится стать полнофункциональной математической системой, и она делает это, объединяя все основные математические системы с открытым исходным кодом в одну.
Когда вы используете функцию Sage, например интеграцию, она вызывает один из содержащихся в ней пакетов с открытым исходным кодом. На самом деле он встроен в Sage. SymPy, с другой стороны, стремится быть автономной системой со всеми функциями, реализованными в ней самой.
Его способность функционировать как библиотека является важной особенностью. Многие системы компьютерной алгебры предназначены для использования в интерактивных средах, но их сложно автоматизировать или расширить.
Его можно использовать интерактивно в Python или импортировать в вашу собственную программу Python. Он также имеет API для легкого расширения с помощью ваших собственных подпрограмм.
Установка SymPy
Просто используйте приведенную ниже команду для установки в вашей среде.
Символы SymPy
Давайте начнем с этого прямо сейчас! Его фундаментальный объект — символ. В SymPy вы можете сгенерировать символ x, написав:
Приведенный выше код генерирует символ x. Символы в нем предназначены для имитации математических символов, представляющих неизвестные значения.
В результате, следующий расчет показан ниже:
Как показано выше, символ x функционирует аналогично неизвестной сумме. Если вы хотите сделать много символов, напишите их следующим образом:
В этом случае вы создали два символа, y и z, одновременно. Эти символы теперь можно складывать, вычитать, умножать и делить по желанию:
Функции SymPy
1. Функция sympify()
Метод sympify() преобразует произвольное выражение в выражение SymPy. Он преобразует стандартные объекты Python, такие как целые числа.
Строки преобразуются в их выражения, а также целые числа и т. д.
2. функция eval()
Эта функция оценивает указанное числовое выражение с точностью до 100 цифр с плавающей запятой.
Функция дополнительно принимает объект словаря с числовыми значениями для символов в качестве подаргумента. Рассмотрим следующую фразу:
Точность с плавающей запятой по умолчанию установлена на 15 цифр. Однако его можно изменить на любое число от 1 до 100.
Следующее уравнение оценивается с точностью до 20 цифр.
3. Функция Lambdify()
Lambdify — это функция, которая преобразует свои выражения в функции Python. Метод evalf() неэффективен при вычислении выражения в широком диапазоне значений.
Lambdify работает аналогично лямбда-функции, за исключением того, что она переводит имена SymPy в имена предоставленной числовой библиотеки, которой обычно является NumPy.
По умолчанию Lambdify применяется к реализациям стандартной математической библиотеки.
Особенности
Здесь перечислены некоторые наиболее важные функции библиотеки; есть еще много не включенных, но вы можете проверить их здесь.
1. Основные возможности
- Основные арифметические операции: поддерживаются операторы +, -, *, / и ** (мощность).
- Полиномиальное расширение
- Целые числа, рациональные числа и числа с плавающей запятой с произвольной точностью
- Тригонометрические, гиперболические и экспоненциальные функции, корни, логарифмы, абсолютное значение, сферические гармоники, факториалы и гамма-функции, дзета-функции, многочлены и специальные функции
- Некоммутативные символы
- Подходящие шаблоны
2. Исчисление
- Интеграция: этот метод использует расширенную эвристику Риша-Нормана.
- Дифференциация.
- Предельные функции
- сериал Лорана Тейлора
3. Многочлены
- Фонды Грёбнера
- Разложение неполных дробей
- Деление, gcd Resultants являются примерами основной арифметики.
4. Комбинаторика
- Перестановки
- Коды Грея и Прюфера
- Комбинации, разделы, подмножества
- Многогранные, рубиковские, симметричные и другие группы перестановок
5. Дискретная математика
- суммирование
- Логические выражения
- Биномиальные коэффициенты
- Теория чисел
Приложения
1. Строительный калькулятор
2. Системы компьютерной алгебры
В отличие от других систем компьютерной алгебры, вы должны вручную объявлять в ней символьные переменные с помощью функции Symbol().
3. Исчисление
Способность системы символьных вычислений выполнять все виды вычислений символически является ее главной силой.
Он может упростить операторы, символически вычислять производные, интегралы и пределы, решать уравнения, взаимодействовать с матрицами и делать многое другое.
Чтобы подогреть ваш аппетит, вот вкус символической силы.
Что еще вы можете сделать с SymPy?
Вместо того, чтобы подробно рассказывать о дополнительных проблемах, позвольте мне предоставить вам список ресурсов, которые помогут вам улучшить свои навыки:
- Матрицы и линейная алгебра: Он может работать с матрицами и выполнять основные операции линейной алгебры. Язык похож на синтаксис NumPy. Однако есть заметные различия. Для начала исследуйте матрицы в библиотеке.
- Выражение: Он использует дерево выражений, которое представляет собой древовидную структуру, для отслеживания выражений. смотреть на деревья выражения если вы хотите узнать больше об их внутренней работе.
- Производные и интегралы: Он может выполнить большую часть того, чему вы научились на вводном занятии по математическому анализу (за вычетом мышления). Вы можете начать с рассмотрения нашей функции дифференциация в SymPy.
- Связь с NumPy: NumPy и SymPy — библиотеки, связанные с математикой. Тем не менее, они принципиально разные! NumPy работает с числами, а с символьными выражениями.
- Упрощения: Он достаточно умен, чтобы автоматически упрощать выражения. Однако, если вы хотите более детально контролировать это, посмотрите на его упрощения.
Заключение
SymPy — мощная библиотека для символьной математики.
Вы можете использовать его для создания переменных и функций, а также символически расширять и упрощать математические операторы и решать уравнения, неравенства и даже системы уравнений/неравенств.
Вы можете писать функции как в тексте скрипта, так и прямо в терминале (или Ноутбуки Jupyter), чтобы получить быструю оценку и лучшее графическое изображение выполненных вычислений.
Готовы ли вы узнать больше о SymPy? Дайте нам знать об этом в комментариях.
 SymPy
SymPy
Функции
Основные возможности SymPy:
Документация
- Basic arithmetic: Support for operators such
as+,-,*,/,**(power) - Упрощение
Trigonometry, Polynomials - Expansion:
of a polynomial - Функции
trigonometric,
hyperbolic,
exponential,
roots,
logarithms,
absolute value,
spherical harmonics,
factorials and gamma functions,
zeta functions,
polynomials,
special functions, … - Substitution: example
- Числа:
arbitrary precision integers,
rationals,
and floats - Некоммутативные выражения
- Проверка соответствия выражения шаблону
Многочлены
Документация
- Basic arithmetic: division, gcd, …
- Разложение на множители
- Разложение, свободное от квадратов
- Gröbner bases
- Разложение на элементарные дроби
- Resultants
Вычисления
Combinatorics
Документация
- Permutations
- Combinations
- Partitions
- Subsets
- Permutation Groups: Polyhedral, Rubik, Symmetric, …
- Prufer and Gray Codes
Discrete math
- Биномиальные коэффициенты
- Summations
- Произведения последовательностей
- Теория чисел generating prime numbers, primality testing, integer factorization, Diophantine equation solving…
- Логические выражения
Матрицы
Документация
- Basic arithmetic
- Eigenvalues/eigenvectors
- Детерминанты
- Inversion
- Solving
- Abstract expressions
Модуль геометрии
Документация
- points, lines, rays, segments, ellipses, circles,
polygons, … - Пересечение
- Tangency
- Подобие
Рисование
Документация
- Coordinate modes
- Рисование геометрических фигур
- Двух- и трёхмерное построение графиков
- Интерактивный режим
- Поддержка цветов
- Matplotlib support
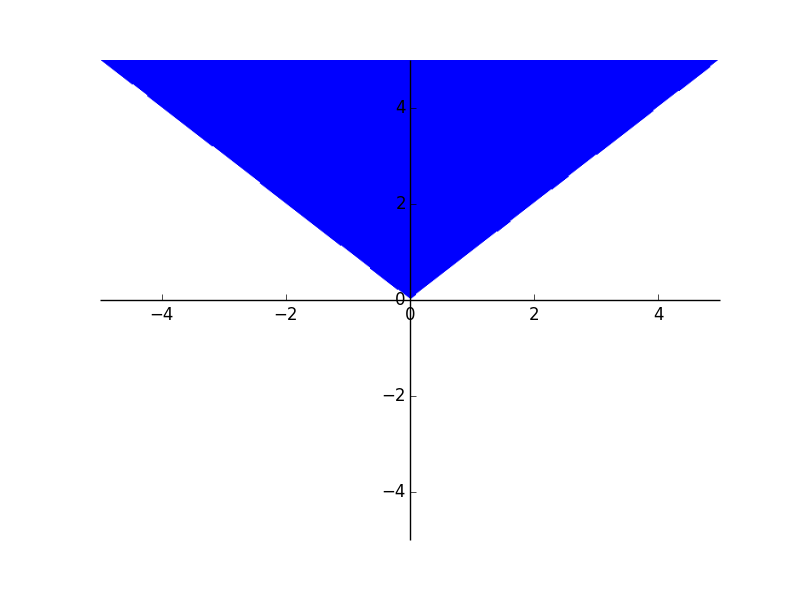
plot(sin(2*sin(2*sin(x))))plot(x, x**2, x**3, (x, -5, 5))plot_parametric(cos(u), sin(u), (u, -5, 5))plot3d(x*y, (x, -5, 5), (y, -5, 5))plot3d_parametric_line(cos(u), sin(u), u, (u, -5, 5))plot3d_parametric_surface(cos(u + v), sin(u - v), u - v, (u, -5, 5), (v, -5, 5))plot_implicit(Eq(x**2 + y**2, 5))plot_implicit(y > x**2)plot_implicit(And(y > x, y > -x))plot3d_parametric_surface(cos(u + v), sin(u - v), u - v, (u, -5, 5), (v, -5, 5))
Физика
Статистика
Документация
- Random variable types:
- Пакеты для дистрибутивов
- Непрерывное равномерное распределение
- Bernoulli distributions
- Binomial distributions
- Hypergeometric distributions
- More…
- Теория вероятностей
- Expected value and variance
- Probability density
Cryptography
Документация
- Shift cipher
- Affine cipher
- Bifid ciphers
- Vigenere’s cipher
- Substitution ciphers
- Hill’s cipher
- RSA
- Kid RSA
- Linear feedback shift registers
- ElGamal encryption
Parsing
Документация
- Conversion from Python objects to SymPy objects
- Optional implicit multiplication and function application parsing
- Limited Mathematica and Maxima parsing: example on SymPy Live
- Custom parsing transformations
Печать
Документация
- Красивая печать (Pretty-printing) Печать с использованием ASCII или Unicode символов. Печать в формате LaTeX
- Генерация кода C, Fortran, Python
- Theano interaction
SymPy — Introduction
SymPy is a Python library for performing symbolic computation. It is a computer algebra system (CAS) that can be used either as a standalone application, as a library to other applications. Its live session is also available at https://live.sympy.org/. Since it is a pure Python library, it can be used as interactive mode and as a programmatic application. SymPy has now become a popular symbolic library for the scientific Python ecosystem.
SymPy has a wide range of features applicable in the field of basic symbolic arithmetic, calculus, algebra, discrete mathematics, quantum physics, etc. SymPy is capable of formatting the results in variety of formats including LaTeX, MathML, etc. SymPy is distributed under New BSD License. A team of developers led by Ondřej Čertík and Aaron Meurer published first version of SymPy in 2007. Its current version is 1.5.1.
Some of the areas of applications of SymPy are −
- Polynomials
- Calculus
- Discrete maths
- Matrices
- Geometry
- Plotting
- Physics
- Statistics
- Combinatorics
SymPy — Installation
SymPy has one important prerequisite library named mpmath. It is a Python library for real and complex floating-point arithmetic with arbitrary precision. However, Python’s package installer PIP installs it automatically when SymPy is installed as follows −
pip install sympy
Other Python distributions such as Anaconda, Enthought Canopy, etc., may have SymPy already bundled in it. To verify, you can type the following in the Python prompt −
>>> import sympy >>> sympy.__version__
And you get the below output as the current version of sympy −
‘1.5.1’
Source code of SymPy package is available at https://github.com/sympy/sympy.
SymPy — Symbolic Computation
Symbolic computation refers to development of algorithms for manipulating mathematical expressions and other mathematical objects. Symbolic computation integrates mathematics with computer science to solve mathematical expressions using mathematical symbols. A Computer Algebra System (CAS) such as SymPy evaluates algebraic expressions exactly (not approximately) using the same symbols that are used in traditional manual method. For example, we calculate square root of a number using Python’s math module as given below −
>>> import math >>> print (math.sqrt(25), math.sqrt(7))
The output for the above code snippet is as follows −
5.0 2.6457513110645907
As you can see, square root of 7 is calculated approximately. But in SymPy square roots of numbers that are not perfect squares are left unevaluated by default as given below −
>>> import sympy >>> print (sympy.sqrt(7))
The output for the above code snippet is as follows −
sqrt(7)
It is possible to simplify and show result of expression symbolically with the code snippet below −
>>> import math >>> print (math.sqrt(12))
The output for the above code snippet is as follows −
3.4641016151377544
You need to use the below code snippet to execute the same using sympy −
##sympy output >>> print (sympy.sqrt(12))
And the output for that is as follows −
2*sqrt(3)
SymPy code, when run in Jupyter notebook, makes use of MathJax library to render mathematical symbols in LatEx form. It is shown in the below code snippet −
>>> from sympy import *
>>> x=Symbol ('x')
>>> expr = integrate(x**x, x)
>>> expr
On executing the above command in python shell, following output will be generated −
Integral(x**x, x)
Which is equivalent to
$\int \mathrm{x}^{x}\,\mathrm{d}x$
The square root of a non-perfect square can be represented by Latex as follows using traditional symbol −
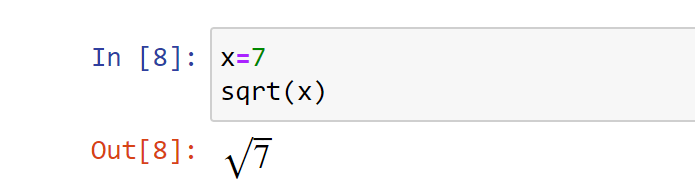
>>> from sympy import * >>> x=7 >>> sqrt(x)
The output for the above code snippet is as follows −
$\sqrt7$
A symbolic computation system such as SymPy does all sorts of computations (such as derivatives, integrals, and limits, solve equations, work with matrices) symbolically. SymPy package has different modules that support plotting, printing (like LATEX), physics, statistics, combinatorics, number theory, geometry, logic, etc.
SymPy — Numbers
The core module in SymPy package contains Number class which represents atomic numbers. This class has two subclasses: Float and Rational class. Rational class is further extended by Integer class.
Float class represents a floating point number of arbitrary precision.
>>> from sympy import Float >>> Float(6.32)
The output for the above code snippet is as follows −
6.32
SymPy can convert an integer or a string to float.
>>> Float(10)
10.0
Float('1.33E5')# scientific notation
133000.0
While converting to float, it is also possible to specify number of digits for precision as given below −
>>> Float(1.33333,2)
The output for the above code snippet is as follows −
1.3
A representation of a number (p/q) is represented as object of Rational class with q being a non-zero number.
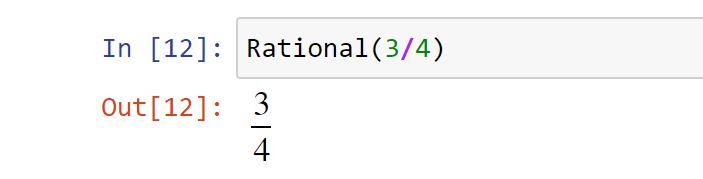
>>> Rational(3/4)
The output for the above code snippet is as follows −
$\frac{3}{4}$
If a floating point number is passed to Rational() constructor, it returns underlying value of its binary representation
>>> Rational(0.2)
The output for the above code snippet is as follows −
$\frac{3602879701896397}{18014398509481984}$
For simpler representation, specify denominator limitation.
>>> Rational(0.2).limit_denominator(100)
The output for the above code snippet is as follows −
$\frac{1}{5}$
When a string is passed to Rational() constructor, a rational number of arbitrary precision is returned.
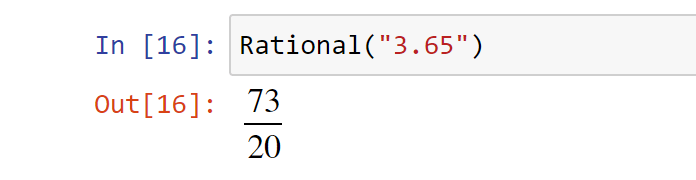
>>> Rational("3.65")
The output for the above code snippet is as follows −
$\frac{73}{20}$
Rational object can also be obtained if two number arguments are passed. Numerator and denominator parts are available as properties.
>>> a=Rational(3,5)
>>> print (a)
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))
The output for the above code snippet is as follows −
3/5
numerator:3, denominator:5
>>> a
The output for the above code snippet is as follows −
$\frac{3}{5}$
Integer class in SymPy represents an integer number of any size. The constructor can accept a Float or Rational number, but the fractional part is discarded
>>> Integer(10)
The output for the above code snippet is as follows −
10
>>> Integer(3.4)
The output for the above code snippet is as follows −
3
>>> Integer(2/7)
The output for the above code snippet is as follows −
0
SymPy has a RealNumber class that acts as alias for Float. SymPy also defines Zero and One as singleton classes accessible with S.Zero and S.One respectively as shown below −
>>> S.Zero
The output is as follows −
0
>>> S.One
The output is as follows −
1
Other predefined Singleton number objects are Half, NaN, Infinity and ImaginaryUnit
>>> from sympy import S >>> print (S.Half)
The output is as follows −
½
>>> print (S.NaN)
The output is as follows −
nan
Infinity is available as oo symbol object or S.Infinity
>>> from sympy import oo >>> oo
The output for the above code snippet is as follows −
$\infty$
>>> S.Infinity
The output for the above code snippet is as follows −
$\infty$
ImaginaryUnit number can be imported as I symbol or accessed as S.ImaginaryUnit and represents square root of -1
>>> from sympy import I >>> I
When you execute the above code snippet, you get the following output −
i
>>> S.ImaginaryUnit
The output of the above snippet is as follows −
i
>>> from sympy import sqrt >>> i=sqrt(-1) >>> i*i
When you execute the above code snippet, you get the following output −
-1
SymPy — Symbols
Symbol is the most important class in symPy library. As mentioned earlier, symbolic computations are done with symbols. SymPy variables are objects of Symbols class.
Symbol() function’s argument is a string containing symbol which can be assigned to a variable.
>>> from sympy import Symbol
>>> x=Symbol('x')
>>> y=Symbol('y')
>>> expr=x**2+y**2
>>> expr
The above code snippet gives an output equivalent to the below expression −
$x^2 + y^2$
A symbol may be of more than one alphabets.
>>> s=Symbol('side')
>>> s**3
The above code snippet gives an output equivalent to the below expression −
$side^3$
SymPy also has a Symbols() function that can define multiple symbols at once. String contains names of variables separated by comma or space.
>>> from sympy import symbols
>>> x,y,z=symbols("x,y,z")
In SymPy’s abc module, all Latin and Greek alphabets are defined as symbols. Hence, instead of instantiating Symbol object, this method is convenient.
>>> from sympy.abc import x,y,z
However, the names C, O, S, I, N, E and Q are predefined symbols. Also, symbols with more than one alphabets are not defined in abc module, for which you should use Symbol object as above. The abc module defines special names that can detect definitions in default SymPy namespace. clash1 contains single letters and clash2 has multi letter clashing symbols
>>> from sympy.abc import _clash1, _clash2 >>> _clash1
The output of the above snippet is as follows −
{‘C’: C, ‘O’: O, ‘Q’: Q, ‘N’: N, ‘I’: I, ‘E’: E, ‘S’: S}
>>> _clash2
The output of the above snippet is as follows −
{‘beta’: beta, ‘zeta’: zeta, ‘gamma’: gamma, ‘pi’: pi}
Indexed symbols can be defined using syntax similar to range() function. Ranges are indicated by a colon. Type of range is determined by the character to the right of the colon. If itr is a digit, all contiguous digits to the left are taken as the nonnegative starting value. All contiguous digits to the right are taken as 1 greater than the ending value.
>>> from sympy import symbols
>>> symbols('a:5')
The output of the above snippet is as follows −
(a0, a1, a2, a3, a4)
>>> symbols('mark(1:4)')
The output of the above snippet is as follows −
(mark1, mark2, mark3)
SymPy — Substitution
One of the most basic operations to be performed on a mathematical expression is substitution. The subs() function in SymPy replaces all occurrences of first parameter with second.
>>> from sympy.abc import x,a >>> expr=sin(x)*sin(x)+cos(x)*cos(x) >>> expr
The above code snippet gives an output equivalent to the below expression −
$\sin^2(x)+\cos^2(x)$
>>> expr.subs(x,a)
The above code snippet gives an output equivalent to the below expression −
$\sin^2(a)+\cos^2(a)$
This function is useful if we want to evaluate a certain expression. For example, we want to calculate values of following expression by substituting a with 5.
>>> expr=a*a+2*a+5 >>> expr
The above code snippet gives an output equivalent to the below expression −
$a^2 + 2a + 5$
expr.subs(a,5)
The above code snippet gives the following output −
40
>>> from sympy.abc import x >>> from sympy import sin, pi >>> expr=sin(x) >>> expr1=expr.subs(x,pi) >>> expr1
The above code snippet gives the following output −
0
This function is also used to replace a subexpression with another subexpression. In following example, b is replaced by a+b.
>>> from sympy.abc import a,b >>> expr=(a+b)**2 >>> expr1=expr.subs(b,a+b) >>> expr1
The above code snippet gives an output equivalent to the below expression −
$(2a + b)^2$
SymPy — sympify() function
The sympify() function is used to convert any arbitrary expression such that it can be used as a SymPy expression. Normal Python objects such as integer objects are converted in SymPy. Integer, etc.., strings are also converted to SymPy expressions.
>>> expr="x**2+3*x+2" >>> expr1=sympify(expr) >>> expr1 >>> expr1.subs(x,2)
The above code snippet gives the following output −
12
Any Python object can be converted in SymPy object. However, since the conversion internally uses eval() function, unsanitized expression should not be used, else SympifyError is raised.
>>> sympify("x***2")
---------------------------------------------------------------------------
SympifyError: Sympify of expression ‘could not parse ‘x***2» failed, because of exception being raised.
The sympify() function takes following arguments: * strict: default is False. If set to True, only the types for which an explicit conversion has been defined are converted. Otherwise, SympifyError is raised. * evaluate: If set to False, arithmetic and operators will be converted into their SymPy equivalents without evaluating expression.
>>> sympify("10/5+4/2")
The above code snippet gives the following output −
4
>>> sympify("10/5+4/2", evaluate=False)
The above code snippet gives the following output −
$\frac{10}{5}+\frac{4}{2}$
SymPy — evalf() function
This function evaluates a given numerical expression upto a given floating point precision upto 100 digits. The function also takes subs parameter a dictionary object of numerical values for symbols. Consider following expression
>>> from sympy.abc import r >>> expr=pi*r**2 >>> expr
The above code snippet gives an output equivalent to the below expression −
$\Pi{r^2}$
To evaluate above expression using evalf() function by substituting r with 5
>>> expr.evalf(subs={r:5})
The above code snippet gives the following output −
78.5398163397448
By default, floating point precision is upto 15 digits which can be overridden by any number upto 100. Following expression is evaluated upto 20 digits of precision.
>>> expr=a/b
>>> expr.evalf(20, subs={a:100, b:3})
The above code snippet gives the following output −
33.333333333333333333
SymPy — Lambdify() function
The lambdify function translates SymPy expressions into Python functions. If an expression is to be evaluated over a large range of values, the evalf() function is not efficient. lambdify acts like a lambda function, except it converts the SymPy names to the names of the given numerical library, usually NumPy. By default, lambdify on implementations in the math standard library.
>>> expr=1/sin(x) >>> f=lambdify(x, expr) >>> f(3.14)
The above code snippet gives the following output −
627.8831939138764
The expression might have more than one variables. In that case, first argument to lambdify() function is a list of variables, followed by the expression to be evaluated.
>>> expr=a**2+b**2 >>> f=lambdify([a,b],expr) >>> f(2,3)
The above code snippet gives the following output −
13
However, to leverage numpy library as numerical backend, we have to define the same as an argument for lambdify() function.
>>> f=lambdify([a,b],expr, "numpy")
We use two numpy arrays for two arguments a and b in the above function. The execution time is considerably fast in case of numpy arrays.
>>> import numpy >>> l1=numpy.arange(1,6) >>> l2=numpy.arange(6,11) >>> f(l1,l2)
The above code snippet gives the following output −
array([ 37, 53, 73, 97, 125], dtype=int32)
SymPy — Logical Expressions
Boolean functions are defined in sympy.basic.booleanarg module. It is possible to build Boolean expressions with the standard python operators & (And), | (Or), ~ (Not) as well as with >> and <<. Boolean expressions inherit from Basic class defined in SymPy’s core module.
BooleanTrue function
This function is equivalent of True as in core Python. It returns a singleton that can be retrieved by S.true.
>>> from sympy import * >>> x=sympify(true) >>> x, S.true
The above code snippet gives the following output −
(True, True)
BooleanFalse function
Similarly, this function is equivalent to Boolean False in Python and can be accessed by S.false
>>> from sympy import * >>> x=sympify(false) >>> x, S.false
The above code snippet gives the following output −
(False, False)
And function
A logical AND function evaluates its two arguments and returns False if either of them is False. The function emulates & operator.
>>> from sympy import *
>>> from sympy.logic.boolalg import And
>>> x,y=symbols('x y')
>>> x=True
>>> y=True
>>> And(x,y), x"&"y
The above code snippet gives the following output −
(True, True)
>>> y=False >>> And(x,y), x"&"y
The above code snippet gives the following output −
(False, False)
Or function
This function evaluates two Boolean arguments and returns True if either of them is True. The | operator conveniently emulates its behaviour.
>>> from sympy import *
>>> from sympy.logic.boolalg import Or
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Or(x,y), x|y
The above code snippet gives the following output −
(True, True)
>>> x=False >>> y=False >>> Or(x,y), x|y
The above code snippet gives the following output −
(False, False)
Not Function
A Logical Not function results in negation of the Boolean argument. It returns True if its argument is False and returns False if True. The ~ operator performs the operation similar to Not function. It is shown in the example below −
>>> from sympy import *
>>> from sympy.logic.boolalg import Or, And, Not
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Not(x), Not(y)
The above code snippet gives the following output −
(False, True)
>>> Not(And(x,y)), Not(Or(x,y))
The above code snippet gives the following output −
(True, False)
Xor Function
The Logical XOR (exclusive OR) function returns True if an odd number of the arguments are True and the rest are False and returns False if an even number of the arguments are True and the rest are False. Similar operation is performed by ^ operator.
>>> from sympy import *
>>> from sympy.logic.boolalg import Xor
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Xor(x,y), x^y
The above code snippet gives the following output −
(True, True)
>>> a,b,c,d,e=symbols('a b c d e')
>>> a,b,c,d,e=(True, False, True, True, False)
>>> Xor(a,b,c,d,e)
The above code snippet gives the following output −
True
In above case, three (odd number) arguments are True, hence Xor returns true. However, if number of True arguments is even, it results in False, as shown below −
>>> a,b,c,d,e=(True, False, False, True, False) >>> Xor(a,b,c,d,e)
The above code snippet gives the following output −
False
Nand Function
This function performs Logical NAND operation. It evaluates its arguments and returns True if any of them are False, and False if they are all True.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nand
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nand(a,b,c), Nand(a,c)
The above code snippet gives the following output −
(True, False)
Nor Function
This function performs Logical NOR operation. It evaluates its arguments and returns False if any of them are True, and True if they are all False.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nor
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nor(a,b,c), Nor(a,c)
The above code snippet gives the following output −
(False, False)
Note that even though SymPy provides ^ operator for Xor, ~ for Not, | for Or and & for And functions as convenience, their normal use in Python is as bitwise operators. Hence, if operands are integers, results would be different.
Equivalent function
This function returns equivalence relation. Equivalent(A, B) is True if and only if A and B are both True or both False. The function returns True if all of the arguments are logically equivalent. Returns False otherwise.
>>> from sympy import *
>>> from sympy.logic.boolalg import Equivalent
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Equivalent(a,b), Equivalent(a,c)
The above code snippet gives the following output −
(False, True)
ITE function
This function acts as If then else clause in a programming language.ITE(A, B, C) evaluates and returns the result of B if A is true else it returns the result of C. All args must be Booleans.
>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True)
>>> ITE(a,b,c), ITE(a,c,b)
The above code snippet gives the following output −
(False, True)
SymPy — Querying
The assumptions module in SymPy package contains tools for extracting information about expressions. The module defines ask() function for this purpose.
sympy.assumptions.ask(property)
Following properties provide useful information about an expression −
algebraic(x)
To be algebraic, a number must be a root of a non-zero polynomial equation with rational coefficients. √2 because √2 is a solution to x2 − 2 = 0, so it is algebraic.
complex(x)
Complex number predicate. It is true if and only if x belongs to the set of complex numbers.
composite(x)
Composite number predicate returned by ask(Q.composite(x)) is true if and only if x is a positive integer and has at least one positive divisor other than 1 and the number itself.
even, odd
The ask() returns true of x is in the set of even numbers and set of odd numbers respectively.
imaginary
This property represents Imaginary number predicate. It is true if x can be written as a real number multiplied by the imaginary unit I.
integer
This property returned by Q.integer(x) returns true of x belong to set of even numbers.
rational, irrational
Q.irrational(x) is true if and only if x is any real number that cannot be expressed as a ratio of integers. For example, pi is an irrational number.
positive, negative
Predicates to check if number is positive or negative
zero, nonzero
Predicates to heck if a number is zero or not
>>> from sympy import *
>>> x=Symbol('x')
>>> x=10
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y")
>>> x,y=5,10
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)
SymPy — Simplification
Sympy has powerful ability to simplify mathematical expressions. There are many functions in SymPy to perform various kinds of simplification. A general function called simplify() is there that attempts to arrive at the simplest form of an expression.
simplify
This function is defined in sympy.simplify module. simplify() tries to apply intelligent heuristics to make the input expression “simpler”. Following code shows simplifies expression $sin^2(x)+cos^2(x)$.
>>> from sympy import *
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2
>>> simplify(expr)
The above code snippet gives the following output −
1
expand
The expand() is one of the most common simplification functions in SymPy, used in expanding polynomial expressions. For example −
>>> a,b=symbols('a b')
>>> expand((a+b)**2)
The above code snippet gives an output equivalent to the below expression −
$a^2 + 2ab + b^2$
>>> expand((a+b)*(a-b))
The above code snippet gives an output equivalent to the below expression −
$a^2 — b^2$
The expand() function makes expressions bigger, not smaller. Usually this is the case, but often an expression will become smaller upon calling expand() on it.
>>> expand((x + 1)*(x - 2) - (x - 1)*x)
The above code snippet gives the following output −
-2
factor
This function takes a polynomial and factors it into irreducible factors over the rational numbers.
>>> x,y,z=symbols('x y z')
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor(expr)
The above code snippet gives an output equivalent to the below expression −
$z(x + 2y)^2$
>>> factor(x**2+2*x+1)
The above code snippet gives an output equivalent to the below expression −
$(x + 1)^2$
The factor() function is the opposite of expand(). Each of the factors returned by factor() is guaranteed to be irreducible. The factor_list() function returns a more structured output.
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) >>> factor_list(expr)
The above code snippet gives an output equivalent to the below expression −
(1, [(z, 1), (x + 2*y, 2)])
collect
This function collects additve terms of an expression with respect to a list of expression up to powers with rational exponents.
>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 >>> expr
The above code snippet gives an output equivalent to the below expression −
$x^3 + x^2z + 2x^2 + xy + x — 3$
The collect() function on this expression results as follows −
>>> collect(expr,x)
The above code snippet gives an output equivalent to the below expression −
$x^3 + x^2(2 — z) + x(y + 1) — 3$
>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y >>> collect(expr,y)
The above code snippet gives an output equivalent to the below expression −
$Y^3+Y^2(x+4z)+y(4xz+2x)$
cancel
The cancel() function will take any rational function and put it into the standard canonical form, p/q, where p and q are expanded polynomials with no common factors. The leading coefficients of p and q do not have denominators i.e., they are integers.
>>> expr1=x**2+2*x+1 >>> expr2=x+1 >>> cancel(expr1/expr2)
The above code snippet gives an output equivalent to the below expression −
$x+1$
>>> expr = 1/x + (3*x/2 - 2)/(x - 4) >>> expr
The above code snippet gives an output equivalent to the below expression −
$\frac{\frac{3x}{2} — 2}{x — 4} + \frac{1}{x}$
>>> cancel(expr)
The above code snippet gives an output equivalent to the below expression −
$\frac{3x^2 — 2x — 8}{2x^2 — 8}$
>>> expr=1/sin(x)**2 >>> expr1=sin(x) >>> cancel(expr1*expr)
The above code snippet gives an output equivalent to the below expression −
$\frac{1}{\sin(x)}$
trigsimp
This function is used to simplify trigonometric identities. It may be noted that naming conventions for inverse trigonometric functions is to append an a to the front of the function’s name. For example, the inverse cosine, or arc cosine, is called acos().
>>> from sympy import trigsimp, sin, cos >>> from sympy.abc import x, y >>> expr = 2*sin(x)**2 + 2*cos(x)**2 >>> trigsimp(expr)
2
The trigsimp function uses heuristics to apply the best suitable trigonometric identity.
powersimp
This function reduces given expression by combining powers with similar bases and exponents.
>>> expr=x**y*x**z*y**z >>> expr
The above code snippet gives an output equivalent to the below expression −
$x^y x^z y^z$
>>> powsimp(expr)
The above code snippet gives an output equivalent to the below expression −
$x^{y+z} y^z$
You can make powsimp() only combine bases or only combine exponents by changing combine=’base’ or combine=’exp’. By default, combine=’all’, which does both.If force is True then bases will be combined without checking for assumptions.
>>> powsimp(expr, combine='base', force=True)
The above code snippet gives an output equivalent to the below expression −
$x^y(xy)^z$
combsimp
Combinatorial expressions involving factorial an binomials can be simplified by using combsimp() function. SymPy provides a factorial() function
>>> expr=factorial(x)/factorial(x - 3) >>> expr
The above code snippet gives an output equivalent to the below expression −
$\frac{x!}{(x — 3)!}$
To simplify above combinatorial expression we use combsimp() function as follows −
>>> combsimp(expr)
The above code snippet gives an output equivalent to the below expression −
$x(x-2)(x-1)$
The binomial(x, y) is the number of ways to choose y items from a set of x distinct items. It is also often written as xCy.
>>> binomial(x,y)
The above code snippet gives an output equivalent to the below expression −
$(\frac{x}{y})$
>>> combsimp(binomial(x+1, y+1)/binomial(x, y))
The above code snippet gives an output equivalent to the below expression −
$\frac{x + 1}{y + 1}$
logcombine
This function takes logarithms and combines them using the following rules −
- log(x) + log(y) == log(x*y) if both are positive
- a*log(x) == log(x**a) if x is positive and a is real
>>> logcombine(a*log(x) + log(y) - log(z))
The above code snippet gives an output equivalent to the below expression −
$a\log(x) + \log(y) — \log(z)$
If force parameter of this function is set to True then the assumptions above will be assumed to hold if there is no assumption already in place on a quantity.
>>> logcombine(a*log(x) + log(y) - log(z), force=True)
The above code snippet gives an output equivalent to the below expression −
$\log\frac{x^a y}{z}$
SymPy — Derivative
The derivative of a function is its instantaneous rate of change with respect to one of its variables. This is equivalent to finding the slope of the tangent line to the function at a point.we can find the differentiation of mathematical expressions in the form of variables by using diff() function in SymPy package.
diff(expr, variable) >>> from sympy import diff, sin, exp >>> from sympy.abc import x,y >>> expr=x*sin(x*x)+1 >>> expr
The above code snippet gives an output equivalent to the below expression −
$x\sin(x^2) + 1$
>>> diff(expr,x)
The above code snippet gives an output equivalent to the below expression −
$2x^2\cos(x^2) + \sin(x^2)$
>>> diff(exp(x**2),x)
The above code snippet gives an output equivalent to the below expression −
2xex2
To take multiple derivatives, pass the variable as many times as you wish to differentiate, or pass a number after the variable.
>>> diff(x**4,x,3)
The above code snippet gives an output equivalent to the below expression −
$24x$
>>> for i in range(1,4): print (diff(x**4,x,i))
The above code snippet gives the below expression −
4*x**3
12*x**2
24*x
It is also possible to call diff() method of an expression. It works similarly as diff() function.
>>> expr=x*sin(x*x)+1 >>> expr.diff(x)
The above code snippet gives an output equivalent to the below expression −
$2x^2\cos(x^2) + \sin(x^2)$
An unevaluated derivative is created by using the Derivative class. It has the same syntax as diff() function. To evaluate an unevaluated derivative, use the doit method.
>>> from sympy import Derivative >>> d=Derivative(expr) >>> d
The above code snippet gives an output equivalent to the below expression −
$\frac{d}{dx}(x\sin(x^2)+1)$
>>> d.doit()
The above code snippet gives an output equivalent to the below expression −
$2x^2\cos(x^2) + \sin(x^2)$
SymPy — Integration
The SymPy package contains integrals module. It implements methods to calculate definite and indefinite integrals of expressions. The integrate() method is used to compute both definite and indefinite integrals. To compute an indefinite or primitive integral, just pass the variable after the expression.
For example −
integrate(f, x)
To compute a definite integral, pass the argument as follows −
(integration_variable, lower_limit, upper_limit)
>>> from sympy import *
>>> x,y = symbols('x y')
>>> expr=x**2 + x + 1
>>> integrate(expr, x)
The above code snippet gives an output equivalent to the below expression −
$\frac{x^3}{3} + \frac{x^2}{2} + x$
>>> expr=sin(x)*tan(x) >>> expr >>> integrate(expr,x)
The above code snippet gives an output equivalent to the below expression −
$-\frac{\log(\sin(x) — 1)}{2} + \frac{\log(\sin(x) + 1)}{2} — \sin(x)$
The example of definite integral is given below −
>>> expr=exp(-x**2) >>> integrate(expr,(x,0,oo) )
The above code snippet gives an output equivalent to the below expression −
$\frac{\sqrt\pi}{2}$
You can pass multiple limit tuples to perform a multiple integral. An example is given below −
>>> expr=exp(-x**2 - y**2) >>> integrate(expr,(x,0,oo),(y,0,oo))
The above code snippet gives an output equivalent to the below expression −
$\frac{\pi}{4}$
You can create unevaluated integral using Integral object, which can be evaluated by calling doit() method.
>>> expr = Integral(log(x)**2, x) >>> expr
The above code snippet gives an output equivalent to the below expression −
$\int \mathrm\log(x)^2 \mathrm{d}x$
>>> expr.doit()
The above code snippet gives an output equivalent to the below expression −
$x\log(x)^2 — 2xlog(x) + 2x$
Integral Transforms
SymPy supports various types of integral transforms as follows −
- laplace_transform
- fourier_transform
- sine_transform
- cosine_transform
- hankel_transform
These functions are defined in sympy.integrals.transforms module. Following examples compute Fourier transform and Laplace transform respectively.
Example 1
>>> from sympy import fourier_transform, exp >>> from sympy.abc import x, k >>> expr=exp(-x**2) >>> fourier_transform(expr, x, k)
On executing the above command in python shell, following output will be generated −
sqrt(pi)*exp(-pi**2*k**2)
Which is equivalent to −
$\sqrt\pi * e^{\pi^2k^2}$
Example 2
>>> from sympy.integrals import laplace_transform >>> from sympy.abc import t, s, a >>> laplace_transform(t**a, t, s)
On executing the above command in python shell, following output will be generated −
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)
SymPy — Matrices
In Mathematics, a matrix is a two dimensional array of numbers, symbols or expressions. Theory of matrix manipulation deals with performing arithmetic operations on matrix objects, subject to certain rules.
Linear transformation is one of the important applications of matrices. Many scientific fields, specially related to Physics use matrix related applications.
SymPy package has matrices module that deals with matrix handling. It includes Matrix class whose object represents a matrix.
Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −
>>> from sympy.matrices import Matrix
Example
>>> from sympy.matrices import Matrix
>>> m=Matrix([[1,2,3],[2,3,1]])
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$
On executing the above command in python shell, following output will be generated −
[1 2 3 2 3 1]
Matrix is created from appropriately sized List objects. You can also obtain a matrix by distributing list items in specified number of rows and columns.
>>> M=Matrix(2,3,[10,40,30,2,6,9])
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$
On executing the above command in python shell, following output will be generated −
[10 40 30 2 6 9]
Matrix is a mutable object. The matrices module also provides ImmutableMatrix class for obtaining immutable matrix.
Basic manipulation
The shape property of Matrix object returns its size.
>>> M.shape
The output for the above code is as follows −
(2,3)
The row() and col() method respectively returns row or column of specified number.
>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$
The output for the above code is as follows −
[10 40 30]
>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$
The output for the above code is as follows −
[40 6]
Use Python’s slice operator to fetch one or more items belonging to row or column.
>>> M.row(1)[1:3] [6, 9]
Matrix class has row_del() and col_del() methods that deletes specified row/column from given matrix −
>>> M=Matrix(2,3,[10,40,30,2,6,9]) >>> M.col_del(1) >>> M
On executing the above command in python shell, following output will be generated −
Matrix([[10, 30],[ 2, 9]])
You can apply style to the output using the following command −
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$
You get the following output after executing the above code snippet −
[10 30 2 9]
>>> M.row_del(0)
>>> M
$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$
You get the following output after executing the above code snippet −
[2 9]
Similarly, row_insert() and col_insert() methods add rows or columns at specified row or column index
>>> M1=Matrix([[10,30]])
>>> M=M.row_insert(0,M1)
>>> M
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$
You get the following output after executing the above code snippet −
[10 40 30 2 9]
>>> M2=Matrix([40,6])
>>> M=M.col_insert(1,M2)
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$
You get the following output after executing the above code snippet −
[10 40 30 6 9]
Arithmetic Operations
Usual operators +, — and * are defined for performing addition, subtraction and multiplication.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5,6],[6,5,4]])
>>> M1+M2
$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$
You get the following output after executing the above code snippet −
[5 7 9 9 7 5]
>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$
You get the following output after executing the above code snippet −
[- 3 -3 -3 -3 -3 -3]
Matrix multiplication is possible only if — The number of columns of the 1st matrix must equal the number of rows of the 2nd matrix. — And the result will have the same number of rows as the 1st matrix, and the same number of columns as the 2nd matrix.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5],[6,6],[5,4]])
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$
The output for the above code is as follows −
[31 29 29 31]
>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$
The following output is obtained after executing the code −
[1 3 2 2 3 1]
To calculate a determinant of matrix, use det() method. A determinant is a scalar value that can be computed from the elements of a square matrix.0
>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$
The output for the above code is as follows −
[10 20 30 5 8 12 9 6 15]
>>> M.det()
The output for the above code is as follows −
-120
Matrix Constructors
SymPy provides many special type of matrix classes. For example, Identity matrix, matrix of all zeroes and ones, etc. These classes are named as eye, zeros and ones respectively. Identity matrix is a square matrix with elements falling on diagonal are set to 1, rest of the elements are 0.
Example
from sympy.matrices import eye eye(3)
Output
Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$
The output for the above code is as follows −
[1 0 0 0 1 0 0 0 1]
In diag matrix, elements on diagonal are initialized as per arguments provided.
>>> from sympy.matrices import diag
>>> diag(1,2,3)
$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$
The output for the above code is as follows −
[1 0 0 0 2 0 0 0 3]
All elements in zeros matrix are initialized to 0.
>>> from sympy.matrices import zeros
>>> zeros(2,3)
$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$
The output for the above code is as follows −
[0 0 0 0 0 0]
Similarly, ones is matrix with all elements set to 1.
>>> from sympy.matrices import ones
>>> ones(2,3)
$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$
The output for the above code is as follows −
[1 1 1 1 1 1]
SymPy — Function class
Sympy package has Function class, which is defined in sympy.core.function module. It is a base class for all applied mathematical functions, as also a constructor for undefined function classes.
Following categories of functions are inherited from Function class −
- Functions for complex number
- Trigonometric functions
- Functions for integer number
- Combinatorial functions
- Other miscellaneous functions
Functions for complex number
This set of functions is defined in sympy.functions.elementary.complexes module.
re
This function returns real part of an expression −
>>> from sympy import * >>> re(5+3*I)
The output for the above code snippet is given below −
5
>>> re(I)
The output for the above code snippet is −
0
Im
This function returns imaginary part of an expression −
>>> im(5+3*I)
The output for the above code snippet is given below −
3
>>> im(I)
The output for the above code snippet is given below −
1
sign
This function returns the complex sign of an expression.
For real expression, the sign will be −
- 1 if expression is positive
- 0 if expression is equal to zero
- -1 if expression is negative
If expression is imaginary the sign returned is −
- I if im(expression) is positive
- -I if im(expression) is negative
>>> sign(1.55), sign(-1), sign(S.Zero)
The output for the above code snippet is given below −
(1, -1, 0)
>>> sign (-3*I), sign(I*2)
The output for the above code snippet is given below −
(-I, I)
Abs
This function return absolute value of a complex number. It is defined as the distance between the origin (0,0) and the point (a,b) in the complex plane. This function is an extension of the built-in function abs() to accept symbolic values.
>>> Abs(2+3*I)
The output for the above code snippet is given below −
$\sqrt13$
conjugate
This function returns conjugate of a complex number. To find the complex conjugate we change the sign of the imaginary part.
>>> conjugate(4+7*I)
You get the following output after executing the above code snippet −
4 — 7i
Trigonometric functions
SymPy has defintions for all trigonometric ratios — sin cos, tan etc as well as well as its inverse counterparts such as asin, acos, atan etc. These functions compute respective value for given angle expressed in radians.
>>> sin(pi/2), cos(pi/4), tan(pi/6)
The output for the above code snippet is given below −
(1, sqrt(2)/2, sqrt(3)/3)
>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)
The output for the above code snippet is given below −
(pi/2, pi/4, pi/6)
Functions on Integer Number
This is a set of functions to perform various operations on integer number.
ceiling
This is a univariate function which returns the smallest integer value not less than its argument. In case of complex numbers, ceiling of the real and imaginary parts separately.
>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)
The output for the above code snippet is given below −
(4, 7, 3 + 4*I)
floor
This function returns the largest integer value not greater than its argument. In case of complex numbers, this function too takes the floor of the real and imaginary parts separately.
>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)
The output for the above code snippet is given below −
(3, 16, 6 — 6*I)
frac
This function represents the fractional part of x.
>>> frac(3.99), frac(Rational(10,3)), frac(10)
The output for the above code snippet is given below −
(0.990000000000000, 1/3, 0)
Combinatorial functions
Combinatorics is a field of mathematics concerned with problems of selection, arrangement, and operation within a finite or discrete system.
factorial
The factorial is very important in combinatorics where it gives the number of ways in which n objects can be permuted. It is symbolically represented as ð‘¥! This function is implementation of factorial function over nonnegative integers, factorial of a negative integer is complex infinity.
>>> x=Symbol('x')
>>> factorial(x)
The output for the above code snippet is given below −
x!
>>> factorial(5)
The output for the above code snippet is given below −
120
>>> factorial(-1)
The output for the above code snippet is given below −
$\infty\backsim$
binomial
This function the number of ways we can choose k elements from a set of n elements.
>>> x,y=symbols('x y')
>>> binomial(x,y)
The output for the above code snippet is given below −
$(\frac{x}{y})$
>>> binomial(4,2)
The output for the above code snippet is given below −
6
Rows of Pascal’s triangle can be generated with the binomial function.
>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])
You get the following output after executing the above code snippet −
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
fibonacci
The Fibonacci numbers are the integer sequence defined by the initial terms F0=0, F1=1 and the two-term recurrence relation Fn=Fn−1+Fn−2.
>>> [fibonacci(x) for x in range(10)]
The following output is obtained after executing the above code snippet −
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
tribonacci
The Tribonacci numbers are the integer sequence defined by the initial terms F0=0, F1=1, F2=1 and the three-term recurrence relation Fn=Fn-1+Fn-2+Fn-3.
>>> tribonacci(5, Symbol('x'))
The above code snippet gives an output equivalent to the below expression −
$x^8 + 3x^5 + 3x^2$
>>> [tribonacci(x) for x in range(10)]
The following output is obtained after executing the above code snippet −
[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]
Miscellaneous Functions
Following is a list of some frequently used functions −
Min − Returns minimum value of the list. It is named Min to avoid conflicts with the built-in function min.
Max − Returns maximum value of the list. It is named Max to avoid conflicts with the built-in function max.
root − Returns nth root of x.
sqrt − Returns the principal square root of x.
cbrt − This function computes the principal cube root of x, (shortcut for x++Rational(1,3)).
The following are the examples of the above miscellaneous functions and their respective outputs −
>>> Min(pi,E)
e
>>> Max(5, Rational(11,2))
$\frac{11}{2}$
>>> root(7,Rational(1,2))
49
>>> sqrt(2)
$\sqrt2$
>>> cbrt(1000)
10
SymPy — Quaternion
In mathematics, Quaternion number system is an extension of complex numbers. Each Quaternion object contains four scalar variables and four dimensions, one real dimension and three imaginary dimensions.
Quaternion is represented by following expression −
q=a+bi+cj+dk
where a, b, c and d are real numbers and i, j, k are quaternion units such that,i2==j2==k2==ijk
The sympy.algebras.quaternion module has Quaternion class.
>>> from sympy.algebras.quaternion import Quaternion >>> q=Quaternion(2,3,1,4) >>> q
The above code snippet gives an output equivalent to the below expression −
$2 + 3i + 1j + 4k$
Quaternions are used in pure mathematics, as well as in applied mathematics, computer graphics, computer vision, etc.
>>> from sympy import *
>>> x=Symbol('x')
>>> q1=Quaternion(x**2, x**3, x) >>> q1
The above code snippet gives an output equivalent to the below expression −
$x^2 + x^3i + xj + 0k$
Quaternion object can also have imaginary co-efficients
>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I) >>> q2
The above code snippet gives an output equivalent to the below expression −
$2 + (3 + 2i)i + x2j + 3.5ik$
add()
This method available in Quaternion class performs addition of two Quaternion objects.
>>> q1=Quaternion(1,2,3,4) >>> q2=Quaternion(4,3,2,1) >>> q1.add(q2)
The above code snippet gives an output equivalent to the below expression −
$5 + 5i + 5j + 5k$
It is possible to add a number or symbol in a Quaternion object.
>>> q1+2
The following output is obtained after executing the above code snippet −
$3 + 2i + 3j + 4k$
>>> q1+x
The following output is obtained after executing the above code snippet −
$(x + 1) + 2i + 3j + 4k$
mul()
This method performs multiplication of two quaternion objects.
>>> q1=Quaternion(1,2,1,2) >>> q2=Quaternion(2,4,3,1) >>> q1.mul(q2)
The above code snippet gives an output equivalent to the below expression −
$(-11) + 3i + 11j + 7k$
inverse()
This method returns inverse of a quaternion object.
>>> q1.inverse()
The above code snippet gives an output equivalent to the below expression −
$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$
pow()
This method returns power of a quaternion object.
>>> q1.pow(2)
The following output is obtained after executing the above code snippet −
$(-8) + 4i + 2j + 4k$
exp()
This method computes exponential of a Quaternion object i.e. eq
>>> q=Quaternion(1,2,4,3) >>> q.exp()
The following output is obtained after executing the above code snippet −
$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$
SymPy — Solvers
Since the symbols = and == are defined as assignment and equality operators in Python, they cannot be used to formulate symbolic equations. SymPy provides Eq() function to set up an equation.
>>> from sympy import *
>>> x,y=symbols('x y')
>>> Eq(x,y)
The above code snippet gives an output equivalent to the below expression −
x = y
Since x=y is possible if and only if x-y=0, above equation can be written as −
>>> Eq(x-y,0)
The above code snippet gives an output equivalent to the below expression −
x − y = 0
The solver module in SymPy provides soveset() function whose prototype is as follows −
solveset(equation, variable, domain)
The domain is by default S.Complexes. Using solveset() function, we can solve an algebraic equation as follows −
>>> solveset(Eq(x**2-9,0), x)
The following output is obtained −
{−3, 3}
>>> solveset(Eq(x**2-3*x, -2),x)
The following output is obtained after executing the above code snippet −
{1,2}
The output of solveset is a FiniteSet of the solutions. If there are no solutions, an EmptySet is returned
>>> solveset(exp(x),x)
The following output is obtained after executing the above code snippet −
$\varnothing$
Linear equation
We have to use linsolve() function to solve linear equations.
For example, the equations are as follows −
x-y=4
x+y=1
>>> from sympy import *
>>> x,y=symbols('x y')
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))
The following output is obtained after executing the above code snippet −
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
The linsolve() function can also solve linear equations expressed in matrix form.
>>> a,b=symbols('a b')
>>> a=Matrix([[1,-1],[1,1]])
>>> b=Matrix([4,1])
>>> linsolve([a,b], (x,y))
We get the following output if we execute the above code snippet −
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
Non-linear equation
For this purpose, we use nonlinsolve() function. Equations for this example −
a2+a=0 a-b=0
>>> a,b=symbols('a b')
>>> nonlinsolve([a**2 + a, a - b], [a, b])
We get the following output if we execute the above code snippet −
$\lbrace(-1, -1),(0,0)\rbrace$
differential equation
First, create an undefined function by passing cls=Function to the symbols function. To solve differential equations, use dsolve.
>>> x=Symbol('x')
>>> f=symbols('f', cls=Function)
>>> f(x)
The following output is obtained after executing the above code snippet −
f(x)
Here f(x) is an unevaluated function. Its derivative is as follows −
>>> f(x).diff(x)
The above code snippet gives an output equivalent to the below expression −
$\frac{d}{dx}f(x)$
We first create Eq object corresponding to following differential equation
>>> eqn=Eq(f(x).diff(x)-f(x), sin(x)) >>> eqn
The above code snippet gives an output equivalent to the below expression −
$-f(x) + \frac{d}{dx}f(x)= \sin(x)$
>>> dsolve(eqn, f(x))
The above code snippet gives an output equivalent to the below expression −
$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$
SymPy — Plotting
SymPy uses Matplotlib library as a backend to render 2-D and 3-D plots of mathematical functions. Ensure that Matplotlib is available in current Python installation. If not, install the same using following command −
pip install matplotlib
Plotting support is defined in sympy.plotting module. Following functions are present in plotting module −
-
plot − 2D line plots
-
plot3d − 3D line plots
-
plot_parametric − 2D parametric plots
-
plot3d_parametric − 3D parametric plots
The plot() function returns an instance of Plot class. A plot figure may have one or more SymPy expressions. Although it is capable of using Matplotlib as backend, other backends such as texplot, pyglet or Google charts API may also be used.
plot(expr, range, kwargs)
where expr is any valid symPy expression. If not mentioned, range uses default as (-10, 10).
Following example plots values of x2 for each value in range(-10,10) −
>>> from sympy.plotting import plot
>>> from sympy import *
>>> x=Symbol('x')
>>> plot(x**2, line_color='red')
To draw multiple plots for same range, give multiple expressions prior to the range tuple.
>>> plot( sin(x),cos(x), (x, -pi, pi))
You can also specify separate range for each expression.
plot((expr1, range1), (expr2, range2))
Following figure plots sin(x) and cos(x) over different ranges.
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))
Following optional keyword arguments may be specified in plot() function.
-
line_color − specifies color of the plot line.
-
title − a string to be displayed as title
-
xlabel − a string to be displayed as label for X axis
-
ylabel − a string to be displayed as label for y axis
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')
The plot3d() function renders a three dimensional plot.
plot3d(expr, xrange, yrange, kwargs)
Following example draws a 3D surface plot −
>>> from sympy.plotting import plot3d
>>> x,y=symbols('x y')
>>> plot3d(x*y, (x, -10,10), (y, -10,10))
As in 2D plot, a three dimensional plot can also have multiple plots each with different range.
>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))
The plot3d_parametric_line() function renders a 3 dimensional parametric line plot.
>>> from sympy.plotting import plot3d_parametric_line >>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))
To draw a parametric surface plot, use plot3d_parametric_surface() function.
plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs) >>> from sympy.plotting import plot3d_parametric_surface >>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))
SymPy — Entities
The geometry module in SymPy allows creation of two dimensional entities such as line, circle, etc. We can then obtain information about them such as checking colinearity or finding intersection.
Point
Point class represents a point in Euclidean space. Following example checks for collinearity of points −
>>> from sympy.geometry import Point >>> from sympy import * >>> x=Point(0,0) >>> y=Point(2,2) >>> z=Point(4,4) >>> Point.is_collinear(x,y,z)
Output
True
>>> a=Point(2,3) >>> Point.is_collinear(x,y,a)
Output
False
The distance() method of Point class calculates distance between two points
>>> x.distance(y)
Output
$2\sqrt2$
The distance may also be represented in terms of symbols.
Line
Line entity is obtained from two Point objects. The intersection() method returns point of intersection if two lines intersect each other.
>>> from sympy.geometry import Point, Line >>> p1, p2=Point(0,5), Point(5,0) >>> l1=Line(p1,p2) >>> l2=Line(Point(0,0), Point(5,5)) >>> l1.intersection(l2)
Output
[Point2D(5/2, 5/2)]
>>> l1.intersection(Line(Point(0,0), Point(2,2)))
Output
[Point2D(5/2, 5/2)]
>>> x,y=symbols('x y')
>>> p=Point(x,y)
>>> p.distance(Point(0,0))
Output
$\sqrt{x^2 + y^2}$
Triangle
This function builds a triangle entity from three point objects.
Triangle(a,b,c)
>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0)) >>> t.area
Output
$-\frac{25}{2}$
Ellipse
An elliptical geometry entity is constructed by passing a Point object corresponding to center and two numbers each for horizontal and vertical radius.
ellipse(center, hradius, vradius)
>>> from sympy.geometry import Ellipse, Line >>> e=Ellipse(Point(0,0),8,3) >>> e.area
Output
$24\pi$
The vradius can be indirectly provided by using eccentricity parameter.
>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4)) >>> e1.vradius
Output
$\frac{5\sqrt7}{4}$
The apoapsis of the ellipse is the greatest distance between the focus and the contour.
>>> e1.apoapsis
Output
$\frac{35}{4}$
Following statement calculates circumference of ellipse −
>>> e1.circumference
Output
$20E(\frac{9}{16})$
The equation method of ellipse returns equation of ellipse.
>>> e1.equation(x,y)
Output
$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} — 1$
SymPy — Sets
In mathematics, a set is a well-defined collection of distinct objects which may be numbers, people, letters of the alphabet, or even other sets. Set is also one of the built-in types in Python. SymPy provides sets module. It contains definitions of different types of set and has functionality to perform set operations such as intersection, union, etc.
Set is a base class for any other type of set in SymPy. Note that it is different from built-in set data type of Python. Interval class represents real intervals and its boundary property returns a FiniteSet object.
>>> from sympy import Interval >>> s=Interval(1,10).boundary >>> type(s)
sympy.sets.sets.FiniteSet
FiniteSet is a collection of discrete numbers. It can be obtained from any sequence object such as list or string.
>>> from sympy import FiniteSet >>> FiniteSet(range(5))
Output
$\lbrace\lbrace0,1,…,4\rbrace\rbrace$
>>> numbers=[1,3,5,2,8] >>> FiniteSet(*numbers)
Output
$\lbrace1,2,3,5,8\rbrace$
>>> s="HelloWorld" >>> FiniteSet(*s)
Output
{H,W,d,e,l,o,r}
Note that, as in built-in set, SymPy’s Set is also a collection of distinct objects.
ConditionSet is a set of elements that satisfy a given condition
>>> from sympy import ConditionSet, Eq, Symbol
>>> x=Symbol('x')
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> s
Output
$\lbrace x\mid x\in[1,10]∧x^2 — 2x =0\rbrace$
Union is a compound set. It includes all elements in two sets. Note that elements that are found in both, will appear only once in the Union.
>>> from sympy import Union >>> l1=[3,1,5,7] >>> l2=[9,7,2,1] >>> a=FiniteSet(*l1) >>> b=FiniteSet(*l2) >>> Union(a,b)
Intersection on the other hand contains only those elements that are present in both.
>>> from sympy import Intersection >>> Intersection(a,b)
ProductSet object represents Cartesian product of elements in both sets.
>>> from sympy import ProductSet >>> l1=[1,2] >>> l2=[2,3] >>> a=FiniteSet(*l1) >>> b=FiniteSet(*l2) >>> set(ProductSet(a,b))
Complement(a,b) retains elements in a excluding elements that are common with b set.
>>> from sympy import Complement >>> l1=[3,1,5,7] >>> l2=[9,7,2,1] >>> a=FiniteSet(*l1) >>> b=FiniteSet(*l2) >>> Complement(a,b), Complement(b,a)
SymmetricDifference set contains only uncommon elements in both sets.
>>> from sympy import SymmetricDifference >>> l1=[3,1,5,7] >>> l2=[9,7,2,1] >>> a=FiniteSet(*l1) >>> b=FiniteSet(*l2) >>> SymmetricDifference(a,b)
Output
{2,3,5,9}
SymPy — Printing
There are several printers available in SymPy. Following is a partial list −
- str
- srepr
- ASCII pretty printer
- Unicode pretty printer
- LaTeX
- MathML
- Dot
SymPy objects can also be sent as output to code of various languages, such as C, Fortran, Javascript, Theano, and Python.
SymPy uses Unicode characters to render output in form of pretty print. If you are using Python console for executing SymPy session, the best pretty printing environment is activated by calling init_session() function.
>>> from sympy import init_session >>> init_session()
IPython console for SymPy 1.5.1 (Python 3.7.4-64-bit) (ground types: python).
These commands were executed −
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()
Documentation can be found at https://docs.sympy.org/1.5.1/.
>>> Integral(sqrt(1/x),x)
$\int \sqrt\frac{1}{x} dx$
If LATEX is not installed, but Matplotlib is installed, it will use the Matplotlib rendering engine. If Matplotlib is not installed, it uses the Unicode pretty printer. However, Jupyter notebook uses MathJax to render LATEX.
In a terminal that does not support Unicode, ASCII pretty printer is used.
To use ASCII printer use pprint() function with use_unicode property set to False
>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)
The Unicode pretty printer is also accessed from pprint() and pretty(). If the terminal supports Unicode, it is used automatically. If pprint() is not able to detect that the terminal supports unicode, you can pass use_unicode=True to force it to use Unicode.
To get the LATEX form of an expression, use latex() function.
>>> print(latex(Integral(sqrt(1/x),x)))
\int \sqrt{\frac{1}{x}}\, dx
You can also use mathml printer. for that purpose, import print_mathml function. A string version is obtained by mathml() function.
>>> from sympy.printing.mathml import print_mathml >>> print_mathml(Integral(sqrt(1/x),x))
<apply>
<int/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<root/>
<apply>
<power/>
<ci>x</ci>
<cn>-1</cn>
</apply>
</apply>
</apply>
>>>mathml(Integral(sqrt(1/x),x))
‘<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>’
Kickstart Your Career
Get certified by completing the course
Get Started

Добрый день уважаемые пользователи. Данная статья ориентированна на начинающих программистов. Как вы знаете для Python существует большое множество библиотек которые помогают с вычислениями. И я хотел бы поделиться одной из библиотек, которая может существенно помочь при вычислениях, но использовать ее в коде я не рекомендую. Но она может значительно облегчить вам жизнь, если вы решаете уровнения и занимаетесь их преобразованием, упрощением для дальнейшего использования.
Библиотека SymPy умеет многое, начиная с решения уравнений и заканчивая построениями графиков, но тут я хотел рассмотреть на примерах, как же работают функции «упрощения» в этой библиотеке на примере решения нескольких простых задач.
Приступим!)
Задача. Найдите значение выражения:
Проведем преобразования:
Проверим наше преобразование с помощью SymPy:
from sympy import * # знак звездочки означает, чт омы импортировали все данные из библиотекиinit_printing(use_unicode = False, wrap_line = False, no_global = True) # формат вывода информацииexpression = (sqrt(13)+sqrt(7))**2/(10+sqrt(91))
expressionСкопируйте этот код и посмотрите на нывод. Библиотека SymPy не дала нам ответ, а вывел очень красиво нашу формулу:
Предлагаю упростить это выражение, т.е. решить его, но для упрощения я буду использовать функцию simplify:
simplify(expression) # функция simplify выполняет упрощение выраженийИ тут мы получаем:
2
Для лучшего понимаю как можно использовать функцию simplify приведем еще пару примеров.
Задача. Найдите значение выражения, если lgb = 5:
Проведем преобразования. Для начала вычислим значение b.
Теперь поставим значение b в наше выражение, которое нужно было вычислить:
Проверим наше преобразование с помощью SymPy:
b = Symbol('b') # введем символ b далее мы сможем его вычислить
expression_b = log(b, 10)
expression_bЭтот код выведет нам следующее сообщение:
После того как мы создадим выражение expression_b давайте вычислим само значение b:
solve_b = solve(expression_b-5, b) # функция slove решает уровнение,тут "-5" эквивалентно "=5"
solve_b = solve_b[0]
solve_bНа выводе получим 100000.
Да, мы уже получили с вами это же числе проводя преобразования в ручную.
Подставим b в выражение:
expression_b_main = log(10 / solve_b**3)
expression_b_mainНа выводе получим:
Да, вывод не всегда удобно читать. Но отметим что, В ответе выше содержится 14 нулей, а логарифм по основанию 10 будет равен — 14.
И именно тут я хочу сделать важное замечание, что в SymPy нужно быть очень внимательными с логарифмами и нужно явно указывать основание. Если его не указать, то по умолчанию основание логарифма будет — е.
Задача. Упростите выражение:
Когда перемножаются степени одинаковых чисел, можно просто сложить показатели степеней.
Проверим наше выражение и упростим его с помощью библиотеки.
a = Symbol('a')expression_a = 2 * a * a**(4/3) * 3 * a**(2/3)
expression_aВыведет , в красивом виде:
Наша библиотека сразу же дала нам упрощенное выражение, перемножив все слагаемые. Результат верный. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующей суммы:
Задача. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующей суммы:
def summa(n):
summa = 0
for x in range(1, n+1, 1):
summa = log(x) + summa
return summaИспользуем нашу функцию:
summa(5)Получим на выводе:
Обратите внимание что функция работает верно. Т.е. наша сумма начинается с i = 1, но поскольку натуральный логарифм т 1 будет равен 0, то в вывод 0 не попадает.
Задача. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующего выражения:
Сразу скажу что не нужно пугаться большой буквы П. В этой записи П оначает что это произведение ряда числе начиная с 1 и до n.
В этом математическом выражении нам необходимо посчитать натуральный логарифм от произведений чисел от 1 до n.
А теперь используем функцию:
multiplication(2)Получим на вывод:
Задача. Проверьте, что функции из предыдущих двух заданий эквивалентны. Объясните, почему это так.
print('Функция из задния 4:', summa(5))
print('Функция из задния 5:', multiplication(5))Тут мы вывели значения которые получили от функций суммы и произведения. Полуим на выводе:
Исходя из свойств логарифмов упростим первое выражение. Поскольку у логарифмов везде одинаковое основание, то мы можем перемножить числа в скобках.
summa_expression_simplify = simplify(summa(5))
summa_expression_simplifyНа выводе получим:
Как мы видим выражения полностью одинаковы.
Задача. Найдите значение выражения.
Воспользуемся SymPy:
x = Symbol('x')expression_g = (4*x-x*x)**(1/3)
expression_g = simplify(expression_g)
expression_gВыведет нам:
Решим данное уравнение:
expression_g_solve = solve(expression_g-0, x) # Найдем корни
expression_g_solveНа выводе получим:
Мы нашли корни уравнения.
Теперь перейдем к решению основного уравнения. На самом деле для решения не нужно было искать корни, это было продемонстрировано для примера.
numerator_g = (4*(2-x)-(2-x)*(2-x))**(1/3)
denominator_g = (4*(2+x)-(2+x)*(2+x))**(1/3)expr_g_main = numerator_g / denominator_g
expr_g_mainНа выводе получим:
Воспользовавшись функцией упрощения, упростим это выражение.
expr_g_main = simplify(expr_g_main)
expr_g_mainНа выводе получим:
И так мы получили ответ 1. Посмотрим как это получилось, приведя поэтапные преобразования:
Задача. Найдите значение выражения.
Упростим выражение в ручную:
В ответе мы получили 5. Проверим наши преобразования используя библиотеку sympy.
x = Symbol('x')
Expression = ((2*x**3)**4-(x**2)**6)/(3*x**12)
ExpressionНа выводе получим:
Наше решение верно. Ответы сошлись.
Задача. Найдите значение выражения при b=2.
Проведем упрощения выражения:
Ответ при b=2 будет -1/2.
Проверим наши вычисления с помощью библиотеки:
b = Symbol('b')
expression_b = (11*a**6*b**3-(3*a**2*b)**3)/(4*a**6*b**6)
expression_bНа выводе получим:
Как видим библиотека сразу сделал упрощение нашего выражения.
expression_g_solve = solve(expression_b+0.5, b)
expression_g_solve[0]На выводе получим:
Поставив свой ответ который мы получили, мы нашли значение b = 2, значит выражение решено верно.
Надеюсь на нескольких простых примерах вы поняли суть работы с SymPy и применением ее в ваших вычислениях. Обращаю внимание, что SymPy не всегда упрошает выражения до самого простого, это было видно по заданиям в этой статье.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Как предпочитаете упрощать выражения при расчетах?
47.83%
Использую библиотеки
11
Проголосовали 23 пользователя.
Воздержались 6 пользователей.


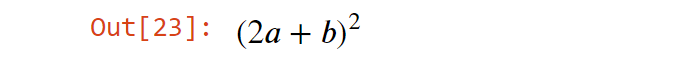

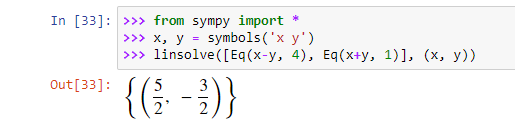
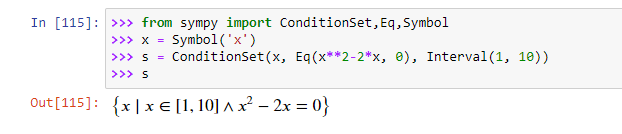









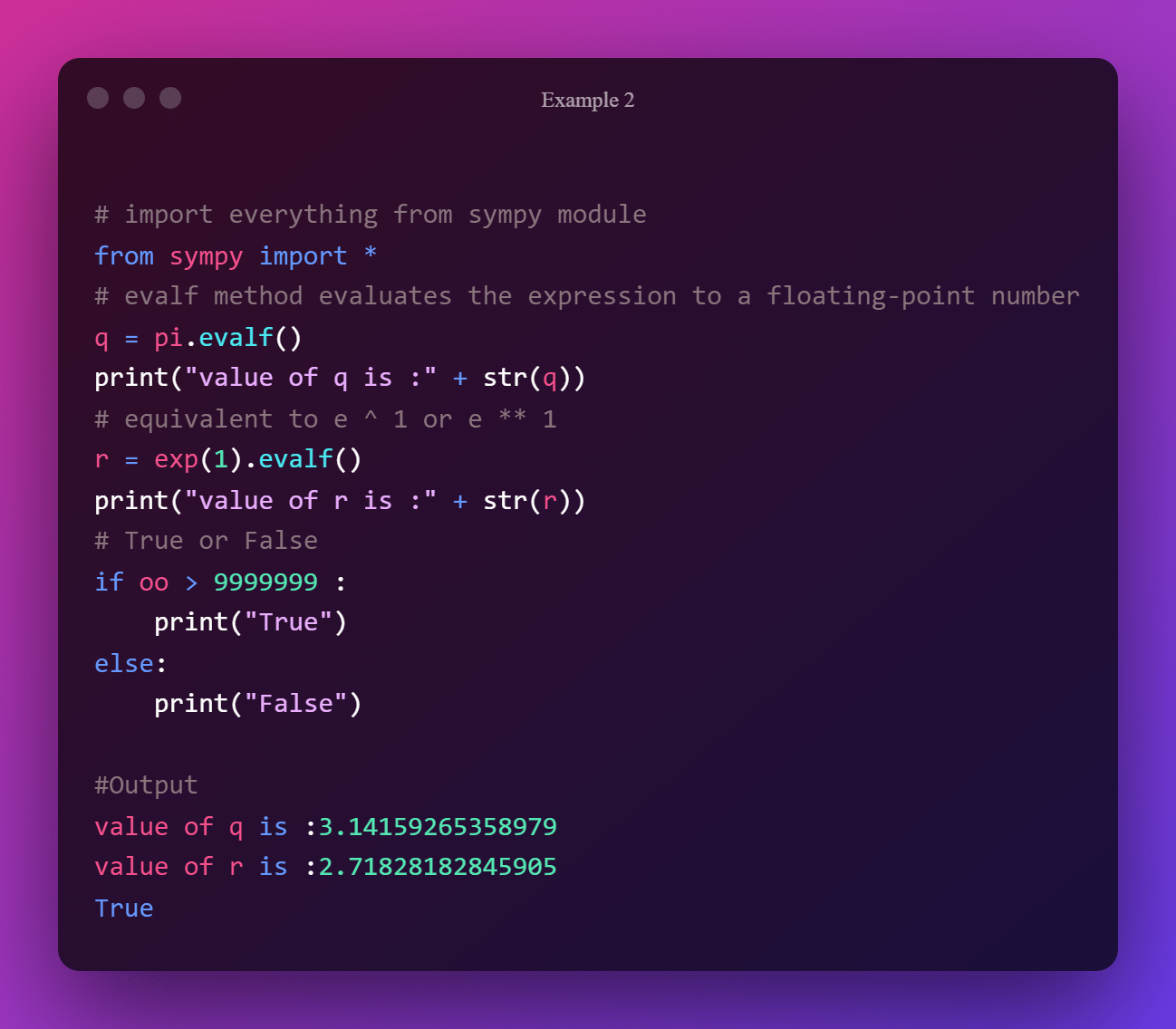


 SymPy
SymPy