Руководство по решению задач по коллоидной химии - Большая энциклопедия инструкций и руководств

Подробное руководство по решению задач в области коллоидной химии

Коллоидная химия исследует системы, в которых один из компонентов имеет размеры в диапазоне от нанометров до микрометров. Коллоидные системы включают в себя растворы, гели, эмульсии, пены, пигменты и другие материалы, имеющие важное значение в многих отраслях науки и техники.

Решение задач в области коллоидной химии может быть сложным из-за того, что коллоидные системы имеют сложную структуру и взаимодействия. Ниже представлено подробное руководство по решению задач в области коллоидной химии.

Шаг 1: Определение типа коллоидной системы

Первым шагом при решении задач в области коллоидной химии является определение типа коллоидной системы. Коллоидные системы могут быть классифицированы на основе фаз, которые они содержат:

Смеси жидкость-жидкость (эмульсии)
Смеси жидкость-твердое тело (сольи, оксиды)
Смеси газ-жидкость (пены)
Смеси газ-твердое тело (дым)

Шаг 2: Определение физических свойств коллоидной системы

Вторым шагом является определение физических свойств коллоидной системы, таких как размер частиц, заряд частиц, степень дисперсности и реологические свойства.

Размер частиц: размер частиц является критическим параметром для коллоидных систем. Коллоидные частицы обычно имеют размер от 1 нм до 1 мкм. Размер частиц определяется с помощью методов, таких как дифракция света или электронная микроскопия.
Заряд частиц: заряд частиц имеет важное значение, поскольку он может влиять на межчастичные взаимодействия и стабильность коллоидных систем. Заряд частиц может быть определен с помощью методов, таких как электрофорез или потенциометрия.
Степень дисперсности: степень дисперсности описывает степень гомогенности или гетерогенности коллоидной системы. Степень дисперсности может быть определена с помощью методов, таких как ультразвуковая спектроскопия или динамический светорассеивающий анализатор.
Реологические свойства: реологические свойства описывают поведение коллоидной системы под воздействием внешних сил. Реологические свойства могут быть определены с помощью методов, таких как реометрия или техника торсионной балансовой микроскопии.

Шаг 3: Определение стабильности коллоидной системы

Третьим шагом является определение стабильности коллоидной системы. Стабильность коллоидной системы зависит от многих факторов, таких как наличие поверхностно-активных веществ, заряд частиц, рН и температура.

Стабильность коллоидной системы может быть оценена с помощью методов, таких как термодинамические расчеты или электрокинетические измерения.

Шаг 4: Определение свойств взаимодействия между частицами

Четвертым шагом является определение свойств взаимодействия между частицами. Взаимодействия между частицами могут быть электростатическими, ван-дер-Ваальсовыми или стерическими взаимодействиями.

Свойства взаимодействия между частицами могут быть определены с помощью методов, таких как рассеяние света, светопропускание, ультразвуковая спектроскопия или микрокалориметрия.

Шаг 5: Решение задач

После того, как произведен анализ коллоидной системы и ее свойств, можно переходить к решению конкретных задач. Решение задач может включать в себя расчет концентрации, расчет заряда частиц, определение степени дисперсности и реологических свойств коллоидной системы.

Вывод

Решение задач в области коллоидной химии может быть сложным, но эффективное использование различных методов и подходов может позволить разобраться в сложных коллоидных системах. Основные шаги в решении задач в области коллоидной химии включают определение типа коллоидной системы, определение физических свойств коллоидной системы, определение стабильности коллоидной системы, определение свойств взаимодействия между частицами и решение конкретных задач.

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Российский химико-технологический университет им. Д. И. Менделеева

Сборник задач по коллоидной химии

Утверждено Редакционным советом университета в качестве учебного пособия

УДК 544.7(076.1) ББК 24.6я7

С23

Авторы: Гаврилова Н. Н., Жилина О. В., Киенская К. И., Назаров В. В., Яровая О. В.

Рецензенты:

Доктор химических наук, профессор химического факультета Московского государственного университета им. М. В. Ломоносова

В. Н. Матвеенко

Доктор химических наук, профессор, заведующий кафедрой технологии химико-фармацевтических и косметических средств Российского химико-технологического университета им. Д. И. Менделеева

Г. В. Авраменко

Сборник задач по коллоидной химии: учеб. пособие / Н. Н. Гаври-

С23 лова, О. В. Жилина, К. И. Киенская, В. В. Назаров, О. В. Яровая. – М. : РХТУ им. Д. И. Менделеева, 2009. – 132 с.

ISBN 978-5-7237-0811-2

Пособие составлено в соответствии с программой курса «Поверхностные явления и дисперсные системы» («Коллоидная химия») и охватывает основные разделы этого курса. В каждом разделе представлены теоретическое введение, примеры решения задач и задачи. В последней части пособия приведены индивидуальные задания (в двух частях), которые включают расчётные задачи на использование основных соотношений из всех разделов.

Предназначается для студентов, обучающихся на дистанционнозаочном отделении РХТУ им. Д. И. Менделеева.

	УДК 544.7(076.1)
	ББК 24.6я7
ISBN 978-5-7237-0811-2	© Оформление. Российский химико-
	технологический университет им. Д.И.
	Менделеева, 2009
	© Гаврилова Н. Н., Жилина О. В., Киен-
	ская К. И., Назаров В. В., Яровая О. В.,
	2009

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ…………………………………………… 4

1.ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ И ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ…………………………………………………………… 5

Примеры решения задач .………………………………	13
Задачи …………………………………………………	18

2.АДСОРБЦИОННЫЕ РАВНОВЕСИЯ …………………………….. 32 Примеры решения задач …………………………………….. 36

Задачи …………………………………………………………. 45

3.КИНЕТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ. МЕТОДЫ ДИСПЕРСИОННОГО АНАЛИЗА……………………. 57

Примеры решения задач …………………………………….. 60

Задачи …………………………………………………………. 69

4.ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ НА ПОВЕРХНОСТЯХ…………. 74 Примеры решения задач …………………………………….. 78

Задачи …………………………………………………………. 81

5.СВОЙСТВА ЛИОФИЛЬНЫХ ДИСПЕРСНЫХ СИСТЕМ………. 88 Примеры решения задач …………………………………….. 92

Задачи …………………………………………………………. 94

6.АГРЕГАТИВНАЯ УСТОЙЧИВОСТЬ И КОАГУЛЯЦИЯ ЛИОФОБНЫХ ДИСПЕРСНЫХ СИСТЕМ……………………….. 98

Примеры решения задач …………………………………….. 100

Задачи …………………………………………………………. 107

7.СТРУКТУРООБРАЗОВАНИЕ И РЕОЛОГИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ …………………………. 112

Примеры решения задач …………………………………….. 118

Задачи …………………………………………………………. 121

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ………………………………… 127

ЛИТЕРАТУРА………………………………………………………. 128 ПРИЛОЖЕНИЯ……………………………………………………… 129

ПРЕДИСЛОВИЕ

Настоящее учебное пособие охватывает основные разделы коллоидной химии – науки о поверхностных явлениях и дисперсных системах. Пособие состоит из семи глав, каждая из которых содержит краткое изложение теоретических основ соответствующего раздела коллоидной химии, примеры решения типовых задач и сами задачи. Кроме этого приведены варианты индивидуальных заданий в форме определённого набора задач.

Первая глава содержит задачи, касающиеся термодинамики поверхностных явлений (адгезия, смачивание, капиллярные явления др.). Во второй главе кратко описаны теории физической адсорбции газов и паров и приведены соответствующие задачи. Вопросы, касающиеся кинетических свойств дисперсных систем, а также методов дисперсионного анализа, базирующихся на этих свойствах, приведены в третьей главе. Соответственно, здесь представлены задачи, касающиеся методов определения размеров частиц дисперсных систем. Четвёртая глава целиком посвящена электрическим явлениям на поверхностях и направлена на ознакомление с теориями строения двойного электрического слоя и с электрокинетическими явлениями. Образование и свойства лиофильных дисперсных систем рассматриваются в пятой главе. Задачи, приведенные в этой главе, касаются в основном свойств растворов коллоидных ПАВ и полимеров как типичных представителей лиофильных систем. В шестой главе представлены задачи, направленные на ознакомление с основными свойствами лиофобных дисперсных систем (агрегативная устойчивость, теория ДЛФО, кинетика коагуляции). Заключительная, седьмая глава знакомит с элементами реологии

иструктурно-механическими свойствами дисперсных систем.

Взаключительной части пособия приведены индивидуальные задания (в двух частях), которые включают расчётные задачи на использование основных соотношений из всех разделов.

1. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ И ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ

Гл. II, с. 21-52, 78-97, 100-113 [1]

Важнейшей особенностью дисперсных систем является их гетерогенность. В свою очередь, гетерогенность объектов коллоидной химии означает наличие межфазной поверхности, а значит и поверхностной энергии.

Поверхностная энергия Гиббса Gs при постоянных температуре и давлении определяется произведением поверхностного натяжения σ на площадь межфазной поверхности s:

Площадь межфазной поверхности зависит от формы и размеров (дисперсности) элементов дисперсной фазы:

sуд =	s	=	k	= kD ,	(1.2)
	d
V

где sуд – удельная поверхность; V – объём дисперсной фазы; k – коэффици-

ент формы частиц; d – диаметр частиц; D = d1 – дисперсность.

Для сферических частиц уравнение (1.2) принимает вид:

sуд =	πd2	6	3	=6D ,
		=		= r	(1.3)
1	πd3	d
	6

где π = 3,14, r – радиус частиц.

Кривизна поверхности Н в данной точке определяется производной площади поверхности по объёму дисперсной фазы:

H = 1	ds				(1.4)

	2 dV
или с помощью соотношения
H = 1		1	+	1	,	(1.5)
	r
2	r
	1	2

где r1 и r2 – радиусы окружностей, получаемых при пересечении поверхности проходящими через нормаль к ней в данной точке двумя взаимно перпендикулярными плоскостями. Следует отметить, что кривизна поверхности может быть как положительной, так и отрицательной. Например, кривизна поверхности сферических частиц радиусом r равна

H = 1	2	= 1	, при этом	ds	= 2 .	(1.6)
dV
2	r	r		r

Поверхностные явления обусловлены тем, что состояние молекул, находящихся в поверхностном слое, иное по сравнению с молекулами, находящимися в объёме тела. Молекулы в объёме тела окружены такими же молекулами, поэтому их молекулярные силовые поля полностью скомпенсированы. Молекулы поверхностного слоя взаимодействуют как с молекулами одной фазы, так и с молекулами другой фазы. В результате равнодействующая молекулярных сил в поверхностном слое не равна нулю и направлена внутрь той фазы, взаимодействие с которой больше. Таким образом, возникает поверхностное натяжение σ, стремящееся сократить поверхность. Поверхностное натяжение можно представить и как работу образования единицы поверхности.

Термодинамически поверхностное натяжение можно выразить как частную производную от энергии Гиббса по величине межфазной поверхности при постоянстве давления, температуры и числа молей компонентов:

	∂G	.	(1.7)
σ=
	∂s p,T ,n
	j

Отсюда следует, что для индивидуального вещества поверхностное натяжение – это удельная энергия Гиббса, т.е. приходящаяся на единицу поверхности.

Внутренняя (полная) энергия поверхностного слоя Us (рассчитанная на единицу площади) связана с поверхностным натяжением уравнением Гиббса–Гельмгольца:

∂G		(1.8)
Us =σ−T
∂T	p
или
Us =σ+qs ,		(1.9)

где qs – теплота образования единицы поверхности; Т – температура. Стремление системы к уменьшению поверхностной энергии Гиббса

выражается в самопроизвольном уменьшении межфазной поверхности (изменение кривизны (дисперсности) элементов дисперсной фазы, протекание коагуляции и т.д.) и уменьшении поверхностного натяжения (проявление процессов адсорбции, адгезии и смачивания, возникновение электрического потенциала и др.).

Изменение кривизны поверхности (дисперсности) вызывает изменение внутреннего давления в телах. Разность давлений р, например, внутри жидкого тела с кривизной поверхности и без неё, называется капиллярным (избыточным) давлением. Связь капиллярного давления с кривизной поверхности описывается уравнением Лапласа:


p =σ	ds	.		(1.10)

	dV
С учетом уравнений (1.5) и (1.6) для сферической поверхности урав-
нение (1.10) принимает вид:
p =±	2σ		,	(1.11)
r

а для цилиндрической поверхности:
p =±σ.		(1.12)
		r

С капиллярным (избыточным) давлением связано специфическое поведение жидкости в капиллярах и пористых телах. При наличии искривлённого мениска жидкость в вертикальном капилляре либо поднимается, либо опускается, что определяется знаком кривизны мениска. В состоянии равновесия капиллярное давление равно гидростатическому давлению столба жидкости высотой h:

p =σ	ds	=(ρ −ρ	0	)gh ,	(1.13)
dV

где ρ – плотность жидкости; ρ0 – плотность воздуха; g – ускорение свободного падения.

При наличии сферического мениска в цилиндрическом капилляре уравнения (1.13) трансформируется в уравнение Жюрена для высоты капиллярного поднятия жидкости:

h =	2σcosθ		,	(1.14)
(ρ−ρ	0	)gr

			к

где rк – радиус капилляра; θ – краевой угол (угол смачивания).

Для плоского капилляра, в котором образуется цилиндрический мениск (например, при погружении в жидкость двух плоскопараллельных пластин), уравнение (1.14) принимает вид:

h =	2σcosθ	,	(1.15)
(ρ−ρ0 )gd

где d – расстояние между стенками капилляра (пластинами).

С изменением кривизны поверхности (дисперсности, удельной поверхности) меняется свободная энергия тела, что находит своё отражение в изменении давления насыщенного пара над веществом по уравнению Кельвина:

ln	p	= σVм	ds	,	(1.16)
p
	RT dV
	s

где p – давление насыщенного пара над поверхностью, имеющей кривизну; ps – давление насыщенного пара над плоской поверхностью; Vм – молярный объём вещества в конденсированном состоянии; R – универсальная газовая постоянная.

Как видно из уравнения (1.16), величина давления насыщенного пара над искривленной поверхностью зависит как от величины, так и от знака кривизны поверхности. При сферической кривизне поверхности (капля жидкости, сферический мениск в капилляре и др.) уравнение Кельвина принимает вид:

ln	p	= ± 2σVм .	(1.17)
ps
	RTr

Выбор знака в правой части уравнения (1.17) определяется знаком кривизны поверхности. Так, например, при наличии в поре (капилляре) вогнутого сферического мениска, кривизна которого отрицательна, давление пара над ним будет описываться уравнением Кельвина в форме:

ln	ps	=	2σVм cos θ	(1.18)
p	RTr

где r – радиус поры; θ – краевой угол, образующийся при смачивании жидкостью стенок поры. Соотношение (1.18) часто называют уравнением капиллярной конденсации.

Дисперсность (кривизна поверхности) также влияет на растворимость частиц:

ln	c	= ±	2σVм	(1.19)
cs	RTr

где с – растворимость частиц дисперсной фазы; сs – растворимость крупных кристаллов; σ – межфазное натяжение.

Из уравнения (1.19) следует, что с уменьшением размеров частиц их растворимость растёт (при положительной кривизне поверхности).

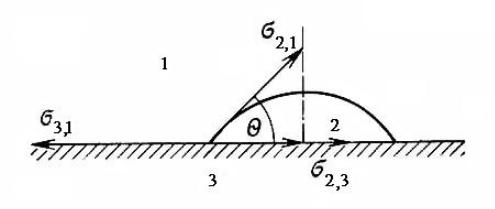
Если жидкость или твёрдое тело имеют поверхность раздела с другой жидкостью или твёрдым телом, то между ними возникает межфазное взаимодействие — адгезия (прилипание). Работа адгезии Wа, характеризующая взаимодействие фаз (она отнесена к единице поверхности), определяется уравнением Дюпре:

Wа =σ2,1 +σ3,1 −σ2,3

(1.20)

где σ2,1 – поверхностное натяжение твёрдого тела или жидкости 2 на границе с газом 1; σ3,1 – поверхностное натяжение жидкости или твёрдого тела 3 на границе с газом 1; σ2,3 – поверхностное (межфазное) натяжение на границе конденсированных фаз.

Из уравнения Дюпре (1.20) следует, что чем больше работа адгезии (взаимодействие между фазами), тем меньше межфазное натяжение σ2,3.

Взаимодействие между жидкой и другой конденсированной фазой можно оценить также с помощью краевого угла (угла смачивания) θ, определяемого уравнением Юнга:

cosθ=	σ3,1 −σ2,3	(1.21)
σ2,1

Краевой угол θ образован касательной к межфазной поверхности, ограничивающей смачивающую жидкость, и имеет вершину на линии раздела трёх фаз (рис. 1.1).

Рис. 1.1. Схематическое изображение капли и векторов сил

Источник

МИНОБРНАУКИ
РОССИИ

Федеральное
государственное бюджетное образовательное учреждение

высшего
образования
«Гжельский государственный университет»

Колледж
ГГУ

УТВЕРЖДАЮ:

Директор колледжа ГГУ

_____________
Т.Г. Колонина

Методические рекомендации к
решению задач

по дисциплине

«Физическая и коллоидная химия »

Специальность:

18.02.05 « Производство тугоплавких неметаллических и
силикатных материалов и изделий»

пос. Электроизолятор,

2017 .г.

Одобрена цикловой комиссией

Общепрофессиональных и специальных технологических
дисциплин

Соответствует государственным требованиями к минимуму
содержания и уровню подготовки выпускников

Автор: Казакова В.Б. – преподаватель
колледжа

Рецензент:
Крючков Ю.Н. – доктор технических наук, преподаватель ГГУ

Пример 1.

При
нормальных условиях плотность двуокиси углерода 1,977 кг/м³. Под каким
давлением нужно сжать газ, чтобы плотность его при 0^оС достигла 10
кг/м³?

Решение

Поскольку
температура газа остается постоянной, то можно использовать следствие из закона
Бойля – Мариотта (2)

откуда

Пример 2.

При
37^оС объем газа равен 0,50 м³. Какой объем займет газ при
100^оС, если давление останется постоянным?

Решение

Используем законы Шарля и Гей-Люссака (4)

откуда

В градусах термодинамической шкалы температура равна:

𝑻₁𝑡₁273=37+273=310^оК

𝑻₂𝑡₂273=100+273=373^оК

Пример 3.

Определить
массу 4 м³ двуокиси углерода при нормальных условиях.

Решение

Μсо₂=44; киломоль СО₂=44 кг. Объем 1 кмоль
газа при нормальных условиях равен 22,4 м³.

Составляем
пропорцию:

Пример 4.

Определить
объем, занимаемый 5,25 кг азота при нормальных условиях.

Решение

Составляем
пропорцию 5,25:28,0 = 𝑣₀:22,4

Пример 5.

Сколько
кубических метров двуокиси углерода при 22^оС и давлении 99280 н/м² можно получить при обжиге 1000 кг известняка с содержанием
90% СаСО₃?

Решение

В 1000 кг
содержится СаСО₃900 кг (остальное приходится на долю
различных примесей).

По уравнению
химической реакции

СаСО_{3 ←}^→ СаО+ СО₂

100 56 44

рассчитываем массу
полученной двуокиси углерода,

Для нахождения
объема этой массы двуокиси углерода при заданных условиях используем уравнение
состояния Клапейрона – Менделеева (11)

Пример 6.

При
27^оС и давлении 106600 н/м² масса 380 см³
газа равна 0,4550 г. Определить грамм- молекулярный вес газа.

Решение

Из
уравнения (11) находим М:

Пример 7.

Вычислить
поверхностное натяжение бензола при 20^оС, если масса 42 капель
бензола, находящихся в объеме между верхней и нижней метками сталагмометра,
равна 1,5672 г. Масса 30 капель воды в том же объеме составляет 2,8180 г.

Решение

Находим
величину поверхностного натяжения воды при 20^оС (см. табл. 2 стр.
257).

Для
нахождения σ_бензвоспользуемся формулой (28)

;

Пример 8.

Поверхностное
натяжение пиридина при 20^оС равно 38,0 н/м; плотность пиридина при этой же
температуре 982 кг/м³ . Чему равен радиус капилляра, в
котором жидкость сможет подняться на 1,60 см?

Решение

По
формуле (29) находим

Пример 9.

Вычислить
динамическую вязкость бензола при 20^оС, если он протекает через
вискозиметр за 91,5 сек. Время прохождения такого же объема воды при той
же температуре равно 2 мин 4,2 сек.

Решение

Для
определения η_бенз воспользуемся формулой (31)

По
таблице^*находим:

1 пз=0,1 н∙сек/м²

Пример 10.

Найти
изменение внутренней энергии при испарении 20 г спирта при температуре
его кипения. Удельная теплота парообразования спирта при этой температуре
858,95 дж/г, удельный объем пара – 607 см³/г (объемом
жидкости пренебречь).

Решение

Для
решения используем уравнение первого закона термодинамики (50)

Q=ΔU+A; ΔU=Q−A.

Q=q Так как спирт кипит, то упругость его паров равна
нормальному атмосферному давлению (p=101325 н/м³).

При
решении необходимо учесть количество граммов спирта, а работу выразить в
джоулях.

A=p∙Δυ=101325∙0,607∙10ֿ³=61,48 дж.

ΔU=20(858,95 – 61,48) = 15949 дж.

Поскольку
ΔU положительно, то, следовательно, при испарении происходит увеличение
внутренней энергии системы.

Пример 11.

Найти
изменение внутренней энергии при испарении 100 г воды при 20^оС,
допуская, что пары воды подчиняются законам идеальных газов и что объем
жидкости незначителен по сравнению с объемом пара. Удельная теплота
парообразования воды равна 2451 дж/г.

Решение

Используем
уравнение состояния идеального газа (10)

pΔυ=nRT,
но pΔυ=A;

A=nRT=∙8,318∙293;

ΔU=100 (2451-)

Происходит
увеличение внутренней энергии на 231,57 кдж.

Пример 12.

Какое
количество тепла выделится при изотермическом сжатии 10 л идеального газа,
взятого при 27^оС и нормальном атмосферном давлении, если объем его
уменьшится в 10 раз?

Решение

Находим
число молей газа

Выделенное тепло
находим по формулам (56) и (53) с учетом числа молей газа. Так при t=const ΔU=0, то Q= A=2,303 nRT lg∙

Q=2,303 lg.

Пример 13.

Тепловой
эффект реакции

C+½Ο₂=CΟ

При
постоянном объеме равен 108,9 кдж/моль при 20^оС. Определить
тепловой эффект этой же реакции при постоянном давлении.

Решение

Находим изменение
числа молей газа при реакции:

Δn=
–½+1=½∙

Используем формулу
(58)

Ōр=Ōυ– Δ nRT=108,9- –8,313∙293∙=107,68 кдж/моль.

Пример 14.

Определить
теплоту сгорания этилена

C₂Н₄+3O₂=2CO₂+2Н₂O+Q̄

Из
следующих данных:

2C+2Н= C₂Н₄–62,01
кдж/моль

C+O₂=CO₂+393,9 кдж/моль

Н₂+½O₂=Н₂O_(ж)+284,9 кдж/моль

Решение

Путем
комбинации заданных термохимических уравнений исключаем из них водород и
углерод, которые не фигурируют в искомом уравнении реакции горения этилена.

Для
этого второе уравнение умножаем на 2 и первое уравнение вычитаем из второго

2C+2O₂=2CO₂+787,8

Полученный
результат складываем почленно с третьим уравнением, предварительно умножив его
на 2.

Или

C₂Н₄+3O₂=

Следовательно,
Q̄=1419,61 кдж/моль.

Тот
же результат можно получить, использовав следствие (62) из закона Гесса:

Q̄=Σ
Q̄_{обр. прод. —}Σ Q̄_{обр. исход.}

Q̄=2∙393,9+2∙284,9—(—62,01)=1419,61
кдж/моль.

Пример 15.

Зная,
что теплота сгорания этана равна 1562 кдж/моль , метана 891,2 кдж/моль,
а водорода 286,3 кдж/моль, вычислить тепловой эффект реакции:

C₂H₆+H₂=2CH₄+ Q̄

Решение

Q̄=Σ
Q̄_{сгор. исход. —}Σ Q̄_{сгор. прод. ;}

Q̄=1562+286,3⎯2·891,5=65,3 кдж/моль.;

Q̄=65,3
кдж/моль.

Пример 16.

Вычислить
теплоту образования этилового спирта при 18^оС и нормальном давлении

2C+3H₂+½O₂=C₂H₅OH+
Q̄

Теплота
сгорания углерода в этих условиях 395,23, водорода до воды 285,95, а этилового
спирта с образованием двуокиси углерода и воды 1368 кдж/моль. (Вода образуется
в жидком состоянии.)

Решение

Для
вычисления Q̄ используем следствие (63) закона Гесса,
учитывая стехиометрические коэффициенты реагирующих веществ в заданном
уравнении реакции.

Q̄=Σ
Q̄_{сгор. исход. —}Σ Q̄_{сгор. прод. ;}

Q̄=2𝑞_о+3𝑞_н_₂▁𝑞_с_₂_н_₅_он;

Q̄=2·395,23+3·285,95⎯1368,0=280,31 кдж/моль.;

Такой
же результат можно получить путем комбинации термохимических уравнений реакций
горения указанных веществ.

Пример 17.

Пользуясь
таблицей стандартных значений ΔΗº₂₉₈, вычислить ΔΗº и Q̄_pдля реакции

CaO₍_ТВ)+CO₂₍_г₎=CaCO₃_(ТВ)

на
1 моль CaCO₃.

Решение

Изменение
энтальпии для реакции находим алгебраическим сложением ΔΗº₂₉₈ участвующих
веществ с учетом стехиометрических коэффициентов (ΔΗº₂₉₈полученных
веществ обозначают со знаком «плюс», а исходных – со знаком «минус»).

ΔΗº_{реакции} = ΔΗº_сас_𝗈_―ΔΗº_са_𝗈_―ΔΗº_со_₂

Находим
по таблице* значения ΔΗº в ккал/моль и переводим их в кдж/моль.

ΔΗº =―1208,6+635,6+394=179,1 кдж/моль.

Q̄_p =179,1 кдж/моль.

Пример 18.

Пользуясь
таблицей значений стандартной свободной энергии ∆F° для важнейших ⁪химических
соединений, установить возможность протекания реакции

C₆H₆+NH₃=C₆H₅NH₂+H₂+∆F°

Решение

Изменение
свободной энергии какой угодно сложной химической реакции можно подсчитать,
пользуясь законом Гесса, аналогично тому как это производится при вычислении
тепловых эффектов.

По
таблице* находим значения ∆F° для бензола, аммиака и анилина.

Примечание.
Изменение свободной энергии в таблице приведено в килокалориях на
килограмм-моль. Для перевода в килоджоули на килограмм –моль необходимо
величину ∆F° реакции умножить на коэффициент 4,19.

C₆H₆+NH₃=C₆H₅NH₂+H₂+∆F°

∆F°с_₆_H_₆=+29400, ∆F°_NH_₃ =―3940, ∆F°_C_₆_H_₆_NH_₂=+35400

∆F°_H_₂=0;

∆F°_{реакции}=∆F°_C_₆_H_₅_NH_₂―∆F°_C_₆_H_₆―∆F°_NH_₃=(35400―29400+3940)4,19=41648,6 кдж/(кг·моль)

Знак
«плюс» у ∆F° данной реакции указывает на невозможность непосредственного
получения анилина из бензола.

Большая
величина ∆F° реакции говорит о том, что анилин в среде водорода является не
совсем устойчивым соединением.

Пример 19.

12
г кислорода охлаждается от 200 до -40^оС. Одновременно
давление повышается от 1 до 60 бар. Каково изменение энтропии, если

Решение

Используем
формулу (68) для вычисления изменения энтропии при изменении состояния газа,
учитывая, что число молей кислорода равно12/32

S₂―S₁=(2,303·8,313 lg дж/град.

Знак
«минус» указывает на то, что при охлаждении газа уменьшается.

Пример 20.

Удельная
теплоемкость жидкого хлора равна 0,9344 дж/град.

Найти
изменение энтропии при нагревании 1 кг жидкого хлора от -50^оС до
-40^оС.

Решение

Применим
формулу (69)

S₂―S₁=с_уд,

S₂―S₁= (0,9344·2,303 дж/град.

Энтропия
повышается.

Пример 21.

Нормальная
температура плавления уксусной кислоты 16,6^оС, теплота плавления ее
равна 194 дж/г. Определить изменение энтропии при плавлении 1 моль
кислоты.

Решение

L=𝑙. M=194·=11640 дж/моль.

Из формулы (70)
находим

S₂―S₁==

Пример 22.

Имеется
1%-ный раствор глюкозы (C₆H₁₂O₆).
Вычислить молярность данного раствора. Плотность раствора принять равной
единице.

Решение

Так
как раствор 1%-ный, то, следовательно, в 100 г раствора содержится 1 г
глюкозы. Масса 1 л раствора равна 1 кг, так как его плотность 1.
Содержание глюкозы в 1 л раствора равно =10 г.

Чтобы
узнать, сколько это будет молей, нужно разделить 10 г на
грамм-молекулярный вес глюкозы (Mс_₆_H_₁₂_O_₆=180), т.е. n==0,055.

Следовательно,
1%-ный раствор глюкозы 0,055 М.

Пример 23.

Какова
нормальность 30%-ной серной кислоты? Плотность этого раствора равна 1,224 г/см³.

Решение

Находим
массу 1 л 30%-ного раствора серной кислоты 1000·1,224=1224 г.

В
нем содержится =367,2 г H₂SO₄,
что составляет ≈7,5 г-экв.

Следовательно,
30%-ный раствор серной кислоты приблизительно 7,5 н.

Пример 24.

Вычислить
молярность 10%-ного раствора серной кислоты.

Решение

Согласно
условию, в 100 г 10%-ного раствора содержится 10 г кислоты и 90 г
воды.

Находим
содержание серной кислоты в 1000 г воды. Оно равно =111,1 г, что составляет =1,13 моль.

Следовательно,
молярность 10% раствора серной кислоты равна 1,13.

Пример 25.

Найти
молярные доли воды и спирта в 40%-ном растворе этилового спирта.

Решение

Согласно
условию, в 100 г раствора содержится 40 г спирта и 60 г
воды.

Вычисляем
количество молей спирта и воды.

n_ь==0,87 моль спирта ; n_а==3,33 моль воды.

Сумма
n_а+
n_ь=4,20
моль.

Используя
формулы (72) и (73), находим для спирта

N_ь==0,87 моль спирта; N_а=0,793.

Пример 26.

Вычислить осмотическое давление
2%- ного раствора глюкозы при 0°С. Плотность раствора принять равной
единице.

Решение

Для вычисления осмотического давления
используем формулу (77)

π= сRТ.

Концентрация
раствора должна быть выражена в кмоль/м³, R — дж/(кмоль • град), π — н/м².

MC₆H₁₂O₆

В 100 кг
2%-ного раствора содержится 2 кг глюкозы. Плотность данного

раствора
принимаем равной 1. Следовательно, в 1000 л или в 1 м³ содержится
20 кг

глюкозы,
что составляет 20/180 кмоль/м³.

π = 20/180
• 8,313 • 10³ • 273 = 2,52 • 10⁵ н/м² = 2,52
бар.

Пример 27.

Какова должна
быть концентрация раствора глюкозы, чтобы раствор этого вещества при 18°С был
изотоничен с раствором, содержащим 0,5 моль/л хлористого кальция ? Кажущаяся степень
диссоциации СаСl₂ в растворе при указанной температуре составляет 65,4%.

Решение

Согласно (77) и
(78) π_гл = c_глRT, а π_СаС_l₂ = ic_CaCl₂RT. Так как π_гл = π_СаС12, то
с_гл = ic_CaCl₂

При диссоциации
каждой молекулы СаС1₂ образуется 3 иона (к = 3); а=0,654. Согласно
(79), i =1+(к—1)a= 1 +
(3 — 1) • 0,654 = 2,308.

Следовательно, с_гл
= 2,308 • 0,5 = 1,154
моль/л.

Пример 28.

Как велико атмосферное давление ,если 0,1 M раствор
хлористого натрия кипит при 99,8°С? кажущаяся степень диссоциации хлористого натрия
в 0,1M растворе равна 84,4%. Давление насыщенного
пара чистой воды при 99,8°С—100600
н/м².

Решение

При
температуре кипения давление пара растворителя над раствором равно атмосферному
давлению. Следовательно, использовав формулу (84) и найдя величину
р_А , тем самым можно определить и величину
атмосферного давления р_А=р_атм. Из
формулы (84)

р_А= р_А⁰ — in_bp⁰_A/ n_a.

Предварительно
находим iи n_а.

i= 1 + a = 1 + 0,844 =
1,844.

В 1 л 0,1 М раствора хлористого натрия содержится 5,85 г NaCl. Число
молей воды равно n_a =
(1000-5,85)/18 = 55,2 моль
(принимаем плотность раствора равной 1).

р_{А =}100600–
(1,844 • 0.1 • 100600) / 55.2 = 100264 H/M2, а
следовательно, и p_атм= 100264H/M2.

Пример 29.

Какова
концентрация в весовых процентах водного раствора глицерина (С₃Н₈0₃),
если он замерзает при —0,52°С?

Решение

Находим
понижение температуры замерзания

Т₃— Т_3р-ля
—Т_3р-ра = 0
—(—0,52) = 0,52.

По формуле (85)
вычисляем моляльную концентрацию раствора

с =(Т₃ )/ Е₃= 0,52 / 1,86 моль в 1000 г воды.

М_глиц
= 92, следовательно, в 1000 г
воды содержится 0,280 • 92 = 25,76 г глицерина.

Общая масса раствора равна 1000 + 25,76= 1025,76 г.

Составляем пропорцию.

В 1025,76 г раствора содержится 25,76 г глицерина

>>100 » » » х »

х =25,76 / 1025,76 = 2,51%.

Таким образом,
раствор глицерина 2,51%-ный (по весу).

Пример 30.

При какой
примерно температуре должен замерзать 40%-ный водный раствор этилового спирта
?

Решение

Используем формулу (87)

Т₃= (E₃m •
1000) / GM = (1,86•40•1000) / (60•46) = 26,95

Т₃T_3р-ля — T_3р-ра= 0 – 26,95 = -26,95

Раствор начнет замерзать примерно при —27° С.

Пример 31.

Вычислите общее и парциальные давления паров жидкостей
над смесью, состоящей из 117,2 г бензола и 884,5 г толуола при
30°С, зная, что зависимость давления пара указанных жидкостей от состава
выражается прямой линией и что при этой температуре давление пара чистого
бензола равно 15756 н/м², а чистого толуола 4892 н/м².

Решение

Находим числа
молей и мольные доли бензола и толуола

M_б = 78,11; М_т = 92,14;

n_b = m_b/
M_б=
117,2 / 78,11 = 1,5 моль;

n_т = m_т/
M_т=
884,5 / 92,14 = 9,6 моль.

По формулам (94)
и (95) вычисляем -парциальные давления паров бензола и толуола над жидкой
смесью

P_б= (1,5 / 1,5 +9,6) • 15756 = 2130 н/м² ;

P_т = (9,6 / 1,5 + 9,6) • 4892 = 4232 н/м² .

Общее давление
паров толуола и бензола над жидкой смесью заданного состава при 30°С равно

P_общ= P_б + P_т
= 2130 + 4232 = 6362 н/м²

Пример 32.

о-Ксилол и n-ксилол
неограниченно смешиваются друг с другом. Давления паров этих жидкостей при 100°
С соответственно равны 28410 н/м²и 36052 н/м². Вычислить отношение числа молей n-ксилола
в парах при температуре 100° С над смесью, содержащей 35 мол. % о-ксилола.

Решение

В смеси
содержится о-ксилола 35, а n-ксилола 65мол.%. Следовательно, молярные
(мольные) доли их в жидкой смеси соответственно равны 0,35 и 0,65.

Находим
парциальные давления -о- и n-ксилола в парах над жидкой смесью

P_о-кс = P⁰_о-ксN_о-кс;

P_n_-кс = P⁰_n_-ксN_n_-кс,

где N_о-кси N_n_-кс–
мольные доли о- и n-ксилола в жидкой смеси

P_о-кс = 28410 • 0,35 = 9943,5 н/м²;

P_n_-кс= 36052 • 0,65 = 23433,8 н/м².

Зная, что
отношение числа молей компонентов в парах равно отношению их специальных
давлений (формула (98) в применении к смешивающимся жидкостям), находим, что

N_о-кс/ N_n_-кс= 9943,5 / 23433,8 = 1 / 2,35.

Следовательно, в
парах на 1 моль о-ксилола приходиться 2,35 моль n-ксилола.

Пример 33.

Смесь камфоры и воды
кипит при нормальном атмосферном давлении (101325 н/м²) при
99° С.

Определить, в каком соотношении будут
переходить вода и камфора в дистиллят. Молекулярный вес камфоры 152,2. Камфора
практически не растворима в воде. Давление паров воды при 99° С равно 97740,9 н/м².

Решение

Так как смесь
кипит, то давление пара камфоры при 99° С равно 101325 — 97740,9 = 3584,1 н/м².

Используем
формулу (99)

M_камф/ Mн₂о = (P_камфМ_камф) / (Pн₂оМн₂о) = (3584,1 •
152,2) / (97740,9 • 18,016) = 1 / 3,23

т. е. с 1 кг камфоры переходит в дистиллят 3,23 кг воды.

Пример 34.

При распределении янтарной кислоты между
водой и эфиром были получены следующие данные: концентрация кислоты (г/10
см³) в водном слое равна 0,121 и 0,07, а в эфире соответственно
0,022 и 0,013.

Показать, что для янтарной кислоты применим закон распределения в
простейшей его форме

Решение

Используем формулу (100)

С₁/ С₂ = 0,121 / 0,022 = 5,50; С₁/
С₂=0,07 / 0,013 = 5,38

Отношение концентраций янтарной кислоты в двух слоях практически
постоянно, следовательно, для данного случая справедлив закон распределения.

Пример 35.

Коэффициент распределения иода
между водой и четыреххлористым углеродом равен 0,0117. Один литр воды
взбалтывают с 200 см³ раствора иода в четыреххлористом
углероде, содержащем 10 г/л иода. Определить равновесную концентрацию
иода в водном слое.

Решение

Используем формулу (100)

Cн₂о
/ Сссl₄=K.

В 200 см³ содержится 2 г
иода.

Обозначим количество иода, перешедшее в 1 л
водного слоя Сн₂о, через х.

Тогда в 200 см’³ раствора
иода в четыреххлористом углероде останется 2-x г иода, а в 1 л 5(2-х) г иода, т.е. Сccl₄ = 5(2-х), но

Cн₂о
/ Сccl₄=К; х/5(2-х)
= 0,0117,

откуда х = 0,117 – 0,0585х;
1,0585х = 0,117; х = 0,1105 г иода.

Следовательно, при взбалтывании
перейдет в 1 л воды 0,1105 г иода.

Пример 36.

Пользуясь правилом Вант-Гоффа и приняв температурный
коэффициент скорости равным 3, вычислить, на сколько нужно повысить
температуру, чтобы скорость реакции возросла в 80 раз?

Решение

Используем уравнение (112)

lg80 = Rt₂ / Rt₁ = (t₂ —
t₁
/ 10) • lgγ;

lg80 = (t₂— t₁ /10)lg3 = (t₂
– t₁) • 0,04771;

t₂ – t₁ = lg80 / 0,04771 =
1,9031 / 0,04771 = 39,89°

Таким образом, для того чтобы
скорость реакции возросла в 80 раз, нужно повысить температуру примерно на
40°С.

Пример 37.

Пользуясь правилом Вант-Гоффа,
вычислить, при какой температуре реакция закончится за 25 мин,
если при температуре 20°С на это требуется 2 ч. Температурный
коэффициент скорости реакции равен 3.

Решение

Между константами скоростей и
временем завершения реакции существует обратно пропорциональная зависимость

Rt₂/Rt₁=
τ_{1 /}τ₂

где τ₁ и τ₂ — время завершения реакции при
температурах t₁ и t₂.

Тогда уравнение (112) можно
записать lg (τ₁ / τ₂₎= (t₂ — t₁ / 10) • lgγ, откуда t₂ — t₁
= 101g (τ₁ / τ₂₎/lgγ, а t₂ = 101g (τ₁ / τ₂₎/ lgγ + t₁ = (101g(120/25) / lg3) +20 = 34,28°

Реакция закончится за 25 мин
при температуре 34,28⁰С.

Пример 38.

Константа равновесия реакции

СН₃СООН
+ С₂Н₅ОН ↔ СН₃СООС₂Н₅ +
Н₂0

равна 4. Определить состав реакционной смеси
при равновесии, если в реакцию введено 1 моль кислоты и 2 моль спирта.

Решение

Используем формулу (114). Обозначим число
молей эфира, образующегося в равновесной смеси, через х. Такое же
количество выделяется и воды — x моль. Количество молей кислоты к моменту равновесия будет
(1—х), а спирта (2—х) моль. Тогда

Kс = С_эфСн₂о
/ С_кС_сп = xx / ((1-x)(2-x)) = 4

Откуда x² = 4(1-х)(2-х); 3x²— 12 + 8 = 0

Решая это квадратное уравнение получим:

Х_1,2 = (12±) /
6 = (12±) /
6,откуда х₁ = 3,154; х₂=0,845.

Первый корень отбрасывается как
неудовлетворяющий условию задачи. Таким образом, в момент установившегося
равновесия в реакционной смеси будет содержаться: эфира – 0,845 моль, воды –
0,845 моль, уксусной кислоты – 0,155 моль, спирта – 1,155 моль.

Пример 39.

При каком разведении концентрация ионов водорода в растворе фенола C₆H₅OH будет
равна 10^-6 г-ион/л? Константа электрической диссоциации фенола 1,28
• 10^-10

Решение

В соответствии с формулой (146)

K_дис
= a²c / 1- a или K_дис = a²/ (1 – a)V

Где V –разведение раствора.

Ввиду малой степени диссоциации фенола можно принять, что 1 – а
≈1. Тогда

K_дис= а² / V

Концентрация ионов водорода в растворе фенола будет равна

Cн₊ = ac_ф или Cн₊= а / V

Следовательно, а = Сн₊V.

Подставляя это значение а в формулу для K_дисполучим

K_{дис =}a² / V = C²н₊ / V = C²н₊V, откуда разведение раствора

V = K / C²н₊ = 1,28 • 10^-10/ (10^-6)²
= 128л

Пример 40.

Пороги коагуляции золя Fe(OH)₃ для электролитов KI и K₂Cr₂O₇ соответственно равны 10,0 и 0,195 ммоль на 1
л золя. Во сколько раз коагулирующая способность двухромовокислого калия
больше, чем у иодистого калия?

Решение

Коагулирующие способности электролитов являются величинами, обратными
их порогам коагуляции

P_KI
= 1 / 10 = 0,1;

P
K₂Cr₂O₇= 1 / 0,195 = 5,1; P_KI

: P K₂Cr₂O₇ =0,1: 5,1 = 1 : 51

Коагулирующая способность двухромовокислого калия для золя Fe(OH)₃
больше, чем иодистого калия, в 51
раз.

Источник