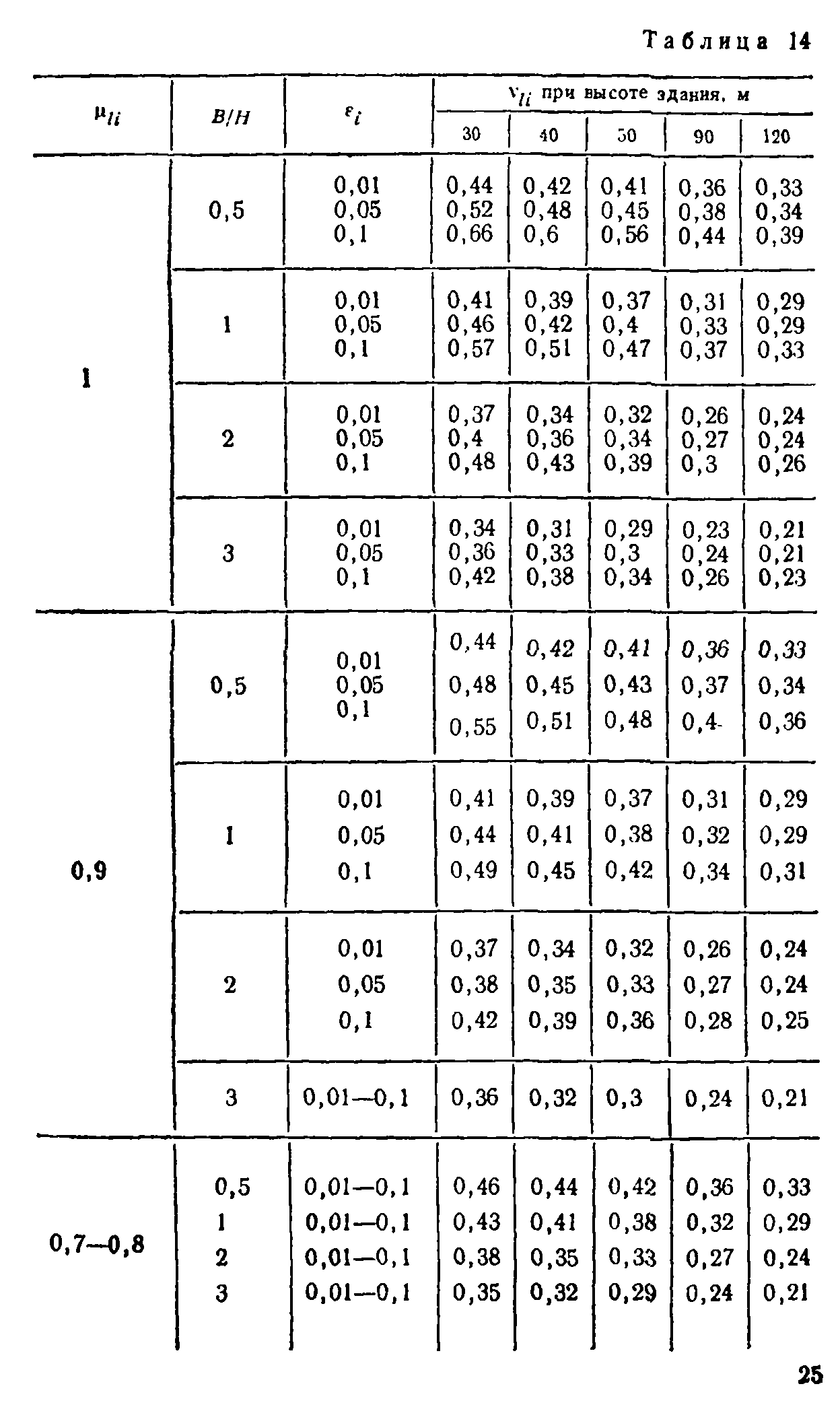
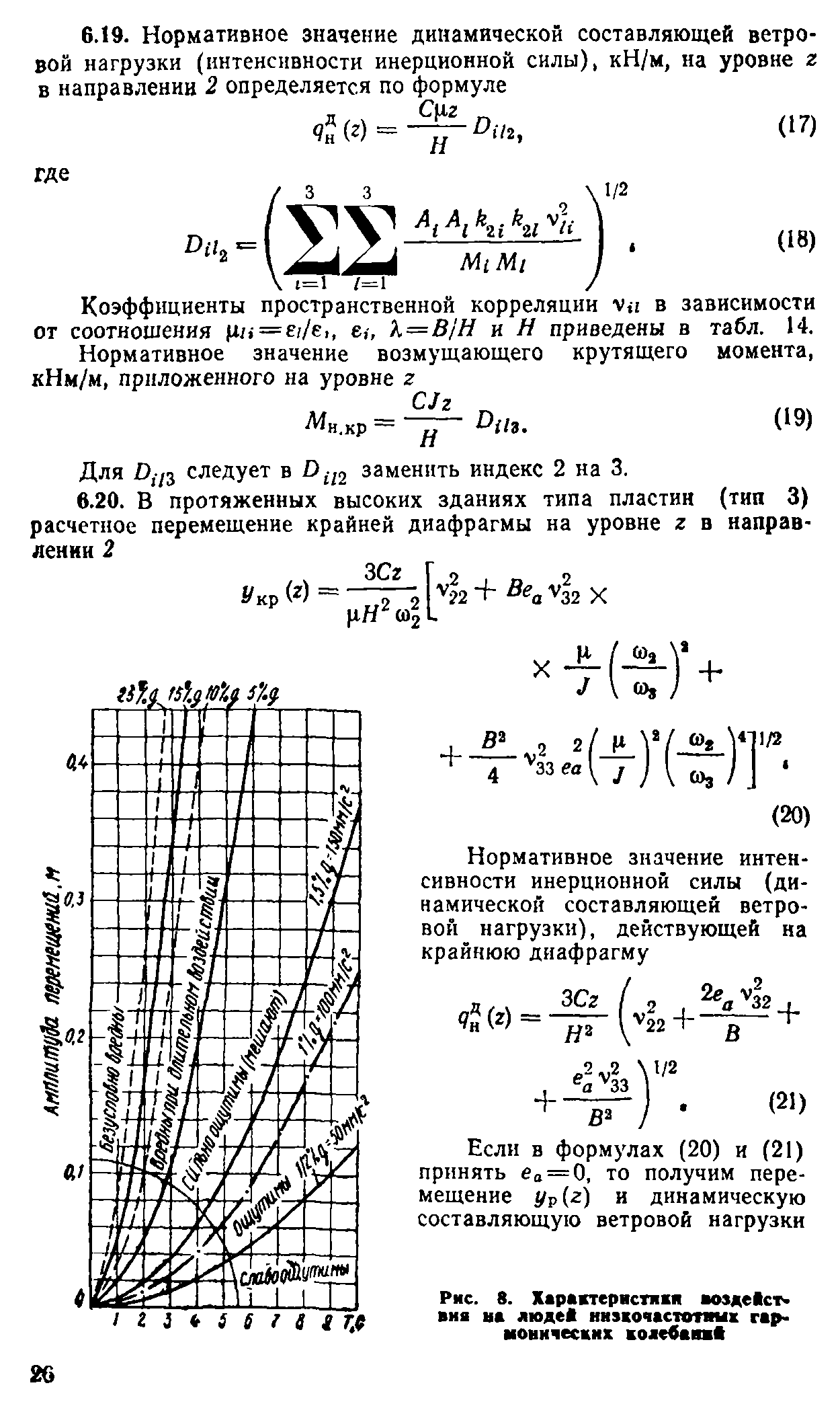
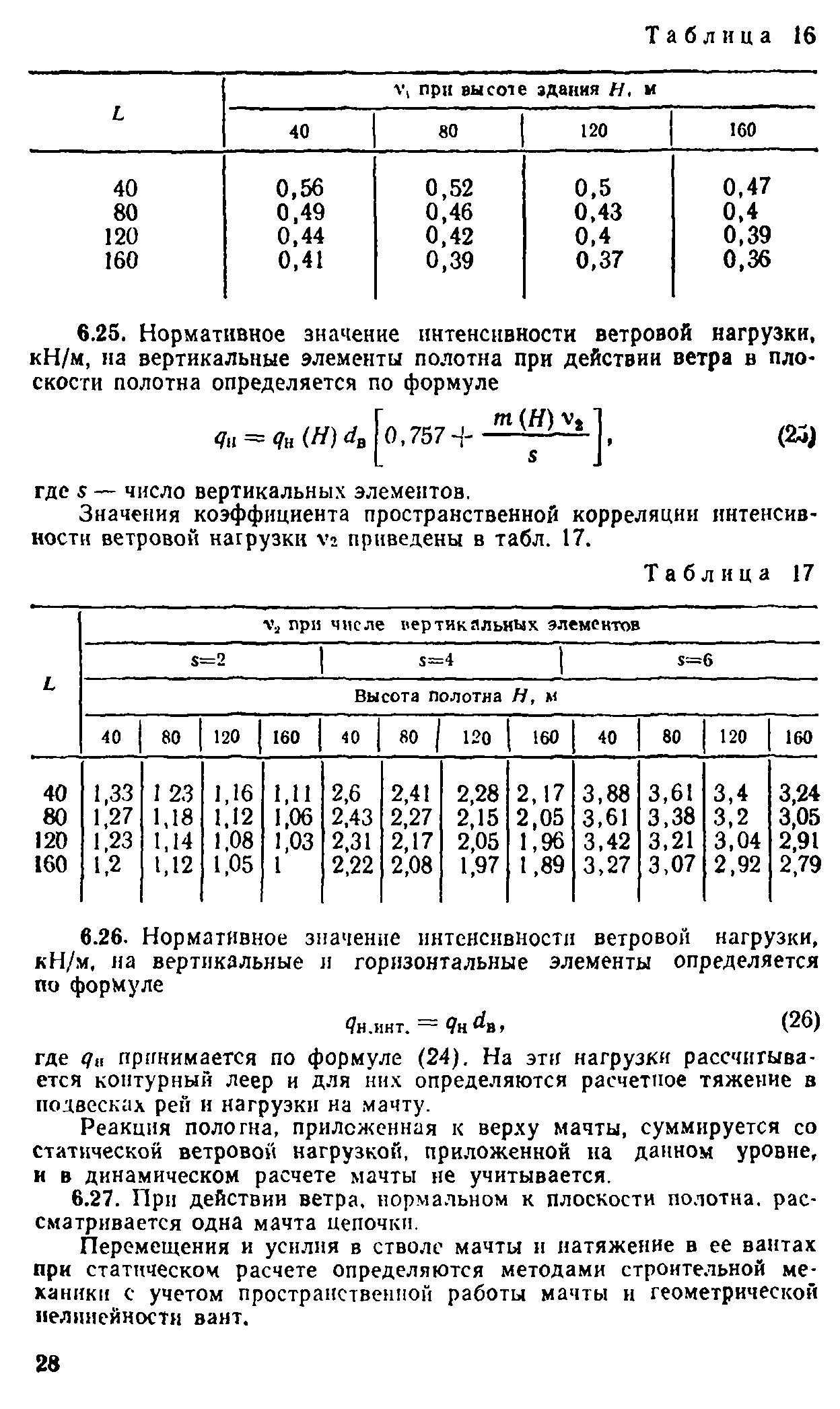
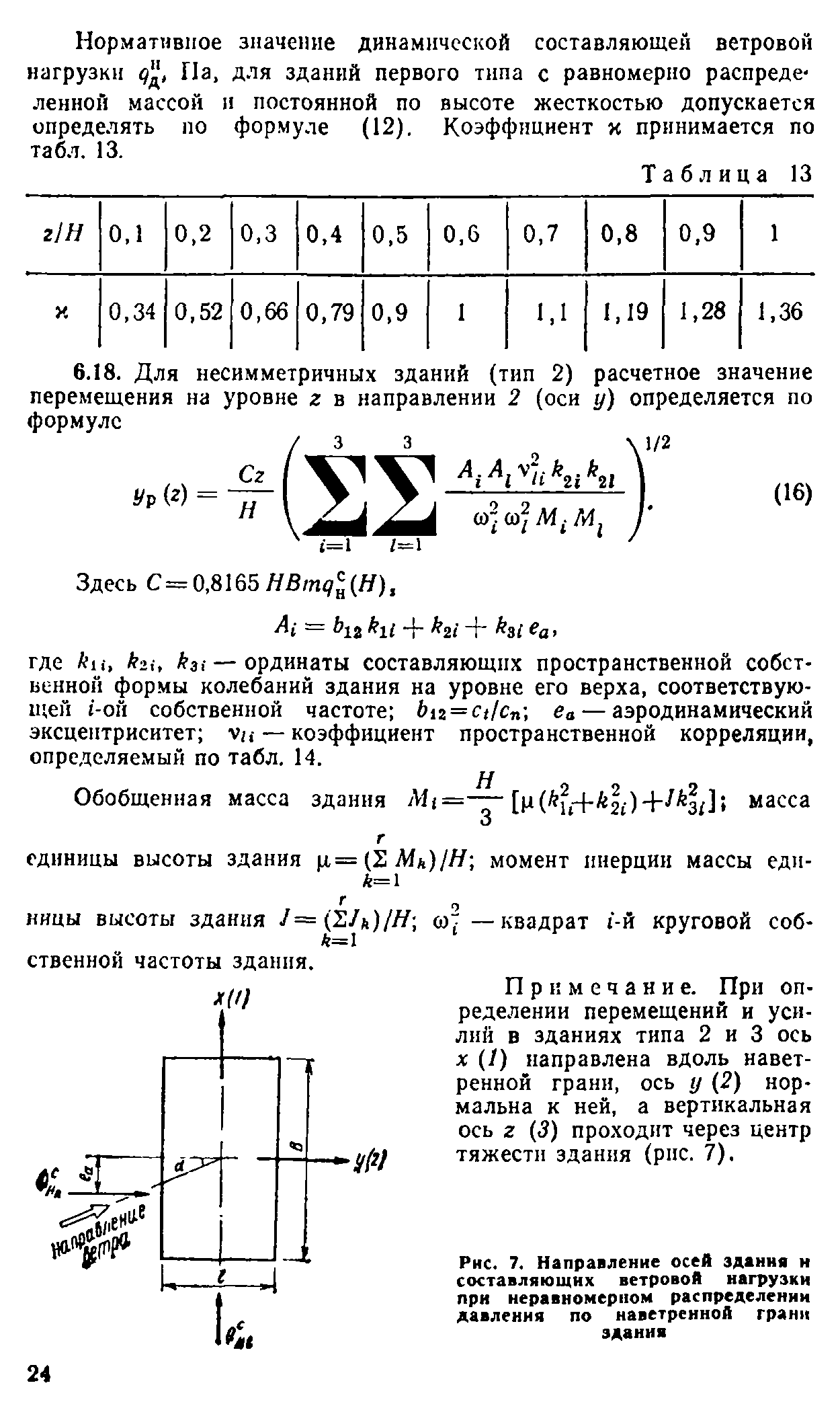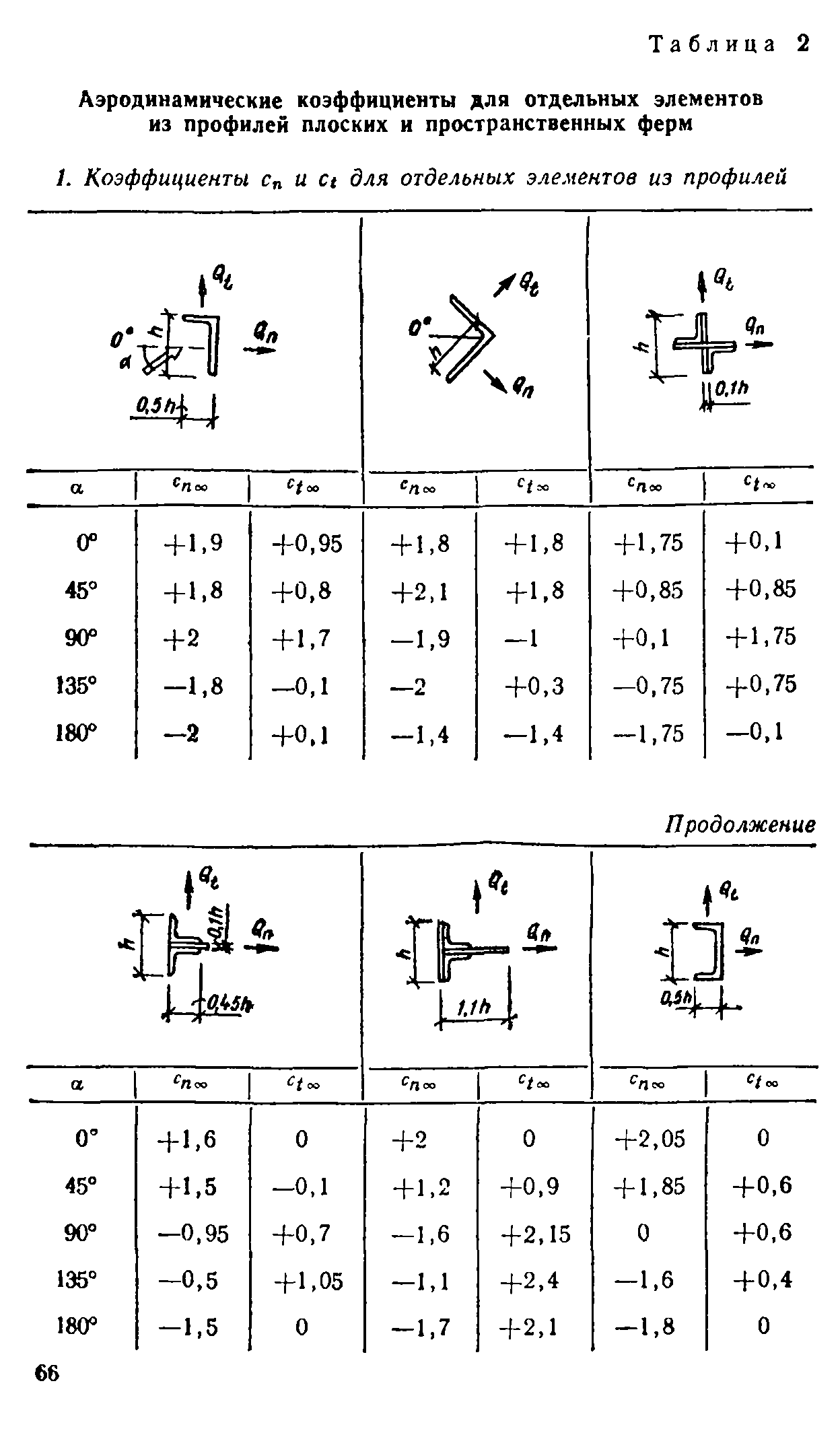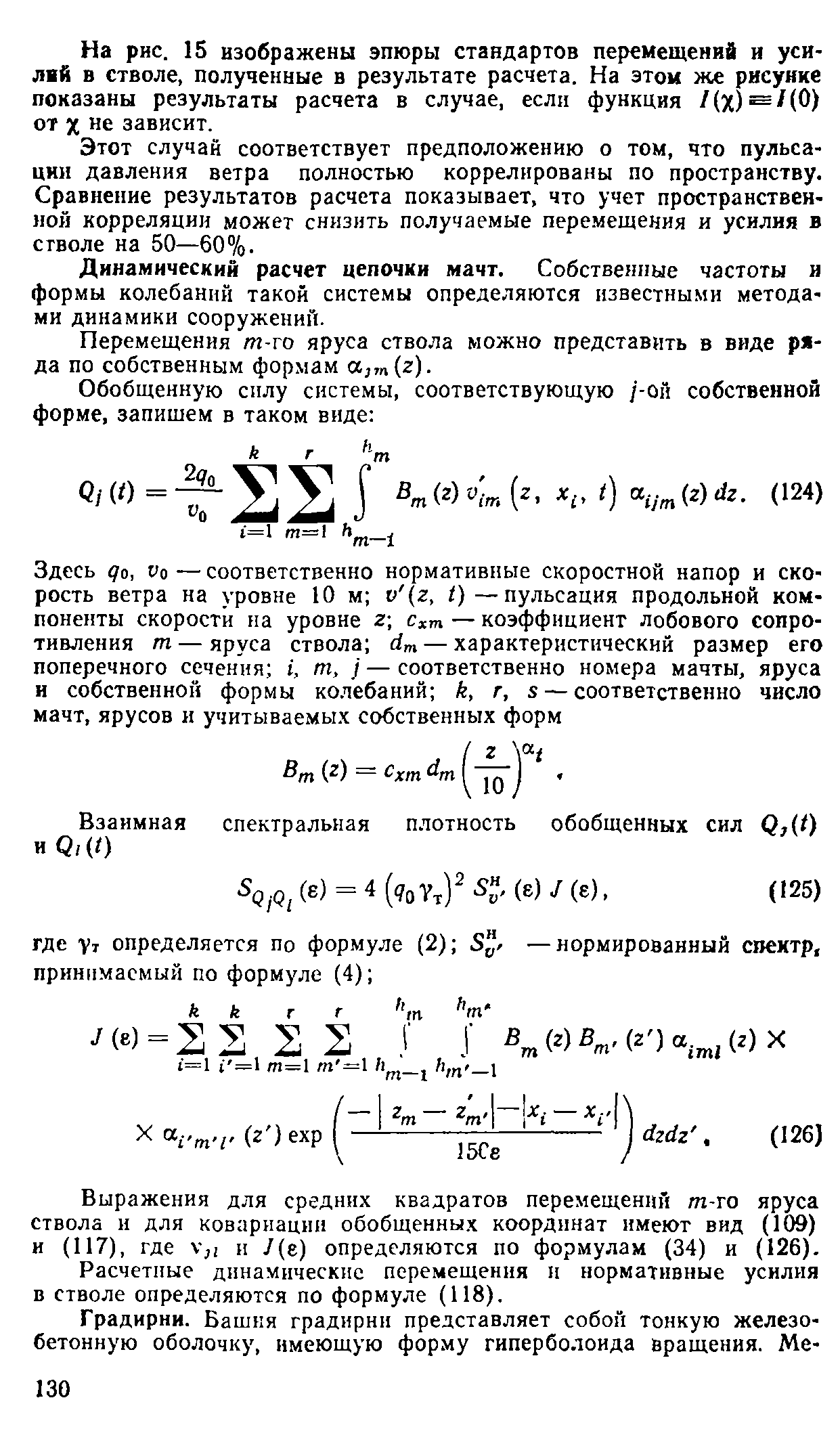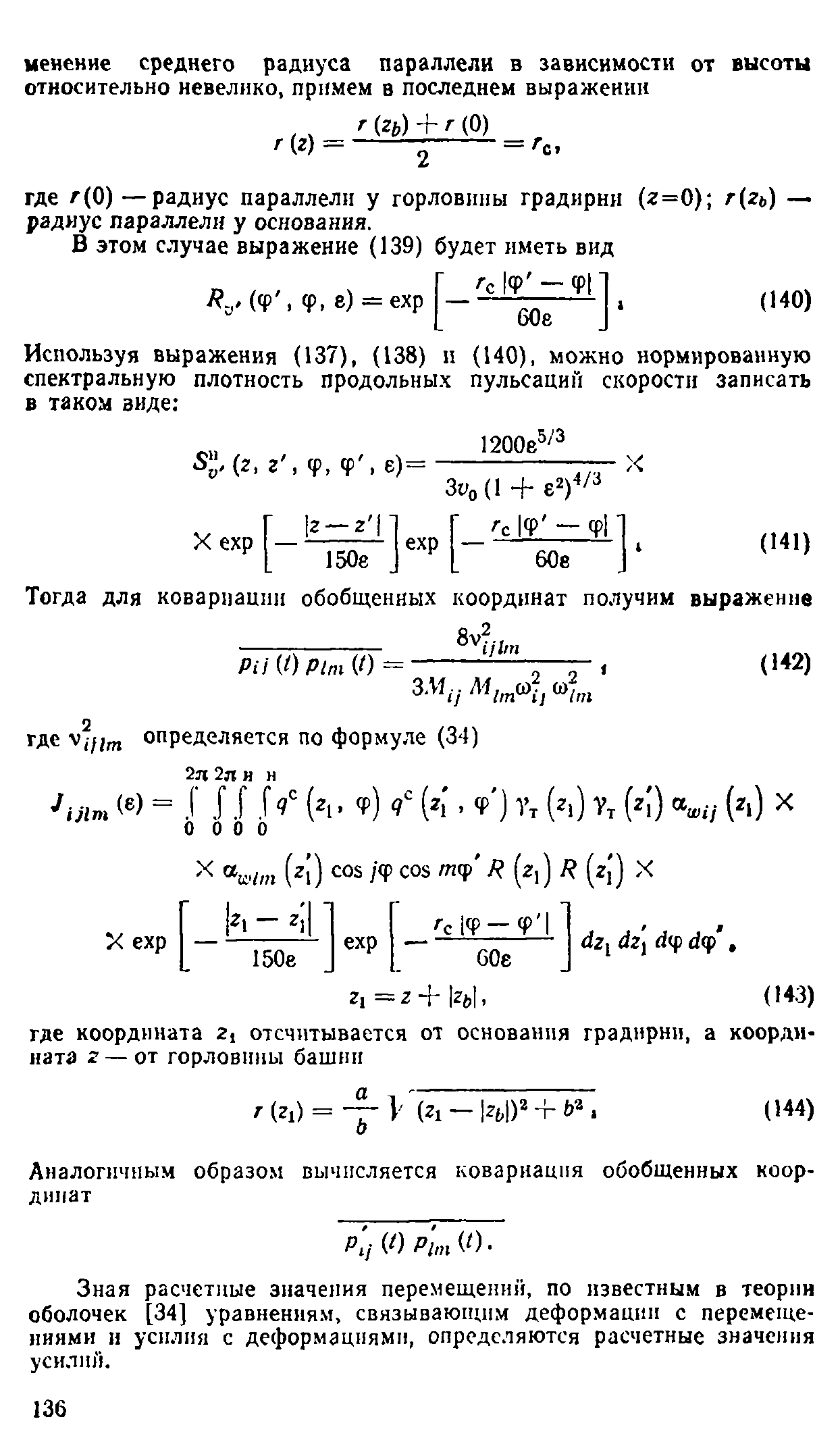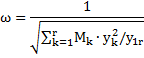| Найти: | |
| Где: | |
| Тип документа: | |
| Отображать: | |
| Упорядочить: |
Скачать Руководство Руководство по расчету зданий и сооружений на действие ветра
Дата актуализации: 01.01.2021

 Руководство
Руководство
Руководство по расчету зданий и сооружений на действие ветра
| Обозначение: |  Руководство Руководство |
| Обозначение англ: |  Guide Guide |
| Статус: | Действует |
| Название рус.: | Руководство по расчету зданий и сооружений на действие ветра |
| Дата добавления в базу: | 01.09.2013 |
| Дата актуализации: | 01.01.2021 |
| Область применения: | Руководство содержит рекомендации по определению ветровой нагрузки на здания и сооружения и указания по динамическому расчету высоких сооружений на действие ветра. В приложениях приведено обоснование основных положений и метода динамического расчета и даны примеры расчета зданий и сооружений на действие ветра. |
| Оглавление: | Предисловие 1. Общие положения 2. Нормативное значение статической составляющей ветровой нагрузки. Коэффициенты перегрузки 3. Нормативные скоростные напоры 4. Изменение скоростных напоров ветра по высоте 5. Ветровая нагрузка на здания, сооружения и конструкции 6. Динамический расчёт высоких сооружений и зданий на действие ветра 7. Аэродинамическая неустойчивость высоких сооружений и гибких конструкций 8. Большеразмерные стекла витрин Приложение 1. Приложение 2. Приложение 3. Приложение 4. Список литературы |
| Разработан: | ЦНИИСК им. В.А. Кучеренко |
| Расположен в: | Техническая документация Строительство Справочные документы Директивные письма, положения, рекомендации и др. |
| Нормативные ссылки: |
|
Особенности расчета металлических решетчатых башен на ветровую нагрузку
В статье рассматриваются некоторые аспекты определения ветровых нагрузок на металлические решетчатые башенные конструкции квадратные в плане, а также особенности расчета последних на ветровое воздействие в ПК ЛИРА-САПР
Определение величины ветровой нагрузки
Ветровую нагрузку следует определять как сумму средней wm и пульсационной wp составляющей. Нормативная величина ветровой нагрузки:
w = wm + wp
Средняя составляющая ветровой нагрузки
Нормативная величина средней составляющей ветровой нагрузки:
wm = w0*k*c
где w0 — нормативное значение ветрового давления; k — коэффициент, учитывающий изменение ветрового давления по высоте; с — аэродинамический коэффициент.
Аэродинамический коэффициент для решетчатых башен и пространственных ферм определяется по формуле:
Ct = Cx(1+η)k1
где Cx — аэродинамический коэффициент отдельностоящей плоской решетчатой конструкции:
Cx = ∑(Cxi*Ai)/Ak
Cxi — аэродинамический коэффициент i-го элемента конструкции; Ai — площадь проекции i-го элемента конструкции; Ak — площадь, ограниченная контуром конструкции.
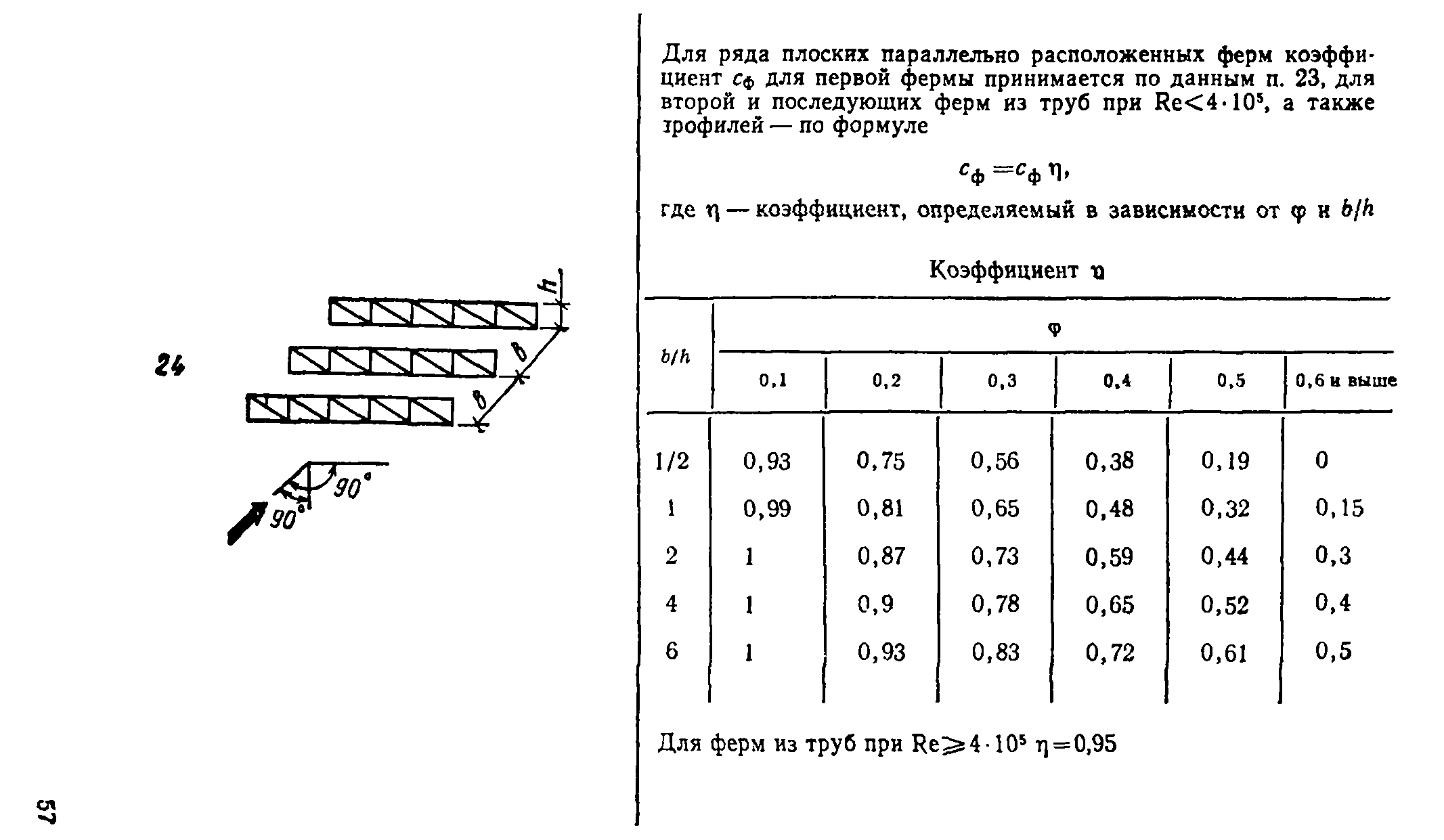
η — коэффициент, учитывающий давление ветра на подветренную грань. Определяется по табл. В.8 СП 20.13330.2016 в зависимости от относительного расстояния между фермами и коэффициента заполнения ферм.
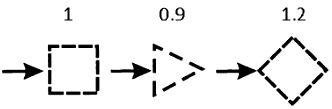
k1 — коэффициент, зависящий от контура поперечного сечения и направления ветра:
Рис. 1. Значение коэффициента k1 в зависимости от ориентации направления ветра по отношению к башне
При определении аэродинамического коэффициента решетчатой конструкции Ct принимается, что направление ветра всегда перпендикулярно грани башни:
Рис. 2. Направления ветра по отношению к башне при определении Ct
Таким образом, при определении Ct коэффициент Cx всегда определяется в предположение воздействия ветра на грань, а соответственно ACk — площадь контура грани вне зависимости от угла атаки ветровой нагрузки.
Переход к аэродинамическому коэффициенту Ct при действии ветра на диагональ осуществляется умножением Ct, вычисленного для грани, на коэффициент k1=1.2.
При определении средней составляющей ветровой нагрузки башня разбивается на конечное количество расчетных полей. Далее для каждого расчетного поля определяется площадь, ограниченная контуром Ak; определяется суммарная площадь проекции элементов башни Ai; определяются аэродинамические коэффициенты элементов башни Cxi; определяются коэффициенты Cx, φ, η, k1; определяется аэродинамический коэффициент для решетчатых башен Ct; вычисляется статическая составляющая ветровой нагрузки.
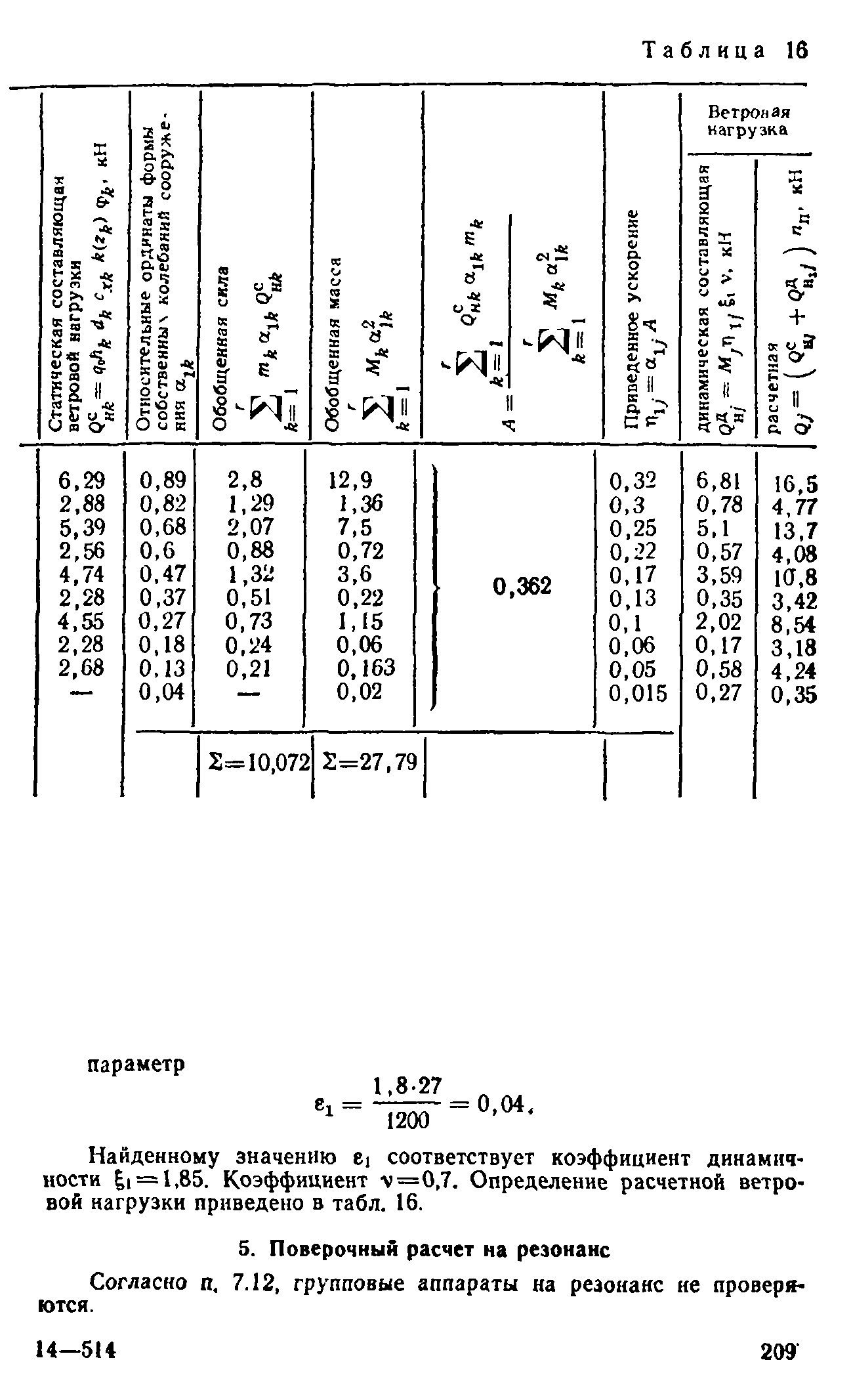
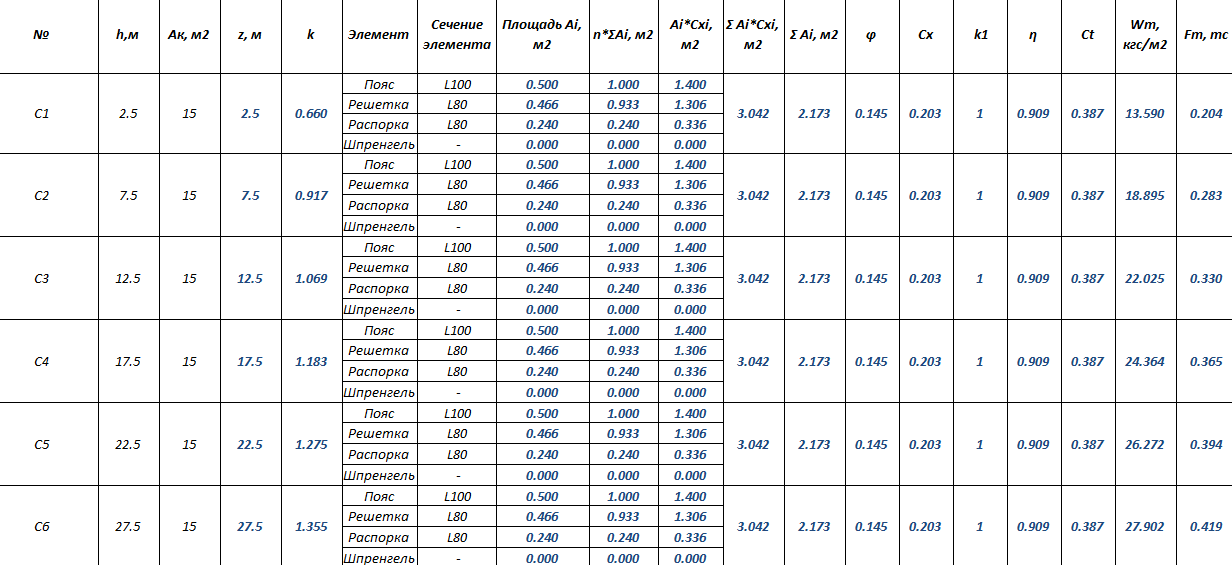
Вычисления удобно выполнять в табличном виде по следующему типу:
Рис. 3. Фрагмент таблицы определения статической составляющей ветровой нагрузки
Пульсационная составляющая ветровой нагрузки
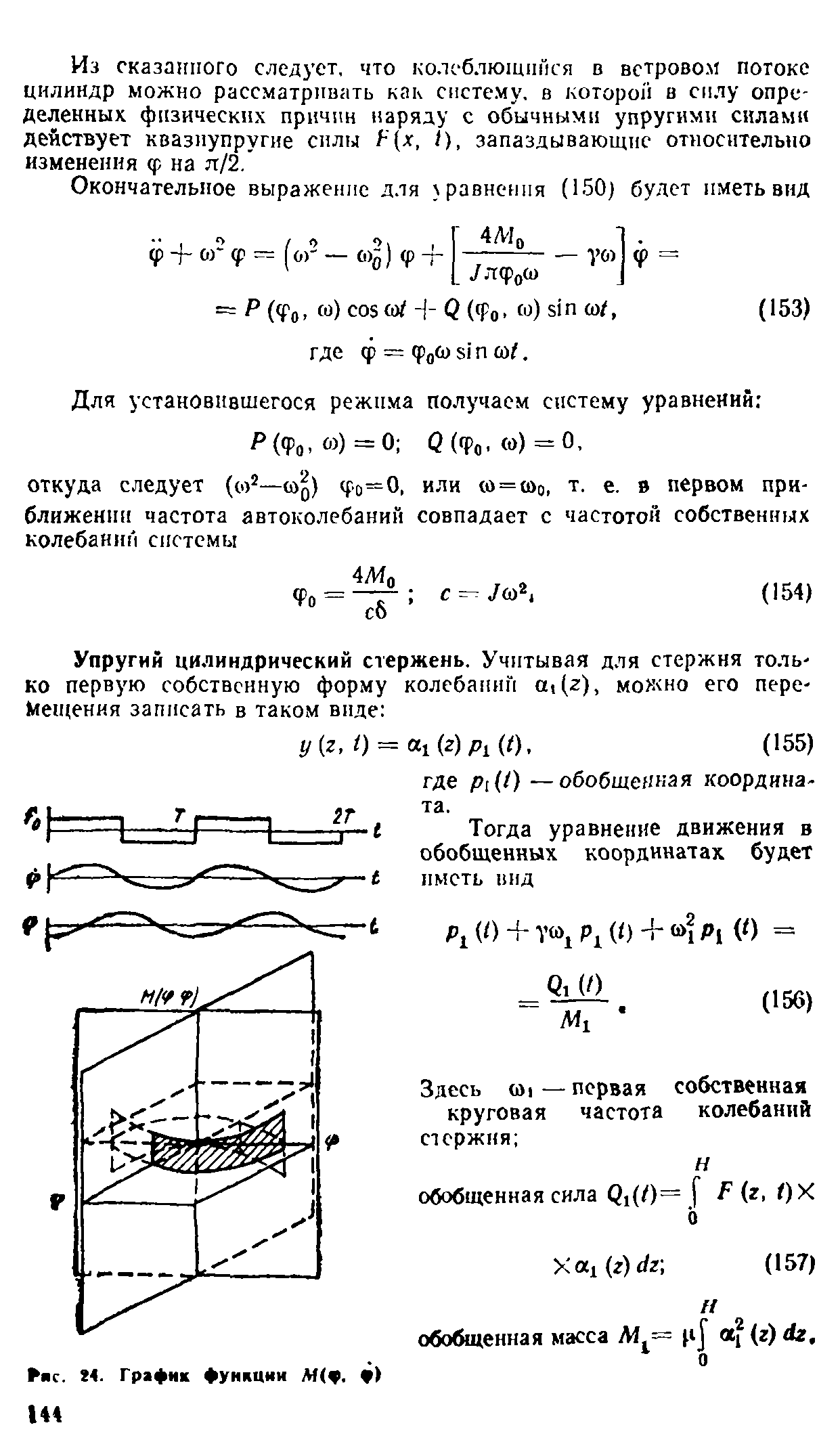
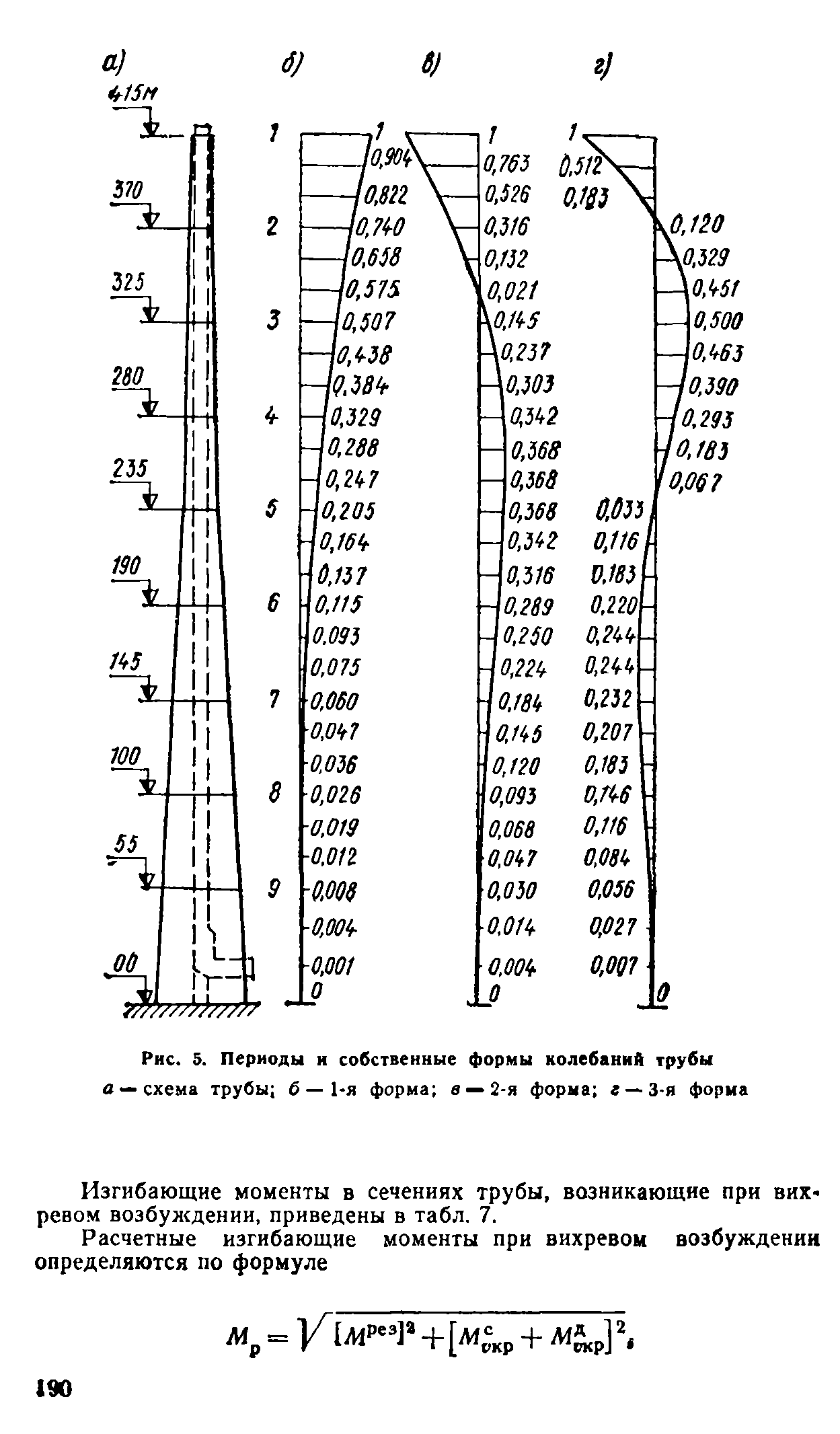
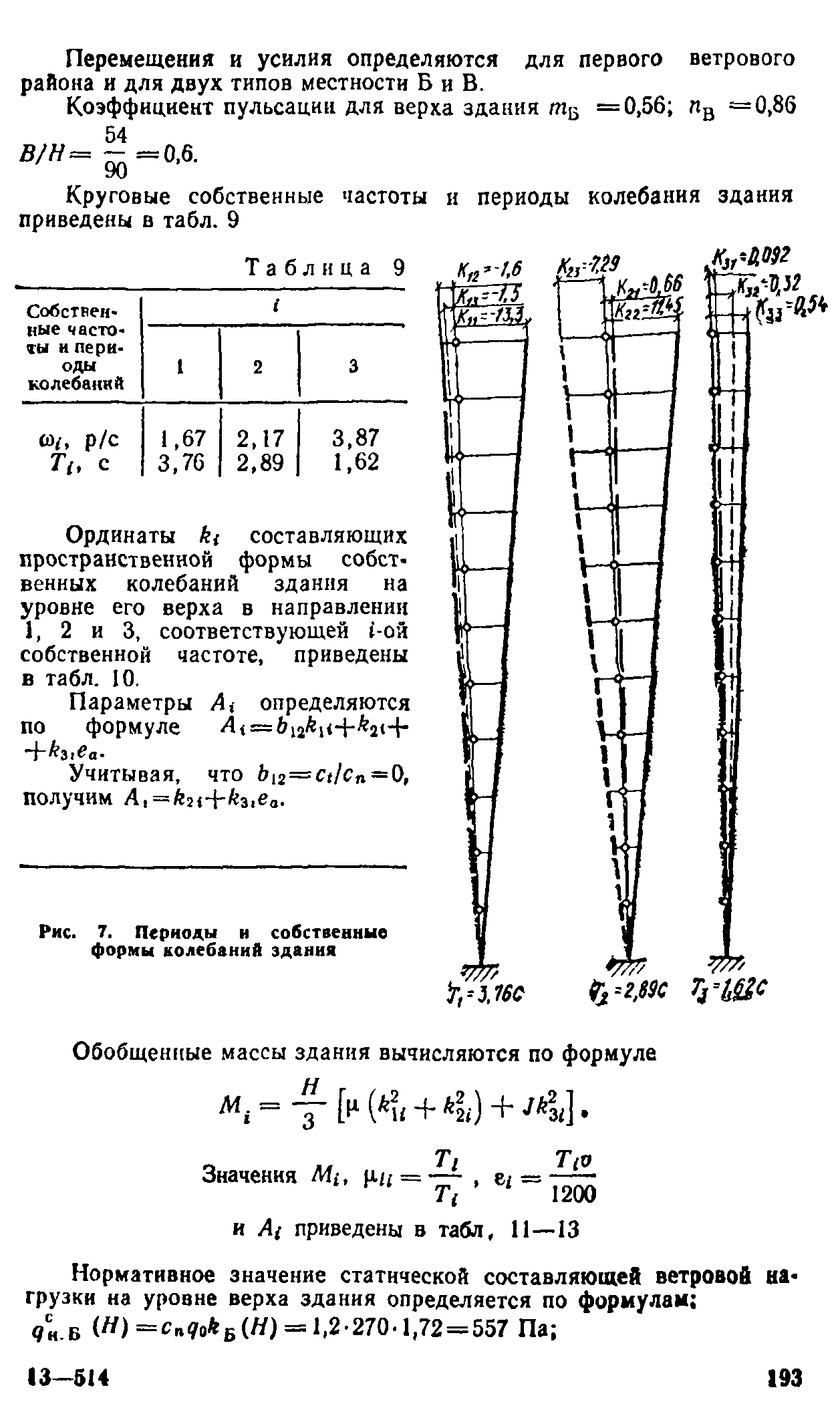
При определении пульсационной составляющей ветровой нагрузки нужно знать собственные формы и частоты колебаний башни.
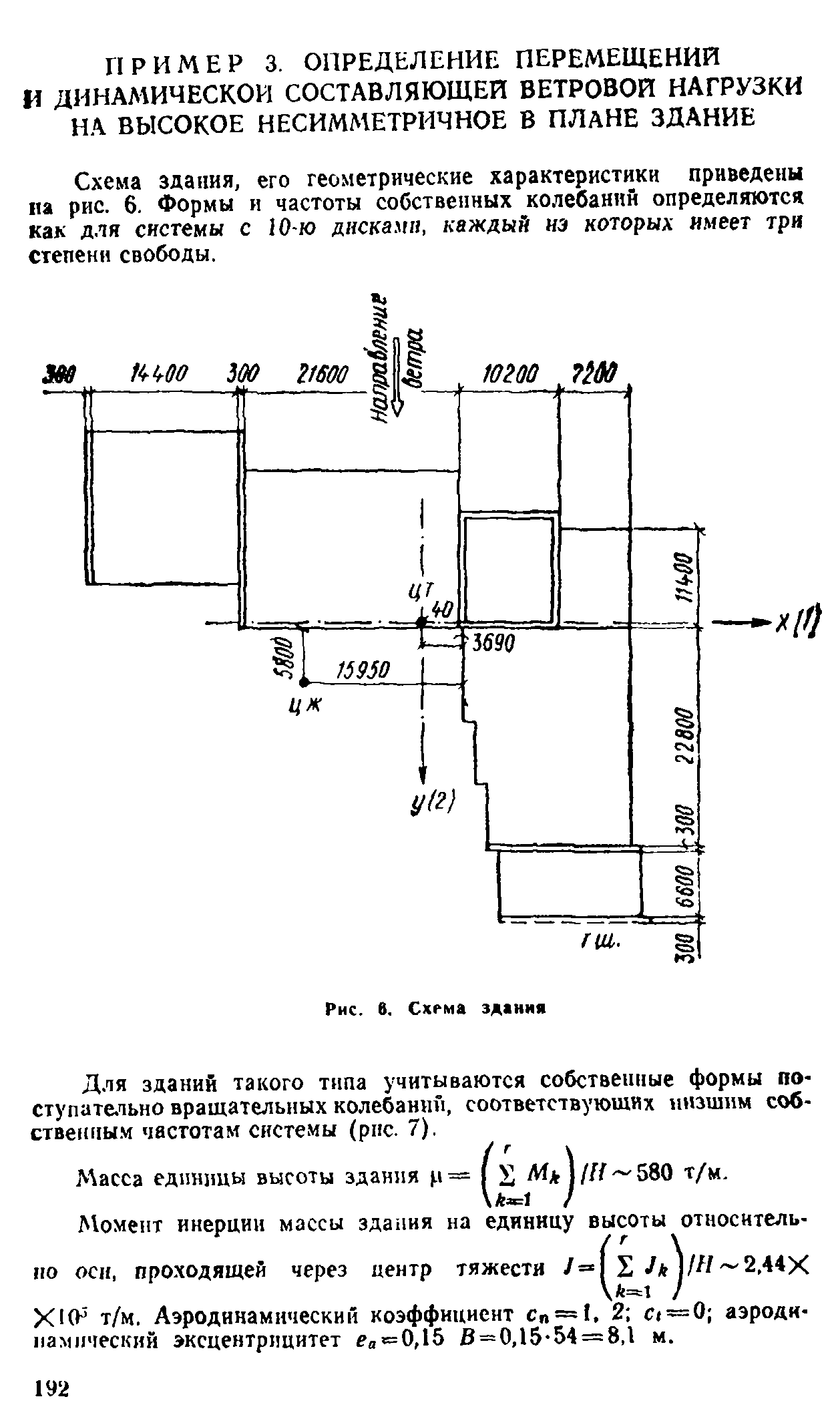
Известно, что круговая частота колебаний может быть определена по формуле ω=√(k/m), где k и m – соответственно жесткость и масса. Жесткость зависит от момента инерции башни. Для квадратных в плане башен момент инерции при действии ветра на диагональ и на грань одинаковые:
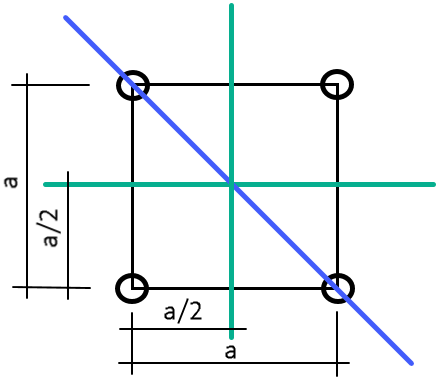
- момент инерции поперечного сечения башни при площади пояса A и размере башни в плане а относительно оси, параллельной грани (зеленой):
Рис. 4. Схема поперечного сечения ствола башни
- момент инерции поперечного сечения башни относительно оси, проходящей через диагональ (синей):
Таким образом, при ветре на диагональ и на грань у квадратной башни одинаковые коэффициент динамичности и ординаты форм колебаний. Поэтому для определения пульсационной составляющей ветровой нагрузки достаточно вычислить частотные характеристики в направлении осей инерции башни, параллельных грани.
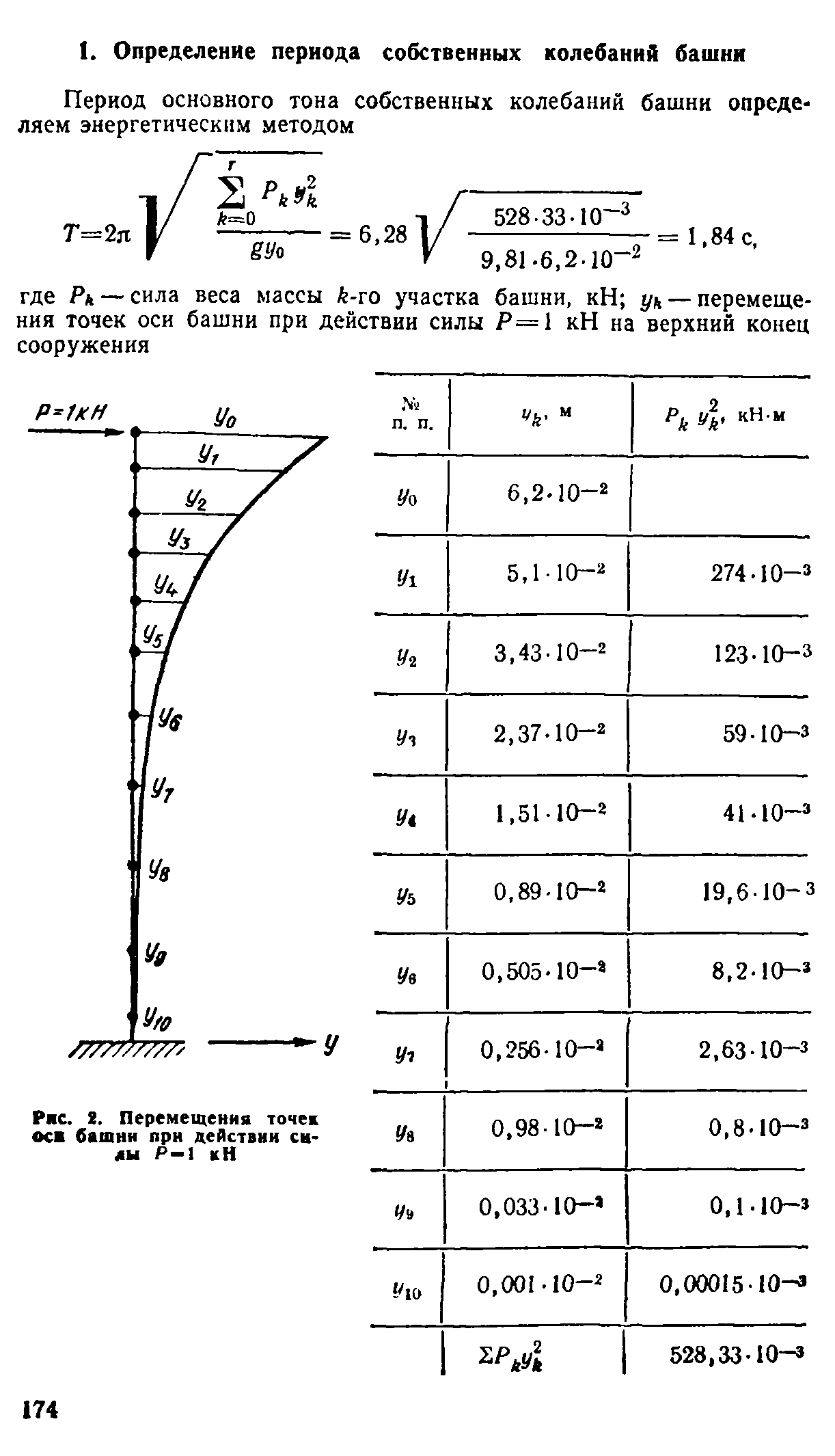
В практике проектирования прежних лет пульсационная составляющая ветровой нагрузки определялась только от основной формы колебаний с круговой частотой:
где yk — перемещение точек оси башни при действии единичной силы, приложенной в уровне ее верха; Mk — приведенная к точке масса соответствующего участка башни; y1r — перемещение верха башни от единичной нагрузки.
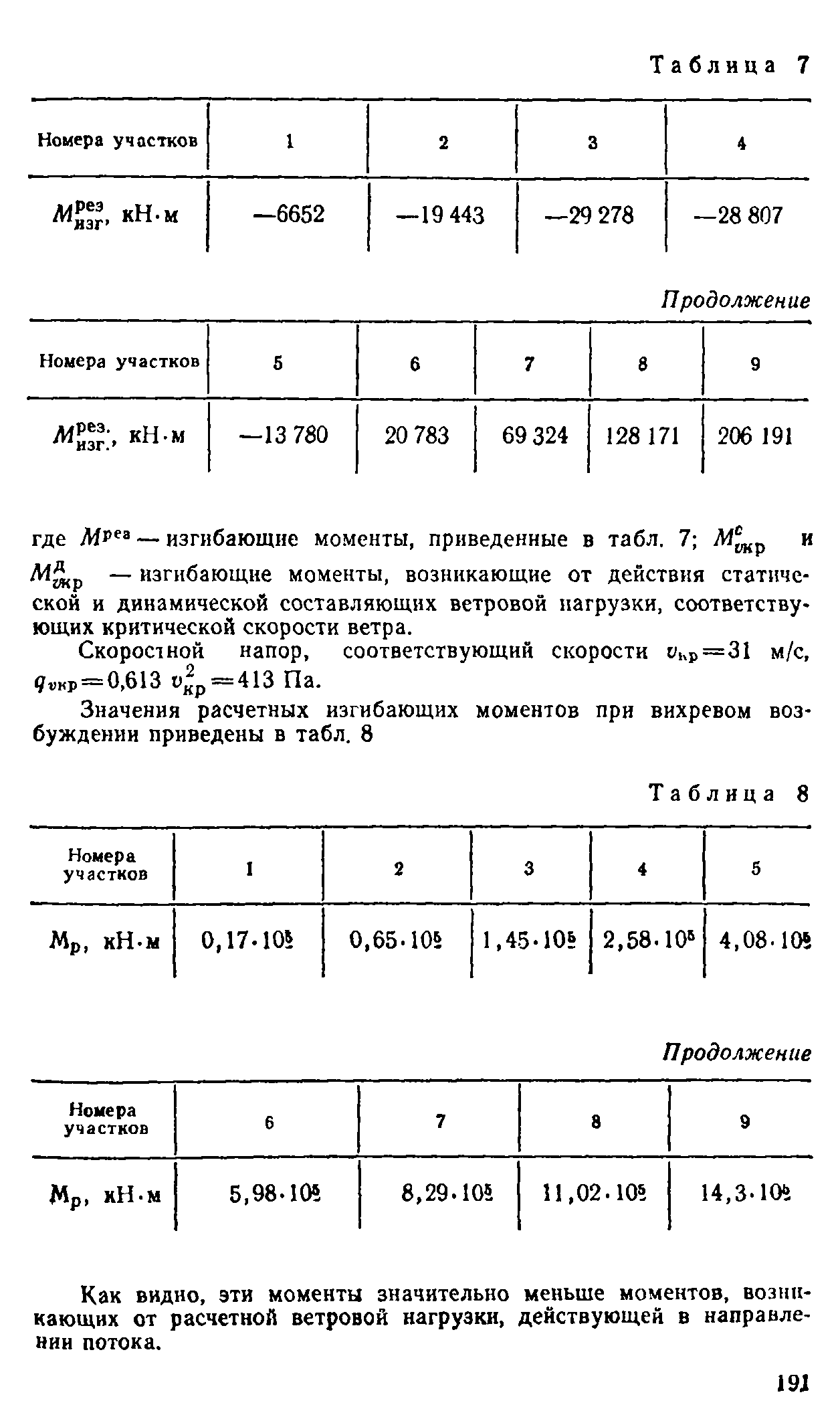
Пульсационная составляющая ветровой нагрузки в общем случае (динамический анализ) определяется по формуле:
где m — масса башни на уровне Z, отнесенная к площади поверхности, к которой приложена ветровая нагрузка; ξ — коэффициент динамичности (зависит от линейной частоты колебаний f=ω/2π); y — горизонтальное перемещение на уровне Z по форме собственных колебаний; ψ — коэффициент, определяется по формуле:
где Mk — масса k-го участка башни; yk — горизонтальное перемещение центра k-го участка (ордината формы колебаний); wpk — равнодействующая пульсационной составляющей ветровой нагрузки на k-й участок:
где ζ — коэффициент пульсаций давления ветра на уровне Z; ν — коэффициент пространственной корреляции пульсаций давления ветра.
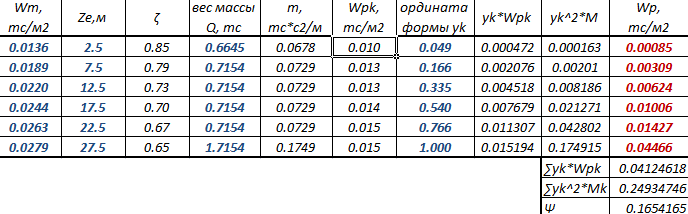
Вычисления удобно выполнять в табличном виде по следующему типу:
Рис. 5. Фрагмент таблицы определения пульсационной составляющей ветровой нагрузки
После определения средней (статической) и пульсационной составляющей ветровой нагрузки, определяется полная ветровая нагрузка w=wm+wp. К расчетной модели ветровая нагрузка обычно прикладывается в виде сосредоточенных сил Fi в уровне пересечения поясов с элементами решетки (Fi=w*Ak/n, где n — число узлов).
Далее выполняется определение усилий в элементах башни.
Ветровая нагрузка на металлическую башню должна быть приложена в 2х вариантах — на грань (для определения усилий в решетке) и на диагональ (для определения усилий в поясах).
Усилия в элементах поясов и нагрузки на фундамент квадратной башни при действии ветровой нагрузки определяются от момента Мд и силы Qд – момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на диагональ. При этом усилия в поясах, лежащих на диагонали (поперечной/перпендикулярной ветру), равны нулю, а усилия в поясах по направлению ветровой нагрузки равны между собой по абсолютной величине, но разные по знаку
Усилия в элементах решетки определяются при действии ветровой нагрузки от Мг и Qг — момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на грань.
Пример расчета башни на полную ветровую нагрузку определенную «ручным» способом
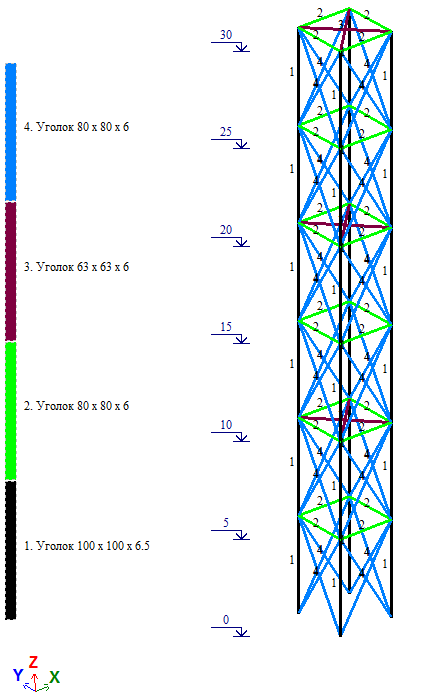
Рассмотрим башню с параллельными поясами высотой 30м. Размер в плане а=3х3м.
Рис. 6. Расчетная модель башни
Нагрузки на башню:
- собственный вес;
- вес оборудования 1тс в уровне верха башни (0.25тс в узел);
- ветер полный на грань;
- ветер полный на диагональ.
Ветровая нагрузка прикладывается как узловая в уровне верха расчетного поля. Величина полной ветровой нагрузки складывается из статической и пульсационной составляющих. Рассматривается 6 расчетных полей по высоте.
Табл. 1
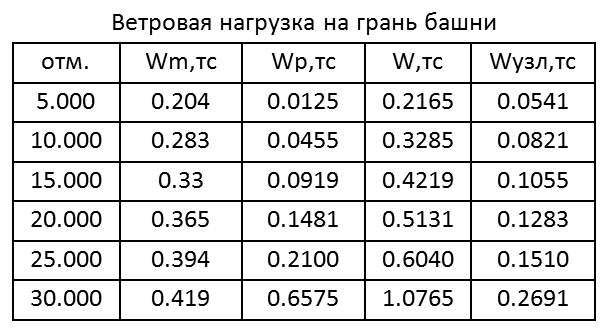
Табл. 2
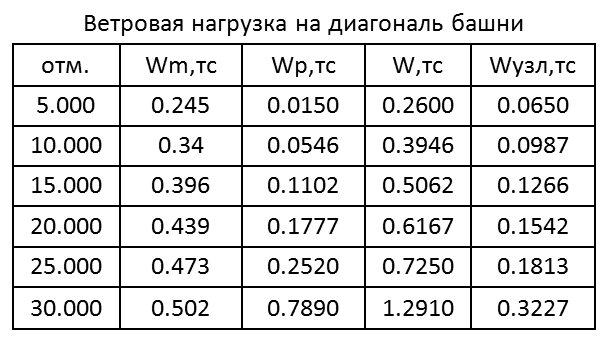
Рис. 7. Схема приложения нагрузок на ствол башни при действии ветра на грань
Рис. 8. Схема приложения нагрузок на ствол башни при действии ветра на диагональ
Ветровая нагрузка на диагональ прикладывается в виде составляющих Х и Y: W(x,y)=W*cos45⁰.
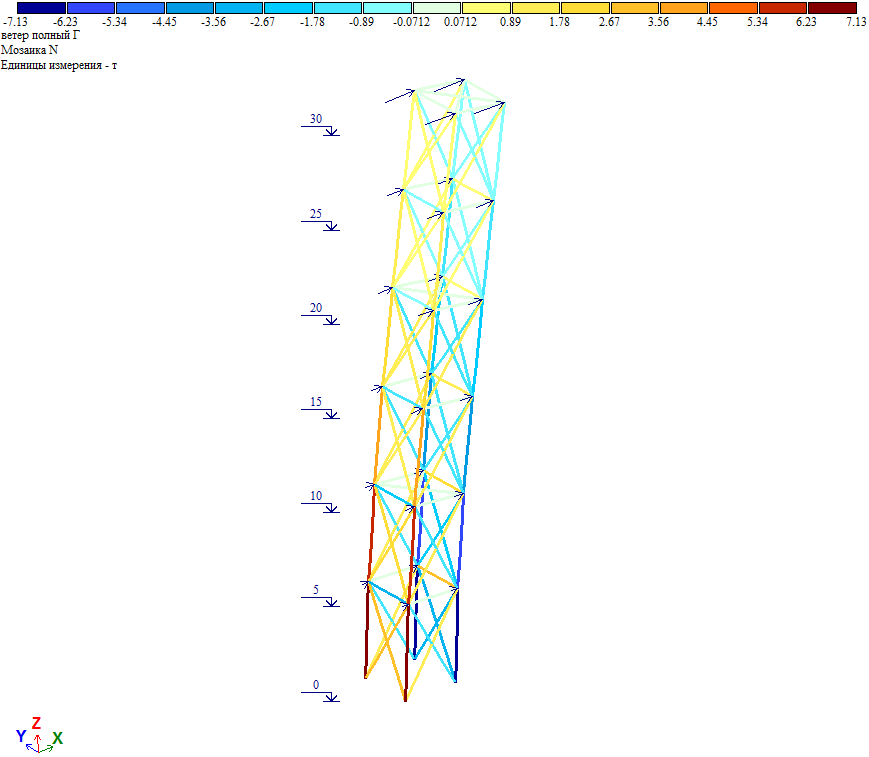
Усилия в элементах башни при действии ветровой нагрузки на грань.
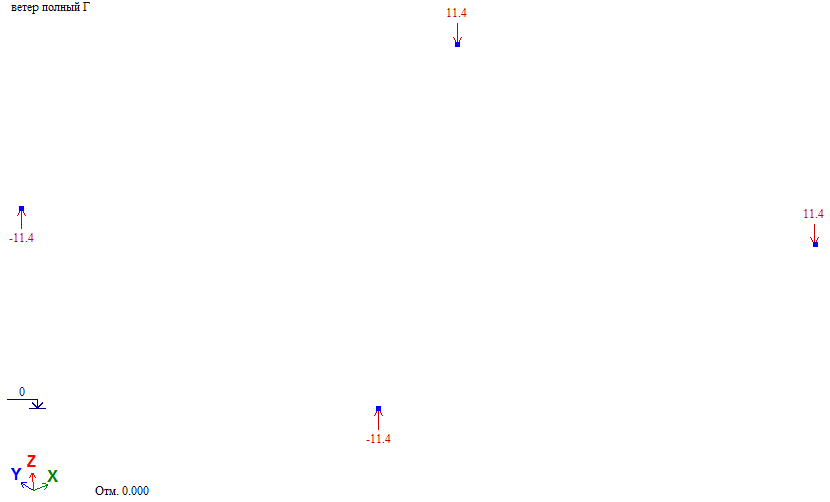
Рис. 9. Усилия от полной ветровой нагрузки при действии ветра на грань
Проверка. Общий момент в основании башни Мг=∑Wiг*Zi=68.35тс*м. Нагрузка на фундамент F=(Мг/а)/2=(68.35/3)/2=11.39тс
Рис. 10. Нагрузки на фрагмент для опорных узлов башни при действии ветра на грань
Как видно результаты программного и «ручного» определения нагрузок на фундаменты сходятся.
Усилия в элементах башни при действии ветровой нагрузки на диагональ.
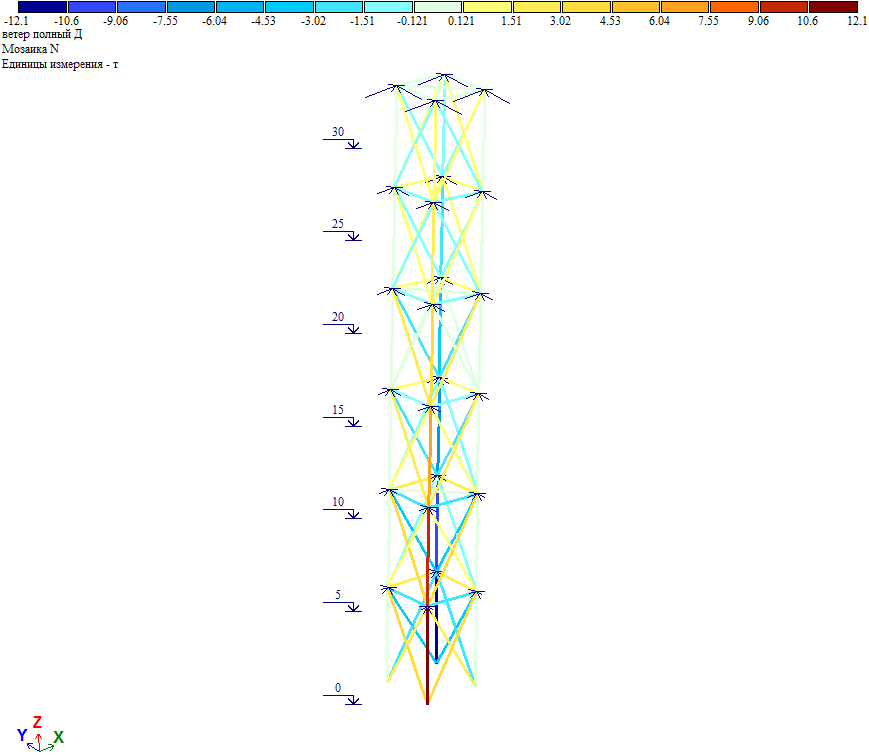
Рис. 11. Усилия от полной ветровой нагрузки при действии ветра на диагональ
Проверка. Общий момент в основании башни Мд=∑Wiд*Zi=82тс*м. Нагрузка на фундамент F=(Мд/а*√2)=(82/3*1.414)=19.33тс
Нагрузки на фрагмент в основании башни:
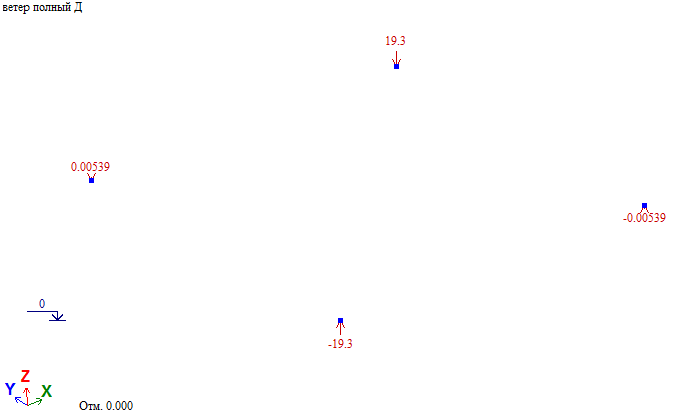
Рис. 12. Нагрузки на фрагмент для опорных узлов башни при действии ветра на диагональ
Моделирование воздействия ветра в ЛИРА-САПР
При конечноэлементном моделировании башня представляется пространственной фермой. Т.к. жесткость и масса конструкции величины не зависимые от внешней нагрузки, то при определении собственных форм и частот колебаний для разных пульсационных загружений имеет место случай кратных форм колебаний, т.е. форм с одинаковой частотой.
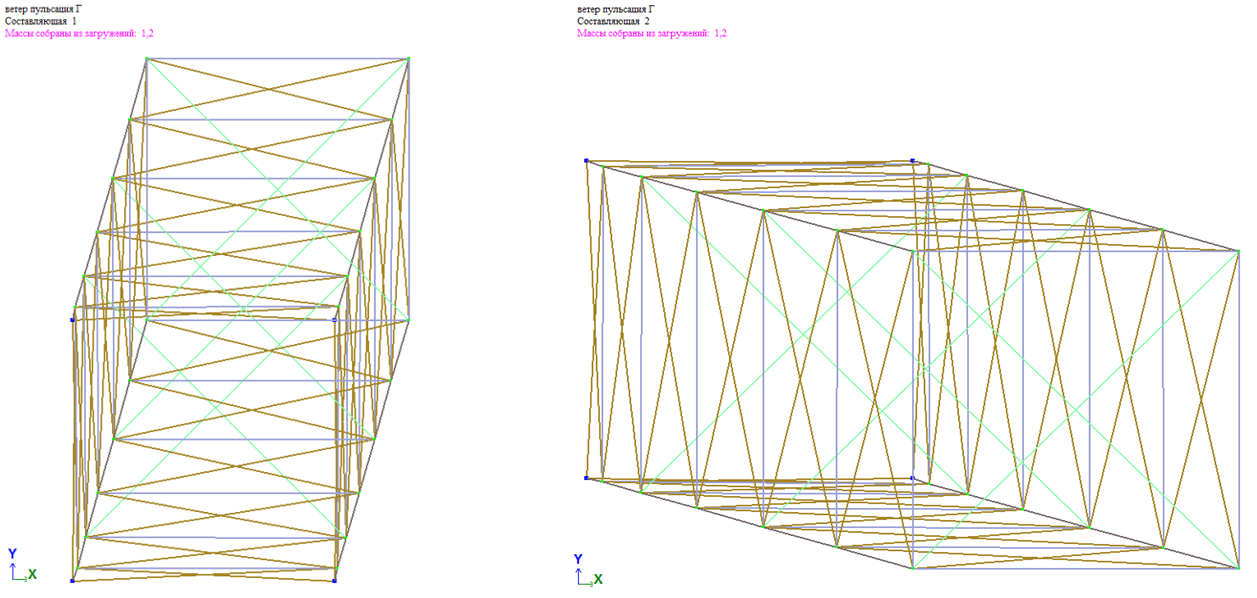
Если частотное уравнение имеет кратные формы, условие ортогональности форм (вдоль граней башни, в данном случае вдоль глобальных осей Х и У) не справедливо. В этом случае существует целое семейство векторов, любая пара из которых может служить собственными векторами для кратных частот. Эта пара будет ортогональна друг другу, но произвольно повернута вокруг вертикально оси башни:
Рис. 13. Пример кратных форм колебаний
Т.к. ординаты форм колебаний учитываются при определении величины пульсационной составляющей ветровой нагрузки, то в случае кратных форм последняя будет зависеть от угла поворота перемещения по кратным формам относительно главных осей сооружения. Если учесть, что угол поворота кратных форм величина случайная, то прогнозировать правильность результатов сложно. В данном случае возможно как уменьшение, так и увеличения вклада ветровой пульсации в усилия в элементах схемы.
Правильный результат будет получен в случае совпадения направления перемещений по одной из кратных форм с направлением ветровой нагрузки.
Для борьбы с кратными формами колебаний применяют разные подходы. Наиболее распространенные из них – изменение геометрии (жесткости) или масс. К примеру, в справке к ПК Abaqus написано:
| «In cases with repeated eigenvalues and eigenvectors, the modal summation results must be interpreted with care. You should add insignificant mass to the structure or perturb the symmetric geometry such that the eigenvalues become unique» | «В случаях с повторяющимися собственными значениями и собственными векторами результаты модального суммирования должны интерпретироваться с осторожностью. Вы должны добавить несущественную массу к конструкции или нарушить симметричную геометрию, чтобы собственные значения стали уникальными» |
При изменении геометрии башня создается прямоугольного сечения с размерами а и k*a (k принимается 1.01-1.05). При изменении масс по одному из направлений прикладываются дополнительные массы (0.01-0.05 от общей массы сооружения по данному направлению).
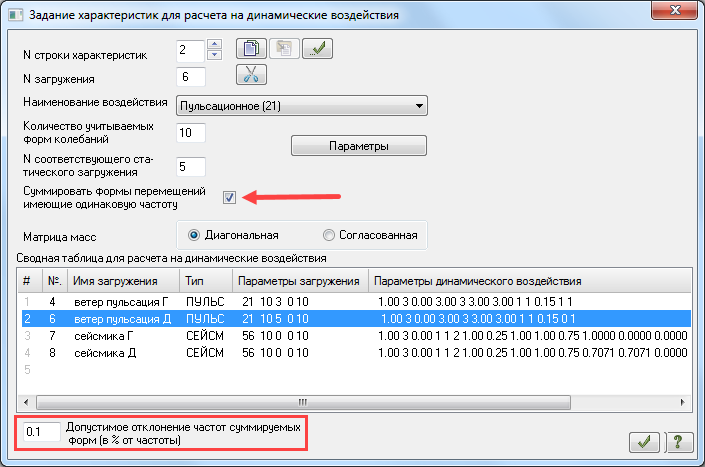
В ЛИРА-САПР версии 2018 появился новый инструмент Суммирование кратных форм. В случае ветровой пульсации направление итоговой формы колебаний принимается по направлению статической составляющей ветровой нагрузки. Так при ветре, заданном на грань, суммарная форма перемещений также будет на грань. При направлении ветра на диагональ, заданном через 2 составляющие вдоль осей X и Y, итоговое направление формы перемещений будет по направлению равнодействующей, т.е. тоже на диагональ.
Рис. 14. Диалог задание характеристик для расчета на динамические воздействия версии 2018
Ниже будут показаны варианты расчета башни на действие пульсационной составляющей ветровой нагрузки с учетом суммирования по формам колебаний и без него. Сравниваться будет НДС схемы при определении величины ветровой пульсации «ручным» способом (см. выше) и программно.
Суммирование кратных форм
К башне, описанной выше, прикладывается статическая составляющая ветровой нагрузки. Пульсационная составляющая определяется программно.
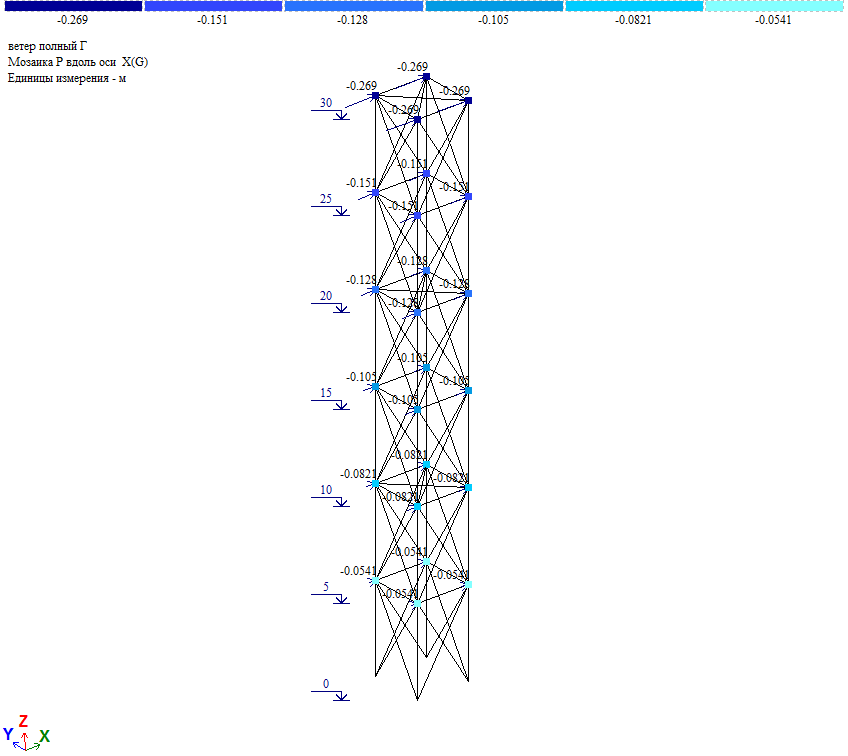
Ветер на грань.
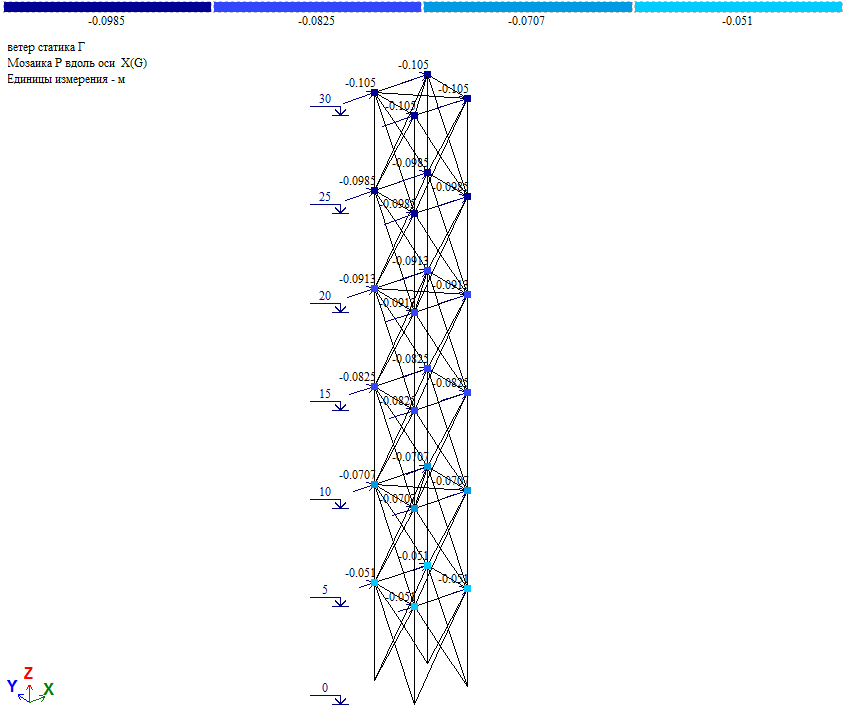
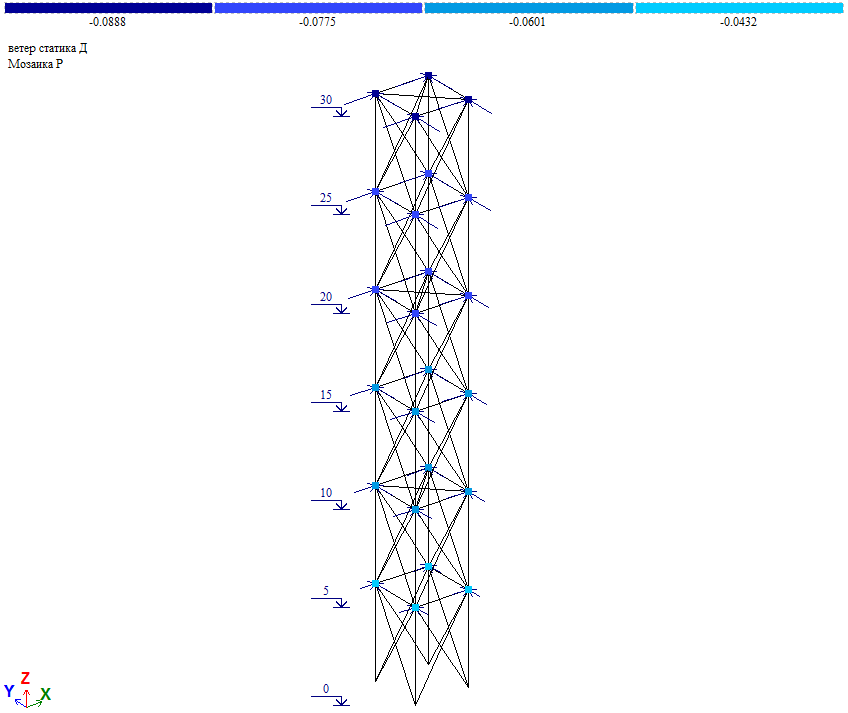
Рис. 15. Схема приложения средней ветровой нагрузки на ствол башни при действии ветра на грань
Величина узловой нагрузки Wm/4 (Wm см. таблицу 2).
Пульсационная составляющая по результатам расчета:
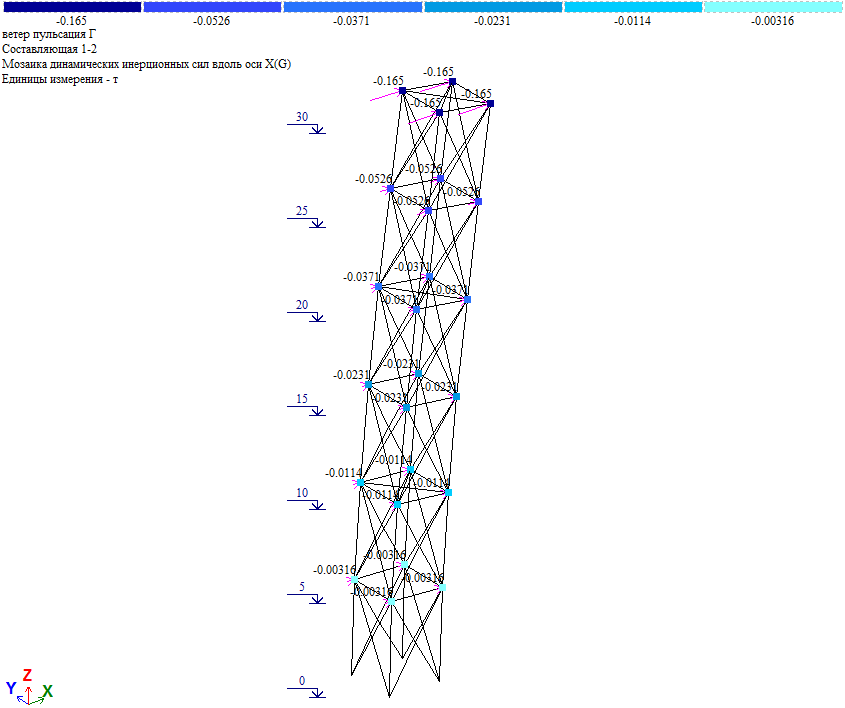
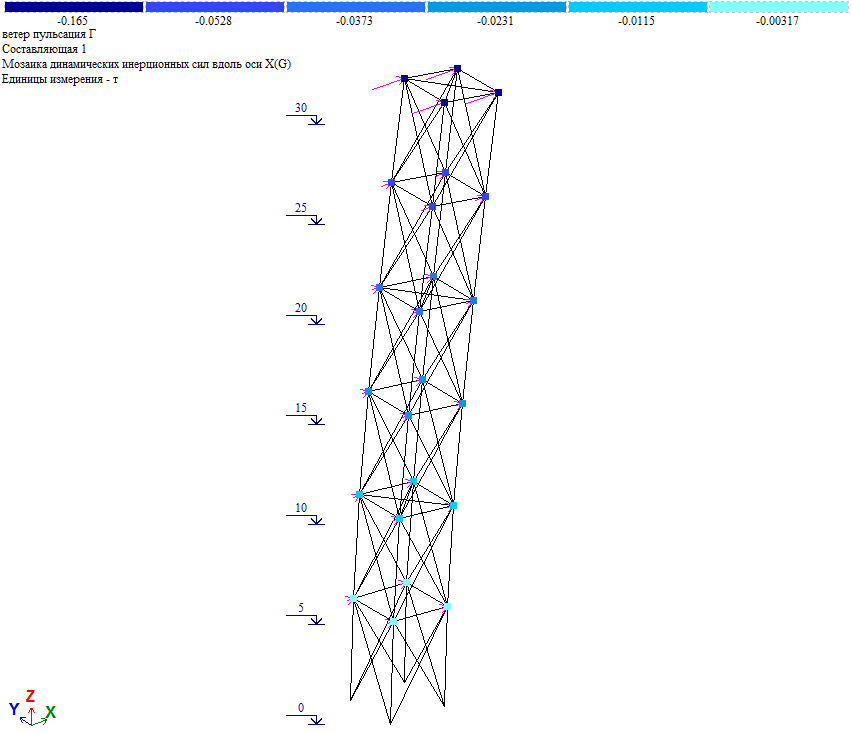
Рис. 16. Пульсационная составляющая ветровой нагрузки при действии ветра на грань
Пульсационная составляющая в уровне отм. +30.000 Wp=0.165*4=0.66тс, что близко к величине нагрузки в таблице 1 (Wp=0.6575тс). Т.е. результаты «ручного» и программного расчета совпадают.
Усилия в элементах башни от полной ветровой нагрузки на грань (получено через РСН):
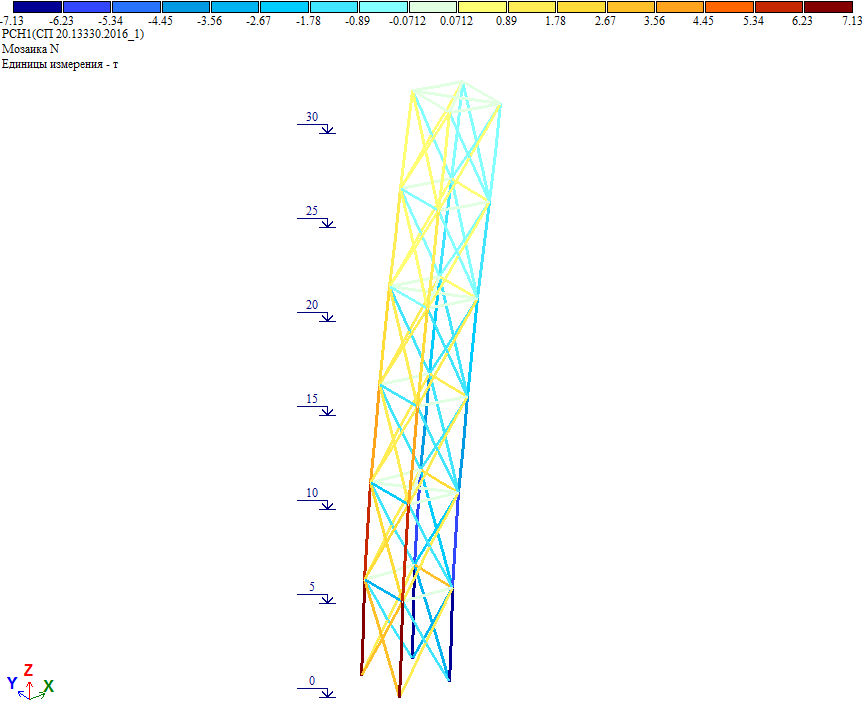
Рис. 17. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на грань
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на грань, определенная «вручную» и приложенная единой нагрузкой.
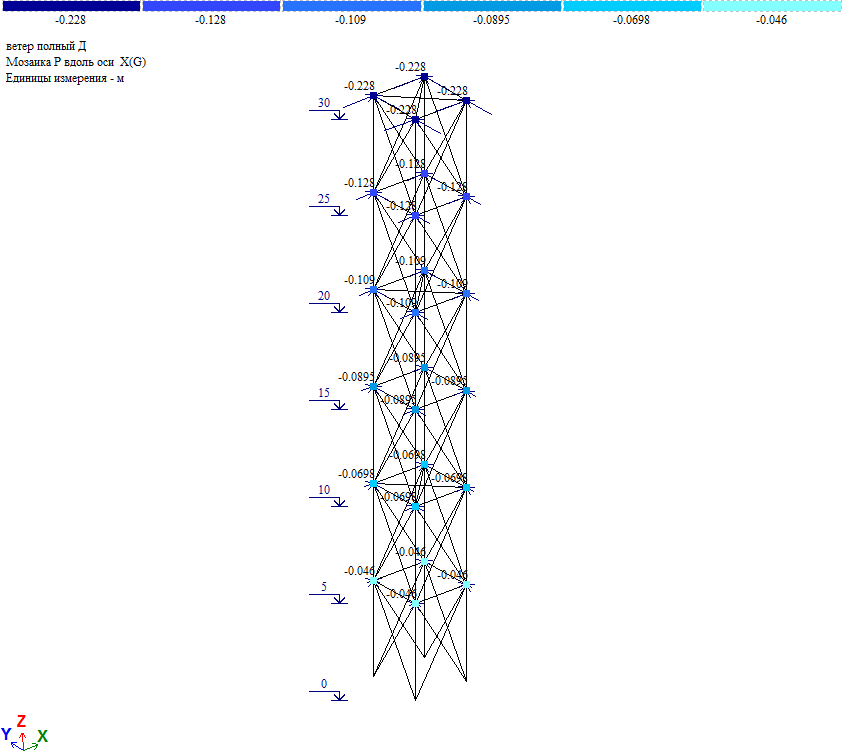
Ветер на диагональ.
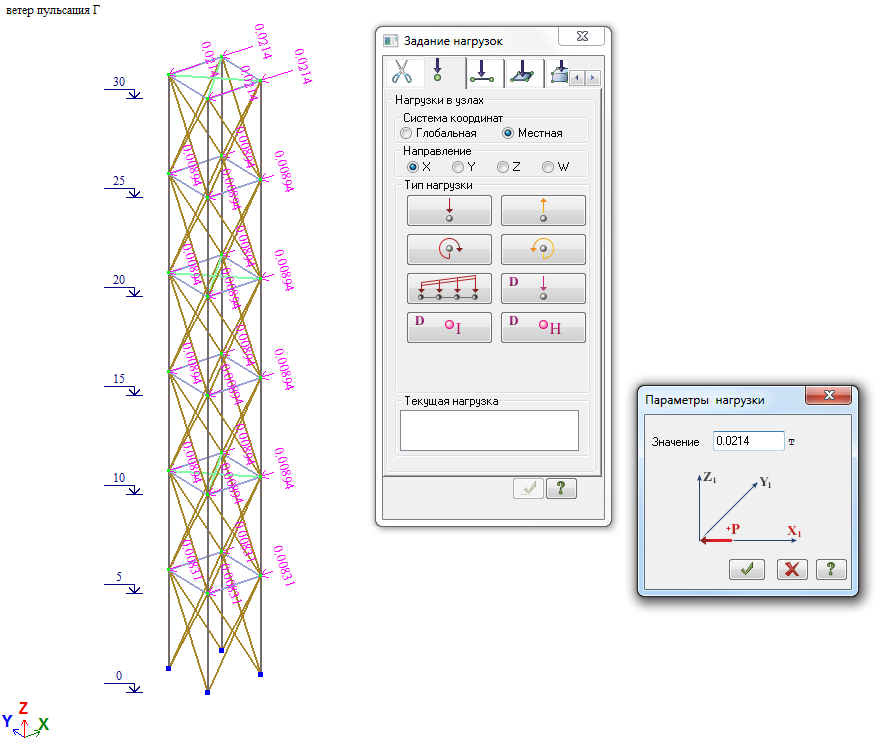
Рис. 18. Схема приложения средней ветровой нагрузки на ствол башни при действии ветра на диагональ
Величина узловой нагрузки (Wm/4)*cos45⁰ (Wm см. таблицу 2).
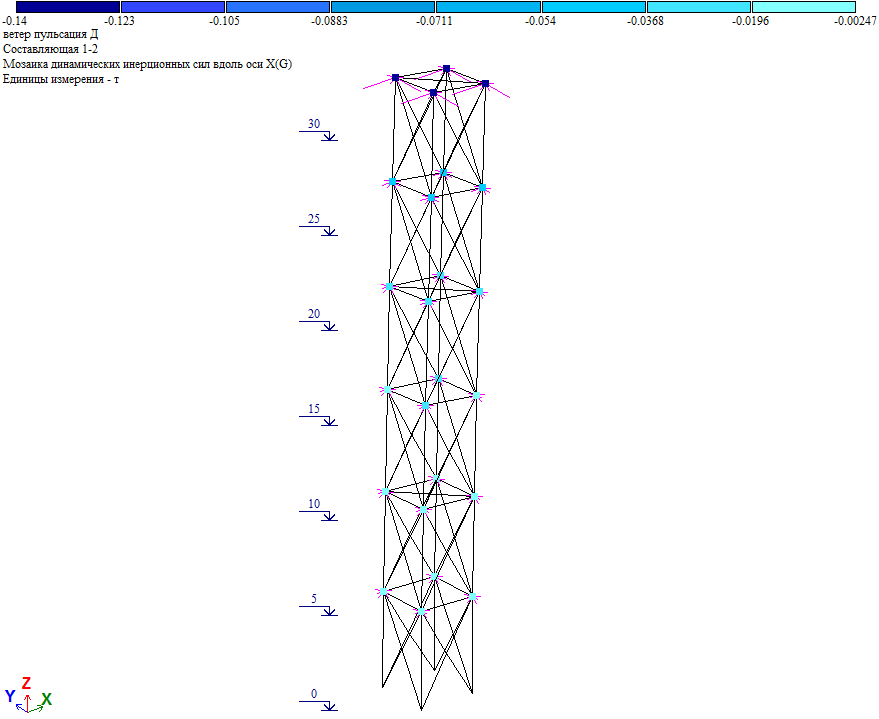
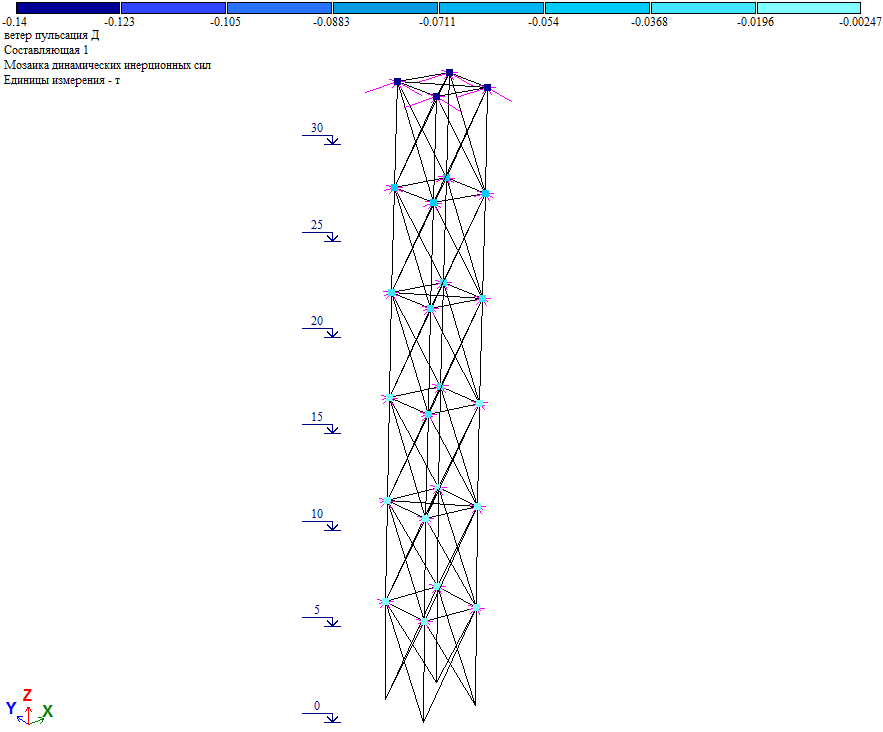
Рис. 19. Пульсационная составляющая ветровой нагрузки при действии ветра на диагональ
Пульсационная составляющая в уровне отм. +30.000 Wp=Wpx/cos45⁰=(0.14*4)/0.7071=0.792тс, что близко к величине нагрузки в таблице 2 (Wp=0.789тс). Т.е. результаты «ручного» и программного расчета совпадают.
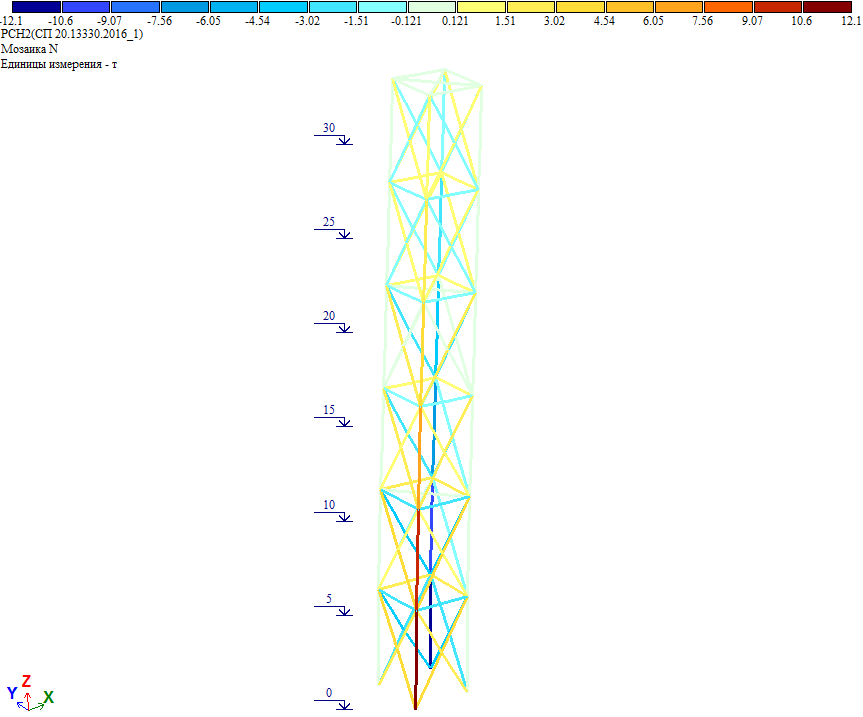
Усилия в элементах башни от полной ветровой нагрузки на диагональ:
Рис. 20. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на диагональ
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на диагональ.
«Управление» кратными формами
При расчете башни без использования функции «Суммировать формы перемещений» кратными формами колебаний следует управлять, чтобы получить ожидаемый результат. Так при ветре на грань следует задать дополнительные веса масс по направлению воздействия ветровой нагрузки:
Рис. 21. Дополнительные узловые веса масс для действия ветра на грань
Величина дополнительных весов масс принимается 0.01-0.05 от общего веса массы сооружения по данному направлению.
Величина суммарной массы представлена в протоколе решения задачи. Т.к. к схеме прикладывается нагрузка вес массы, то массу из протокола расчета следует увеличить в g раз.
В примере выше для каждого уровня принята величина дополнительной массы, пропорциональная массе сооружения на данном уровне.
Рис. 22. Пульсационная составляющая ветровой нагрузки при действии ветра на грань
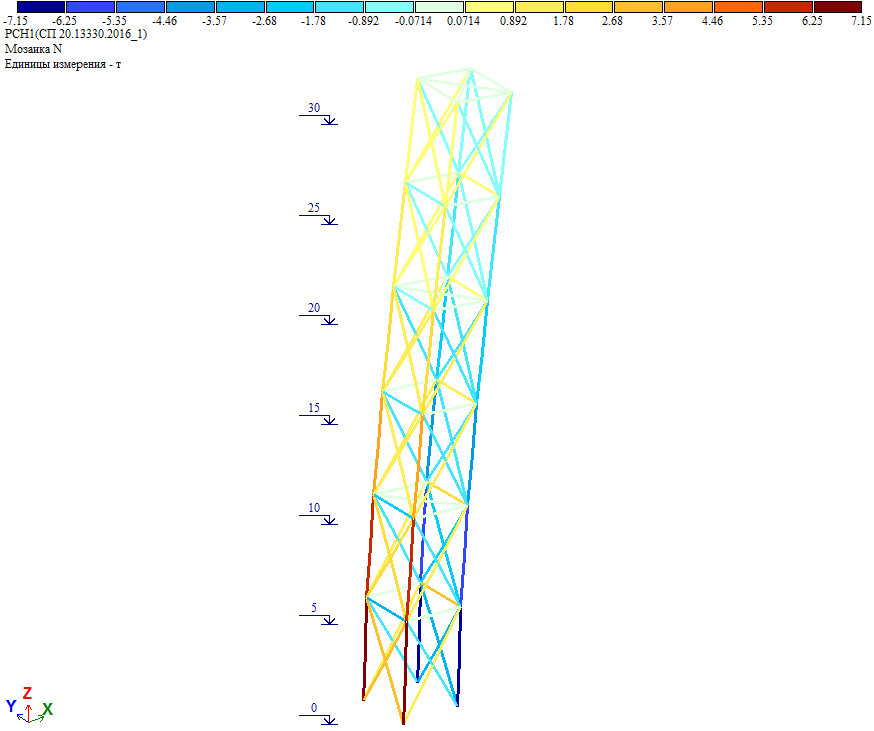
Рис. 23. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на грань
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия. Максимальное продольное усилие увеличилось на 100%*(7.15-7.13)/7.13=0.28%.
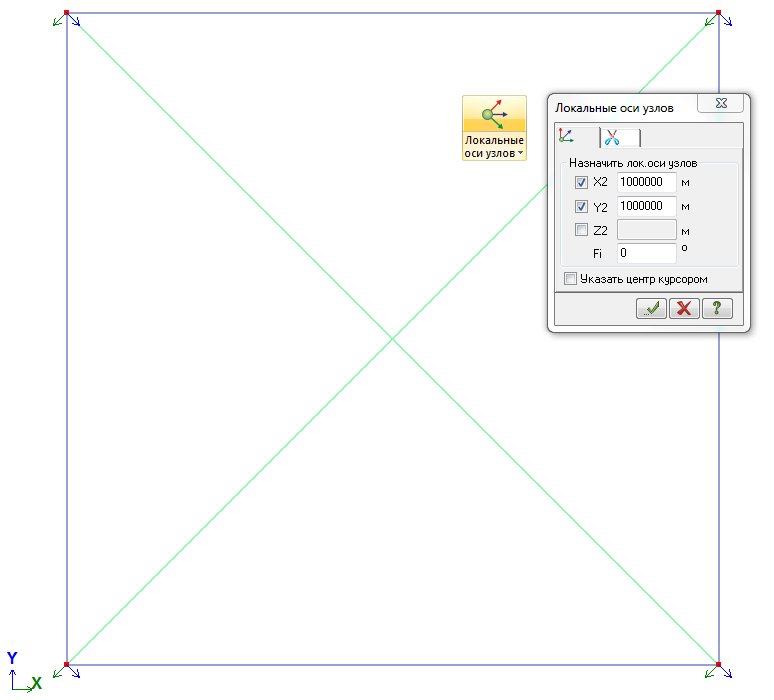
При действии ветра на диагональ следует ввести локальную систему координат узлов по направлению ветра. Для этого нужно отметить узлы, к которым прикладывается нагрузка, вызвать диалог «Локальные оси узлов» и указать в качестве координат точки, из которой будет смотреть ось X2, достаточно большие величины:
Рис. 24. Введение местных осей узлов
В итоге для узлов местные оси Х2 будут параллельны и сонаправлены с ветровым воздействием. Итоговая форма колебаний при определении величины ветровой пульсации также будет совпадать с направлением ветра на диагональ.
Т.к. веса масс при динамическом расчете приложены всегда в локальной системе координат узла (если локальная система координат не вводится, то локальные оси узлов совпадают по направлению с глобальными осями схемы), то при расчете башни на диагональное воздействие ветра следует формировать отдельный файл задачи. В противном случае формы колебаний будут не пригодны для получения корректных пульсационных инерционных сил для загружения ветра на грань. В этом случае результаты расчета двух задач (ветер на грань и на диагональ) можно «склеить» в Метеоре (Вариации моделей). Но всего этого можно избежать, если воспользоваться новой функцией «Суммировать формы перемещений»
Инерционные силы:
Рис. 25. Пульсационная составляющая ветровой нагрузки при действии ветра на диагональ
Рис. 26. Усилия в элементах башни от полной ветровой нагрузки при действии ветра на диагональ
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия.
РУКОВОДСТВО
ПО РАСЧЕТУ ЗДАНИЙ И СООРУЖЕНИЙ НА ДЕЙСТВИЕ ВЕТРА
УДК 624.042.4
Рекомендовано к изданию секцией динамики сооружений научно-технического совета ЦНИИСК им. Кучеренко.
Руководство по расчету зданий и сооружений на действие ветра. — М.: Стройиздат, 1978. … с. /Центр, науч.-исслед. ин-т строит, конструкций им. В. А. Кучеренко.
Руководство содержит рекомендации по определению ветровой нагрузки на здания и сооружения и указания по динамическому расчету высоких сооружений на действие ветра. В приложениях приведено обоснование основных положений и метода динамического расчета и даны примеры расчета зданий и сооружений на действие ветра.
Руководство предназначено для инженерно-технических работников проектных и научно-исследовательских институтов.
Табл. 58, рис. 55.
Р
$0213—523
447(01 )-78
Инструкт.-иормгг., II «ип,—47—77
© Стройиздат, 197$
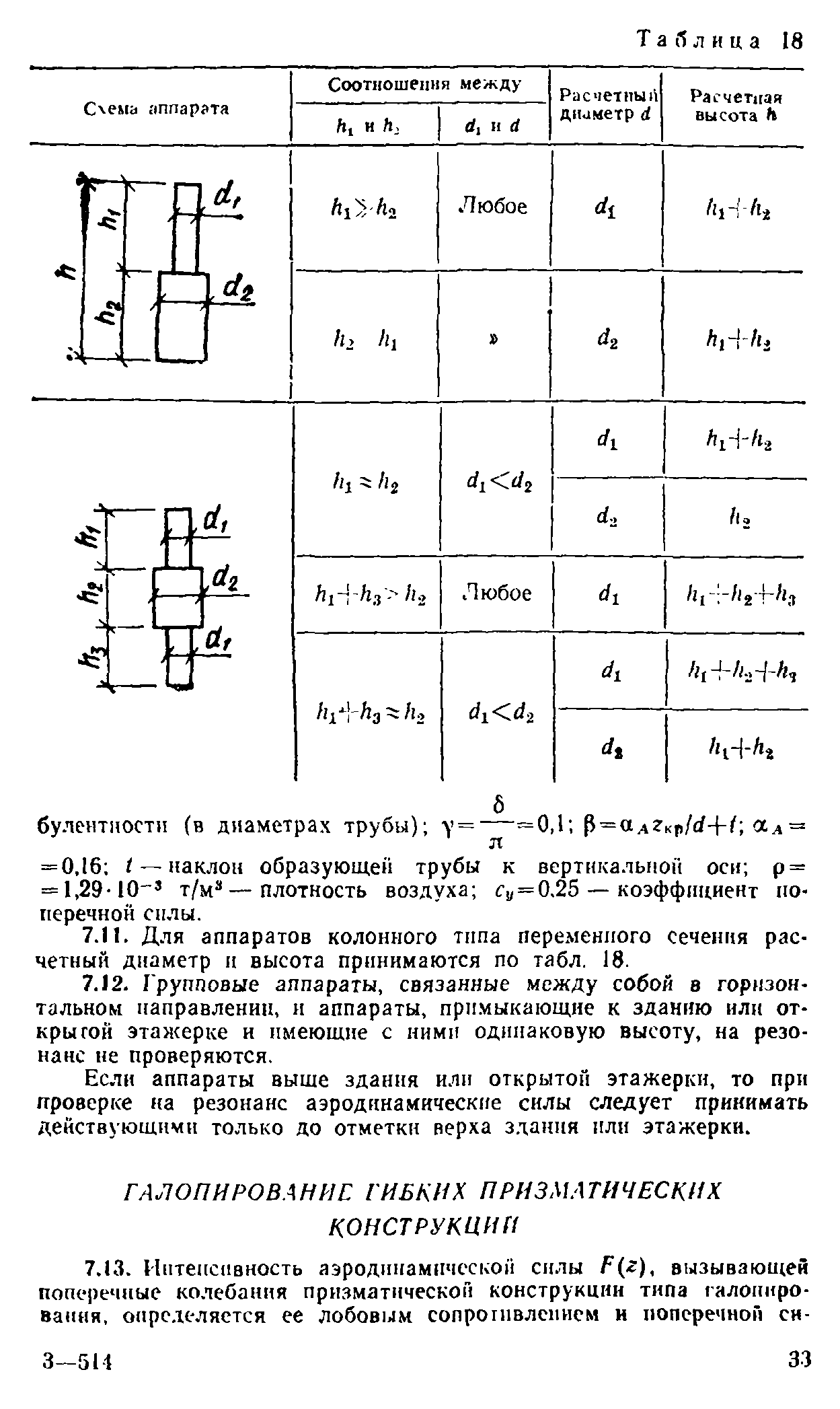
5.5. Нормативное значение равнодействующей ветрового давления на отдельные элементы и конструкции определяется по формуле
<?£ <*) — cqol (г) 5, (5)
Для составляющих (г) в направлении скорости ветра (лобового сопротивления) Q*H(z) и в перпендикулярном к ней направлении (поперечной силы) Q£H (z) аэродинамический коэффициент с соответствует коэффициентам с% и для составляющих Q{| (z) в направлении осей конструкции — коэффициентам сп и ct (рис. 3).
Аэродинамические коэффициенты сп и а совпадают с сх и су при ветре, нормальном к наветренной грани.
ОДНОЭТАЖНЫЕ ЗДАНИЯ
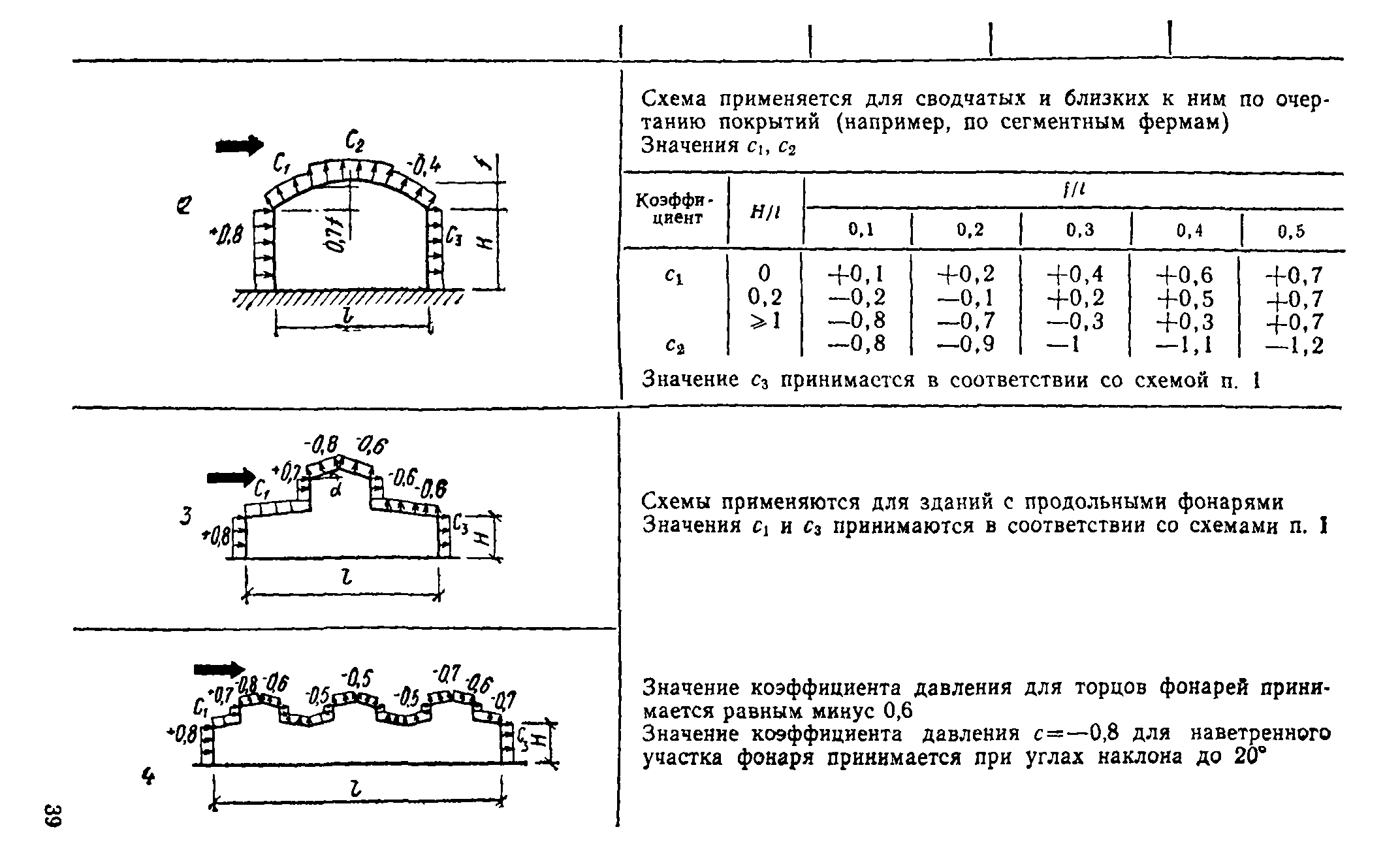
5.6. Для зданий (пп. 1—7, табл. 1, прил. 1) с открывающимися проемами (окна, ворота, двери), равномерно распределенными по периметру здания, или проницаемыми стенами из асбестоцементных или других листов (независимо от наличия проемов) при расчете ограждений наружных стен, стоек и ригелей фахверка, импостов остекления значения аэродинамических коэффициентов для ограждения должны приниматься равными: с= + 1—при расчете на положительное давление: с=—0,8 — при расчете на отрицательное давление.
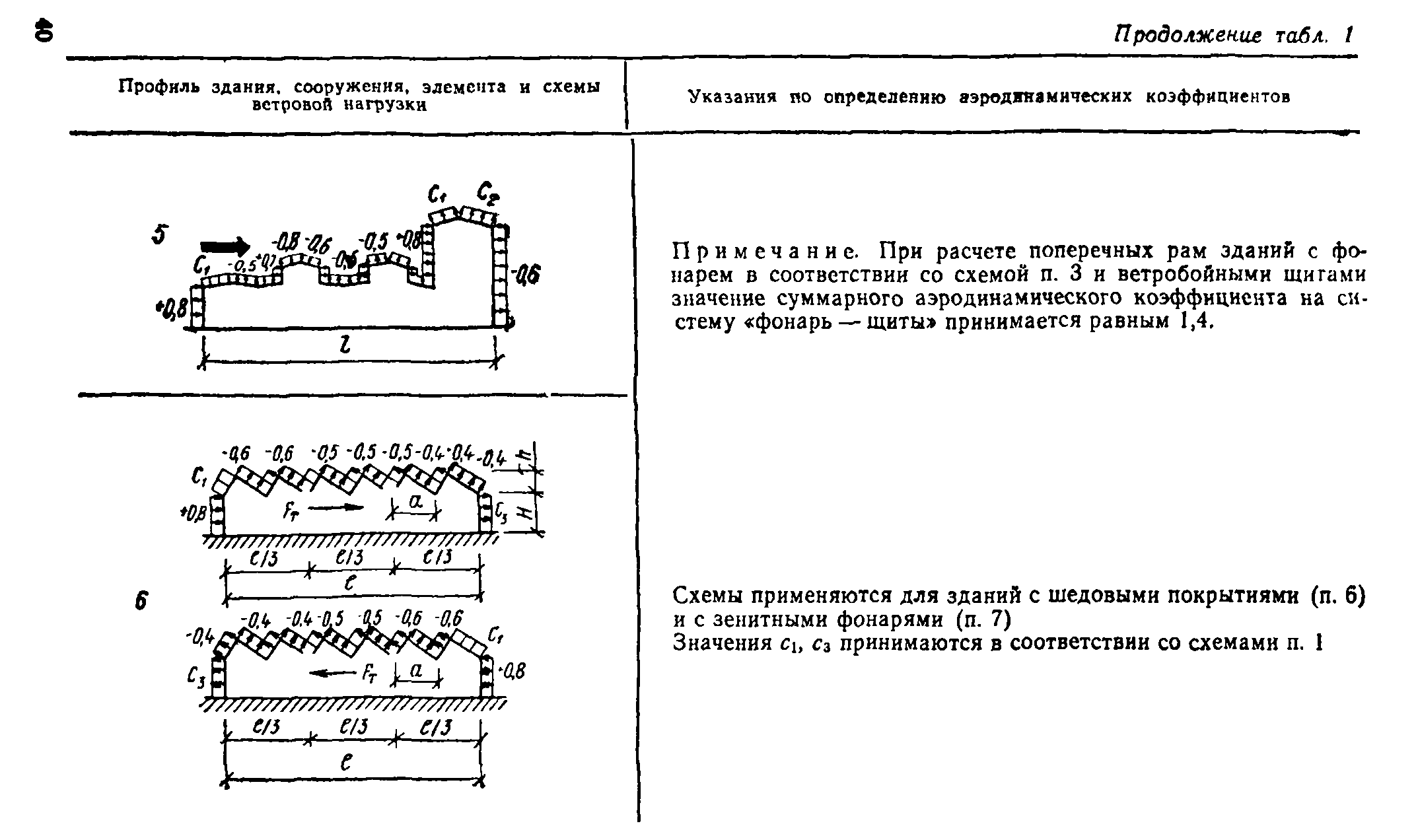
5.7. При расчете поперечных рам зданий с продольными фонарями или с зенитными (при а>4Л) фонарями (пп. 4, 5, 7, табл. 1, прил. 1) учитывается ветровая нагрузка, действующая иа наветренные и заветренные стойки рамы, и горизонтальная составляющая ветровой нагрузки, действующая на фонари.
Распределение ветровой нагрузки на здания с продольными фонарями, приведенное в пп. 4, 5, табл. 1, прил. 1, принимается при п<4Л; при а >4/* схема ветровой нагрузки принимается по п. 7 указанной таблицы.
Для зданий с шедовыми покрытиями (п. 6 той же таблицы) или с зенитными фонарями при a^4h вместо горизонтальных составляющих, действующих на второй (от наветренной стороны здания) и последующие фонари, должна быть учтена сила трения FT| определяемая по формуле
FT = (0,001 а + 0,02) q0 kt (z) Snn, (6)
где а — угол наклона наветренной грани фонаря к горизонту, град; к% (г)—коэффициент, принимаемый по табл. 2, прил. 1; S —площадь горизонтальной проекции покрытия здания (без площади первого фонаря); пп — коэффициент перегрузки (п. 2.2).
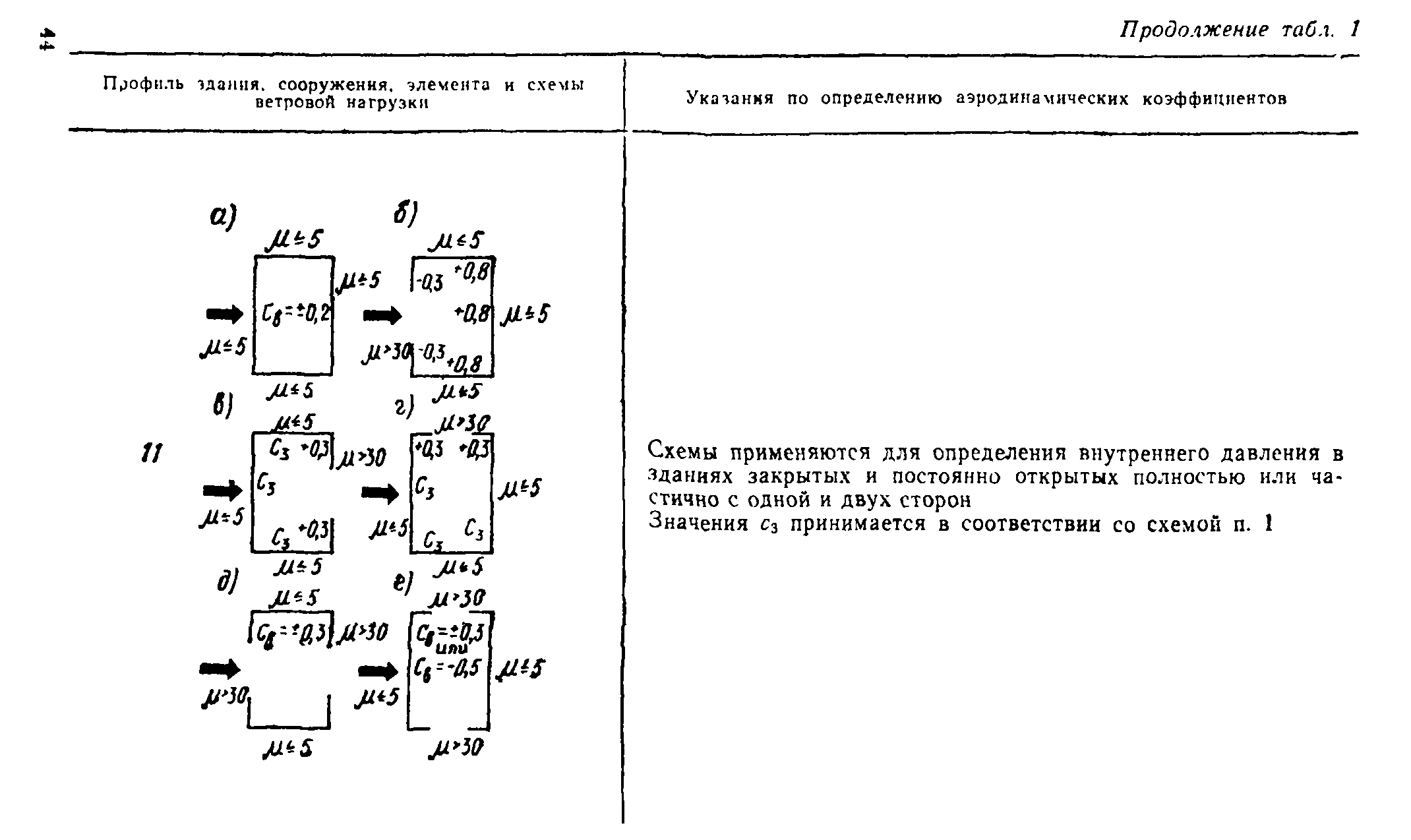
ВНУТРЕННЕЕ ДАВЛЕНИЕ В ЗДАНИЯХ
5.8. Внутреннее давление в помещениях одноэтажных и многоэтажных зданий равно давлению на внешнюю поверхность рассматриваемого помещения. В тех случаях когда на одном или нескольких фасадах имеются участки различной проницаемости,
внутреннее давление для каждого помещения устанавливается соответственно его проницаемости и направлению ветра.
В закрытых зданиях с проницаемостью ограждений ко
эффициент внутреннего давления сш во всех помещениях принимается равным ±0,2 (п. 11а, табл. 1, прил. 1).
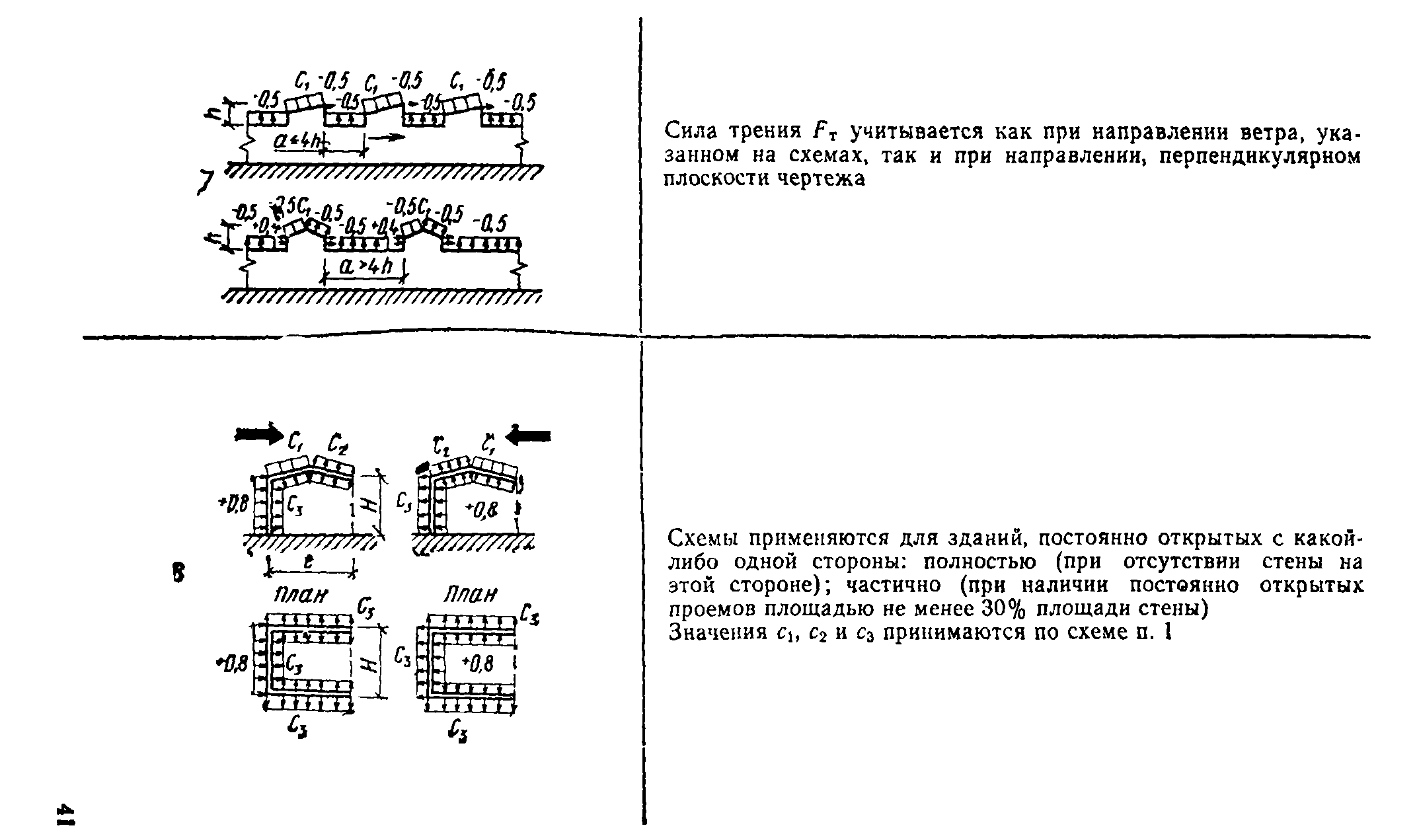
В зданиях с одной открытой стеной, имеющей р>30 (другие стены имеют проницаемость р<5), коэффициенты са принимаются, если открыта сторона здания: наветренная — по п. 116; заветренная — по п. 11в; параллельная ветру — по п. 11г.
В зданиях с двумя открытыми стенами, имеющими р>30 (другие стены имеют проницаемость р<5), коэффициенты сй принимаются, если открыты стороны здания:
наветренная и заветренная — по п. 11д; параллельные ветру — по п. Не.
Если здание имеет стены с проницаемостью 30>ц>5, то коэффициенты Си определяются линейной интерполяцией между их значениями для закрытого и открытого с одной стороны здания Так, если наветренная стена здания имеет р=15, а другие стены |л<5, то для наветренной грани сй = —0,3, для других стен
св ~1 0,3 -J- 0,5 “ ~ — 0,5j
Ветровая нагрузка на конструктивные элементы ограждения определяется путем суммирования действующих на них внешнего и внутреннего давления.
5.9. В закрытых одноэтажных промышленных зданиях (пп. 1—7, табл. 1, прил. 1) и в многоэтажных зданиях высотой до 30 м расчетная ветровая нагрузка на внутренние стены должна приниматься равной 0,4^о, на легкие перегородки (весом не более 100 даН/м2) — 0,2?о, но не менее 100 Па.
При высоте зданий более 30 м расчетная ветровая нагрузка на внутренние стены и перегородки определяется с учетом коэффициента kt{z), принимаемого по табл. 2 для местности типа Б.
Расчетная ветровая нагрузка на внутренние стены и перегородки многоэтажного здания, монтируемые одновременно с его каркасом при отсутствии наружного стенового ограждения, принимается но эксплуатационному случаю с учетом того, что в период монтажа здания они могут быть дополнительно раскреплены.
ВЫСОКИЕ ЗДАНИЯ
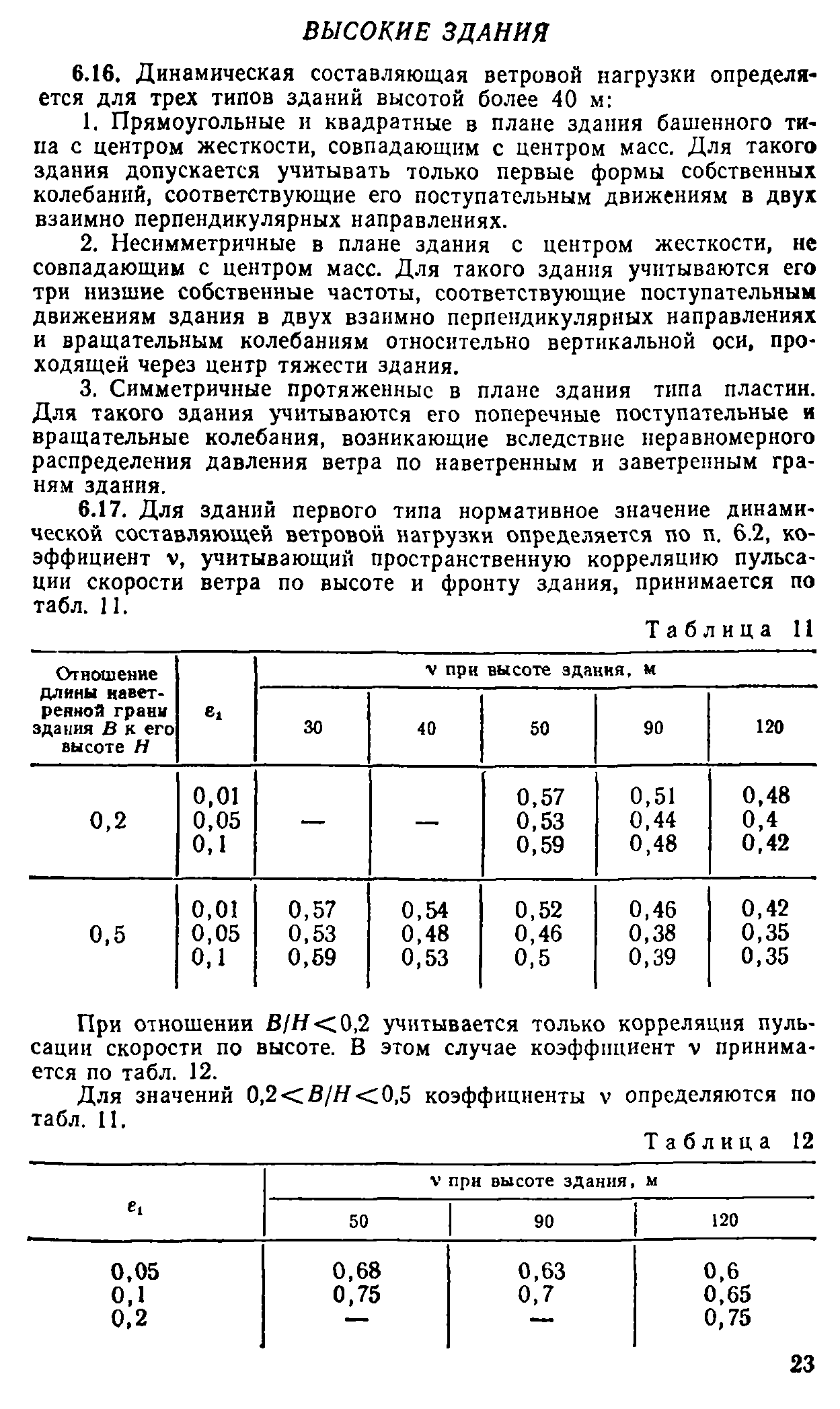
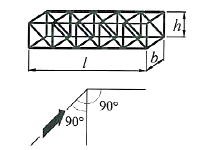
5.10. Для прямоугольных и квадратных в плане зданий повышенной и большой этажности коэффициенты лобового еопротивле-
Н I
имя определяются по табл. 4 в зависимости от и , где Н —
о а
высота здания, / — его ширина (размер в направлении потока), В — длина наветренной грани здания.
Промежуточные значения коэффициентов допускается определять линейной интерполяцией между указанными в таблице значениями.
12
В таком здании при ///* = 0,2—0,5 давление ветра по его наветренной и заветренной граням распределяется неравномерно. Эксцентриситет равнодействующей этого давления относительно центра наветренной грани, возникающий при угле между направлениями потока ветра и нормалью к этой грани порядка 40—50°, может быть принят равным 0,15 В.
Аэродинамические коэффициенты сп для этих углов атаки вет
|
Таблица 4 |
|||||||||||||||||||
|
ра, определяемые как разность коэффициентов давления на наветренную и заветренную грани, могут быть приняты равными 1,1 при //5=0,5 и 1,3 —при //5=0,2; коэффициент с* = 0,5.
5.11. Для здания с лоджиями в продольных стенах при ветре, нормальном к торцу, кроме ветровой нагрузки, определяемой в соответствии с пп. 2.1 и 2.2, для каждой стены с лоджиями должна быть учтена сила трения FT — = 0 ,\qokt{z)Snn, где S=tf5 — площадь продольной стены.
СООРУЖЕНИЯ ЦИЛИНДРИЧЕСКОЙ И СФЕРИЧЕСКОМ ФОРМЫ
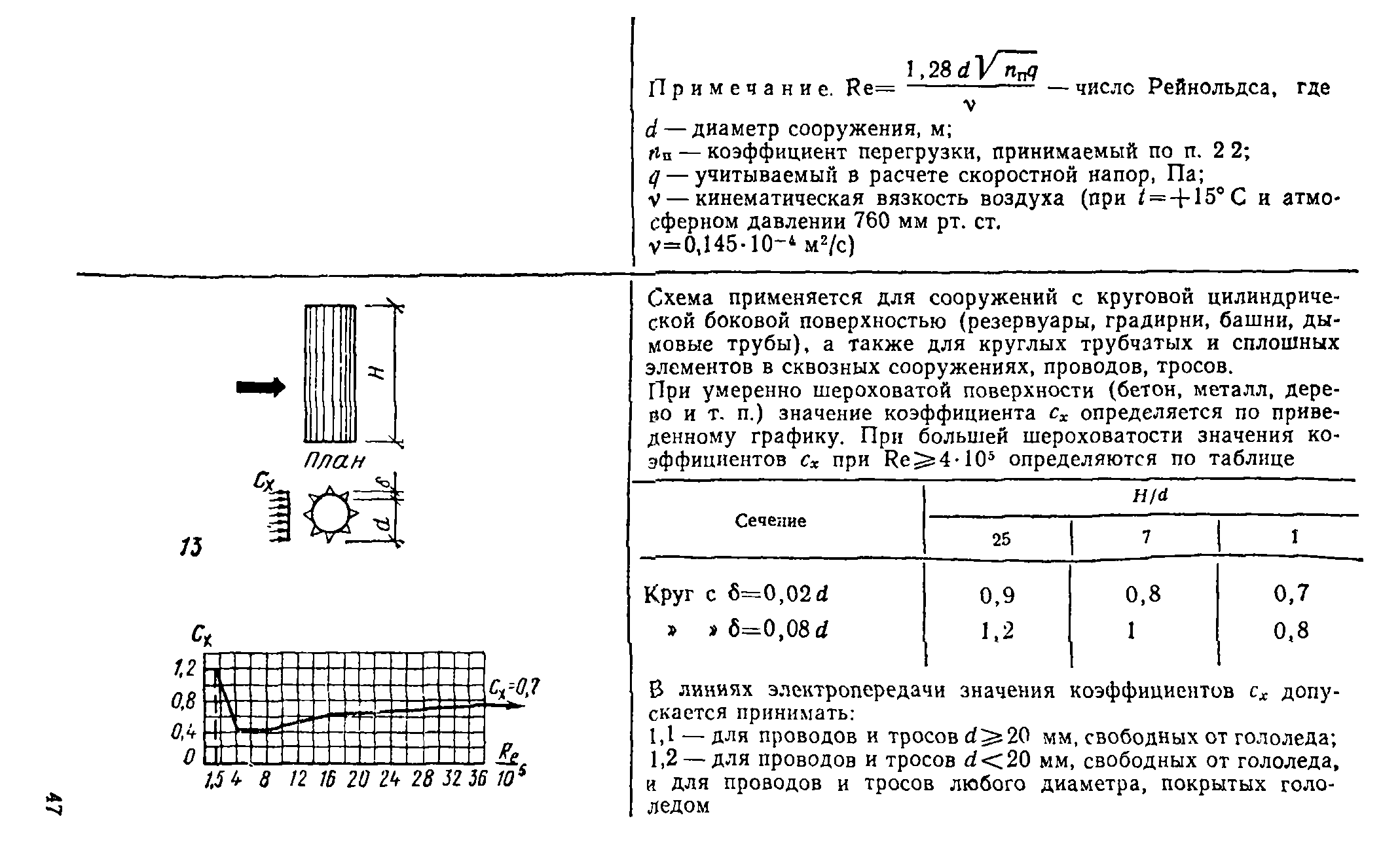
5.12. Высокие сооружения цилиндрической формы (дымовые трубы, мачты, градирни и т. п.) и элементы сквозных сооружений (трубчатые или из прокатных профилей) относятся к классу плохо обтекаемых тел.
Вследствие наличия трения в воздухе, около такого тела (например, бесконечного цилиндра), обтекаемого воздушным потоком, образуется так называемый пограничный слой, в котором скорость потока быстро падает до нуля у поверхности тела. Толщина этого слоя зависит от вязкости среды.
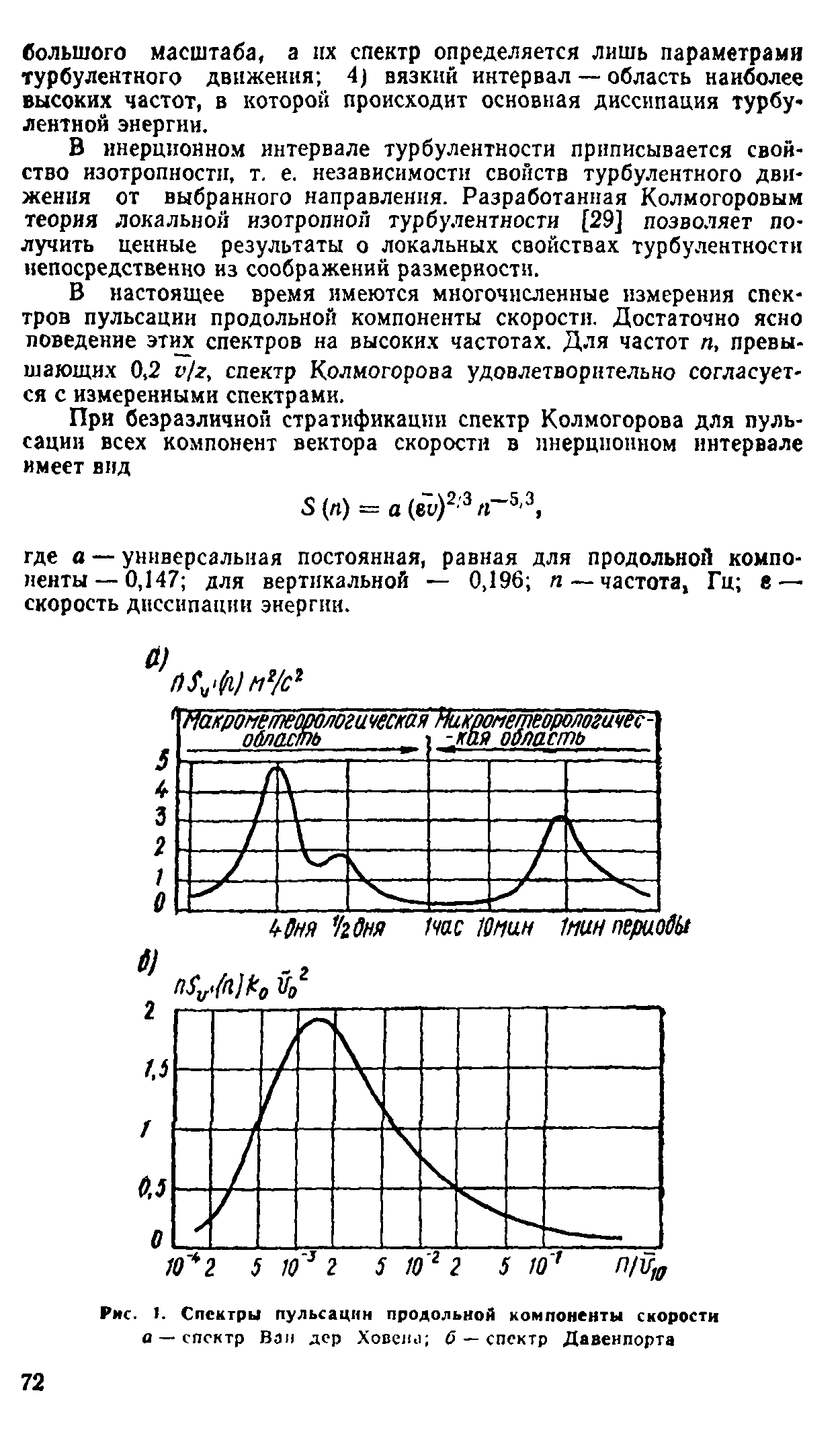
В начале движения, когда скорость мала, поток вокруг тела приближается к потенциальному. Пограничный слой служит своего рода прослойкой между потоком и цилиндром, и если в критических точках имеется повышенное давление, то оно передается телу через пограничный слой. Этим давлением пограничный слой как бы вытесняется к точкам В и Д, вследствие чего возникают течения от А к В и Д и от С к В и Д; с другой стороны, пограничную зону обтекает потенциальный поток. От этих противоположных токов за точками В и Д образуются симметричные парные вихри, которые смываются потоком. Такое расположение вихрей, однако, не является устойчивым, поэтому при дальнейшем увеличении скорости и соответственно числа Рейнольдса расположение вихрей становится асимметричным. Вихри отрываются попеременно с обеих сторон цилиндра, правильно чередуясь через определенные промежутки времени и образуя вихревую дорожку, которая называтся дорожкой Бенара — Кармана (рис. 4). Этот тип движения сохраняется в широком диапазоне чисел Рейнольдса. Наконец, при Re=l05—2 * 105 пограничный слой становится турбулентным и срывается с поверхности цилиндра.
13
Рис. 4. Характер обтекания цилиндра потоком жидкости
й — начало движения цилиндра; б — зарождение вихрей за цилиндром; в — неустойчивое состояние парных вихрей; г — периодический срыв вихрей за
цилиндром
Турбулизация пограничного слоя приводит к заметному смещению линии отрыва вихрей по направлению к концу тела, так что область вихреобразований — турбулентный след за телом сужается, что приводит к уменьшению силы сопротивления. Коэффициент лобового сопротивления падает в несколько раз в сравнительно узком интервале чисел Рейнольдса. Это явление называется кризисом сопротивления.
На явление кризиса влияет степень турбулентности набегающего на тело потока. Чем она больше, тем ранее (при меньших Re) наступает турбулизация пограничного слоя.
Различают следующие области изменения коэффициента сх при увеличении Re: докритическая при Re<1,5-105, критическая при 1,5* 105<Re<8* 105, закритическая при 8-105<Re<107 и транскритическая при Re>107.
Периодический отрыв вихрей наблюдается при обтекании не только цилиндров, но также и других тел. Однако для призматического тела линии отрыва вихрей совпадают с угловыми точками поперечного сечения; коэффициент сх для таких тел от числа Рейнольдса практически не зависит.
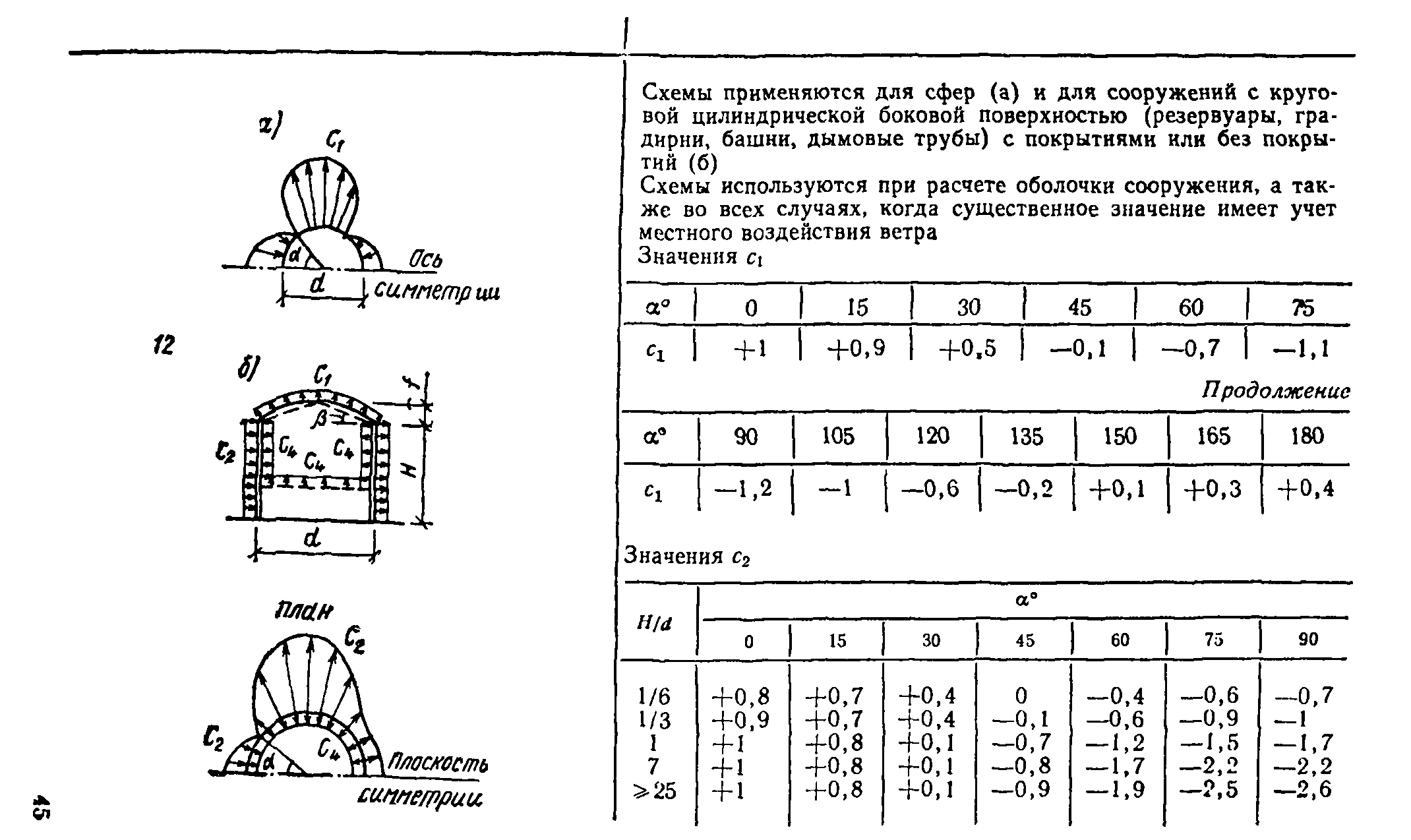
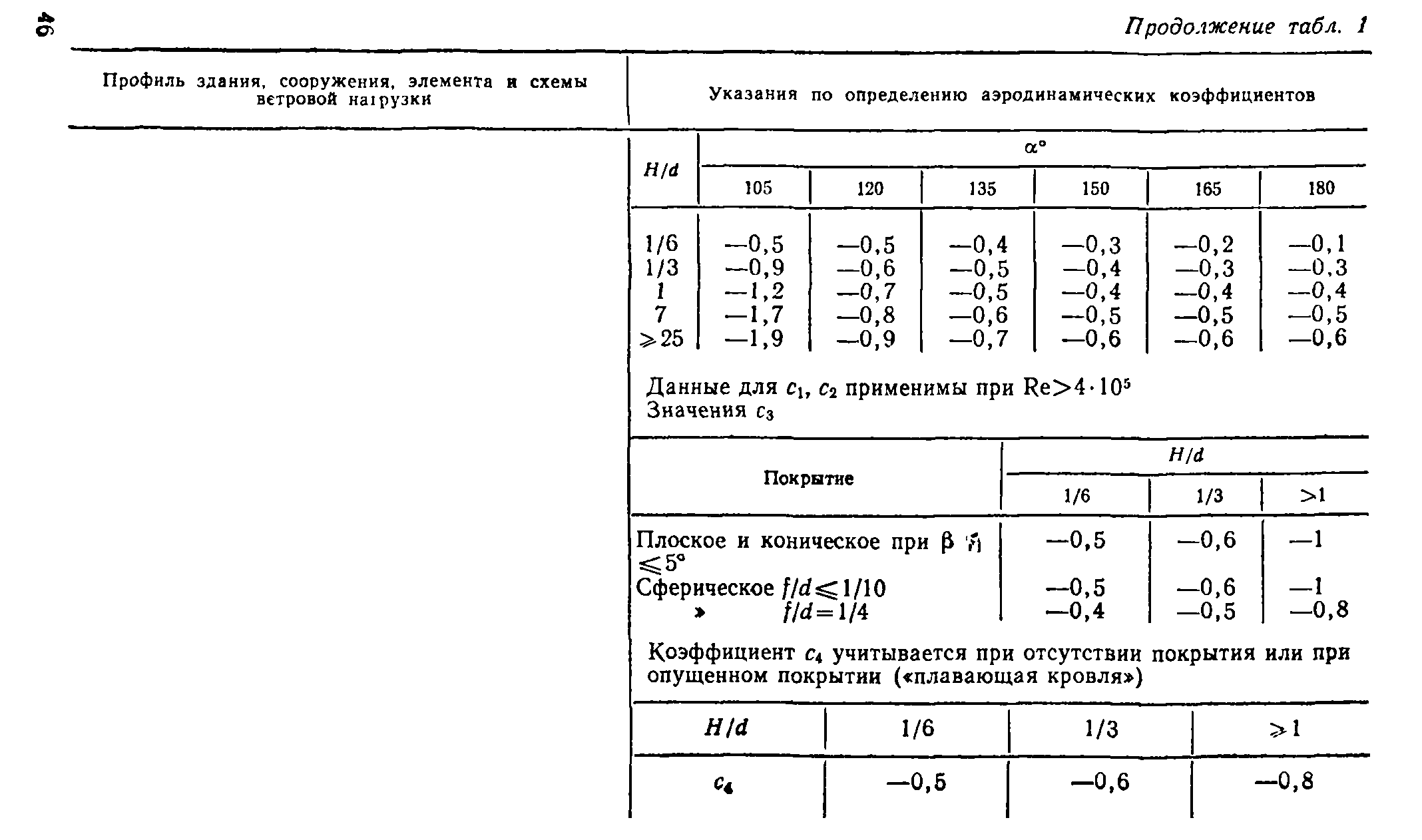
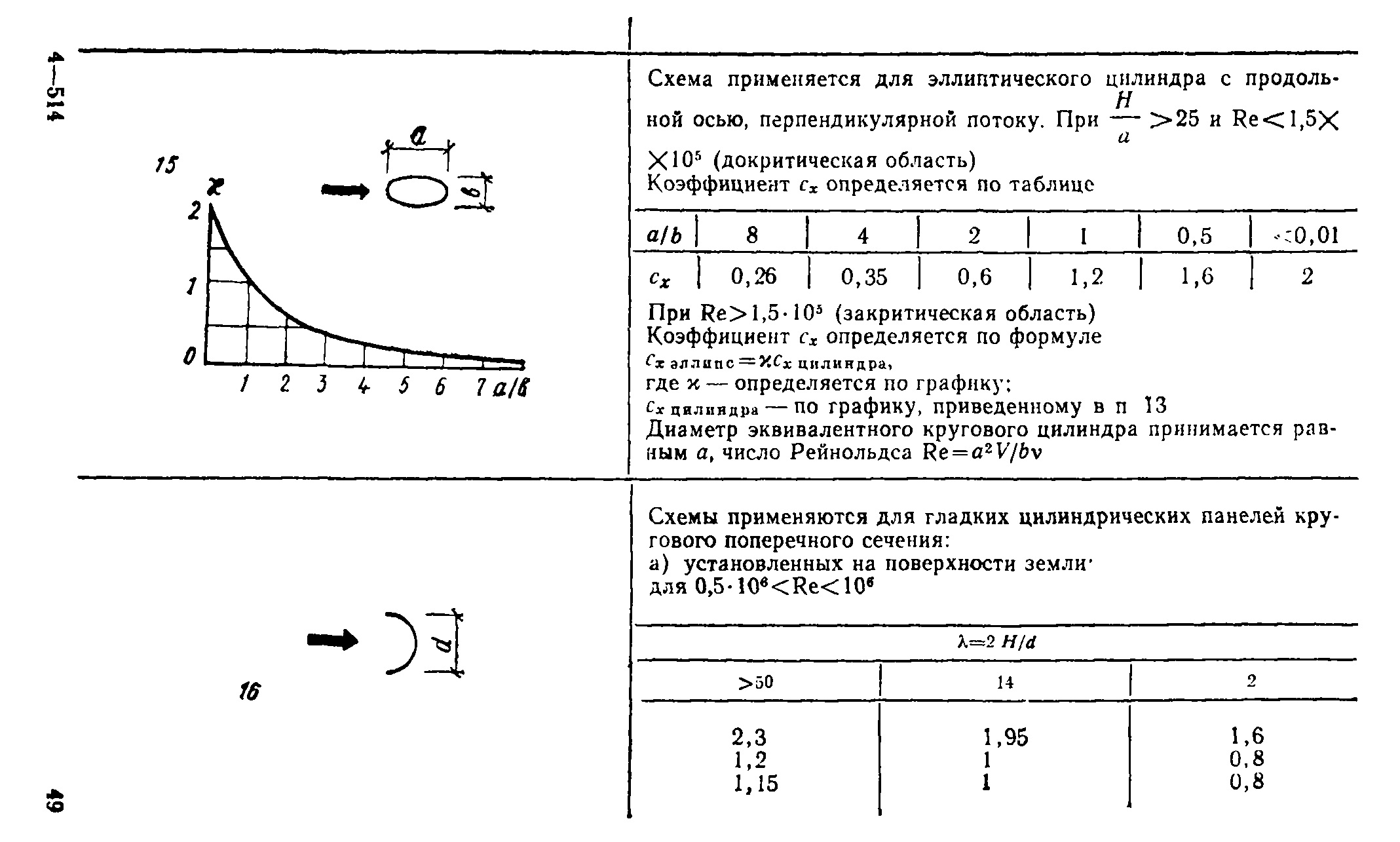
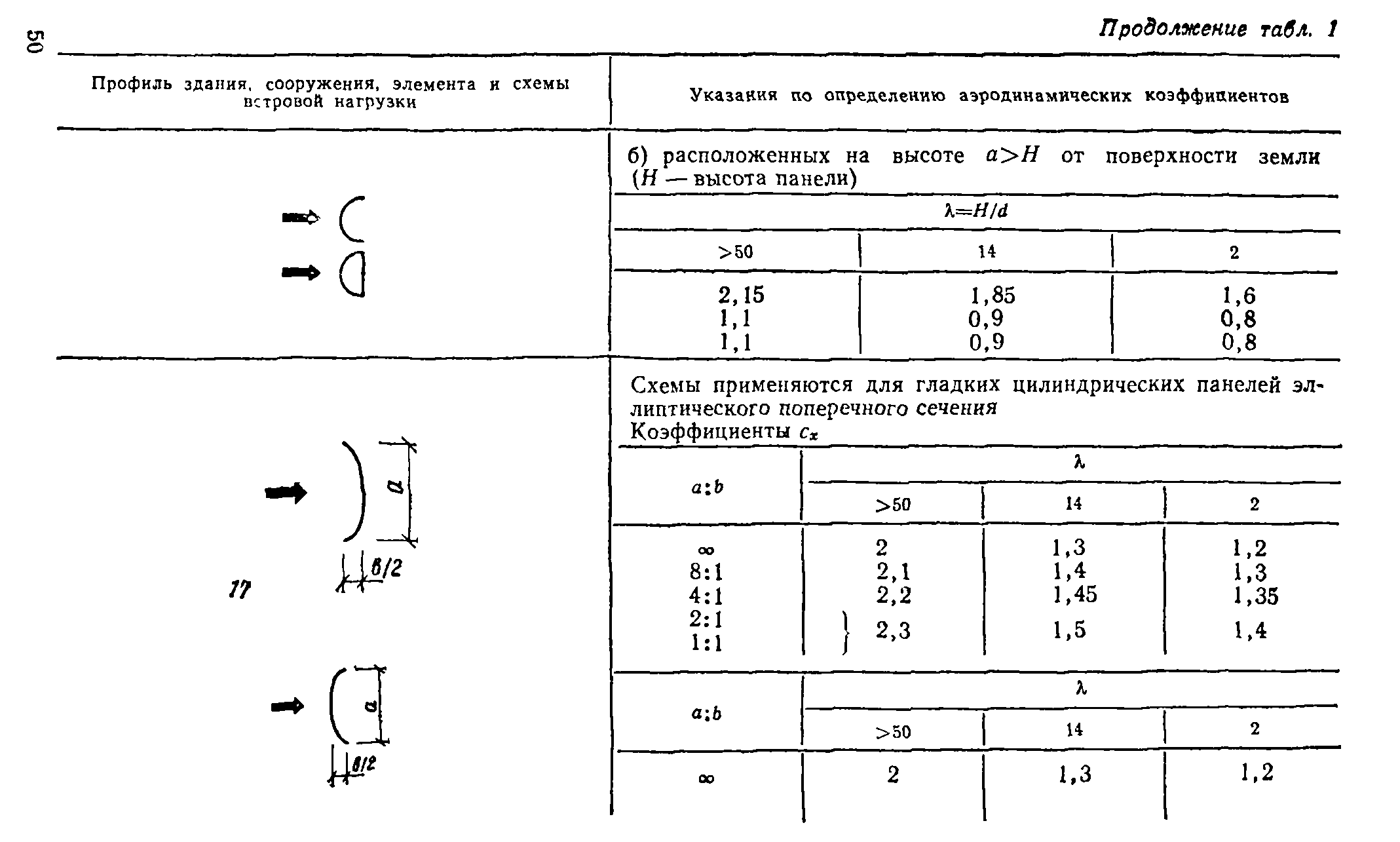
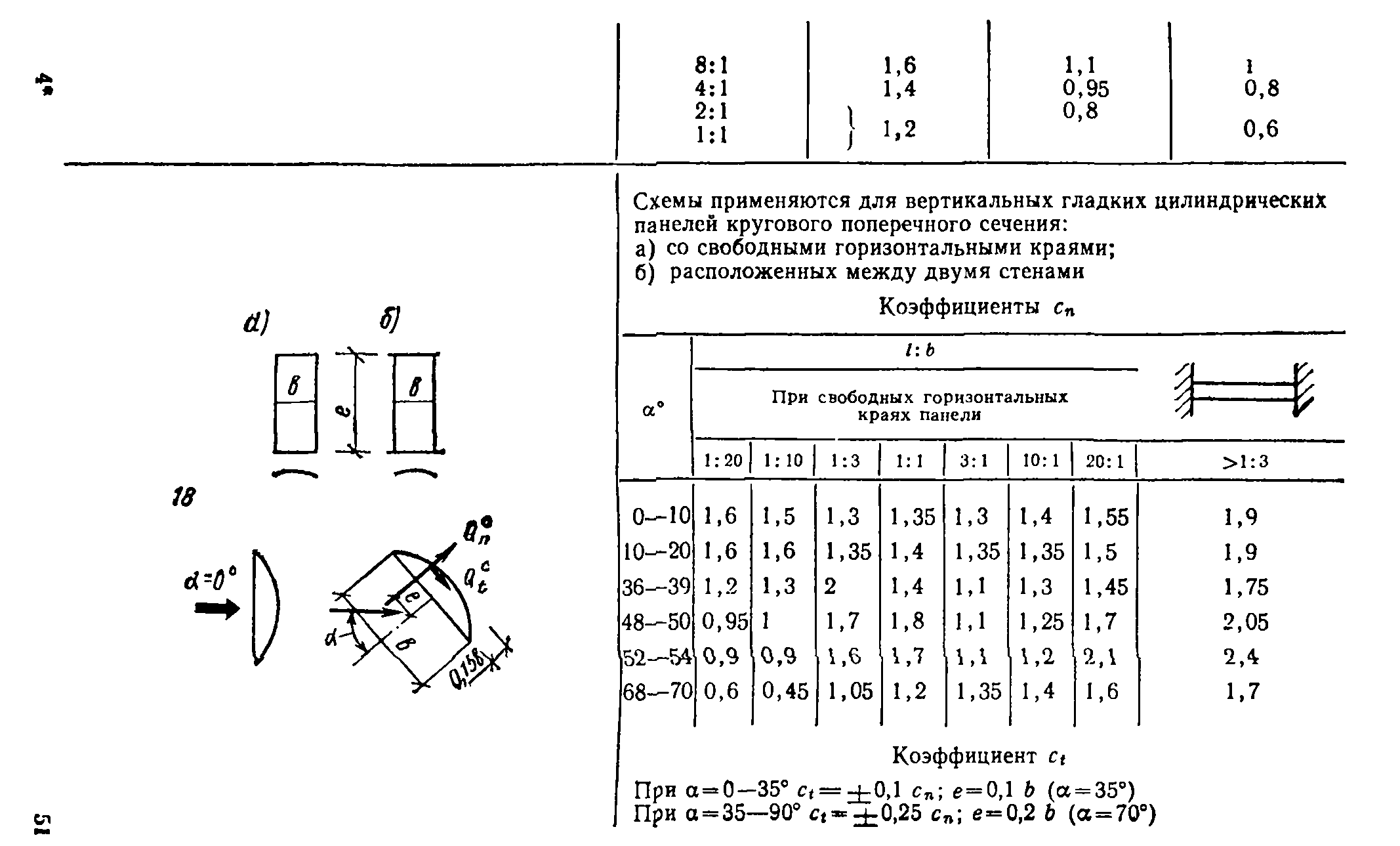
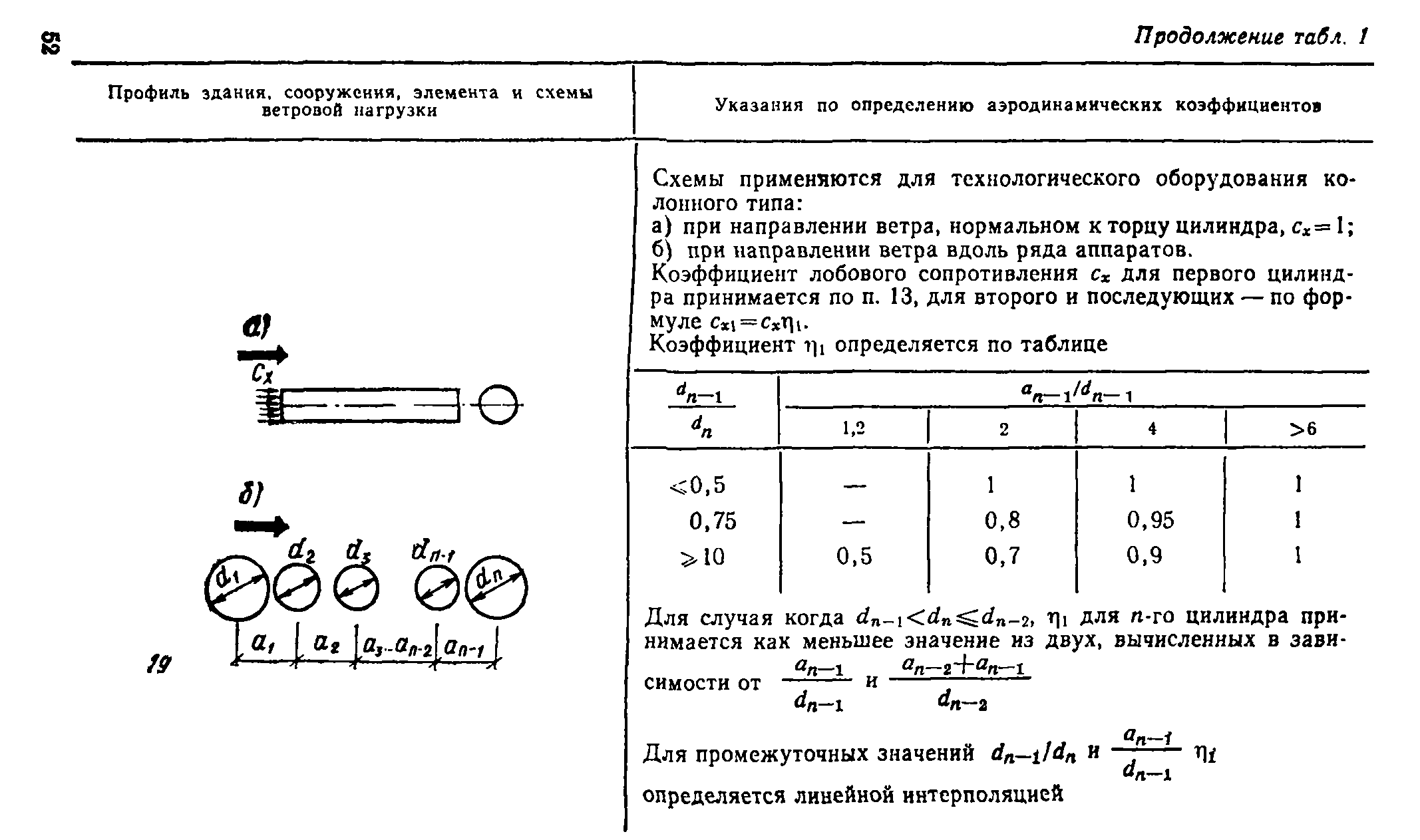
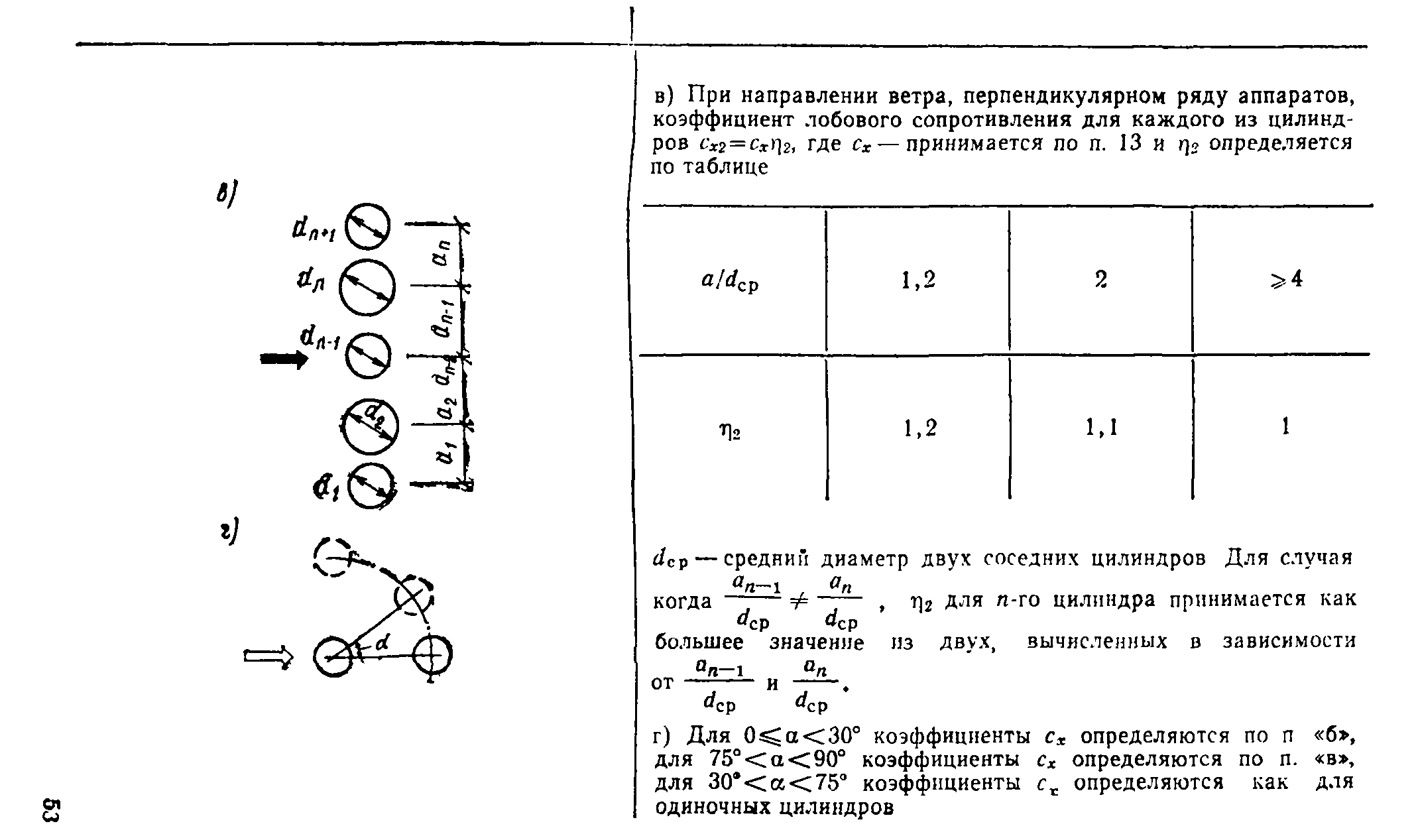
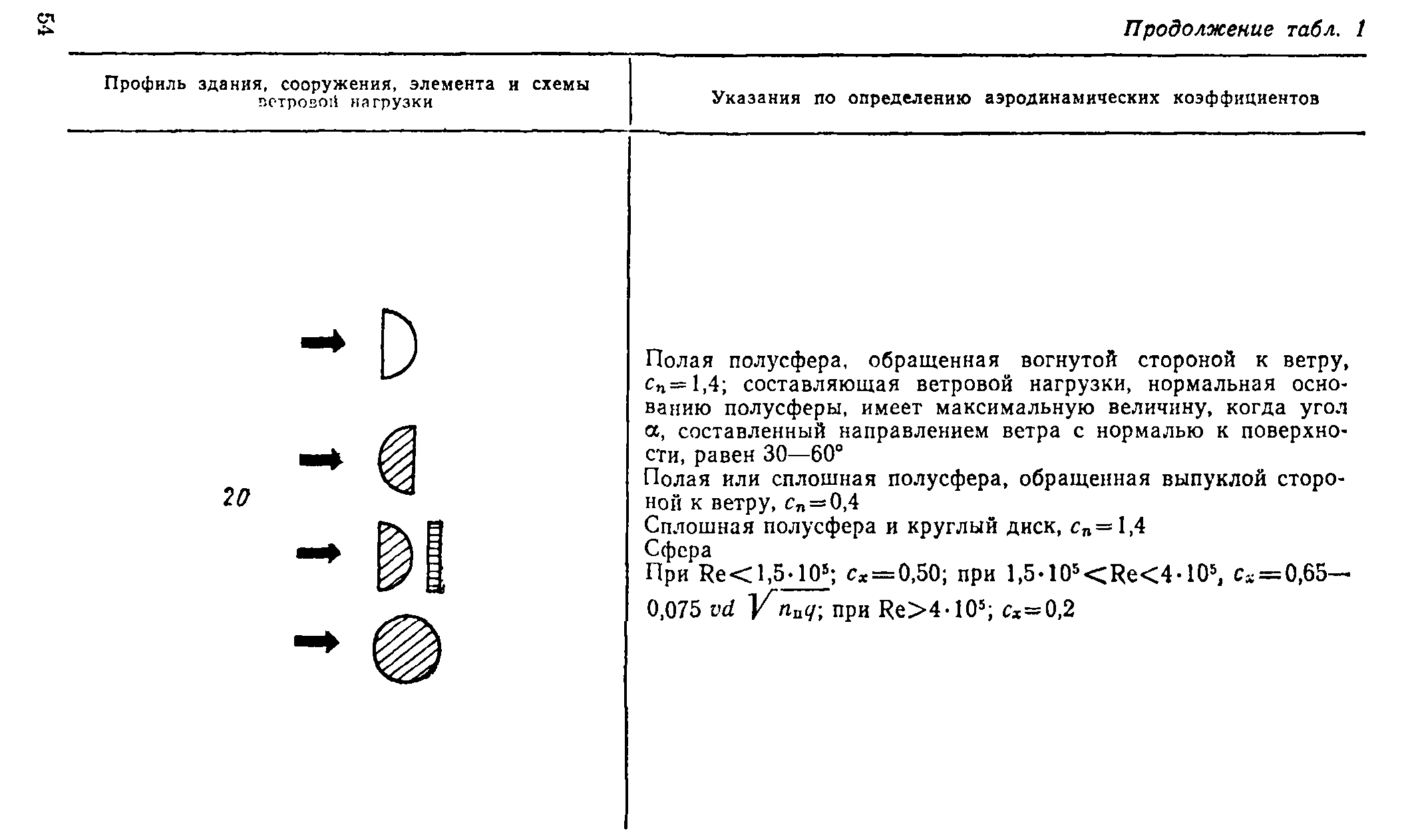
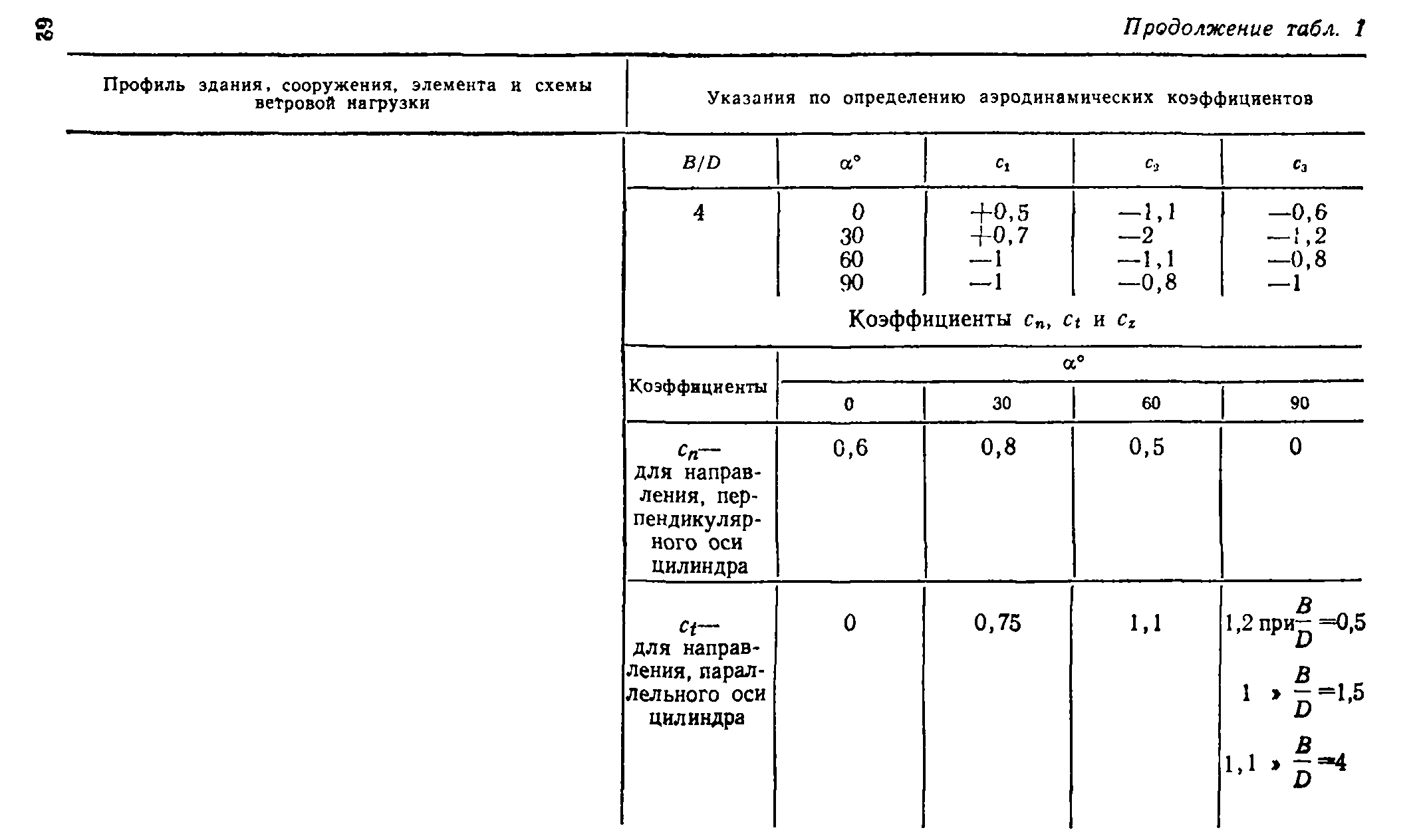
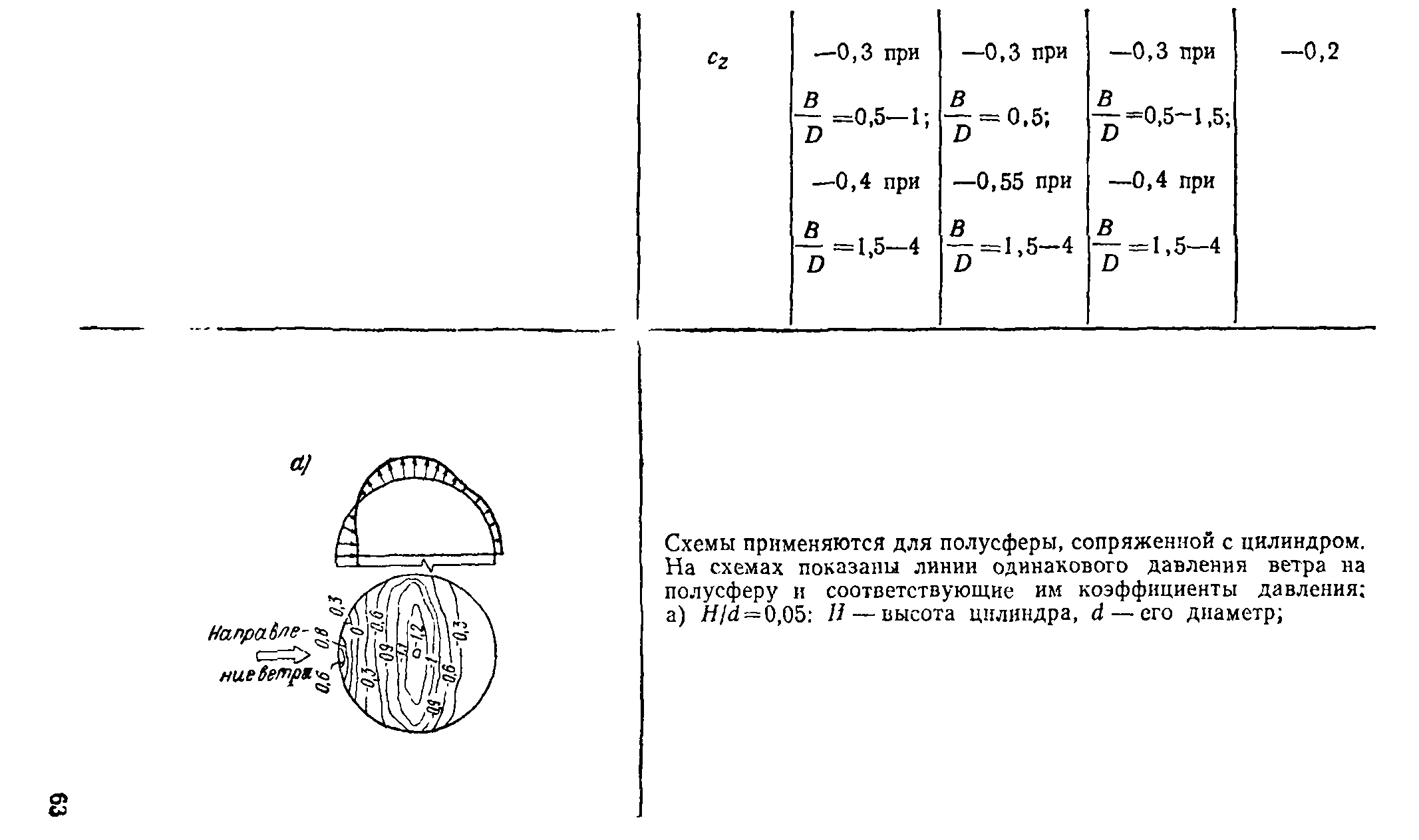
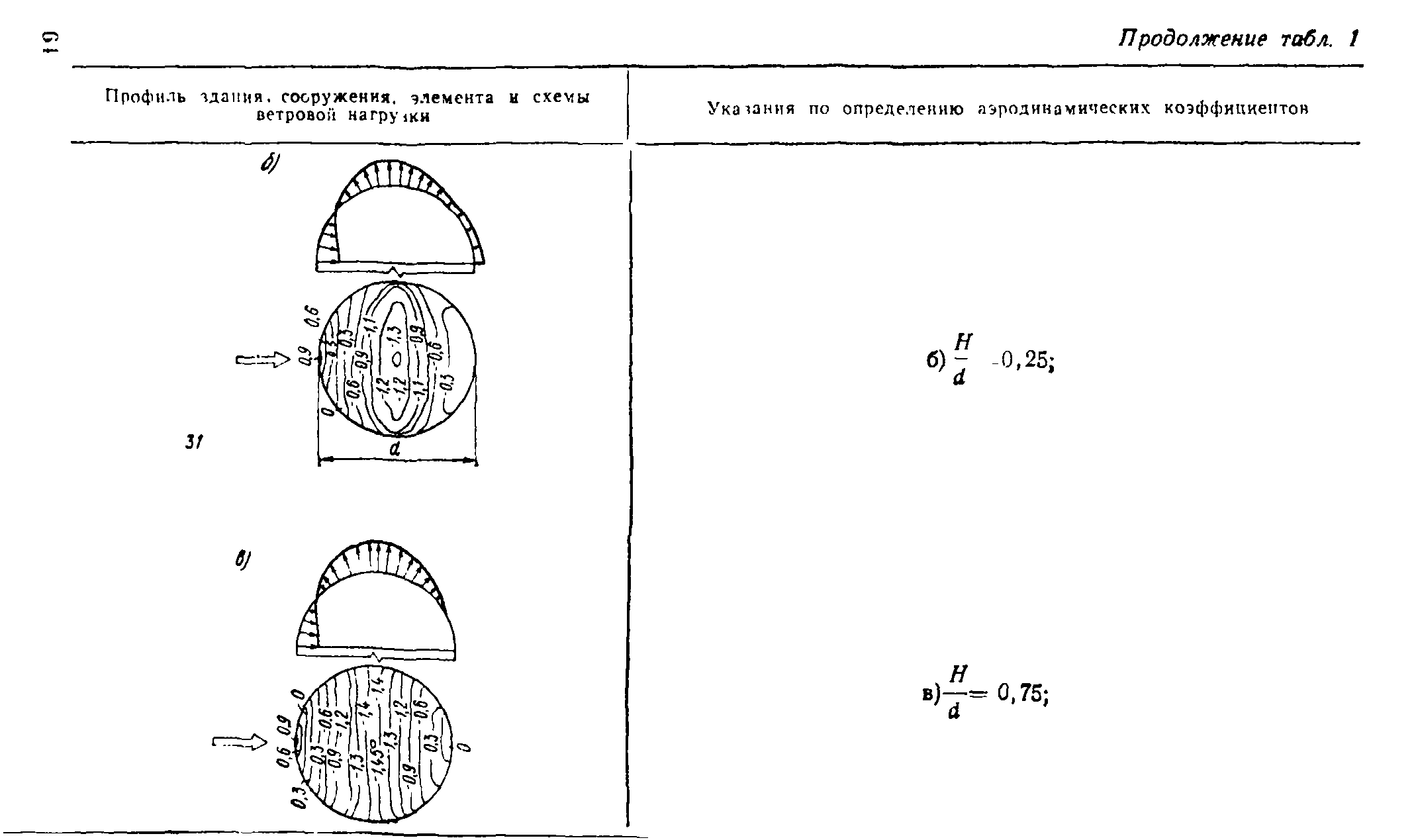
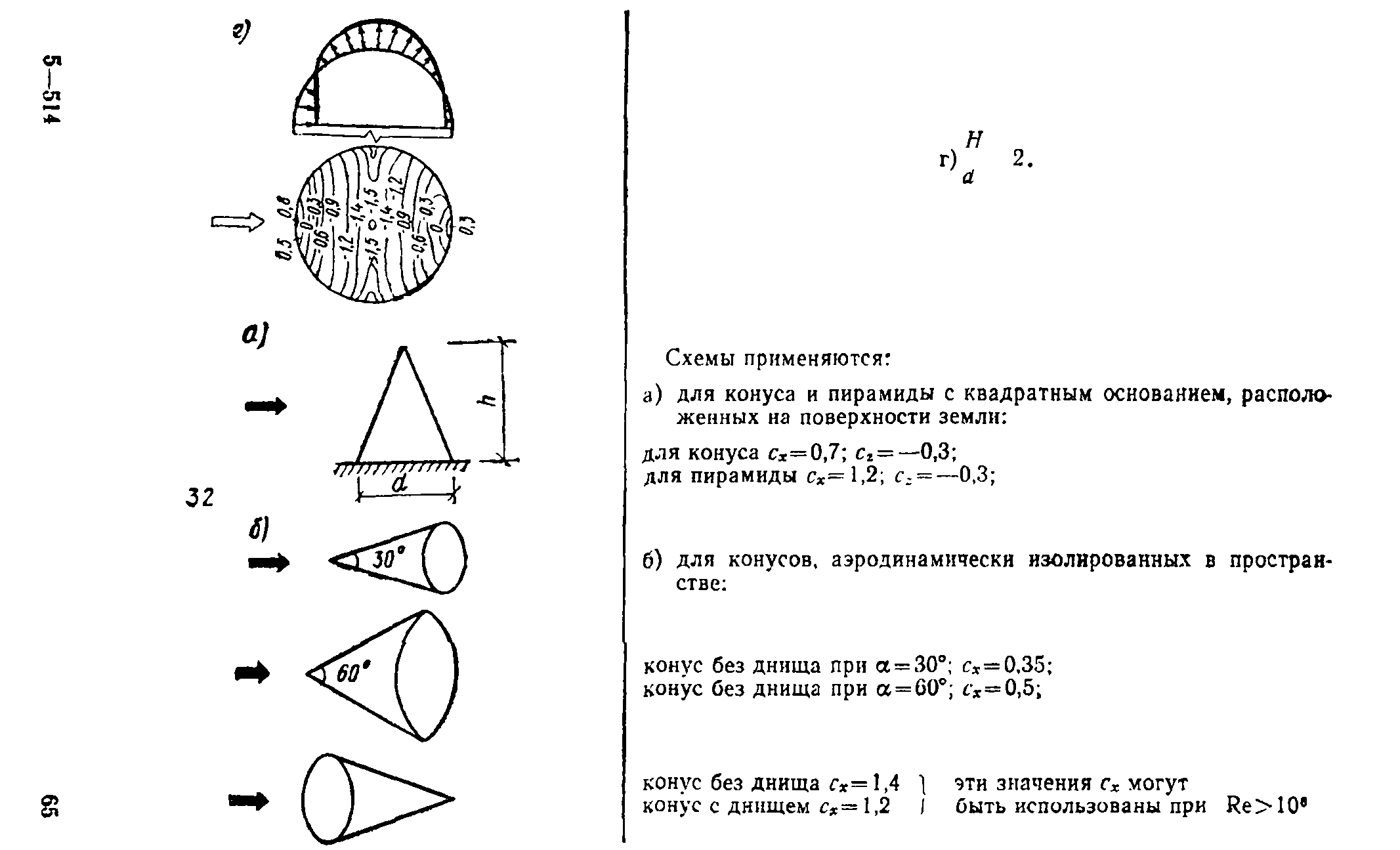
В пп. 12—20, табл. 1, прил. 1 приведены схемы распределения ветровой нагрузки и аэродинамические коэффициенты (коэффициенты давления и лобового сопротивления) для сферы, сооружений с круговой цилиндрической поверхностью (резервуары, башни, дымовые трубы), эллиптического цилиндра, цилиндрических панелей кругового и эллиптического поперечных сечений, аппаратов колонного типа и конструкций, образуемых из сфер. Там же даны коэф-
14
фициенты сх для цилиндров с ребрами (выступами), для проводов и тросов.
5,13. Коэффициенты давления для оболочки градирни, наружная поверхность которой не имеет меридиональных ребер (умеренно пероховатая поверхность), принимаются по п. 12, табл. 1, прил. 1 для Hjd = 1. Коэффициенты давления для оболочки градирни с меридиональными ребрами, расположенными на расстоянии не более 1/50 длины окружности, и отношением высоты ребра к среднему диаметру оболочки 6/rf^3,5*l0~4 (с шероховатой наружной поверхностью) принимаются по п. 14, табл. 1, прил. 1. Там же приведены коэффициенты разложения в ряд Фурье эпюры давления ветра по поверхности оболочки для умеренно шероховатых и шероховатых поверхностей.
Кроме внешнего давления на оболочку должно учитываться также распределенное по ее поверхности внутреннее давление с коэффициентом 0,5.
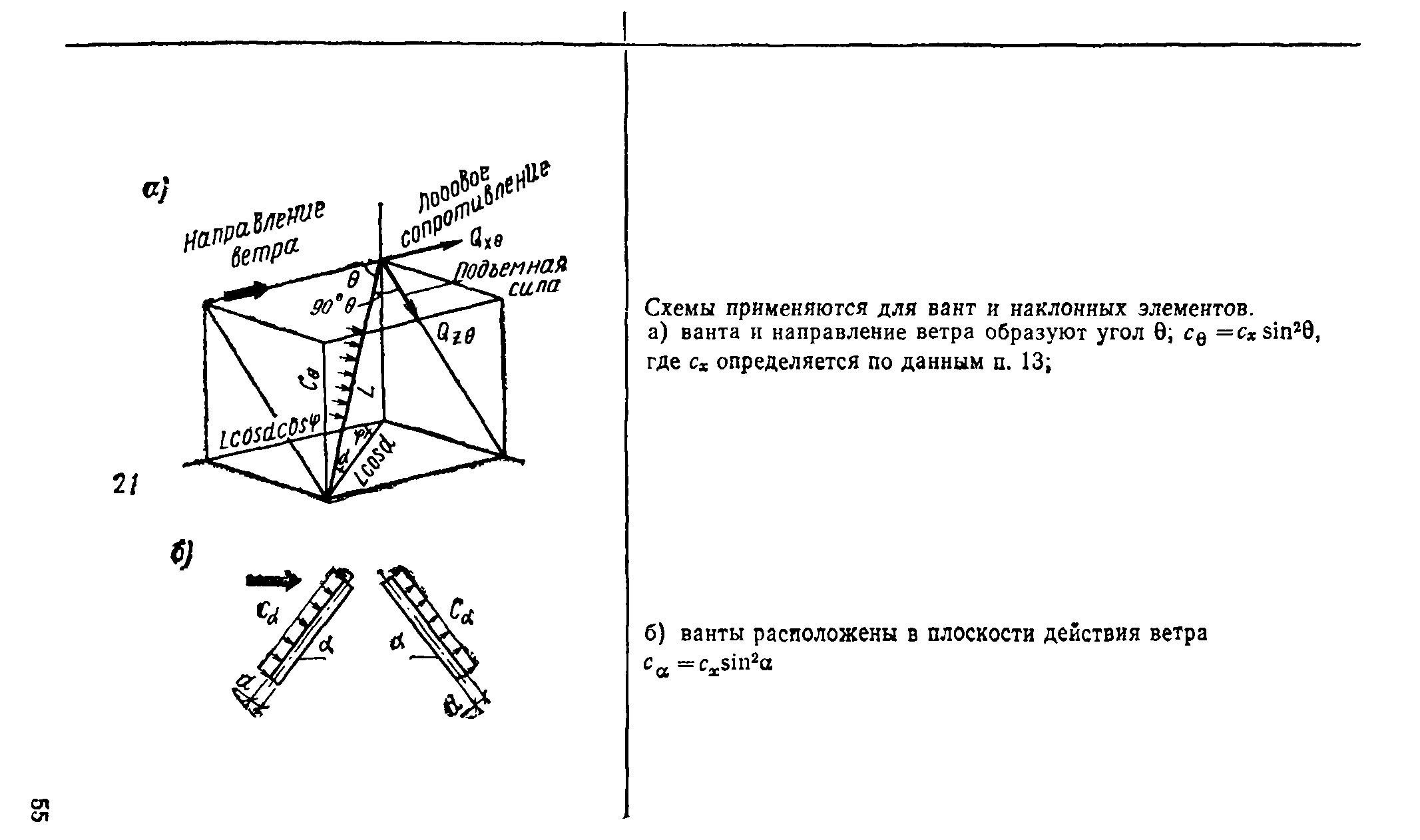
Б.14. Нормальное к хорде ванты или наклонного трубчатого элемента нормативное значение ветровой нагрузки определяется по формуле
Qi(z)=q0ktU)ceS, (7)
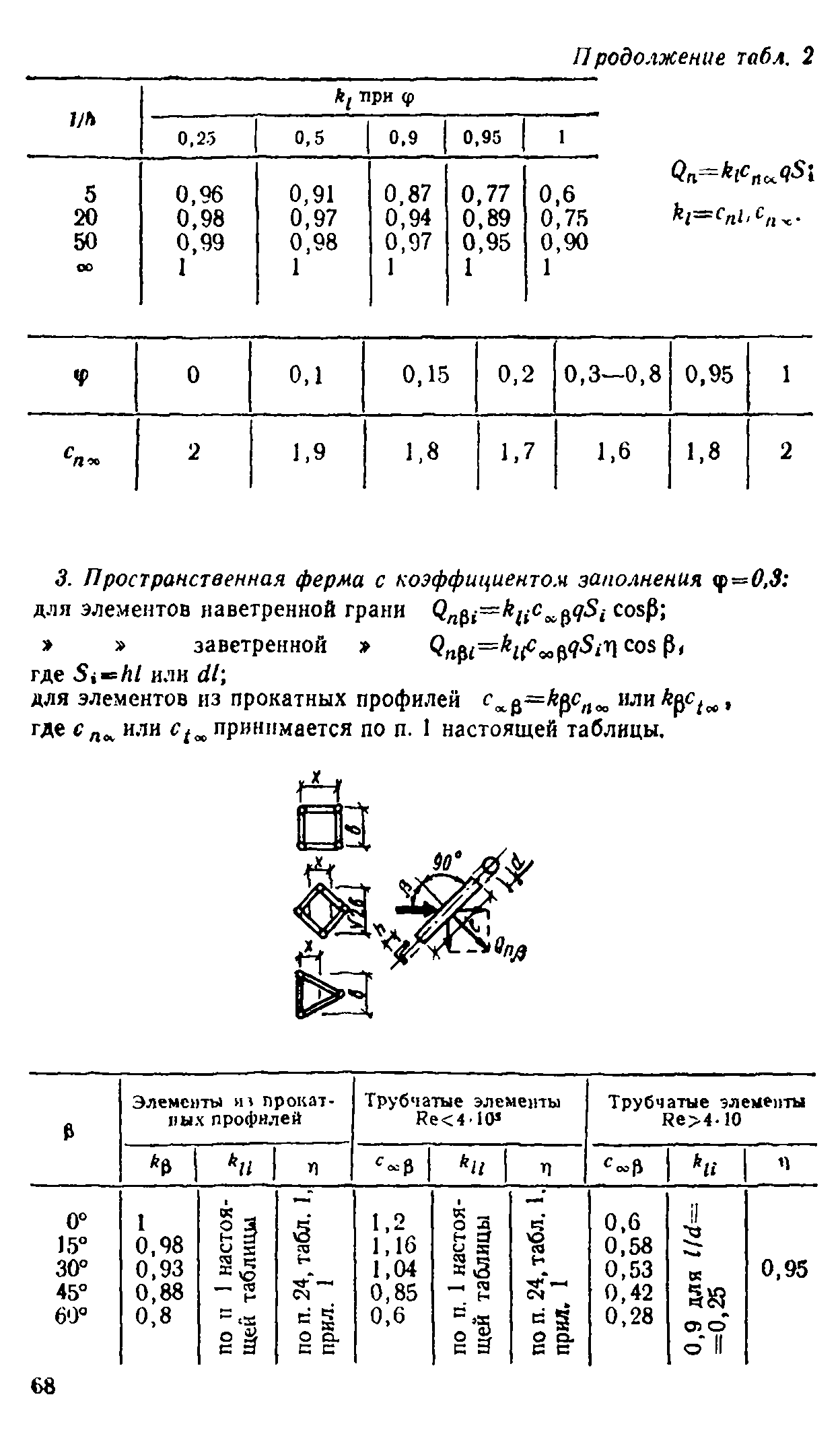
где с0 =*схе sin 0+с20 cos 0; 0—угол между вантой и направлением ветра; cos0=cosacos cp; a — угол наклона ванты к горизонту; <Р— угол между плоскостями действия ветра и ванты (см, п. 21, табл. 1, прил. 1).
Для элементов с Re^l,5*105 аэродинамические коэффициенты с*0 и £20 принимаются по табл. 5.
Таблица 5
|
ев |
10 I |
20 |
30 |
40 |
60 |
60 |
70 |
80 |
90 |
|
схй |
0,05 |
0.1 |
0,2 |
0,35 |
0,6 |
0,8 |
1,03 |
1,16 |
1,2 |
|
0,04 |
0,15 |
0,27 |
0,36 |
0,45 |
0,43 |
0,33 |
0,18 |
0 |
Если плоскости действия ветра н ванты совпадают (ср=0), то а = 0.
Приближенные значения с© и са могут быть вычислены по формулам, приведенным в упомянутом п. 21.
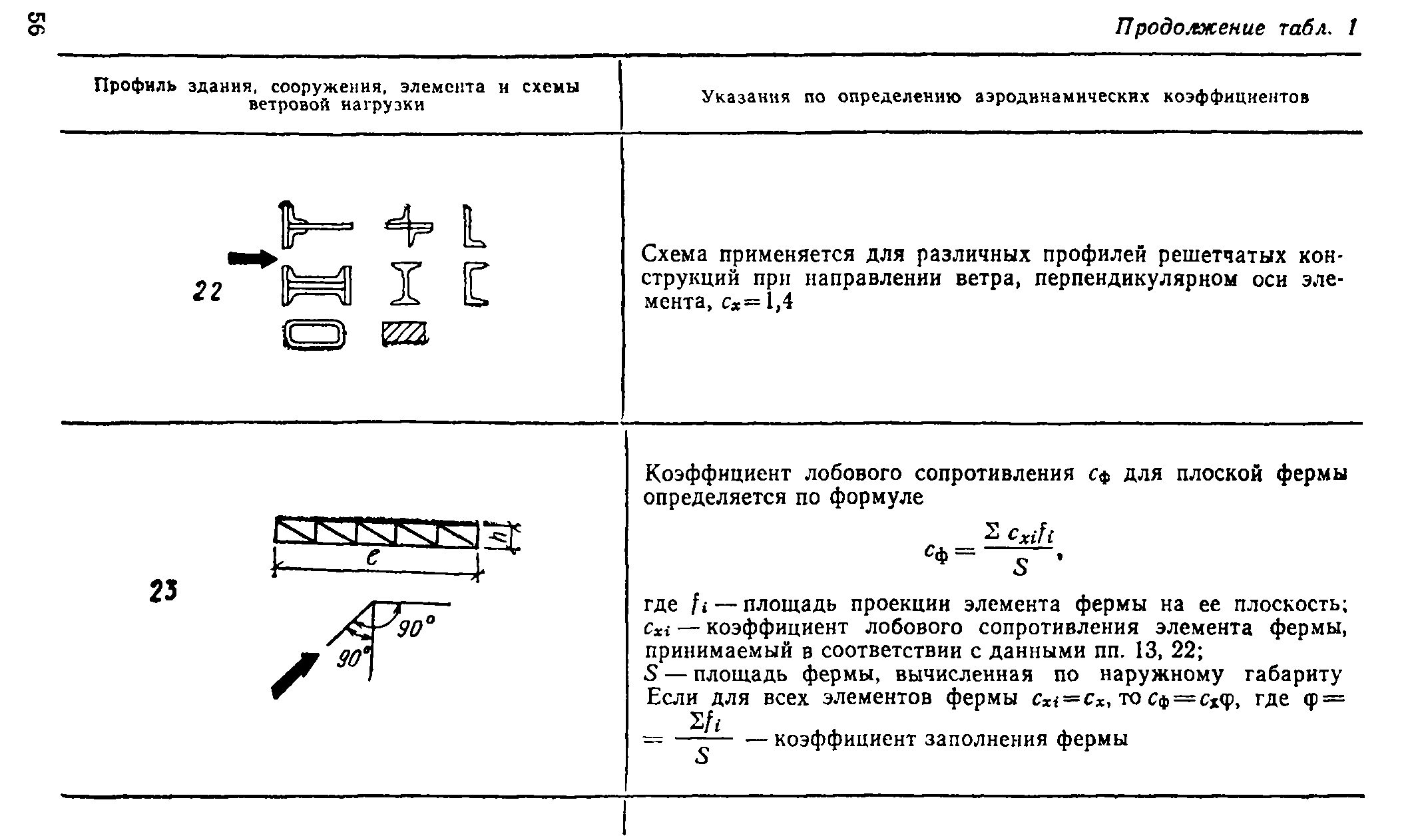
РЕШЕТЧАТЫЕ КОНСТРУКЦИИ
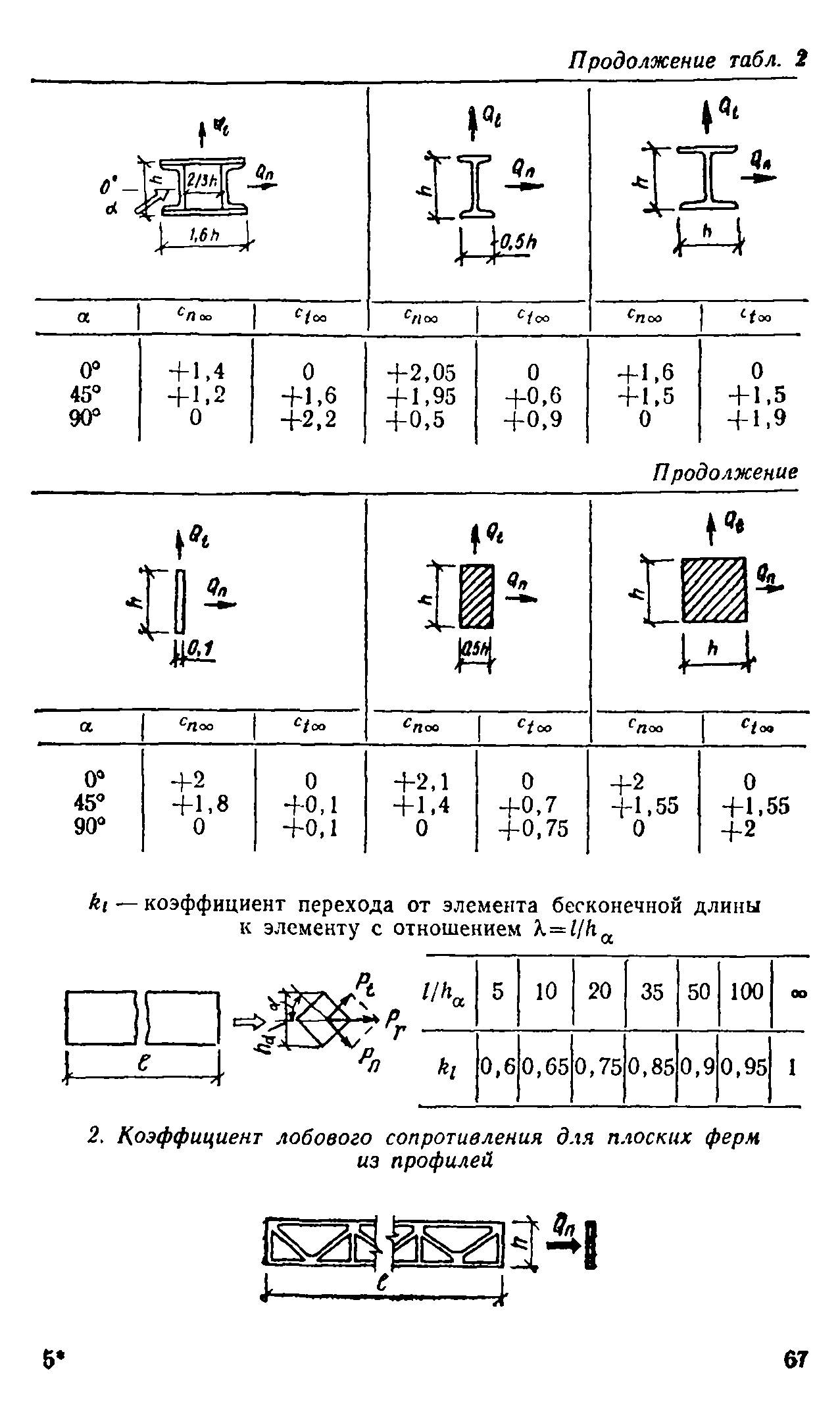
5.15. Аэродинамические коэффициенты сп и ct для конструктивных элементов решетчатых конструкций из простых и составных профилей приведены в табл. 2, прил. 1. Они зависят от угла атаки а и ог отношения Я высоты элемента к его характеристическому размеру.
Нормативное значение ветровой нагрузки на такие элементы определяется по формулам
(*) = к1 ел°о <?о/ W S и фн (г) = bt с to, %t (г) s.
15
ПРЕДИСЛОВИЕ
Руководство составлено к главе СНиП II-6-74 «Нагрузки и воздействия. Нормы проектирования».
В Руководстве приведены основные положения по определению ветровой нагрузки на здания и сооружения, а также указания по динамическому расчету высоких сооружений башенного типа (башни, дымовые трубы и т. п.), высоких зданий, антенно-мачтовых систем, градирен и др.
Рассмотрены вопросы аэродинамического возбуждения высоких сооружений и гибких призматических конструкции.
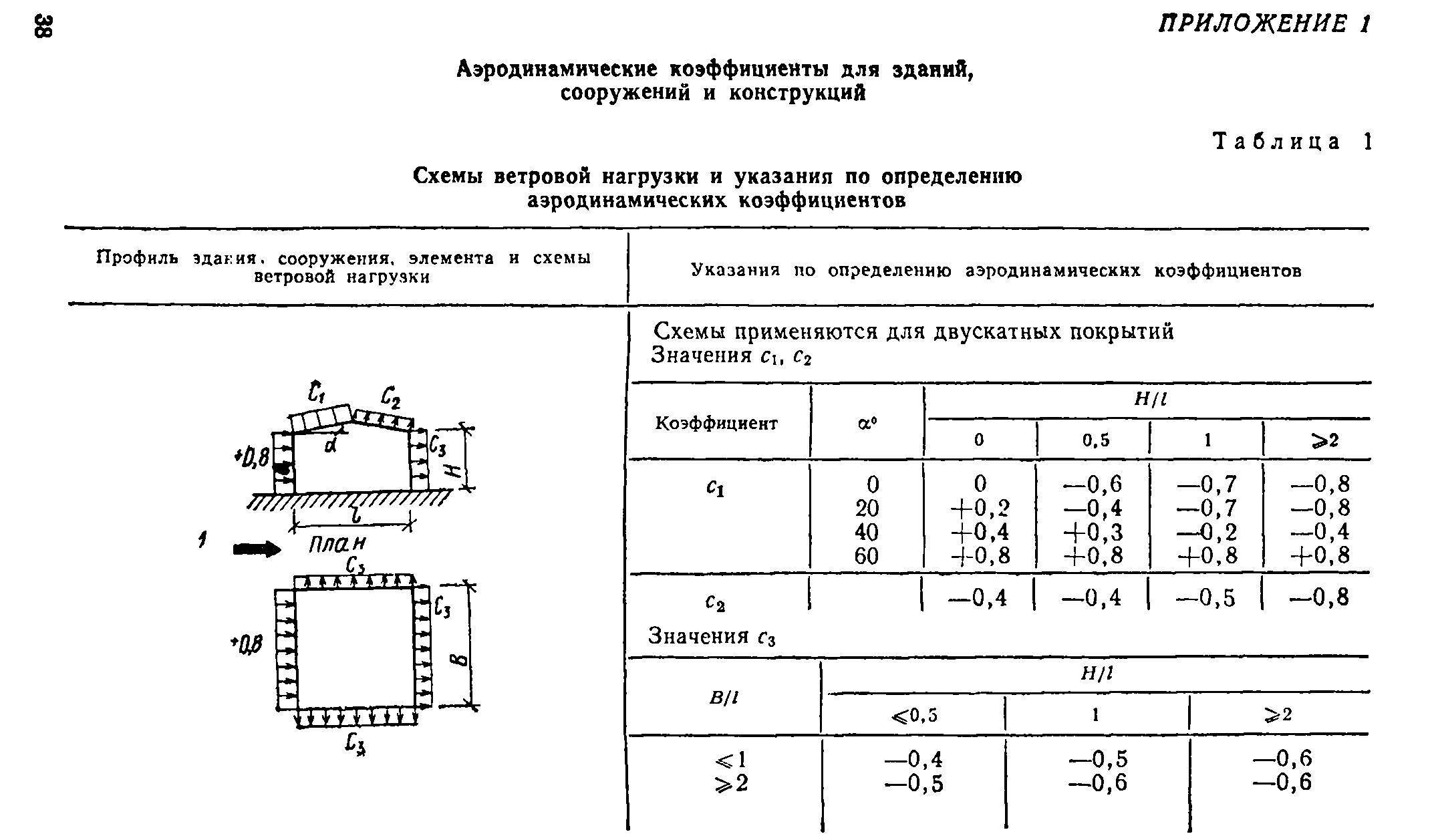
В прил. 1 приведены аэродинамические коэффициенты для зданий, сооружений и конструкций.
Прил. 2 содержит обоснование основных положений по определению статической составляющей ветровой нагрузки и метода динамического расчета высоких зданий и сооружений на действие турбулентного ветра.
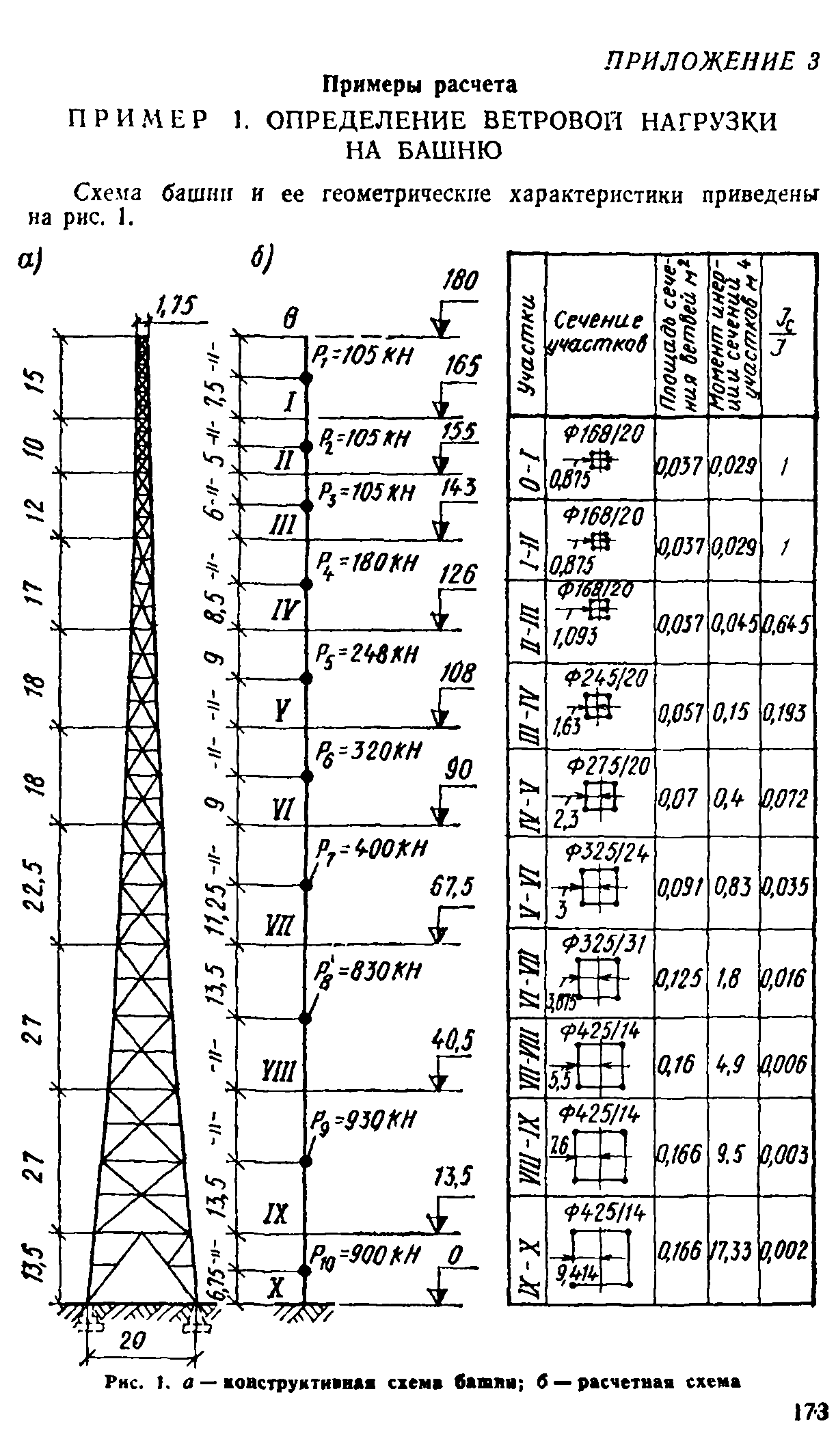
В прил. 3 даны примеры расчета высоких зданий н сооружений на действие ветра.
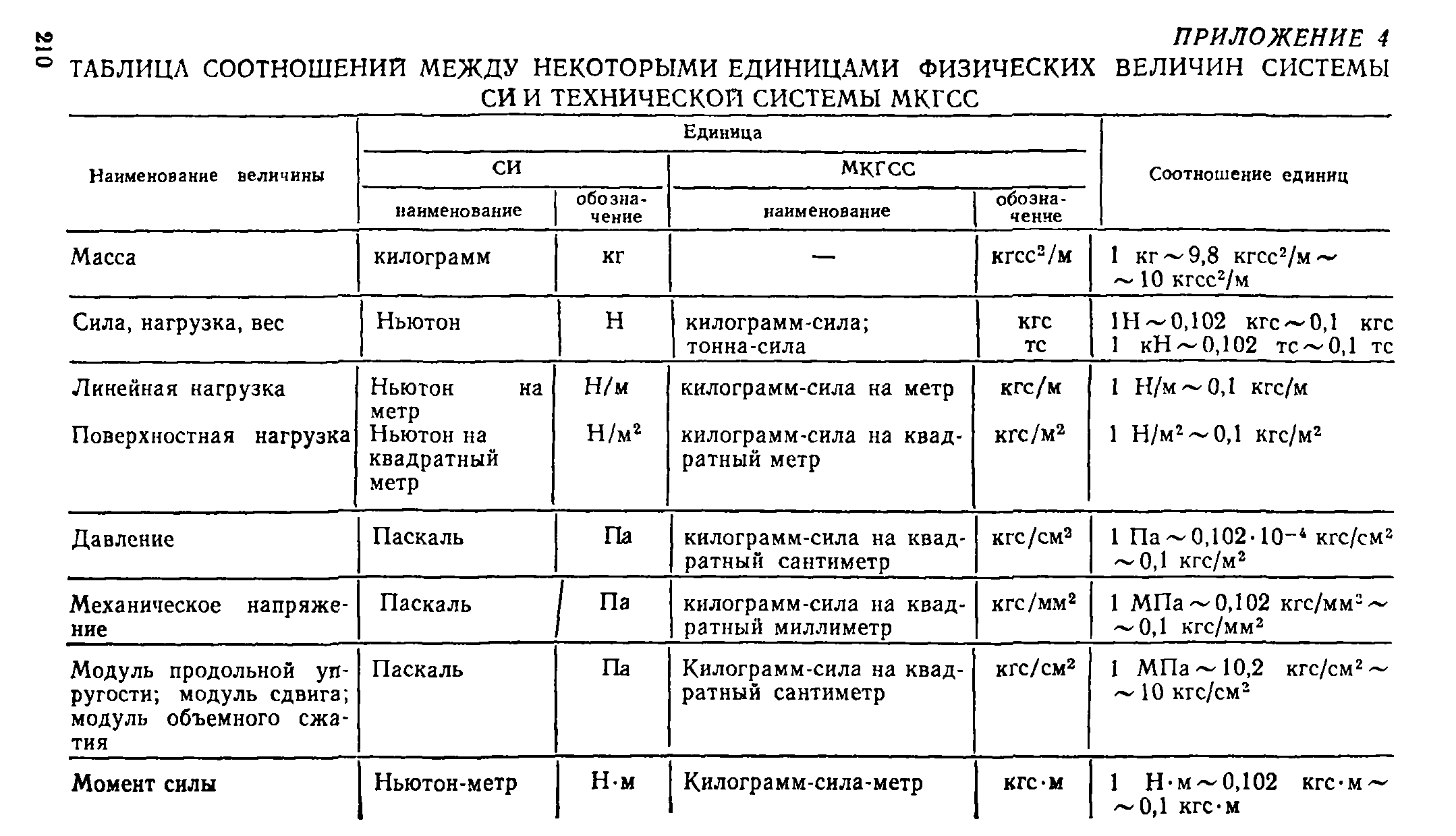
В Руководстве единицы физических величин приняты в системе СИ. Таблица соотношений между единицами этой системы и технической системы МКГСС дана в прил. 4.
Руководство разработано в отделении динамики сооружений Нейтрального научно-исследовательского института строительных конструкций им. В. А. Кучеренко канд. техн. наук М. Ф. Барштейном,
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Настоящее Руководство составлено к главе СНиП 11-6-74 «Нагрузки и воздействия. Нормы проектирования» и распространяется на проектирование промышленных, гражданских и сельскохозяйственных зданий и сооружений.
1.2. Здания и сооружения, проектируемые с учетом настоящего Руководства, должны удовлетворять требованиям главы СНиП 11-6-74 «Нагрузки и воздействия», а также требованиям, предъявляемым действующими нормативными документами к аналогичным зданиям и сооружениям.
1.3. Ветровая нагрузка на здания и сооружения должна определяться как сумма статической и динамической составляющих.
Статическая составляющая, соответствующая установившемуся скоростному напору, должна учитываться во всех случаях. Динамическая составляющая, вызываемая пульсациями скоростного напора, должна учитываться при расчете: сооружений с периодом собственных колебаний более 0,25 с (мачт, башен, дымовых труб, опор линий электропередачи, аппаратов колонного типа, транспортерных галерей, открытых этажерок и т. п.); многоэтажных зданий высотой более 40 м; поперечных рам одноэтажных однопролетных производственных здании высотой более 36 м при отношении высоты к пролету более 1,5.
1.4. Для высоких сооружении круговой цилиндрической формы (дымовых труб, мачт и т. п.) необходимо также производить поверочный расчет на резонанс, возникающий при таких скоростях ветра, когда частота срыва вихрей совпадает с собственной частотой колебаний сооружений поперек потока.
Примечание. В гибких призматических конструкциях при определенных скоростях ветра могут возникнуть колебания поперек потока, связанные с явлением аэродинамической неустойчивости таких тел. Указания по расчету и мероприятия по уменьшению колебаний таких конструкций устанавливаются на основании данных аэродинамических испытаний.
2. НОРМАТИВНОЕ ЗНАЧЕНИЕ СТАТИЧЕСКОЙ СОСТАВЛЯЮЩЕЙ ВЕТРОВОЙ НАГРУЗКИ.
КОЭФФИЦИЕНТЫ ПЕРЕГРУЗКИ
2.1. Нормативное значение статической составляющей ветровой нагрузки д* (г) должно опредляться по формуле
Чп(г) = qot(z)c, Па, (I)
где
<?о< (*) = <?о kt (г);
П
qo = pvQ/2—нормативный скоростной напор ветра на высоте 10 м над поверхностью земли, принимаемый по п. 3.1; р — плотность воздуха, кг/м3; v0 — скорость ветра на высоте 10 м над поверхностью земли, м/с; kt(z)— коэффициент, учитывающий изменение скоростного напора по высоте, принимаемый в соответствии с указаниями, изложенными в пп. 4.1—4.4; с—аэродинамический коэффициент, принимаемый по табл. 1, прил. ],
4
2,2. Коэффициент перегрузки для ветровой нагрузки на здания па должен приниматься равным 1,2; на высокие сооружения, где ветровая нагрузка имеет решающее значение, лп=1,3, если в нормах проектирования этих сооружений не приводится другое значение этого коэффициента. Коэффициент перегрузки пп для дымовых труб высотой от 150 до 300 м рекомендуется принимать равным 1,4, выше 300 м — 1,5.
3. НОРМАТИВНЫЕ СКОРОСТНЫЕ НАПОРЫ
3.1. Нормативный скоростной напор ветра (qn) для данного географического района устанавливается на основе статистическою анализа климатологических данных по скоростям ветра в этом районе (районы СССР принимаются по карте, приведенной в главе СНиП 11-6-74 «Нагрузки и воздействия. Нормы проектирования»).
Скоростные напоры qo в зависимости от района СССР должны приниматься по табл. 1.
|
Таблица 1 |
||||||||||||||||
|
Для обозначенных на карте горных и мало изученных районов скоростной напор ветра допускается уточнять по данным Гидрометеорологической службы, а также по результатам обследования районов строительства с учетом опыта эксплуатации. При корректировке нормативный скоростной напор допускается определять по формуле
Яо =- 0.613 (осе’о)2, Па, (2)
где vo — скорость ветра (при двухминутном интервале осреднения), превышаемая в среднем один раз в пять лет, если техническими условиями, утвержденными в установленном порядке, не регламентированы другие периоды повторяемости скорости ветра; а=0,75+-5
+ —* — коэффициент к скоростям ветра, полученным из обработки
Е’О
наблюдений по флюгеру, принимаемый не более единицы; при использовании малоинерционных анемометров коэффициент а принимается равным единице.
Указания по определению скорости ветра заданной обеспеченности (с заданным периодом повторяемости) даны в п. 3, прнл. 2.
3.2. В случаях когда при расчете здания (сооружения) имеют значения ветры одного-двух румбов, допускается при наличии достоверных данных о скоростях ветра по различным направлениям учитывав направление ветра и определять его скорость заданной обеспеченности по указаниям п. 3, прил. 2,
5
4. ИЗМЕНЕНИЕ СКОРОСТНЫХ НАПОРОВ ВЕТРА ПО ВЫСОТЕ
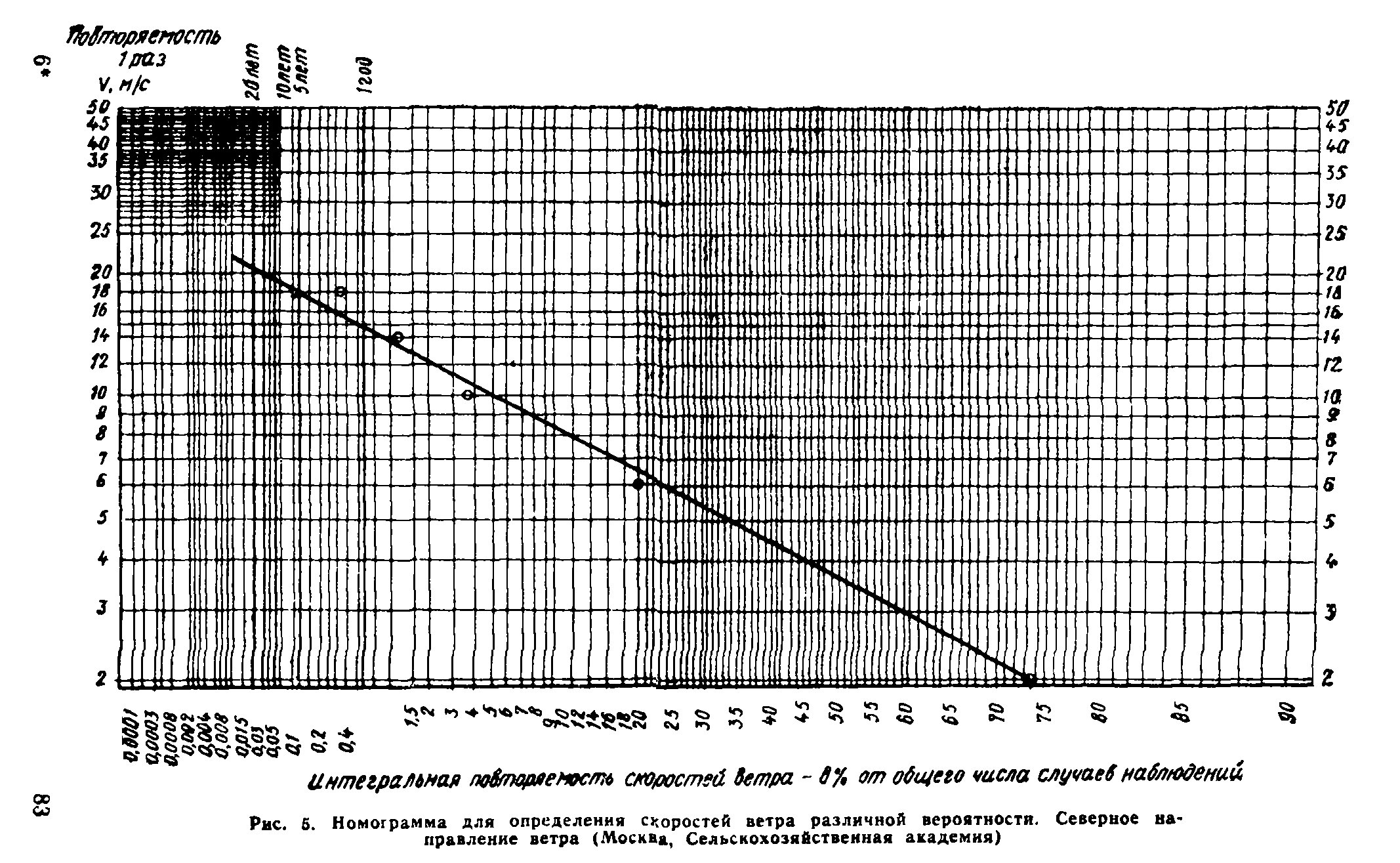
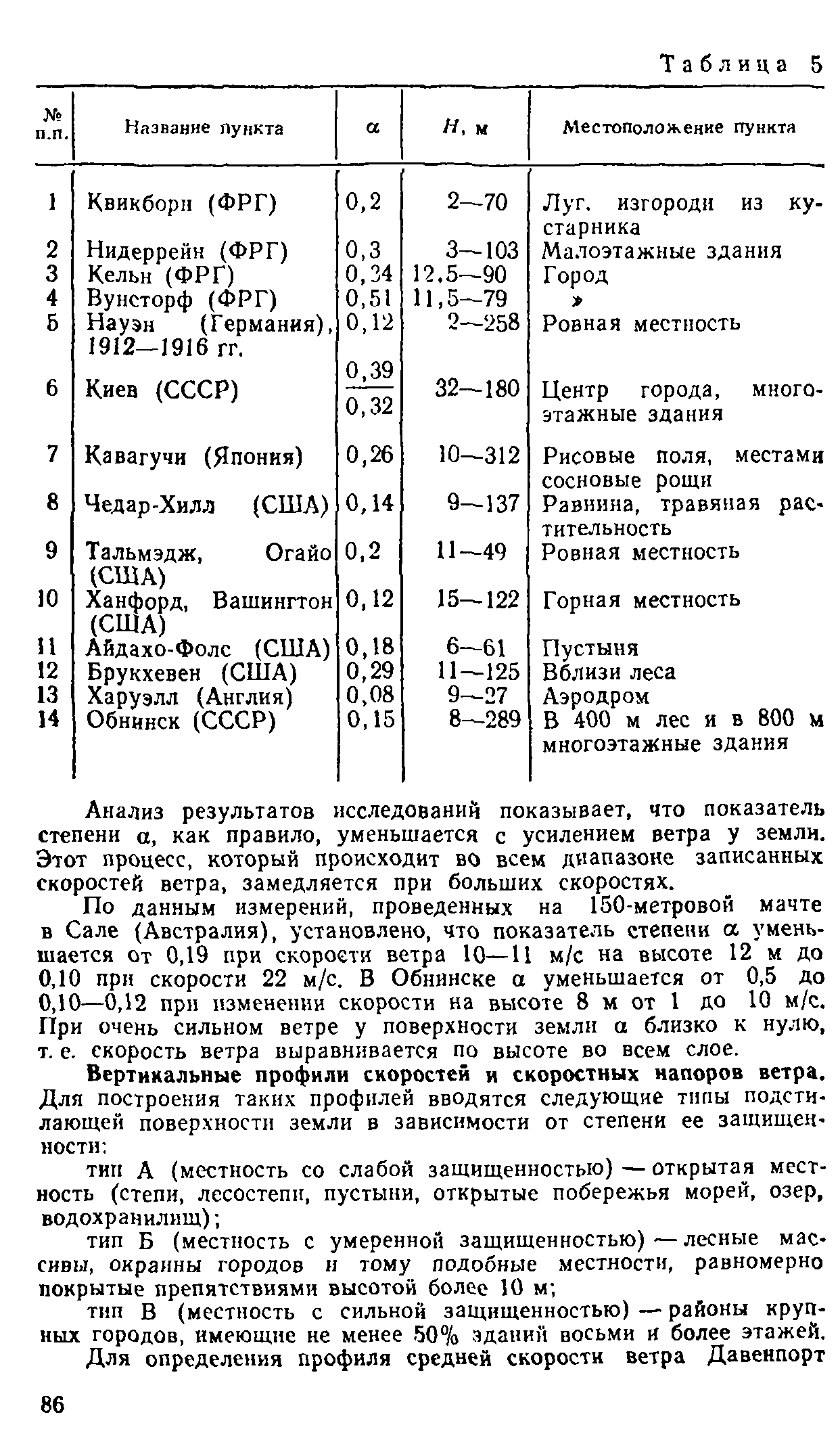
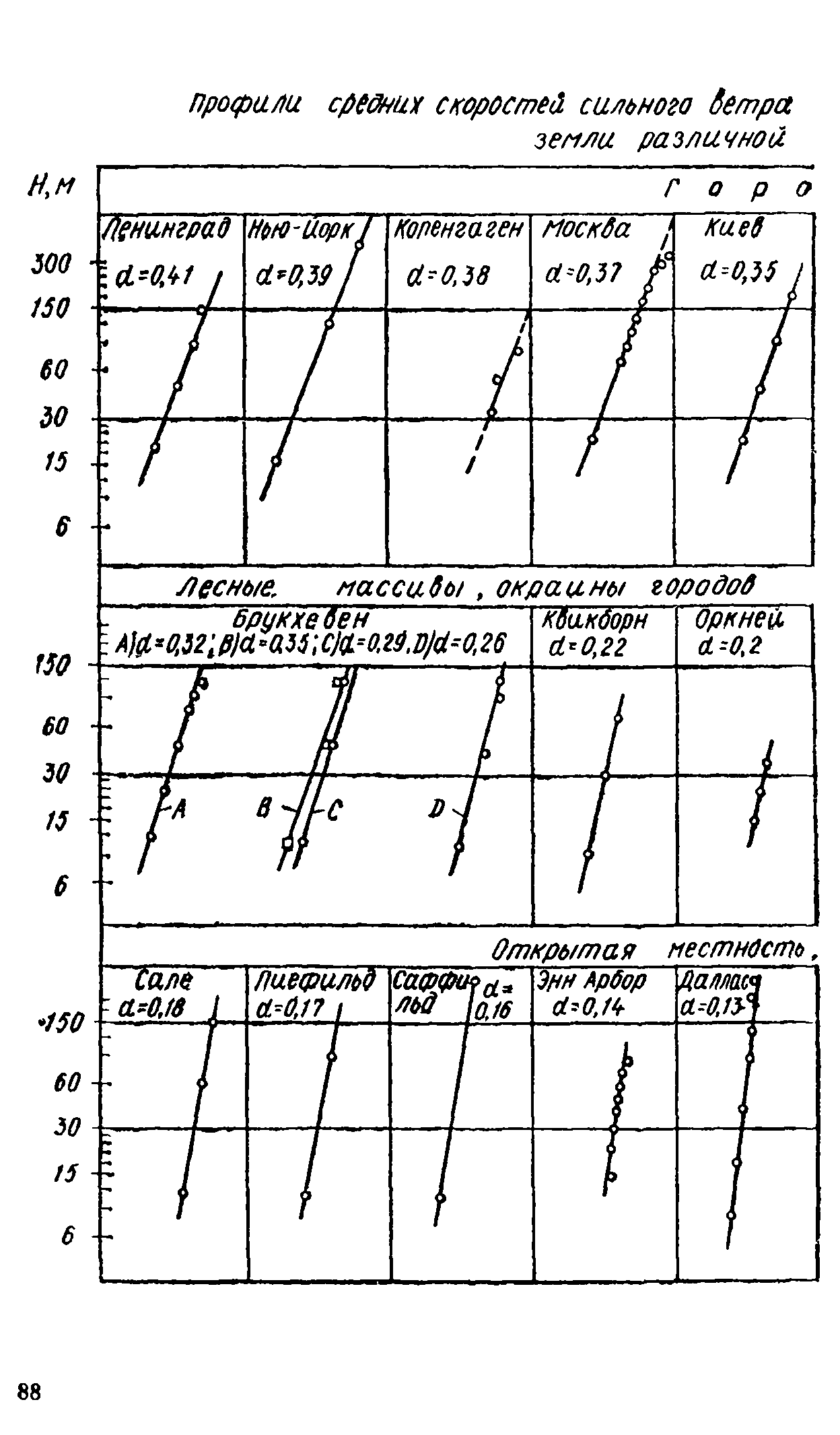
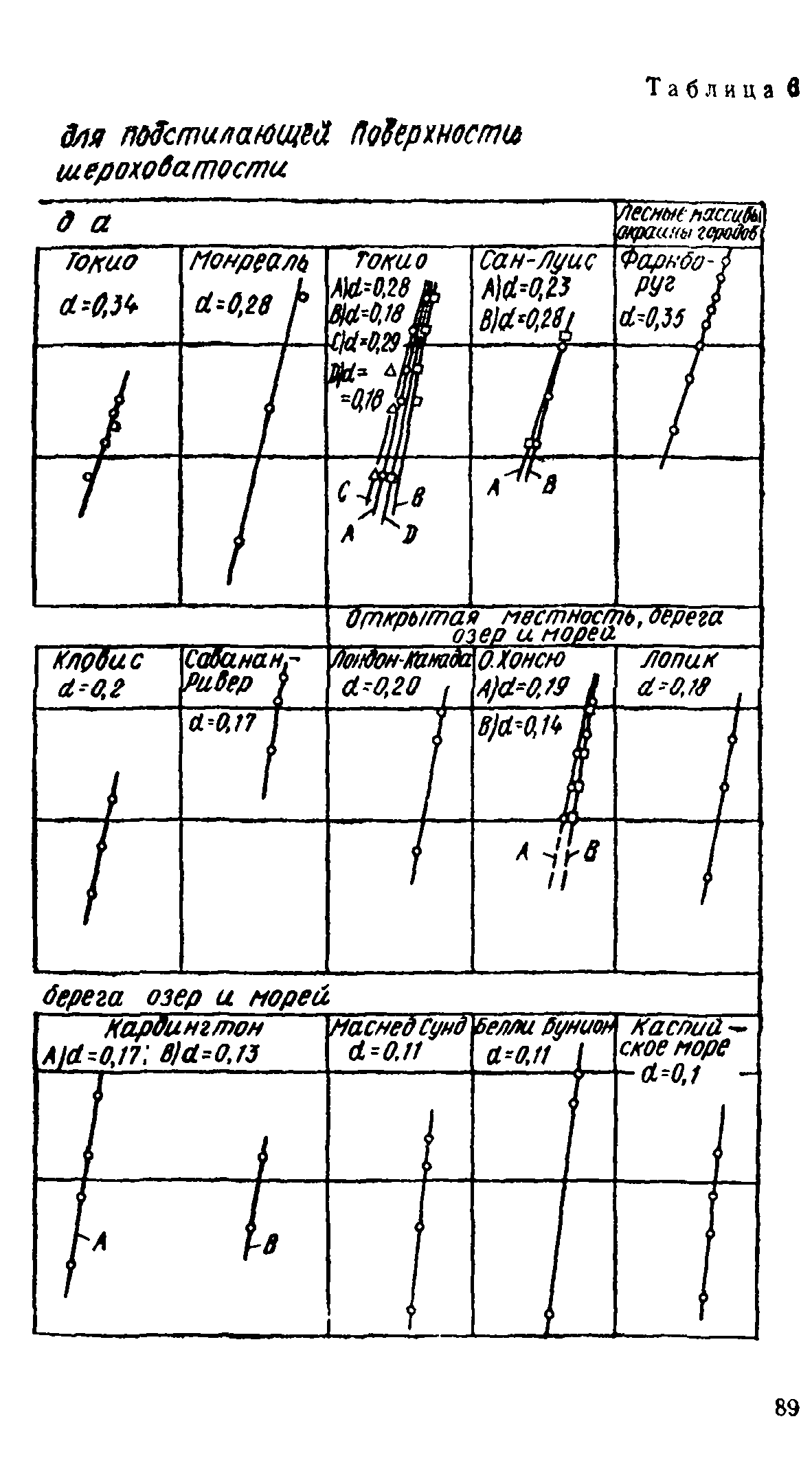
4.1. Для определения скоростного напора ветра q<n(z) по высоте сооружения используется степенной закон изменения нормативной скорости ветра с высотой в нижнем слое атмосферы. Показатель степени в этом законе зависит от шероховатости подстилающей поверхности и от самой скорости ветра (см, п. 4, прил. 2).
В зависимости от шероховатости подстилающей поверхности земли различают местности типа А, Б и В. К типу А относятся открытые местности (степи, лесостепи, пустыни, открытые побережья морей, озер, водохранилищ). К типу Б относятся города, лесные массивы и тому подобные местности, равномерно покрытые препятствиями высотой более 10 м. К типу В относятся районы крупных городов, имеющие не менее 50% зданий восьми и более этажей.
В главе СНиП II-6-74 приняты два профиля для нормативных скоростных напоров: один для открытой местности (тип А), другой для городов и лесных массивов (тип Б).
Жилые районы в крупных городах со зданиями повышенной этажности и высокими зданиями (25—30 этажей) при надлежащем обосновании могут быть отнесены к местности типа В.
Вертикальные профили скоростных напоров для местности типа БиВ применяются в тех случаях, когда эти местности в направлении действия ветра имеют протяженность не менее 1,5—2 км, при этом в зависимости от шероховатости эти профили могут меняться для разных направлений.
Для сооружений, возводимых в открытом море, скоростной напор определяется по скорости, записанной в районе расположения сооружения.
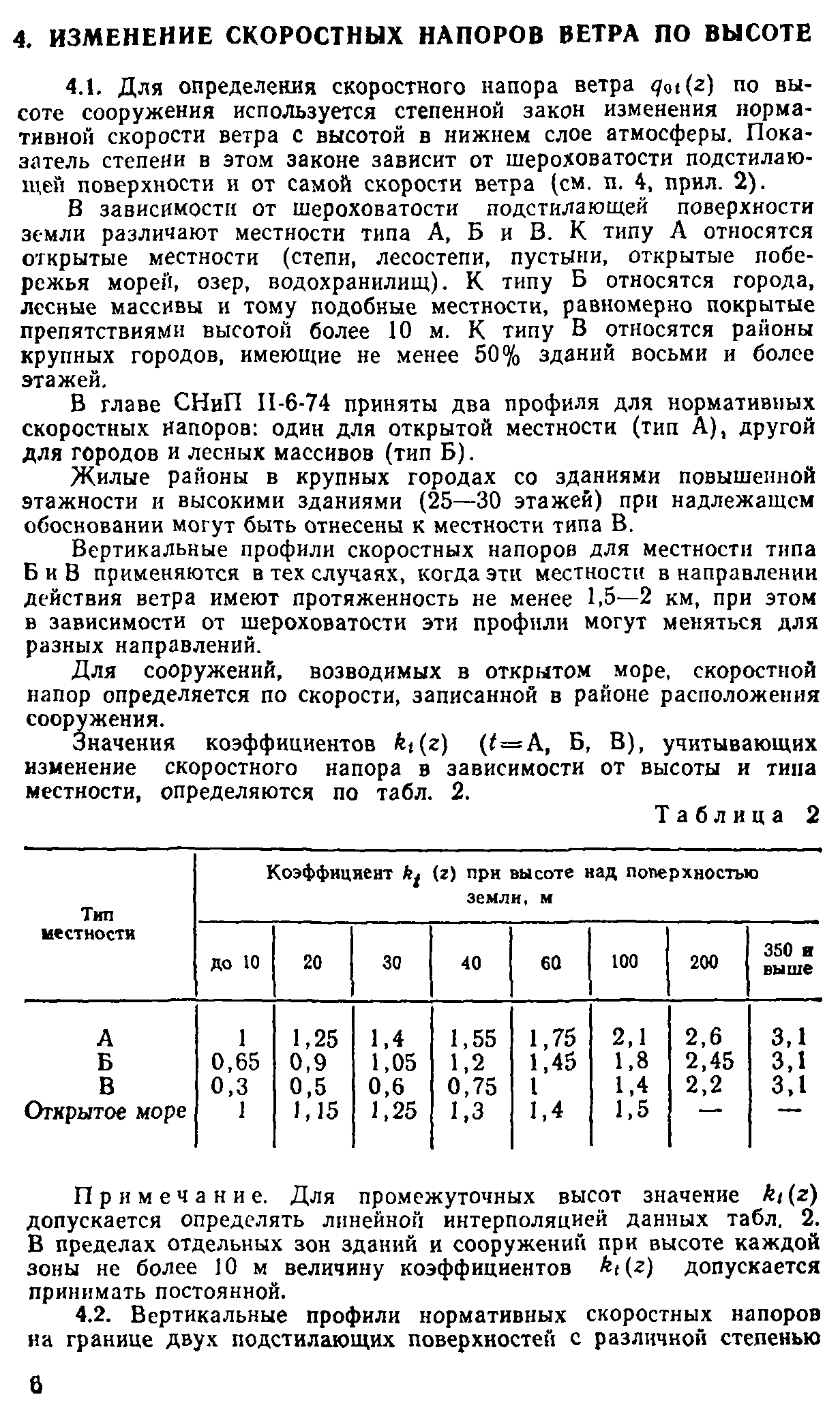
Значения коэффициентов ftt(z) (*=А, Б, В), учитывающих изменение скоростного напора в зависимости от высоты и тина местности, определяются по табл. 2.
Таблица 2
|
Тип местности |
Коэффициент ki |
(г) при высоте над поперхностью земли, м |
||||||
|
до Ю |
20 |
30 |
40 |
6Q |
100 |
200 |
350 я выше |
|
|
А |
1 |
1,25 |
1,4 |
1,55 |
1,75 |
2,1 |
2,6 |
3,1 |
|
Б |
0,65 |
0,9 |
1,05 |
1,2 |
1,45 |
1,8 |
2,45 |
3,1 |
|
В |
0,3 |
0,5 |
0,6 |
0,75 |
1 |
1,4 |
2,2 |
3,1 |
|
Открытое море |
1 |
1,15 |
1,25 |
1.3 |
1,4 |
1.5 |
-” |
Примечание. Для промежуточных высот значение k\ (г) допускается определять линейной интерполяцией данных табл, 2. В пределах отдельных зон зданий и сооружений при высоте каждой зоны не более 10 м величину коэффициентов kt(z) допускается принимать постоянной.
4.2. Вертикальные профили нормативных скоростных напоров на границе двух подстилающих поверхностей с различной степенью
б
|
aj 6) |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Рис. 1. Условные уровни от которых отсчитывается высота сооружения |
2—£
а —в точке A: zc*=Zi\ на участке ВС гс—г\+ -z\ за точкой О
2с-га. На участках АВ и CD zc определяется линейной интерполяцией; б — на участках АВ и ВС: zc=zx\ за точкой Огс~гг
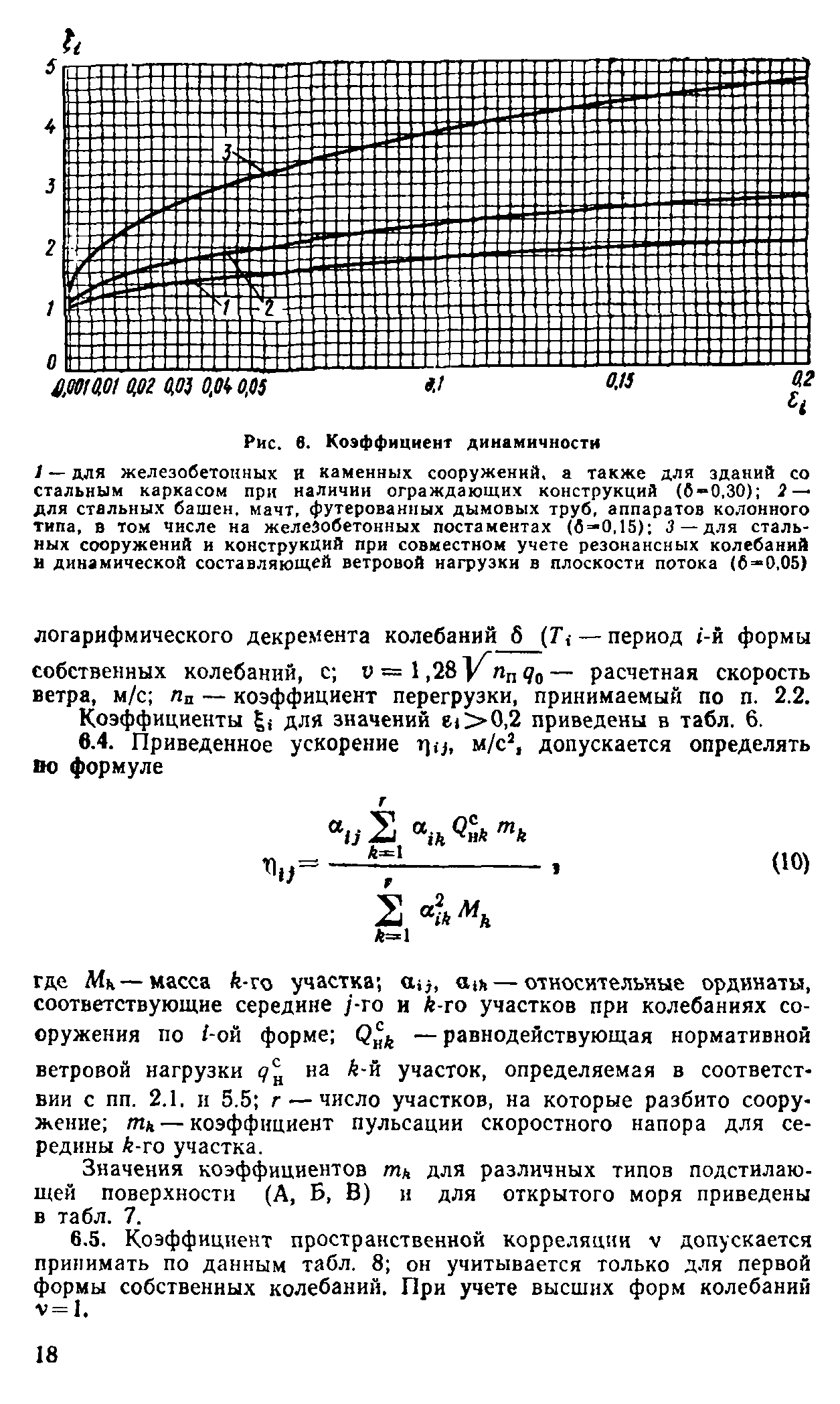
защищенности (см. л. 4, прил. 2) определяются по формулам! при z > б 9о1 (2) = <7о *1 (2); при 2 < б до1 (г) = q0 (б) (г/б)2а*, (3)
где *, (г) = (10) (г/10)2а>.
Параметр £i(10) относится к местности, расположенной выше по потоку, принимается по табл. 2. Показатели степени си и а2 относятся к местностям, расположенным соответственно выше и ниже по потоку.
Глубина внутреннего пограничного слоя б, зависящая от расстояния х от границы до точки, для которой строится переходной профиль, принимается по табл. 3.
Таблица 3
|
Граница местностей типа |
«1 |
аа |
Глубина пограничного слоя б при расстоянии х, м |
|||
|
50 |
200 |
500 |
2000 |
|||
|
А И Б |
0,16 |
0,22 |
11 |
35 |
70 |
215 |
|
Б и В |
0,22 |
0,33 |
19 |
55 |
110 |
340 |
|
Б и А |
0,22 |
0,16 |
9 |
22 |
55 |
165 |
|
В и Б |
0,33 |
0,22 |
13 |
42 |
90 |
260 |
4.3. Для зданий высотой до 5 м, расположенных на местности типа А, скоростной напор, определяемый по табл. 1, допускается сьижать на 25%.
4.4. Для зданий высотой до 40 м, расположенных в местности типа В, скоростной напор принимается как для местности типа Б.
4.5. Если поверхность земли вокруг здания не горизонтальна, то при уклоне t ^ 0,3 высота сооружения Н определяется от его основания.
При уклонах 0,3</<2 и 1^2 условный уровень zCt от которого отсчитывается высота сооружения, определяется по рис. 1,
7
5. ВЕТРОВАЯ НАГРУЗКА НА ЗДАНИЯ, СООРУЖЕНИЯ И КОНСТРУКЦИИ.
АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ
ОБЩИЕ УКАЗАНИЯ
5.1. Ветровая нагрузка на здания (сооружения) зависит от нх формы, положения в пространстве и проницаемости ограждений.
Различают многоугольные (квадратные, прямоугольные и т. п.) и круглые в плане здания и сооружения, навесы, решетчатые сооружения, конструкции специальных форм.
По своему положению в пространстве конструкции могут быть установлены на поверхности земли или примыкать к плоскостям больших размеров; аэродинамически изолированы в пространстве, если расстояние до земли или до соседней стены более их размера по вертикали или по нормали к стене; заключены между двумя параллельными плоскостями больших размеров.
Конструкции, расположенные на поверхности земли и примыкающие к плоскости больших размеров (другое здание или стена), с аэродинамической точки зрения подобны конструкции высотой 2// (рис. 2, а) или длиной 2В (рис. 2,6). Конструкции расположенные на поверхности земли и заключенные между двумя параллельными плоскостями больших размеров, подобны конструкции с бесконечной длиной (рис. 2,в).
Проницаемостью ограждения р, %, называется отношение суммарной площади проемов ограждения отдельной грани здания к ее общей площади.
Различают здания закрытые, имеющие небольшие равномерно распределенные проемы со средней проницаемостью ограждений р^5%. При р=0 здание герметически закрыто. Жилые и гражданские здания практически являются закрытыми зданиями; частично открытые с ограждениями, имеющими среднюю проницаемость 5%<р<30%; открытые со средней проницаемостью ограждения р>30%. Частично открытые и открытые здания имеют одну или несколько стен, открытых частично или полностью.
Примечание. При проектировании зданий необходимо учитывать, что в ряде случаев давление ветра на здание в процессе монтажа (при отсутствии наружных стен) может быть больше, чем в законченном здании.
5.2. Схемы распределения ветровой нагрузки и значения аэродинамических коэффициентов с должны приниматься в соответствии с указаниями табл. 1, прил. 1; при этом промежуточные значения коэффициентов допускается определять линейной интерполяцией.
Аэродинамические коэффициенты принимаются:
а) для отдельных поверхностей или точек зданий и сооружений — как коэффициенты давления, которые следует учитывать при определении ветровой нагрузки, нормальной к рассматриваемой поверхности и относящейся к единице площади этой поверхности.
Положительным значениям коэффициента давления соответствует направление давления к поверхности сооружения, а отрицательным значениям — направление от поверхности сооружения.
Поверхности, подверженные непосредственному воздействию потока ветра, называются наветренными, заветренные поверхности воспринимают воздействия отсоса (отрицательного давления). Ко-
8
|
Рис. 2. Положение конструкции в пространстве |
а, б — конструкция расположена на поверхности земли или примыкает к плоскости больших размеров; в — конструкция заключена между двумя параллельными плоскостями больших размеров
эффиаиенты давления изменяются от точки к точке поверхности. Для простоты при определении ветровой нагрузки принимаются их значения, осредненные по отдельным граням или зонам поверхности;
б) для отдельных элементов и конструкций — как коэффициенты лобового сопротивления сх и поперечной силы си, которые следует учитывать при определении составляющих общего сопротивления тела, действующих по направлению скорости потока и перпендикулярно ему и относящихся к площади проекции тела на плоскость, перпендикулярную потоку, и как коэффициент подъемной силы сг при определении вертикальной составляющей общего сопротивления тела. Последняя относится к площади проекции тела на горизонтальную плоскость;
в) при направлении ветра под углом а к наветренной стороне конструкции — как коэффициенты сп и ct, которые должны учитываться при определении составляющих общего сопротивления тела, действующих в направлении его осей и относящихся к площади наветренной грани.
В случаях, не предусмотренных табл. 1, прил. 1 (иные формы зданий и сооружений, учет при надлежащем обосновании других направлений ветрового потока или составляющих общего сопротивления тела по другим направлениям и т. п.), аэродинамические коэффициенты необходимо принимать по справочным и экспериментальным данным.
ВЕРТИКАЛЬНЫЕ ПОВЕРХНОСТИ
5.3. Коэффициенты давления принимаются: для наветренных вертикальных поверхностей с=+0,8, для заветренных с~—0,6.
Для вертикальных и отклоняющихся от вертикальных не более чем на 15° поверхностей в зданиях с многорядным расположением фонарей и другим сложным профилем (если в табл. 1, прил. 1 нет соответствующих схем) коэффициенты давления принимаются для крайних и возвышающихся промежуточных поверхностей: наветренных с = +0,7, заветренных с==—0,6; для промежуточных поверхностей (наветренных и заветренных) с——0,5.
Ветровая нагрузка на вертикальную стену равна разности на-1рузок на наветренную и заветренную плоскости стены. Коэффнцн-
9
енты давления для этих плоскостей учитываются со своими знаками. Принимается, что плоский характер стен не нарушается выступами, балконами, лоджиями.
ЗАКОНЫ ПОДОБИЯ. СОСТАВЛЯЮЩИЕ ВЕТРОБОИ НАГРУЗКИ
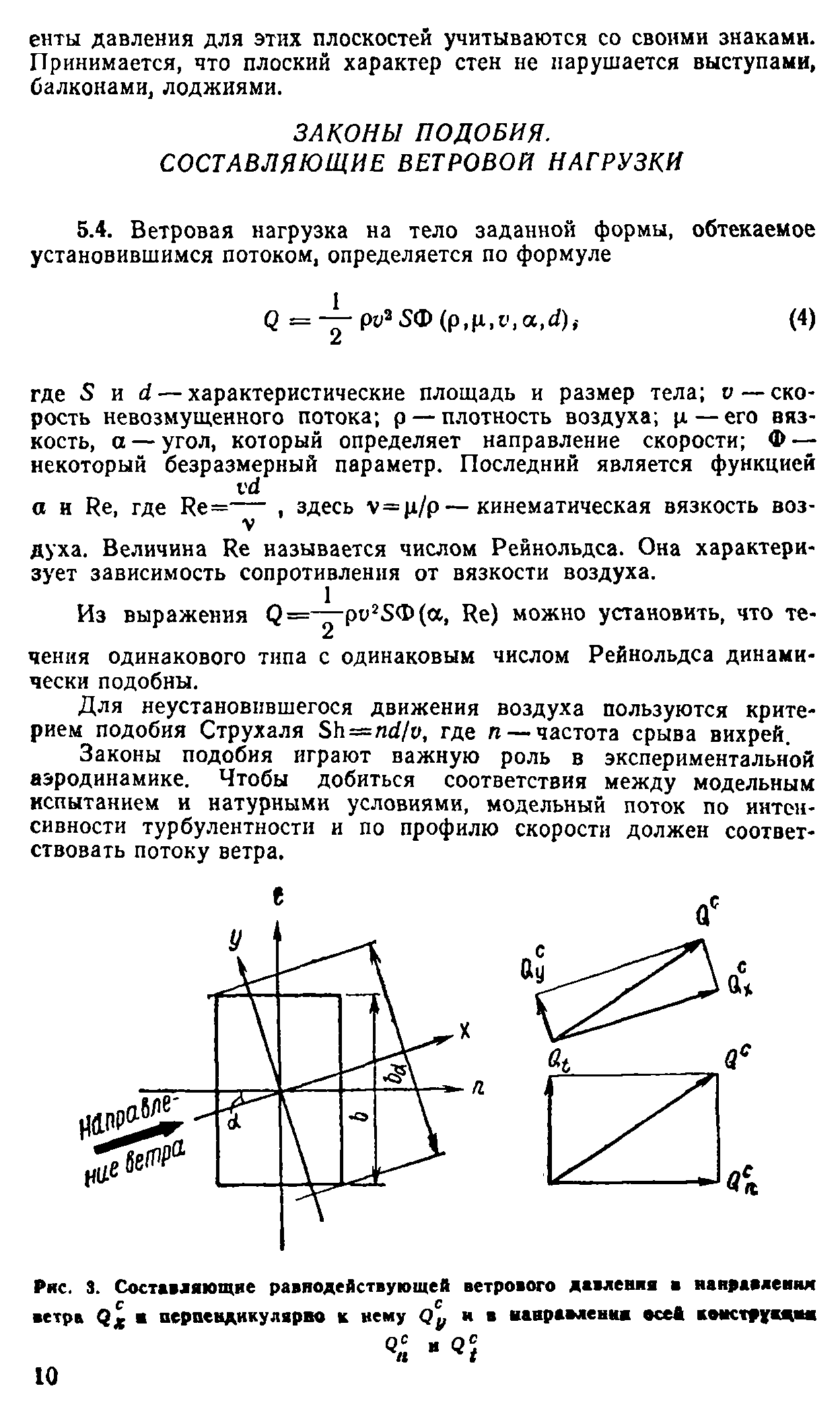
5.4. Ветровая нагрузка на тело заданной формы, обтекаемое установившимся потоком, определяется по формуле
Q =-^-руа 5Ф (p.n.t’.a.d), (4)
где 5 и d — характеристические площадь и размер тела; v — скорость невозмущенного потока; р — плотность воздуха; р. — его вязкость, а —угол, который определяет направление скорости; Ф — некоторый безразмерный параметр. Последний является функцией vd
а и Re, где Re—— , здесь v=p/p—кинематическая вязкость воз-v
духа. Величина Re называется числом Рейнольдса. Она характеризует зависимость сопротивления от вязкости воздуха.
Из выражения Q=— pu2S<D(a, Re) можно установить, что течения одинакового типа с одинаковым числом Рейнольдса динамически подобны.
Для неустановившегося движения воздуха пользуются критерием подобия Струхаля Sh=m//p, где п — частота срыва вихрей.
Законы подобия играют важную роль в экспериментальной аэродинамике. Чтобы добиться соответствия между модельным испытанием и натурными условиями, модельный поток по интенсивности турбулентности и по профилю скорости должен соответствовать потоку ветра.
е
|
Рис. 3. Составляющие равнодействующей ветрового давления в направления ветра Q# а перпендикулярно к нему qJ и в нанр вменив осей комструящия |
ас
п Q
10


 СНиП II-6-74 «Нагрузки и воздействия»
СНиП II-6-74 «Нагрузки и воздействия»