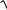Руководство к решению задач по курсу аналитической химии

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

                    Г. Н. Шрайбман
РЕШЕНИЕ ЗАДАЧ
ПО АНАЛИТИЧЕСКОЙ
ХИМИИ
Учебное пособие

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кемеровский государственный университет»
РЕШЕНИЕ ЗАДАЧ
ПО АНАЛИТИЧЕСКОЙ ХИМИИ
Учебное пособие
3-е издание, переработанное и дополненное
Кемерово 2015

УДК 543(076.1):378.147.227
ББК Г4я73-41
Ш 85
Печатается по решению редакционно-издательского совета
Кемеровского государственного университета
Рецензенты:
д. х. н., профессор, ведущий научный сотрудник Института углехимии и химического ма¬
териаловедения СО РАН Е. В. Остапова,
к. х. н., доцент кафедры аналитической химии и экологии Кемеровского технологического
института пищевой промышленности О. В. Беляева
Авторы:
Г. Н. Шрайбман, П. Д. Халфина, О. Н. Булгакова, Н. В. Иванова
Шрайбман , Г. Н.
Ш 85 Решение задач по аналитической химии: учеб. пособие. - 3-е изд., перераб и
доп. / Г. Н. Шрайбман [и др.]; под ред. Г. Н. Шрайбман; Кемеровский государст¬
венный университет. - Кемерово, 2015. - 208 с.
ISBN 978-5-8353-1821-6
Учебное пособие разработано по дисциплине «Аналитическая химия» в со¬
ответствии с требованиями Федерального государственного образовательного
стандарта высшего профессионального образования по специальности «Фундамен¬
тальная и прикладная химия». В пособии приведена методика решения типовых за¬
дач и задач повышенной сложности по основным разделам аналитической химии:
химическому равновесию в гомогенных и гетерогенных системах, гравиметриче¬
скому и титриметрическому анализу, методам разделения и концентрирования. В
каждом разделе дано краткое теоретическое введение, облегчающее понимание ме¬
тодики расчетов, и включены задания для самостоятельного решения. Приложение
содержит необходимую справочную информацию. Пособие направлено на разви¬
тие у студентов навыков самостоятельной работы при выполнении контрольных и
индивидуальных заданий, на формирование правильного подхода к оформлению
решения задач в соответствии с рекомендованными обозначениями величин и еди¬
ниц СИ в химии.
Пособие предназначено для студентов специальности «Фундаментальная и
прикладная химия», а также может использоваться студентами направления подго¬
товки «Химия» и другими направлениями подготовки при проведении аналитиче¬
ских расчетов.
УДК 543(076.1):378.147.227
ББК Г 4 я 73-41
ISBN 978-5-8353-1821-6	© Шрайбман Г. Н., Халфина П. Д.,
Булгакова О. Н., Иванова Н. В., 2015
© Кемеровский государственный университет, 2015

ПРЕДИСЛОВИЕ
Аналитическая химия - одна из важнейших химических дисцип¬
лин, изучаемых студентами химического и биологического факультетов.
Она является научной основой химического анализа. В связи с этим при
изучении аналитической химии предусматривается усвоение теоретиче¬
ских разделов и приобретение практических навыков химика-аналитика
в ходе выполнения объемного лабораторного практикума. Глубокому ус¬
воению теоретических основ современных аналитических методов и
грамотному проведению расчетов на всех стадиях анализа способствует
решение задач, касающихся теории и практики различных разделов ана¬
литической химии.
Основная задача данного пособия - детальное обсуждение реше¬
ния типовых задач по важнейшим разделам теоретической аналитиче¬
ской химии в пределах программы курса (ионным химическим равнове¬
сиям в гомогенных и гетерогенных системах), а также рассмотрение
расчетов в гравиметрии и титриметрии, базирующихся на знании ион¬
ных равновесий. Каждому такому разделу посвящена отдельная глава. В
начале главы приводится краткое теоретическое введение с пояснения¬
ми к формулам, используемым для расчетов, обсуждаются границы их
применения. Каждое из рассматриваемых положений иллюстрируется
расчетным примером. В конце главы предлагаются задачи для само¬
стоятельного решения. Обсуждаются вопросы статистической обработ¬
ки и представления результатов количественного анализа. В специаль¬
ном приложении содержится необходимая справочная информация.
Пособие предназначено для оказания методической помощи в са¬
мостоятельной работе при выполнении индивидуальных заданий и кон¬
трольных работ студентами химического факультета, а также студентами
биологического факультета очной и заочной форм обучения. Для студен¬
тов-химиков особую ценность представляет глава, посвященная расчетам
при протекании окислительно-восстановительных реакций. В ней круг
рассматриваемых примеров значительно шире, чем в известных сборни¬
ках задач и упражнений по аналитической химии.
Решение задач занимает в химическом образовании важное место,
так как это один из приемов обучения, посредством которого обеспечи¬
вается более глубокое и полное усвоение учебного материала и выраба¬
тывается умение самостоятельного применения приобретенных знаний.
Студент, избравший химическую специальность, должен овладеть в со¬
вершенстве простейшими приемами умственной деятельности (выделе-
3

ние главного, сравнение, анализ, обобщение и др.), развить творческое
мышление.
Разработанное пособие направлено на формирование профессио¬
нальных компетенций:
-	знание основ теории фундаментальных разделов химии (прежде всего
неорганической, аналитической, органической, физической, химии высоко¬
молекулярных соединений, химии биологических объектов, химической тех¬
нологии);
-	понимание необходимости и способность приобретать новые знания
с использованием современных научных методов и владение ими на уровне,
необходимом для решения задач, имеющих естественнонаучное содержание
и возникающих при выполнении профессиональных функций.
Обращаясь к студентам, которые пожелают воспользоваться дан¬
ным пособием, мы можем дать ряд общих рекомендаций:
■	не стремитесь решать задачу по предложенному образцу; вос¬
пользуйтесь им, если не сможете самостоятельно найти путь решения;
■	решая задачу, попытайтесь осознать свою собственную деятель¬
ность (понять сущность задачи и представить ход ее решения);
■	проанализируйте содержание задачи, определите тему, раздел
АХ, которому она посвящена;
■	продумайте общий ход решения задачи и последовательность
действий;
■	определитесь в химических понятиях, математических действи¬
ях, обозначениях физических величин, используемых в данной задаче;
■	в решении выделите химическую и математическую часть;
■	в решении задач не ставьте на первое место получение указанно¬
го ответа, объясните ход решения задачи и убедитесь в его логичности и
правильности, попытайтесь сформулировать обратную задачу, решить ее
или поищите другой способ решения.
Умение решать задачи развивается в процессе обучения, и разви¬
вать это умение можно только одним путем - постоянно, систематически
решать задачи. Желаем Вам успехов!
Авторский коллектив выражает благодарность В. А. Ананьеву и
Р. Ш. Халиуллину за помощь в оформлении пособия.
Мы будем признательны всем, кто выскажет замечания и пожела¬
ния по данному учебному пособию.
Авторы
4

ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ И РЕКОМЕНДАЦИИ
1.1.	Условные обозначения и размерности величин
2- +
Х - формула частицы вещества (например, KMnO4, SO42-, H+ и др .);
n(X) - количество вещества, моль;
с(Х) - молярная концентрация, моль/л;
z* - число эквивалентности; 1/z* = f^β. - фактор эквивалентности;
n(1∕z*X) или п(Х) в титриметрии - число молей эквивалентов вещества Х;
β(1∕z*X) или с(/'экв(Х)) - молярная концентрация эквивалента вещества Х,
моль/л (ранее - г-экв/л);
[Х] - равновесная молярная концентрация вещества Х, моль/л;
w(X), % - массовая доля вещества Х, %;
Т(Х) - титр вещества Х, г/мл;
Т(В/А) - титр рабочего раствора вещества В по определяемому веществу А, г/мл;
S(X) - растворимость вещества Х, моль/л;
33
r - плотность раствора, кг/м3 или г/см3 (г/мл);
V - объем раствора, мл, л;
m - масса, г;
I - ионная сила раствора;
g - коэффициент активности z-того иона;
a(i) или αi - активность иона, моль/л;
ОХ) или ax - доля частиц вещества Х или самого вещества Х в растворе,
степень диссоциации, доля свободных ионов и др.;
h(X) - степень гидролиза вещества Х;
К, К', K0 - реальная, условная и термодинамическая константы равновесия;
Ks (ранее - ПР) - константа растворимости малорастворимого электролита;
Ksh - константа автопротолиза растворителя (для воды - Kw);
Kα, Kb - константы кислотности и основности (константы диссоциации ки¬
слоты и основания); для многоосновных кислот - Kα1, Kα2 и т. д.
Kh - общая константа нестойкости комплексного соединения;
b n - общая константа образования (устойчивости) комплексного соединения;
bn = 1∕Kh = K1-K2-K3-.. Kn ; (K1, K2... Kn - ступенчатые константы образования);
b1 = K1; b2 = K1×K2; b3 = K1××K2×K3 и т. д.
Е Ox/Red, E0'ox∕Red, Eoχ∕Red - стандартный, формальный, равновесный
окислительно-восстановительные (электродные) потенциалы.
Примечания: 1) значения термодинамических констант простых равновесий и Другие
справочные Данные привеДены в таблицах Приложения по пособию Ю. Ю. Лурье [1];
2) размерности величин приведены в системе СИ и распространенных в учебной литера¬
туре еДиницах.
5

1.2.	Правила вычисления. Условие значимости цифр
Результаты анализа должны быть вычислены с той же точно¬
стью, что и выполненные измерения. С этой целью при расчете ре¬
зультатов всегда сохраняют одну лишнюю цифру по сравнению с
числом цифр в конечном результате, т. е. используют значащие
цифры. Значащими называют все достоверно известные цифры
плюс первая из недостоверных. В конечном результате число ок¬
ругляют с учетом значащих цифр, а лишнюю цифру отбрасывают.
При представлении числа, выражающего результат измерения или
вычисления с учетом значащих цифр, следует помнить, что нули в
начале числа незначимы (в числе 0,0015 - две значащие цифры, в
0,0150 - три); нули, стоящие между цифр - всегда значимы. При
представлении чисел с нулями, стоящими после цифр, значащие
цифры должны быть четко показаны, например, степенным выра-
2
жением (5,00·10 - три значащие цифры) или указанием нуля после
запятой (200,0 - четыре значащие цифры).
При проведении любого расчета нужно уметь округлять полу-
O	T-I	О	О	1	о
ченный результат. Если за первой недостоверной цифрой следует
цифра 5, округление проводят до ближайшего четного числа. На¬
пример, число 12,245 следует округлить до 12, 24; число 12,255 -
до 12,26.
Рассмотрим некоторые правила округления для основных
арифметических действий, наиболее часто встречающихся при рас¬
чете химических равновесий и результатов химических методов
анализа.
Сложение и вычитание. Значимость суммы или разности
определяется значимостью числа с наименьшим числом десятич¬
ных знаков. Например, при сложении чисел 4; 0,21 и 22,3 значи¬
мость определяется недостоверностью числа 4. Тогда сумму чисел
26,51 следует округлить до 26. При отбрасывании цифры 5 округ¬
ляют до ближайшего четного числа. При сложении чисел со степе¬
нями приводят показатели степеней к наибольшему числу, а далее
поступают в соответствии с приведенным правилом. Например:
-5 -2 -4 -
сумма чисел 4·10 , 3,00·10 и 1,5·10 , преобразованных в 0,004·10
2 -2 -2 -2
, 3,00·10 и 0,015·10 , должна быть выражена числом 3,02·10
-2
(значимость суммы определяется значимостью числа 3,00·10 ).
6

Умножение и деление. Число значащих цифр произведения
(или частного) величин, измеренных с разной точностью, определя¬
ется значимостью сомножителя с наименьшим числом значащих
цифр. Например, перемножение чисел 1,5 и 2,35 дает произведение
3,525, которое представляют числом с двумя значащими цифрами,
т. е. 3,5. С учетом приведенных правил рекомендуется округлять
результат после проведения всех арифметических действий.
Возведение в степень. Относительная недостоверность ре¬
зультата возведения в степень увеличивается в число раз, равное
степени (то есть при возведении в квадрат - удваивается).
Извлечение квадратного корня. Относительная недостовер¬
ность результата √X вдвое меньше относительной недостоверности
числа х, поэтому в некоторых случаях после извлечения корня чис¬
ло значащих цифр увеличивается. Например -∖∣2,0 × 10-4 = 1,41 × 10-2,
поскольку относительная недостоверность для значащих цифр чис¬
ла 2,0×10-4 равна ±0,1, а результата извлечения корня: ±0,1/2 = ±0,05,
поэтому в его значащие цифры включается вторая после запятой.
Логарифмирование. Число значащих цифр в мантиссе равно
числу цифр, которое содержал нестепенной член числа. Характери¬
стика логарифма, определяющаяся порядком логарифмируемого
числа, не входит в число значащих цифр, например:
lg2,3×10-4 = -3,62; lg2,30×10-4 = -3,617.
Абсолютная недостоверность логарифма примерно в 2,5 раз
меньше относительной недостоверности числа под логарифмом.
Например, если относительная погрешность логарифмируемой ве¬
личины 5×10-4, то точность логарифма 2×10-4. Для антилогарифмов
число значащих цифр, соответственно уменьшается, например:
antlg3,19 = 1,6×103.
Следует помнить, что округление проводят после окончания
всех математических действий, всех расчетов. Результат измере¬
ния (определения) и его погрешность следует выражать числом с
одинаковым количеством цифр после запятой. Например, пред¬
ставляя средний результат анализа, имеющий четыре значащих
цифры и две из них после запятой, при указании границ довери¬
тельного интервала после запятой должно быть не более двух цифр:
X ± Dx = (14,48 ± 0,04) %.
7

Пример 1.1. Раствор H2SO4 для создания среды в титримет-
рии приготовили, сливая остатки трех растворов: 50 мл, 5,25 мл и
14,5 мл с разными концентрациями. Определите объем получен¬
ного раствора.
Ре ше ние . V = 50 + 5,45 + 14,7 = 70,15 мл.
Наименьшее число значащих цифр в объеме 50 мл, поэтому
округленный результат содержит 2 значащих цифры: V = 70 мл.
Пример 1.2. Для раствора H2SO4, полученного по условию
-3
примера 1.1 (количество вещества H2SO4 в 50 мл равно 4,0-10' , в
5,25 мл - 0,25-10-4, а в 14,5 мл - 2,0-10-4 моль) вычислите: а) общее
количество вещества H2SO4; б) молярную концентрацию.
Ре ше ние : а) при сложении взятых количеств кислоты сле¬
дует уравнять показатели степени, приводя их к наибольшему
числу:
n(⅛SO4) = 4,0-W3 +0,025-W3 + 0,20-10'3 = 4,225- W3 моль.
Округление проводим по первому слагаемому, имеющему
-3
наименьшее число десятичных знаков, т. е. n (H2SO4) = 4,2-10'
моль;
б) концентрация серной кислоты: ^H2SO4) = n (H2SO4)//';
^H2SO4) = (4,0+0,025+0,20)-10’3/( 50 + 5,45 + 14,7)-10’3 =
= 6,023-10-2 моль/л.
Округление проводим до 2-х значащих цифр, ориентируясь на
числа 50 и 4,0, тогда результат расчета концентрации:
^H2SO4) = 6,0-10-2 моль/л.
Пример 1.3. Определите массовую долю серы в сухом угле,
если по данным весового анализа из навески угля 2,6448 г (с влаж¬
ностью 2,58 %) получено 0,3248 г весовой формы ВаSO4.
Ре ше ние. После подстановки величин в расчетную формулу
(гл. 7) получаем:
( s) = M(S) - m((BaSO4) -100 -100
W( ) = M(BaSO4) - ma ■ (100- w(H2O))
32,06 - 0,3248-100-100
233,39 - 2,6448-(100 - 2,58)
=1,7316 %.
8

Результат округляем до сотых долей процента, ориентируясь
на число 2,58 с наименьшим числом значащих цифр.
Пример 1.4. Вычислите и округлите результат:
1,76×10-5
250
25,0.
Решение. При вычислении получаем величину:
1 76×10-5 × — = 1,76 ×10- 4.
25,0
Все числа, входящие в формулу, имеют одинаковое число
значащих цифр, но абсолютные и относительные недостоверности
их отличаются. При отсутствии в задании абсолютных недостовер¬
ностей этих трех чисел считаем их равными ±1 в последней знача¬
щей цифре каждого числа. Тогда относительные недостоверности
составят:
0,01∙10-5∕1,76∙10-5 = 0,006,
1/250 = 0,004,
0,1/25,0 = 0,004,
а их сумма равна:	0,006 + 0,004 + 0,004 = 0,014.
Абсолютная недостоверность результата равна:
0,014×1,76×10-4 = 0,02×10-4.
Поскольку недостоверность в последней цифре превышает 1,
рекомендуется округлить результат до 2-х значащих цифр, а имен¬
но: до 1,8×10-4.
Пример 1.5. Вычислите рН 9,8×10-4 М раствора сильной ки¬
слоты НА.
Решение. Для сильной кислоты:
рН = -lgc(HA) = -lg(9,8×10-4) = 4 - 0,9912 = 3,0088.
В коэффициенте величины c(HA) всего две значащие цифры
(9,8), поэтому мантиссу округляем до двух цифр: рН = 3,01.
9

1.3.	Чувствительность аналитических реакций
Аналитическими реакциями, пригодными для качественного
анализа, являются реакции, сопровождающиеся каким-нибудь
внешним эффектом: выпадением и растворением осадка, выделени¬
ем газообразных веществ, изменением окраски. Выбирая реакции
для химического анализа, руководствуются законом действующих
масс и представлениями о химическом равновесии в растворах. Для
успешного проведения аналитической реакции необходимо соблю¬
дать ряд тех или иных условий, обеспечивающих получение досто¬
верных результатов. Такими условиями являются рН раствора,
температура, маскирование или удаление мешающих ионов. Одна¬
ко даже при соблюдении всех этих условий аналитическая реакция
может не дать положительного эффекта, если недостаточна кон¬
центрация обнаруживаемого иона в растворе. С концентрацией об¬
наруживаемого иона в растворе связано понятие «чувствитель¬
ность» аналитической реакции.
Чувствительность аналитических реакций характеризуется
преДелом обнаружения cmιn (спред) и открываемым минимумом т;
преДельным разбавлением ^ед; минимальным объемом предельно
разбавленного раствора Vmin, показателем чувствительности рст|п.
ПреДел обнаружения ст|п (спред) (г/мл) - минимальная или пре¬
Дельная концентрация; это наименьшая концентрация иона или
вещества (далее - компонента) в растворе, при которой он может
быть обнаружен с помощью данной аналитической реакции с за¬
Данной Доверительной вероятностью.
ПреДел обнаружения т (мкг) - открываемый минимум; это
наименьшая масса определяемого компонента, с заданной довери¬
тельной вероятностью обнаруживаемая данной аналитической ре¬
акцией в минимальном объеме предельно разбавленного раствора.
ПреДельное разбавление, 7првд (мл/г) - максимальный объем
раствора, в котором обнаруживается 1 г компонента с помощью
данной реакции.
Минимальный объем преДельно разбавленного раствора, Vmin
(мл) - наименьший объем анализируемого раствора, необходимый
для обнаружения компонента в данной аналитической реакции.
10

Эти характеристики чувствительности связаны между собой
соотношением:
6 / 6
m = с ■ - V i -106 =-⅛l-106	(. |)
min min . (1.1)
пред
В качественном анализе обычно используют реакции с с11П11 от
-3	-8
10 до 2·10 г/мл. Открываемый минимум ионов изменяется от
~ 10 мкг в реакциях осаждения до ~ 0,2 мкг в реакциях образо¬
вания окрашенных комплексных соединений. Иногда для т поль¬
зуются обозначением 1 g (1 гамма), равным 1 мкг.
Показатель чувствительности, рсть , аналитической реакции
равен:
рстт	1дстт	lg(1/Vпред) lg ^пред·
В количественном химическом анализе показателем чувстви¬
тельности является нижняя граница определяемых содержаний
(тн или сн), являющаяся метрологической характеристикой кон¬
кретной методики.
3+
Пример 1.6. Предельное разбавление ионов Al при обна¬
ружении микрокристаллоскопической реакцией равно 150000 мл/г,
Vmin исследуемого раствора составляет 0,06 мл. Вычислить откры¬
ваемый минимум.
Ре ше ние . По формуле (1.1) находим:
m = VmiiL·-106 = 0,06 -10 = 0,4 мкг = 0,4 g.
V∏ψ,i	150000	’ '
Пример 1.7. Для обнаружения ионов меди действием раство¬
ра аммиака Vmin равен 0,05 мл, открываемый минимум этой реакции
0,2 мкг. Определить предельную концентрацию ионов меди в рас¬
творе.
Решение . С учетом формулы (1.1) рассчитываем стт:
стт
V ■
тт
-10-6
0,2 -10-6
0,05
= 1: 250000 = 4-10-6
г/мл.
m
Пример 1.8. Предельно допустимая концентрация (ПДК) иона
аммония в питьевой воде 2,0 мг/л. Предел обнаружения его по ре-
11

акции с реактивом Несслера составляет 0,002 мкг. Проверьте расче¬
тами возможность обнаружения иона аммония в 1,0 мл воды при
содержании, равном ПДК.
Ре ше ние . Рассчитаем минимальную концентрацию иона
аммония в растворе, при которой реакция с реактивом Несслера да¬
ет положительный эффект:
m
Cmin
×10-6
min
0,002 -10-6
1,0
= 2 ×10 -9
г/мл.
Сравнивая полученное значение Cmin с величиной ПДК, со¬
ставляющей 2,0 мг/л или 2,0·10-6 г/мл, можно видеть, что ион аммо¬
ния легко может быть обнаружен, поскольку чувствительность дан¬
ной реакции высокая: cmin значительно ниже ПДК.
Пример 1.9. Катионы серебра Ag+ можно обнаружить реакци¬
ей с хромат - ионами CrO42- по образованию кирпично-красного
осадка Ag2CrO4 при минимальном объеме 0,02 мл в водном раство¬
ре нитрата серебра с молярной концентрацией c(AgNO3) равной
0,0004 моль/л. Определите для иона Ag+ открываемый минимум,
предельное разбавление и показатель чувствительности в данной
аналитической реакции.
Ре шени. Найдем Cmin иона Ag+, зная c(AgNO3):
Cmin = C(AgNO3)-M(Ag)-10-3 =0,0004-107,868-10-3 = 4-10"5 г/мл.
Вычислим показатель чувствительности:
рСтхп = - IgCmin = - lg4-10-5 = 4,4.
Используя формулу (1.1), найдем т и Кпред:
m = Cmin ×Vmin ×106 = 4×10-5 ×0,02×106 = 0,8 мкг = 0,8 g,
‰ = 1∕cmιn = 1/4-10-5 = 2.5-10' мл/г.
Задачи для самоконтроля
1.	Сколько значащих цифр содержится в числах 0,1250; 0,015; 2,50·10-4;
250; 0,01280?	Ответ: 4; 2; 3; 3; 4.
2.	Представьте в нормальном виде объемы мерной колбы 1000 мл и
250 мл, если погрешность измерения объема 1 мл. Какова относитель¬
ная недостоверность для их объема.
Ответ: 1,000·103 мл, 2,50·102 мл; 0,001, 0,004.
3.	Произведите арифметические действия и округлите результат:
12

а) 6,75 + 0,443 + 15,28; б) 0,10 + 0,1 + 10;
в) 10,1378 - 10,03; г) 4,183·10-2 + 3,1·10-3 + 5,13·10-4;
д) 1,23· 10 3 × 5,0 : 25; е^0,252 + 0,22 + 0,12.
Ответ: а ) 22,47; б) 10; в) 0,11; г) 4,54· 10-2; д ) 2,5· 10-4; е) 0,34.
4.	Представьте результат расчета рН смеси равных объемов 3,25·10-4 М
-3
раствора соляной и 1,1·10 М азотной кислот.	Ответ: 3,15.
5.	Найдите концентрацию ионов ОН- в растворе, если его рН 8,3.
Ответ : 2 · 10-6.
6.	Открываемый минимум для реакции обнаружения Ti4+ с помощью хро¬
мотроповой кислоты равен 2,0 мкг при объеме 0,50 мл. Вычислить предель¬
ное разбавление и минимальную концентрацию.
Ответ: 2,5 ×105 мл/г; 4,0×10-6 г/мл.
7.	Открываемый минимум при обнаружении ионов K+ с Na3[Co(NO2)6] равен
4 мкг, предельное разбавление раствора равно 50000 мл/г. Вычислить мини¬
мальный объем раствора, необходимый для обнаружения K+. Ответ: 0,05 мл.
8.	Предельная концентрация CN- в реакции с AgNO3 1:50000 г/мл. Каков
открываемый минимум, если реакция удается с каплей объемом 3,0×10-4 мл?
Ответ: 0,006 мкг.
2-	-5
9.	Реакция на ион SO42- с BaCl2 удается в 5,6·10-5 М растворе Fe2(SO4)3.
Вычислить открываемый минимум, если минимальный объем равен 1,0 мл.
Ответ: 16 мкг .
2+
10.	Открываемый минимум для реакции обнаружения ионов Ni2+ с помо¬
щью диметилглиоксима равен 0,003 мкг. ПДК никеля в воде 0,1 мг/л. Можно
ли обнаружить ионы никеля в капле воды объемом 0,05 мл при содержании,
равном ПДК?	Ответ: можно, т. к. 6· 10-8 г/мл < 0,1 мг/л.
11.	В 1 л воды растворили 0,14 г Fe2(SO4)3 ^9Н2О: а) будет ли наблюдаться
3+
реакция на ион Fe с реагентом К4ре(С^б], если предельная концентрация
ионов Fe3+ составляет 3·10-8 г/мл? б) можно ли с помощью такой реакции об¬
наружить железо в воде при его содержании на уровне 0,05 ПДК (ПДК со¬
-8	-5
ставляет 0,3 мг/л)?	Ответ: а) 3·10-8 г/мл < 3·10-5 г/мл (будет); б) нельзя:
-8
3·10-8 г/мл > 0,3·0,05 мг/л; необходимо концентрирование более чем в 2
раза.
13

ГЛАВА 2. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РЕАЛЬНЫХ
СИСТЕМАХ
Химические реакции, используемые в аналитической химии,
проводятся в растворах и являются в той или иной степени обрати¬
мыми. В связи с этим теория химического анализа базируется на
законах химического равновесия. Для понимания химической реак¬
ции необходимо знание её стехиометрии, термодинамики и кинети¬
ки. Термодинамика касается направления и глубины протекания
реакции и через свободную энергию Гиббса отражается в термоди¬
намических константах равновесия К0 (или КТ), которые для разных
видов простых равновесий приведены в справочной литературе, в
том числе, в таблицах 2 - 4 приложения. Кинетика дает представ¬
ление о механизме и скорости реакции.
При рассмотрении законов химического равновесия следует
различать идеальные и реальные системы. В идеальных системах
ионы и молекулы свободны от влияния других частиц и способны
полностью проявить свою химическую природу. К таким системам
приближаются бесконечно разбавленные растворы. В реальной
системе частицы испытывают влияние со стороны окружающих
ионов и молекул. Вследствие этого при участии в химических ре¬
акциях даже в разбавленных растворах они проявляют себя как бы
в меньшей концентрации, чем она есть в действительности. Поэто¬
му для описания поведения ионов в реальных системах вместо кон¬
центрации используют величину, называемую активностью а. В
идеальной системе активность частицы равна её концентрации, а в
реальной она обычно меньше концентрации.
Отклонение поведения ионов в растворе от идеального может
быть связано с их электростатическими и химическими взаимодейст¬
виями. Именно они учитываются при расчетах химических равнове¬
сий в растворах электролитов. Химические реакции могут протекать
между ионами, а также при специфических сольватационных взаимо¬
действиях ионов с молекулами растворителя (например, при гидроли¬
зе). При этом следует помнить, что влияние химических взаимоДейст¬
вий на химическое равновесие во много раз сильнее, чем Действие
электростатических сил. Поэтому в практических расчетах влияни¬
ем электростатических взаимоДействий пренебрегают при протека¬
14

нии в растворах побочных химических реакций: ионную силу раствора
считают равной нулю, gi = 1 и σi = с (см. раздел 2.1).
2.1.	Влияние электростатических взаимодействий
на поведение ионов в растворе. Ионная сила раствора.
Коэффициент активности
Характеристикой электростатического поля в растворе и ме¬
рой электростатических взаимодействий ионов является ионная си¬
ла раствора I связанная с концентрацией ионов с (моль/л) и их за¬
рядами Zi соотношением:
2 i =1
Ионной силой раствора определяется коэффициент активно¬
сти иона gi. Измерить величину g индивидуального иона невозмож¬
но, поэтому пользуются экспериментально определяемым средним
коэффициентом активности g±. Для электролита типа AmBn:
m+n
(2.2)
Например, для 0,01 М раствора MgCl2 g± = 0,528. Это означает,
что раствор ведет себя так, как будто его концентрация в 0,528 раз
меньше, чем 0,01 М. Т. е. коэффициент активности является неко¬
торой мерой отклонения реальной системы от идеальной. В то же
- 2+
время отклонение в проявлении свойств ионов Cl и Mg в реакци¬
ях от концентраций (0,02 и 0,01 моль/л) будет разным, поскольку gi
для иона зависит от I раствора, от Zi и, строго говоря, от ионного
радиуса (пример 2.1). Связь I и gi очень сложна, и для разбавленных
водных растворов выражается формулами Дебая и Хюккеля (ионы
при этом рассматриваются как точечные заряды и различие в их
размерах не учитывается):
lggi =-0,5 Zf 4I при
( I£0,01);
при
(I £ 0,1).
(2.3)
В практических расчетах для оценки коэффициентов активно¬
сти используют ряд постулатов, упрощающих расчеты:
15

1.	Коэффициенты активности ионов равного заряда, независимо
от знака и размера, приблизительно равны.
2.	Растворы, содержащие только нейтральные молекулы, можно
считать идеальными (I = 0, g =1).
3.	Разбавленные растворы электролитов (особенно - слабых!)
приближаются к идеальным (I ® 0, g ® 1).
Поэтому при расчете величины gi можно пользоваться табли¬
цами, в которых приведены значения g для одно-, двух-, трех-, че¬
тырехзарядных ионов независимо от типа иона (например табл. 1
приложения).
Коэффициент активности является мерой отклонения реаль¬
ной системы от идеальной. Он связывает концентрацию иона и его
активность а:
аА = Гл [А],
где [А] - равновесная концентрация иона А. Активность имеет
размерность концентрации (моль/л).
Следует помнить, что при расчетах любого из четырех видов
химических равновесий с применением табличных (термодинами¬
ческих) констант равновесия получают значения активностей
частиц, а не их равновесные концентрации. Расчет равновесных
концентраций при I > 0 проводится с учетом g с использованием
уравнения (2.11), связывающего различные константы.
Пример 2.1. Вычислить ионную силу, коэффициенты актив¬
ности и активность ионов в 0,010 М растворе MgCl2 .
Решение.
MgCl2:
Уравнение диссоциации сильного электролита
MgCl2 ® Mg2+ + 2Cl- .
Начальная концентрация (моль/л) с: 0,010	-	-
Равновесные концентрации (моль/л) [...]:	-	0,010	0,020.
По формуле (2.1) вычисляют ионную силу раствора:
i = 1 ∑ c z2 = с(м§2+ Zg2++ с(с1 - )⅞-
2	∑ °i i 2
0,01 - 22 + 0,02 -12
2
= 0,03
Коэффициенты активности можно найти в табл. 1 приложения: при
I = 0,03 для двухзарядного иона gMg2+ = 0,54; для однозарядного
иона gCl- = 0,88. Расчеты по формулам (2.3) при 0,01 £ i = = 0,03 £0,1
16

приводят к близким к справочным значениям g:
lggMg2+
lggCl- =
- 0,5 - 22√0,03
1 + 70,03
=-0,295; gMg2+
= 0,51;
- 0,5 -12 70,03
1 +70,03
= -0,0738; gCl-
= 0,84.
Активности ионов соответственно равны:
2+
aMg2+ = ,∙Ug∣Mg ] = 0,51∙0,010 = 0,051 моль/л,
aCl- = TCι-∙[CΓ] = 0,84∙0,020 = 0,0168 = 0,017 моль/л.
Пример 2.2. Во сколько раз изменится активность ионов во¬
дорода в 0,010М растворе HCl, если в 1,0 л такого раствора раство¬
рить 3,4 г сульфата алюминия?
Ре ше ние . Для 0,010 М раствора HCl: I = 0,01;
дН+ = gCl- = 0,91; аН+ = дН+^Н+] = 0,91∙0,010 = 0,0091 моль/л.
Молярная концентрация раствора Al2(SO4)3 при растворении в
HCl:
C(Al2(SO4)3) = m/MV = 3,4/(342·1,0) = 0,010 моль/л.
В полученном растворе сильных электролитов устанавлива¬
ются равновесия:
HCl ® H+ + Cl-	и Al2(SO4)3 ® 2Al3+ + 3SO42-,
C:	0,01	-	-	0,01	-	-
[..]: -	0,01	0,01 -	0,02	0,03.
В величину I (формула 2.1) вносят вклад все ионы, находя¬
щиеся в растворе:
n
I=2 ∑ ' =
2 i =1
0,01 -12 + 0,01 -12 + 0,02 - 32 + 0,03 - 22
2
= 0,16.
При I= 0,16: дН+ = 0,80;
аН+ = дН+-[Н+] = 0,80∙0,010 = 0,0080 моль/л.
Отношение полученных активностей (0,0091/0,0080) показы¬
вает, что при введении в раствор HCl соли Al2(SO4)3 активность ио¬
нов водорода уменьшилась всего в 1,14 раз, в то время как ионная
сила раствора увеличилась в 16 раз.
17

Пример 2.3. Вычислить ионную силу и активности ионов в
растворе, полученном при сливании по 100 мл 0,050 М раствора
NaOH и 0,040 М HCl.
Ре ше ние . При сливании растворов протекает реакция ней¬
трализации с образованием достаточно слабого электролита - воды,
диссоциацией которой пренебрегаем. Данные указывают на избы¬
ток взятой щелочи.
NaOH + HCl ¾ NaCl + ⅛0.
С учетом разбавления с: 0,05∙0,1	0,04∙0,1	_
(0,1+0,1) (0,1+0,1)
и после расчета	с: 0,025	0,020	-
[...]: 0,025-0,02 -0,020.
- - + 2
В растворе присутствуют ионы OH , Cl , Na , для которых z = 1.
i = 0,5∙(0,005 + 0,005 + 0,020 + 0,020) = 0,025.
Соответственно g± = 0,88 и активности ионов составляют:
aNa+ = g⅛+∙[Na+] = 0,88∙(0,0050+0,020) = 0,022 моль/л;
acι- = gcι-∙[Cl-] = 0,88∙0,020 = 0,0176 = 0,018 моль/л;
аон- = Zoh-∙[OH^] = 0,88∙0,0050 = 0,0044 моль/л.
Проверкой решения может быть выполнение принципа электроней¬
тральности раствора в целом:
[Na+] = [Cl-] + [OH-] или 0,025 = 0,02 + 0,005.
2.2.	Влияние химических факторов на равновесие.
Молярная доля компонента в растворе
Образующиеся в растворе ионы могут вступать в различные
реакции с другими ионами и молекулами. Поэтому наряду с основ¬
ной химической реакцией в растворе могут протекать конкури¬
рующие (побочные) реакции. Например, в водном растворе Na2CO3,
наряду с диссоциацией соли на ионы Na+ и CO32-, могут протекать
побочные реакции протонирования аниона. Протонирование может
осуществляться ионами Н+, образующимися в результате диссо¬
циации воды или введенными в раствор с какой-либо кислотой:
CO32- + H+ ⅛ HCO3-,
HCO3- + H+ ⅛ H2CO3.
Поэтому в растворе анион присутствует в виде трех частиц с
2- -
разной равновесной концентрацией: [CO3 ], [HCO3 ] и [H2CO3].
18

2-
Общую (аналитическую) концентрацию, с(СО3 ), можно предста¬
вить как сумму равновесных концентраций всех форм (условие ма¬
териального баланса):
с(СО32-) = ^Na2CO3) = [CO32-] + [HCO3-] + [H2CO3].
Равновесная концентрация каждой формы связана с общей
концентрацией вещества коэффициентом a, называемым молярной
долей соответствующей формы. В данном примере для раствора
Na2CO3:
[CO32-] = θ(CO32-)<(Na2CO3); [HCO3-] = aHCO3-MNa2CO3);
[H2CO3] = aH2CO3MNa2CO3).
Сумма молярных долей всех форм вещества равна единице
(или 100 %). Таким образом, чтобы найти равновесную концентра¬
цию формы, зная общую, необходимо вычислить а. Для расчета а -
молярной доли любой формы кислоты HnA при заданных условиях
(заданной концентрации ионов водорода), а также для расчета [H+],
обеспечивающей нужную равновесную концентрацию частицы в
растворе, используют общую формулу:
Ka1 × Ka2 ×...× Ka(n-m) ×[H+ ]m
a	[H+г+Kλ	×[H+Г-1	+ κai	×	κa2	×[H+Г-2+....+κai	×κa2 ......Kaa	·[H+∏ (2.4)
Смысл индекса m (изменяется от 1 до п) понятен из уравнения ма¬
териального баланса для кислоты HnA:
с(Н„А) = [А” -] + |11.V 1 -] + + ∖H.Λ-m -] + + [HnA].
2- -
Например, для равновесных форм H2CO3: CO3 , HCO3 и H2CO3
молярные доли вычисляют по формулам, вытекающим из (2.4):
a(CO2- ) = JCOtL =	Ka1 × Ka2
( 3 ) ^H2CO3 ) [H+ ]2 + Kα1 × [H+ ] + Ka1 × Ka2 ,
(2.5)
a(HCO3-) =
[HCO- ]
W)
Ka1 × [H + ]
[H+ ]2 + Ka1 × [H+ ] + Ka1 × Ka√
a(H2CO3) = JH2CO3L _

V 2	3 с(Н^03) [H+ ]2 + Ka1 × [H+ ] + Ka1 × Ka2 ,
где ^H2CO3) = [CO32-] + [HCO3-] + [H2CO3].
(2.6)
(2.7)
Если ион в растворе участвует в реакциях комплексообразо¬
вания и при этом получаются формы с разным количеством лиган¬
дов, то расчет молярных долей форм проводят по формулам:
19

[M m+ ]
c(M m+)
	1

1 + b -[L]1 +.... + b ∙[LΓ ,
а(М m+)
a(∖H.m') =
[MLm+ ]
c(M m+)
b1 - [L]1
1 + b1 - [L]1 +.... + βn ∙ [L]n
(2.8)
(2.9)
а(МЦ;+) =
[MLmt ] =	b ■ [L]n
c(Mm+)	1 + b1 -[L]1 +.... + bn ∙[L]n
(2.10)
где L - лиганд (для простоты записи - нейтральная частица);
с(Мт+ ) = [Мт+] + ^Lm+] + ... + ^L^+].
Молярную Долю рассчитывают и используют, с оДной сторо¬
ны, Для вычисления равновесной концентрации частицы в условиях
побочных взаимоДействий, а с Другой - при определении условий,
которые необхоДимо созДать в растворе Для маскирования иона и
поДавления его реакционной способности.
Пример 2.4. Какая из форм серы преобладает в 0,10 М рас¬
творе (NH4)2S при рН = 6,0? (Ионную силу раствора не учитывать).
Определите равновесные концентрации всех серосодержащих форм
частиц в растворе.
Ре ше ние . (NH4)2S - сильный электролит, нацело диссо¬
циирует, поэтому общая концентрация форм, содержащих серу,
равна исходной концентрации соединения, т. е. по условию матери¬
ального баланса:
<<(NH4)1S) = 0,10 моль/л = t(S) = [S2-] + [HS-] + [H2S].
Главная реакция:	(NH4)2S ® 2NH4+ + S2-.
2- + -
Побочные реакции:	S + Н → HS ,
HS- + Н+ ⅛ H2S.
По формуле (2.4) или формулам (2.5-2.7) для вычисления мо¬
лярных долей всех форм двухосновной кислоты вычисляют a и
равновесные концентрации форм серы с учетом констант кислот¬
ности H2S и рН раствора (главная и побочные реакции протекают
при рН = 6, или [H+] = 1,0-10-6):
20

a(S2-)
= [S-]
<<S)
1 ×10-7 × 2,5 ×10-13
(1,0 ■ 10-6)2 +1 ■ 10-7 × 1,0 ■ 10-6 +1 ■ 10-7 × 2,5 × 10-13
= 1×10-7 × 2,5 ×10-13
=	1,1×10-12
= 2,3 ■ 10-8;	[S2- ] = с(Б) ■ α(S2-) = 0,10 ■ 2,3 ■ 10-8 = 2,3 ■ 10-9 моль/л;
a(HS-)
= [HS-]
с^)
1×10-7 ×1×10-6
1,1×10-12
= 9,1.10-2; [HS-] = 0,10.0,091= 9,1.10-3моль/л;
a(H2S)
= [H2S]
<*S)
= (1,0 ×10-6)2
^ 1,1×10-12
=0,91;
[H2S] =0,10.0,91=0,091 моль/л.
Проведенные вычисления показывают, что при таких услови¬
ях в растворе преобладает молекулярная форма, т. е. H2S.
Пример 2.5. Для начала осаждения ZnS из 1 .10-4 М раствора
2- -18
Zn(NO3)2 в растворе необходимо создать [S ], равную 2,5.10
моль/л. Будет ли выпадать осадок ZnS из такого раствора соли цин¬
ка, если насытить раствор сероводородом при [H+] = 0,2 моль/л
(^H2S) = 0,1 моль/л)? Если нет, то какую концентрацию ионов во¬
дорода следует создать в растворе для достижения достаточной
концентрации S2-?
Ре ше ние . Осадок ZnS выпадет, если в указанных условиях
2- -18 2- +
[S ] будет больше, чем 2,5.10 моль/л. Вычисляем [S ] при [H ] =
0,2 моль/л по формуле (2.4) или (2.5):
[S2' ] = с(И 2S) ∙α(S2" ) = 0,1
	1 ■ 10-7 ■ 2,5 ■ 10-13

(0,2)2 +1 ■ 10-7 ■ 0,2 +1 ■ 10-7 ■ 2,5 ■ 10-13
= 6 ■10-20 моль/л.
Вычисленная с учетом условий задачи [S2-] меньше необходимой для
выпадения осадка ZnS, следовательно, осадок не выпадет. Тогда необ¬
ходимо решить уравнение (2.4) или (2.5) относительно [H+], достаточ¬
ной для [S2-] ≥ 2,5×10-18 моль/л.
2_) ≥ [S2- ] ≥ 2,5 ■ 10-18 ≥	1 ■ 10-7 ■ 2,5 ■ 10-13	,
а(	) ≥ ^H2S) ≥	0,1	≥ [H+]2 +1 ■ 10-7 ■ [H+ ] +1 ■ 10-7 ■ 2,5 ■ 10-13 ;
1≥
	1 ■ 10 -3	,
[H+]2 +1 ■ 10-7 ■ [H+] + 2,5 ■ 10-20;
21

[H+]2 £ 1 ∙10-3; [H+] £3,2 ∙10-2моль/л.
Пример 2.6. Рассчитайте молярную долю и равновесную кон¬
центрацию ионов серебра в 0,010 М растворе AgNO3 в присутствии
2,0 М NH3.
Решение.
Главная реакция:
AgNO3 ® Ag+ + NO3-.
Побочные реакции:
Ag+ + NH3 ⅛ [Ag(NH3)]+ ,
[Ag(NH3)]+ + NH3 ⅛ [Ag(NH3)2]+.
dAg') = [Ag+] + [Ag(NH3)+] + [Ag(NH3)2+] = 0,01 моль/л.
(условие материального баланса)
Молярную долю, a(Ag+), и [Ag+] можно вычислить по форму¬
ле (2.8) с учетом табличных значений констант устойчивости ком¬
плексных ионов. Равновесную концентрацию лиганда - [NH3] при
этом можно принять равной исходной, поскольку побочные реак¬
ции протекают при большом избытке аммиака.
a(Ag+)
	1

1 + b ■ [NH3] + b2 ■ [NH3]2
	1

1 +103,32 ■ 2 +107,23 ■ 22
10-8;
[Ag+] = ^Ag^aAg^ = 0,01∙1,5^10-8 = 1,5-10-10 моль/л.
2.3.	Направление химических реакций.
Способы выражения констант равновесия.
Ступенчатые и общие константы равновесия
Термодинамические (табличные) константы (К0) простых
равновесий пригодны для расчетов при условии, что поведение ис¬
ходных и конечных продуктов не осложняется электростатически¬
ми или конкурирующими химическими взаимодействиями. При
расчетах равновесий с использованием термодинамических кон¬
стант получаются активности компонентов. Поэтому в реальных
условиях удобнее пользоваться реальными (концентрационными)
константами (К), которые выражаются через равновесные концен¬
22

трации, а также условными (К), которые связаны с общими концен-
трациями.
Для реакции:
аА + ЬВ ¾ сС + dD
К0
с d
аС ' aD
ab
aA ’ aB
К0 = f(T,P);
[С]c ∙ [D]d
[A]a ∙ [В]b
К = f(T,P,I);
с d
К ' = ^Cr-D, К ' = f (T, P, I ,а).
сА ∙ сВ
Все три константы связаны между собой через соответствую¬
щие, рассмотренные выше, коэффициенты:
К0 = К gC ' gD = Кf gC ' gD
~ 'gA ∙gb	'gA ∙gb аА ■ аВ ■
а ∙aD
(2.11)
Таким образом, при расчетах равновесных (или общих) кон¬
центраций в реальных системах необходимо оценить меру различ¬
ных влияний и через указанные коэффициенты и К0 рассчитать
значения К (или К'). При этом следует помнить, что химические
факторы оказывают более сильное влияние, чем электростатиче¬
ские, поэтому при наличии конкурирующих реакций, как правило,
принимают ионную силу I = 0 и g = 1.
Химическая реакция может протекать только в том случае, ко¬
гда она термодинамически возможна и константа равновесия её
больше единицы. По величине константы равновесия можно оце¬
нить направление, полноту протекания реакции и возможность её
регулирования. При 104 > К > 10-4 равновесие реакции можно сме-
7
стить в нужную сторону, например избытком реагента. При К >10
реакция протекает в прямом направлении практически до конца
-7
(такие реакции применимы в количественном анализе); при К < 10
реакция практически не идет.
Любая химическая реакция может быть преДставлена как
совокупность ступенчатых процессов, а общая константа равно¬
весия такой реакции может быть выражена как произведение
ступенчатых констант.
Пример 2.7. Рассчитайте константу равновесия реакции, опи¬
сывающей растворение CaCO3 a) в HCl ; б) в CH3COOH.
Решение. Представляем уравнения реакций в молекуляр¬
ной и ионно-молекулярной форме:
23

а) CaCO3 (тв) + 2HCl ⅛ CaCl2 + H2CO3 и
CaCO3 (тв) + 2H+ ⅛ Ca2+ + H2CO3.
Записываем уравнения ступенчатых реакций, описывающих
распад или образование слабых и малорастворимых электролитов и
соответствующие им константы:
1) CaCO3fra3 ⅛ Ca2+ + CO32- , К = [Ca2+]∙ [CO32^] = Ks';
2)	CO32- + H+ ⅛ HCO3- ,	K2 = [HCO3-]/[H+][CO32’] = 1/K„2;
3)	HCO3- + H+ ⅛ H2CO3,	K3 = [H2CO3’]/[H+] [HCO3-] = 1/Ka1.
Составляем выражение общей константы равновесия и под¬
ставляем табличные значения соответствующих констант:
К = Kv KrK3 = KS'/KaK = 3,8■10■9/4,5■10■7■4,8■10■ii = 1Л108.
К > 107, значит CaCO3 растворится в HCl даже без избытка ки¬
слоты.
б) CaCO^) + 2CH3COOH ¾ Ca(CH3COO)2 + H2CO3 ,
CaCOз(Tв.) + 2CH3COOH ¾ Ca2+ + 2C¾COO" + H2CO3.
Уравнения и константы ступенчатых процессов:
1)	CaCO3fra3 ⅛ Ca2+ + CO32^ ,	K1 = [Ca2+HCO32^] = Kx0;
2)	2CH3COOH ⅛ 2CH3COO- + 2H+,	K2 = Ka2.
Ступени 3) и 4) те же, что 2) и 3) в примере 2.7а,
т. е. K3 = 1/Ka2, K4 = 1/Ka1.
Рассчитываем общую константу равновесия:
К = KvKrK3K4 = Ks0K2 /KarKav
К =3,8■10■9■(1,76■10■5)2/4,5■10■7■4,8■10■ii = 5А10’2.
Вычисленное значение K указывает на смещение равновесия
влево, в сторону исходных веществ. Однако поскольку K > 10-4,
можно сместить равновесие вправо избытком уксусной кислоты и
провести растворение CaCO3.
Пример 2.8. Определите возможность растворения AgI в NH3.
Ре ше ние . Для ответа на вопрос рассчитаем общую кон¬
станту равновесия согласно схеме, использованной в примере 2.7.
AgI + 2NH3 ⅛ [Ag(NH3)2]+ + I-.
Ступенчатые процессы:
1)	AgIfra.) ⅛ Ag+ + I-,	K = [Ag+H I-] = Ks0;
2)	Ag+ + 2NH3 ⅛ [Ag(NH3)2]+, K2 = [A^W]»]2 = bi,
K = Kv K2 = Ks°-βl = 8,3■10■17■1,7■107 = 1A10'9.
24

-7
Поскольку полученное значение К < 10 , можно сделать вы¬
вод о том, что осадок AgI не растворится даже в избытке аммиака.
Задачи для самоконтроля
1.	Во сколько раз изменится активность ионов водорода в 0,0050 М рас¬
творе HNO3 при добавлении в него ¾SO4 до концентрации 0,10 М?
Ответ: уменьшится в 1,2 раза.
2.	Вычислите активность ионов хлора в растворе, 1,00 л которого содержит
0,050 моль соляной кислоты и 0,050 моль хлорида хрома. Ответ: 0,16.
3.	Вычислить ионную силу и активность сульфат-ионов в 0,012 М растворе
соли NaCr(SO4)2.	Ответ: 0,11; 0,010 моль/л.
4.	К 100 мл 0,025 М раствора нитрата железа (III) добавили 150 мл 0,25 М
3+	-3
азотной кислоты. Вычислить активность ионов Fe3+. Ответ: 1,9·10-3 моль/л.
2¬
5.	Вычислить молярную долю S2- и равновесную концентрацию этого иона
в 0,20 М растворе (NH4)2S при рН 7,0 (ионную силу раствора не учитывать).
Ответ: a(S2-)=1,2-10-6; [S2-] = 2,5-10-7 моль/л.
6.	Рассчитайте молярную долю и равновесную концентрацию ионной
формы [Ag(NH3)]+ в 0,01 М растворе AgNО3 в присутствии 2 М NH3.
Ответ: a([Ag(NH3)]+) = 6-10-5; [Ag(NH3)+] = 6-10-7 моль/л.
7.	Рассчитайте константу равновесия реакции взаимодействия Agd c рас¬
твором NH3 и сделайте вывод о возможности растворения осадка.
-3
Ответ: 3,0-10-3; растворяется в избытке.
8.	По величине константы равновесия определите возможность растворе¬
-24
ния Fe(OH)3 в NH4Cl.	Ответ: 1,2-10-24; не растворяется.
9.	Можно ли использовать для количественных определений реакцию
47
“нейтрализации” аммиака уксусной кислотой? Ответ: К = 3-104, что < 107;
нельзя.
25

ГЛАВА 3. КИСЛОТНО-ОСНОВНОЕ
(ПРОТОЛИТИЧЕСКОЕ) РАВНОВЕСИЕ
3.1. Расчет [H+], [OH-], рН, рОН
в растворах сильных и слабых кислот и оснований
В практике аналитической химии широко используются ки¬
слотно-основные реакции для разделения, растворения, определения
ионов, создания условий для взаимодействия частиц в растворе и др.
Поэтому необходимо научиться рассчитывать равновесные концен¬
трации ионов H+, OH- φH, рОЩ, а также степени диссоциации a
(доли распавшихся на ионы) слабых кислот и оснований (протоли¬
тов) в растворах. Поведение кислот и оснований в растворах зависит
от свойств растворителя. Вода и ряд других растворителей (напри¬
мер метанол) обладают амфотерным характером, что можно пред¬
ставить реакцией автопротолиза с образованием катиона лиония
(для воды - гидроксония, H3C)') и аниона лиата (для воды - О^).
112О + I НО ¾ H^+ + ОИ- (упрощенно: I НО ¾ H+ + О! ),
CH3OH + CH3OH ¾ CH3OH2+ + CH3O-.
ион лиония	ион лиата
Константа автопротолиза растворителя KsH (для воды - KW или
ионное произведение воды) отражает закономерность, существую¬
щую в кислотно-основных системах в данном растворителе при 25°С:
для воды KsH = KW = 10-14, для этанола KsH = 8,0·10-20,
-17
для метанола KsH = 2,0·10 .
Учитывая, что активность чистого растворителя (стандартное
состояние вещества) равна 1, справедливы выражения:
Kw = а(11,;О>а(О| I-) = ∏I' IJdII | = 10 14
(в чистой воде ионная сила I мала, g i близки к 1);
Ksh = a(CΗ3OH3)∙a(CΗ3O ) = [CH3OH24HCH3O-] = 2,0· 10'17.
При расчетах, связанных с кислотно-основным равновесием и
кислотно-основными взаимодействиями в растворах слабых про¬
толитов, считают табличные термодинамические значения кон¬
стант KsH, KW, Ka , Kb равными соответствующим значениям кон¬
центрационных констант, связанных с равновесными концентра¬
циями компонентов. Исключение составляют случаи, когда следу¬
26

ет учитывать ионную силу раствора I и коэффициенты активно¬
сти ионов gi (пример 3.3).
В качестве характеристик кислотности используются отри¬
цательные Десятичные логарифмы активности (при приближен¬
ных расчетах без учета ионной силы - логарифмы концентрации)
ионов лиония и лиата (для воды Н3О+ и ОН-). Знак «»» используется
в случаях, когда надо подчеркнуть приближенность расчетов, чаще
же используется знак «=».
Для воды: pH = - lg а(Н3О+) = - Ig а(^) » - lg[H+];
pOH = - Ig а(О^) » - lg [OH’];
Соответственно: [H+] = 10-pH; [OH-] = 10-pOH; [H+]-[OH-] = 10-pKW;
рН + рОН = рК, = 14.
В чистой воде, нейтральном водном растворе:
[Н+] = [ОН-] =10-7; рН = рОН = 7.
Для метанола (см. также пример 3.7):
pH = -lg а(И') » -lg[CH3O⅛+];
pOH = -lg а^^) » -lg[CH3O-];
рН + рОН = (-lg[CH3O¾+]) + (-lg[CH3O-]) = рКн = 16,7
и нейтральному раствору в метаноле соответствует рН = 8,35.
Эти соотношения используют для вычисления равновесной
концентрации одного из ионов растворителя, если концентрация
другого известна.
При описании поведения сильных и слабых кислот и основа¬
ний следует помнить о том, что сильные протолиты в водных рас¬
творах диссоциируют практически полностью, степень диссоциа¬
ции (ионизации) a близка к 100 %. Диссоциация слабых кислот
(НА) и оснований (В) протекает обратимо и описывается соответ¬
ствующими константами равновесия Ка и Kb.
НА + Н2О ⅛ Н3О+ + А-
к-та 1 осн 2	сопр. к-та 2 сопр. осн.1
или (в упрощенном виде): НА ¾ Н+ + А ,
[H + ][A- ].
[HA] ;
В + Н2О ⅛ ВН+ + ОН-,
осн. 1	к-та 2	к-та1
Kb
= [BH+ ][OH- ]
"	[B]
(3.1)
(3.2)
27

Из реакций следует, что для одноосновных протолитов в воде спра¬
ведливо:
[НзО+] = [А-]	и	[ВН+] = [ОН-].
Если НА и В - кислотно-основная сопряженная пара и В соответст¬
вует А-, то при умножении (3.1) на (3.2) получаем важное соотно¬
шение, связывающее свойства компонентов конкретной кислотно¬
основной сопряженной пары в данном растворителе. Для водного
раствора справедливо:
[H+][A-] [HA][OH-] k
—	- K1
(3.3)
[A-]
SH SH
Ка ∙ Kb = kSH.
W
Ka-Kb

a b [HA]
а для растворителя SH:
При растворении в воде солей, в состав которых входит ани¬
он слабой кислоты (CH3COONa, KCN и др.), катион слабого осно¬
вания (NH4CI, (CH3)2NH2CI и др.) или тот и другой вместе
(CH3COONH4), ионы слабых протолитов вступают во взаимодей¬
ствие с молекулами воды (реакция гидролиза), в результате чего
среда раствора становится кислой или щелочной. Только в случае
равной силы слабых протолитов среда может оказаться близкой к
нейтральной, как, например, в растворе ацетата аммония.
Реакция гидролиза характеризуется константой равновесия,
соответствующей протолитическому поведению гидролизующей¬
ся частицы (Кь или Ка), называемой также константой гиДролиза
(Кгидр.). Участвующая в таком протолитическом равновесии частица
соли характеризуется степенью гидролиза h, имеющей тот же
смысл, что и степень ионизации слабой кислоты или основания.
Например, для соли KCN с анионом слабой кислоты уравне¬
ние реакции гидролиза (гидролиз “по аниону'', среда щелочная):
+ OH-	и [HCN] = [OH-].
сопр. осн.2
CN- + Н2О ¾ HCN
осн.1 к-та2 сопр. к-та1
K
Kгидр. = Kb (CN -)  	w
(3.4)
N2H5+ + H2O ⅛ N2H4 + H3O+
к-та 1 осн. 2 сопр. осн.1
= [HCN]∙[OH- ] » [OH- ]2
Kа (HCN) -	[CN- ]	» C(KCN).
Для соли с катионом слабого основания, например N2H5Cl (соляно¬
кислый гидразин), протекает гидролиз “по катиону”, среда кислая:
и	[N2H4] = H3O+].
сопр.	к-та 2
28

Kεudp. = Ka (N2H5+)
kw
Kb (N2H4)
=[N2H4] ■ [H3O+]» [H3O+]2
[N2H+]	C(N2H5Cl), (3.5)
(поскольку для сопряженных протолитов в воде Ka×Kb= Kw по фор¬
муле (3.3)).
Для соли, в которой и катион, и анион - ионы слабых протолитов,
например CH3COONH4:
NH4+ + CH3COO - + H2O ¾ NH3H2O + CH3COOH
к-та1	осн.2	амфолит	сопр.осн. 1	сопр. к-та 2
(протекает гидролиз “по катиону” и “по аниону”, среда зависит от
Ka и Kb продуктов реакции: при Ka > Kb - среда кислая и наоборот).
k	= [NH3 ■ H2O] ■ [CH3COOH]=	K	 (
гидр.	[NH4CH3COO]	Ka (CH3COOH) ■ Kb (NH3 ■ H2O). (3.6)
Для кислой соли с катионом сильного основания, например
NaH2PO4, Na2HPO4, NaHCO3 и др., анион может участвовать в двух
протолитических реакциях, т. е. является амфолитом. Реакции ам¬
фолита H2PO4-:
1)	H2PO4- + H2O ¾ H3PO4 + OH- (гидролиз),
основание
2)	H2PO4- + H2O ⅛ HPO42- + H3O+ ,
кислота
(упрощенно: 2) H2PO4
2- +
HPO4	+ H (ионизация по
Ka2(H3PO4)).
Для реакции 1)
k = K = K = Kw = [H,PQtHOH] = [H,PO4]∙Kw ;
1 r'gp b1 Ka2	[H>POt- ]	[H2PO4-]∙[H ]’
для реакции 2) K2 = Ka2
= [H+ ] 4HPO42-]
[H2PO4- ]
От соотношения К1 и К2 зависит реакция среды раствора соли.
Аналогично, проявляя свойства амфолитов, ведут себя катионы ос¬
новных солей, аминокислоты (см. пример 3.16). При выводе формул
для точных расчетов помимо выражений констант равновесия, ис¬
пользуют уравнения нейтральности, материального баланса, про¬
тонного баланса и другие приемы (см. пример 8.22). В случае водно¬
го раствора NaH2PO4 при расчете рH учитывают вышеприведенные
уравнения (2) и (1), а также диссоциацию воды. Тогда справедливо:
29

[H+] = [HPO42-] - [H3PO4] + [ОН-]из воды.
Заменяя концентрации компонентов в правой части уравнения
через соответствующие константы, [H+], [H2PO4-] и группируя чле-
ны, получаем:
[H+ ] l [H2PO4- ]∙[H+ ] =	O. ] ι Kw
Kai	[H+ ]	[H+ ]·
Решая последнее уравнение относительно [H+], получаем:
[H+ ] - Ka1 ∙ Ka2 ∙ [H2PO4 ] + Ka1 ' KW
N	Kal + [H2PO4 - ]
(3.7)
Формула (3.7) упрощается при пренебрежении малыми величинами
и при допущении [H2PO4-] ≈ ^H2PO4-).
Например, если [H2PO4-] >>Ка1, то Ка1 ∙ Rw мало. Тогда справедливо:
[H+ ] ≈ √Kai ∙ Ka2 ∙ .	(3.8)
Для приближенных расчетов разных случаев кислотно-основного
равновесия можно воспользоваться формулами таблицы 3.1. Значе¬
ния Ка, Кь для водных растворов и рК приведены в табл. 2 и 3 при¬
ложения.
В случаях, когда н ел ьзя считать равновесную концентрацию
ионизирующегося вещества равной его аналитической концен¬
трации (не соблюдается условие с/К > 400, соответствующее
степени диссоциации менее 5 %); когда необходим учет ионной
силы раствора, проводятся точные расчеты равновесных кон¬
центраций ионов (примеры 3.2 - 3.5).
Пример 3.1. Рассчитайте рН, рОН и степень диссоциации
0,10 М раствора СН3СООН.
Решение. СН3СООН - слабая кислота, Ка = 1,74 10-5:
СН3СООН ¾ СН3СОО- + Н+,
с:
[...]:
с
с - [H+]
[H+]	[H+]
([СН3СОО-] = [H+]).
Проверка условия с/Ка= 0,10/1,74 10-5 > 400 показывает, что
расчет можно провести по приближенным формулам:
_ [CH3COO-][H + ] [H+ ]2
с
[CH3COOH]
K а
30

[H+ ] = JKa -C(CH3COOH) = √1,74-10~5 -10-1 = 1,32-10-3моль/л
рН = 2,88; рОН = 14 - 2,88 = 11,12;
a = [Н+]/с = 1,32-10-3/0,10 = 1,32-10-2 (1,32 %).
Таблица 3.1
Формулы для приближенного расчета [Н+] и [OH-]
в водных растворах кислот и оснований
Тип электролита
Концентрация иона, моль/л
Сильная кислота НА
Сильная кислота Н2А
[Н+] = с(НА)
[Н+] = 2с(НА)
Сильное основание В
[ОН-] = с(В)
Слабая кислота НА
Слабая кислота Н2А
[H+] = JКа ■ с(НА)
[H+ ]=JКа1 · с(Н2А) (если К.1 >>K2)
Слабое основание В
[ОИ - ] = J Кь-с(В)
Гидролизующиеся соли:
по катиону или катионо-
кислота (Ка= Кгидр)
по аниону или
анионооснование
{Кь = КгиДр)
по катиону и аниону
K - с	,
!Ή+] =	w соли или γh +1 = Ik
LH ]	д	к	ИЛИ [И ]	k гиДр.
\	кь
[OH-] =	KW ' ссоли	и [OH-] = /к	с
[OH ] = ^	к	ИЛИ Loh ]	к гиДр. Ссоли
+ KW Ka
[H] = V Kb
Гидролизующиеся
кислые соли:
амфолиты типа H2PO4-
2
амфолиты типа HPO4
[H+ ] = J Ka1- Ka 2
[H+ ] = J Ka 2- Ka 3
Пример 3.2. Рассчитайте рН, рОН и a 0,0050 М раствора
СН3СООН.
Ре ше ние . СН3СООН - слабая кислота, Ка = 1,74-10-5:
СН3СООН ¾ СН3СОО- + Н+,
с:	с	-	-
[...]:	с - [H+]	[H+]	[H+].
31

Поскольку с/Ка = 0,005/1,74 10-5 < 400, то необходимы точные рас¬
четы [H+], т. е. нельзя пренебречь [H+] в разности (с- [H+]):
откуда:
k - [CH3COO-][H+] - [H+]2
а	[CH3COOH]	(с - [H+])’
[H + ]2 + Kа [H + ] - Kас - 0.
Решаем квадратное уравнение относительно [H+]:
[H+]2 +1,74 10-5[H+]-8,7 10-8 -0;
[H+]-
-1,74 ∙ 10-5 +√34,83∙I0 8
2
- 2,86 10-4 моль/л ;
рН = - lg(2,86 10-4) = 3,54; рОН = 14 - 3,54= 10,46;
a = [Н+]/с(СH3COOH) = 2,87 10 4 0.0050 = 0,057 (5,7 %).
Пример 3.3. Рассчитайте рН 0,010 М раствора муравьиной
кислоты в присутствии 0,010 М NaCl.
Решение. Отношение с/Ка = 0,01/1,8 10-4 < 400 указывает на
необходимость точных расчетов. Нужно учесть также ионную силу.
НСООН ¾ НСОО- + Н+,
с:	с	-	-
[...]: с - [H+]	[H+]	[H+].
С учетом соотношения (2.11) термодинамической и реальной
констант:
k = [HCOO-][H+ ] 7. + 7hcoo- - [H+ ]2 g
а [HCOOH]	Yhcooh	с - [H+ ]
I = (0,01∙12 + 0,01∙12)∕2 = 0,01; g = }Hcqq- = 0,91;
2
+
(3.9)
gHCOOH = 1;
Ка l∕g) = [H+]2∕(c- [H+]) = 1,8 ∙10"4∕0,912 = 2,17∙10"4;
[H+]2 + 2,17 10-4[H+]- 2,17 10-6 - 0;
[H+] = - 2,17∙10 -4 +V 8>74∙10 t -1,37 ∙ 10 -3;
2
[H+] = 1,4∙10^3 моль/л;	рН = 2,8.
Пример 3.4. Рассчитайте рН 1,00 10-4 М раствора фенола.
32

Ре ше ние . Ka = 1,0×10-10, Ka < 10 -6 и с£ 10-4, поэтому необхо¬
димо учесть автопротолиз воды:
С6H5OH + ^О ⅛ Сб^О- + Ы3О+,
2Ы2О ¾ ОЯ" + IНО'.
Запишем уравнение электронейтральности:
[Сб^О-] + [OH-];
K с
[C6H5O-] = -^~;
65	[H+ ]’
[OH-] = Kw/[H+].
[H+] =
= [C6H5O- ][H+];
Ka
с
[OH-][H+] = Kw;
[н+]=!''с+k-
Тогда:
[H+ ] [H+ ]
откуда [H+ ] = J Ka с + Kw =J W10 -W4 +10-14 = 1,41 ■ W7 моль/л;
рH = 7 - 0,15 = 6,86.
Без учета автопротолиза воды:
[H+]	= J 10-10 ■ 10 -4 = 10-7 моль/л;
рH = 7, расчет менее точен.
Подобный подход необходим и при расчете рH очень разбав¬
ленных (с < 10-4) растворов сильных протолитов.
Пример 3.5. Рассчитайте рH и h 0,10 М раствора Na3AsO4.
Ре ше ние . Определяем тип гидролизующейся соли (тип про¬
толита).
Na3AsO4 + H2O ¾ Na2HAsO4 + NaOH,
AsO43- + H2O ⅛ HAsO42- + О^,
с:	с	-	-
[...]: с - [OH-]	[OH-]	[OH-].
3-
Гидролиз протекает по аниону, т. е. AsO4 - слабое основа-
2- -
ние. Очевидно, что [HAsO4 ] = [OH ]. 11айдем константу гидролиза
(Км), если Ка2 = 2,9540-п:
K	10 - 14
Kb1 = Kp =	=	- = 3,39 ■ 10 -3
b1	гидр .	K a2	2,95 ×10 -12	.
Поскольку с/Кгидр= 0,1/3,3940-3 = 29,5 < 400, необходим точный
расчет [OH-]:
33

k = [HAsO42- ][OH- ] = [OH - ]
гиДр.	IAsO4 ]	с - ГОИ - ],
отсюда:
[OH-]2 +3,39×10-3[OH-]-3,39×10-4 =0.
Решаем квадратное уравнение:
ГОИ ] =
- 3,39-10-3 +√11,49 -10-6 +13,56 -10-4
2
= 1,68 -10 2 моль/л;
рОН = 1,8;	рН = 14 - рОН = 14 - 1,8 = 12,2.
Находим степень гидролиза h:
h = [ОИ"]/с = 1,68-10-2/0,1 = 0,17 (17 %).
Пример 3.6. К 50 мл 0,10 М раствора №2СО3 добавлено 25 мл
0,20 М раствора HCl. Вычислить рН полученного раствора.
Ре ше ние . После смешивания двух растворов получаем:
V = 75 мл;	с(№2СО3) = 50-0,1/75 = 0,067 моль/л;
с(ИС1) = 25-0,2/75 = 0,067 моль/л.
В результате взаимодействия протолитов в растворе образуется
кислая соль (амфолит) согласно уравнению реакции:
№2СО3 + НС1 ¾ NaI 1СО3 + NaCl.
-7	-11
Для угольной кислоты Ка1 = 4,5×10 , Ка2 = 4,8×10	. При расчете
[H+]
можно воспользоваться приближенной формулой из табл. 3.1
или (3.8):
[H+] »Vка1 - ка2 =√4,5-10-7 - 4,8-10-11 = 4,65-10-9моль/л; рН = 8,3.
Пример 3.7.* К 20 мл 0,20 М раствора соли аммония в без¬
водном метаноле добавили 10 мл 0,20 М раствора метилата натрия
в безводном метаноле. Определите: а) рН исходного раствора соли;
-17
в)	рН полученного раствора, если для метанола KSH = 2,0·10 ;
Ke(NH3) в метаноле (Kfew2) = 1,0· 10-7.
Решение:
а)	в метанольном растворе протекает протолитическая реакция:
NH4+
кислота 1
+ СИ3ОН →→ NH3 + СИ3ОИ2+,
основание 2 основание 1	кислота 2
с:	0,2
[ ]:	0,2-x
x
x.
34

мет.
K а
Ksh = 2,0 × 10-17
Km 1,0 × 10 -7
_ [NH3]∙[CH3OH2+] _
= 2,0×10-10 ;
x2	» x2
[NH4 + ]	0,2 - x ~ 0,2 ∙
Откуда х = [CH3OH2+] = 6,3 · 10-6 моль/л и рН = - lg[CH3OH2+] = 5,2.
б) протолитическая реакция взаимодействия при сливании
мет.
K а
двух растворов:
NH4+	+ CH3O-
NH3	+
кислота 1
основание 2
основание 1
CH3OH,
кислота 2
с :
[.. ]:
0,2
0,2 ∙ (20 - 5) + χ
I
30
0,2
х
0,2 × 5
30
- х.
Значение константы равновесия реакции:
K р = 1/ K м'ет·= 1/1-10-7 = 1 ∙107
указывает на ее практическую необратимость и возможность при¬
ближенных расчетов. Используя эту константу или формулу для
расчета рН в растворе, содержащем кислотно-основную сопряжен¬
ную пару (3.11), можно вычислить рН полученного раствора:
Кр = [NH4+]∙[CH3O-] 15∙ x	,
откуда рОН = - lg [CH3O-] = - Ig (5/15-107) = 7,5;
рН = pKsh - рОН = 16,7 - 7,5 = 9,2.
3.2.	Буферные растворы
Важным случаем кислотно-основного равновесия является
равновесие в растворах, содержащих кислотно-основные сопря¬
женные пары и обладающих буферным действием (буферные рас¬
творы). Их готовят разными способами: растворяя в воде слабую
кислоту и ее соль (буферный раствор кислотного типа); слабое ос¬
нование и его соль (буферный раствор основного типа); две соли
многоосновных кислот разной степени замещения (например
NaH2PO4 и Na2HPO4); проводя реакцию частичной нейтрализации
многоосновной кислоты сильным основанием. Буферное действие
35

подобных систем проявляется в способности поддерживать рН в
растворе практически неизменным при внесении в него или образо¬
вании в нем некоторых количеств сильной кислоты или основания
вследствие замены сильного протолита образующимся слабым.
В растворе, содержащем сопряженную пару, например НА и
А-, устанавливаются равновесия:
НА ⅛ Н+ + А-,
А- + Н2О ⅛ НА + ОН-.
Концентрация ионов водорода в таком растворе (с учетом ав¬
топротолиза воды) выражается уравнением:
[H+]-Ka
с(НА) - {[H+] - [OH-]}
с (А -) + {[H+] - [OH - ]}
(3.10)
При достаточно высоких концентрациях НА и А- можно счи¬
тать, что [HA] » с(11А) и [А-] » с(А~), поэтому, пренебрегая величи¬
ной {[H+] - [OH - ]} , получаем формулу для приближенной оценки рН
в буферных растворах:
[H + ] - Kа
с (НА)
с (А -)
или
рН = рКа - lg
с(НА)
с(А -)
(3.11)
Каждый буферный раствор характеризуется сопротивляемо¬
стью к изменениям рН. Количественно ее выражают буферной ем¬
костью π. Она определяется числом молей эквивалентов сильной
кислоты или основания, которые нужно добавить, чтобы изме¬
нить рН раствора на единицу:
p-- Аскисл ;	p- ^осн
dpH ;	dpH ’
(3.12)
где fa - прирост концентрации сильной кислоты или основания,
вызвавший изменение показателя кислотности среды на АрН.
Буферная емкость связана с концентрацией компонентов буферной
системы:
p-	2,3	^)-с(А-)
с(НА)+с(А-)
(3.13)
36

и с константой диссоциации кислоты Ка:
p- 2,3 [H+ ]
Ka ([НА] + [А - ])
(Ka + [Н+ ])2
(3.14)
Зная буферную емкость, можно найти изменение рН раствора
при добавлении сильной кислоты или основания, определить состав
буферной смеси и решать другие вопросы. См. также пример 3.16.
Пример 3.8. К 12 мл 0,030 М раствора муравьиной кислоты
прибавлено 15 мл 0,15 М раствора формиата калия. Вычислить рН
полученной смеси.
Решение. НСООН и НСООК являются компонентами бу¬
ферной смеси (кислотой и сопряженным основанием). Рассчитаем
их концентрации после смешения (V = 27 мл):
с(НСООН) = (12∙ 0,03)∕27 = 0,013 моль/л,
с(НСООК) = (15 ∙ 0,15)∕27 = 0,083 моль/л.
Рассчитаем рН кислотного буфера:
с(НСООН)	0,013
рН - pKα - lg—	- 3,8 - Ig-		 4,6
a с( НСООК)	0,083	.
Пример 3.9. К 20 мл 0,20 М раствора двухзамещенного фос¬
фата калия прибавлено 10 мл 0,25 М раствора HCl. Определить рН
раствора.
Решение. При смешивании данных растворов происходит
реакция:
HPQ42- + H+	⅛ H2PQ4 .
основание	кислота
Количество добавленной сильной кислоты меньше, чем K2HPO4.
Поэтому, наряду с образовавшейся в результате реакции солью
KH2PO4, в растворе будет оставаться K2HPO4. Рассчитаем концен¬
трации анионов (солей) в образовавшемся буферном растворе с
учетом разбавления и взаимодействия:
[H2PO4-] = с(1 IT().l ) = KHCl)∕K = (10 ∙ 0,25)∕30 = 0,083 моль/л;
[HPO42-]= (n(HPO42-) -n(HCl))/V = (20 0,2-10 0,25)/30 = 0,050
моль/л.
37

Находим рН раствора: pH=pKa2 -Ig с(Н7Р°| ) = 7,21-Ig0,083 = 6,99.
2	с(НРО42 -)	0,050
Пример 3.10. Сравнить эффективность двух буферных рас-
творов:
1)	с(СН3СООН) = 0,10 М, с(СН3СОО№) = 0,10 М;
2)	с(СН3СООН) = 0,030 М, с(СН ;С()()∖a) = 0,17 М.
Ре ше ние . Рассчитаем рН каждого буферного раствора:
pH1 = pKa
- lg
с (СН 3 СООН)
с (СН 3СОО№)
= 4,76 - Ig — = 4,76
0,1
pH2 = 4,76- Ig0,03=5,50
2	0,17
Эффективность буферного раствора будем оценивать по вели¬
чине буферной емкости. Для этого к каждому буферному раствору
“добавим” 0,01 моль ИС1 (v). При этом рН каждого раствора изме¬
нится вследствие протекания реакции:
СН3СОО- + Н+ ¾ СН3СООН.
pH1 = 4,76 - Ig 0,1 + 0,01 = 4,76 - 0,09 = 4,67;
1 0,1- 0,01
D pH 1 = 4 ,76 - 4 ,67 = 0 ,09 ;
pH2 = 4,76 - lg0,03 + 0,01 = 4,76 + 0,59 = 5,35;
2	0,17- 0,01
DpH2 = 5,50-5,35= 0,15.
Рассчитаем буферную емкость с учетом формулы (3.12):
г(Н+)	0 01	0,01
p1 =r(—) = — = 0,11; P2 =÷7 = 0,07
1 DpH 0,09	2	0,15	.
Первый буферный раствор обладает большей буферной емко¬
стью, так как в этом растворе с(СН3СООН) = с(СН3СОО-).
Пример 3.11. Определить состав аммонийной буферной смеси
с рН 9,25, при добавлении к 0,50 л которой 25 ммоль NaOH значе¬
ние рН изменяется не более, чем на 0,050.
Решение . Найдем Dс(ОН~), соответствующее добавляемой
в буферный раствор щелочи:
38

.\оОН ) = (25∙10'3)∕0,5 = 0,05 моль/л.
Найдем необходимую буферную емкость по формуле (3.12):
р=Ас(ОН -)
DpH
= 0,05/0,05 = 1.
Рассчитаем константу кислотности Ка иона аммония:
К	10-14
Ka (NH4+) =	w— = —		 = 5,6 ∙10-10
a " K (NH3) 1,76 ∙10-5	∙
Зная π, Ka, и [H+] = 10-9,25 = 5,6∙10^1°, рассчитаем сбуф. по фор¬
муле (3.14):
Сбуф. = r(NH4+) + c(NH3);
= P- (Ka(NH4+)+[H+ ])2 = 1-(5,6 ∙10-10 + 5,6∙10-10)2
= 2,3 - Ka (NH4+) - [H+ ] = 2,3 - 5,6 -10-10 - 5,6 -10-10
c(NH+) + c(NH3)
=1,74 моль/л.
Из уравнения (3.11) находим отношение компонентов:
c(NH+) = [H+ ] = 5,6 -10-10 = 1
c(NH3)	Ka	5,6 -10-10	.
Следовательно, состав смеси: c(NH4+) = 0,87 и c(NH3) = 0,87 моль/л.
3.3.	Расчеты при приготовлении растворов протолитов
с заданным значением рН
При решении задач на указанную тему следует:
а)	установить конкретный случай кислотно-основного взаимо¬
действия (протолитической реакции): сильная, слабая кислота; силь¬
ное, слабое основание; амфолит; гидролизующаяся соль; буферный
раствор; написать уравнения протолитических взаимодействий;
б)	подобрать соответствующие формулы для расчета [H+], рН
и др. и преобразовать их относительно неизвестной величины -
концентрации раствора, или соотношения концентраций (для бу¬
ферного раствора);
в)	по найденному значению концентрации вычислить, если не¬
обходимо, другие величины: массу вещества, объем раствора и др.
Пример 3.12. В каком объеме воды необходимо растворить
3
1,000 г 17,58 % раствора HNO3 с ρ = 1,100 г/см , чтобы рН получен¬
ного раствора был равен 1,50?
39

Ре ше ние . HNO3 (М = 63 г/моль) - сильная кислота, поэто¬
му рН в растворе связан с концентрацией соотношением (табл. 3.1):
рН = - lg[H+] = - lg c(HNO3).
Зная рН, можно рассчитать молярную концентрацию полу¬
ченного раствора:
c(HNO3) = 10"рН = 10-1,5 = 0,03 моль/л.
Рассчитаем массу HNO3 в 1г раствора с ρ = 1,1 г/мл:
τ(HNO3) = 1-17,58/100 = 0,1758 г,
а также объем этого раствора: V = m/ρ = 1/1,1 = 0,9 мл.
Находим объем полученного раствора с концентрацией 0,03 моль/л:
V = v/c = 0,1758 ■ 1000/0,03 -63 = 93,0 мл.
Необходимо добавить объем воды V= 93,0 - 0,9 = 92,1 мл.
3
Пример 3.13. Сколько мл 10,1 % (ρ = 1,11 г/ см ) раствора
NaOH нужно добавить к 1000 мл 0,0010 М раствора NaOH, чтобы
рН был равен 12?
Ре ше ние . Исходный (1) раствор NaOH имеет рН:
рН = 14 + lg c(NaOH) = 14 - 3 = 11.
Следовательно, добавлением 10,1 % -го раствора нужно повысить
рН на 1 и c(NaOH) повысится до 0,010 моль/л (раствор 2). При
смешивании растворов 1 и 2 справедливо правило:
c1-V1 + c2-V2 = c3(V1 + V2).
Рассчитаем c1: c1 = ρ-w-V/M = 1,11-0,101-1000/40 = 2,803 моль/л;
2,803 V1 + 10-3-1000 = W2-(1000 + V1);
2,791-V1 = 9;	V1 = 3,22 мл.
Пример 3.14. Какую навеску NH4Cl следует растворить в 100
мл воды, чтобы рН был равен 5,5?
Ре ше ние . При растворении NH4Cl в воде протекает реакция:
NH4Cl + НОН ¾ ^4ОН + HCl,
NH4+ + НОН ⅛ Nl 14О11 + Н+.
Рассчитаем константу гидролиза по формуле (3.5):
К
гидр.
KW
= K a =	=
a	Kb
10-14
1,76 -10-5
=5,68-10-10.
Используя формулу (3.5), рассчитаем концентрацию соли:
40

^NH4Cl)»
К
гидр.
[NH4OH] ∙[H+ ] - [H+ ]2
[NH+ ]	- [NH+ ]
[H+ ]
^nh4ci) - [H+],
[H+ ]2 - (10-5,5)2
Кгидр. ~ 5,68 ∙10-10
-1,76 10-2моль/л.
Вычислим навеску NH4Cl:
m(NH4Cl) = ^H4Cl)∙<NH4Cl) V = 1,76∙10-2 ∙ 53,5∙0,1 = 0,09416 г.
Пример 3.15. Какую массу бензоата натрия нужно добавить к
500 мл 0,016 М раствора бензойной кислоты, чтобы получить рас¬
твор с рН 4,42?
Решение. При растворении бензоата натрия в растворе
бензойной кислоты (Ка = 6,6 10-5) образуется буферный раствор.
С6Н5СООН ⅛ С6Н5СОО- + Н+,
С6Н5СОО- + Н2О ⅛ С6Н5СООН + ОН-.
r, t(C6H5COO- )∙[H+ ] c(C6H5COO- )∙10-ph
Ка

а	i<C6H5COOH)	e(C6H5COOH) ’
Из этого выражения можно найти молярную концентрацию соли:
-	6,65 10 -5 0,016	3
с(C6H5COO )  	 42		 0,0278 моль/дм3.
Тогда навеска бензоата натрия (М (С6Н5СОО№) = 144 г/моль):
m = c М V = 0,0278 144 500/1000 = 2,00 г.
Пример 3.16. * Буферные системы на основе a-аминокислот
поддерживают рН в физиологических средах, в плазме крови; ис¬
пользуются в анализе. В частности, из 0,100 М водного раствора
аминоуксусной кислоты (глицина) и 0,100 М растворов HCl или
NaOH готовят буферные растворы с рН соответственно 1,10 ÷ 3,50
или 8,53 ÷ 12,9 на фоне 0,1 М NaCl. В водном растворе глицина
+
преобладает его биполярный таутамер: H3 N- CH2 -COO-
+
φKα(-COOH) = 2,3; рКа( - NH3) = 9,6). Используя указанные кон¬
центрации растворов и приведенные справочные данные (ионную
силу не учитывать):
а) вычислите рН в 0,100 М водном растворе глицина с обосновани¬
ем расчетной формулы; б) рассчитайте объем 0,100 М раствора
глицина, необходимый для приготовления 1000 мл буферного рас-
41

твора с рН 3,00 (с буферной емкостью π = 0,027).
Решение : а)глицин - амфолит, для которого через урав¬
нения материального баланса или электронейтральности и соответ¬
ствующих Ка, можно вывести формулу для расчета [H+]:
1) HA + H2O ¨ H2A+ + OH-
k = [H2A+] × [OH- ] =	Kw
1 [HA]	Ka (-COOH;
2) HA + H2O ® H3O+ + A- K 2 =
[H± ] ■ [A- ]
[HA]
+
= K a ( - NH3);
3) H2O ® H+ + OH-
Kw= [H+]∙ [OH-];
w
+
[H+] = [A-] - [H2A+] + [OH-] = k-(-nh^×[HA] —[HA] ■ [H"] +k j
2	[H+]	Ka(-COOH ) [H+]
Преобразуя последнее выражение относительно [H+], получаем: ·
[H] = ^
K ( COOH)∙ K ( .VH,)∙∣H∖∣ ■ K ( COOH)∙ K,
[HA] ± Ka (-COOH)
]к„ (-COOH) ■ K (- NHj).
Расчет по выведенной формуле (считая [HA] ≈ 0,1) и приближен¬
ной формуле приводит к рН = 6,86.
б)	для получения “кислого” буферного раствора к Vr мл 0,1 М
глицина нужно добавить V(HCl) мл 0,1 М HCl для частичного пере¬
вода основания в сопряженную кислоту:
H3N- CH2 - COO- ± H±-	®H3N- CH2 - COOH,
основание НА	сопряженная кислота Н А+
± с ×V
се,ф. = [ha] ± Ih 2 A ] = v ± V(Н	= 0,1· Vr, так как Kr + V(HCl) = 1 л.
Расчет V1- можно провести через уравнение для буферной емкости (π):
p= 2,3×[H± ]×
K (-COOH) ■ сб>ф,
(Ka (-COOH) ± [H+])2
0,027 = 2,3×1×10-3 ×
5,01∙10-3 ■ 0,1∙ Vr
(5,01∙10-3 ± 1∙10-3)2
откуда Vr = 0,849 л = 849 мл (850 мл);	V(HCl) = 151 мл.
Для расчета можно также использовать уравнение (3.11), учитывая,
что V(HCl) = 1-Vr:
42

[H2A + ]
[HA]
[H+] = Ka(-COOH )-
= Ka(-COOH )-
0,1 - V(HCl) - [H + ] -1
0,1 - Vγ - 0,1 - V(HCl) + [H+]
с последующей проверкой буферной емкости по формуле (3.13).
Задачи для самоконтроля
1.	Рассчитайте рН и a 0,100 М раствора NH4OH.	Ответ: 11,2; 1,33 %.
2.	Рассчитайте рН и a 0,00200 М раствора NH4OH. Ответ: 10,2; 9,0 %.
3.	Рассчитайте рН и a 0,010 М раствора HCOOH.
4.	Рассчитайте рН и h 0,0300 М раствора Na2CO3.
5.	Рассчитайте рН и h 0,010 М раствора Na3PO4.
6.	Рассчитайте рН 0,100 М раствора NaHCO3.
Ответ: 3,1; 8,1 %.
Ответ: 11,4; 7,98 %.
Ответ: 12; 73 %.
Ответ: 8,33.
7.	К 100 мл 0,10 М раствора фтороводородной кислоты прибавлено 5,0 г
фторида натрия. Вычислить рН этого раствора.	Ответ: 4,3.
8.	Вычислить рОН и рН буферной смеси, содержащей 0,100 моль гидро¬
ксида аммония и 0,0100 моль нитрата аммония.	Ответ: 10,2; 3,75.
9.	К 50 мл 1%-го раствора ацетата натрия добавлено 20 мл 0,1 М раство¬
ра соляной кислоты. Вычислить рН полученного раствора. Ответ: 5.
10.	В 250 мл воды растворено 3,4563 г двухзамещенного фосфата калия.
К этому раствору добавлено 50,0 мл 0,1078 М раствора соляной кислоты.
Вычислить рН полученного раствора.	Ответ: 7,63.
11.	Как изменится рН буферной смеси, содержащей 0,10 М NH3 и 0,20 М
NH4Cl, если в 1,0 л такого раствора добавить 0,01 моль HCl? Чему равна бу¬
ферная емкость такой смеси?	Ответ: ∆рН = -0,067; π = 0,15.
12.	Какую навеску ацетата калия следует растворить в 500 мл раствора,
чтобы рН раствора был равен 9,0?	Ответ: 8,6 г.
13.	Какую навеску гидрокарбоната натрия следует растворить в 100 мл
раствора, чтобы рН раствора был равен 9,06?	Ответ: 0,05 г.
14.	В каком объеме следует растворить навеску соды Na2CO3 0,005 г, что¬
бы рН раствора был равен 9,0?	Ответ: 9,9 мл.
15.	В каком объеме следует растворить навеску ацетата натрия 0,03 г,
чтобы получить раствор с рН, равным 8?	Ответ: 209 мл.
16.	Определите рН 0,20 М раствора нитрата аммония в безводном этано¬
ле. Какой объем 0,20 М раствора этилата натрия в безводном этаноле следует
добавить к 20 мл этого раствора соли аммония для получения раствора с рН
9,55? Для этанола Ksh = 8,0· 10-20; для NH3 Kf. = 8,0· 10-10.
Ответ: рН = 5,35; 9,4 мл.
17.	В условиях примера 3.16 определите, при каком рН в растворе преоб¬
ладает анион H2N-CH2-COO-.	Ответ: при рН > 11,6 его концентрация
примерно в 100 раз выше сопряженной формы.
43

ГЛАВА 4. РАВНОВЕСИЕ В РАСТВОРАХ
КОМПЛЕКСНЫХ СОЕДИНЕНИЙ
Реакцию комплексообразования в растворе можно определить
как реакцию взаимодействия между ионами металла (комплексооб-
разователя) и лигандами. Значительная часть свойств комплексных
соединений обусловлена электронной конфигурацией центрального
атома, донорными и акцепторными свойствами лигандов и приро¬
дой связи между ионом металла и лигандами. Основными призна¬
ками комплексного соединения является наличие координационной
связи, сохранение структуры в растворе и частичная диссоциация
по типу слабого электролита. Термодинамическая устойчивость
комплексного иона определяется энергией связи металла с лиган¬
дом и выражается константой равновесия реакции комплексообра¬
зования (β), называемой константой устойчивости (табл. 4 прило¬
жения). Образование комплексов происходит ступенчато, причем
каждая ступень характеризуется константой равновесия (К1,
K2,...Kn). В упрощенном виде процесс можно представить следую¬
щим образом (принимая ионную силу равной нулю):
1)	M + L ¾ ML,
2)	ML + L ¾ ML2,
K2 =
3) MLn-1 + L ¾ MLn,
[ML] -	= [ML] ;
[M][L] ;	β1 [M][L] ;
[ML2] ;
[ML][L];
= [ML2]
β2	[M][L]2
(для 2-х ступеней);
k = [MLn ]	.
n [MLn -1][L];
β = [M][iL]'· (для n стУпеней).
Например, для равновесий в растворе, содержащем ионы кад-
мия и аммиак:
Cd2+ + NH3 ±
♦ [Cd(NH3)]2+ b1 = [Cd(NH3)2+] = 3,24 -102;
3	1 [Cd2+][NH3]
Cd2+ + 2NH3 ⅛ [Cd(NH3)3]2+,
Cd2+ + 3NH3 ⅛ [Cd(NH3)3]2+,
Cd2+ + 4NH3 ⅛ [Cd(NH3)4]2+,
b = [Cd(NH,)2+ ]
b2 [Cd2+ ][NH3]2
= 2,95-104;
b4=
[Cd(NH3)2+ ]
[Cd2+ ][NH3]4
=3,63-106.
b = [Cd(NH3)3+ ]
' [Cd2+ ][NH3]3
= 5,89 -105 ;
44

Комплексообразование широко используется в анализе для
обнаружения ионов, маскирования мешающих ионов; с целью пре¬
дупреждения осаждения и растворения малорастворимых соедине¬
ний; изменения окислительно-восстановительного потенциала, а
также для проведения количественного анализа. Зная константы
устойчивости и условия проведения реакции, можно рассчитать
равновесную концентрацию любой комплексной формы или сво¬
бодного иона в растворе. В основе расчета лежит условие матери¬
ального баланса (см. раздел 2.2).
Пример 4.1. Рассчитайте равновесную концентрацию ионов
серебра в 0,010 М растворе AgNO3 в присутствии 2,0 М раствора
аммиака (см. также пример 2.6, раздел 2.2).
Ре ше ние . В растворе устанавливаются равновесия:
Ag+ + NH3 ⅛ [Ag(NH3)]+ и [Ag(NH3)]+ + NH3 ⅛ Ag(NH3)2]+,
[Ag(NH3) ± ]
[Ag± ][NH3]
= 2,09 ■103;
b = K1 ∙ K2 =
[Ag(NH3)± ]
[Ag± ][NH3]2
= 1,62 ∙107.
Составляем уравнение материального баланса, учитывая, что
ионы серебра в растворе к моменту равновесия переходят в ком¬
плексные ионы и частично остаются в свободном виде:
c(Ag+) = [Ag+] + [Ag(NH3)+] + [Ag(NH3)2+].
Выражаем [Ag(NH3)+] и [Ag(NH3)2+] из соответствующих кон¬
стант устойчивости:
[Ag(NH3)± ] = b1[Ag±][NH3], [Ag(NH3 )2± ] = b2[Ag±][NH3]2
и подставляем в уравнение материального баланса:
c(Ag±) = [Ag± ] ± ^1[Ag+ ][NH3] ± y¾[Ag± ][NH∪2 = [Ag± ] ∙ (1± β[NH3] ± β[NH3]2).
Отсюда: [Ag+] = o(Ag+)∙c(Ag+) ,
где a(Ag+) (тождественные обозначения: aAg+, или a0) - молярная
доля свободных (гидратированных) ионов Ag+:
a(Ag+) =	-		2 =		7—2 = 1,5· 10-8,
1± b1 ∙[NH3] ±b2 ∙[NH3]2 1±2,09∙103∙2 ±1,62∙107 ∙22
(поскольку c(NH3) >> c(Ag+), то [NH3] » c(NH3));
[Ag+] = c(Ag+)∙α(Ag+) = 0,01∙1,5∙10-8 = 1,5∙10-10 моль/л.
В расчетах часто вместо констант устойчивости используют
обратные им константы нестойкости Kh, характеризующие равнове-
45

сие в реакции диссоциации комплексного соединения. Например,
для соединения [MLn]:
[MLn] ¾ M + nL;
[M]∙[L]n
[ML n ]
т. е. Кн = 1∕βn.
Исходя из значений констант нестойкости комплексных соедине¬
ний, можно вычислять концентрации ионов, присутствующих в
растворах комплексных соединений, а также степень их ионизации.
Пример 4.2. Вычислить концентрацию ионов Ag+, CN- и сте¬
пень ионизации комплексного иона в 0,100 М растворе K[Ag(CN)2].
Решение. Комплексное соединение K[Ag(CN)2] диссоции¬
рует в водном растворе по типу сильного электролита:
K[Ag(CN)2] ® K+ + [Ag(CN)2]-.
Далее комплексный ион [Ag(CN)2]- (lgβ2 = 19,85 и β2 = 7,08 1019)
диссоциирует по типу слабого электролита по суммарному уравне¬
нию:
[Ag(CN)2]-
⅛ Ag+ +
2CN-,
с:	0,1
-
-
[...]:	0,1-х
х
2х.
К.(Ag(CN)-) - [Ag+ ][CN-]2
-1-
1	19 -1,41 ∙10-20
н	[Ag(CN)- ]
- b2(Ag(CN)2-) -
7,08 1019
Предполагаем, что x << 0,1, тогда	(0,1 - х) » 0,1;
4х3/0,1 = 1,41.10-20; x = 7,1.10-8 моль/л;
[Ag+] = 7,1.10-8 моль/л;	[CN-] = 2[Ag+] = 1,4.10-7 моль/л.
Степень ионизации комплексного иона:
a = 7,1.10-8 100/0,1 = 7,1.10-5 %.
Пример 4.3. К 0,20 М раствору сульфата меди добавили рав¬
ный объем 2М раствора аммиака. Вычислить концентрацию иона
Cu2+, если считать, что в растворе образуются комплексные ионы
[Cu(NH3)4]2+.
Решение. Образование комплексного иона можно пред¬
ставить суммарным уравнением:
С u2+
+ 4NH3
⅛ [Cu(NH3)4]2+ ,
с:	0,1
1,0
-
46

c/2:	0,05	0,5	- (с учетом разбавления);
[.. ]:	x	0,5-4∙0,05+4x	0,05-x .
Подставляем значения равновесных концентраций в выраже¬
ние для β4 (lgβ4 =12,03) и, пренебрегая величиной х в разностях,
проводим расчет х:
b4 =
[Cu(NH3)2+ ]
[Cu2+ ][NH3]4
,	4 = 1012,03 = 1,07 ∙1012∙
x ∙0,34	;
x = [Cu2+] = 5,8∙10-12 моль/л.
Влияние одноименного иона на равновесие в растворах ком¬
плексных соединений учитывается подобно тому, как это показано
в примерах вычисления растворимости осадков (примеры 6.11, 6.12
раздела 6.2).
Пример 4.4. Рассчитайте степень образования [HgC 13] , если
известно, что равновесная концентрация иона С1- в растворе равна
-2
1,0∙10 моль/л (определена экспериментально).
Ре ше ние . Степень образования или молярную долю ком¬
плексных ионов ртути [HgC 13]-, т. е. a3, можно вычислить по фор¬
муле (см. 2.8 - 2.10), подставляя в нее справочные значения кон¬
стант устойчивости и [Cl-]:
[HgCl3] =	b3[Cl- ]3

C(Hg) 1+b1[Cl- ]+b2[Cl- ]2 +b3[Cl- ]3 +b4[Cl- ]4
1,18∙1014(1∙10-2)3
1+5,5∙106 ∙1∙10-2 +1,66∙1013 ∙(1∙10-2)2 +1,18∙1014(1∙10-2)3 +1,66∙1016(1∙10-2)4
=0,0607;
a3 = 6,1 %.
Пример 4.5. Определите, какой комплекс преобладает в раство-
-2
ре, содержащем 1∙10^ моль/л кадмия (II) и 1 моль/л аммиака?
Решение. В растворе, содержащем ионы кадмия и аммиак,
устанавливаются следующие ступенчатые равновесия:
Cd2+ + NH3 ⅛ [Cd(NH3)]2+,
[Cd(NH3)]2+ + NH3 ⅛ [Cd(NH3)2]2+,
[Cd(NH3)2]2+ + NH3 ⅛ [Cd(NH3)3]2+,
[Cd(NH3)3]2+ + NH3 ⅛ [Cd(NH3)4]2+.
47

Общие константы образования (устойчивости) соответствую¬
щих комплексных ионов (см. выше) составляют:
β I = 3,24-102; β2 = 2,95-104; β3 = 5,89 -105; β4 = 3,63-106.
2+
Учитывая, что c(NH3) >> c(Cd ), полагаем [N⅛] = c(NH3) = 1 моль/л.
Расчет молярных долей соответствующих форм с учетом фор¬
мул (2.8 -2.10) показывает, что в растворе преобладает комплекс со¬
става [Cd(NH3)4 ]2+ (α4 =0,853):
[Cd2+ ]	1
a0 = i	- =	т =
0 c(Cd) 1+ b1[NH3]+...+ b4[NH3]4
	1

1 + 3,24 -102 + 2,95 -104 -12 + 5,89 -105 -13 + 3,63 -106 -14
= 2,35×10-7 ;
a0 = 2,35×10-5%;
a1 = [Cd(NH3) ] =b1[NH3] -a0 = 3,24 -102 -1 - 2,35 -10-7 = 8 -10-5;
c(Cd)
a1 =8×10-3%;
a2 = [Cd(NH3), ] = b2[NH3]2 - a0 = 2,95 -104 -12 - 2,35 -10-7 = 7 -10"3;
c(Cd)
a2 =0,7%;
a3 = [Cd(NH3)3 ] = b3[NH3]3 -a0 = 5,89 -105 -13 -2,35 -10^7 = 0,140;
c(Cd)
a3 =14,0 %;
α4 = [Cd(NH3)4 ] = b4 [NH3 ]4 - a0 = 3,63 -106 -14 - 2,35 -10-7 = 0,853;
c(Cd)
a4 =85,3 %.
Пример 4.6. Какое количество вещества NH4SCN необходимо
ввести в 1 л 5,0-10-5 М раствора Hg(NO3)2, чтобы снизить концен-
2+ -11
трацию ионов Hg до 1,0· 10 моль/л за счет образования ком¬
плексных ионов [Hg(SCN)4]2-?
Решение . Реакция образования комплекса:
Hg2+ + 4SCN- ⅛ [⅛(SCN)4]2-
b = [Hg(SCN)4-]
'4 [Hg2+][SCN-]4
= 5,9 ×1019.
48

Отсюда:
5 10 -5	-4
- 4	г:	ттт - 5,4 ∙ 10 моль/л;
V1∙10-11∙5,9∙1019	.	,
[SCN - ] - J[Hg(SCN)2~]
У [Hg2+ ]∙β4	-4	5	-4
c(SCN-)-[SCN-]+4[Hg(S4CN)24-]-5,4 10-4+4 5 10-5 -7,4 10-4 моль/л.
В 1 л раствора необходимо внести 7,4 ∙ 10-4 моль соли NH4SCN.
Пример 4.7. Рассчитайте максимальное значение рН, при ко¬
тором в 0,0200 М растворе Cd(NO3)2 99,0 % кадмия находится в ви-
2+
де гидратированных ионов Сd , а 1,0 % - в виде гидроксокомплек-
са [Cd(OH)]+ (lgβ1 = 4,3).
Решение . Составим уравнение материального баланса:
c<Cd) = [Cd]2+ + ^ОН+].
Из условия задачи следует: ^d]2+ = 0,0200·0,99 = 1,98· 10-2 моль/л,
а [CdОН+] = 2,0· 10-4 моль/л. Из константы устойчивости присутст¬
вующего в растворе гидроксокомплекса кадмия найдем [OH-]:
-	[CdOH ] 4 -1,99∙ 104;
[Cd2+][OH-]4
[OH-]-
[CdOH+ ]
b [Cd2+ ]
2,0∙10-4
1,99 ∙10-4∙ 1,98 ∙10-2
- 5,1 10 -7.
Отсюда lg[OH ] = - 6,30; pH = 7,70.
Пример 4.8. Вычислите условную константу образования
2-
комплексоната никеля NiY (комплекс никеля с анионом этилен-
диаминтетрауксусной кислоты (ЭДТА) Y4- состава 1:1) в буферном
растворе, содержащем 0,050 М NH3 и 0,10 М NH4Cl.
Решение . Реакция образования комплексоната никеля
Ni2+ + Y4- ⅛ NiY2-
в указанных условиях сопровождается побочными реакциями обра¬
зования аммиакатов никеля и протонирования аниона слабой четы¬
рехосновной кислоты - Y4-. В таком случае равновесие образова¬
ния NiY2- описывается условной константой:
й,	[NiY2-]	[NiY2-]	a
b ' - -t—⅛	, л - —⅛	-7- ∙ aλr 2+ ∙ av4- - b ∙ au.2 + ∙ av4-
с XNi2+ )∙ с '(Y4') [Ni2+ ]∙[Y4-] Ni y	Ni y ,
49

2+ 2+
где с'(Ni ) = [Ni ]/aNi2+.- общая концентрация ионов металла, не
прореагировавших с Y4- (свободные ионы никеля и входящие в со¬
став всех аммиакатов); с'(Y4-) = [Y4-]/aY4- - общая концентрация
всех форм ЭДТА, за исключением входящих в комплексонат нике¬
ля (свободные ионы Y4- и протонированные формы).
2- 18
b(NiY ) = 4,17∙10 , а для аммиачных комплексов никеля
β1 = 4,68∙102; β2 = 6,17∙104; β3 = 2,51∙106; β4 = 2,95∙107 , β5 = 1,26∙108;
8
β6 = 1,02∙10 (из табл. 4 приложения). Рассчитаем молярную долю
свободных ионов металла aNi2+ с учетом формулы (2.8):
1
a т. 2+ = 	’
Ni	1+b1∙[NH3]+b2∙[NH3]2 +...+b6 ∙[NH3]6
aNi2+ =1/(1 + 4,68∙ 102∙0,05 + 6,17∙ 104∙0,052 + 2,51∙ 106∙0,053 +
+ 2,95∙107 ∙0,054 +1,26∙108∙0,055 +1,02∙108∙0,056) = 1/717,75 =
1,39· 10-3.
Доля свободных лигандов Y4- зависит от рН, задаваемого ам¬
миачным буферным раствором. Значение рН определяется по фор¬
муле (3.11):
рН = рКа - lg(c(NH4+yc(NH3)) = 14 - р Kb - lg(c(NH4+yc(NH3));
рН = 14 - 4,75 - lg(0,1/0,05) = 8,95 » 9.
Молярную долю aY4- при рН = 9 можно рассчитать по форму¬
лам (2.4, 2.5) или взять из табл. 7 приложения: aY4- = 0,052.
Используя найденные значения a, вычислим условную кон¬
станту образования комплексоната никеля:
β'(NiY2 ) = β(NiY2-Va^Ом- = 4,17∙ 10l8∙ 1,39· 10-3∙0,052 = 3,01∙10l4.
Задачи для самоконтроля
1.	Вычислите равновесные концентрации ионов калия, ртути и хлорид-
иона в 0,10 М растворе K2[Hg(Cl)4]. Ответ: 0,2; 1,9∙10-4; 7,5∙10-4 моль/л.
2.	Вычислите равновесную концентрацию ионов кобальта(Ш) в 0,10 М
растворе хлорида кобальта (III), содержащего 0,60 моль/л аммиака.
Ответ: 1,4∙10-6 моль/л.
3.	Рассчитайте равновесную концентрацию Hg(II) в 0,0100 М растворе
Hg(NO3)2 в присутствии 0,0800 М KI.	Ответ: 5,8∙ 10-27 моль/л.
4.	Рассчитайте равновесную концентрацию Ag(I) в растворе, содержащем
0,10 М [Ag(NH3)2]+ и 0,50 М NH3.	Ответ: 2,4∙ 10-8 моль/л.
50

5.	Рассчитайте равновесную концентрацию Со(П) в растворе, содержащем
25,96 г/л хлорида кобальта и 2,8 моль/л аммиака, если считать, что в растворе
Э-1-	7
образуются комплексные ионы |Со(\Н3)| .	Ответ: 8,5∙10- моль/л.
+ 2+
6.	Рассчитайте степени образования [Cu(NH3)3]+ и [Cu(NH3)4]2+ в растворе
с равновесной концентрацией аммиака 0,10 моль/л. Ответ: 9,8 %, 90,0 %.
2¬
7.	Сколько граммов NaOH необходимо для образования [Zn(OH)4]2-
2+
из 50,0 мл 0,8 М ZnCl2, если концентрация Zn2+ в конечном растворе
не превышает 1,0 10-13 моль/л (Mr (NaOH) = 39,98).	Ответ: 7,14 г.
8.	Сколько молей КОН необходимо добавить к 1 л 0,0560 М раствора
Pb(NO3)2, чтобы равновесная концентрация ионов РЬ(11) понизилась до 3,5-10-5
моль/л за счет образования [РЬ(ОН)3]- ?	Ответ: 0,17 моль.
9.	Рассчитайте условную константу образования комплексоната кадмия в
0,0100 М растворе КС\.	Ответ: 2,8-104.
51

ГЛАВА 5. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНОЕ
РАВНОВЕСИЕ
5.1.	Оценка окислительно-восстановительной
способности веществ и направления
окислительно-восстановительной реакции
Окислительно-восстановительная реакция протекает с изме¬
нением степеней окисления элементов, входящих в ту или иную
форму реагирующих веществ. Направление окислительно-восста¬
новительной реакции (3) и глубина ее протекания, как и в других
химических равновесиях, могут быть определены по константе
равновесия, являющейся произведением констант (раздел 2.3) по¬
луреакции восстановления (1) и полуреакции окисления (2).
1)	Ox1 + ne ¾ Red1,
2)	Red2 - ne ¾ Ox2,
3)	Ox1 + Red2 ¾ Red1 + Ox2,
К10
К20
aRed1
aOx1×
aen
aOx2
aRed2
×ae-n
aRed1 ×
aOx2
9
К 30 =
aOx1 × aRed2
Окисленная и восстановленная формы вещества представляют
собой сопряженную пару (Ox1/Red1; Ox2/Red2) или редокс- пару,
подобно паре кислота - сопряженное основание в кислотно¬
основном равновесии. Подобие этих систем проявляется также в
невозможности осуществления в растворе полуреакций приема и
отдачи электронов, как и полуреакций приема и отдачи протона
(основанием и сопряженной кислотой - глава 3).
Чаще направление окислительно-восстановительной реакции
и глубину ее протекания оценивают, сравнивая стандартные
Eox/Red потенциалы, а в реальных условиях - формальные потен-
0'
циалы EOx/Red (примеры 5.5 - 5.8).
52

Стандартные потенциалы EO0x/Red измеряют в гальваническом
элементе (рис. 5.1) относительно стандартного водородного элек¬
трода, E02H+/H которого принят за нуль при любой температуре. Их
приводят в справочных таблицах (табл. 5 приложения) для полуре¬
акций восстановления. В стандартных условиях активности всех
участников полуреакции равны 1, т. е. EO0x/Red не зависит от ион¬
ной силы раствора и концентрации реагентов. Чем больше EO0x/Red ,
тем более сильным окислителем является окисленная форма пары и
более слабым восстановителем - ее восстановленная форма.
Для определения направления реакции в близких к стандарт¬
ным условиях необходимо сравнить EO0x /Red и EO0x /Red полуреак¬
ций и найти DEq = E⅛x /Red - E⅛x/Red . Это соответствует вычи¬
танию из одной полуреакции восстановления другой полуреакции
восстановления. При DE0 > 0 реакция окисления-восстановления
протекает слева направо (пример 5.1), а при DE0 < 0 - в обратном
направлении (пример 5.7).
Использование для оценки окислительно-восстановительной
способности веществ удобной термодинамической характеристики,
которой является окислительно-восстановительный (электродный,
редокс-) потенциал, связано с отличительной особенностью полу¬
реакций окисления и восстановления - возможностью их разделе¬
ния в пространстве. Полуреакции можно осуществить в виде ка¬
тодного (восстановление) и анодного (окисление) процессов в галь¬
ваническом элементе - электрохимической ячейке, служащей ис¬
точником тока. Электрический ток возникает при переносе элек¬
тронов, т. е. энергия химической реакции преобразуется в электри¬
ческую (рис. 5.1).
Для этого компоненты полуреакций помещаются в отдельные
сосуды, которые соединяют солевым мостиком. Им может быть
стеклянная трубочка, заполненная инертным гелем, пропитанным
сильным электролитом, не участвующим в редокс- реакциях (KCl
на рис. 5.1). В каждый сосуд, погружается проволочка (пластинка)
либо из инертного металла, либо из металла, участвующего в полу¬
реакции. Металл и компоненты полуреакции составляют полуэле¬
мент или электрод. Электроды подсоединяют к гальванометру или
53

потенциометру - внешней цепи. При замыкании цепи гальванометр
покажет наличие тока.
Анод:	Катод:
Zn0 - 2e = Zn2+ 2H+ + 2е = H2 (с.
(окисление)	(восстановление)
Рис. 5.1. Схема гальванического
элемента: 1 - анод, 2 - катод,
3 - гальванометр
На рис. 5.1 один полуэле¬
мент состоит из цинковой пла¬
стинки, погруженной в раствор
ZnSO4 (a(Zn2+) = 1 моль/л) (цин¬
ковый электрод). Другой - из
платиновой пластинки, покрытой
губчатой Рt (для лучшей адсорбции
Н2, который подается под давлением
101,3 кПа), погруженной в раствор
с а(Н+) = 1 моль/л - стандартный
водородный электрод (с.в.э.). При
замыкании цепи электроны от
цинка будут переходить к ионам
Н+ и начнется суммарная реакция
до установления равновесия, ко-
торая протекала бы и в растворе между Zn и кислотой:
4) 2Н+ + Zn ⅛ Н2(газ) + Zn2+.
Измеренная при этом ЭДС близка к величине:
ЭДС =
Екатода Еанода Е 2H+/H2
- = 0 - (- 0,76) =
= - E°Zn2+/Zn = 0,76 В.
2+
Если вместо электродной пары Zn /Zn в левый сосуд помес¬
тить пару Cu2+/Cu, при замыкании цепи стрелка гальванометра от¬
клонится в другую сторону, поскольку электроны от водорода
(анода) будут переходить к ионам Cu2+, в результате чего медь из
раствора будет осаждаться на медном электроде (катоде), что соот¬
ветствует суммарной реакции:
5) Н2(газ) + Cu2+ ⅛ 2Н+ + Cu .
Тогда: ЭДС = ЕкаТОда - Еанода = E°Cu2+/Cu - E°2h+/H? = 0,34 - 0 =
Е Cu2+∕Cu 0,34 В.
Различие в направлении отклонения стрелки измерительного
прибора в этих двух случаях указывает на различие в направлении
самопроизвольно протекающей в гальваническом элементе химиче-
2+ +
ской реакции. Сила окислителя уменьшается в ряду: Cu > Н >
2+
Zn , а сила восстановителя уменьшается в ряду: Zn > Н2> Cu.
54

Схематически гальванический элемент представляют, указы¬
вая слева направо: анод (присваивают знак «-»); границу раздела
фаз (вертикальная черта); электролиты в анодном полуэлементе;
границу раздела полуэлементов (две вертикальные черты); элек¬
тролиты в катодном пространстве; границу раздела фаз (вертикаль¬
ная черта); катод (присваивают знак «+»). Для гальванического
элемента рис. 5.1 границей раздела полуэлементов (катода и анода)
в растворе служит солевой мостик с KCl.
Упомянутые гальванические элементы (см. также примеры
5.21-5.23):
(-) Zn I ZnSO4 (1 M) Il M2SO4 (0,5 M) IН2, Pt (+),
(-) Pt, Н21N.-SO: (0,5 M) I I CuSO4 (1 M) I Cu (+).
На практике для измерения потенциалов вместо с.в.э. используют
электрод сравнения с известной величиной потенциала, чаще всего
хлорсеребряный или насыщенный каломельный (пример 5.23).
Пример 5.1. В каком направлении протекает реакция между
Fe3+ и I- ?
Решение. Табличные значения E°Ox/Red для полуреакций:
1)	Fe3+ + e ⅛ Fe2+,	£°Fe3+;Fe2+ = + 0,77В,
2)	I2 + 2e ⅛ 2I- ,	E°I2/2I_ = + 0,54 В.
Уравнивая число электронов и вычитая из полуреакции вос¬
становления (1) (с участием предполагаемого окислителя) полуре¬
акцию восстановления (2)(с участием предполагаемого восстано¬
вителя) и меняя знаки в уравнении на положительные, получаем:
3) 2Fe3+ + 2I- ⅛ 2Fe2+ + I2 ,
DE° = Е°Feз+/Fe2+ -	= 0,77 - 0,54 = 0,23 B.
DE° > 0, поэтому реакция 3) протекает в прямом направлении.
5.1.1.	Расчет стандартного потенциала полуреакции,
являющейся сочетанием двух полуреакций
Для определения неизвестного Е0 можно использовать спра¬
вочные данные о Е0 двух полуреакций, сочетанием которых можно
представить полуреакцию для новой пары:
55

1)	Ох1 + ne ¾ Red1 - с табличным значением Е°1;
2)	Ох2 + me ¾ Red2 - с табличным значением Е°2;
3)	Ох2 + (m + n)e ¾ Red1 - с неизвестным значением Е°3.
0 nE10 + mE20
e3 -	,	.
m+ n
(5.1)
Пример 5.2. Рассчитать Е0 полуреакции:
H2SO3 + 6H+ + 6e ⅛ H2S + 3H2O,
если известны: ES0/H S - 0,171 B и EH0 SO /S - 0,450 B.
Решение. Представим полуреакции, для которых Е0 из¬
вестны и полуреакцию (3), потенциал которой надо вычислить:
1)	S + 2H+ + 2e ¾ H2S,
2)	H2SO3 + 4H+ + 4e ¾ S +
3H2O,

3)	H2SO3 + 6H+ + 6e ¾ H2S +
3H2O,
Е0 =
0,171 В;
Е0 =
0,450 В;
Е0 = ?
Используя формулу (5.1) находим потенциал:
E0 -
EH2SO3/H2S
2 ∙ 0,171+4 ∙ 0,450
6
- 0,357 B.
Пример 5.3. Рассчитайте EN0O / N O для полуреакции
2NO2 + 6H+ + 6e ⅛ N2O + 3H2O,
исходя из величин EH0 NO2 / N2O -1,29 B и EN0O2/HNO2 -1,09 B.
Решение. Представим полуреакции с известными Е0:
2HNO2 + 4H+ + 4e ⅛ N2O + 3H2O,
NO2 + H+ + e ⅛ HNO2,
Е0 = 1,29 B,
E0 = 1,09 B.
После удвоения второй полуреакции (для уравнивания коэффици¬
ентов при HNO2) и сложения, получаем:
2NO2 + 6H+ + 6e ⅛ N2O + 3H2O,	Е° = ?
E0
NO2/N2O
4EHNO2 / N2O + 2ENO2/HNO2	4×1,29+ 2×1,09
6 - 6
-1,22 B.
56

5.2.	Вычисление потенциала в реальных условиях.
Уравнение Нернста
В реальных условиях химического равновесия величина потен¬
циала зависит от температуры и активностей окисленной и вос¬
становленной форм. Количественно эта зависимость равновесного
потенциала пары (E) выражается уравнением Нернста:
для полуреакции	Ox + ne ¾ Red
RT	aOx
уравнение Нернста E = Eo + 	In	,	(5 ?)
nF a
Red
где: R - универсальная газовая постоянная (8,31 Дж×моль'1К'1);
F - число Фарадея (96493 Кл-моль’1);
T - абсолютная температура (К);
Е - равновесный потенциал.
После подстановки постоянных величин и переходя к деся¬
тичным логарифмам, получаем коэффициенты 0,059 при 25° С и
0,058 при 20° С.
Тогда уравнение Нернста при 25° С можно записать так:
E = E° +
0,059 lg aox
n	aRe d '
(5.3)
Обычно вместо активностей в расчетах используют концен¬
трации окисленной и восстановленной форм, пренебрегая различи¬
ем в величинах коэффициентов активностей обеих форм, которые
при близких значениях сокращаются в уравнении (5.3).
Пример 5.4 . Вычислить EB/2Br_, если [Вг2]ж = 0,21 моль/л, а
[Br -] = 0,012 моль/л.
Ре ше ние . Записываем уравнение полуреакции:
Вг02(ж) + 2e ⅛ 2Вг _,	E°Br2/2Br_ = +1,07 B.
Записываем уравнение Нернста для данной полуреакции:
EBr2/2Br- = E° Bγ2∕2Bγ- + (0,≡2)⅛([bΓ2HbΓ-]⅛
Eb,2bγ-= 1,07 + (0,059/2).lg(0,21/0,0122) = 1,07 + 0,029'3,163 = 1,16 В.
57

5.3.	Влияние электростатических и химических взаимодействий
на величину потенциала. Формальный потенциал
В тех случаях , когда на величину равновесного потенциала
влияют электростатические и химические факторы (см. главу 2),
удобно пользоваться общими концентрациями окисленной и вос¬
становленной форм (c0x и cRed).
Поскольку, а = gac, то уравнение Нернста приобретает вид:
e = e о	+ 0,059
^Ox/Red	^Ox/Red ^,^
n
lg
gOxaOx
gRedaRed
0,059
+ —

n
c
lg'	,(5.4)
c Red
где сумма первых Двух членов преДставляет собой формальный
»
потенциал E°'Ox/Red. Он равен равновесному потенциалу при общих
концентрациях окисленной и восстановленной форм, равных 1, и
заДанных концентрациях всех Других веществ, присутствующих в
системе, но не меняющих степень окисления.
'
Как видно из уравнения (5.4), формальный потенциал E°', в
отличие от станДартного E°, зависит от ионной силы, глубины
протекания конкурирующих реакций и концентрации частиц, не
являющихся окисленной и восстановленной формами, но прини¬
мающих участие в полуреакции. Именно формальный, а не стан¬
дартный потенциал следует использовать для оценки направления
окислительно-восстановительной реакции в реальных условиях.
Например, для полуреакции:
AsO43- + 2H+ + 2e ⅛ AsO33- + H2O,
согласно (5.4), уравнение Нернста для равновесного потенциала
можно представить, помня о том, что a(H2O) = 1 (стандартное со¬
стояние), в виде:
E 3	3 = E» 3	3 + 0059Ig gAs°4 " - + 0059lga(Н+)2 +
AsO43-/AsO33-	AsO43-/AsO33-	2 g - ×a	-	2
AsO33-	AsO33-
0,059 l с(AsO3-)
+	2 g с (AsO3-).
/
Формальный потенциал E° при этом можно представить как:
58

eo	e>	ι 0,059 gA<'a⅛ ι 0,059 _(Н+ )2
4/Asθ3- =	∕Asθ3- + ~,g	3 a 3	) '	(5.6)
AsO33- AsO33-
5.3.1.	Влияние ионной силы на потенциал
Коэффициенты активности ионов - участников окислительно¬
восстановительной полуреакции входят в числитель и знаменатель
выражений (5.4) - (5.6). Поэтому легко видеть, что заметное влия-
Z
ние ионной силы на величину E и Eo может проявляться, когДа
окисленная и восстановленная формы элементов входят в состав
ионов с сильно отличающимися зарядами, или при разном числе ио¬
нов в правой и левой части полуреакций. В частности, в выражениях
(5.5) и (5.6) ионная сила раствора будет оказывать влияние на E и
E°, в основном через g+, поскольку JAs043- » ‰θ33-.
Пример 5.5. Рассчитать формальный потенциал пары
Fe3+/Fe2+ при ионной силе, равной 0,1 и 0,01.
Ре ше ние . Записываем уравнение полуреакции:
Fe3+ + 1e ¾ Fe2+,	E° = 0,77 B.
При I = 0,1 gFe3+ = 0,16, gFe2+ = 0,43;
при I = 0,01 gFe3+= 0,44, gFe2+= 0,67.
С учетом вышеприведенных уравнений и (5.3) можно записать
при молярных долях a 3+ и a 2+, равных 1 и n = 1:
Fe3+	Fe2+
e°' = e° + 0,059lg(ge3+∕ge2+).
При I = 0,01	E° = 0,77 + 0,059lg(0,44∕0,67) = 0,77 - 0,011 =
= 0,76 B.
При I = 0,1	E° = 0,77 + 0,059lg(0,16∕0,43) = 0,77 - 0,025 =
= 0,74 B.
Проведенные расчеты показывают, что с ростом ионной силы
раствора снижается окислительная способность ионов Fe3+. Однако
при изменении ионной силы в 10 раз потенциал изменяется всего
лишь на 0,02 В (на 2,6 %) даже для ионов с зарядом окисленной и
восстановленной форм, отличающимся в 1,5 раза (Fe3+ и Fe2+).
59

5.3.2.	Влияние рН раствора на величину потенциала
Влияние рН на величину потенциала проявляется для полуре¬
акций, протекающих с участием «ионов среды» - Н+ и ОН-, причем
оно может быть настолько значительным, что способно изменить
направление (пример 5.7) окислительно-восстановительной реакции.
Пример 5.6. Рассчитайте равновесный и формальный потен¬
- 2+ - + 2+
циалы пары MnO4 /Mn (строго говоря, пары MnO4 , 8Н /Mn ),
если [MnO4-] = 0,20 и [Mn2+] = 0,1 моль/л при pH = 5 и рН = 1.
Решение. Записываем уравнение полуреакции:
MnO4- + 8H+ + 5e ⅛ Mn2+ + 4H2O, E°MnO4-7Mn2+ = 1,51 B.
С учетом вывода, сделанного в примере 5.5, и ввиду отсутст¬
вия данных о составе раствора, будем считать I = 0, а g ионов рав¬
ными 1. Тогда равновесный потенциал пары MnO4-/Mn2+ можно
вычислить по уравнению Нернста вида (5.4) или (5.5), а по уравне¬
нию, подобному (5.6) - формальный.
E ,	= E°	, „ + (0,059∕5)⅛[H+]8 + (0,059∕5)lg[MnO+
MnO4-/Mn2+	MnO4-/Mn2+	[Mn2+]
При рН = 5 или [H+] = 10-5 моль/л, в отсутствие побочных реакций
(a = 1):
£MnO4-/Mn2+ = 1,51 + (0,059∕5)lg(10-5)8 + (0,059/5)lg(0,2/0,1) = 1,042 В;
E°'MnO4-/Mn2+ = E°MnO4-/Mn2+ + (0,059/5)lg[H+]8 = 1,51 + (0,059/5)lg(10-5)8 = 1,038 В.
При рН = 1 или [H+] = 10-1 моль/л, в отсутствие побочных реакций
(a = 1):
E MnO4-/Mn2+ = 1,51 + (0,059/5)lg(10-1)8 + (0,059/5).lg(0,2./0,1) = 1,420 В;
E°'MnO4-/Mn2+ = E°MnO4-/Mn2+ + (0,059/5)lg[H+]8 = 1,51 + (0,059/5)lg(10-1)8 = 1,416 В.
Сравнивая E° (при рН=0) и E° для пары MnO4 /Mn при различных
рН, можно видеть сильную зависимость окислительной способно¬
сти формы MnO4- от рН, проявляющуюся в её увеличении с ростом
кислотности раствора.
Пример 5.7. Определите направление реакции взаимодейст¬
вия иода с арсенитом натрия при рН =0, рН = 4 и рН = 8.
60

Ре ше ние . Реакция взаимодействия иода с арсенит-ионом:
AsO33 + I2 + H2O ¾ AsO43 + 2I + 2H+.
Полуреакции и стандартные потенциалы пар:
I2 + 2e ⅛ 2I-,	E° I2/2I_ = 0,54 В.
As043∙ + 2H+ + 2е ⅛ As°33- + H2O, e°a^a^ = 0,57 В.
Сравнение Eo данных пар показывает, что арсенат-ион являет¬
ся более сильным окислителем, чем иод. Если, как это предполага¬
ется по реакции, окислителем считать иод, то:
Do = 0,54 - 0,57 = _ 0,03 В, т. е. ЛЕ° < 0.
Следовательно, в стандартных условиях (аН+ = 1, рН = 0) рав¬
новесие данной реакции будет смещено влево, иод не будет окис¬
лять арсенит.
3-	3-
Вычислим формальные потенциалы пары AsO4 ∕AsO3 с уче¬
том рН по формуле (5.6) (EI /2I- от рН не зависит). При рН = 4:
E0'-
AsO43-∕AsO33
E0-
AsO43- ∕AsO33
+0059lgα(н+)2 =0,57+0,059lg<10 4 )2 =0,334В;
при рН = 8:
E0' 3	3 = 0,57 + 0059 lg(10-8)2 = 0,098B
AsO3- ∕ AsO3-	2
43
/
Сравнивая EoI /2I- с полученными значениями Eo AsO 3-∕AsO 3-, ви-
3-	3-
дим, что с ростом рН формальный потенциал пары AsO4 ∕AsO3
/
уменьшается, EoI /2I- становится значительно больше, чем EoAsO 3-∕AsO 3-, зна¬
чит арсенит будет окисляться иодом и реакция пойдет в прямом
направлении.
При рН 4: DEo' = 0,54 - 0,334 = 0,206 В, т. е. DEo' > 0;
при рН 8: DEo' = 0,54 - 0,098 = 0,442 В, т. е. DEo' > 0.
5.3.3.	Влияние комплексообразования на величину потенциала
Окисленная или восстановленная формы системы могут связы¬
ваться в комплексы или образовывать малорастворимые соединения.
В таких случаях образуется новая пара, стандартный потенциал ко¬
торой связан с потенциалом пары Ox∕Red через константу, характе¬
ризующую побочную реакцию. В случае образования комплекса -
это константа устойчивости комплекса b, а в случае образования ма¬
61

лорастворимого соединения - константа растворимости малораство¬
римого электролита или произведение растворимости ∕∖s.
Учет комплексообразования можно провести через молярные
доли форм по общему уравнению (5.4) с использованием (2.8). При
условии преобладания комплекса одного состава - OxLm, для кото¬
рого
bm = [OxLm]/[Ox][L]m
и при участии OxLm в полуреакции
OxLm + ne ¾ Red + mL
уравнение Нернста примет вид:
E = E0
OxL /Red	Ox/Red
m
n
n
n
0,059	1	0,059	1	0,059	[OxLm]
+ — l^^+— lgπτm+“— l⅛dτ (57)
bm	n	[L]m n	[Red] .	(5.7)
43
E0
OxL /Red
m
Аналогично, при связывании восстановленной формы в комплекс:
E	= E0
Ox/RedL	Ox/Red
m
0,059	0,059 m 0,059 [Ox]
+—- b+—- ⅛[L]++— ⅛-_ (5.8)
n
n
n
E0
Ox/RedL
m
Суммы первых трех членов в этих уравнениях представляют собой
Z	/
формальные потенциалы пар: E° OxL Red и E° OxRedL .
Формулы (5.7 - 5.10) могут быть использованы и в решении об¬
ратных заДач - вычисления соответствующих констант по значе¬
ниям потенциалов (примеры 5.9, 5.11).
Пример 5.8. Рассчитать формальный потенциал окислитель¬
но-восстановительной пары, образованной ионами Fe3+ и Fe2+, в 2М
растворе фторида аммония, если [Fe3+] = [Fe2+] = 0,0010 моль/л.
Решение. Ионы Fe3+ (окисленной формы) вступают в реак¬
ции комплексообразования с ионами F-. Поскольку ионы F- взяты в
большом избытке, можно считать, что в растворе протекает реакция
Fe3+ + 5F- ⅛ [FeF5]2-
и образуется пара [FeF5]2-/Fe2+.
Рассчитаем E°'[FeF5]2-,Fe2+ по формуле (5.7):
E [К·. 5 2 l..2- E°[FeF5]2-/Fe2+ + 0-°59 ∣g<∣ b + 0,059lg(W]5);
справочные данные: E°Fe3+/Fe2+ = 0,77 B; lgb5 = 16,1; b5=1,26.1016;
62

£°'FeF5]2-/Fe2+ = 0,77 + 0,0591g(1∕1,26'10l6; + 0,0591g(1∕25) = - 0,27 В.
Следовательно, связывание Fe3+ , т. е. окисленной формы в
комплекс, привело к сильному снижению стандартного потенциала
3+	2+	3+
Fe ∕Fe и, соответственно, окислительных свойств Fe .
Учет конкурирующих реакций можно провести и по формуле
(5.4), предварительно вычислив молярную долю свободных ионов
3+
Fe (a 3+) по формуле (2.8):
Fe3+
1
aFe3+
= 2 04×10-1^
1 +106,04 × 2 + 1010,74 × 22 +1013,74 × 23 +1015,74 × 24 +1016,1 × 25 ’	;
£°'[FeF5]2-/Fe2+ = ‰∕Fe2+ + 0,059lg(a1,1„)=0,77 + 0,0591g(2,0410-1s> = -
0,27 В.
Результаты расчетов двумя способами получаются одинако¬
выми, что указывает на правильность предположения о преоблада¬
нии формы [FeF5]2- и об отсутствии необходимости учета других
форм комплексных ионов.
Пример 5.9. Вычислите константу устойчивости комплексно-
2¬
го иона ^d(CN)4] ', если для полуреакции:
[εd(CN)4]2- + 2е = Сd + 4CN- Е° = - 0,907В.
Реше ние. Найти величину b4 для комплекного иона
2-
^d(CN)4] ' можно, используя формулу (5.7), согласно которой
E0
OxL ∕Red
m
E0
Ox∕Red
0,059
+ —

n
lg
Стандартный потенциал E°Cd2+∕Cd = - 0,403 В. Тогда:
- ⅛A = ( Е°| С'с1(С\)4 ∣2-∕('d, 4CN- - e°Cc∣2∙ Cd У2/0-059 =
= (- 0,907 + 0,403)×2∕0,059 = -17,1;	b4 = 1,22.1017
5.3.4.	Влияние образования малорастворимых соединений
на потенциал
Пусть окисленная форма образует осадок с анионом А:
Ox + A ¾ OxA^	K°s = α(Ox) × а(А);	а(Ox) × = K0/а(A).
Ox + e ¾ Red и полная полуреакция: OxA + e ¾ Red + А.
63

После подстановки и преобразования получаем уравнение Нернста
(5.9)
Е0
Е OxA /Red
Аналогично, если восстановленная форма малорастворима:
E0
Ox / Re dA
(5.10)
Пример 5.10. Как изменится потенциал пары BrO3 /Br , если в
раствор ввести AgNO3? Ионную силу не учитывать.
Ре ше ние . В этом случае в осадок связывается восстанов¬
ленная форма по реакции:
Ag+ + Br- ⅛ AgBr I	Ks(AgBr) = 5,3 10-13.
Для полуреакции BrO3- + 6Н+ + Ag+ + 6е ⅛ AgBrI + 3Н2О
уравнение Нернста имеет вид уравнения (5.9).
С учетом E°BrO3-/Br- = 1,45 B вычисляем E°BrO3-/AgBr:
E°BrO3-/AgBr = 1,45 + (0,059/6)lg(1/5,3 10-13) = 1,45 + 0,12 = 1,57 В.
Следовательно, окислительно-восстановительный потенциал
пары увеличивается при связывании в малорастворимое соедине¬
ние восстановленной формы, при этом возрастает сила окислителя.
Пример 5.11. Определите K0S(CuI), если известны потенциалы
пар: E°Cu2+/Cu+ = 0,153 В и E°Cu2+/CuI = 0,858 В.
Ре ше ние . По условию очевидно, что восстановленная
форма первой пары образует малорастворимое соединение CuI. Ис¬
пользуя формулу (5.10), рассчитываем K0S (CuI):
lg KS = (EOx/Re dA EOx/Re d ) × 1/0,059;
(EC0u2+/CuI -EC0u2+/Cu+ )/0,059 = (0,858-0,153)/0,059 =11,95;
K0S (CuI) = 1,12 10-12.
64

Пример 5.12.* К 10,0 мл 0,010 М раствора Pb(NO3)2, содер¬
жащего также 4,00×10-4 М K3[Fe(CN)6], добавили некоторый объем
0,0340 М раствора K4[Fe(CN)6]. Количество добавленного
K4[Fe(CN)6] меньше стехиометрического в реакции взаимодействия
с ионами свинца. Потенциал платинового электрода, погруженного
в полученный раствор, равен 0,705 В (по отношению к с.в.э.). Вы¬
числите а) равновесную концентрацию ионов Pb2+ в полученном
растворе (с учетом ионной силы, соответствующей 0,1 М KNO3);
б) величину потенциала платинового электрода в растворе при сте¬
хиометрическом количестве добавленного K4[Fe(CN)6].
Для справки: Λ^s(Pb2[Fe(CN)6]) = 9,55×10-19,
E	3-	4- = 0,364 В.
[Fe(CN)6]3- /[Fe(CN)6]4-	В
Ре ше ние . Реакция взаимодействия:
1) 2Pb2+ + [Fe(CN)44- ⅛ Pb2[Fe(CN)4;.
коэффициенты активности составляют: g Pb2+= 0,44; g[Fe(CN)6]4- = 0,037.
Равновесный потенциал платинового электрода для полуреакции:
2) [Fe(CN)43- + 1е ⅛ [Fe(CN)6]4-
определяется по уравнению Нернста вида:
а) при количестве K4[Fe(CN)6], меньшем стехиометрического
по реакции осаждения 1), в растворе остаются ионы Pb2+, в присут¬
ствии которых:
a([Fe(CN) 6]4-) = 2
KS0
aPb2+
То есть в присутствии ионов Pb2+ равновесный потенциал платино¬
вого электрода фактически определяется полуреакцией:
3) [Fe(CN)6]3- + 2Pb2+ + 1е ⅛ Pb2[Fe(CN)6U.
После подстановки в уравнение Нернста выражения для
a([Fe(CN)6]4- ) получаем уравнение вида (5.10). Решаем его, под¬
ставляя имеющиеся данные:
0,705 = 0,364+0,059×lg4×10-4-0,059×lg9,55×10-19+0,059×2lg0,44+0,059×2lg[Pb2+];
65

0,705 = 1,185 + 0,059×2lg[Pb2+];
lg[Pb2+] = - 0,480/2·0,059 = - 4,068;	[Pb2+] = 8,55× 10-5 моль/л;
б) при стехиометрическом количестве добавленного осадителя
2+
в реакции 1) концентрация [Pb ] будет определяться растворимо¬
стью Pb2[Fe(CN)6]:
9,55 ×10	= 3,22 ∙ 10 -6 моль/л;
S = з
3
22 ×gP2b 2+ ×g[
	KS	= з
2gPb -×gi Fe (CN )614 -	V' 44	3'
[Pb2+] = 2 S = 6,44·10-6 моль/л.
Тогда равновесный потенциал платинового редокс-электрода будет
равен:
Е = 1,185 + 0,059 2lg[Pb2+] = 1,185 + 0,059 2lg(6,44 10-6) = 0,572 В.
5.4.	Расчеты с использованием константы равновесия
окислительно-восстановительной реакции
5.4.1.	Расчет константы равновесия по стандартным
и формальным потенциалам
Направление реакции, полноту её протекания, а также равно¬
весные концентрации компонентов или растворимость веществ в
ходе окислительно-восстановительной реакции, можно оценить по
ее константе равновесия (см. разделы 2.3, 5.1), которая в справоч¬
никах не приводится, но связана с табличными значениями стан¬
дартных потенциалов. Термодинамическую константу (К0) можно
вычислить по формуле:
1 jκ0	(E(Ox) - E(Red))n DEn
lg K =	0.05.,	= 00T9,	(5Л1)
где n - число электронов, передаваемых в ходе реакции окисли-
00
тельно-восстановительного взаимодействия; Е (Ox) и Е (Red) - стан¬
дартные потенциалы пар предполагаемого окислителя и восстано¬
вителя. В реальных условиях вместо стандартных потенциалов
следует воспользоваться формальными и вычислить условную кон-
Z
станту равновесия К.
66

Пример 5.13. Вычислить константу равновесия реакции окис¬
ления иодом арсенит-иона с учетом кислотности среды в условиях
примера 5.7.
0 0z
Ре ше ние . Воспользуемся данными о Е и Е для полуре¬
акций, полученными в примере 5.7.
Уравнение реакции: AsO33- + I2 + H2O ¾ AsO43- + 2I- + 2H+;
полуреакции и потенциалы пар:
I2 + 2e ⅛ 2I-,	E0 = 0,54 В;
рН = 0; рН = 4; рН = 8;
AsO43 + 2H++2е ⅛ AsO33 + H2O, E0=0,57 В; Е0= 0,334 В; Е0= 0,098 В.
В стандартных условиях (рН = 0) рассчитаем термодинамиче¬
скую константу равновесия К0
указанной реакции по формуле
(5.11). В качестве окислителя предполагается I2.
1дК0
(e∣2∕2I- easo3-∕AsO33-)'2 = (0,54-0,57)∙2
0,059	=	0,059
1,02; К0=10-1,02=0,096.
Поскольку К0 < 1, равновесие реакции смещено влево. Вычислим
значения К' при других значениях рН. При рН = 4:
Ig К ,=
(EI2∕2I-
E'°	3	3 ) ■ 2
AsO43 - ∕ AsO33 -
0,059
(0,54 - 0,33) ■ 2
0,059
= 7,12; К' = 1,3 ■ 107;
при рН = 8:	1gK' = (0,54 - 0,1)∙2∕0,059 = 14,9; K = 1015.
Расчеты показывают, что для практически полного смещения
равновесия вправо необходимо создать рН > 4.
Пример 5.14. Вычислить константу равновесия реакции:
2Cu2+ + 4I- ⅛ 2CuU + I2.
Реше ние . Представим полуреакции и соответствующие им Е0:
Cu2+ + 1e ⅛ Cu+,	Е0 = 0,159 В;
I2 + 2e ⅛ 2I-,	Е’ = 0,536 В.
Предложенную реакцию можно представить как сумму ступенчатых
процессов, характеризующихся соответствующими константами:
67

2Cu2+ + 4I- ⅛ 2Cu+ + I2,
2I- + 2Cu+ ⅛ 2CuU,
(0,159-0,536)×2
K1 = 10	0,059	= 1,66 ×10 "l3;
K2 =
1
K2(CuI)
1
(1,1 × 10-12)2
= 8,26 ×1023.
Общая константа равновесия суммарной реакции равна про¬
изведению K1-K2 (см. также раздел 2.3):
К = KvK = 1,66∙10-13∙8,26∙1023 = 1,37-1011.
Значение константы показывает, что реакция будет протекать
до конца даже при стехиометрическом соотношении реагирующих
веществ.
5.4.2.	Вычисление равновесных концентраций
по величине константы
Пример 5.15. Вычислить равновесные концентрации частиц в
растворе, содержащем H3AsO4, H3AsO3, H+, I2, I-. Считать, что
с(Н+) = 2,0 моль/л; C(H3AsO4) = c(H3AsO3) = c(I-) = c(I2) = 0,1 моль/л.
(Ионную силу не учитывать).
Ре ше ние . В растворе присутствуют две пары:
E0
H3AsO4 /H3AsO3
=0,56 B и EI02/2I-
= 0,536 B. Их сравнение позволяет
предположить реакцию
H3AsO4 + 2I- + 2H+ ⅛ H3AsO3 + I2 + H2O,
(0,56-0,536)-2
для которой K = 10	0,059	= 6,51.
Величина K > 1, реакция протекает в прямом направлении,
причем дополнительное смещение равновесия происходит из-за из¬
бытка (по условию) ионов Н+ по отношению к стехиометрическо¬
му. Для расчета равновесных концентраций необходимо воспользо¬
ваться выражением константы равновесия через равновесные кон-
центрации:
К = [H3AsO3]×[I2]∕([H3AsO4]×[Γ]2×[H+]2) = 6,51.
H3AsO4 + 2I- + 2H+ ⅛ H3AsO3 +	I2	+ H2O,
Обозначим исходные и равновесные концентрации (в недостатке I-).
68

с:
0,1 0,1 2,0 0,1 0,1
[..]: 0,1-0,05+х 2х 2,0-0,1+2х 0,1+0,05-х 0,1+0,05-х
Подставляя в выражение для константы равновесия обозна¬
ченные равновесные концентрации, получаем:
651 =	(0,15 - х )2
,	(0,05 + х)∙(2х)2×(1,9 + 2х)2 .
Решая уравнение методом подстановки, находим х = 0,038.
[H3AsO4] = 0,05 + 0,038 = 0,088 моль/л;
[H3AsO3] = [I2] = 0,15 - 0,038 = 0,112 моль/л;
[I-] = 0,038 2 = 0,076 моль/л;
[H+] = 1,9 + 0,076 » 1,98 моль/л.
Пример 5.16.* Вычислить равновесные концентрации ионов
3+	2-
Cr , Cr2O7 и Н2О2 в растворе, содержащем 0,2 моль CrCl3 и
0,3 моль Н2О2 в 1 литре, считая, что рН поддерживается равным 1.
Решение. Рассматривая полуреакции и Е0:
1) Н2О2 + 2Н+ + 2e ⅛ 2Н2О,	Е = 1,77 В;
2)	Cr2O72- + 14Н+ + 6e ⅛ 2Cr3+ + 7 Н2О,	Е = 1,33 В,
предполагаем протекание реакции 3) - окисления ионов хрома
(III). Константа равновесия этой реакции (п = 6):
lg κ = (1,77 -1,33)6 = 44,75; к = 5,6∙1044
0,059	.
Обозначим исходные и равновесные концентрации для участ¬
ников реакции:
3) 2Cr3+ +
3Н2О2 + Н2О ⅛ Cr2O72-
+ 8Н,+
с:
0,2
0,3	-
10-1,
[..]:
х
1,5х	0,1
10-1.
Подставляем соответствующие величины в выражение для К и на¬
ходим равновесные концентрации:
K =5,62 1044
= [Cr2θ7-]{H+]8 = 0,1∙(10-1)s,
=[Cr3+ ]2∙ [H2O2]3 = х 2 ∙ (3/2 х)3 ’
x=[Cr3 + ]=^5,27∙10-55 =1,4 ∙10-11 моль/л ;
69

[H2O2] = 1,5×[Cr3+] = 2,1×10-11 моль/л.
5.4.3.	Вычисление растворимости веществ
в окислительно-восстановительной реакции
Пример 5.17. Вычислить растворимость железа (г/л) в 0,500 М
уксусной кислоте.
Решение . Сравнение стандартных потенциалов пар
Е°2Н+/Н2= 0 и ЕFe2+/Fe = - 0,473 В, а также вычисленная по ступенча¬
тым константам общая константа равновесия:
(0-(-0,473)∙2
к = ка ■ Kox/Red = (1,76∙ 10-5)2 ∙ 10	0,059	= 3,35∙ 106
указывают на протекание прямой реакции:
Fe + 2CH3COOH ⅛ Fe2+ + 2C¾COO- + ‰
C:	0,5	-	-	-
[,,,]:	2х	0,25 -х	0,5 -2х	0,25 - х.
С учетом высокого значения K (3,35∙106>> 1), предполагается
низкое значение х (х << 0,25 моль/л).
Растворимость Н2 при 25° С составляет 8∙10-4 моль/л, поэтому
в выражение константы подставляем эту величину равновесной
концентрации Н2, а не завышенное значение 0,25 моль/л.
3,35∙106
(0,25 - х) ∙ (0,5 - 2х)2 ∙ 8 ∙10-4 » 0,25 ∙ 0,52 ∙ 8 ∙10-4
4х2	4х2
х = -y∣ 3,73 ∙10 12
=1,93∙10-6 (действительно, х << 0,25).
Растворимость железа равна 0,25 моль/л или 0,25∙56 = 14 г/л.
Пример 5.18. Вычислить растворимость сульфида никеля в
2М HNO3.
Ре ше ние . E0 2- = -0,48B, E0 -	= 0,96B.
S / S2 -	NO3- / NO
Реакцию растворения NiS в HNO3 (реакция 3) можно предста¬
вить как сумму двух процессов:
1)	3NiS ⅛ 3Ni2+ + 3S2-,	K1 = (K0s )3 для NiS;
2)	3S2- + 2NO3- + 8H+ ⅛ 3S + 2NO + 4H2O, K2 = K(„ κ,j;
70

(0,96 - (- 0,48))∙6
К = (К0 )3 ∙ Kox/Red = (3,2 ∙ 10-l9 )3 ∙ 10	0,059
= 3,28 10-56 2,46 10146 =9,04 1090;	т . е. К >>1.
Введем обозначения исходных и равновесных концентраций
частиц в растворе. Сравнение стехиометрических соотношений ио¬
нов NO3- и H+ и их исходных концентраций показывает, что ионы
Н+ взяты в недостатке. Поэтому, с учетом стехиометрических соот¬
ношений, выразим убыль концентрации взятых частиц (ионов ки¬
слоты) и добавление продуктов реакции через исходную концен¬
трацию ионов Н+. За х обозначим концентрацию одной частицы,
расходующейся или образующейся вследствие частичной обрати¬
мости реакции (для общего случая взаимодействия). Учитывая, что
-3
растворимость NО при 25° С ~ 2,1-10' моль/л, что меньше его кон¬
центрации 0,5 моль/л (4/8), способной образоваться по данной ре¬
акции (из-за необратимости реакции х мало), в расчетах используем
-3
именно величину растворимости NО - 2,1-10' моль/л.
3) 3NiS + 2NO3-	+ 8H+ ¾ 3Ni2+ + 2NO + 3S +
4H2O,
с:	2 2 - - -
[..]:	2-4/8+2х 2 - 2 + 8х 6/8- 3х 4/8 - 2х -.
(2,1 10-3!!!)
9 04 -1090 = (0,75 - 3х)3 -(2,1-10-3)2 ;
,	(1,5 + 2 х)2-(8 х)8	’
2,35∙10-11
9,04 ∙1090
= 2,00 10-13 .
х = 8
Следовательно, растворимость NiS в 2 М HNO3 составляет:
S(NiS) = [Ni2+] = 6/8 = 0,75 моль/л.
Для данной реакции, протекающей необратимо, расчет можно
было провести сразу по концентрации компонента, взятого в недос¬
татке. Подробная же запись для вычисления х сделана, чтобы пока¬
зать, как провести такой расчет в любом случае с К > 1.
Пример 5.19.* Вычислить растворимость HgS в 6 М HNO3.
Решение. Для уравнения реакции:
3HgS + 2NO3' + 8Н+ ⅛ 3Hg2+ + 2NO + 3S + 4H2O,
71

рассуждая как в примере 5.16 с той же KoxfRed, получаем существен¬
ное отличие в величине общей константы равновесия из-за разли¬
чия в величинах К 0s для HgS и NiS.
К = (tf0s (HgS))3 К.е, = (1,6∙10-52)3∙2,76∙10146 = 1,13∙10-9, т. е. К>> 1.
В этом случае за х обозначим концентрацию одной образую¬
щейся частицы в ходе реакции с К << 1. Равновесные концентрации
ионов в левой части уравнения выразим как разности исходных и
образующихся, с учетом стехиометрических коэффициентов:
3HgS + 2NO3- +
8Н+ ⅛
3Hg2+ +
2NO + 3S + 4H2O,
c:
6
6
-
- -
[..]:
6 - 2х
6 - 8х
3х
2х	-
[..]:
2(3 - х)
8(0,75-х)
3х
2х	-.
Подставляем равновесные концентрации в выражение для
константы и решаем уравнение:
[Hg2+ ]3 ∙[NO]2
[NO3 - ]2 ∙[H+]8
(3 х)3 ∙(2 х)2
88 ∙(0,75- х)8 ∙22 ∙(3-х)2
=1,13∙10-9
х = 0,155; S(HgS) = [Hg2+] = 3х = 3∙0,155 = 0,465 моль/л.
При этом [NO] = 2х = 0,31 моль/л, что больше s(NO), составляющей
-3
2,1 ∙10 моль/л. Следовательно, расчет необходимо повторить с
[NO] = 2,1∙10-3 моль/л (справочные данные по растворимости NO):
1	10=	(3х)3 ■ (2J-W3)2
88 ∙ (0,75 - х)8 ∙ 22 ∙ (3 - х)2 ’
откуда:	х = 0,481; s(HgS) = [Hg2+] = 3х = 0,481×3 = 1,44 моль/л.
5.5.	Расчеты с использованием ЭДС гальванического элемента
При проведении подобных расчетов используются два урав¬
нения Нернста с разными редокс- парами или разными концентра¬
циями компонентов редокс- пар. В свою очередь, концентрация
компонентов редокс- пары может быть связана с любым видом
взаимодействий в растворе из рассматриваемых в главах 2,3,6 и
разделах 5.2-5.3. Расчеты с использованием ЭДС гальванического
72

элемента приближают к пониманию изучаемого в дальнейшем по¬
тенциометрического метода анализа.
Пример 5.20. Приведите схему и вычислите ЭДС гальваниче¬
ского элемента, составленного из редокс- пар Pb2+/Pb и Zn2+/Zn при
стандартных активностях всех участников и константу равновесия,
протекающей в нем окислительно-восстановительной реакции.
Ре ше ние . Справочные данные:
E°Pb2'Pb - 0,126 В, e°Z112∙∕11 - 0,764 В.
В гальваническом элементе должна протекать самопроизволь¬
ная реакция с DE° > 0 (разд. 5.1). Для этого катодом должен быть
свинцовый электрод, анодом - цинковый.
Схема гальванического элемента:
(-) Zn I Zn2+ (а = 1 моль/л) I I Pb2+ ((а = 1 моль/л) I Pb (+).
ЭДС = DE° = E°Pb2+/Pb - E°/n2+/Zn = - 0,126 - (- 0,764) = 0,638 В.
По формуле (5.11) находим для реакции:
Pb2+ + Zn ¾ Pb + Zn2+
lgK0 = ^ePb2+ /Pb EZn / Zn) ■ 2 De ■ n
g	0,059
0,059
1021.
= 0,638∙ 2
= 0,059
= 21,63 и K0 = 4,24∙
Пример 5.21. Приведите схему гальванического элемента, оп¬
ределите его ЭДС и константу протекающей в нем реакции. Эле¬
мент состоит из свинцового полуэлемента (свинцовой пластинки,
погруженной в раствор, содержащий взвесь PbSO4 в 0,10 M
Na2SO4), цинкового полуэлемента (цинковой пластинки в 0,020 М
растворе ZnSO4) и солевого мостика с KNO3.
Ре ше ние . Рассматривая стандартные потенциалы редокс-
пар (E°Pb2+/Pb= - 0,126 В и E°/n2+//n= - 0,764 В), можем установить ка¬
тод и анод в данном гальваническом элементе согласно раздела 5.1
(см. также пример 5.20): сила Pb2+ как окислителя выше, чем Zn2+,
значит цинковый полуэлемент - анод, а свинцовый - катод.
Схема элемента:
(-) ZnI ZnSO4 (0,020 M)II Na2SO4 (0,10 М), PbSO4I Pb (+).
Полуреакция на аноде:	1) Zn - 2е ¾ /n2+,
73

а в катодном полуэлементе совокупность реакций:
2) Pb2++ 2е ⅛ Pb и 3) Pb2++ SO42- ⅛ PbSO4,
приводящих (разд. 5.3.4) к полуреакции:
4) PbSO4 + 2е ⅛ Pb + SO42-.
Вычислим, пренебрегая влиянием ионной силы и учитывая связы¬
вание Pb2+ в малорастворимое соединение, потенциалы соответст¬
вующих электродов по уравнению Нернста (см. формулы (5.3) и
(5.9) при α(Red) = 1):
^Zn2+∕Zn = ^°Zn2+∕Zn+ (°,°≡)1g[Zn2+];
Е2п2+/2п = - 0,764 + (0,059 2)'lg0,ιι20 = - 0,814 В.
Е° ,PbSO4∕Pb ='^2+«. + (0,059/2)lg^s(PbSO4) + (0,059/2) Ig
(1/[SO42-]);
Е0'pbso4/Pb = - 0,126 + (0,059/2) lg1.6∙ 10 8 + (0,059/2)lg (1/0,10)=-
ч		0,326 В.
Е PbSOyPb
ЭДС = Е - Е	= Е°'
катода анода	PbSO4/Pb
- Л/..'· z.. = - 0,326 - (-0,814) = 0,488 В.
Для протекающей в гальваническом элементе реакции
PbSO4 + Zn° ⅛ Pb + Zn2+ + SO42-,
можно вычислить константу равновесия по формуле (5.11):
lg K ' =
⅛/ - e- / zn )∙2 = (-0,326 - (-0,764)) ∙ 2
0,059	0,059
=14,85;
7 ?
К' = 7,04 1014.
Пример 5.22. Вычислите ЭДС гальванического элемента:
(-) Pt, ⅛∣NH4Cl (1,76· 10’'2M) IIAgNO3 (0,010 M), NH3 (2,0
М)|А8 (+).
Решение. Справочные данные: Е°Ag+/Ag = 0,800 В· ПрИ вЫ¬
числениях пренебрежем влиянием ионной силы.
ЭДС = ■ Екзтодз.- Еан°да ^H+/^ - ’^Ag+ZAg·
Равновесный потенциал водородного электрода зависит от рН,
+ -2
значение которого при c(NH4 ) = 1,76 ∙10' моль/л составляет 5,5
(пример 3.14).
Реакция в анодном полуэлементе: H2 -2е ¾ 2H+.
E°2H+/H2 = 0, давление водорода - 1 атм. По уравнению Нернста:
74

= (0,059∕2),1g [H+]2 = - 0,059 рН = - 0,059-5,5 = - 0,324 В.
На катоде вместо равновесия Ag+ + е ¾ Ag в присутствии избытка
NH3 устанавливается равновесие [Ag(NH3)2]+ + е ¾ Ag + 2NH3.
В таком случае вычисление равновесного потенциала можно
провести по формуле (5.7), учитывая, что bAg(NH )+ = b2 = 1,62 ×107 и
α(Ag) =1:
E	=E 0	+∩∩59ig	1

Ag(NH3)+ /Ag	Ag(NH3)+ /Ag
Ag(NH3)2+
+0,0591⅛-b7+0,0591g[Ag(∖H3 )2 ].
[NH3]2	3 2
В условиях большого избытка лиганда:
[Ag(NH3)2+] » c(Ag+) = 0,010 моль/л;
[NH3] = c(NH3) - 2 c(Ag+) = 2 - 2-0,01 = 1,98 моль/л.
fAg(NH1)+/Ag=	0-800+0-059(1g(1/1-62·l07)+1g(l/l,982)+1g0-0l0)	=
0,221 В.
Можно провести расчет равновесного потенциала катода как
серебряного электрода, рассчитав [Ag+] в условиях комплексообра¬
зования. В примере 4.1 для указанных условий найдена aAg+, рав¬
ная 1,5×10-8.
[Ag+] = c(Ag+)-aAg+ = 0,01∙ 1,5∙10-8 = 1,5∙10-10 моль/л.
fAg+,Ag = f°Ag+,Ag + 0,0591g[Ag+] = 0,80 + 0,0591g(1,5∙ 10-10) =
0,221 В.
ЭДС = Екатода.- Еанода = 0,221 - (- 0,324) = 0,545 В.
Пример 5.23.* Вычислите равновесную и аналитическую
концентрацию (с учетом ионной силы) ионов свинца в растворе ка¬
тодного полуэлемента, если после добавления к 20,0 мл раствора
соли свинца 1,30 мл 0,0340 М ^[Fe(CN)6] измеренная величина
ЭДС гальванического элемента
(-)Hg | Hg2C1g, KC1 (нас.) I IKNO3 (0,1 М), Pb2+(?), |Fe(CW,∣i (■!.(’)■ Ki1 М) | Pt (+)
оказалась равной 0,463 В и известно, что добавленное количество
R4IFe(CN)6] меньше стехиометрического. (Справочные данные
приведены в примере 5.12).
Ре ше ние . Анодом здесь служит насыщенный каломельный
электрод (н.к.э.), потенциал которого равен 0,242 В. Н.к.э. часто
используют в электрохимических ячейках как электрод сравнения.
75

Потенциал анода вычислим по величине ЭДС и известному потен¬
циалу катода:
ЭДС = Екатода.- Еанода , откуда: Екатода = Еанода + ЭДС = 0,242 + 0,463 = 0,705 В.
Катодом является инертный электрод (Pt), потенциал которого зави¬
сит от активности компонентов редокс- пары [Fe(CN)6] /[Fe(CN)6] .
Ее восстановленная форма, в свою очередь, зависит от активности
ионов Pb2+ (пример 5,12). Далее решение следует проводить как в
примере 5.12 а), где найдено:
[Pb2+] = 8,55-10-5 моль/л.
Аналитическая концентрация соли свинца (с0) определяется
суммой прореагировавшего (n1) по реакции
2Pb2+ + [Fe(CN)6]4" → Pb2[Fe(CN)6∏
2+
и оставшегося (n2) количеств Pb с учетом объемов раствора.
V1 = c(K4[Fe(CN)6])∙ K(K4[Fe(CN)6])∙2 = 0,034∙ 1,3∙2∙ 10-3 = 8.81 -10 5 моль,
v2 = [Pb2+] - Ираствора = 8,55-10^5 -21,3-10 3 = 0,18-10^5 моль,
⅛(Pb2+) = (V + V2)/K(l = (8,84 + 0,18)-10_5/0,020 = 4,51 -10- моль/л.
Задачи для самоконтроля
1.	Будет ли протекать реакция между хлоридом олова(П) - SnCl2 и бром-
31
ной водой - Br2? Ответ подтвердить расчетом К. Ответ: Да. К = 1,5×10 .
2.	Вычислить равновесный окислительно-восстановительный потенциал
пары Cl2/2Cl- при [С12]ж = 0,20 моль/л; [Cl-] = 0,002 моль/л. Ответ: E = 1,5 B.
3.	Определить формальный окислительно-восстановительный потенциал
пары MnO47Mn2+ при pH = 2.	Ответ: E° = 1,3 B.
4.	Вычислить значение формального потенциала редокс-пары IO3-/I2 при
ионной силе, равной 0,10 и рН = 1,0.	Ответ: E° = 1,1 B.
5.	Вычислить значение формального потенциала пары Ag+/Ag в 0,10 M
растворе аммиака.	Ответ: E° = 0,49 B.
2+
6.	Рассчитайте стандартный потенциал системы Cu2+/CuI, если стандарт-
2+ +
ный потенциал системы Cu2+/Cu+ равен 0,0159 В.	Ответ: E° = 0,87 B.
7.	Оцените направление и полноту протекания реакции:
SO42- + 2I- + 2H+ → H2SO3 + I2 + 2H2O при pH = 1,0.
-33
Ответ: K = 10-33; влево, практически не идет.
8.	Вычислите потенциал водородного электрода в растворе, полученном
при добавлении к 50,0 мл 0,200 н. раствора Na2CO3 50,0 мл 0,100 М HCl.
Ответ: - 0, 492 В.
9.	Вычислить растворимость золота (Е°Аи3+/Аи = 1,50 B) в 1,2 М HNO3 по
реакции: Au + NO3- + 4H+ → Au3+ + NO + 2H2O.	Ответ: 4-10-12 моль/л.
76

10.	* Можно ли осадок Cr(OH)3, выделенный в результате осаждения ам¬
миаком из 20 мл 2,0 М раствора Cr(NO3)3, полностью растворить при 25° С в
20 мл раствора, 1 литр которого содержит 6,0 моль NaOH и ~ 6 моль Н2О2.
Ответ подтвердите расчетами, используя необходимые справочные данные.
Ответ: осадок растворится.
11.	* Вычислите равновесный потенциал редокс- пары (HgY2-∕Hg^), Y4-)
в растворе, полученном добавлением к 10 мл 0,0010 М раствора нитрата
кальция 10 мл 0,0010 М раствора ЭДТА. Считайте молярную долю аниона
ЭДТА - aY4- = 1; E’HgY^Hg^XY4- = +0,210 В и [HgY2-] = 7,24∙ 10-4 моль/л.
Ответ: 0,303 В.
12.	Вычислите ЭДС гальванического элемента:
Ag | AgNO3 (0,010 M), NH3 (0,50 М) || Hg2C12, KC1 (0,10 M) | Hg.
Ответ: 0,018 В.
13.	Вычислите ЭДС гальванического элемента:
Pt | Fe2+ (0,05М), Fe3+(0,1M) || Мп2+(0,05М), MnO4-(0,1M), CH3COOH
(1M) | Pt
Ответ: 0,50 В.
77

ГЛАВА 6. ГЕТЕРОГЕННОЕ РАВНОВЕСИЕ В СИСТЕМЕ
ОСАДОК - РАСТВОР
Реакции осаждения и растворения представляют один из наи¬
более важных для аналитической химии видов гетерогенного рав¬
новесия. Они широко используются для обнаружения, разделения и
количественного определения катионов и анионов.
В системе осадок - раствор, т. е. в насыщенном растворе ма¬
лорастворимого электролита типа AmBn, устанавливаются равнове¬
сия, которые можно представить в виде (заряды ионов упущены
для упрощения записи):
AmBn (та)——1 ® mA + nB
AmB
n (р-р)
Для соединений с ионной решеткой (большая часть сильных
электролитов) преобладает равновесие 1 (ионная растворимость).
Для соединений с молекулярной решеткой (очень слабые электро¬
литы) - равновесие 2 (молекулярная растворимость).
Термодинамическую константу равновесия 1 - равновесия
между малорастворимым соединением и его ионами в растворе -
называют термодинамическим произведением растворимости
(табл. 6 приложения). Эту константу можно выразить следующим
образом (aAmBn = 1):
0	m n
KS = aA aB
(устаревшее обозначение - ПРТ).
Эта константа связана с реальным (концентрационным) KS и
/
условным Ks произведением растворимости (см. также раздел 2.3,
выражение (2.1)) через коэффициенты активности g и молярные до¬
ли a соответствующих ионов. Учитывая, что для иона А, например,
активность аА = сА-дА-аА , причем сАаА = [A], получаем выражение:
	 lr' „,m ^ m „,n ^ n	∕<1∖
= KSgA aA g aB ,	(6.1)
Txr   г a -∣m гт* in „ τz'   m n
где KS = [A] [В] , а KS = сА сВ .
При невысоких значениях ионной силы раствора I (g близки к 1), а
также в отсутствие конкурирующих реакций (а = 1), K0s = Ks = Ks .
78

Тогда в расчетах можно по табличному значению K0S найти в на¬
сыщенном растворе общие концентрации ионов А и В, которые
только в этом случае равны равновесным. В тех случаях, когда ио¬
ны, образующие осадок, участвуют в побочных реакциях (пример
2.5), или существенны электростатические взаимодействия, при
расчетах следует пользоваться соотношением (6.1).
Произведение растворимости позволяет провести расчеты ус¬
ловий образования или оценить растворимость осадков в данном
растворителе, в том числе и при протекании химических реакций.
6.1.	Определение условий выпадения осадка
и разделения ионов
Малорастворимое соединение начинает выделяться в виде твер¬
дой фазы, когда произведение концентраций (точнее, активностей)
ионов данного электролита (так называемое ионное произведение,
обозначаемое ИП) достигает величины произведения растворимости.
Если ИП < K0S , осадок не образуется, т. е. растворяется.
Пример 6.1. Образуется ли осадок гидроксида марганца, если
к 20 мл 0,20 M раствора хлорида марганца прилить 10 мл 1,0 М
раствора NaOH?
Решение. Образование осадка происходит по реакции:
Mn2+ + 2OH- ⅛ Mn(OH)2I
Значение K0S(Mn(OH)2) = 4.10-14. Так как реакция протекает в
растворе сильных электролитов, необходимо провести расчет с
учетом ионной силы раствора. Находим концентрации ионов в рас¬
творе после разбавления:
2+ 20 0,2 -
c(Mπ2+) = 20—10 = 0,133 моль/л;	c(Cl ) = 2 ∙0,133 = 0,266 моль/л;
- + 1 10
c(OH_) = c(Na+) = 10+20
= 0,333 моль/л.
Вычисляем ионную силу раствора по формуле (2.1):
I = 0,5 ∙ (eZ2(Mn2+) + cZ 2(CΓ) + cZ 2(OH-) + cZ 2(Na+);
I = 0,5·(0,133 ·22 + 0,266 12 + 0,333 12 + 0,333 12) = 0,73.
По табл. 1 приложения для полученного значения I находим
коэффициенты активности:
79

gOH- = g Cl- = g Na+ = 0,89; g Mn2+ = 0,63.
Вычисляем ионное произведение с учетом того, что ионы в
растворе взаимодействуют по основной реакции в соответствии с
равновесными концентрациями, равными общим, побочных реак-
2+
ций нет (не учитываем гидролиз Mn ), a = 1.
ИП = ClMn’>;,-Ml'-c’(Ol I >∙∕oh = 0,133 -0,63- (0,333 )2 -0,892 = 7,36 -10-3.
ИП > K0S, следовательно, осадок выпадет.
Пример 6.2. Может ли образоваться осадок Mg(OH)2, если
смешать равные объемы 0,5 M MgCl2 и 0,1 M раствора NH4OH?
Расчет провести без учета ионной силы раствора.
Ре ше ние . При сливании двух равных объемов суммарный
объем увеличивается вдвое, а концентрация веществ уменьшается
вдвое, т. е. концентрация MgCl2 станет равной 0,25 моль/л, а
NH4OH - 0,05 моль/л.
[Mg2+] = c(Mg2+) = c(MgCl2) = 0,25 моль/л.
Равновесную концентрацию OH- рассчитываем, используя констан¬
ту диссоциации NH4OH: Kb = 1,76·10-5.
[OH-] = J Kb■ cb =/1,76- 10-5-0,05 = 9,38∙10^4 моль/л.
Взаимодействие ионов с образованием осадка протекает по реакции
(K0S(Mg(OH)2) = 5,0·10-12):
Mg2+ + 2OH- → Mg(OH)2L.
ИП = [Mg2+]∙[OH-]2 = 0,25∙(9,38∙10-4)2 = 2,2∙10-7;
ИП > K0S (Mg(OH)2), т. е. осадок выпадет.
Пример 6.3. Найдите pH начала выпадения осадка Fe(OH)2 из
0,10 M раствора FeSO4. При каком значении pH осаждение будет
практически полным?
Ре ше ние . Образование осадка можно представить уравне¬
нием:
Fe2++ 2OH → Fe(OH)2L.
KS(Fe(OH)2) = [Fe2+][OH-]2 » K0S(Fe(OH)2 = 1,1∙10-15.
Так как FeSO4 - сильный электролит, [Fe2+] = C(FeSO4).
[OH-] = x K /[Fe2+] = √1,1 -10-15 / 0,1 = 1,05∙10-7 моль/л; pOH = 7; pH = 7.
Следовательно, при pH = 7 начнется выпадение осадка
Fe(OH)2 из 0,10M раствора FeSO4.
80

ОсажДение (связывание) иона считается практически пол¬
ным, если его концентрация в растворе становится < 10 6 моль/л.
Тогда [OH-] = √ Ks0/[Fe2 +] =√1,1-10-15/10 ^6 = 3,3∙10-5 моль/л; pH = 9,5.
Таким образом, при pH = 9,5 образование осадка из 0,10 M
раствора FeSO4 практически закончится.
В растворе могут присутствовать несколько ионов, участвую¬
щих в реакциях образования осадков с одним и тем же реагентом.
Это используется при объединении ионов в одну аналитическую
группу аналитических классификаций катионов и анионов. По схе¬
ме расчета, подобной приведенной в примере 6.4, можно рассчи¬
тать условия начала и конца совместного осаждения группы катио¬
нов. Практический интерес представляет также определение воз¬
можности разделения двух ионов (при достаточно заметной разни¬
це в K0S их соединений с одним и тем же реагентом), т. е. возмож¬
ности их фракционного осаждения.
Пример 6.4. Какой осадок выпадет первым и какая доля пер¬
вого иона останется в растворе к началу осаждения второго, если к
раствору, содержащему по 0,10 моль/л нитратов кальция и бария,
постепенно добавлять 0,10 М карбонат аммония. Возможно ли ко-
2+ 2+
личественное разделение ионов Ba и Ca с такой концентрацией
при осаждении карбонатом аммония?
Решение. K0s (BaCO3) = 4,0 -10-10; K0s(CaCO3) = 3,8 -10-9.
Ионную силу учесть в данном случае сложно, поскольку ме¬
няется ионный состав раствора в ходе осаждения. Однако её изме¬
нения одинаково скажутся на изменении коэффициентов активно¬
сти ионов, входящих в состав осадков, и не повлияют на общий вы¬
вод. Поэтому будем считать g ионов равными единице и K0s = Ks.
Найдем [CO32-] для начала осаждения ионов Ba2+, т. е. [CO32-]Ba2+:
[CO32-]Ba2+ = K0s(BaCO3)/[Ba2+] = 4,0 10-10/0,1 = 4,0 10-9 моль/л,
и для начала осаждения ионов Ca2+:
[CO32-]Ca2+ = K0s(CaCO3)/[Ca2+] = 3,8 10-9/0,1 = 3,8 10-8 моль/л;
2- 2- 2+
[CO3 ]Ba2+ < [CO3 ]Ca2+, поэтому для Ba раньше будет дос¬
тигнуто соотношение ИП > K0s, и осадок BaCO3 выпадет первым.
K началу осаждения Ca2+ в растворе останется [Ba2+]Ca2+:
81

∣Ba'∣la = K0s (Ba(.'<>;) ∣Co∕ |( a = 4,0·10'Ι0/3,8 ∙ 10-8 = 1,0 ∙ 10-2 моль/л.
-2
Это составляет 1,0 10 100/0,1 = 10 % от первоначального количест¬
ва, следовательно, полного разделения ионов не произойдет, они бу¬
дут соосаждаться.
При практически полном осаждении доля иона в растворе со¬
ставляла бы величину менее 1,0 10-6 100/0,1 = 0,001 %.
Пример 6.5.* Найдите условия количественного разделения
2+ +
Pb и Tl путем насыщения сероводородом (c(¾S) = 0,1 моль/л)
раствора, содержащего по 0,10 моль/л каждого катиона.
Решение. Представим равновесия двух главных реакций:
Pb2+ + S 2- ⅛ PbS 4-,	Ks(PbS) = 2,5 ∙102';
2Tl+ + S2- ⅛ Tl2S 4,	AK(TBS) = 5,0 ∙10-21.
Найдем концентрации S2-, необходимые для начала осаждения
ионов, пренебрегая влиянием ионной силы:
∣S2 ∣∣.∣√∙ = ∕Os PbS) ∣PbK = 2,5∙ 10 2//0,1 = 2,5 ∙ 10-26 моль/л;
[S2-]τl2+ = AK(Tl-S) ∣TT∣2 = 5,0 -10 2 ∣0,1) = 5,0 -10 19моль/л.
Следовательно, первым будет осаждаться PbS. Для количест¬
венного осаждения Pb2+ (∣Pb2+∣ < 10-6) необходима ∣S2-∣, равная:
∣S''∣p∣.∙ ■ = Ks(PbS)/[Pb2+] = 2,5 ∙ 10-27/10-6 = 2,5 ∙ 10“21 моль/л.
При сравнении полученной величины с концентрацией S2-,
при которой начинает осаждаться Tl2S, видно, что осаждение ионов
Pb2+ к этому моменту практически закончится. Таким образом, для
полного разделения этих ионов следует поддерживать концентра-
2-	-21	-19
цию S между 2,5 ∙10 и 5,0 ∙10 моль/л. Поскольку ¾S - слабая
кислота, концентрация ионов S2-, т. е. условия осаждения, зависят
от рН раствора. Поэтому найдем интервал рН, обеспечивающий
2-
указанные концентрации S , используя выражение (2.5).
2-
Предварительно вычислим молярные доли для иона S в этих
двух случаях при c(¾S) = 0,1 моль/л:
a = ⅛ = ^l0 = 10-20	= ∣'	=5,010-18;
1 c(H2S)	0,1	2 c(H2S)	0,1
-20
1 ∙ 10-7∙ 2,5 ∙ 10-13
[H+]2 +1 ∙ 10-7 ∙ [H+ ]+1 ∙ 10-7 ∙ 2,5 ∙ 10-13.
82

Решая последнее уравнение относительно [H+], получаем
[H+]1= 1,0 моль/л и [H+]2 = 0,070 моль/л. Таким образом, в интервале
рН от 0 до 1,2 в данном случае будут осаждаться только ионы Pb2+.
Пример 6.6.* Установите возможность образования осадка
AgOCN, если в раствор, содержащий 1,0×10-2 М HNO3 и 1,0×10-3 М
NaOCN, ввести AgNO3 до концентрации 1,0×10-4 моль/л. Гидролизом
ионов Ag+ пренебречь. (Ks(AgOCN) = 2,3 ∙ 10-7; K0α(HOCN) = 2,7∙ 10-4).
Реше ние. Реакция образования осадка:
Ag+ + OCN- ¾ AgOCNi.
Условие осаждения: [Ag+HOCN-Ig2 ≥ K0s.
По величине ионной силы в исходном растворе, равной 0,011,
находим gAg+ = gOCN- = gH+ = g± = 0,90.
Из условия задачи [Ag+] = 1,0×10-4 моль/л (a =1).
Равновесную концентрацию [OCN-] можно найти из системы
двух уравнений (поскольку Kα = [Н+НОС\-]/ [НОС\] = 3,3∙10-4):
[OCN-]/ [НОС\] = 3,3∙10-4 /1,0∙10-2 = 3,3∙10-2 и
[OCN-] + [НОС\] = 1,0∙ 10-3,
или предварительно вычислив Kα (HOCN) (пример 3.3).
Kα = K,lJg±2 = 2,7∙ 104 0,81 = 3,340^4.
Учитывая, что c(OCN-) = [OC∖ ] + [НОС\] = 1,0∙ 10 3 моль/л и
молярная доля aOCN- = Kα /( Kα + [Н+]), с учетом уравнения (2.4) на¬
ходим [OCN-]:
[OCN-]∙= a0C∖- ∙coc∖- = 1,0-∣0"3-3,3-10"4 /(3,3∙10-4 + 1,0∙10-2) =
=3,2∙10-5 моль/л;
[Ag+]∙[OCN-]∙g±2 = 1,0∙10-4 ∙3,2∙10-5 ∙0,81 = 2,6∙10-9 , что < K0s.
Осадок не выпадет.
6.2.	Вычисление растворимости малорастворимого электролита
Растворимостью малорастворимого электролита AmBn назы¬
вают его общую концентрацию в насыщенном растворе, которая
обозначается как S (моль/л). В случае преобладания в системе оса¬
док - раствор равновесия 1 (стр. 75), т. е. ионной растворимости, S
может быть выражена через общие концентрации ионов А и В.
83

Если в 1 л раствора перешло S моль электролита AmBn в реак¬
ции 1), то, в отсутствие избытка какого-либо из ионов, уравнение
реакции растворения можно представить следующими обозначе¬
ниями концентраций ионов через величину растворимости S:
1) AmBn (тв.)
¾ mA +
nB,
а:
ms×gA×aA
ns×gβ×aβ,
с:
ms
ns,
[ ]:
ms×aA
ns×aβ.
Соответственно а = с = [ ], если для ионов a = 1 и g = 1.
Подставляя в выражение (6.1) эти обозначения, получаем для K0S
малорастворимого электролита AmBn уравнение в общем виде:
0 m m m n n n m n m+ n m m n n
Ks = (mS)	×gA	-aA	× (nS)	×gβ	a = m	× n	∙S	-gA	-aA	×g	aB	(6.2)
и выражение для растворимости электролита AmBn:
S - 'mjκy
s -	+n	∕m^' ×nn ×am∙α"Β·γm-gnB
(6.3)
При отсутствии побочных реакций (aA = aβ - 1) и при I - 0
(gA = д = 1) выражение упрощается, и растворимость определяется
только природой электролита и температурой (через величину K0S):
(6.4)
В присутствии избытка одноименного иона, например В с
концентрацией св:
AmBn (тв.)
а:
→ mA	+	nB,
mS-gA-aA	(^+св^дв-ав.
Поскольку одноименный ион уменьшает растворимость, смещая
равновесие влево, в расчетах часто пренебрегают величиной nS в
сумме (nS + св). Тогда Для приближенного расчета растворимости
в присутствии одноименного аниона справедливы выражения:
тУ	m cm n	(г г\
Ks = m ×S ×cβ ,	(6.5)
s = - Jks/	(6.6)
Аналогично, в присутствии избытка катиона (зДесь - ион
Ат+) с введенной концентрацией сА для приближенного расчета
растворимости справеДливо выражение:
84

s =
1 κs ∕
n∖ /с cA
(6.7)
Таким образом, согласно выражениям (6.3, 6.7 и 6.8), раство¬
римость малорастворимого электролита зависит от его прироДы
и температуры; от побочных реакций ионов; от ионной силы рас¬
твора, создаваемой посторонними электролитами (“солевой эф¬
фект”); от присутствия одноименных с осадком ионов.
В обратной задаче может быть вычислена константа рас¬
творимости малорастворимого электролита, если известна вели¬
чина его растворимости.
Пример 6.7. Вычислить K0s(Ca3(PO4)2), если в 1 л растворяет¬
ся 2,2∙10-4 граммов фосфата кальция.
Реше ние. Найдем растворимость s (моль/л) соли в воде:
m	2,2 ∙10-4	-7
s = l∙(Ca,(POl).) = — = -312-1- = 7,1 ∙ 10 7 моль/л.
При такой низкой концентрации ионов в растворе величиной ионной
силы можно пренебречь и считать g = 1. Пренебрегая побочной ре¬
акцией гидролиза аниона, можно считать a = 1. Равновесие в систе¬
ме описывается уравнением:
Са3(РО4)2(тв) ⅛ 3Ca2+ + 2PO43-.
а = с = [...]:	3s	2s
Вычисляем K0s в соответствии с выражениями (6.1) и (6.2):
K’s= Ks= Ks = [Ca2+]3∙[PO43 -∣2 = (3s)3∙(2s)2 = 108.s,' = 108 (7,1∙10'7)5 = 1,9∙10-29.
Пример 6.8. Определить растворимость сульфата бария в
воде. Сколько граммов этой соли растворяется в 1 л воды, если
K0s (RaSO4) = 1,1 ∙ W10?
Ре ше ние . Поскольку в растворе отсутствуют посторонние
электролиты, пренебрежем влиянием ионной силы. Побочных ре¬
акций не происходит. Как в примере 6.6 при g = 1 и a = 1 по выра¬
жению (6.4) рассчитаем растворимость s:
ВaSO4(тв) ¾ Ва + SO4 .
[ ]:	s s
85

Тогда растворимость в г/л будет соответствовать массе соли m в 1 л
раствора: m = ^(BaSO4) ∙ S = 233∙ 1,05∙ 10-5 = 2,4 ∙10^3 г.
Пример 6.9. Определить растворимость сульфида висмута в
воде, если K0s(Ri2S3) = 1,0 ∙10-97 (без учета гидролиза).
Решение. Равновесие в системе выражается уравнением:
2Bi3+ + 3S2-.
2s	3s
В i2S3( 'ic.)
[...]:
Вычисления проводим аналогично предыдущему примеру, исполь¬
зуя выражение (6.4) (ионная сила мала):
108 = 1,56∙10 20 моль/л.
6.2.1.	Влияние ионной силы раствора на растворимость
В присутствии посторонних ионов, создающих вокруг ионов
осадка ионную атмосферу, но не вступающих с ними в химические
реакции, I ≠ 0, и, согласно выражению (6.3), наблюдается увеличе¬
ние растворимости осадка вследствие уменьшения знаменателя, на¬
зываемое “солевым эффектом”. В этом случае, а также при доста¬
точно большой концентрации собственных ионов, т. е. при высоком
значении K0s ( >1 10-5), учитывают ионную силу раствора и раство¬
римость вычисляют по формуле (при a = 1):
(6.8)
Пример 6.10. Определить растворимость PbCl2 в воде.
Решение. Так как K0s (PbCl2) = 1,6 10-5, что больше 1·10-5,
при расчете растворимости следует учесть влияние ионной силы
раствора. Равновесие в системе выражается уравнением:
PbC^™.) ⅛ Pb2+ + 2Cl-.
Из значения K0s проведем оценку растворимости по формуле
(6.4):
86

s » m↑i'7ni × l = ^1,6×1°∕4 = 1,6∙10-2 моль/л.
Ионную силу раствора вычисляем по формуле (2.1):
I = 0,5(1,6∙10-2∙22 + 2∙1,6∙10-2∙12) = 0,048.
По табл. 1 приложения находим: gPb2+ = 0,47; gCl-= 0,86 и рас¬
считываем растворимость хлорида свинца по формуле (6.8) с уче¬
том ионной силы:
1,6∙10-5/
∕4∙ 0,47∙ 0,862
= 2,3×10-2 моль/л.
Проведенные вычисления свидетельствуют о возрастании рас¬
творимости вследствие влияния ионной силы.
Пример 6.11. Сравните растворимость сульфата свинца в воде
с растворимостью в 0,10 М растворе нитрата калия.
Решение. K0s(PbSO4) = 1,6.10-8. Так как K0s <10-5, при рас¬
чете ионной силы можно учесть только вклад сильного индиффе¬
рентного электролита KNO3. Вычисляем ионную силу раствора:
I = 0,5(0,1×12 + 0,1×12) = 0,1.
При этом g Pb2+ = g SO42--= 0,43. Рассчитаем растворимость хло¬
рида свинца в водном растворе нитрата калия по формуле (6.8):
si = s (в KNO3) =	g	^1fv10Z0.13 =2,9× 1" 4 моль/л.
Растворимость PbSO4 без учета ионной силы (в воде без KNO3):
s2 = s (в воде) = "^^nAll =1,6108 = 1,3'10 4 моль/л;
sjs2 = 2,9' 10-4/1,3 × 10-4 = 2,23.
Вследствие “солевого эффекта” растворимость повышается в 2,23
раза.
6.2.2.	Влияние одноименного иона на растворимость осадка
Пример 6.12. Рассчитать (без учета и с учетом ионной силы
раствора) растворимость CaCO3 в воде, в 1 литре которой растворе¬
но 0,010 моль CaCl2.
87

Решение. K0s(CaCO3) = 3,8 10-9. CaCl2 - сильный электро¬
лит, образующий при диссоциации в растворе одноименный с
2+ 2+
осадком ион Ca , причем c(Ca ) = c(CaCl2). Обозначим общие
концентрации ионов в насыщенном растворе CaCO3:
CaCO3(m)	⅛ Ca2+	+ CO32-,
[ ] = с:	S + c(Ca2+) S(m = n = 1).
2+
Пренебрегая значением S в сумме (S + c(Ca )) и используя
формулы (6.2) и (6.7) при a = 1, получаем выражения:
K,S = c(Ca2+) ∙ да' S gcO32- и S = [CO32-] = K's/(c(Ca2+) ∙ да' gCO32-).
Ионная сила раствора определяется, в основном, ионами
сильного электролита CaCl2 по формуле (2.1):
I = 0,5(0,01 ∙ 22 + 0,01 ∙ 2 ∙ 12) = 0,03;	дс а2' = gcO?- = 0,54.
Тогда, с учетом ионной силы раствора,
S = [CO32-] = 3,8·10-9/0,01 ∙0,542 = 1,3 ∙10-6 моль/л.
Без учета ионной силы (д =1), но с учетом влияния одноимен¬
ного иона растворимость составляет:
S = [CO32-] = 3,8·10-9/0,01= 3,8∙10-7 моль/л.
Растворимость CaCO3 в воде при д = 1 и a = 1:
S = ^2+] = [CO32-] = √K0- = √3,8∙ 10^9 = 6,2 ∙ 10-5 моль/л.
Проведенные расчеты свидетельствуют о существенном
уменьшении растворимости в присутствии одноименного иона,
причем это влияние более значительно, чем “солевой эффект”.
Пример 6.13. Рассчитать растворимость Fe(OH)3 в воде.
Решение. Особенностью решения данной задачи является
необходимость учета ионов OH из воДы как оДноименных ионов
при вычислении растворимости гидроксидов, если произведение
растворимости очень мало. K0S(Fe(OH)3) = 6,3·10-38. В этом случае
принимаем концентрацию одноименного иона (аниона), [OH-] »
-7
1,0·10 моль/л. Растворимость вычисляем по выражению (6.6) с
учетом стехиометрических коэффициентов реакции:
Fe(OH)3ni3 ⅛ Fe3+	+	3OH-.
[.] = с:	S	(3S+10-7) »10-7
(Учитывать ионную силу при низких концентрациях не требуется).
88

1 K	K0
S - [Fe3+]=- v—T = KT - KS ∣O∣ I Г - 6,3 ■ 10-38∕( 10-7)3 - 6,3 ■ 10-17 моль/л.
m с	с
Без учета “нейтральности” среды при низкой растворимости ве¬
ществ растворимость Fe(OI)3 составила бы:
- 2,2×10 моль/л,
что в 3500000 раз выше.
6.2.3.	Влияние конкурирующих реакций на растворимость
Ионы осадка могут вступать в реакции с компонентами рас¬
твора. Общая растворимость осадка в этих случаях складывается из
всех форм, которые образует катион и анион. Наибольшее практи¬
ческое значение имеет учет влияния комплексообразования катио¬
на и протонирования аниона слабой кислоты, вхоДящих в состав
малорастворимого электролита.
Если рН при растворении создается и поддерживается буферным
раствором, то предварительно следует вычислить ∣I+] соответственно
конкретным условиям, а затем рассчитывать молярную долю свобод¬
ных ионов и проводить расчет растворимости по выражению (6.3).
ОДнако Для малорастворимых электролитов, способных рас¬
творяться в кислотах или основаниях опреДеленной концентрации,
расхоДующихся в хоДе реакции растворения, расчет растворимо¬
сти слеДует провоДить по общей константе равновесия реакции
растворения (примеры 6.16 - 6.17; см. также главы 2 и 5, примеры
5.15 - 5.17).
При растворении осадков в воде в ряде случаев следует рас¬
сматривать в качестве конкурирующих реакции гидролиза, которые
для катиона могут сопровождаться образованием гидроксоком-
плексов, а для аниона слабой кислоты - протонированием. в этом
случае в практических расчетах принимают слеДующее основное
Допущение: при низкой растворимости соли (низкой концентрации
гиДролизующихся частиц) среДа раствора опреДеляется Диссоциа¬
цией воДы и близка к нейтральной, т. е. [H+] ≈ [OH-] ≈ 10-7 моль/л
(пример 6.18).
89

Обычно при наличии конкурирующих реакций не учитывают
влияние ионной силы (глава 2, раздел 2.2).
Пример 6.14. Рассчитать растворимость AgI в 1,0 М растворе
аммиака.
Ре ше ние . В насыщенном растворе AgI в присутствии NH3,
наряду с основной реакцией:
AgI0,.) ⅛ Ag++ I-	(K0s = 8,3∙10^17)
протекают конкурирующие реакции (lgb1 = 3,32; lgb2 = 7,23):
Ag++NH3 ⅛ [Ag(NH3)]+,
b = [Ag(NH3)+ ]
b1 [Ag + ][NH3F
[Ag(NH3)]+ + NH3 ⅛ [Ag(NH3)2∣+,
b = [Ag(NH3)2+ ]
b2 [Ag+ ][NH3]2
Растворимость AgI определяется общей концентрацией ионов серебра в
растворе:
s = c(Ag+) = [Ag+] + [Ag(NH3)+] + [Ag(NH3)2+].
По формуле (2.8) (см. пример 2.6) вычисляем молярную долю ио¬
нов Ag+:
= 	1

aAg+ = 1 + b1[NH3 ]+b2 [NH3 ]2
1 -8
	3	7—г = 6 17∙10
1+ 2,09 '103 '1+1,62'107 '12
Пренебрегая ионной силой, по формуле (6.3) (aI- = 1) вычисляем s (AgI):
8,3 ∙10-17
6,17 ∙10-8
3,7∙10-5 моль/л.
Проведенные расчеты показывают, что связывание катиона в
растворе в комплекс приводит к повышению растворимости мало-
растворимого электролита.
Пример 6.15. Рассчитать растворимость CaCO3 при pH 5,0.
Ре ше ние . В данном примере pH задано в явном виде, при¬
чем подразумевается поддерживание рН буферным раствором.
В растворе CaCO3 (K0s = 3,8∙10-9) наряду с основной реакцией
CaCO3fn,) ⅛ Ca2+ + CO32-
протекают побочные реакции связывания ионов CO32- ионами водо-
- 2-
рода в HCO3 и H2CO3 (разд. 2.2). Молярную долю CO3 находим по
выражению (2.5):
90

a
2,07×10-9.
CO
2¬
3
	4,5 ■ 10-7× ■ 4,8 ×10-11

(1 ■ 10-5)2 +1 ■ 10-5 ■ 4,5 ■ 10-7 + 4,5 ■ 10-7 ■ 4,8 ■ 10-11
Растворимость вычисляем по формуле (6.3) при aCa2+ - 1:
3,8 ■ 10-9 =
2 07 10-9	1,35 моль/л.
Протонирование аниона слабой кислоты повышает раство¬
римость подобных малорастворимых электролитов.
Пример 6.16. Вычислите массу CaCO3, способного раство¬
риться в 50 мл 2,0 М уксусной кислоты.
Ре ше ние . В данном примере pI в ходе растворения не за¬
дано в явном виде и не поддерживается постоянным из-за расхода
СН3СООН:
CaCO3(„) + 2CH3COOH ⅛ Ca2+ + 2CH3COO- + H2CO3.
∣...]:	2 - 2S S	2S	S
Общая константа равновесия реакции (см. раздел 2.3, пример 2.7(б)):
К - Ks0Ka2 /—2—1 - 3,8· 10-9∙(1,74∙ 10-5)2∕4,5∙ 10-7∙4,8∙ 10-11 - 5,33×10-2.
Подставляем в выражение константы реакции равновесные концен¬
трации и находим растворимость S, решая квадратное уравнение:
- = [Ca2 + ]∣CH3COO-]2∣H2CO3] =	4S4	= 5 3340_2.
∣CH3COOH]2	(2 - 2S )2	,	’
S2 + 0,231S - 0,231 - 0;
S - - 0,231 + √ O,O53 + 0,924 =	= 0,38 моль/л;
2
2
m(CaCO3) - SVM - 0,38∙0,05∙100 - 1,9 г.
Подобным образом рассчитывается растворимость малорас¬
творимых гидроксидов в кислотах. Обратной задачей является на¬
хождение концентрации кислоты в растворе для растворения опре¬
деленного количества осадка (пример 6.17).
Пример 6.17. Какую концентрацию муравьиной кислоты
следует создать в растворе, чтобы в 100 мл растворилось 0,2137 г
Fe(OH)3?
91

Решение. Растворение Fe(OH)3 в муравьиной кислоте при¬
водит к образованию ионов Fe3+ в растворе. По их концентрации
можно судить о растворимости Fe(OH)3 в указанных условиях:
^Fe3+) = [Fe3+] = S(Fe(OH)3) = m∕( KM(Fe(OH)3);
S = 0,2137/(0,1 106,85) = 2,00 10-2 моль/л.
Fe(OH)3(.re) + 3НС ООН ¾ Fe3+
[...]:	3x-3S S
[...]:	3х-3 0,02 0,02
+ 3НСОО- + 3H2O,
3S
3	0,02.
Вычисляем общую константу равновесия для реакции раство¬
рения К (раздел 2.3), подставляем в неё выражения равновесных
концентраций и решаем полученное уравнение относительно
с(НСООН), обозначая ее через 3х:
К = KS0 Ka3/KW3 = 6,3 10-38 (1,8 10-4)3/(10-14)3 = 3,67 10-7;
К = 0,02√0,06)i = 3,67-10-7;	(0,06)ί = 18,4∙10-6; 0,06 = 2,64∙10-2;
(3х - 0,06)3	(3х - 0,06)3	3х -0,06
7,92 10-2 х = 0,158 10-2 + 6,00 10-2 = 6,16 10-2; х = 0,78;
с(НСООН) = 3х = 2,34 моль/л.
Пример 6.18.* Вычислить растворимость сульфида ртути(1) в
воде с учетом гидролиза.
Решение. Основная реакция при растворении:
Hg2S(τ,i ⅛ Hg22+ + S2-	(K,s (Hg2S) = 1 ∙10-47).
В общем случае, в побочных реакциях гидролиза могут участ¬
вовать и катион, и анион. Однако сравнение констант гидролиза по
2+
первой ступени показывает, что гидролизом ионов Hg2 можно
пренебречь и учитывать только протонирование аниона ионами во¬
дорода из воды:
Hg22+ + H2O ⅛ Ид2(ОН)+ + H+, Kagp= Кг/К^ОН)4) = 10-14· 109= 10'5;
S2' + И2О ⅛ HS' + ОН-, Кгидр.2= Kw∕Ka2(H2S) = 10-14Z2,5 ∙10-13 = 4∙10-2;
К	<< К
Кгидр .1	Кгидр .2
Допускаем, что pH ≈ 7 создается только диссоциацией воды, по¬
скольку низкая концентрация подвергающихся гидролизу ионов S2-
мало повлияет на среду раствора. Найдем долю свободных ионов
S2- с учетом формулы (2.5) (для H2S Ka1 = 1∙10-7 , Ka2 = 2,5∙10^13).
	1-10-7 -2,5-10-13		 -6
a2 = (1-10-7)2 +1-10-7 -1-10-7 +1-10-7 -2,5-10-13 = 1,310 ;
92

s=,
∕2i Λ-as, =	∙1∙1,3∙10-6 = 1>2'10^14 моль/л.
Без учета гидролиза растворимость Hg2S была бы ниже:
-16
s = 3J1'10 ^∕2 1 = 1,4 × 10 16 моль/л.
Следовательно, в результате гидролиза ионов осадка повышается
его растворимость.
6.2.4.	Вклад молекулярной растворимости
в общую растворимость
Если при растворении осадка общий процесс является суммой
равновесий 2 и 3:
AmBn (тв) -	® AmBn (р-р) -	® mA + nB,
то общая растворимость малорастворимого электролита AmBl
складывается из ионной и молекулярной растворимостей.
Молекулярная растворимость s0 - это составляющая раство¬
римости, обусловленная наличием в растворе недиссоциированных
(нейтральных) молекул. Константа K0 равновесия (2) может быть
легко вычислена из произведения растворимости AmBn, табличных
констант устойчивости комплексов и констант ионизации кислот (в
соответствии с природой AmBn в растворе). В общем виде для рав¬
новесия (2):
K0 = [AmBn (р-р)] = s0.	(6.9)
Например, для малорастворимого комплексного соединения
AB при ионной силе, близкой к нулю, справедливо:
b = [AB]/[A][B];	Ks = [A][B] » K0s;	K0 = s0 = Ksb .	(6.10)
Аналогично, для малорастворимых кислот типа НА:
Ko = so = KsK .	(6.11)
Общая растворимость (без учета сложной ассоциации ионов, в от¬
сутствие побочных реакций и избытка одноименных ионов) для
осадка типа АВ:
s = vK + Ко.	(6.12)
Для сильных электролитов λ∕K° >>K0, а для очень слабых K0 >>y[K^.
Подробнее о молекулярной растворимости - в рекомендованной
литературе.
93

Пример 6.19. Оценить вклад молекулярной растворимости в
общую растворимость AgCl.
Решение. В насыщенном растворе AgCl устанавливаются
равновесия:
AgCV.) -¾→Ag‰) -¾→ Ag+ + Cl-,
S - [AgCl^J + [Ag+] - К0 + √K;.
По формуле 6.10 находим K0 :
K0 - S0 - -sb(AgCl) - 1,78∙10"10∙1,10∙103 - 1,96∙10-
7;
S- √1,78· 10-,° + 1,96· 10 7 - 1,33∙10'5 + 0,02· 10 5 - 1,35· 10 '
моль/л.
В данном случае молекулярной растворимостью можно пренеб¬
речь, т. к. она составляет всего 0,02 10-5 100/1,33 10-5 - 1,5 % от
ионной растворимости.
Пример 6.20.* Вычислите: 1) концентрацию [OH-], при кото¬
рой растворимость Al(OH)3 в его насыщенном растворе мини¬
мальна, и величину минимальной растворимости Al(OH)3; 2) рас¬
творимость Al(OH)3 в 0,100 М KOH; 3) объем 1,00 М KOH, необ¬
ходимый для полного растворения 1,00 г Al(OH)3, суспендиро¬
ванного в 100 мл воды.
Ре ше ние . 1. Для осадка Al(OH)3, образующего с реагентом
OH- разные комплексные формы, растворимость определяется
суммарной концентрацией всех форм (уравнение материального
баланса):
S = c(Al3+) - [Al3+] + [AlOH2+] + [Al(OH)2+] + [Al(OH)3] + [Al(OH)4-].
Для последовательных реакций комплексообразования выра-
жения констант:
1)Al3+ + OH- → AlOH2+,
2)Al3+ + 2OH- → Al(OH)2+,
β - [AlOH2 + ] = [AlOH2 + ][OH-]2 .
β1	[Al3+ ][OH- ] ^	Ks0	;
β - [Al(OH) + ] = [Al(OH)+][OH- ] .
[Al3+][OH-]2	’
β3 - [Al(OH) 3]/ KS0 ;
KS0
3)	Al3+ + 3OH- → Al(OH)3 ,
[Al(OH)3] - S0 - β3∙Ks0 - собственная или молекулярная растворимость;
4)	Al3+ + 4OH- → Al[(OH)4]-,	β4 - [Al(OH)-]4 - [A0l(OH)-].
[Al3+][OH-]4	-S ∙[OH-]
94

s = Ks0
Подставляя вместо равновесных концентраций их значения из
выражений констант в уравнение для растворимости, получаем:
—1~τ + b 2 +-b- + β3 +β4'[OH-] .
[4 [OH-]3 [OH- ]2 [OH-]	J
(6.9)
Наименьшая растворимость smin(Al(OH)3) будет наблюдаться при
pH, когда преобладает недиссоциированная форма Al(OH)3, т. е.
aAl(OH) должна быть максимальной. Тогда из выражения для мо¬
лярной доли Al(OH)3:
aAl(OH)3
	b3[OH- ]3

1 + b1[OH- ] + b2[OH- ]2 +b3[OH- ]3 +b4[OH- ]4
нужное значение [OH-] можно найти, приравнивая к нулю da/ d[OH-] .
da/d[OH-]= 3 + 2β1[OH-] + β2[OH-]2 - β4[OH-]4 = 0.
Используя справочные значения констант при решении последнего
уравнения, получаем: [OH-] ≈ 2,65·10-8 (pOH = 7,6; pH = 6,4).
- -8
smin при [OH ] ≈ 2,65·10 находим из уравнения (6.9):
smin = 5,4·10-10 + 1,1·10-8 + 2,4·10-7 + 10-6 + 2,65·10-7 = 1,5·10-6 моль/л,
(основной вклад в растворимость дают три последних слагаемых).
2.	В присутствии избытка щелочи s = [Al(OH)3] + [Al(OH)4-].
Первое слагаемое s0 = β3∙Ks0 - мало и
s ≈ [Al(OH)4^] = β√∙Ksθ∙[OH-] = 1033∙10-32∙(0,1 - s).
Отсюда s/(0,1 - s) = 10; s = 0,091 моль/л. (Коэффициенты активно¬
сти однозарядных анионов близки (OH- и Al(OH)4-), ионную силу
можно не учитывать).
3.	ν(Al(OH)3) = m/M = 1,00/78,0 = 1,28·10-2 моль.
Для реакции: Al(OH)3 + OH- → Al[(OH)2]-
K = [Al(OH)- ]/[OH- ] = Ks0∙β4 = l-0·∣0-32'l-0·∣033 = 10.
Объем V(KOH) для растворения Al(OH)3 складывается из V1 для
перевода в раствор и V2 для обеспечения данной концентрации.
F1(KOH) = V(Al(OH)3)/c(KOH) = 1,28 ∙ 10-2/1,00 = 1,28∙10-2 л (12,8 мл);
K=10 = [Al(OH)- ]/[OH-] = (1,28 ∙10-2∕(0,1 + F1 + F2))/(1,00 ∙F2/(0,1 + F1 + V1));
F2(KOH) = 1,28'10-2 /10 = 1,28·10-3 л (1,3 мл);
F(KOH) = 12,8 + 1,3 = 14,1 мл.
95

Задачи для самоконтроля
1.	В 1,00 л воды растворяется 0,0794 г TlI. Вычислите KS этого соединения.
Ответ: KS (TlI) = 5,75 10-8.
2.	Выпадет ли осадок сульфата свинца, если к 500 мл 0,010М раствора нит¬
рата свинца прилить 1 мл 0,0010М раствора сульфата натрия? Ответ: да.
3.	Вычислить растворимость AgCl в 0,05 М растворе AgNO3. Ионную силу
раствора не учитывать.	Ответ: 3,6 10-9 моль/л.
4.	Определить растворимость BaSO4 в воде и в 0,010 М растворе NaCl.
Ответ: 1,05 10-5 моль/л; 1,6 10-5моль/л..
5.	Сколько граммов серебра содержится в 200 мл насыщенного раствора
фосфата серебра?	Ответ: 1,0 10-4 г.
6.	Образуется ли осадок гидроксида магния, если к 20 мл 0,20 М хлорида
-7
магния, прибавить 10 мл 2,0 М аммиака? Ответ: ИП = 5,2 10-7 , образуется.
7.	Определить растворимость CaF2 при pH = 3.	Ответ: 4,08 10-4 моль/л.
8.	Вычислить концентрацию ионов магния в растворе, если, после осажде-
-2
ния его в виде гидроксида, pH раствора равен 10.	Ответ: 6,0 10-2 моль/л.
9.	Сравнить растворимость AgCl в насыщенном растворе и в 0,010 М рас¬
творе NH3.	Ответ: 1,33 10-5 и 5,41 10-4 моль/л (в NH3 в 40 раз больше).
10.	* Вычислите: а) растворимость Al(OH)3 в 0,10 М КОН; б) концентра¬
цию КОН, обеспечивающую растворение 0,390 г Al(OH)3 в 100 мл щелочи.
Ответ: S = 0,072 моль/л; ^KOH) = 0,055 моль/л.
11.	* Можно ли осадок Cr(OH)3, выделенный в результате осаждения ам¬
миаком из 20 мл 2,0 М раствора Cr(NO3)3, полностью растворить при 25° С в
20 мл 6,0 М раствора NaOH? Ответ подтвердите расчетами.
Ответ: не растворится, растворится только в избытке щелочи.
12.	* Рассчитайте значение рН раствора и укажите систему, поддерживаю¬
щую рН, для разделения ионов Ba2+ и Sr2+ при их осаждении в виде хроматов
0,10 М хроматом калия. Ионную силу и разбавление растворов не учитывать.
-1	-7
(Ka1 = 2,1∙10- , Ka2 = 3,2∙10- для H2CrO4). Ответ: рН 5; например, ацетатный
буфер с соотношением с(СН3СООН)/с(СН3СОО-) = 1,76.
96

ГЛАВА 7. РАСЧЕТЫ В ГРАВИМЕТРИИ
Гравиметрический анализ или гравиметрия - это метод коли¬
чественного анализа, основанный на измерении массы вещества из¬
вестного состава, химически связанного с определяемым компонен¬
том. Он основан на законе сохранения массы вещества при химиче¬
ских превращениях. Существует три типа гравиметрических опре¬
делений:
1.	Определяемую составную часть выделяют из вещества и
взвешивают. Это может быть минеральная часть пробы после уда¬
ления при сгорании органической части.
2.	Определяемую составную часть удаляют и взвешивают ос¬
таток. Так чаще всего определяют летучие соединения, влагу в
пробах разного происхождения (методы отгонки).
3.	Определяемую составную часть превращают в соответст¬
вующее химическое соединение, которое выделяют и взвешивают.
Аналитические определения чаще ведут по третьему типу, ис¬
пользуя реакции осаждения (методы осаждения). Основные этапы
анализа включают:
а)	растворение навески ma анализируемого вещества;
б)	осаждение путем добавления некоторого избытка реагента - оса¬
дителя для превращения компонента А в осаждаемую форму;
в)	фильтрование полученной смеси для отделения осадка;
г)	промывание осадка для удаления адсорбированных примесей;
д)	высушивание или прокаливание для превращения осадка в гра¬
виметрическую (весовую) форму);
е)	взвешивание гравиметрической формы (m(B)) и проведение вы¬
числений. Общую схему гравиметрического анализа можно пред-
ставить в виде:
A + R ® AR
® B
определяемый	осадитель осаждаемая
ион (компонент)	форма (о.ф.)
гравиметрическая
форма (в.ф .)
Некоторые примеры гравиметрических определений приведе¬
ны в табл. 7.1. Из примеров видно, что осаждаемая и гравиметриче¬
ская формы могут быть представлены разными химическими со¬
единениями.
Массу определяемого компонента m(A) и его массовую долю
97

Примеры гравиметрических определений неорганических компонентов
Таблица 7.1
Компонент
Реагент
Уравнение реакции
осаждения
Осаждаемая
форма
Измеряемая
величина
Весовая
форма
Cl-
(Br-, I-)
AgNO3
Cl- + Ag+ — AgCU
AgCl
Масса AgCl после
высушивания осадка
AgCl
Mg2+
(NH4)2HPO4
+ NH4OH
Mg2+ + HPO4 2- + NH4OH ®
— MgNH4PO4. + H2O
MgNH4PO4
Масса Mg2P2O7
после прокаливания
осадка MgNH4PO4
Mg2P2O7
PO43-
MgCl2 +
NH4Cl
Mg2+ + PO4 3- + NH4+ ®
—— MgNH4PO4.
MgNH4PO4
Масса Mg2P2O7
после прокаливания
осадка MgNH4PO4
Mg2P2O7
Ni2+
диметил-
глиоксим
NiCl2 + 2HC4H7O2N2 —
—Ni(C1IhO)A2R.. +2HCl
Ni(C4H7O2N2)2
Масса высушенного
осадка Ni(C4H7O2N2)2
Ni(C4H7O2N2)2
SO42-
(сульфаты)
BaCl2
SO42- +Ba2+ — BaSO4.
BaSO4
Масса BaSO4 после про¬
каливания осадка
BaSO4
Fe3+
(Al3+, Sn4+)
NH3 +H2O
Fe3+ + 3NH3 + 3H2O —
Fe(OH)3. + 3NH4+
Fe(OH)3
Масса Fe2O3
после прокаливания
осадка Fe(OH)3
Fe2O3
Са2+
(Mg2+, Zn2+)
(C2H5)2C2O4
(H2C2O4)
Ca + (C2H5)2C2O4 + 2H2O—
CaC2O4. + 2C2H5OH + 2H+
CaC2O4
Масса CaO после
прокаливания осадка
CaC2O4
CaO

w(A) (%) рассчитывают по формулам:
m(A) =Fm(B);	(7.1)
w(A)=m(В)·F∙100/ma.	(7.2)
В приведенных формулах F - гравиметрический фактор (на¬
зываемый также аналитическим множителем, фактором пере¬
счета). Он показывает, массу определяемого компонента (г), соот¬
ветствующую 1 г гравиметрической формы.
Гравиметрический анализ является абсолютным методом - не
требует образцов сравнения (эталонов). На основании данных гра¬
виметрического элементного анализа может быть также установле¬
на формула анализируемого соединения. Погрешность метода
обычно составляет 0,05 - 0,2 %.
7.1.	Гравиметрический фактор и его значение
Гравиметрический фактор F вычисляют как отношение мо¬
лярной массы определяемого компонента М(А) к молярной массе
гравиметрической (весовой) формы М(В):
F=a · ma	(7 3)
b М ( В)
где а и b - коэффициенты, обеспечивающие равенство числа молей
определяемого компонента в числителе и знаменателе.
Гравиметрический фактор можно рассчитать и в тех случаях,
когда определяемый компонент не входит в состав гравиметриче¬
ской формы, если известны стехиометрические соотношения между
соединениями. Например, при определении серы методом отгонки
по схеме S→H2S→CdS→CuS→CuO:
F = 1M(S) =04030
1М (CuO)
Желательно, чтобы значение F было мало для снижения относи¬
тельной погрешности результата анализа и повышения чувстви¬
тельности гравиметрических определений.
Следует заметить, что Для расчетов в гравиметрии использу¬
ются не округленные, а табличные значения относительных атом¬
ных и м ол е кулярн ых масс. Гравиметрические факторы для ряда оп¬
ределяемых компонентов приводятся в справочных таблицах по
аналитической химии (например Ю. Ю. Лурье).
99

Пример 7.1. Вычислить гравиметрический фактор:
а)	при гравиметрическом определении кальция по схеме:
Са ® СаС2О4 Н2О ® СаО;
прокаливание проводят при определенной температуре для получе¬
ния в.ф. СаО:
СаС 7VН2О ® СаО + ∞2↑ + CO↑ + Н2О
б)	при определении содержания магния в виде в.ф. Mg2P2O7.
Решение. Вычислим F по формуле (7.3):
а)	F - 1M(Ca) = 4	'' = 0,7147 ;
1M(CaO) 56,08
б)	F =	2M(Mg) = 2-24,31 = 0,2184.
M(Mg2P2O7)	226,6
В случае б) а = 2, b = 1, так как одна молекула Mg2P2O7 содержит
два атома магния.
Пример 7.2. При гравиметрическом анализе фосфор опреде¬
ляют по схеме: P ® PO43- ® (NH4)3[PMo12O40] ® PbMoO4 .
Вычислите гравиметрический фактор а) при определении
фосфора как элемента и б) при определении фосфора в виде P2O5.
Решение: а) в формуле (7.3) в этом случае а = 1, b = 12, по¬
скольку из 1 моль Р получается 1 моль (NH4)3[PMo12O40], но 12 моль
PbMoO4, тогда:
1М (P)	30,974
= 12M(PbMoO4)=12-367,13 = 0,007031;
б) в этом случае на 1 моль P2O5 согласно схеме, приходится 24 моль
PbMoO4, тогда а = 1, b = 24, и
F=—1M (Р2°5)—= 141,94 =0,01611
24M(PbMoO4) 24-367,13
Пример 7.3. Сравните чувствительность гравиметрического
определения фосфора в виде Mg2P2O7 и PbMoO4 (пример 7.2).
Решение. Гравиметрический фактор при определении фос¬
фора в условиях примера 7.2: F = 0,007031, а в виде гравиметриче-
2M(Р )	_ 2-30,974 _
ской формы Mg2P2O7: f - M(Mg2P2O7) —Έ6Τ - 0’2734.
Если считать минимальную массу гравиметрической формы (в.ф.),
100

равной 0,1 г (т (B)min.- 0,1 г), то из (7.1) следует:
т(Р)ып.- m(A) =Fm(B)
Тогда при в.ф. Mg2P2O7 т(Р)тп - 2,734· 10-2 г ,
при в.ф. PbMoO4	т(Р)тт. - 7,031· 10-4 г ,
min.
и в этом случае можно определить почти в 40 раз меньшую массу
фосфора.
Вывод: чем меньше гравиметрический фактор, тем меньшую
m(A) можно определить и тем выше чувствительность анализа.
В более общем случае, при определении массовой доли, чув¬
ствительность гравиметрии зависит не только от F, но и от размера
навески та, от величины массовой доли определяемого компонента
w(A)(%):
т(В)тт.- та- w(A)/(F100).
В связи с этим, масса пробы для анализа берется не произвольно, а
предварительно проводится ее расчет.
7.2.	Расчет величины навески анализируемой пробы
При предварительных расчетах величины навески вещества
для анализа (та) следует учитывать массу гравиметрической фор¬
мы, а также ориентировочное содержание определяемого компо¬
нента А в анализируемом веществе. В свою очередь, масса грави¬
метрической формы зависит от погрешности весов и от структуры
осаждаемой формы. Погрешность взвешивания на аналитических
весах составляет 0,0002 г, а относительная погрешность гравимет¬
рического определения должна быть не более 0,2 %, поэтому вели¬
чина погрешности весов не должна превышать 0,2 % от минималь¬
ной массы гравиметрической формы т(B)min. (г). C учетом этого
имеем: т(В)тт. ≥ 2·10-4·100 /2·10-1 или т(В)тт. ≥ 0,1 г.
Зависимость массы гравиметрической формы от структуры
осадка связана с влиянием его объема на размеры выбираемой ворон¬
ки для фильтрования и тигля для прокаливания осадка (табл. 7.2).
Учитывая рекомендованную массу гравиметрической формы
т(В), F, а также ориентировочное содержание компонента А в про¬
бе - w(A), %, массу навески можно оценить по формуле:
w( А)
(7.4)
101

Таблица 7.2
Рекомендуемая масса гравиметрической формы для разных
типов осадков
Тип осаждаемой формы
т(В), г
Аморфный (типа Fe2O3 хН2О), скрытокристаллический
Кристаллический, легкий (типа СаСО3)
Кристаллический, тяжелый (типа BaSO4)
Кристаллический, очень тяжелый (типа PbSO4)
0,1
0,1 - 0,2
0,2 - 0,4
£ 0,5
Пример 7.4. Какой должна быть навеска чугуна с массовой
долей серы около 2 % для ее гравиметрического определения в виде
сульфата бария?
Ре шение. Вычисляют фактор пересчета:
F = M(S)	= 0,1373.
M(BaSO4) 233,4
По формуле (7.4) получают массу навески с учетом ожидаемой
массы в.ф. 0,4 г (осадок кристаллический, легкий) и ориентировоч¬
ного содержания серы 2 %:
ma = 0,4×0,1373×100∕2 = 2,746 г.
Т. о. надо взять навеску около 3 г и затем провести взвешива¬
ние с точностью аналитических весов.
Пример 7.5. Какую навеску зерна следует взять для определе¬
ния влажности, если допустимое содержание влаги в зерне £ 3 %?
Решение. Минимальная потеря массы при высушивании не
должна быть меньше 0,1 г, что соответствует 3 % от навески, зна¬
чит:
ma = 0,1× 100/3 ≥ 3,3 г.
7.3.	Расчет количества осадителя
Важным этапом гравиметрического анализа является осаждение
определяемого компонента. При выборе осадителя выполняется ряд
требований, среди которых практическая необратимость (разд. 2.3,
7
гл. 6) реакции осаждения (К > 10 ). Расчет количества осадителя
102

может быть проведен по массе определяемого компонента, по массе
осаждаемой формы, по массе гравиметрической формы.
Во всех случаях расчет основан на выполнении закона эквива¬
лентов (8.1) в химической реакции. Для общей схемы гравиметри¬
ческого анализа:
xA + zR ® cAR ® yB,
где x, z, c и y - стехиометрические коэффициенты, легко установить
соотношения количества участников: на x моль определяемого ком¬
понента А необходимо z моль осадителя R, а образуется y моль гра¬
виметрической формы B (пример 7.8). При расчете массы осади¬
теля nι(R) справедливы формулы:
по массе определяемого компонента:
массе осаждаемой формы:
по массе гравиметрической формы:
m(R) =
zM (R) - m(A)
xM (A)
m(R) =
; (7.5)
zM(R) - m(AR).
cM (AR)	;
m(R) =
zM (R) - m( B)
yM ( B)
по
(7.6)
(7.7)
Расчет объема раствора осадителя V основан на определении
объема раствора с заданной концентрацией, содержащего требуе¬
мую массу осадителя m(R). В зависимости от способа выражения
концентрации раствора применимы следующие формулы:
для массовой доли:
V - m(R) -100,	(7.8)
w(R) r
где w(R) и r - массовая доля (в %) и плотность раствора осадителя;
m(R) 1000
для молярной концентрации: V	;
для молярной концентрации эквивалента:
v =	m( R)-1000
= c(f3κβ,(R)R)-M(f3κβ(R)) ∙
ОсажДение считают количественным (полным),
(7.9)
(7.10)
если после
осаждения равновесная концентрация определяемого компонента в
растворе не превышает 10-6 М и остаточное количество осаждаемо¬
го вещества не выходит за пределы точности взвешивания на ана¬
литических весах (0,0002 г). Для более полного выделения осаж¬
даемого компонента вводят избыток осадителя, вплоть до двукрат¬
ного по сравнению с величиной, рассчитанной с учетом стехиомет¬
рии реакции.
103

Избыток осадителя зависит от его летучести и растворимости
осаждаемой формы: летучий осадитель рекомендуется брать в 2-
кратном избытке, а для нелетучего осадителя рекомендуемый избы¬
ток около 30 %.
Пример 7.6. Рассчитать (с учетом 1,5-кратного избытка) объ¬
ем 2 н. раствора H2SO4, необходимый для осаждения бария из на¬
вески 0,5234 г BaCl2×2H2O.
Решение. Масса (г) осадителя m(H2SO4) может быть выра¬
жена по известной массе определяемого компонента (7.5)
при x = z = c = y=1:
BaCl2×2H2O + H2SO4 = BaSO4. + 2HCl + 2H2O,
m(H2SO4) = ''''''"'''.mBa''''''1 = ⅛0^ = 0,2100 r.
M(BaCl2 ×2H2O)	244,31
Рассчитывают (7.10) объем 2 н. раствора H2SO4:
m(H2SO4)×1000	0,2100×1000
V=	, v 2—λ-	=—	=2,142 мл.
M(1∕2H2SO4)×c(1∕2H2SO4)	49,03∙2
Необходимый объем с учетом 1,5-кратного избытка:
V = 2,142×1,5 =3,2 мл.
Пример 7.7. Рассчитать (с учетом 1,5-кратного избытка) объ¬
ем 2,5 % раствора гидроксида аммония (r = 0,989 г/мл), необходи¬
мый для осаждения алюминия из 1,234 г аммонийных квасцов
NH4Al(SO4)2×12H2O.
Решение. Коэффициенты x и z для реакции равны 1 и 3:
NH4Al(SO4)2×12H2O + 3NH4OH = Al(OH)3. + 2(NH4)2SO4 + 12H2O.
Массу осадителя (г) можно вычислить по формуле (7.5):
m(NH4OH) =
3M(NH4OH) × m(NH4Al(SO4)2 × 12H2O)
M(NH4Al(SO4)2 × 12H2O)
m(NH4OH) =
3 × 35,046 × 1,234
453,32
= 0,2862 г.
Объем раствора NH4OH найдем по формуле (7.8):
m(NH4OH)
w(NH4OH) ×r
0,2862
2,5 × 0,989
×100 = 11,58 мл.
Необходимый 1,5-кратный объем: 11,58×1,5 = 17,4 мл (~ 18 мл).
104

Пример 7.8. Рассчитать объем осадителя в виде 0,05 M рас¬
твора Na2HPO4 для осаждения магния в виде MgNH4PO4 из 100 мл
0,02 М раствора MgCl2 с избытком осадителя до 120 %.
Решение. Уравнение реакции осаждения:
MgCl2 + Na2HPO4 + NH4OH - MgNH4PO4; + 2NaCl + H2O.
Из уравнения видно, что на 1 моль MgCl2 расходуется 1 моль
Na2HPO4 (x=z=y=1). Количество MgCl2 в растворе:
n (MgCl2) - c(MgCl2> V(MgCl2) - 0,02·0,100 - 0,002 моль,
что равно необходимому по реакции количеству Na2HPO4. Тогда
V(Na2HPO4) - c(MgCl2} V(MgCLmXaJIPOl) - 0,002/0,05 - 0,04 л (40 мл).
C учетом избытка осадителя (120 %): V = 40· 120/100 - 48 мл.
7.4.	Расчет потерь при промывании осадка
Для освобождения осадка от адсорбированных примесей при¬
меняют промывание. Крупнокристаллические легко фильтрующие¬
ся осадки с низкой растворимостью промывают водой, кристалли¬
ческие осадки с высокой растворимостью - раствором электролита,
имеющего с осадком одноименный ион (разд. 6.2.2). Аморфные и
скрытокристаллические осадки промывают раствором электролита,
например, нитрата или хлорида аммония (предотвращают пептиза¬
цию осадка), которые при прокаливании осадка улетучиваются.
Существует два приема промывания осадка: промывание на
фильтре и промывание декантацией. Первый способ рекомендуется
для очистки объемистых аморфных осадков, второй - для кристалли¬
ческих. При этом во всех случаях более эффективно многократное
промывание небольшими порциями, чем при меньшем числе раз
большими порциями при одном и том же объеме промывной жидко-
сти.
Концентрацию сп отмываемого вещества в объеме V0 промыв¬
ной жидкости, остающейся в осадке и не стекающей через фильтр
после n-го промывания, можно рассчитать по формуле:
с
n
X n
У
=с0
V0
V0 +V
(7.11)
где с0 - начальная концентрация отмываемого вещества, г/мл;
V- объем каждой очередной порции промывной жидкости, мл;
V0 - объем жидкости, удерживаемой осадком.
105

Приведенная формула позволяет также оценить общий объем
промывной жиДкости. Эту зависимость можно использовать толь¬
ко для ориентировочного расчета, поскольку на самом деле осадок
следует отмывать не только от посторонних веществ, находящихся
в смачивающей жидкости, но также и от адсорбированных ве¬
ществ. Использовать большой объем промывной жидкости нельзя,
поскольку потери за счет растворимости могут превысить погреш¬
ность взвешивания. Можно рассчитать потери при промывании за
счет растворимости осадка, исходя из произведения растворимости
и состава промывной жидкости.
Пример 7.9. Для промывания осадка BaSО4 массой 0,5000 г
используют 250 мл воды. Вычислить массовую долю потерь осадка
за счет промывания водой. Во сколько раз уменьшатся потери осад¬
ка, если для промывания использовать 250 мл 5,05×10-4 М раствора
H2SO4 (ионную силу не учитывать)?
Решение. Допустим, что при промывании осадка происхо¬
дит образование насыщенного раствора (K0s(BaSО4) = 1,1×10-10). В
связи с этим вычисляем растворимость осадка, исходя из KS по
формуле (6.4):
= [Ba2+ ] = [ SO4-] = √ 1,1 - 10-10 = 1.05-10 5 моль/л.
Масса осадка BaSО4, растворяющегося в 250 мл промывной
воды, соответствует потерям осаждаемой формы (т^.ф.). Это со¬
ставит с учетом ^(BaSO4) = 233,4 г/моль:
ms,0.φ. = 1,05· 10 '-233,4-0,25 = 0,0006 г .
Массовая доля потерь осадка равна:
w = (т$о.ф./то.ф.)-100 = 0,0006-100/0,5000 = 0,12 %.
Следует отметить, что на практике указанные потери должны
быть меньше, так как насыщения промывных вод, как правило, не
происходит.
2-
При промывании разбавленным раствором H2SO4: [SO4 ] » ^H2SO4)
и растворимость осадка определяется по формуле (6.6):
S = Ks{BaSΘ4)/'[SO42"] = 1,1-10"10∕5,05-10"4 = 2-10"7 моль/л.
т&лф. = 2-10^7-233,4-0,25 = 0,000012 г,
что меньше погрешности взвешивания на обычных аналитических
весах.
106

Массовая доля потерь осадка составит:
w = (msr0.φ.∕m0.φ.) ∙100 = 0,000117-100/0,5000 = 0,0023 %.
Потери уменьшаются примерно в 51 раз.
Пример 7.10. Для гравиметрического определения хлорида в
каменной соли пробу 100 мг растворили в 100 мл раствора. Рассчи¬
тать, какое количество осадителя 0,1 М раствора нитрата серебра
следует добавить к раствору, чтобы потери вследствие неполноты
осаждения хлорида серебра не превысили 0,001 %. Солевым эф¬
фектом пренебречь.
Ре шение. Допустим, что соль практически полностью со¬
стоит из хлорида натрия. Определим количество NaCl в пробе:
m(NaCl)	100 мг
V(NaCl) -— 	—-	-1,7 ммоль
M (NaCl) 58,44 мг/ммоль	'
Потери хлорида не должны превысить 0,001 %, чему соответствует
количество вещества NaCl, равное:
V(NaCl) -
1,7 ммоль 10-3
100
-1,7 10-5ммоль .
Определим эквивалентное количество осадителя:
V(NaCl) = V (AgNO3) = c(AgNO3) ∙ V(AgNO3);
V (AgN О 3)
ν (NaCl)
с (AgN О 3)
1,7
0,1
-17 мл.
Таким образом, после добавления эквивалентного количества оса¬
дителя объем раствора составляет:
V = 100 мл + 17 мл = 117 мл.
Допустим, что при добавлении избыточного количества осадителя
объем раствора практически не увеличится. Тогда максимальное зна-
чение концентрации хлорид-иона в растворе не превысит значения:
с (Cl-) -
V(NaCl) -1,7-10^5
V ~ 117
-1,4 1 0 -7 ммоль/мл
-7
или 1,4 10 моль/л.
Исходя из величины K0S (AgCl) = 1,78 10-10, находим минимальную
концентрацию серебра в растворе:
^Ag +) -
Aj0(AgCl) -1,78 ∙ 10-10
[Cl-] - 1,4 ∙ 10-7
1,3 10-3 моль/л.
Находим избыточное количество раствора AgNO3 из соотношения:
107

c(AgNO3> V(Ag≡3‰5. - c(Ag+)· V;
1,3 ×10-3 ×117
V(AgNO3)ra6.= ,	—	= 1,5 мл.
Общее количество осадителя: Vo6u - 17 мл + 1,5 мл - 18,5 мл.
Пример 7.11. Сколько граммов кальция будет потеряно при
промывании моногидрата оксалата кальция 0,2 л воды и таким же
объемом 0,1 % раствора оксалата аммония?
Решение. Осадок частично растворяется в промывной жид¬
кости, поэтому задача сводится к расчету растворимости (S) осадка
в воде в присутствии одноименного иона. Пренебрегаем влиянием
ионной силы и протеканием конкурирующих химических реакций.
Если осадок промывают водой, то
5 = √Ks°(CaC2O4 ·H2O) =42,99 ·10-9 = 5,5 · 10 5моль/л.
Если промывают раствором оксалата аммония, то при
c((NH4)2C2O4) - т(((NH4)2C2О4)//(М(((NH4)2C2O4)· V) »
» 0,1/(124·0,1) - 8· 10-3 моль/л,
2-	-3
[C2O4 -] » C((NH4)2C2O4) - 8· 10- моль/л, тогда с учетом (6.6):
= Kθ(CaC2O4 ■ H2O) = 2,99·10 "
=	[C2O2· ]	= 8 ·10-3
= 3,7×10-7 моль/л.
При промывании водой масса потерь:
m5 (Ca) - 5,46×10-5×0,2×40,08 - 4,4 ×10-4 г ,
что превышает величину допустимой погрешности.
При промывании раствором оксалата аммония:
m5 (Ca) - 3,7×10-7×0,2×40,08 - 3,0 ×10-6 г.
Пример 7.12. Какое максимальное количество воды можно
использовать для промывания хлорида серебра массой 0,2 г?
Решение. C учетом погрешности гравиметрического анализа
(£0,2 %) потеря осадка должна быть не более 4×10-4 г, что соответст¬
вует количеству AgCl:
V(AgCl) - 4· 10-4/143,32 - 2,8· 10^6 моль.
Рассчитываем растворимость хлорида серебра в воде (принимая ко¬
эффициенты активности равными единице):
S = √Ks(AgCl) = 1,78 ·10 l' = 1,33 · 10-5 моль/л.
108

Следовательно, объем воды для промывания не может быть больше,
чем V= К AgCl) S(AgCl) = 2,8-101,33-10 ' =0,210 л или 210 мл.
Пример 7.13. Сравните соотношение концентраций примеси в
растворе и маточном растворе, удерживаемом осадком (сп/с0), если
общий объем промывной жидкости 100 мл и объем V0 удерживае¬
мого осадком раствора 1 мл, а промывание осадка ведется порция¬
ми: а) двумя по 50 мл; б) четырьмя по 25 мл и в) десятью по 10 мл.
Сравните концентрацию примесей в растворе после промывания
осадка в условиях а) - в), если концентрация примеси в маточном
растворе с0 = 0,01 моль/л.
Решение.Расчет проведем с использованием формулы (7.11):
а)
С2 =
Со
' 1 T
1 + 50 у
= 3,8 ×10-4,
моль/л;
б)	cC
co
в)	c
co
1 + 25 J
1 Y0
ч1+10,
= 2,2 × 10 - 6
= 3,9 ×10 -11
с- с0·3,8· 10 1 10 '∙3,8-10 4 3,8· 10 '■
с4 = 10-2×2,2×10-6 = 2,2×10-8 моль/л;
с10 = 10-2×3,9×10-11 = 3,9×10-13 моль/л;
1
4
Проведенные расчеты свидетельствуют о большей эффективно¬
сти многократного промывания при неизменном общем объеме про¬
мывной жидкости.
7.5.	Расчет результатов анализа в гравиметрии
Расчеты результатов гравиметрического анализа проводят с
использованием формул (7.1) и (7.2), если анализируемая проба
взвешивается. Если для анализа отбирается определенный объем,
проводят несложные пересчеты. Важно правильно установить гра¬
виметрический фактор (примеры 7.1 - 7.3). По данным анализа
можно установить компонентный состав пробы, элементный состав
вещества, формулу соединения и др. Суммирование погрешностей
в гравиметрии рассматривается в гл. 9.
Пример 7.14. При гравиметрическом определении свинца из
2,000 г сплава получено 0,6048 г PbSO4. Вычислить массовую долю
свинца в сплаве.
109

Решение. Рассчитывают гравиметрический фактор F (пере¬
счета PbSO4 на Pb) по формуле (7.3):
F - 207,2/303,25 - 0,6833
и по формуле (7.2) определяют массовую долю свинца в навеске:
w(Pb) - 0,6833·0,6048·100/2,0000 - 20,66 %.
Пример 7.15. Рассчитать массовую долю карбонатов кальция и
магния в известняке, если из навески его 0,9866 г в результате ана¬
лиза получено 0,3755 г CаO и 0,4105 г Mg2P2O7.
Решение. Вычисляют (7.3) гравиметрический фактор (для пере¬
счета весовой формы CаO на определяемое вещество CаCO3):
F - 100,09/56,08 - 1,7848
и затем по формуле (7.2) - массовую долю CаCO3:
K(CnCO3) - 1,7848·0,3755· 100/0,9866 - 67,93 %.
Аналогично вычисляют массовую долю MgCO3, подставляя выра¬
жение для фактора пересчета Mg2P2O7 на MgCO3 из (7.3) в (7.2):
w(MgCO,) = M (MCKWMAK)·100 = 2 · 84,°3·°,4105 ·100 = 3148 %
3	M(Mg2P2O7) × ma	222,06 × 0,9866
Пример 7.16. Вычислить по результатам гравиметрического
анализа число молекул воды в кристаллогидрате ацетата свинца,
если из его навески 0,3243 получено 0,2593 г сульфата свинца.
Решение. Обозначим через M(A) молярную массу кристал¬
логидрата Pb(CH3COOH)2 · xH2O.
Значения молярных масс:
M(PbSO4) - 303,2 г/моль; M(Pb(CH3COO2)) - 325 г/моль; M(H2O) - 18 г/моль.
Гравиметрическое определение проведено по схеме:
Pb(CH3COOH)2 xH2O ® PbSO4 (о.ф.) ® PbSO4 (в.ф.).
Решая выражение, получаемое подстановкой (7.3) в (7.1), от¬
носительно М(А), находим молярную массу кристаллогидрата:
M(A) - M(PbSO4) · ^Pb(CH3COO2) · хН2О)/т (PbSO4);
M(A) - 303,2·0,3243/0,2593 -379.
Поскольку M(A) - M(Pb(CH3COO2)) + JtM(H2O),
x - (379-325)/18 - 3
и формула кристаллогидрата Pb(CH3COOH)2 · 3H2O.
110

Задачи для самоконтроля
1.	Какую массу технического сульфата натрия с массовой долей Na2SO4
90 % нужно взять для гравиметрического анализа, чтобы масса осадка BaSO4
была равной 0,5 г?	Ответ: 0,3313 г.
2.	При определении магния осаждением в виде MgNH4PO4 масса прока¬
ленного осадка не должна превышать 0,3 г. Рассчитать массу образца для
анализа с массовой долей MgCO3 40%.	Ответ: 0,5680 г.
3.	Какой объем раствора ВаС12 с массовой долей 10 % нужно взять для
осаждения сульфата из 100 мл 0,05 М раствора Na2SO4?	Ответ: 10,4 мл.
4.	Определите массу 5 % раствора H2SO4, необходимую для осаждения
2+
Pb2+ из навески 0,5865 г сплава с массовой долей свинца 12 %?
Ответ: 0,664 г.
2+
5.	Рассчитайте объем 10 % раствора H2SO4 для осаждения Pb из раство¬
ра 0,6856 г сплава с массовой долей свинца 15 %.	Ответ: 0,5 мл.
6.	Какой объем раствора H2SO4 плотностью 1,1 г/мл требуется для осаж¬
дения бария из раствора 0,4880 г BaCl2∙2H2O?	Ответ: 1,2 мл.
7.	Определите массовую долю потерь из 0,3 г осадка РЬСгО4, полученного
в объеме 300 мл в условиях эквивалентного осаждения?	Ответ: 0,004 %.
8.	Определите массовую долю потерь осадка PbSO4 массой 0,5 г вследст¬
вие его растворимости, если осадок получен в объеме 200 мл при избыточной
концентрации H2SO4 0,02 моль/л.	Ответ: 0,01 %.
9.	При гравиметрическом определении свинца потери осадка за счет про¬
мывания не должны превышать 0,0002 г. Можно ли осадок PbSO4 промывать
водой объемом 250 мл?	Ответ: нельзя.
10.	При анализе технического сульфата натрия пробу 0,1500 г растворили
в 150 мл воды. Сульфат-ион осадили 0,05 М раствором хлорида бария. Сколь¬
ко этого раствора следует добавить, чтобы потери вследствие неполноты
осаждения были не более 10-5 г? Влиянием солевого эффекта пренебречь.
Ответ: 22 мл.
11.	Рассчитайте потери кальция при промывании осадка СаС^4 ∙ H2O 250 мл
воды. При какой общей концентрации оксалата в промывной жидкости с рН
4,00 потери при промывании 0,1 г осадка 250 мл этой жидкости не превысят
0,1 % по массе? Ионную силу не учитывать. М(Са) = 40,08; ^СаС^/! ∙ H2O) =
=146,11.	Ответ: потери Са 4,8 ∙ 10^4 г; ^C2O42-) = 2,26 -10-3 моль/л.
12.	При анализе силиката из навески 0,7524 г получили смесь хлоридов ка¬
лия и натрия массой 0,2415 г. В этой смеси затем определяли калий в виде
K2PtCl6, получили осадок массой 0,2760 г. Вычислить массовую долю K2O и
Na2O в силикате.	Ответ: 10,64 % Na2O и 7,11 % K2O.
13.	При анализе раствора Fe2(SO4)3 железо осадили в виде гидроксида и
прокалили. Масса весовой формы оказалась равной 0,2875 г. Вычислить мас¬
су железа в растворе и массу соли Fe2(SO4)3. Ответ: 0,2010 г (Fe) и 0,7199 г.
111

14.	При анализе минерала массой 0,5076 г получили сумму оксидов алю¬
миния, железа и титана массой 0,2078 г. При дальнейшем анализе из суммы
оксидов определили массовую долю TiO3 2,78 %, Fе2O3 3,56 %. Алюминий
определяли по разности. Вычислить содержание алюминия, железа и титана.
Ответ: 1,67 % Ti; 2,49 % Fe; 18,30 % Al.
15.	А. Вычислить гравиметрический фактор для определения P2O5 в виде
Mg2P2O7. В. Oпределить содержание общего фосфора в почве в виде P2O5
(мг/кг), если из навески почвы массой 20,0 г получено после всех операций
0,0360 г Mg2P2O7. С. Вычислить объем 0,05 М раствора MgCl2 для осаждения
фосфора в виде MgNH4PO4 из той же навески (с учетом 20 % избытка).
Ответ: В. 1148 мг/кг. C. 17,8 мл.
16.	А. Вычислить аналитический множитель для определения NaF в виде
PbClF. В. Oпределить содержание NaF (г/л) в растворе, если масса высушен¬
ного осадка PbClF после осаждения фторида из 200 мл раствора оказалась
равной 0,3069 г. С. Вычислить объем 0,1 М раствора Pb(NO3)2 (с учетом 1,5-
кратного избытка) для осаждения ионов фтора в виде PbClF из того же рас¬
твора.	Ответ: В. 0,2463 г/л. С. 17,6 мл.
112

ГЛАВА 8. РАСЧЕТЫ В ТИТРИМЕТРИИ
8.1.	Сущность титриметрии
Титриметрия или титриметрические методы количествен¬
ного анализа основаны на измерении объема раствора реактива В,
израсходованного на реакцию с определяемым веществом А. Рас¬
твор реактива (титрант, рабочий раствор) должен при этом иметь
известную концентрацию. Различают рабочий раствор с «приготов¬
ленным титром», установленным титром (по другому раствору с
известной концентрацией) и полученный растворением вещества
«фиксанала» или «стандарт-титра» (ампулы с точной навеской) в
мерной колбе соответствующего объема.
Титр - способ выражения концентрации раствора, опреде¬
ливший название метода и показывающий массу растворенного
вещества в граммах в 1 миллилитре раствора (г/мл). Процесс по¬
степенного добавления титранта к раствору определяемого веще¬
ства называют титрованием. При титровании наступает момент,
когда рабочий раствор В и определяемое вещество А прореагиру¬
ют между собой в эквивалентных количествах, т. е. в строгом со¬
ответствии со стехиометрией реакции. В таком случае справедлив
закон эквивалентов, составляющий основу расчетов в титриметрии:
(8.1)
При титровании важно зафиксировать конец реакции, назы¬
ваемый точкой стехиометричности или точкой эквивалентности
(ТЭ). Для экспериментального установления конечной точки тит¬
рования (КТТ), по возможности наиболее близкой к ТЭ, использу¬
ют изменение окраски индикатора или какого-либо физического
свойства раствора.
К химической реакции титрования предъявляются следующие
требования: 1) строгая стехиометричность, отсутствие побочных
реакций; 2) высокая скорость; 3) практическая необратимость
7
(∕√≥ 10 ), обеспечивающая количественное превращение реагирую¬
щих веществ в продукты реакции; 4) наличие подходящего индика¬
тора или другого способа фиксирования ТЭ.
В титриметрии используют мерную посуду: мерные колбы -
для приготовления растворов; пипетки - для отмеривания опреде-
113

ленного объема раствора и бюретки - для измерения объема тит¬
ранта.
Титриметрические методы характеризуются быстротой анали¬
за, простотой оборудования, возможностью автоматизации. Чувст-
-3	-4
вительность методов не превышает 10 - 10 моль/л, относитель¬
ная погрешность ≥ 0,5 %.
8.2.	Методы, приемы и способы титрования
В титриметрии используют реакции всех типов: с переносом
протона, электрона, электронной пары, осаждения. В соответствии
с типом реакции, титриметрические методы разделяют на 4 боль¬
шие группы, в каждой из которых выделяют группы по названию
применяемых титрантов (табл. 8.1).
По приемам титрования различают прямое, обратное и тит¬
рование заместителя (табл. 8.2). При прямом титровании титрант
В непосредственно добавляют из бюретки к титруемому веществу
А. Такой прием применим только при выполнении всех требований
к реакции титрования. В случае их несоблюдения или для практи¬
ческой целесообразности используют прием обратного титрова¬
ния, для осуществления которого необходимы два рабочих раство¬
ра титрант В1 и титрант В2. Первый добавляется к определяемому
веществу А в избытке для доведения реакции до конца, затем избы¬
ток В1 оттитровывается титрантом В2 для определения количества
не прореагировавшего с веществом А титранта В1. Закон эквивален¬
тов для обратного титрования можно представить следующим
уравнением (см. также табл. 8.3):
(8.2)
Пример 8.1. Ион NH4+, являющийся в воде очень слабой кисло¬
той (Λ≥5,68-10'10), нельзя оттитровать рабочим раствором NaOH
приемом прямого титрования из-за высокой обратимости реакции.
Поэтому к пробе, содержащей соль аммония, добавляют определен¬
ный объем титрованного раствора NaOH (В1), обеспечивающий избы¬
точное количество щелочи по отношению к ионам аммония, после че¬
го удаляют аммиак и избыток NaOH титруют рабочим раствором НС1
(B2), т. е. последовательно выполняются две реакции:
114

NH4Cl + NaOH - NH3↑+ NaCl + H2O,
NaOH + HCl - NaCl + H2O.
Тогда:	n(NH4Cl) - n(NH4+) - n(N) - H(NOH) - n(HCl).
Пример 8.2. О'ехиометрическая реакция
5NO2- + 2MnO4- + 6H+ - 2Mn2+ + 5NO3- + 3H2O
осложняется реакцией разложения азотистой кислоты в кислой среде:
2HNO2 ® NO↑ + NO2↑ + H2O
и поэтому из-за летучести оксидов азота теряется определяемое
вещество. В связи с этим применяют обратное титрование: к анали¬
зируемому нитриту добавляют избыток KMnO4 (B1), подкисляют и
после окончания реакции оттитровывают оставшийся перманганат
рабочим раствором B2 - щавелевой кислоты или соли Мора (Fe2+).
В этом случае: n(NO2-) - n(MnO4-) - n((Fe2+).
Титрование заместителя используют при отсутствии подхо¬
дящего индикатора, при несоблюдении стехиометричности или при
медленном протекании реакции. В этих случаях к определенному
объему вещества А добавляют вспомогательный реагент, количест¬
венно взаимодействующий с А, а получающийся продукт реакции
(в количестве, эквивалентном А) оттитровывают подходящим тит¬
рантом В. Закон эквивалентов при титровании заместителя имеет
выражение как при прямом титровании: n(A) = n(B).
115

Таблица 8.1
Важнейшие методы химического титриметрического анализа
Метод титрования,
тип реакции (равновесия)
Разновидности
методов
Рабочие
растворы
Индикаторы
для установления KTT
Вещества, определяемые
прямым титрованием
Кислотно-основное
(метод нейтрализации)
Кислотно-основные
индикаторы:
ОН +H+ = H2O
An +H+ = HAn
Ацидиметрия
HCl, H2SO4
метиловый красный,
метиловый оранжевый,
бромкрезоловый зеленый,
Основания, соли типа:
Na2CO3, Na2B4O7, KCN,
NaHCO3, фенолят натрия
H+ + ОН = H2O
HAn + ОН = H2O + An
Алкалиметрия
NaOH, KOH
фенолфталеин,
бромтимоловый синий и др.
Кислоты, соли типа:
NaH2PO4, Na2HPO4, RNH3Cl
Окислительно-
восстановительное
(редоксиметрия)
Перманганатометрия
KMnO4
Окраска KMnO4
Fe2+, H2C2O4 и другие
неорганические и
органические восстановители
αθxι + ARcd2 = i∕Rcd∣ + AOx2
Иодометрия
I2, (Na2S2O3 ∙2H2O)
Крахмал (1% р-р)
Окислители и
восстановители
Дихроматометрия
K2Cr2O√
Ред окс-индикаторы:
дифениламин, ферроин и др.
Восстановители
Броматометрия
KBrO3, (+KBr)
Метиловый оранжевый
Фенол,оксихинолин и др.
Комплексометрическое
M + Ln = [MLn]
Комплексонометрия
Na2C10H14O8N2∙2H2O
(ЭДТА, трилон Б,
комплексон III)
Металлохромные
индикаторы:
эриохром, мурексид и др.
Катионы,
образующие с ЭДТА
лабильные комплексы
Осадительное
м + X = MXsL
Аргентометрия:
метод Mopa
AgNO3
K2CrO4
Br', Г в слабокислой
среде
метод Фаянса
AgNO3
Эозин, флуоресцеин
(адсорбционные)
Br , Г, Cl , CN , SCN
при pH < 7
Тиоцианатометрия:
метод Фольгарда
AgNO3, NH4SCN
Ионы Fe3+
в кислой среде
Прямое: Ag+
Обратное: BL, CF, S2 . CN
SCN , CO32, CrO42, PO43

Таблица 8.2
Классификация приемов титрования
Приём
титро¬
вания
Уравнения реакций,
примеры
Измеряе¬
мые вели¬
чины
Рабочие
раство¬
ры
Прямое титрование
A + B ® продукты
1)	HCOOH + OH-® HCOO- + H2O
2)	5Fe2+ + MnO4- + 8H+ ® 5Fe3++ Mn2+ +
4H2O
3)	C6H5OH + BrO3- + 5Br- + 6H+®
® C6H2Br3OH + 3HBr + 3H2O
4)	Mg2+ + H2Y2- ® MgY2- + 2H+
5)	Cl- + Ag+ ® AgCU
V(A) (пи¬
петка)
V(B) (бю¬
ретка)
B
NaOH
KMnO4
KBrO3
Na2H2Y
AgNO3
Обратное титрование
A + B1( избыток) ® продукты +
^(остаток)
^(остаток) + B2 ® продукты
1)	CaCO3 + 2H+ ® Ca2+ + CO2 + H2O
Н+(остаток) + OH-® H2O
2)	Ca2+ + C2O42- ® CaC2O4j.
5C2O42- (остаток) + 2MnO4- + 16H+ ®
® 10CO2 + 2 Mn2+ + 8H2O
3)	Al3+ + H2Y2-®AlY- + 2H+
Н^2-(остаток) + Mg2+® MgY2- + 2H+
4)	Cl- + Ag+ ® AgCU
Ад+(остаток) + SCN- ® AgSCNv
V(A) (пипет¬
ка)
V(B1) (пи¬
петка)
V(B2) (бю¬
ретка)
B1
B2
HCl
NaOH
Na2C2O4
KMnO4
Na2H2Y
MgSO4
AgNO3
NH4SCN
Титрование заместителя
A + D ® C (заместитель А) + продукты
C (заместитель А) + В® продукты
1)	2Cu2+ + 4I- ® I2 + 2CuIv
I2 + 2S2O32- ®2I- + S4O62-
2)	4NH4++ 6CH2O ® 4H+ + (CH2)6N4 +
6H2O
H+ + OH-® H2O
3)	Mn+ + MgY2- ® Mg2+ + MY(n-4)
Mg2+ + H2Y2- ® MgY2- + 2H+
V(A) (пипет¬
ка)
V(B) (бю¬
ретка)
B
Na2S2O3
NaOH
Na2H2Y
(ЭДТА)
Пример 8.3. При определении иона NH4+ можно провести ре¬
акцию с формальдегидом, в результате которой выделяется эквива¬
лентное количество протонов, являющихся заместителями NH4+.
4NH4+ + 6СН2О = (CH2)6N4 + 4H+ + 6H2O.
117

Ионы H+ оттитровывают раствором NaOH. При этом справед¬
ливо:
n(NH4+) - n(NaOH).
Пример 8.4. При определении свинца проводят последова¬
тельно несколько стехиометрических реакций:
Pb2+ + CrO42- - PbCrO4^	(осаждение),
2PbCrO4 + 2H+ - 2Pb2+ + Cr2O72-+ H2O	(растворение),
Cr2O72-+ 6I- + 14H+ - 2Cr3+ + 3I2 + 7H2O (получение заместителя),
I2 + 2S2O32- - 2I-+ S4O62-	(титрование).
Выделившийся в эквивалентном количестве иод титруют ра¬
бочим раствором тиосульфата натрия. В результате:
n(Pb2+) - n(I2) - n(S2O32-).
Oбычно в титриметрии проводят несколько параллельных
титрований. При этом используют один из двух способов: спосо6
отдельных навесок и способ пипетирования (аликвот). Использо¬
вание в расчетах - в табл. 8.3. В спосо6е пипетирования пробу (на¬
веска сухого вещества или объем раствора), содержащую опреде¬
ляемое вещество А, переводят в мерную колбу вместимостью Vm.k,
а на титрование отбирают пипеткой равные объемы Vn - аликвоты.
В способе отдельных навесок пробу помещают в колбу для титро¬
вания, при этом навеску вещества там же растворяют в небольшом
объеме растворителя, затем проводят титрование, измеряя объем
израсходованного титранта V(B). Метод пипетирования является
более экспрессным и менее трудоемким, но и менее точным, чем
метод отдельных навесок.
8.3.	Способы выражения концентрации растворов
в титриметрии
Все расчеты в титриметрии связаны с законом эквивалентов и
понятием «эквивалент». Эквивалентом называют реальную или ус¬
ловную частицу вещества, которая в Данной реакции равноценна
(эквивалентна) оДному иону воДороДа или оДному электрону. Ш-
пример, зквивалент NaOH, HCl, NaCl - реальная частица, соответ¬
ствующая молекуле этих веществ. Эквивалент H3PO4 , в зависимо¬
сти от числа участвующих в реакции протонов, может представлять
реальную молекулу H3PO4 или условную часть молекулы: 1/2H3PO4
118

или 1/3H3PO4. Дробь, показывающую, какая часть молекулы или
иона является эквивалентом, называют фактором эквивалентно¬
сти f3κβ. Фактор эквивалентности рассчитывают на основе стехио¬
метрии реакции. Число, показывающее, сколько эквивалентов со¬
держится в молекуле, называют числом эквивалентности и обозна¬
чают z : f3κf, -1/z . Молярная масса эквивалента вещества - это
масса оДного моля эквивалента этого вещества, равная произвеДе¬
нию фактора эквивалентности на молярную массу вещества. Ш-
пример, для вещества В:
M	В) = Лкв(В) M(B) = 1/z* (В) M(B).	(8.3)
8.3.1.	Вычисление молярной массы эквивалента
Пример 8.5. Вычислим молярные массы эквивалентов фос¬
форной кислоты, участвующей в реакциях нейтрализации:
H3PO4 + NaOH - NaH2PO4 + H2O,	‰(H3PO4) - 1;
M(1H3PO4) = 1 M(H3PO4) - 1 98 - 98,00 г/моль;
H3PO4 + 2NaOH - Na2HPO4 + 2H2O,	‰(H3PO4) - 1/2;
M(1/2H3PO4) = 1/2M(H3PO4) - 1/2 98 - 49,00 г/моль;
H3PO4 + 3NaOH - Na3PO4 + 3H2O,	‰(H3PO4) - 1/3;
M(1/3H3PO4) =1/3M(H3PO4) - 1/3 98 - 32,66 г/моль.
Пример 8.6. Молярная масса эквивалента KMnO4 зависит от
среды, в которой проводят восстановление. Поэтому с учетом числа
принимаемых электронов fκχKMnO4) составляет 1, 1/3, 1/5. Ш-
пример, в кислой среде:
MnO4- + 8H+ + 5e - Mn2+ + 4H2O,	fκ(KMnO4) - 1/5;
M(1/5KMnO4) =1/5M(KMnO4) -1/5 158,03 - 31,61 г/моль.
^которые затруднения возникают при определении эквива¬
лентной массы анализируемого вещества, не участвующего в реак¬
ции прямого титрования, а определяемого косвенным путем (на¬
пример при титровании приемом замещения). В этом случае полез¬
но установить химические соотношения между реагирующими ве¬
ществами и после этого определить молярную массу эквивалента.
Пример 8.7. Азот в органических соединениях, например в
C9H9N3, можно определить по следующей схеме:
C9H9N3 + реагент o¾¾κa ® 3NH3 + продукты,
119

NH3 + H+ = NH4+.
Из схемы видны следующие соотношения:
1 C9H9N3	° 3 NH3 ° 3 H+ ° 3 N,
1 M(C9H9N3) ° 3 M( NHs) ° 3M(H+) ° 3M(N),
т. е. 1 молекула C9H9N3 содержит 3 эквивалента, а
Z3k6(C9H9Ns) = 1/3;	М(1/3C9H9Ns) = 1 3 М( CJIA'.))∕wβ(N) = 1.
Пример 8.8. Свинец определяют методом окислительно-вос¬
становительного титрования с использованием приема замещения по
следующей схеме операций:
2+ 2-
Pb + CrO4 = PbCrO44	(осаждение и фильтрование осадка),
2PbCrO44 + 2H+ = 2Pb2+ + Cr2O72- + H2O	(растворение осадка),
Cr2O72- + 6Fe2+ + 14H+ = 2Cr3+ + 6Fe3+ +7 H2O	(титрование).
Отсюда: 2Pb2+° 2CrO∣'" ° Cr2O72" ° 6Fe2+° 6e;
2M(Pb2+)∕6 ° 2M(CrO42")∕6 ° M(Cr2O72")∕6 ° 6M(Fe2+)∕6 ° 6 моль e/6;
∕UPb2+) = 1/3; M(1∕3 Pb2+) = 1∕3M(Pb2+).
8.3.2.	Способы выражения концентрации растворов
При приготовлении рабочих растворов и вычислениях резуль¬
татов в титриметрии обычно используют следующие способы вы¬
ражения концентрации:
с(В) - молярная концентрация вещества В, моль/л;
c(f3κβ (В)В - молярная концентрация эквивалента вещества В, моль/л.
c(f3κβ.(B)B) = n(f3κβ.(B)B)∕V(B),	(8.4)
гДе V(B ) - объем раствора (л), содержащего n моль эквивалентов
B; соответствует старому названию - нормальная концентрация.
с(В) = /экв*&экв.(В)В).	(8.5)
В методиках анализа, установленных стандартами, разре¬
шены только единицы системы СИ. В частности, размерность
объема при выражении молярной концентрации - дм3. Такие вне¬
системные размерности объема, как литр (л), миллилитр (мл) яв¬
ляются разрешенными в химии и используются в учебной и научной
литературе, в том числе на страницах пособия.
Не рекомендуется использовать термины “молярность” и “нор¬
мальность” раствора, но эти понятия применяются в контекстах после
величины концентрации, например: ...0,1 молярный раствор, ...0,1
120

нормальный раствор. Разрешаются сокращенные обозначения, напри¬
мер 0,025М H2SO4 - 0,025 молярный раствор H2SO4, т. е. в одном лит¬
ре раствора содержится 0,025 моль вещества H2SO4; 0,050 н. H2SO4 -
0,050 нормальный раствор H2SO4, т. е. в одном литре раствора содер¬
жится 0,050 моль эквивалента вещества H2SO4.
T(В) - титр раствора вещества В, г/мл. Oн показывает массу
вещества В в одном миллилитре раствора:
Т(В) = m(B)/V(B).	(8.6)
С использованием T(B) возможен простой расчет навески вещества,
необходимой для приготовления определенного объема рабочего
раствора с заданным титром.
Т(В/А) - титр рабочего раствора В по опреДеляемому веще¬
ству А, г/мл (условный титр). Oн показывает, какая масса вещества
А эквивалентна или оттитровывается одним миллилитром рабочего
раствора В. Например, выражение T(KMnO4ZFe) - 0,001396 г/мл оз¬
начает, что 1 мл такого раствора KMnO4 эквивалентен (оттитровы-
вает) 0,001396 г Fe. Такой способ выражения концентрации удобен
при серийных анализах, т. к.
m(A) = V(B) -Т(В/А).	(8.7)
Между указанными способами выражения концентрации су¬
ществует простая связь:
с&кв(В)В) = Т(В) ЮООШ^жв^В),	(8.8)
с(В) = Т(В) ×1000∕M^),	(8.9)
T(В/A) = T(В)× ∖AAκ∣A∣A) ∖AA.VAA>).	(8.10)
с&квМВ) = Т(В/А) ×1000∕ Mfcκβ(A)A),	(8.11)
с(В) = T@/A)-1000/M(A).	(8.12)
В анализе чаще всего пользуются растворами с концентрациями
~0,002 или 0,1 моль/л. I Ic' применяются 1 М растворы, так как в этом
случае велика капельная ошибка титрования, т. е. ошибка при добав¬
лении одной лишней капли титранта с высокой концентрацией.
Использование в титриметрии концентрации с (OkiAV) В) (моль
эквивалента В в одном литре раствора) связано с удобством расче¬
тов, т. к. при одинаковых концентрациях растворов веществ А и В
реакции идут между равными объемами этих веществ (согласно за¬
кону эквивалентов):
n(A) = n(B)) или с V1K1.. (В)В) V(B) = с^экв. (A)A) V(A).
121

Выражение закона в обозначениях, встречающихся в ранее из¬
данной литературе: (N×V)A = (N×V)B.
В практике титриметрии часто пользуются так называемым
поправочным коэффициентом k, который показывает степень от¬
клонения практической концентрации полученного раствора от его
теоретического (расчетного) значения:
k = c(B).∕c(B)meop. или k = T(B)./ T(B)теор. ■
(8.13)
Например, если при приготовлении 0,1000 М раствора HCl
практическое значение концентрации полученного раствора оказа¬
лось равным 0,09983 моль/л, то на этикетке можно записать:
«0,1000 М HCl (k = 0,09983)». И, наоборот, если в условиях задачи
(эксперимента) используется, например, «0,2000 н. раствор ZnSO4
(k = 1,01)», то в расчетные формулы следует подставить:
c(1/2ZnSO4) = c(1/2ZnSO4)meop-k = 0,2000·1,01 = 0,2020 моль/л.
8.3.3.	Расчеты при приготовлении рабочих растворов
и установлении их концентрации
Пример 8.9. Сколько граммов дихромата калия необходимо
взять для приготовления 500 мл раствора K2Cr2O7 с титром, равным
0,005882 г/мл? Определите молярную концентрацию и молярную
концентрацию эквивалента K2Cr2O7 в полученном растворе, если
fκβ. (K2Cr2O7) = 1/6.
Р е ш е н и е. Из формулы (8.6):
m(K2Cr2O7) = T(K2Cr2O7)×V(K2Cr2O7).
В данном случае m(K2Cr2O7) = 0,005882 500 = 2,941 г.
По формулам 8.9 и 8.8 находим соответствующие молярные
концентрации дихромата. M(K2Cr2O7) = 294,1 г/моль.
c(K2Cr2O7) = T(K2Cr2O7)-1000/M(K2Cr2O7);
c(K2Cr2O7) = 0,005882× 1000/294,1 = 0,02000 моль/л;
c(1/6 K2Cr2O7) = T(K2Cr2O7)×1000/ М(1/6 K2Cr2O7);
с(1/6 K2Cr2O7) = 0,005882-1000/(1/6-294,1) = 0,12 моль/л.
Пример 8.10. Сколько нужно добавить воды к 100 мл 0,8000 н.
раствора HCl, чтобы получить 0,2000 н. раствор?
122

Р е ш е н и е. Исходя из выражения закона эквивалентов (8.1)
и учитывая, что количество кислоты при разбавлении сохраняется,
справедливо:	^(HCl)- V1(HCl) = с2(Ж1)- V2(HCl);
0,8000-100 = 0,2000-V2(HCl); V2(HCl) = 0,8000-100/0,2000 = 400 мл,
V2(HCl) = V1(HCl)+V(H2O); V(H2O) = V2(HCl)-V1(HCl) = 400-100 = 300 мл.
Пример 8.11. Приготовлен 0,02500 н. рабочий раствор КMnO4
для перманганатометрии. Определить его молярную концентрацию,
титр и титр по железу.
Р е ш е н и е. В соответствии с примером 8.6:
‰(KMnO4) = 1/5;	M(1∕5KMnO4) = 31,61 г/моль.
Тогда, пользуясь формулами (8.5), (8.8), (8.9) и (8.12) нахо¬
дим:
e(KMnO4) = 1∕5√1∕5KMnO4) = 1/5-0,02500 = 0,005000 моль/л,
T(KMnO4)-= 0,005000-158,03/1000 = 0,0007902 г/мл;
или, через молярную концентрацию эквивалента:
T(KMnO4) = с(1/5KMnO4)-М(1/5KMnO4)/1000,
T(KMnO4)-= 0,02500-31,61/1000 = 0,0007902 г/мл,
T(KMnO4∕Fe)-= e(1∕5KMnO4)- M(Fe)∕1000,
T(KMnO4∕Fe) = 0,02500-55,85/1000 = 0,001396 г/мл.
Пример 8.12. Во сколько раз следует разбавить 20,24 % - ый
3
раствор ⅛SO4 (р = 1,012 г/см ) для приготовления 0,1 н. раствора?
Р е ш е н и е. Вычислим e1(⅛SO4) - молярную концентрацию
исходного раствора кислоты:
^^O^ = w∙10∙ρ∕M(Η2SO4) = 20,24∙10∙1,012∕98,08 = 2,088 моль/л.
По условию необходимо приготовить раствор с ^^SO^. Её опре¬
деляем по формуле 8.5:
^^SO^ = 1/2 с^ШН^) = 1/2-0,1000 = 0,05 моль/л.
Тогда:	C1(Н2SO4)/с2(Н2SO4) = 2,088/0,05 = 41,76.
Такая кратность разбавления неудобна на практике. Можно разба¬
вить раствор в 40 раз, т. е. получить раствор с концентрацией:
C2(Н2SO4) = C1(Н2SO4)/40 = 2,088/40 = 0,05220 моль/л;
с^ШН^) = 2·^^) = 2∙0,05220 = 0,1044 моль/л.
Согласно (8.13), k = 0,1044/0,1 = 1,044.
Например, при приготовлении 1 литра рабочего раствора ки¬
слоты, т. е. V2 = 1000 мл, необходимо с помощью пипетки взять
123

V1(H2SO4) и довести в мерной колбе до метки:
K1(⅛SO4) = C2(H2SO4)×1000/C1(H2SO4) = 0,05220× 1000/2,088 = 25,00 мл.
Пример 8.13. Из 2,500 г Na2CO3 приготовлено в мерной колбе
500 мл раствора. Вычислить для этого раствора: а) T(Na2CO3),
б) молярную концентрацию, в) молярную концентрацию эк¬
вивалента Na2CO3, если предполагается титрование приготовленно¬
го раствора рабочим раствором НС1 с индикатором метиловым
оранжевым, г) определить молярную концентрацию НС1 и
T^Cl/Na^O^, если на титрование 25,00 мл раствора соды израс¬
ходовано 23,35 мл раствора НС1.
Р е ш е н и е:
а)	T(Na2CO3) = m(Na2CO3)/V(Na2CO3) = 2,500/500 = 0,005000 г/мл;
б)	согласно (8.9), c(Na2CO3) = T(Na2CO3>1000/M(Na2CO3),
c(Na2CO3) = 0,005000× 1000/106,0 = 0, 04717 моль/л.
При титровании с метиловым оранжевым реакция протекает до II2CO3:
Na2CO3 + 2НС1 = ¾CO3 + 2NaCl.
Тогдаj^kb (Na2CO3) = 1/2; M(1/2Na2CO3) = 53,00 г/моль;
в)	по формуле (8.8) находим:
c(U2Na2CO3) = T(Na2CO3>1000/M(1/2Na2CO3),
c(1/2Na2CO3) = 0,005000× 1000/53,00 = 0,09434 моль/л;
г)	по формулам (8.1) и (8.12) находим c^Cl) и T(BCVNa2CO3):
c^Cl) = c(1/2Na2CO3) V(Na2CO3)/V(TOl),
c(TOl) = 0,09434·25,00/23,35 = 0,1010 моль/л;
T(TOVNa2CO3) = c(TOl>M(1/2Na2CO3)/1000 = 0,1010×53,00/1000;
T(TOV^CO3) = 0, 005353 г/мл.
Пример 8.14. Рассчитайте поправочный коэффициент 0,1 н.
раствора AgNO3, если на титрование 0,09850 г NaCl израсходовано
16,50 мл этого раствора.
Р е ш е н и е.	AgNO3 + NaCl = AgClv + NaNO3.
M(NaCl) = 58,44 г/моль; /экв. (NaCl) = /экв. (AgCl) = 1.
Для определения концентрации использовано прямое титрование
отдельных навесок, следовательно, согласно формулам табл. 8.3:
124

m(NaCl) =
AAgNO3) - V(AgNO3) - М(NaCl)
1000
Из этого выражения находим:
W(NaCl) -1000
^a8n°3) = V (AgNO3) - М (NaCl)
с
к =	:
с
теор.
0,09850 -1000
16,50 - 58,44
0,1022
0,1
= 0,10220 моль/л;
= 1,022.
Задачи для самоконтроля
1.	До какого объема следует разбавить 900 мл 0,5 М раствора НО, чтобы
получить 0,1 М раствор?	Ответ: до 4500 мл.
2.	Вычислите молярную концентрацию раствора, полученного при сме¬
шивании 500 мл 2 М и 1500 мл 0,5 М растворов NaOH. Ответ: 0,8750 М.
3.	Какой объем 27,3 %-ного раствора КОН (r = 1,260 г/мл) необходимо
взять для приготовления 1,00 л 2,00 М раствора?	Ответ: 326 мл.
4.	Вычислите молярную концентрацию I I2SOi, если титр раствора равен
0,004852 г/мл.	Ответ: 0,04951 моль/л.
5.	Вычислите AHCl) и титр раствора, полученного смешиванием 50,00 мл
раствора HCl с титром 0,02370 г/мл и 550,0 мл 0,1925 М раствора HCl.
Ответ: 0,2306 моль/л; 0,008416 г/мл.
6.	Вычислите навеску NaCl, необходимую для приготовления 250,0 мл
рабочего раствора с T(NaCl/Ag) = 0,01080 г/мл.	Ответ: 1,4629 г.
7.	Вычислите навеску K2Cr2O7 для приготовления 500,0 мл 1,000 н. рас¬
твора. Определите T(K2Cr2O7/Fe).	Ответ: 2,4515 г; 0,005585 г/мл.
8.	Вычислите навеску Na2S2O3∙5H2O, необходимую для приготовления
12,5 л 0,2000 н. раствора для иодометрии. Определите молярную концентра¬
цию раствора.	Ответ: 621 г; 0,2000 моль/л.
9.	Навеску 0,6000 г H2C2O4-2H2O растворили в мерной колбе на 100 мл.
На титрование 20,00 мл полученного раствора израсходовали 18,34 мл рас¬
твора NaOH. Определить молярную концентрацию NaOH и его титр по
H2C2O4.	Ответ: 0,1038 моль/л, 0,004671 г/мл.
10.	Найти молярную концентрацию NaOH, если на титрование 16,78 мл
его затрачено 17,21 мл раствора соляной кислоты с титром 0,003604 г/мл.
Ответ: 0,1013 моль/л.
125

8.4. Расчеты результатов анализа в титриметрии
Расчетные формулы определения массы вещества m(A) для
разных приемов и способов титрования, при различных способах
выражения концентрации рабочего раствора, приведены в таблице
8.3. Прежде чем приступать к вычислениям, следует представить
уравнения протекающих реакций, определить прием и способ тит¬
рования, а также, с учетом протекающих реакций, найти молярную
массу эквивалента определяемого вещества.
Приведенные формулы легко дополняются необходимыми
множителями для вычисления содержания компонента A в анали¬
зируемой пробе.
Шпример, от массы определяемого компонента m(A) можно
перейти к его массовой доле w(A) (%) через отношение m(A) к мас¬
се навески та: w(A) - m(A)·100/ma.
Пример 8.15. Oпределить массу железной проволоки, кото¬
рую растворили в серной кислоте, а на титрование полученного
раствора израсходовали 40,00 мл рабочего раствора KMnO4 c
T(KMnO4/Fe2+) - 0,005585 г/мл.
Р е ш е н и е. Титрование прямое, способ - отдельных навесок.
Fe + H2SO4 - FeSO4 + H2↑ (растворение),
2KMnO4 + 10FeSO4 + 8H2SO4 - 2MnSO4 + 5Fe2(SO4)3 + K2SO4 + 8H2O,
m(Fe) - m(Fe2+) - ДKMnO4/Fe2+)∙ V(KMnO4) - 0,005585×40,00 - 0,2230 г.
Пример 8.16. Швеска кальцинированной соды массой 0,1267 г
растворена в воде и оттитрована в присутствии индикатора метило¬
вого оранжевого 22,65 мл 0,1002 н. раствора HCl. Вычислить массо¬
вую долю Na2CO3 в образце.
126

Таблица 8.3
Формулы для расчета массы определяемого вещества по результатам титрования при разных способах
выражения концентрации титранта
Способ
расчета
Прием титрования
Прямое и заместителя
Обратное (по остатку, по избытку)
По c(f3κβ В)
(по молярной
концентрации
эквивалента
рабочего
раствора)
Способ отдельных навесок:
c(f3κβB)-V(B)-M(f3κβ А)
Способ отдельных навесок:
[c(f3κβ B1)-V(B1) c(f3κβB2)-V(B2)J-M(f3κβА)
нIyrlJ
1000
Способ пипетирования (аликвот):
c(f3κβB)-V(B) ■ M(f3κβA)-Vmk
п IyrlJ
1000
Способ пипетирования (аликвот):
[c(f3κβ B1)-V(B1) c(f3κβ B2)-V(B2)J -M(f3κβ A)-Vmk
HlyrlJ
1000· Vn.
п IyrlJ
1000· Vn.
По T(B)
(по титру
рабочего
раствора В)
Способ отдельных навесок:
T(B)-V(B)-M(f3κβА)
т(А) =	.
M(f3κβ В)
Способ пипетирования (аликвот):
T(B)-V(B) -M(f3κβ A) -Vmk
т(А) =	.
M(f3κβB)- Vn
Способ отдельных навесок:
T(B1)-V(B1)	T(B2)-V(B2)
m(A) - [	]-M(f3κβA).
M(f3κβ B1)	M(f3κβ B2)
Способ пипетирования (аликвот):
T(B1)-V(B1)	T(B2)-V(B2)	Vmk
m(A) - [	]-M(f3κβA)-
M(f3κβ B1)	M(f3κβ B2)	Vn
По T(BZA)
(по титру
рабочего
раствора В по
определяемому
веществу А)
Способ отдельных навесок:
m(A) = T(BZA)-V(B).
Способ пипетирования (аликвот):
Vmk
m(A) - T(BZA) ■ V(B) ■
Vn.
Способ отдельных навесок:
m(A) = [T(B1∕A)- V(B1) - T(B2ZA) ∙ V(B2)J.
Способ пипетирования (аликвот):
Vmk
m(A) = [T(B1∕A)- V(B1) - T(B2ZA)- V(B2)J	.
Vn

Р е ш е н и е. Проведено прямое титрование по реакции
Na2CO3 + 2HCl = H2CO3 + 2NaCl.
Индикатор метиловый оранжевый имеет переход окраски в
кислой среде, что указывает на оттитровывание не одного, а двух
эквивалентов Na2CO3) (см. пример 8.13).
M(1∕2Na2CO 3) = 1/2 M(Na2CO 3) = 105,99/2 = 52,99 г/моль;
w(Na2CO 3) =
С(HCl) - V(HCl) - M(1∕2Na2CO3)
1000
100
W
нав.
w(Na2CO 3) =
0,1002 - 22,65 - 52,99 -100
1000 - 0,1267
= 94,92 %.
Пример 8.17. Навеску 3,017 г пестицида, содержащего 20,86 %
формальдегида обработали 50,00 мл 1,0 М (k = 0,9022) раствора
NaOH в присутствии пероксида водорода:
HCOH + OH- + H2O2 = HCOO- + 2H2O.
Избыток щелочи оттитровали раствором HCl c T(HCl) = 0,03798 г/мл.
Какой объем HCl израсходован на титрование?
Р е ш е н и е. В данном примере использован прием обратного
титрования по способу отдельных навесок. Учитывая условие зада¬
чи, найдем массу HCOH в навеске пестицида:
W(HCOH) = w^.WHCOH) = 3,017-20,86/100 = 0,6293 г.
Поскольку содержание HCOH определялось обратным титровани¬
ем, то согласно табл. 8.3 справедливо:
_ WNaOH) - V(NaOH) - с(НС1) - V(HCl)) - M(HCOH)
W(HCOH)	;
1000
/эКв. (HCOH) = 1;
T(HCl) ×1000
*<hci> = M(Hc1)
M(HCOH) = 30,01 г/моль;
0,03798 -1000
λc.	= 1,0420 моль/л;
^NaOH) = K-стеOp(NaOH) = 0,9022-1,0 = 0,9022 моль/л.
Преобразуем выражение для расчета W(HCOH) относительно V(HCl):
V(HCl) =
W(HCOH) -1000
M (HCOH) - с(НС1) ,
^NaOH) - V(NaOH)
e(HCl)
0,9022 × 50,00
0,6290 ×1000
V(HCl) =0,9012,0242500,00
■ 30,01 -1,0420 = 43,29 - 20,12 = 23,17 мл.
128

Пример 8.18. 1,1622 г поваренной соли растворили в воде и
раствор разбавили до 200,0 мл. К 20,00 мл этого раствора прибавили
25,00 мл 0,1000 н. раствора AgNO3. На титрование избытка AgNO3
израсходовали 5,080 мл 0,0900 н. раствора NH4SCN. Определить мас¬
совую долю хлорида натрия в образце соли.
Р е ш е н и е. Проведено обратное титрование способом алик¬
вот. Для расчета используем (табл. 8.3) уравнение:
w(NaCl) = C(AgNQ) × V(AgNOj) -c(NH4SCN) × V(NH4SCN)) ×M(NaCl). Умж. . 100
1000	Vn тнав. ’
В соответствии с уравнением реакции (см. пример 8.14):
fkβ. (NaCl) = 1,	/(NaCl) = 58,44 г/моль.
w(NaCl) =
(0,1000 × 25,00 - 0,0900 × 5,80) × 58,44 200	100
1000 20 1,1622
= 99,46 %.
Пример 8.19. Из 25,00 мл раствора свинец осадили в виде
PbCrO4, осадок отфильтровали, растворили в кислоте и добавили
избыток KI. На титрование выделившегося иода израсходовали
31,50 мл 0,1010 н. раствора Na2S2O3. Рассчитайте количество свин¬
ца в растворе (г) и молярную концентрацию ионов свинца в исход¬
ном растворе.
Р е ш е н и е. В данном примере проведено определение ионов
Pb2+ приемом титрования заместителя согласно реакциям :
(осаждение);
(растворение);
(замещение);
(титрование).
Pb2+ + CrO42- = PbCrO4v
2PbCrO4 v +2H+ = Cr2O72- + 2Pb2+ + H2O
Cr2O72- + 6I- + 14H+ = 2Cr3+ + 3I2 + 7H2O
I2 + 2S2O32- = S4O62- + 2I-
По закону эквивалентов (см. также пример 8.8):
n(Pb2+) = n(CrO42-) = n(I2) = n(S2O32-);
2Pb2+ ° 2CrO42- ° Cr2O72- ° 3I2 ° 6S2O32- ° 6e;
Λ.,<Pb"l = 1/3; М(1/3 Pb2+) = 1/3M(Pb2+) = 207,2/3 = 69,07 г/моль.
Для расчета содержания свинца при титровании по заместите¬
лю можно использовать формулу (см. табл. 8.3):
™ 2Л c(Na2S2O3) × V(Na2S2O3) × 1/3 × M(Pb2+)
m(Pb ) =		;
1000
129

0,1010 - 31,50 - 69,07
1000
W(Pb2+) =
= 0,2197 г;
2+	W(Pb2+ ) ×1000	0,2197×1000
с(РЬ ) =	z , 2.4 = ∏< лл эл7 п = 0,0424 моль/л.
V × M(Pb2+ )	25,00 × 207,2
Пример 8.20.* При получении экстракционной фосфорной
кислоты из фосфоритной муки протекают следующие основные ре¬
акции:
а) Ca3(PO4)2 + 3H2SO4 = 3CaSO4; + 2H3PO4 или
б) 2Ca3(PO4)2 + 5H2SO4 = 5CaSO4; + Ca(H2PO4)2 + 2H3PO4.
От направления процесса зависит состав реакционной массы.
Контроль процесса осуществляется методом кислотно-основного
титрования.
Для анализа взяли 5,00 мл фильтрата реакционной массы и раз¬
бавили в мерной колбе до 250,0 мл. H титрование аликвоты 25,00 мл
с индикатором метиловым оранжевым (м.о.) израсходовано 20,10 мл
раствора NaOH с T(NaOHH2SO4), равным 0,004901 г/мл. H титро¬
вание такого же объема с фенолфталеином (ф.ф.) израсходовано
35,80 мл того же раствора NaOH. Интервал рH перехода окраски
м.о. 3,1 - 4,4; ф.ф. 8,2 - 9,8.
Установите, при избытке или недостатке H2SO4 проводился
процесс, в результате которого получена указанная реакционная
масса. Вычислите концентрации каждого из компонентов в реакци¬
онной массе (г/л).
Р е ш е н и е.
Возможные реакции титрования (см. разделы 8.5, 8.6):
H2SO4 + 2NaOH = Na2 SO4 + 2H2O (с м.о. и с ф.ф.),
H3PO4 + NaOH = NaH2PO4 + H2O (с м.о.),
поскольку рЯта! = 1/2(рКа1+ рКа2) = 1/2(2,15+7,21) = 4,68;
H3PO4 + 2NaOH = Na2HPO4 + 2H2O (с ф.ф.),
поскольку рИ^ = 1/2(рКа2+ рКаз) = 1/2(7,21+12,3) = 9,76;
Ca(H2PO4)2 + 2NaOH = CaHPO4 + Na2HPO4 + 2H2O (с ф.ф.).
Для случая а) 1/2V(NaOH с ф.ф.) < V(NaOH с м.о.);
для случая б) 1/2V(NaOH с ф.ф.) > V(NaOH с м.о.).
По данным анализа: 1/2V(NaOH с ф.ф.) = 35,80/2 = 17,9 мл,
что < V(NaOH с м.о.) = 20,10 мл, следовательно, реакционная масса
130

содержит H2SO4 и ¾PO4.
Найдем расход щелочи на 1 эквивалент ¾PO4:
∆V1(NaOH) = V(NaOH с ф.ф.) - V(NaOH с м.о.) = 35,8 - 20,1 = 15,7 мл.
Найдем расход щелочи на 2 эквивалента H2SO4:
∆V2(NaOH) = V(NaOH с м.о.) - ∆V1(NaOH) = 20,1 - 15,7 = 4,4 мл.
Z,. . .	T(NaOH/H2SO4)∙DV2(NaOH)∙1000-V^,
P(H2S°4) = 	V	—	 =
пробы п
X¾PO4) =
0,004901×4,40×250×1000
=	= 43,1 г/л;
5,00×25,0
T((NaOHH2SO4) × 1000 × D V1((NaOH) × M(H3PO4)) × Vm.k. · 1000
M(1≡2SO4) -Vnpo6u ∙ Vn ∙1000
p(¾PO4) =
0,004901 × 15,7 × 98,0 × 250 × 1000
49,0 × 5,00 × 25,0
= 307,8 г/л.
Задачи для самоконтроля
Во βcex задачах переД проведением pac4emoβ следует npe∂cmaβumb уравне¬
ния протекающих реакций, определить метод, прием и способ титрования.
1.	Только граммов Н3РО4 содержится в растворе, если при титровании
с метиловым оранжевым израсходовано 25,50 мл 0,2000 М раствора NaOH.
Ответ: 0,4998 г.
2.	Определить жесткость воды, если к 100 мл ее прибавили 25 мл
0,1110 н. раствора Na2CO3 и после фильтрования осадка избыток карбоната
был оттитрован 15,20 мл HCl с титром 0,003645 г/мл (по метиловому оран¬
жевому).	Ответ: Ж = c(1/2(Ca2++Mg2+)) = 12,55 ммоль/л.
3.	Из 0,5320 г нитрата аммония приготовили 100,0 мл раствора. К 20,00
мл этого раствора добавили в избытке нейтральный раствор формалина, в ре¬
зультате реакции с которым выделилась азотная кислота в количестве, экви¬
валентном NH4NO3. На титрование HNO3 израсходовано 12,50 мл 0,1030 М
раствора NaOH. Влажность нитрата аммония 2,4 %. Рассчитать массовую до¬
лю в сухом нитрате аммония: а) NH4NO3; б) азота.
Ответ: а) 99,2 %, б) 34,7 %.
4.	На титрование раствора, приготовленного растворением 0,7353 г
сплава серебра в азотной кислоте, израсходовано 26,50 мл раствора роданида
аммония, титр которого по азотнокислому серебру равен 0,008550 г/мл. Рас¬
считать массовую долю серебра в сплаве.	Ответ: 19,57 %.
5.	Исследуемый раствор хлорида никеля разбавлен в колбе до 250 мл. К
10,00 мл этого раствора прибавлено 15,00 мл 0,0100 М ЭДТА, избыток кото-
131

рого оттитрован 4,50 мл 0,0100 М сульфата магния. Сколько граммов никеля
содержится в исследуемом растворе?	Ответ: 0,1550 г.
6.	* При анализе сухого растительного материала пробу 1,000 г под¬
вергли окислительной минерализации. Полученную золу растворили в раз¬
бавленной кислоте и отфильтровали в мерную колбу вместимостью 200 мл.
Аликвоту 50,0 мл после подкисления до рH 2 оттитровали, израсходовав 3,90
мл 0,0100 М ВаС12 (в вводно-органической среде с индикатором нитхромазо).
Другую аликвоту 50,0 мл, создав рH 11, оттитровали, израсходовав 2,15 мл
0,0100 М ЭДТА с мурексидом. Вычислить содержание серы и кальция в рас¬
тительном материале (г/кг).	Ответ: 4,99 г/кг, 3,44 г/кг.
7.	Какую навеску силиката, с массовой долей Fe2O3 около 4%, следует
взять для прямого комплексонометрического титрования железа (III), чтобы
израсходовать около 20 мл 0,0200 М раствора трилона Б?	Ответ: 0,8 г.
8.	К 25,00 мл раствора нитрата ртути (II) добавили избыток комплексона-
та магния. Ш титрование выделившихся ионов магния израсходовано 2,45 мл
0,05145 М раствора трилона Б. Вычислить нормальную концентрацию и титр
раствора нитрата ртути (II).	Ответ: 0,0924 н.; 0,01500 г/мл.
9.	Для анализа отобрали 20,0 мл сточной воды, содержащей соединения
железа, окислили их до железа (III) и осадили в виде гидроксида. Промытый
3
осадок растворили в HCl и оттитровали, израсходовав 4,0 см 0,0505 М рас¬
твора ЭДТА. Вычислите массовую концентрацию (мг/л) железа в сточной
воде.	Ответ: 571 мг/л.
10.	Швеску пиролюзита массой 0,2060 г обработали концентрированной
соляной кислотой. Хлор, который образовался в результате реакции, погло¬
тили раствором иодида калия. Выделившийся иод оттитровали 0,05200 н.
раствором тиосульфата натрия, затратив 42,52 мл. Определить массовую до¬
лю MnO2 в руде.	Ответ: 46,60 %.
11.	*Растворы (а - в) могут содержать HCl, H3PO4, NaH2PO4 (один из компо¬
нентов или в разумном сочетании). Укажите вещества и их концентрацию в
растворе (мг/мл), если на титрование 2-х отдельных аликвот (по 25,00 мл) этого
раствора 0,1200 М раствором NaOH с индикаторами бромкрезоловым зеленым
и тимолфталеином (табл. 8.12) средний объем NaOH составил, соответственно:
а) 13,12 мл и 35,19 мл; б) 18,72 мл и 23,60 мл; в) 13,33 мл и 26,65 мл.
Ответ: а) H3PO4 (6,17), NaH2PO4 (5,16); б) HCl (2,42), H3PO4 (2,30);
в) H3PO4 (6,27).
12.	* Выполните все условия и задания примера 8.20, но при измененных
данных анализа: «Ш титрование аликвоты 25,00 мл с м.о. израсходовали
14,40 мл раствора NaOH с T(NaOH∕H2SO4) = 0,004901 г/мл. H титрование
аликвоты 25,00 мл с ф.ф. израсходовали 32,80 мл того же раствора NaOH».
Ответ: H3PO4, 282 г/л; Ca(H2PO4)2), 93,6 г/л.
132

8.5.	Построение кривых титрования
В процессе титрования изменяются равновесные концентра¬
ции титруемого вещества А, титранта В, продуктов реакции и соот¬
ветственно свойства раствора. Cвойствами, связанными с концен¬
трацией А, являются равновесный потенциал E в окислительно¬
восстановительном титровании, величина pH - в кислотно-ос¬
новном, pM - в осадительном и комплексометрии. Ход реакции
титрования можно изобразить графической моделью или кривой
титрования.
Кривой титрования называют график зависимости параметра
системы, связанного с концентрацией титруемого вещества, титран¬
та или продукта реакции от состава раствора в процессе титрования
(например от объема титранта V(B) или степени оттитрованности f).
По оси ординат в химических методах титриметрии, как правило,
откладывают логарифм концентрации или логарифмически связан¬
ную с ней величину (например Е). В таком случае получаются полу¬
логарифмические (монологарифмические) кривые титрования.
Кривые титрования помогают выбрать индикатор, оценить по¬
грешность, наглядно проследить за ходом титрования.
При расчете кривых титрования прибегают к некоторым до¬
пущениям, не оказывающим заметного влияния на конечный ре¬
зультат. К таким допущениям относится:
1)	пренебрежение изменением объема раствора в ходе титро¬
вания (более справедливо при использовании титранта В с более
высокой концентрацией, чем А);
2)	пренебрежение малыми концентрациями выводимых из
сферы реакции ионов при образовании прочных продуктов (вода,
осадки, комплексы). Погрешность при этом пренебрежении тем
меньше, чем выше константы равновесия реакции титрования, т. е.
когда К > 107.
Если принимаемые допущения несправедливы, происходит на¬
рушение плавного хода кривой титрования. Тогда следует пользо¬
ваться более точными формулами расчета равновесий в соответст¬
вии с рекомендациями, приведенными в главах 3 - 6. Cм. также при¬
меры 3.2, 3.4, 8.22.
Пусть исходное количество А: n0(A) = с0(/экв(А)А) У(А).
^гласно закону эквивалентов (8.1), в каждый момент титрования
133

справедливо соотношение:
n(A) = n(B) или c(J3κβ.(B)B)-V(B) = cff3κβ.(A)A)-V(A).
В ТЭ:	B = no(A) или cfnβ.(В)В) -Vn(B) =	(A)A) -V(A);
Vt3 (B) = с0(f3KB.(A)А) - V(A)	(8 14)
T	с(/экв.(B)B)	.	( . )
Отношение количества оттитрованного в данный момент ве¬
щества A к исходному количеству A называют степенью оттитро-
ванности f :
n(B) = e(f.„( B)B)-V( B) =	B) B)-V (B) = V( B)	1
f n0(A) Cf(A)AW(A) c(f,κe,(B)B)-Vτ3(B) Vt3(B) (8.15)
При равных концентрациях A и В справедливо: f = V(B)/V(A).
Степень оттитрованности может быть выражена в %. Очевид¬
но, что до ТЭ f < 1 или f < 100 %, после ТЭ f > 1 или f > 100 %, в ТЭ
f = 1 или f = 100 %.
При построении кривых титрования задаются молярными кон¬
центрациями эквивалентов c(f,κβ(Α)Α)-и c(fκβ(B)B)- и начальным объ¬
емом раствора определяемого вещества (V(A)). Затем по закону эк¬
вивалентов рассчитывают V(B) в ТЭ. Принимают его за 100% и рас¬
считывают объемы V(B) в промежуточных точках, соответствующих,
например: 10 %; 50 %; 90 %; 99 %; 99,9 %; 101,1 %; 101 % и 110 %
добавленного титранта или задаются f (см. табл. 8.4 - 8.12). Такой
выбор значений объемов обусловлен плавным изменением кривой
вдали от ТЭ и резким вблизи (рис. 8.1 - 8.3). Резкое изменение рас¬
считываемого параметра (pH, pM или E) вблизи ТЭ называется скач¬
ком титрования и связано с крутизной кривой. Границы скачка рас¬
ширяются при снижении требований к точности титрования.
В кислотно-основном титровании рассчитываемым параметром
состава раствора является pH, осадительном и комплексонометриче¬
ском - pM , окислительно-восстановительном - равновесный потен¬
циал E.
Для реакции титрования: A + B = продукты
целесообразно рассчитывать параметр состава раствора До ТЭ по
концентрации титруемого раствора вещества A и, если необходи¬
мо, проДукта его превращения, пренебрегая концентрацией B. По¬
сле ТЭ - по избытку Добавленного титранта B, пренебрегая кон¬
центрацией A.
В ТЭ в растворе преобладают продукты реакции. Концентра-
134

ции A и B малы и расчет параметра системы, связанного с концен¬
трацией A, проводится через константу соответствующего равнове¬
сия: в кислотно-основном через KW и Ka или Kb; в осадительном -
через Ks ; в комплексонометрическом - через константу устойчиво -
сти комплексного соединения β; в окислительно-восстановитель¬
ном - через соответствующие значения Е0 редокс-пар A и В
(см. табл. 8.4-8.11).
Величина скачка титрования определяется константой равно¬
весия, концентрацией реагирующих веществ, температурой, приро¬
дой титруемого вещества и титранта, наличием посторонних ве¬
ществ и др. При правильном выборе индикатора для визуального
обнаружения ТЭ интервал перехода его окраски должен полностью
или частично укладываться в пределы скачка титрования (рис. 8.1).
При несовпаДении рТ инДикатора (или среДнего значения ин¬
тервала перехоДа инДикатора) с точкой эквивалентности (ТЭ)
титрование заканчивается при так называемой конечной точке
титрования - КТТ. Это является причиной инДикаторных ошибок.
Пояснения к расчету индикаторных ошибок титрования и необхо¬
димые формулы приведены в разделе 8.6.
Расчетные формулы в табл. 8.6 и других даны без вывода и
предполагают усвоение теоретических разделов и расчетов химиче¬
ских равновесий, в том числе, приведенных в разделах 2 - 6 глав. С
выводами сделан расчет кривой титрования многоосновного осно¬
вания Na2CO3 (пример 8.22).
8.5.1.	Расчет кривых кислотно-основного титрования
Метод кислотно-основного титрования основан на реакции
нейтрализации. Oн позволяет определять содержание кислот или
оснований в растворе, причем роль таких кислот и оснований могут
играть гидролизующиеся соли и амфолиты (см. табл. 3.1, 8.4). Oe-
новными рабочими растворами в методе нейтрализации являются
растворы сильных кислот (соляной, серной и др.) и щелочей. При
визуальном титровании применяют различные кислотно-основные
индикаторы, примеры которых приведены в табл. 8.12. В инстру¬
ментальных методах точку эквивалентности определяют по кривой
титрования, полученной экспериментально с помощью индикатор¬
ного электрода, потенциал которого является функцией р11.
135

Пример 8.21. Рассмотрим построение кривых титрования 0,20
М рабочим раствором NaOH 50 мл 0,10 М растворов кислот: силь¬
ной - HCl, слабой - CH3COOH и слабой катионокислоты - катиона
солянокислого анилина C6H5NH3Cl. Для этих протолитов fκβ=1.
^гласно формулам (8.14) и (8.15), в этих случаях V(NaOH) в
ТЭ составляет:
Vt3 (NaOH) =
со (A) × V(A)
c(NaOH)
0,1 · 50
0,2
= 25 мл,
что соответствует f = 100 %. Промежуточные значения и другие
расчетные данные для построения кривых титрования представле¬
ны в табл. 8.4 - 8.6.
Для качественной и количественной оценки состава раствора в
ходе титрования следует вспомнить расчеты протолитических рав¬
новесий, приведенные в разделах глав 2 и 3. правочные значения
Ka и Kb приведены в табл. 2 и 3 приложения.
При титровании протекают следующие протолитические ре¬
акции:
1)	H+ + OH- ⅛ H2O,	К = 1/Kw = 1014;
2)	CH3COOH + OH- ⅛ CH3COO- + H2O,
К = KJKw = 1,76·10-5/10-14= 1,76∙109;
3)	C6H5NH3+ + OH- ⅛ C6H5NH2 + H2O,
К = KJKw = 1/Кь = 1/3,31· 10-10 = 3,02∙109.
Из рассмотрения химических равновесий реакций титрования
следует:
-	в случае 1) в ТЭ среда нейтральная (pH = 7);
-	в случаях 2) и 3) в ТЭ среда щелочная (pH > 7); причина это¬
го - присутствие в растворе в ТЭ слабых оснований CH3COO- (2) и
C6H5NH2 (3);
-	Kb для CH3COO- (Kb = Kw/Ka = 5,68∙10-10) близка к Kb для
C6H5NH2, поэтому ход кривых для случаев 2) и 3) тождественен
(рис. 8.1).
Как видно из рис. 8.1, при титровании сильной кислоты кри¬
вая (1) симметрична относительно линии нейтральности. Благодаря
большей величине скачка для кривой 1 можно использовать доста¬
точно широкий круг индикаторов. Для кривых 2 и 3, например ме¬
тиловый оранжевый непригоден.
Таким образом, величина скачка на кривой кислотно-основ-
136

ного титрования зависит от природы (силы) титруемых протолитов. С
уменьшением Ka возрастает pH раствора в ТЭ. Если величина скачка
становится меньше интервала перехода индикатора (pKud ± 1), то ви¬
зуальное титрование становится невозможным.
При построении кривых титрования оснований кислотой ис¬
пользуют ту же схему подхода к расчетам, рассматривая изменение
состава раствора при титровании и подбирая формулы для расчета
[OH-], [H+] и pH.
Таблица 8.4
Данные для расчета и построения кривой титрования 0,10 М
раствора HCl 0,20 М раствором NaOH
K(NaOH)
Состав
раствора, %
pH-
опреде¬
ляющие
компонен¬
ты
Расчетные формулы
для [H+]
pH
мл
f, %
HCl
NaO
H
до т.э.
0
0
100
-
HCl
[H+ ] = c(HCl) =
C100 - fλ
= C0(HCl) × 100 j
° \ 100 ,
1,0
12,50
50
50
-
1,3
22,50
90
10
-
2,0
24,75
99
1
-
3,0
24,90
99,6
0,4
-
3,4
H
25,00
100
-
-
H2O
[H+] =JkW
7,0
после т.э.
25,10
100,4
-
0,4
NaOH
[OH - ] = C (NaOH)
[H+ ] = Kw =
[OH-]
=	KW ×100
= C0(NaOH) ×( f -100)
10,9
25,25
101
-
1
11,3
27,50
110
-
10
12,3
137

Таблица 8.5
Данные для расчета и построения кривой титрования 0,10 М
раствора слабой кислоты CH3COOH 0,20 М раствором NaOH
K(NaOH)
Состав
раствора, %
pH-опреде¬
ляющие
компонен¬
ты
Расчетные формулы
для [H+]
рН
мл
f, %
CH3C
OOH
NaO
H
до т. э.
0
0
100
-
CH3COOH
[H+ ] =JKa ∙ c⅛(CH3COOH)
2,9
12,50
50
50
-
CH3COOH
+
CH3COO-
(бУфеР)
[H+ ]=Ka
× C(CH3COOH) =
4,8
22,50
90
10
-
× C(CH3COONa)=
5,7
24,75
99
1
-
k (100- f)
=k f
6,7
24,90
99,6
0,4
-
7,2
H
25,00
100
-
-
H2O,
CH3COO-
[H + ] =
[ ] У
KwKa
с (CH3COOH)
8,9
после т. э.
25,10
100,
4
-
0,4
NaOH
[OH^ ]=C(NaOH)
[H+ ] = Kw =	Kw-100
[	] [OH ] C0 (NaOH)( f -100»
10,9
25,25
101
-
1
11,3
27,50
110
-
10
12,3
Таблица 8.6
Данные для расчета и построения кривой титрования
0,10 М раствора C6H5NH3Cl 0,20 М раствором NaOH
K(NaOH)
Состав
раствора, %
pH-
опреде¬
ляющие
компо¬
ненты
Расчетные формулы
для [H+]
рН
мл
f, %
C6H5N
H3Cl
NaOH
до т. э.
0
0
100
-
C6H5NH3+
[ff+ ] =
[ ] ί
kW × c0(C6 H, NH1CI)
Kb
2,8
12,50
50
50
-
C6H5NH3+
+
C6H5NH2
[H+ ] = Kw c(C6H5NH3Cl) =
]	Kb	C(C6¾≡2)
Kw (100 - f)
Kb	f
4,6
22,50
90
10
-
5,6
24,75
99
1
-
6,6
24,90
99,6
0,4
-
7,0
138

Окончание табл. 8.6
Λ
H
25,00
100
-
-
H2O,
C6H5NH2
[ H+]=	Kw
JKi CC6 H 5 № 2)
8,8
после т. э.
25,10
100,
4
-
0,4
NaOH
[OH- ] = C(NaOH)
Γ11+ ] = kw =	kw ∙100
[	] [OH- ] c(NaOH)(/ -100)
10,9
25,25
101
-
1
11,3
27,50
110
-
10
12,3
V (NaOH), мл
Рис. 8.1. Кривые кислотно-основного титрования:
1 - HCl; 2 - CH3COOH; 3 - C6H5NH2Cl.
-7
Для определения очень слабых кислот и оснований (K < 10 )
в титриметрии используется ряд приемов, описанных в рекомендо¬
ванной учебной литературе: обратное титрование, прием замеще¬
ния, усиление кислотных свойств за счет комплексообразования
или перехода к неводным и смешанным растворителям, определение
ТЭ инструментальными методами и др. В случае многоосновных ки¬
слот (оснований), смесей кислот (оснований) возможно их раздель¬
ное ступенчатое титрование (примеры 8.22, 8.23) с выраженными
скачками титрования, если константы кислотности (основности)
или константы соответствующих реакций титрования отличаются
не менее, чем в 104 раз.
139

Пример 8.22.* Построить кривую титрования 100 мл 0,10 М
раствора Na2CO3 0,10 М рабочим раствором HCl, считая относи¬
тельную погрешность титрования (погрешность измерения объема)
±1 % и пренебрегая изменением ионной силы раствора. (Следует
заметить, что подобная постановка задачи представляет интерес в
основном для приобретения навыков расчета более сложных случа¬
ев протолитических взаимодействий).
Ре ше ние .
1.	Проведем некоторые предварительные рассуждения и расчеты .
При титровании слабого основания CO3 сильной кислотой могут протекать
последовательно две реакции с соответствующими константами:
1)	CO32_ + H+ ¾ HCO3_, K1 = [HCO, ]I[H'][CO,2 ] = 1∕Ka2 = <4.8× 10 "ι 1 = 2,1×10l0;
2)	HCOf + H+ ≈ ⅛CO3, K2 = [H2CO⅛],∣H'∣∣UCOi_] = 1∕Ka,ι = l-l.5×0i ) = 2,2∙106.
Значения констант равновесия показывают, что реакции 1) и 2) проте¬
кают практически количественно, а их отношение (K1IK2 = 2,1×1010∕2,2×106),
равное 104 (отличаются на 4 порядка), свидетельствует о возможности сту-
2_
пенчатого титрования CO32_ с двумя выраженными скачками.
Расчет кривой до 1-ой ТЭ соответствует построению кривой титрова¬
ния слабого одноосновного основания, т. к. при этом титруется один эквива-
2_
лент слабого двухосновного основания CO32_ с константой основности
Kb1(CO32_):
.∙.OC2 = KwK = О'4 -IKH11 = 2,1∙1<T,.
Далее титруется продукт реакции 1) _ амфолит HCO3 , для которого величи¬
на константы основности составляет:
KbHCOil = .C -(C'OC I = Kw∕Kαi = 10_14 I4,5∙10-7 = 2,2·10_8,
что превышает величину константы кислотности HCO3 :
(K„(HCO3_) = Ka2(H2CO3) = 4,8∙10~π).
В начальный момент титрования HCO3_, соответствующий 1-ой ТЭ при тит¬
ровании Na2CO3, концентрация HCO3_ вдвое меньше начальной концентрации
2_
CO32_ вследствие двукратного увеличения объема:
c„(HCO3_) = ^CO 2 Oi ОСС ( v (∖il COii + HJHClW,
oiHCOC) = C(HCl)VHClWV(Na2CO3) + K(HClW.
С учетом предварительных рассуждений, формул (8.14), (8.15), а также
условий примера 8.21, для построения кривой титрования Na2CO3, зададим
значения степени оттитрованности f и соответствующих объемов HCl в точ¬
ках кривой: V(HCl) _ общий добавленный объем титранта к 100 мл раствора
Na2CO3; Нраствора_ общий объем титруемого раствора (V(Na2CO3) + V(HCl))
(табл. 8.7). В последнюю строку таблицы внесены результаты проведенных
ниже расчетов для построения кривой титрования (в скобках приведены для
сравнения значения рН в указанных точках при приближенных расчетах).
140

2.	Проведем вычисления рН в соответствующих точках, внося результа¬
ты в нижнюю строку табл. 8.7 и представляя в виде кривой на рис. 8.2.
В первой точке f = 0,	V(HCl) = 0.
Среда раствора определяется концентрацией слабого анионооснования CO3 :
CO32_ + H2O ¾ HCO3_ + OH_,	K>ι(CO32") = 2,1∙10-4 (см. выше).
2_ 2_
Соотношение c0(CO3 ')∕Kb1(CO3 ) >> 400, поэтому расчет проводим по при¬
ближенной формуле (табл. 3.1), преобразовав ее для расчета рН:
рН = рKw _ 1/2рКь1 + 1∕2lgCo(CO32>= 14 _ 3,68/2 _ 1/2 = 11,66.
Таблица 8.7
Данные для построения кривой титрования 100 мл 0,10 М Na2CO3 0,10 М
рабочим раствором HCl (с учетом разбавления)
До
1-ой ТЭ
1-ая
ТЭ
До 2-ой ТЭ
2-ая
ТЭ
После
2-ой ТЭ
V(HCl),
мл
0
50,0
90,0
99,0
100
101
110
150
190
199
200
201
210
f
0
0,50
0,90
0,99
1,00
1,01
1,10
1,50
1,90
1,99
2,00
2,01
2,10
Vэаствора,
мл
100
150
190
199
200
201
210
250
290
299
300
301
310
рН
11,66
10,32
9,37
8,54
(8,32)
8,33
8,13
(8,35)
7,30
6,35
5,40
4,41
(4,35)
3,91
3,49
2,49
До 1-ой ТЭ титрование проводится по реакции 1). При этом в растворе
_ 2_
образуется кислотно-основная сопряженная пара HCO3 /CO3 , в достаточно
широком пределе концентраций обладающая буферным действием.
Расчет рН при V(HCl) 50 и 90 мл можно провести, используя формулу (3.11):
рН = рКа2 _ lg(c(HCO3~)∕c(CO32~)),
рН = рк . _ lg{c(HCl)×F(HCl)∕(c0(CO32-)×F(Na2CO3) - C(HCl)-V(HCl))),
рН = рК„2 _ lg f /(1-f).
Подставляя в уравнения справочные и подготовленные данные, получа¬
ем значения рН для соответствующего участка кривой титрования. Например,
при V(HCl) = 90,0 мл (f = 0,90):
рН = 10,32 _ lg (0,9 /(1 - 0,9) = 9,37.
_ 2_
Вблизи ТЭ при c∣[[C'O; ) >> с(CX)3 ), в частности, приf = 0,99, расчет
по приближенной формуле для буферного раствора приводит к значению рН
8,32, в результате чего нарушается ход кривой. В таких точках следует прово¬
дить расчеты через равновесные концентрации, которые можно вычислить с
учетом совокупности равновесий и соответствующих констант:
1.	НОЭ3_ ¾ Н+ + CO32_,	К = Ka2(R2CO3) = 4,8×10-11.
2.	НОТ + H2O ¾ ¾CO3 + OH_,	К2 = Kw/Ka1 = 10"14 /4,5×10"7 = 2,2-10_8.
3.	H+ + ОН_ ¾ H2O,	К3 = 1/Kw = 1014.
141

Общая константа K123 = K1-K2-K3 = 4,8-10 11∕4,5-10 7 = 1,07-10 4 характеризует
суммарное уравнение с исходными (C) и равновесными ([ ]) концентрациями
частиц:
2 HCO3-	¾
CO32-	+
H2CO3,
с:
0199 = 4,975-10-2
0∙1<100 - 99) = 5,025-10-4
-
199
199
[ ]:
4,975 10-2 - 2х
5,025 10-4 +х
х .
Подставляя значения равновесных концентраций в выражение для K1,2,3, по-
лучаем уравнение:
k	= [CO 32- ]-[H2CO3] = (5,025 -10 -4+х)-х =1 07 -10 - 4
1,2,3 [HCO3 - ]2	(4,975 -10 -2 - 2 х )2 ,	,
решение которого приводит к значению х = 3,155-10-4. Вычисляем равновес¬
ные концентрации компонентов кислотно-основных сопряженных пар и, под¬
ставляя в соответствующие уравнения, получаем значение рН:
[H2CO3] = х = 3,155-10-4;	[HCO3"] = 4,975-10-2 - 2-3,155-10"4= 4,91-10-2;
[CO32-] = 3,155-10-4+ 5,025-10-4 = 8,18-10-4;
pH = pKa2 - lg([HCO3"]∕[CO32"]) = 10,32- lg(4,91∙10'2∕8,18-10-4) = 8,54;
(или pH = pKai - lg<∣H3CO,∣∕∣HCO3 I) = 6,35- lg(3,155-10-4∕4,91-10-2) = 8,54).
В 1-ой ТЭ f = 1, pH создается амфолитом HCO3- - уравнение (3.8), из
которого получаем выражение для pH:
pH =1∕2(pKa1+pKa2)=1∕2(6,35+10,32)=8,335=8,33 .
После 1-ой ТЭ и До 2-ой ТЭ по реакции 2) начинается титрование
HCO3-, причем в 1-ой ТЭ c0(HCO3-) = 1∕2c0(CO32-) = 0,050 моль/л.
При соизмеримых количествах HCO3- и H2CO3 в образующемся буфер¬
ном растворе, например в интервале K(HCl) от 110 до 190 мл, расчет pH мож¬
но проводить по приближенной формуле для буферного раствора, т. е. через
c(HCO3-) и c(H2CO3) или через степень оттитрованности f. Например, при
K(HCl) = 110 мл и f = 1,10, получаем:
pH = pKai - lg(c(H2CO3)∕c(HCO3-));
pH = pKai - lg{(c(HCl)-K(HCl) - c(HCl)-K(HCl}ra)∕(c<>(CO32-)-K(Na2CO3) -
- C(HCl)-K(HCl) + c(HCl)-K(HC‰)} = 6,35 - lg((f- 1)∕(2 -f)) = 7,30.
При большом избытке той или иной формы (вблизи ТЭ) расчет pH сле¬
дует проводить через [HCO3-] и [H2CO3], вычисляя их подобно тому, как это
было показано выше. Например, при K(HCl) = 101 мл (f = 1,01):
CO32-
2 HCO3-
0,05-200- 0,1-1	-2
’	’ = 4,925-10 2
+	H2CO3,
01-1 = 4,975-10-4,
201
4,975-10-4+х.
C:
[ ]:
201
4,925-10-2-2х
х
Подставляя значения равновесных концентраций в выражение для K1,2,3, по¬
лучаем уравнение, решение которого приводит к значению х = 3,12×10-4.
142

К	= [CO32 - ]∙[H2CO3] = х <4,975 ∙10 -4 + х) =1 07 ×10 - 4
1,2,3	[HCO3-]2	(4,925 ∙10-2-2х)2 ,	,
тогда [CO32_]= x = 3,12· 10_4;	[H∞3^] = 4,925·10_2 - 2·3,12·10_4= 4,863·10_2;
[H2CO3] = 4,975·10_4 + 3,12· 10_4 = 8,095· 10_4;
рH = fiKa∣ _ lg([H2CO3]I[HCO3^]) = 6,35 - lg(8,095 · 10_4/4,863 · 10^2) = 8,13.
Вблизи 2-ой ТЭ, в начале второго скачка на кривой титрования, в част¬
ности при V(HCl) = 199 мл, когда мала [HCO3_], можно провести расчет [H+]
по формуле (3.10), считая [H+] >> [0H_]:
[H+]=K 1	-[H ] = 4,5·10-7 · 0,1·99/299 -[H ] = 3,86·10-5; рH = 4,41.
a1 ^HCO3-)+[H+]	’	0,1·1/299 +[H+]
Во 2-ой ТЭ f=2, рH создается слабой двухосновной кислотой H2CO3,
концентрация которой втрое меньше ^(Na^O^:
^H2CO3) = 0,1· 100/300 = 3,33 ·10"2.
При концентрации Н2СО3, превышающей растворимость СО2, равную при комнатной
температуре 4,5·10 , при расчете рН следует использовать величину молярной раство¬
римости СО2.
Объем HCl, мл
Рис. 8.2. Кривая титрования 0,10 М раствора Na2CO3 0,10 М раствором HCl
Различие Ktt1, Ktt2 и соотношение с(H2CO3)IKа1(H2CO3)>>400 позволяют
провести расчет рH по приближенному уравнению (табл. 3.1):
рH = 1^,1 - 1I2lgс(H2COз)·= 1/2(6,35 - lg3,33· 10_2) = 3,91.
После 2-ой ТЭ рН раствора определяется избыточной концентрацией силь¬
ной кислоты, подавляющей диссоциацию слабой угольной кислоты.
Например при V(HCl) = 201 мл (f = 2,01):
[H+] = aHClX V(HCl) _ K(HαWf‰4>. = 0,1·(201-200)/301 = 3,23· V
μH = 3,49.
143

Как видно из рис . 8.2, кривая титрования Na2CO3 имеет два
скачка. Однако первый из них, при протекании реакции 1, имеет
меньшую крутизну и величину. Интервал перехода фенолфталеина
выходит за границы скачка. Поэтому титрование Na2CO3 по второ¬
му скачку с индикатором метиловым оранжевым по реакции:
2- +
CO3 + 2H ¾ H2CO3 будет иметь более высокую точность.
Пример 8.23. Оцените значения pH в точках эквивалентности,
границы второго скачка (погрешность определения объема считать
±1,0 %) при титровании смеси кислот: 0,10 М HIO3 и 0,10 M
CH3COOH 0,10 M раствором NaOH, а также точность определения
первого иона водорода при его титровании до точки эквивалентно¬
сти.
Ре ше ние . В данной смеси присутствуют кислоты разной
силы (pKα(HIO3) = 0,77; pKa(CH3COOH) = 4,76), каждая из которых
может быть независимо оттитрована щелочью, и последовательно -
из смеси, поскольку константы кислотности отличаются на 4 по¬
рядка. Первой реагирует с NaOH более сильная кислота HIO3:
1)	HIO3 + OH- ¾ H2O + IO3-;
2)	CH3COOH + OH- ¾ H2O + CH3COO-.
В 1-ой ТЭ pH раствора можно оценить, учитывая проявление
свойств анионооснования ионом IO3- (гидролиз) и диссоциацию
CH3COOH, т. е. провести расчет по приближенной формуле для ам¬
фолита, в котором основная и кислотная функции распределены на
две частицы.
3)	IO3- + H2O ¾ HIO3 + OH-;
4)	CH3COOH ⅛ H+ + CH3COO-.
pH1-31 = 1∕2(pKa(HIO3) + pKa(CH3COOH)) = (0,77 + 4,76)∕2 = 2,765 » 2,8.
Точность титрования первого иона водорода (от HIO3) можно
охарактеризовать, выразив из Ka(HIO3) отношение оттитрованной
части к неоттитрованной, а затем к общей для данной кислоты:
[IO3-]∕[HIO3] = Ka ∕[H+] = 1,7 10-1∕10-2,765 = 1,7 10-1∕1,718 10-3 = 98,95∕1.
Точность титрования составляет: 98,95 100∕(1+98,95) = 99 %.
Вторая ТЭ (f = 2) и границы второго скачка рассчитываются
подобно приведенным в примере 8.22 (табл. 8.7), при этом не учи¬
тывается вклад гидролиза IO3- в pH среды и разбавление раствора.
144

Нижняя граница второго скачка титрования соответствует f = 1,99.
При этом среду раствора можно оценить по буферной смеси, со¬
стоящей на 99 % из сопряженного основания CH3COO- и на 1 % -
из CH3COOH:
pH = pKa(CH3COOH) - lg((2 -f)∕(f-1)) = 4,76 - lg(2 - 1,99)∕(1,99 - 1)) = 6,76;
pH132 = 7 + 1∕2pKa(CH3COOH) + 1∕2lgc(CH3COOH) = 8,88.
Верхняя граница второго скачка титрования определяется избы¬
точной концентрацией NaOH при f = 2,01:
pH = pKw + lg(c(NaOH) (f-2)) = 14 - lg(0,1 (2,01 - 2)) = 11.
Таким образом, границы второго скачка находятся в пределах pH
6,8 - 11.
Пример 8.24*. Рассмотрите возможность титрования 0,20 М
раствора соли аммония 0,20 М растворами: а) NaOH в воде; б) этила¬
та натрия в безводном этаноле, считая константу автопротолиза эта¬
нола KSff = 8,0·10-20, константу ионизации NH3 в этаноле - 8,0·10-10.
Рассчитайте долю неоттитрованного NH4+ (%) при титровании
до точки эквивалентности в случаях а) и б). Какие условия являют¬
ся более приемлемыми? Вычислите pH в точках эквивалентности
для а) и б).
Ре ше ние . Титрование в воде идет по реакции:
NH4+ + OH- → NH3 + H2O,
константа равновесия которой:
К =	ES	= К = ½ = 1∕(1,76∙10-5) = 5,7-104
р [NH+ ]-[OH" ] Kw /Кь	’	■
При титровании в этаноле (см. пример 3.7) протекает реакция:
NH4+ + C2H5O- 5→ NH3 + C2H5OH
с константой равновесия:
k =	[NH3]	= Kf-
р [NH +] - [C2H5O- ] КЭтн
=1∕(8 10-10)=1,25 109
В точке эквивалентности в обоих случаях (NH3) = 1∕2c(NH4+) = 0,10 моль/л.
Концентрации титруемой катионокислоты в точках эквива¬
лентности можно вычислить через Кр. При титровании в воде со¬
гласно уравнениям реакций титрования:
[NH4+] = [OH-];	[NH3] = 0,1 - [NH4+] ≈ 0,10 моль/л;
145

[NH4+] =
[NH3]
0,10
5,7-104
-3
= 1,3·10 моль/л.
Ί
Доля неоттитрованного иона х вычисляется из отношения:
x(NH4+) =
[NH+ ] = 1,3 -10-3
c(NH3) = 0,1
= 1,3 ·10-2 или 1,3 %.
При титровании в этаноле: [NH4+] = [C2H5O_];
[NH4+] =
0,10
V 1,25 ×109
= 8,9·10-6 моль/л; x(NH4+) = 8,9·10-5 или ≈ 0,01%.
Таким образом, при неводном титровании в этаноле доля не-
оттитрованного иона NH4+ значительно меньше (вследствие мень¬
шей обратимости реакции).
В точках эквивалентности среда определяется константой ос¬
новности и концентрацией слабого основания. С учетом приведен¬
ных выше соотношений проще провести расчеты по формулам:
pH = 14 _ pOH = 14 _ (_lg[NH4+]) = 14 + lg(1,3 · 10-3) = 14 _ 2,9 = 11,1 _ в воде;
в этаноле: pH = _lg[C2H5OH2+] = pKSH + lg[C2H5O_] = 19,1 + lg(8,9∙ 10-6) = 14,0.
8.5.2.	Расчет кривых окислительно-восстановительного
титрования
Классификация методов окислительно-восстановительного
титрования (редоксиметрии) приведена в табл. 8.3. Методы редок-
симетрии основаны на изменении потенциала окислительно-вос¬
становительной системы в ходе титрования вследствие изменения
концентрации окисленной и восстановленной форм реагирующих
веществ. Полнота протекания реакции зависит от разности стан¬
дартных (или формальных) потенциалов окислительно-восстано¬
вительных пар. Для реакции в общем виде:
n2Ox1 + n1Red2 ¾ n1Ox2 + n2Red1 ,,
lgk = .[Ox2]"1 - [Redl]"2 = (E - E) - n
ё	i5[Ox1]n2 - [Red2]n1	0,059 ’
где n= n1-n2 - количество электронов, участвующих в реак¬
ции.
8
Например, при n1 = n2 = n необходима К не менее 10 (для пре¬
вращения исходных веществ в продукты реакции на 99,99 %), а lgK
не менее 8. Следовательно:
146

(E01 - E02)n∕0,059 ≥ 8;	(E01 - E02)n ≥ 0,472.
Тогда при n1 = n2 = n = 1	(E1 - E2)>0,472В;
при n1 = n2 = n = 2	(E01 - E02) ≥0,236 В и т. д.
Величина изменяющегося в ходе титрования равновесного по¬
тенциала определяется значениями стандартных потенциалов ре-
докс-пар титранта В и определяемого вещества А, а также концен¬
трациями реагентов. Для построения кривых титрования необходи¬
мо записать уравнения полуреакций для титранта и определяемого
вещества и найти в справочнике или табл. 5 приложения соответст-
0
вующие им значения стандартных потенциалов Е .
n2Ox1 + n1Red2 i→ n1Ox2 + n2Red1,
0x1+ nιe ¾ Redb	Eox1/Red1;
0x2+ n2e i→ Red2,	EOx2/Red2.
Для построения кривой титрования в координатах E - V(B) (рис. 8.3)
расчет E в ходе титрования проводят по уравнению Нернста, связан¬
ному с концентрациями компонентов окислительно-восстановитель¬
ных пар (см. главу 5).
В случаях, когда в полуреакциях участвуют ионы H+ или OH-, оп¬
ределяющие среду раствора, E и ЕТЭ зависят от [H+] (сравните табл.
8.8 и табл. 8.9). При расчетах допускается, что pH практически не
меняется в ходе титрования. При этом до ТЭ удобно пользоваться
полуреакциями с участием титруемого вещества А, после ТЭ - с
участием титранта В.
Если титруемое вещество (с индексом 1) - восстановитель, то до ТЭ:
E = E10 + 0,059lg [OX1] = E10 + 0059Ig—f—;
1	n1	[Red1]	1	n1	100 - f
^eeо i 0,059 lg [Ox2]	eo i 0,059 f -100
после ТЭ: e = Е2 +	Igro , 1 = Е2 +	lg 1	.
n2	[Red2]	n2	100
Если титруемое вещество окислитель, то до ТЭ:
Е Е0 i 0,059	100- f;	e Е0 i 0,059lg 100
e = E1 +	Ig		—; после ТЭ: E = E1 +	lg
n1	f	n2	f -100
f
В области ТЭ устанавливается смешанный потенциал, который для
простых редокс- реакций можно представить в виде:
E
ТЭ.
= n1 × ei0 + n2 × Е2
n1 i n2	.
147

Для расчета ЕТЭ в общем случае используют формальный прием
сложения двух полуреакций с уравненным числом электронов (пу¬
тем умножения на n2 и n1) и решения полученного уравнения отно -
сительно ЕТЭ (пример 8.25).
Пример 8.25. Рассмотрим построение кривых титрования 100 мл
0,1 н. раствора соли Fe2+: 1) 0,1 н. раствором соли Ce4+;
2) 0,1 н. раствором KMnO4, т. е. раствором с c(1/5KMnO4) = 0,1 моль/л
в среде 1 н. H2SO4 ([H+] = 1 моль/л).
Расчет проведем в интервале ±10 % от V^ (100 мл). Начальную
точку при V(B) = 0 в редоксиметрии не рассчитывают, а также пре¬
небрегают влиянием ионной силы раствора.
1)	Fe2+ + Ce4+ ⅛ Fe3+ + Ce3+,
Fe3++ 1e ⅛ Fe2+ , n=1; E01 = E^l=+0,77B;
Ce4+ + 1e ⅛ Ce3+, n2=1; E02 = E^. lce+ = +1,44B.
2)	5Fe2+ + MnO4- + 8H+ ⅛ 5Fe3+ + Mn2+ + 4H2O,
Fe3+- 1e ⅛ Fe2+ ,	щ=1; E0ι = E°f^ , Fe2+ = +0,77 B;
MnO4- + 8H+ + 5e ⅛ Mn2+ + 4H2O, n2 =5; E02 = E0	= +1,51B
4 2 2 2	MnO4- / Mn2+
Выведем выражение для ЕТЭ во втором, более общем случае.
Уравнения Нернста для полуреакций окисления Fe2+ перманганатом
калия представим в виде (выражения умножены на соответствую¬
щие количества электронов в полуреакциях):
5Е
MnO4- /Mn2+
= 5Е
0
МnO - / Mn
2+
+ 0,059 lg[H+ ]8 + 0,059lg[Mn°O⅛
[Mn2+]
=5 Е
ТЭ
[Fe3+]
Е^3+ /Fe2+ = Еpe+/pe+ + 0,059lg[Fe2+ ] = ЕТЭ .
При их сложении получаем:
6 ЕТЭ
5Е
0
МnO - / Mn
2+
0
+ Е 0Fe3+ /Fe2+
+0,059 lg[H+ ] 8 + 0,059 lg
[M∏O1] [Fe3+ ]
[Mn2+ ] ×[Fe2+ ];
ЕТЭ = (5Еθ _пл 2+ + £0Fe3+/Fe2+ )/6 + 0,059/6lg|H+ ]8+ 0,059/6·lg[Mn(°4] ·l''e'l.
ТЭ V МЮ 4 /Mn2+	7	’	-II ,	[Mn2+ ] [Fe2+ ]
В соответствии с уравнением реакции титрования (2) можно пред¬
ставить соотношение равновесных концентраций в ТЭ:
[Fe3+] = 5[Mn2+],	[Fe2+] = 5[MnO4-].
148

После подстановки и сокращений получаем выражение для ЕТЭ:
ЕТЭ = (5 ЕМпО4- /Mn2 + + Е0F/Fe2+ )/6 + 0,059/6lg[H + ]8 ,
т. е. ЕТЭ в данной системе зависит от рН.
Кривые титрования показаны на рис. 8.3, результаты расчетов
для реакций (1) и (2) представлены в виде таблиц 8.8 и 8.9.
Если титрование Fe2+ раствором KMnO4 в кислой среде про-
3+
водить в присутствии H3PO4, то продукт реакции - ионы Fe - бу-
2+	3
дут связываться в комплекс [Fe(H2PO4)]2+ (b = 3,16×103). Легко по¬
казать, что при рН » 0, создаваемом 1 н. H2SO4, в присутствии 1 М
H3PO4 равновесная концентрация дигидрофосфат-ионов, [H2PO4-]
-3
равна 6,94×10 моль/л.
Значения Е на этом участке (до ТЭ) и в ТЭ можно вычислить,
0	0'
заменяя в формулах табл. 8.9 значение EF0e3+ / Fe2+ = +0,77B на E ', кото¬
рое можно получить с использованием формулы (5.7).
Таблица 8.8
Данные для расчета и построения кривой титрования
0,10 н. раствора соли Fe 2+ 0,10 н. раствором соли Ce4+
Объем В
(Ce4+)
Состав раство¬
ра, %
По-
тенци-
ал-
опре-
де-
ляю-
щая
систе¬
ма
Расчетные
формулы
E, B
мл
f,%
Fe3+∕Fe
2+
Ce4+/Ce
3 +
до т. э.
90
90
90/10
-/90
Fe3+,
Fe2+
E=$ + 0'059lg f
1	n1	100-f
0,83
99
99
99/1
-/99
0,89
99,9
99,9
99,9/0,1
-/99,9
0,95
П
H
100
100
100/-
-/100
Fe3+,
Ce3+
7~, 0	I	T 0
E = n1E10 +n2E20
n1 + n2
1,10
после т. э.
100,1
100,1
100/-
0,1/100
Ce4+,
Ce3+
E=E2+0059Igf-100
2	n2	100
1,26
101
101
100/-
1/100
1,32
110
110
100/-
10/100
1,38
149

Таблица 8.9
Данные для расчета и построения кривой титрования 0,10 н. раствора
соли Fe 2+ 0,10 н. раствором KMnO4 при рН = 0
Объем
KMnO4
Состав раствора,
%
Потен¬
циал-
опреде¬
ляющая
система
Расчетные
формулы
Е,В
мл
f,%
Fe3+∕Fe2+
MnO4
/Mn2+
до т. э.
90
90
90/10
-/90
Fe3+,
Fe2+
E — E1 + 0,059lg f
1	∏	100-f
0,83
99
99
99/1
-/99
0,89
99,9
99,9
99,9/0,1
-/99,9
0,95
100
100
100/-
-/100
Fe3+,
Mn2+,
H+
00
E = n1 × E10 + n2 × E20 -
n1 + n2
0,059	1
	lg
n1 + n2	[H +]8
1,39
после т. э.
100,
1
100,1
100/-
0,1/100
MnO4-,
Mn2+,
H+
z7 z70	0,059
E — Е 2 +	×
П 2
f - 100	+ 8
× Ig-	[ H + ]8
100
1,47
101
101
100/-
1/100
1,49
110
110
100/-
10/100
1,50
E θ'	= E 0
Ox/Red	Ox/Red
0,059 1 0,059
+	lg b +

bm	n
lg— ∙
[L]m ;
n
1
E °,
Fe3+/Fe2+
=0,77+
0,059
1
1	0,059
3,16×103	1
lg 3
6,94×10-3
=0,69 В
При этом получаются следующие значения равновесного потенциа¬
ла Е при соответствующих объемах титранта:
V(KMnO4), мл:	90,0;	99,0;	99,9;	100.
Е, В:	0,75;	0,81;	0,87;	1,37.
Сравнение этих данных с приведенными в табл. 8.9, а также
сопоставление хода кривых (3) и (2) рис. 8.3, показывает увеличе¬
ние скачка титрования на кривой (3). Это происходит вследствие
0	Q,
уменьшения EF0e3+ /Fe2+ = +0,77 B до EF0e3+/Fe2+ = +0,69 B за счет
связывания в комплекс окисленной формы (Fe3+).
150

Объем рабочего раствора, мл
Рис. 8.3. Кривые окислительно-восстановительного
титрования 0,10 н. раствора FeSO4: 1 - 0,10 н. Ce(SO4)2; 2 ,3 - 0,10 н. KMnO4
в среде 1 н. H2SO4 (3 - в присутствии 1 М H3PO4)
Таким образом, анализ кривых редокс- титрования показывает, что:
■	при n1= n2 кривая симметрична относительно ТЭ (кривая 1);
■	при n1≠ n2 ЕТЭ смещен к ветви кривой, соответствующей паре
с большим Е0 (например, кривые 2, 3);
■	скачок титрования возрастает с увеличением DE = E02 - E01
или DE, т. е. зависит от факторов, влияющих на редокс-по-
тенциал (с ростом pH для реакции (2) величина скачка уменьша-
3+
ется; при связывании в комплекс ионов Fe величина скачка уве¬
личивается вследствие понижения Е до ТЭ).
Для окислительно-восстановительного титрования использу¬
ются индикаторы разных типов. При выборе окислительно¬
восстановительных индикаторов (табл. 8.14) необходимым усло¬
вием является попадание Еинд. и ЬЕинд. - интервала изменения его
окраски в границы скачка титрования.
151

8.5.3.	Расчет кривых титрования в методах осаждения
В индикаторных методах осадительного титрования наиболее
широко используются разные варианты аргентометрии (табл. 8.1 и
8.2). Значительно реже применяют титрование солями Hg22+ (мерку-
рометрия, индикаторы - дифенилкарбазид, бромфеноловый синий);
K4[Fe(CN)6] (индикатор - дифениламин) и др. Полнота связывания
определяемого вещества A титрантом B зависит от K0S образующего¬
ся малорастворимого соединения. Величина K0S определяет возмож¬
ность прямого титрования и влияет на величину скачка титрования.
Пример 8.26. Проведем расчет кривых титрования по методу
осаждения в координатах pM(A) - V(B) при образовании малорас¬
творимых соединений состава 1:1 на примере титрования 20,0 мл
0,10 М раствора NaCl 0,20 М раствором AgNO3.
Реакция титрования:
Cl- + Ag+ ⅛ AgCli, K = 1∕K0S (AgCl) = 1∕1,78×10-10 = 5,62×109.
Объем титранта в ТЭ (f = 100 %) составляет 10,00 мл (согласно
формуле 8.14). Формулы и результаты расчета (без учета разбавле¬
ния раствора) приведены в таблице 8.10, ход кривой титрования
представлен на рис. 8.4.
Таблица 8.10
Изменение pCl и pAg при титровании 20,00 мл 0,10 М раствора
NaCl 0,20 М раствором AgNO3
I(AgNOi)
Состав
раствора, %
Расчетные формулы
pCl =
=-lg[Cl-]
+
д ≤
М) "м
T
О- Il
мл
f, %
A
(Cl-)
B
(Ag+)
0
0
100
-
[A] = c⅛(A) × (100 f Ί
\ 100 ,
[B] = K0S /[A]
1
9
до т. э.
9,00
90
10
-
2
8
9,90
99
1
-
3
7
9,99
99,9
0,1
-
4
6
H
10,00
100
-
-
[A] = [B] vK
5
5
после т. э.
10,01
100,1
-
0,1
K0	K0
[A] = kS =	KS
] [B] с (B). {f-100∣
0( ) L 100 J
[B] = K /[A]
6
4
10,10
101
1
7
3
152

Окончание табл. 8.10
11,00
110
10
8
2
20,00
200
-
100
9
1
Анализ приведенных уравнений позволяет заметить, что скачок на
кривой осадительного титрования возрастает с уменьшением
K0S(AB), а также с увеличением концентрации титранта В и титруе¬
мого вещества А.
V (AgNO3), мл
Рис. 8.4. Кривые осадительного титрования 0,10 М раствора NaCl 0,20 М
раствором AgNO3: 1 - изменение pCl, 2 - изменение pAg
8.5.4.	Расчет кривых титрования в методе комплексонометрии
Комплексонометрическое титрование основано на способно¬
сти ионов металлов образовывать устойчивые комплексные со¬
единения с органическими полидентатными лигандами анионами
аминополикарбоновых кислот, из которых чаще всего использует¬
ся комплексон III (трилон Б, ЭДТА). Так называют двунатриевую
соль этилендиаминтетрауксусной кислоты (H4Y), кристаллогидрат
которой (Na2H2Y×2H2О) хорошо растворим в воде. В реакциях
ЭДТА проявляет себя как шестидентатный лиганд и образует бес¬
цветные октаэдрические комплексы состава МеY(n-4), т. е. реагиру¬
153

ет с ионами металлов в молярном отношении 1:1.
В комплексонометрии применяют металлохромные индика¬
торы - красители, способные образовывать окрашенные внутри-
комлексные соединения с ионами металлов: кислотный хром тем¬
но-синий, хромоген черный специальный ЕТ-00 (эриохромовый
черный Т), мурексид и др. В условиях титрования комплекс MeInd-
должен иметь окраску, резко отличающуюся от окраски свободного
индикатора, и прочность его должна быть значительно меньше
прочности комплекса МеY(n'4).
В частности, эриохромовый черный Т имеет синюю окраску
при рН 7-10. С катионами металлов образует комплексы красного
цвета, поэтому в ТЭ, вследствие перехода ионов металла из ком¬
плекса с индикатором в комплекс с ЭДТА, появляется синяя окра¬
ска свободного индикатора. В растворах ЭДТА устанавливается
равновесие между различными протонированными формами и де-
4-
протонированным анионом Y :
H4Y ⅛	H3Y-	+	H+	pKaι = 2,00,
H3Y- ⅛	H2Y2-	+	H+	pKa2 = 2,67,
H2Y2- ⅛	HY3	+	H+	pKa3 = 6,16,
HY3- ⅛	Y4-	+	H+	pKa4 = 10,26.
При pH 0 - 1,5 существуют незаряженные молекулы H4Y. Пол¬
ностью депротонированный анион Y4- образуется при pH ≥ 11, а при
3-
рН 8-9 преобладает HY . В связи с этим, комплексонометрическое
титрование проводят в присутствии буферов. Большая группа ионов
МП+ титруется в среде аммиачного буферного раствора с эриохромо-
вым черным Т. Поэтому для ряда катионов возможны побочные ре¬
акции комплексообразования: с NH3, c OH- и др. Их следует учиты¬
вать при выборе условий титрования и при вычислении условной
(см. разделы 2, 3, 4) константы реакции титрования К'= b'MY).
Реакцию образования комплексоната металла (титрования)
можно представить в упрощенном виде (упуская заряды):
M + Y ¾ MY.
При протекании побочных реакций M и Y их равновесные кон-
центрации выражают через аналитические и молярную долю частицы
(формулы (2.4), (2.5), (2.8)).
154

1
1+b1×[L]+b2 ×[L]2 +K+bn ×[L]n .
Значения aY4- при разных значениях рН приведены в табл. 7,
значения bn - в табл. 4 приложения. Условная константа равновесия
реакции титрования вычисляется по формуле (в случае Zn2+, Ni2+,
Cd2+ и др.):
[MY]
β c(M) - c(Y) b m,^ y' ' ·	(8.16)
Если ион Мп+ не вступает в побочные взаимодействия (Ca2+, Mg2+),
Ofan+ = 1 и формула (8.16) преобразуется в (8.17):
β'=-[MYL~=β.c^i 4-
c(M) ∙c(Y)	γ
(8.17)
Кривая титрования в комплексонометрии строится в координатах
рМ - K(B). Для вычисления рМ = -lg[M] ионов, участвующих в по¬
бочных реакциях, используют соотношение:
[M] = аМп+^с(М).
Пример 8.27. Рассмотрим построение кривых титрования в
среде аммиачного буфера (c(NH3) = 0,2 моль/л) с учетом разбавле¬
ния раствора:
1)	50,00 мл 0,1 М MgSO4 0,1 M ЭДТА при pH 7, 9 и 10;
2)	50,00 мл 0,01 M NiSO4 0,01 M ЭДТА при pH 10
(b(MgY2-) = 1,32×109 и b(NiY2-) = 4,17×1018).
Поскольку M и Y реагируют в соотношении 1:1, в обоих случаях
справедливо: УТЭ (Y) = 50,00 мл.
2+
Ион Mg не образует комплексов с NH3, поэтому аМп+ = 1.
2+
Для иона Ni необходимо вычислить cNi2+ по формуле (2.8), ис¬
пользуя табличные значения βn. Можно считать, что [NH3] = c(NH3)
2+
вследствие большого избытка по отношению к c(Ni ).
=	1

a2+ 1+4,7× 102 -0,2+6,2- 10 -0,22 + 2,5-10 -0,23 +3,0-107 -0,24 +1,3-10 -0,25 +1,1-10 -0,26 ,
cNi2+ = 8,3× 10 .
Используя табличные значения aγ4- , вычисляем для всех случаев β↑
β''(MgY2-) = βMgY2-)- Cγ4-;
β'NiY2-) = β (NiV2-)-αγ4-c⅛2+.
155

рН
7
9
10
aγ4-
. 1,8-10 4
5,2-10 2
0,35
β{MgY2-)
6,3∙105
6,9∙107
4,6∙108
/KNiY2 )
-
-
1,21∙1013
Далее определяем K(B) = К(ЭДТА) = K(Y) для точек кривых титро¬
вания и проводим расчеты рМ. При вычислениях руководствуемся
теми же правилами, как и для других типов реакций:
-	с(М) до ТЭ определяется оставшейся неоттитрованной частью;
-	в ТЭ общая концентрация всех форм М (кроме MY) равна об¬
щей концентрации протонированных форм Y и вычисляется через
условную константу β' (MY) и [MY] = c0(M)∙K(M)∕( K(M)+K(Y));
-	после ТЭ расчет с(М) проводится через β' (MY) и избыток
титранта.
Необходимые формулы и результаты расчетов приведены в
табл. 8.11, кривые титрования - на рис. 8.5.
Таблица 8.11
Данные для расчета и построения кривых титрования
растворов MgSO4 и NiSO4 раствором ЭДТА в условиях
примера 8.27
V(Y),
мл
Расчетные формулы
pH 7
pH 9	pH 10
pM = -lg[Mg2+]
aMg2+ = 1
pM =-lg[Ni2+]
αNi2+ = 8,3∙10
0
[M] = an+ -C0(M)
1,0
1,0
1,0
7,1
до т. э.
25,0
[M] a	V(M)∙ C0(M)-K(Y)* C(Y)
1,5
1,5
1,5
7,6
40,0
2,0
2,0
2,0
8,0
|M| aM.	K(M)+K(Y)
49,0
3,0
3,0
3,0
9,1
49,9
-
4,0
4,0
10,1
н
50,0
[M] = α	C0(m) - V(m)
3,6
4,6
5,0
12,8
' "'	' mn+ ∖β'∙ (K(M) + K(Y))
после т. э.
50,1
[M] -a	"":Mi	K(M)
-
5,1
6,0
15,5
m ■ β'∙ C(Y) (K(M) + K(Y))
C(Y) - C(Y)-K(Y)- C0(M)∙K(M)
( )	K(M)+ K(Y)
51,0
4,1
6,1
7,0
16,5
60,0
5,1
7,1
8,0
17,5
75,0
5,5
7,5
8,4
17,9
Анализ кривых титрования (рис. 8.5) и расчетных формул по¬
казывает, что:
156

·	pM не зависит от pH раствора до ТЭ, но зависит в ТЭ и после
ТЭ;
·	величина скачка титрования и положение ТЭ зависит от величи¬
ны pH - чем больше pH, тем больше скачок титрования;
·	на величину скачка титрования влияют концентрация ионов ме¬
талла и все факторы, определяющие ионное равновесие и константу
устойчивости комплексоната; чем больше· aγ4- и амп+, тем больше
скачок.
V (ЭДТА), мл
Рис. 8.5. Кривые комплексонометрического титрования MgSO4 (1-3) и
NiSO4 (4) при разных значениях рН: 7(1), 9 (2), 10 (3,4), создаваемых
аммиачным буфером с c(NH3) = 0,2 моль/л
Задачи для самоконтроля
При решении приведенных задач используйте данные табл. 8.12 и 8.14 для
выбора подходящих индикаторов кислотно-основного и окислительно-восстано¬
вительного титрования, где это возможно.
1.	Рассчитайте рН в области скачка (при f, равной 99,9 % и 100,1 %) кри¬
вой титрования 100 мл 0,01 н. NaOH: а) 0,01 н. HCl и б) 0,1 н. HCl. Как влия¬
ет концентрация титранта на величину скачка?
Ответ: скачок а ) от рН 9 до рН 5; б) от рН 9 до рН 4.
2.	Рассчитайте рН в ТЭ и в области скачка (при f, равной 99,9 и 100,1 %)
кривой титрования 100 мл 0,1 М NH3 0,1М HCl. Как влияет сила основания
на величину скачка (с учетом предыдущей задачи)?
Ответ: рНТЭ = 5,1; скачок от рН 6,2 до рН 4,0.
157

3.	Вычислите pH в точке эквивалентности при титровании 20 мл 0,20 М
раствора соли аммония в безводном этаноле 0,20 М раствором метилата на¬
трия, если для метанола Ksh = 2,0· 10-17; Ce(XH3) в метаноле (KBMem) = 1,0· 10-7.
Ответ: рН = 12,7.
4.	Рассчитайте значения рН в точках эквивалентности (без учета разбав¬
ления) при титровании 100 мл 0,10 М H3AsO4 0,10 M раствором NaOH. C ка¬
кой точностью можно оттитровать первый ион водорода в этих условиях?
Ответ: рНТЭ1 = 4,51; рНТЭ2 = 9,15; рНТЭ3 = 12,3; 99,45 %.
5.	Рассчитайте рВг в ТЭ и области скачка (при f равной 99,9 %, 100 % и
100,1 %) кривой титрования 100 мл 0,05 М раствора NaBr 0,1 М рабочим рас¬
твором AgNO3. Укажите способ установления ТЭ.
Ответ: в ТЭ рВг = 6,1; скачок рВг от 4,3 до 8,3.
6.	Рассчитайте (с учетом разбавления) рМ в ТЭ и области скачка (при f,
равной 99,9 %, 100 % и 100,1 %) кривой титрования 100 мл 0,01 М раствора
Са^О3)2 0,01 М раствором ЭДТА при рН 9. Вычислите условную константу
равновесия реакции. Ответ: β' =2,0×109; рМТЭ = 5,8; скачок рМ от 5,3 до 6,3.
7.	Рассчитайте Е в ТЭ и области скачка (при f, равной 99,9 %, 100 % и
100,1 %) кривой титрования 100 мл 0,05 М раствора FeSO4 0,1 М рабочим
раствором Ce(SO4)2. Определите Cfwe(Ce(SO4)2).
Ответ: в ТЭ Е =1,25В; скачок от Е = 0,95В до Е = 1,56В; f3kβ(Ce(SO4)2 = 1.
8.	Рассчитайте Е в ТЭ и в области скачка (при f, равной 99,0 %, 100 % и
101 %) кривой титрования 100 мл 0,05 М раствора H2SO3 0,05 М рабочим
раствором KMnO4 в присутствии 1 н. H2SO4. Вычислите K(KMnO4) в ТЭ и
молярную массу эквивалента H2SO3 в данной реакции.
Ответ: V = 40,0 мл; ЕТЭ = 1,13В; скачок от 0,26 до 1,47 В;fκβ. (H2SO3) = 1/2.
8.6.	Индикаторные погрешности титрования
Как было сказано выше, при несоответствии интервала пере¬
хода индикатора и ТЭ, титрование заканчивается при так называе¬
мой конечной точке титрования - КТТ, что является причиной ин¬
дикаторных погрешностей титрования (ПТ). Титрование может
быть закончено до ТЭ или после ТЭ, в результате чего возникают
отрицательные (недотитровывания) и положительные (перетитро-
вывания) систематические ПТ. Их можно оценить по кривым тит¬
рования или расчетным способом (графический способ - в реко¬
мендованной учебной литературе).
158

Расчет индикаторных погрешностей кислотно-основного
титрования
Согласно ионно-хромофорной теории индикаторов, интервал
перехода окраски индикатора DрН ≈ рКа ± 1 (табл. 12). Середина
области перехода окраски (при этом рН близко к рКа) называется
показателем титрования с данным индикатором или рТ индикатора.
Индикаторные погрешности отсутствуют, когда рТ индикатора
практически совпадает с рН в ТЭ. Основой для выбора индикатора
является расчет и построение кривой титрования, определение
области скачка и рН в ТЭ.
Таблица 8.12
Важнейшие кислотно-основные индикаторы
№
Индикатор
Интервал рН
перехода
р^«
(I = 0)
рТ
Изменение
окраски
1.
Тимоловый
синий
1,2 - 2,8
1,65
2,0
Красная - желтая
2.
Метиловый
оранжевый
3,1 - 4,4
3,50
4,0
Красная - желтая
3.
Бромкрезоловый
зеленый
3,9 - 5,4
4,90
4,9
Желтая - синяя
4.
Метиловый
красный
4,4 - 6,2
5,00
5,5
Красная - желтая
5.
Бромкрезоловый
пурпурный
5,2 - 6,8
6,4
6,0
Желтая -
фиолетовая
6.
Бромтимоловый
синий
6,0 - 7,6
7,30
7,0
Желтая - синяя
7.
Феноловый
красный
6,4 - 8,2
7,90
7,5
Желтая - красная
8.
Тимоловый
синий
8,0 - 9,6
9,20
8,5
Желтая - красная
9.
Фенолфталеин
8,2 - 9,8
9,5
9,0
Нет - красная
10.
Тимолфталеин
9,3 - 10,5
9,6
10,0
Нет - синяя
При правильно выбранном индикаторе индикаторная ПТ не
должна превышать заданную погрешность измерения объема рас¬
твора в титриметрии. Типы (виды) индикаторных ПТ кислотно-
159

основного титрования и названия, встречающиеся в разных учебни¬
ках и сборниках задач, происхождение погрешностей и формулы для
расчета приведены в табл. 8.13. Формулы легко выводятся из опре¬
деления погрешности титрования как отношения недотитрованно-
го или перетитрованного количества кислоты или основания к пер¬
воначально взятому для титрования (то есть к произведению
c0(Λ)∙K(Λ)). Погрешность выражают в %, а вид и знак устанавлива¬
ют по ходу процесса (кривой) титрования и составу раствора в КТТ
(табл. 8.13, примеры 8.28 и 8.29).
Таблица 8.13
Индикаторные погрешности кислотно-основного титрования
Тип ПТ
(обозначение,
название)
Происхождение, знак
Формула
для расчета ПТ(%)
Н+-погрешность
(Н+-ошибка),
протонная,
водородная.
В растворе избыток
сильной кислоты:
1)	перетитровано
сильной к-той (+);
2)	недотитрована
сильная к-та (-).
ПТ-± 10’рр ∙(Ka + Kb)-100
с0, А ∙KA
ОН--погрешность
(ОН--ошибка),
гидроксидная
В растворе избыток
сильного основания:
1)	перетитровано
щелочью (+);
2)	недотитрована
щелочь (-).
ПТ = ± 10-'14-рТТ ∙ (Ka + Kb)∙100
с0, А ∙KA
НА-погрешность
(НА-ошибка),
кислотная
В растворе избыток
слабой кислоты:
недотитрована
слабая к-та (-)
ПТ	10<pKa - рТ ) ∙ 100
1 + 10 (PKa - Pp)
(ПТ - -10 (pKa - рТ ) ∙100
при 10 (pKa - рТ > << 1)
МеОН-
погрешность
(МеОН-ошибка),
основная
В растворе избыток
слабого основания:
недотитровано
слабое основание (-)
10 (Pκb + Pp-14) ∙ 100
ПР	1 + 10< Pκb + Pp-∣4)
(ПТ --10'pκb+рТ-14) ∙100
при 10 (PKb+Pp-14) << 1)
160

Пример 8.28. Выберите подходящие индикаторы, определите
тип индикаторных погрешностей и рассчитайте ПТ при титровании
а) HCl и б) CH3COOH рабочим раствором NaOH в условиях приме¬
ра 8.21, если считать относительную погрешность измерения объе¬
ма 0,4 %.
Решение: а) как следует из табл. 8.4 и рис. 8.1(1), для слу¬
чая титрования HCl при погрешности определения объема 0,4 %
область скачка на кривой титрования соответствует изменению рН
от 3,4 до 10,9, а рНТЭ равен 7,0. Следовательно, для титрования
можно выбрать индикаторы от № 2 до № 10 (табл. 8.12), т. к. их рТ
и интервалы перехода окраски находятся в области скачка кривой.
Однако используемые для расчета ПТ формулы показывают, что чем
ближе рТ и рНТЭ, тем меньше ПТ. «Идеально» подходит бромтимо¬
ловый синий, поскольку его рТ 7 практически совпадает с рНТЭ.
Рассчитаем величину ПТ с двумя индикаторами: с рТ < рНТЭ и
с рТ > рНТЭ и проверим их пригодность для титрования в заданных
условиях.
С индикатором метиловым красным (рТ 5,5 < рНТЭ) в растворе
остается неоттитрованная сильная кислота, следовательно, возни¬
кает протонная ошибка со знаком «-» (см. формулы в табл. 8.13):
ПТ =
 10 p - (Va + VB) -100
с0,А ×VA
_ 10_5·-5 ∙ (50 + 25) -100
0,1 ∙ 50
= - 0,005 %.
С индикатором фенолфталеином (рТ 9,0 > рНТЭ) в растворе -
избыток сильного основания, в результате чего ПТ представляет
собой ОН- - ошибку (гидроксидную)	со знаком «+»:
ПТ=
+ 10 4- ∙ (Va + VB) -100
С0,А ∙ VA
10_(14_ 9)
∙ (50+ 25) ∙100
0,1 ∙ 50
= + 0,015 %.
+
В данном случае оба индикатора пригодны, поскольку вычис¬
ленные значения ПТ не превышают заданную погрешность титро¬
вания (0,4%), но с метиловым красным систематическая индика-
торная погрешно сть меньше.
б) При титровании CH3COOH (табл. 8.5, рис. 8.1(2)) для той
же точности титрования (99,6 %) величина скачка меньше и состав¬
ляет 7,2 - 10,9, а рНТЭ - 8,9. Круг пригодных индикаторов сужается
до № 7 - № 9. Для индикаторов с рТ > рНТЭ, как и в случае (а), ПТ
соответствует ОН-- ошибке (гидроксидной) со знаком «+».
161

Например, при выборе фенолфталеина (рТ = 9,0):
ПТ =
+10-(14-рТτ · (Va + VB ) ·100
c0,A ' VA
∣0 ιl490i × (50+ 25) ×100
0,1· 50
+ 0,015 %,
а при выборе тимолфталеина (рТ = 10,0) погрешность возрастает в
10-(14-10,0) ·(50+25)·100
10 раз:	∏T = +	0TT5δ— 	= + 0>15 %∙
Выбор фенолфталеина приводит к меньшей индикаторной погреш¬
ности титрования CH3COOH, но могут использоваться оба индика¬
тора.
При титровании с индикаторами, для которых рТ < рНТЭ, в
растворе остается неоттитрованная слабая кислота, т. е. присутст¬
вует НА-ошибка (кислотная) со знаком «-» (см. табл. 8.13). Если
использовать индикатор бромтимоловый синий (рТ 7,0), то вычис¬
ленная ПТ не удовлетворяет заданной точности, индикатор не при-
годен:
ПТ =
10p -рТ) · 100
1 +10 (pKa - рТ)
10(4'76-7'0; ×100
1 +10(4,76-7,0)
10 -2,24 · 100
1 +10 - 224
= -0 57% ,
или при проведении расчета по приближенной формуле:
ПТ = - 10(pKa-рТ × 100 =- 10(4,76-7,0; × 100 = -0,58 % .
Пример 8.29. Какой индикатор позволяет оттитровать 0,1000 М
гидразин (pKb = 6,03) 0,1000 М раствором HCl с меньшей погреш¬
ностью: бромкрезоловый пурпурный (рТ 6,0) или метиловый крас¬
ный (рТ 5,5)?
Решение. Реакция титрования:
^Н4(основание) + H+ = ^Н5+(сопряженная кислота)
приводит к образованию слабой сопряженной кислоты N2H5+ с
рКа =14 - pKb. Тогда рНТЭ < 7 и вычисляется с учетом того, что
c(N2H5+) = c0(N2H5+)∕2 и рКа = 7,97:
рНТЭ = 1/2(рКа - lg c(N2H5+)) = 1/2(7,97+1,3) = 4,64.
Сравнивая рТ индикаторов и рНТЭ, видим, что в обоих случаях ос¬
тается неоттитрованный гидразин, поэтому для оценки ПТ рассчи¬
тываем МеОН-ошибку (основную) со знаком «-». С бромкрезоло¬
вым пурпурным (рТ 6):
162

10 ( pKb + рТ _ 14 ) × 100
1 + 10 (pKb + pt _14)
ПТ = _
10 (6,03+6,0_14 ) ×100
1 + 10 (6,°3 + 6,0_ 14)
= _1,1 % ;
и с метиловым красным (рТ 5,5):
ПТ = _
10 (6,03 + 5,5_14) ∙ 100
1 + 10 (6,03 + 5,5_ 14)
= _0,34 %
Из предложенных индикаторов метиловый красный позволяет про¬
вести титрование гидразина с меньшей погрешностью.
Расчет индикаторных погрешностей
окислительно-восстановительного титрования
При использовании окислительно-восстановительных (редокс)
индикаторов потенциал в ТЭ (ЕТЭ) может не совпадать с потенциа¬
лом ЕКТТ, который связан с Е0инд. (табл. 8.14) и интервалом перехода
его окраски ∆E.
Таблица 8.14
Примеры распространенных окислительно-восстановительных
индикаторов
№
Индикатор
еЕ, в
Окраска
окисленной
формы
Окраска
восстановлен¬
ной
формы
1.
2,2' -Дипиридил
(комплекс с рутением)
+1,33
Бесцветная
Желтая
2.
Нитрофенантролин
(комплекс с Fe2+)
+1,25
Бледно-голубая
Красная
3.
N-фенилантраниловая
кислота
+1,08
Фиолетово¬
красная
Бесцветная
4.
о-Фенантролин
(с Fe2+ - ферроин)
+1,06
Бледно-голубая
Красная
5.
2,2' -Дипиридил
(комплекс с Fe2+)
+0,97
Бледно-голубая
Красная
6.
о-Дианизидин
+0,85
Красная
Бесцветная
7.
Дифениламинсульфонат
+0,84
Красно¬
фиолетовая
Бесцветная
8.
Дифенилбензидин
+0,76
Фиолетовая
Бесцветная
9.
Дифениламин
+0,76
Фиолетовая
Бесцветная
10.
Метиленовая синь (рН 0)
+0,53
Синяя
Бесцветная
11.
Индигокармин (рН 0)
+0,29
Синяя
Бесцветная
163

Полуреакция восстановления и интервал перехода индикатора:
∆E = Еинд± 0,059/n.
Indox+ ne = Indred,
Наиболее часто в полуреакции восстановления (окисления) индика¬
тора участвуют 2 электрона. Для индикаторов № 1 - № 6 Е0инд. сла¬
бо зависит от рН. При расчете ПТ необходимо:
-	вычиелить облаать Cκa4κa и значение ЕТЭ (см. разд. 8.5.2);
-	выбрать подходящий индикатор (разд. 8.5) c u3βeCTHbiM
Еинд, вычислить его интервал перехода ∆E и установить ЕКТТ,
т. е. потенциал, соответствующий окончанию изменения ок-
ражи индикатором;
-	сраβнить ЕКТТ C ЕТЭ для выбора редокс-nары учаотников реакции
титрования и уравнения Нерн^а для расчета ПТ.
Например, если ЕКТТ < ЕТЭ при титровании βосстаноβителя (при¬
мер 8.30-а), то реакция не завершена; из уравнения Нернста для по¬
луреакции титруемого компонента находят (объемы раствора в чис¬
лителе и знаменателе одинаковы):
[Red]	количество неоттитрованного восстановителя
Сумма числителя и знаменателя здесь составляет 100 % титруемого
вещества. Индикатор считается пригодным, если ПТ не превышает
0,1 - 0,2 %.
Пример 8.30. Выберите подходящие индикаторы, определите
тип индикаторных погрешностей и рассчитайте ПТ при титровании
2+	4+
раствора соли Fe раствором соли Се .
Решение. Как следует из табл. 8.8 и рис. 8.3 (кривая 1, пример
8.25), область скачка (при относительной погрешности измерения объ¬
ема 0,1 %) на кривой титрования 0,95 - 1,26 В, а ЕТЭ = 1,10 В. Следова¬
тельно, для титрования можно выбрать индикаторы от №3 до № 5
(табл. 8.14).
Выберем для рассмотрения порядка расчета два индикатора:
а)	с Еинд < Етэ - 2,2'-дипиридил, для которого Етд = +0,97 В;
б)	с Е0инд > ЕТЭ, например нитрофенантролин (Е0инд = +1,25 В).
В случае а) интервал перехода индикатора:
∆E = Е>ияд.± 0,059/n = 0,97 ± 0,059/2 = 0,97 ± 0,03;
∆E = 0,94 - 1,0 В.
164

Изменение окраски заканчивается при ЕКТТ = 1,0 В. В раство¬
ре остаются неоттитрованными ионы Fe2+ (оттитрованные ионы -
ионы Fe3+). Для расчета ПТ используем уравнение Нернста для ре-
докс- пары титруемого компонента (Fe3+/Fe2+):
[Fe3+]	[Fe3+ ]
ЕКТТ = 1,0 В = E°Fe3+ /Fe2+ + 0,059lg[--2+] = 0,77 + 0,0591g[--2+];
[Fe ]	[Fe ]
1g[Fe+ ] 1,0 _ 0,77	[Fe3+ ]
g[Fe2+ ]	0,059	3,9; [Fe2+ ]	10 '/1.
[Fe3+] + [Fe2+] = 103,9 + 1 ≈ 103,9.
Тогда: ПТ = - [Fe2+]/([Fe3+] + [Fe2+]) = - 1/103,9 = - 1,26·10-4 (- 0,013 %).
В случае б) интервал перехода индикатора нитрофенантролина
P 2+
в виде комплекса с Fe составляет:
∆E = Еинд,± 0,059/n = 1,25 ± 0,059/2 = 1,25 ± 0,03;
∆E =1,22 - 1,28 В.
Изменение окраски заканчивается при ЕКТТ = 1,28 В и раствор
перетитровывается. В этом случае ПТ имеет положительный знак и
рассчитывается по уравнению Нернста для редокс-пары, образуе-
4+
мой титрантом С- .
Тогда количество Ce3+ (после ТЭ образования Ce3+ не происхо¬
дит) соответствует количеству взятых для титрования ионов
2+ 4+
Fe , а количество Се - их перетитрованному количеству.
[Ce4+ ]	[Ce4+]
Ектт = 1,28 В = Е0 Се/ Се3+ + 0,0591g[c-3+] = 1,44 + 0,0591g[c-3+j;
1g
[Ce4+ ] =
[Ce3+ ]
1,28 _ 1,44
0,059
[Ce4+]	-2,71
ПТ = т—= 10-2,71∕1 = + 0,00194 или + 0,19 %.
[Ce3+]
Таким образом, оба выбранных индикатора оказались приемлемыми.
Расчет индикаторных погрешностей комплексонометрического
титрования
В конечной точке титрования общие концентрации опреде¬
ляемого иона с(М) и титранта e(Y) можно представить выражения¬
ми (для упрощения записи в общем виде упустим заряды ионов):
с(М) = с'(M) + [MY],	(8.18)
165

C(Y) = C'(Y) + [MY],	(8.19)
где C'(M) - концентрация всех форм определяемого иона, кро¬
ме входящего в комплекс MY; с '(Y) - концентрация всех форм тит¬
ранта, кроме входящего в комплекс MY.
Условные константы устойчивости (см. выражение 8.16) свя¬
зывают [MY], C'(M), C'(Y):
[MY]
β- b(MY)-aMM ∙ a - C,(M)-C,(Y) ; [MY] = β⅛'(M)∙ c'(Y);
[MY] _ C(M) - Cz(M)
c'(y) -ом/ = c'(m)-У.	(8.20)
Отсюда относительная погрешность титрования (ПТ) опреде¬
ляется выражением (с учетом (8.18) и (8.19)):
ПТ - c (Y)- c (M) = C(Y)- C(M)
c(M)	c(M)
Подставляем в это уравнение выражение для c'(Y) (8.20):
C(M)-Ck(M)-c,(m)
ПТ- C(M)∙β'	- c(M)-C(M) - c(M)
c'(M) ∙β' - c(M) c(M) .
c(M)
Вблизи ТЭ с'(М) очень мала, поэтому (с(М) - с'(М)) » с(М),
1
C(M)
следовательно:	ПТ - , „„ п,
c (M) - β
’ c(M) .	(8.21)
Выражение (8.21) тождественно выражению: ПТ = f - 1. Если
конечная точка титрования находится после точки эквивалентности
(степень оттитрованности f > 1), то относительная погрешность бу¬
дет положительной. В случае недотитровывания, т. е. когда конеч¬
ная точка титрования будет зафиксирована с помощью индикатора
до точки эквивалентности (f < 1), ПТ будет со знаком «-».
Конечная точка титрования определяется интервалом перехо¬
да окраски индикатора (интервалом рМ, в котором индикатор ме¬
няет свою окраску):
DрM = lgβ{MInd) ±1, где рМ = - lg[M] и β(MInd) = /(MInd)∙ om- αnd-.
Интервал перехода окраски DрM индикатора эриохром чер¬
ный Т (рК^ИМ2-) = 11,5), образующего комплексы с ионами ме-
2+ 2+
таллов при рН 10, составляет для ионов: Co - (18,5 ± 1); Cu -
166

(19,9 ± 1); Pb2+ - (11,7 ± 1); Cd2+ - (10,8 ± 1); Zn2+ - (10,8±1); Mg2+
- (5,5 ± 1); Ca2+ - (3,9 ± 1).
Пример 8.31. Рассчитайте погрешность титрования 0,10М
раствора MgSO4 0,10 М раствором ЭДТА в присутствии индикатора
эриохром черный Т в аммиачном буферном растворе при рН 10 и
c(NH3) = 0,2 моль/л (см. условия в примере 8.27).
Решение . В данных условиях aMg2+ = 1,	pMgτ3 = 5,
2- 8
β '(MgY ) = 4,6·10 (пример 8.23). Интервал перехода окраски ин¬
дикатора: DpMg = 5,5 ± 1 или в интервале концентраций магния от
3,6·10-5 до 3,6·10-7. Точка эквивалентности попадает в указанный
2+
интервал, индикатор считается пригодным для титрования Mg ,
КТТ наступает после ТЭ, когда с'(Mg) = [Mg2+] = 3,6· 10-7 моль/л.
Погрешность титрования Mg2+ с «эриохром черным Т»:
ПТ=- 2T⅛	2— c(Mg+) =	71	T - 3,6×10 = 6,03×10-3 (0,6%).
c'(Mg2+) √(MgY^) c(Mg2+) 3,6∙10-7 · 4,6×108	0.1
Пример 8.32. Докажите возможность использования индика-
то-ра эриохром черный Т для титрования 0,010 М раствора
Zn(NO3)2 0,010 М раствором ЭДТА при рН =10 и c(NH3) = 0,10
моль/л. Рассчитайте погрешность титрования при использовании
этого индикатора.
2-
Решение.1. Рассчитаем условную константу β ' (ZnY ).
Общие константы устойчивости для аммиачных комплексов Zn2+
(табл. 4 приложения): β1 = 1,6·102, β2 = 1,8·104, β3 = 6,5·106, β4 = 7,8·108.
Для свободных ионов Zn2+ по формуле (2.8) предварительно рас¬
считаем aZn2+:
aZn2+ = 1/(1+1,6·102·0,1+1,8·104·10-2+6,5·106·10-3+7,8·108·10-4) =
1,840-5.По табл. 7 и табл. 4 приложения находим αΥ4- = 3,5·10-1,
lgβ(ZnY2-) = 16,26. Константа устойчивости комплекса Zn2+ с ЭДТА
при заданных условиях с учетом выражения (8.16):
β ' = 1016,26·1,8·10-5·3,5·10-1 = 1,15·1011.
В точке эквивалентности:
c'(Zn2+) =
C0(Zn2+) · V (Zn2+)
∖b'× (V (Zn2+) + V (Y))
0,01
\ 1,15 · 1011 · 2
= 2,085 ·10-7 моль/л,
167

pZn = -1g[Zn2+] = -1g (ε'(Zn2+) × αzn.+) = -1g( 2,085 × 10"7 × 1,8× 10-5) = 11,4.
Интервал перехода окраски индикатора эриохром черный Т в
случае титрования ионов цинка при рН 10: DpZn = 10,8 ± 1, т. е. от
9,8 до 11,8 или от 1,6·10-10 до 1,6·10-12 моль/л. Точка эквивалентно¬
сти попадает в интервал концентраций, при которых индикатор ме¬
няет свою окраску. Следовательно, эриохром черный Т пригоден
2+
для титрования Zn при заданных условиях.
2. Конечная точка титрования наступает при [Zn2+], рав¬
ной 1,6·10-12 моль/л, отсюда концентрация всех форм Zn2+, за ис¬
ключением связанных в комплекс с ЭДТА, составляет:
c'(Zn2+) = [Zn2+]∕azn2+ = 1.6-10 12/1,8· 10 5 = 8.9· 10 8 моль/л.
ПТ =	1	c(Zn ) =
c'(Zn2+) b(ZnY' ) c(Zn2 +)
	1

8,9 ×1ff8 ×1,15 ×1011
_ 8,9 -H∣'
0,01
=8,9×10-5 (0,01%).
Задачи для самоконтроля
1.	Определите вид, знак и величину индикаторной погрешности титрова¬
ния 100 мл 0,100 М раствора НСООН 0,100 М раствором NaOH с бромтимо¬
ловым синим.	Ответ: кислотная, - 0,056 %.
2.	Определите вид, знак и величину индикаторных погрешностей титро¬
вания 100 мл 0,100 М раствора KCN 0,100 М раствором HC1 а) с бромтимо¬
ловым синим, б) с метиловым оранжевым.
Ответ: а) основная, - 0,50 %; б) протонная, + 0,200 %.
3.	Определите вид, знак и величину индикаторной погрешности титрова¬
ния 20 мл 0,100 М раствора аскорбиновой кислоты 0,100 М раствором NaOH
в присутствии фенолфталеина, если ее рКа1 = 4,04 и рКа2 = 11,34.
Ответ: гидроксидная, + 0,01 %.
4.	Рассчитайте величину скачка титрования 0,1000 М раствора метилами¬
на 0,2000 М HC1 при относительной погрешности измерения объема 0,1 % и
установите пригодность индикаторов для титрования: фенолфталеина и
бромкрезолового зеленого. Ответ: DрН 3,53; - 2,45% (не пригоден); +0,02 %.
5.	Рассчитайте индикаторную погрешность титрования 100 мл 0,05 М
раствора соли железа (II) раствором дихромата калия с молярной концентра¬
цией эквивалента 0,05 моль/л в кислой среде а) с дифениламином; б) с фер¬
роином.	Ответ: а) - 60,5 %; б) - 0,001 %.
168

6.	Предложите схему расчета индикаторной погрешности осадительного
титрования NaCl по методу Мора. Рассчитайте индикаторную погрешность
титрования 20 мл 0,0500 М NaCl 0,0500 М раствором AgNO3, если концен¬
трация индикатора K2CrO4 1∙10-3 моль/л и κ0S(Ag2CrO4) = 1,1∙10-12.
Ответ: 0,13 %.
7.	Докажите возможность использования индикатора эриохром черный Т
для титрования 0,5 М раствора Cd(NO3)2 0,5 М раствором ЭДТА при рН 10 и
C(NH3) = 1 моль/л. Рассчитайте погрешность титрования при использовании
этого индикатора.	Ответ: 0,0049 %.
169

ГЛАВА 9. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
КОЛИЧЕСТВЕННОГО АНАЛИЗА
При получении результатов количественного анализа, как пра¬
вило, проводят несколько аналитических операций, начиная с отбо¬
ра и подготовки проб, используют несколько последовательно из¬
меренных величин. Каждое измерение физической величины, каж¬
дая операция вносят свой вклад в общую погрешность результата
анализа. Например, любое титриметрическое определение включа¬
ет в себя: 1) погрешность определения титра рабочего раствора, ко¬
торая зависит от точности взвешивания и правильности измерения
объема; 2) погрешность титрования анализируемого вещества, за¬
висящую от правильности измерения объемов и правильности ус¬
тановления точки эквивалентности с помощью индикаторов (инди¬
каторные ошибки титрования). Погрешности необходимо уметь
выявлять, оценивать, знать и использовать способы их уменьшения.
Например, в титриметрических методах анализа стремятся к отно¬
сительной погрешности, не превышающей 0,1 %, в гравиметриче¬
ских - 0,05 %.
Оценка погрешностей (ошибок) результата связана с требова¬
ниями к точности химического анализа, являющейся одной из его
метрологических характеристик.
9.1.	Классификация и оценка погрешностей
количественного анализа
По способу вычисления различают абсолютную Dx и отно¬
сительную D (ранее d) погрешности.
Если среднее арифметическое значение x для n полученных
результатов анализа составляет:
x - (x1 + x2 + x3 +... + xn)/n = ∑xi /n,
то абсолютную погрешность выражают как
Dx - x - m,
где m - истинное содержание определяемого компонента (напри¬
мер, известное для стандартного образца или контрольной пробы).
Очевидно, что абсолютная погрешность может быть положи¬
тельной или отрицательной, в зависимости от того, каким полу¬
170

чился результат: завышенным или заниженным по сравнению с ис¬
тинным (рис. 9.1).
Относительная погрешность может быть выражена в долях
или процентах и обычно не имеет знака:
d=∣(j-μ)/m=D∣/m или d,% = ∣(χ-m)∣×ιoo/m = D∣*100/μ.
По происхождению погрешности делят на систематические,
случайные и промахи (грубые ошибки).
Погрешность определения, обусловленная постоянно дейст¬
вующей причиной, неизменная во всех измерениях, сохраняющая
знак от опыта к опыту или закономерно изменяющаяся, называется
систематической погрешностью. Погрешность, случайным обра¬
зом изменяющаяся от опыта к опыту, называется случайной по¬
грешностью. Грубые погрешности или промахи резко искажают ре¬
зультат анализа, вызываются небрежностью и обычно легко обна-
руживаются.
а)
Воспроизводимость
•_о	∙
.∙	∙.
П равильность
©_®
х 1	х3
X2 X	Х5
х 4	μ
б)
-·-·— о ·—·—·	©	®
Xi Хз	X X2	X4	X5	μ
в)
•—·- о	©-·—·
Х4 X5 X Xi μ Хз Х2
г)
•-•©-О-·—·
X3 (промах)
xi x5 μ	X	x2 x4
Рис. 9.1. Воспроизводимость и правильность химического анализа.
Результаты: а) невоспроизводимы и неправильны; б) воспроизводимы, но не¬
правильны; в) воспроизводимы и правильны; г) воспроизводимы и правиль¬
ны, но есть промах
171

С систематическими погрешностями связана правильность
анализа, со случайными погрешностями - воспроизводимость.
Правильность и воспроизводимость являются метрологическими
характеристиками анализа и входят в понятие «точность анализа».
Воспроизводимость результатов анализа характеризует
рассеяние единичных результатов относительно среднего.
Правильность характеризует отклонение полученного ре¬
зультата от истинного и показывает, насколько близка к нулю
систематическая погрешность. Систематические погрешности
выявляют и устраняют. Если же устранение невозможно, то при
постоянном значении систематической погрешности ее учитывают,
вводя поправку. Для выявления используют различные приемы и
методы, например “введено - найдено”, анализ стандартного об¬
разца, “двойной или тройной добавки”.
Оценка случайных погрешностей проводится методами ма¬
тематической статистики. В обычной практике выполняют ограни¬
ченное число параллельных измерений n (обычно 3-5), называемое
выборочной совокупностью данных или просто выборкой (в отли¬
чие от генеральной совокупности - при п ® ¥). При n < 20 матема¬
тическую обработку результатов проводят с использованием рас¬
пределения Стьюдента, связывающего вероятность попадания ве¬
личины в данный доверительный интервал и объем выборки п.
Среднее для ряда параллельных определений, x = ∑ xi / n, является
наиболее вероятным значением измеряемой величины.
Характеристики случайной погрешности (воспроизводимости) для
2
выборки: выборочная дисперсия s (или V) , стандартное отклоне¬
ние s и относительное стандартное отклонение sr:
i=n
∑(xi - x)2
*2 = i=1

n -1	’
*=1
∑ (xl - x)2
i=1

n -1	,
* ×100 о/
*r =	Z—,%.
X
2
С ними связаны Дисперсия среДнего sx (или Vx) и стандартное от-
∑ (X1 - X )2
*2 — V — i=1

клонение среднего sx:	** = vx = n(n -1) ,
∑ (x - x )2
i=1
* = V = 1 —

* v x )|	n(n -1)	.
При обработке данных химического анализа определяют гра-
172

ницы Доверительного интервала C = x- μ, вводя число степеней
свободы f = n - 1.
Доверительный интервал (С) - это интервал значений, в кото¬
ром для данного вида распределения случайных величин (при от¬
сутствии систематических погрешностей), при заданной довери¬
тельной вероятности P и числе степеней свободы f лежит истинное
значение определяемой величины:
		t P f ' s
x - m = ± —,	= с.
^4n	'
Доверительная вероятность попадания величины внутрь довери¬
тельного интервала в химическом анализе принята равной 0,95 или
95 %. Это означает, что в рассчитанный интервал попадут 95 из 100
значений. Коэффициенты tP,f - коэффициенты нормированных от¬
клонений Стьюдента приведены в табл. 8 приложения. Зависимость
tP,f от f показывает, что с возрастанием числа степеней свободы, т. е.
числа параллельных результатов, увеличивается и точность анали¬
за, поскольку доверительный интервал характеризует воспроизво¬
димость и, в какой-то мере, правильность результатов химического
анализа. С учетом доверительного интервала истинное значение
m = x ± p ,f
(9.1)
представляют выражением:
t P f · S

-J=— = x ± C.
√n
Оценка промахов (выбраковка результатов). Перед обра¬
боткой данных методами математической статистики необходимо
выявить промахи и исключить их из числа обрабатываемых резуль¬
татов. Для выявления промахов используют различные критерии, в
частности, Q-критерий. Проверку соответствия Q-критерию про¬
водят следующим образом. Все параллельные результаты распола¬
гают в последовательности их убывания или возрастания. При этом
(xmax, - xmin.) = R - размах варьирования. Затем рассчитывают Qkn:
Оэксп.	(хподозрителъное - xcocedHee)/R	(хподозрителъное — хсоседнее)/(хтах. - xmin. ) (9.2)
и сравнивают с критическим значением Qma6n при доверительной ве¬
роятности 0,90 (табл. 9 приложения).
Если О)ксп. < Qma6n., то промах отсутствует и подозрительный ре¬
зультат оставляют в составе выборки. Если же О)ксп. > Qma6n., то по-
173

дозрительное значение является промахом, грубой погрешностью;
его отбрасывают.
Q-критерий рекомендуется применять к выборкам с n ≥ 5. При
малой выборке (n = 3 - 4) заметно отличающийся от других резуль¬
тат просто отбрасывают, а определение повторяют и после этого оце¬
нивают случайную погрешность. Если n ≥ 10, промахи можно уста¬
новить с помощью 3s - критерия, проверяя для каждого отклонения
∣dz∙∣ = xi - x выполнение условия ∣di∙∣ £ 3s, позволяющего оставить ре¬
зультат в составе выборки.
Пример 9.1. Контрольный раствор соли кальция имеет
концентрацию с (1∕2CaCl2), равную 0,1056 моль/л. Студентом
было получено методом перманганатометрии среднее значение
x = с (1∕2CaCl2) = 0,1040. Вычислите абсолютную и относи¬
тельную погрешности.
Решение. Абсолютная погрешность результата:
∆x = x - μ = 0,1044 - 0,1056 = - 0,0012.
Относительная погрешность:
Δ = ∣∆x∣ /μ = 0,0012/0,1056 = 0,0114 или 1,14 %.
Пример 9.2. При определении содержания аскорбиновой ки¬
слоты в пробе картофеля по новой методике пробоподготовки по¬
лучены следующие результаты (мг/100 г): 14,50; 14,43; 14,54; 14,45;
14,44; 14,52; 14,58; 14,40; 14,25; 14,49. Оцените:
а)	наличие грубых погрешностей (промахов);
б)	воспроизводимость результатов анализа.
Решение.
а) наличие промахов оценим по Q-критерию. Представим экс¬
периментальные данные в порядке возрастания: 14,25; 14,40; 14,43;
14,44; 14,45; 14,49; 14,50; 14,52; 14,54; 14,58. Проверим подозри¬
тельные значения 14,25 и 14,58. Вычислим Q-критерий для этих ве¬
личин:
Qwcrii = (14,40 - 14,25)∕(14,58 - 14,25) = 0,45;
Qwcni = (14,58 - 14,54)∕(14,58 - 4,25) = 0,12.
Из табл. 9 приложения при P = 0,90 и n = 10 Qma6j = 0,41;
174

Q^m1 > 0,41, a Q3κcn.2< 0,41, следовательно, значение 14,25 не¬
достоверно и его исключаем, сокращая объем выборки до n = 9.
б) после исключения промаха найдем среднее и характеристи¬
ки воспроизводимости: дисперсию s2, стандартное отклонение s и
относительное стандартное отклонение sr:
x =(14,40+14,43+14,44+14,45+14,49+14,50+14,52+14,54+14,58) / 9 = 14,48;
s=
0,082 + 0,052 + 0,042 + 0,032 + 0,012 + 0,022 + 0,042 + 0,062 + 0,102
9-1
=5,82×10-2;
sr = s / x = 5,82× 10-2 /14,48 = 4,02× 10-3 или 0,04 %.
Пример 9.3. Используя условия примера 9.2 и считая, что со¬
держание аскорбиновой кислоты для той же пробы картофеля, оп¬
ределенное по стандартной методике составляет 14,58 мг/100 г,
рассчитайте доверительный интервал и установите, свидетельству¬
ют ли полученные результаты о наличии систематической погреш¬
ности при работе по новой методике?
Решение.
Для расчета доверительного интервала при числе степеней
свободы f = 9 - 1 = 8 и доверительной вероятности P = 0,95 из табл. 8
приложения находим коэффициент Стьюдента tP,f = 2,31.
Находим полуширину доверительного интервала, оставляя знача¬
щие цифры:
×s
tP,f
2,31 × 5,82 · 10-2
√9
= 4,48 ×10 -2 = 0,04
Таким образом, среднее содержание аскорбиновой кислоты лежит в
границах
x ± С = 14,48 ± 0,04 или ^(кислоты), мг/100 г = 14,48 ± 0,04.
Истинное значение содержания аскорбиновой кислоты14,58 не по¬
паДает в Доверительный интервал, слеДовательно, такой метоД
пробоподготовки картофеля к анализу имеет систематическую
погрешность, причину которой наДо выяснять.
Пример 9.4. При анализе стандартного образца, содержащего
1,44 % Ag, были получены результаты (%): 1,31; 1,45; 1,42; 1,32; 1,30.
Определить стандартное отклонение, доверительный интервал и сде-
175

лать выводы о наличии систематической погрешности в использо¬
ванном методе определения серебра.
Решение. Проверим наличие грубых погрешностей по
Q-критерию. Располагаем экспериментальные данные в порядке
возрастания численных значений: 1,30; 1,31; 1,32; 1,42; 1,45. Пред¬
полагаем, что значение 1,45 является результатом грубой погрешно¬
сти. Рассчитываем для него Q-критерий:
Q^ = (1,45-1,42)∕(1,45-1,30) = 0,2.
Для Р = 0,90 и n = 5 Qma6n. = 0,56 (табл. 9 приложения). Вычислен¬
ное значение Q-критерия Qkcn < 0,56, следовательно, грубая по¬
грешность отсутствует.
Находим среднее значение из пяти определений:
_ 1,31 +1,45 +1,42 +1,32 +1,30 1 „ А
x =	= 1,36.
5
Вычисляем стандартное отклонение:
(0,05)2 + (0,09)2 + (0,06)2 + (0,04)2 + (0,06)2 = 6 96 ×1θ. 2
s 1
5 -1
По табл. 8 приложения для Р = 0,95 и f = 5 - 1 = 4 находим tP,f = 2,78
и рассчитываем полуширину доверительного интервала для x:
tP,f s	6,96×10-2
-f = 2,78	” = 0,09.
√n	√5	’
Результат представляем в виде: w(Ag),% = 1,36 ± 0,09.
Наличие систематической погрешности можно выявить, как в
x ± C = 1,36 ± 0,09.
предыдущем примере, проверяя попадает ли истинное значение со¬
держания серебра в доверительный интервал. В данном случае для
Ag m = 1,44 % попадает в границы доверительного интервала, сле¬
довательно, систематическая погрешность в этом методе определе¬
ния серебра отсутствует.
Ответить на вопрос задачи о присутствии систематической
погрешности можно, используя критерий Стьюдента и сравнивая
вычисленное значение tκn с табличным значением t - критерия при
Р = 0,95 и f = 4, равным 2,78:
t
эксп
X - m∣ ∙ Vn	∣1,3 6 -1,44∣
S ~ 0,0696
×√5 = 2,57.
176

Поскольку 1)ксп < tma6jl, делаем вывод о вероятном отсутствии сис¬
тематической погрешности.
Пример 9.5. При определении ванадия были получены ре¬
зультаты: 8,00×10-4; 8,40×10-4 г. Чему равен доверительный интер¬
вал? Сколько параллельных определений необходимо провести для
достижения доверительного интервала с полушириной 0,41 ×10-4?
Решение. Находим среднее значение:
x = 8,00 × 10-4 + 8,40 · 10-4
•X
2
Вычислим стандартное отклонение:
По табл. 8 приложения находим 1P,f = 12,7 (для Р = 0,95 и f = 1) и
вычисляем полуширину доверительного интервала:
Требуется же получить доверительный интервал с полушириной 0,41 ×10-4.
Найдем необходимое для этого соотношение 1P,f и n:
1
1 Р , f
или —^должно быть £1,45.
При n = 4 значение критерия 10,95. 3 = 3,18, а отношение 3,18A∕4 > 1,45;
при n = 5 значение критерия 10,95. 4 = 2,78, а отношение 2,78/75 <1,45.
Таким образом, для сужения границ доверительного интерва¬
ла до ±0,41 ×10-4 необходимо провести 5 параллельных определений.
9.2.	Сравнение результатов двух методов
количественного анализа
Методами математической статистики можно сравнить выбо¬
рочные совокупности (выборки) по воспроизводимости (сравнение
дисперсий) и правильности (сравнение средних).
Сравнение двух выборочных дисперсий проводят, когда ре¬
зультаты получены двумя разными методами, в двух лабораториях,
на двух приборах, двумя аналитиками и т. д. При сравнении снача-
177

22
ла находят дисперсии s1 и s2 (или, соответственно, V1 и V2) для со¬
ответствующих выборок с f1 = n1 - 1 и f2 = n2 - 1.
Для ответа на вопрос, значимо или незначимо отличаются
Дисперсии, провоДят сравнение с табличным значением критерия
Фишера Ftc6ji вычисленного значения критерия Фишера - Рэксп.
F^n вычисляют по формуле, деля большую дисперсию на
меньшую:
F
)ксп
sL
if
Vl
и2.
(9.3)
Значения Ftc6ji можно взять из табл. 10 приложения. В этой таблице
число степеней свободы f большей дисперсии находится в горизон¬
тальном ряду. Если Ftc6ji > F^n при Р = 0,95 (или Р = 0,99), расхо¬
ждение между выборками незначимо, дисперсии однородны.
Сравнение средних результатов двух выборок проводят,
если проверка их по критерию Фишера указывает на незначимость
расхождения дисперсий, т. е. на одинаковую воспроизводимость
результатов сравниваемых выборок. Для сравнения используют 1 -
распределение. Сначала рассчитывают средневзвешенную диспер¬
сию s2 (или V) по формуле:
s2 = (n1 -1) × s12 + (n2 -1) × s2	(9 4)
n1 + n2 - 2	,	( . )
затем вычисляют 1-критерий:
(9.5)
nI ∙ n2
n1 + n2
Сравнивают 1та6л и 1)ксп при числе степеней свободы f = п1 + п2- 2 и до¬
верительной вероятности Р = 0,99 (или уровне значимости р = 0,01).
Если 1та6л < 1)ксп, то расхождение значимо. Если 1та6л > 1)ксп, то
расхождение между средними двух выборок незначимо, и резуль¬
таты можно рассматривать как одну выборочную совокупность с
п1 + п2 количеством результатов.
Пример 9.6. Определите, существует ли значимое различие
между выборочным средним значением результатов определения
массовой доли серы в каменном угле (%): 2,10; 2,12; 2,13; 2,15;
178

2,15 и средним генеральной совокупности (истинным значением)
m = 2,15 %, полученным для n = 80.
Ре шение . Найдем среднее для выборки и стандартное от¬
клонение отдельных результатов:
_	2,10 + 2,12 + 2,13 + 2,15 + 2,15
x _	_ 2,13,
5
s=
(0,03)2 +(0,01)2 +(0,00)2 +(0,02)2 +(0,02)2
=2,12×10-2.
N	5-1
Как в примере 9.4, находим значение величины t3κcn∖
t
эксп
(2,15 - 2,13) ×√5
2,12 × 10-2
Сравниваем 1эксп с tτa6j коэффициента Стьюдента (табл. 8 приложе¬
ния), значение которого при f = 4 и Р = 0,95 равно 2,78. Поскольку
полученное среднее значение x не отличается значимо от истинного
значения m (среднего генеральной совокупности), делаем вывод о
вероятном отсутствии систематической погрешности.
Пример 9.7. Массовую долю (%) CuO в минерале определили
методом иодометрии и методом комплексонометрии. По первому
методу получили результаты: 38,20; 38,00; 37,66. По второму 37,70;
37,65; 37,55. Значимо ли различаются результаты данных методов?
Решение. Вычислим среднее значение для каждого метода:
x1 =
38,20 + 38,00 + 37,66
3
= 37,95;
_	37,70 + 37,65 + 37,55
x2 _			_ 37,63.
3
Рассчитаем дисперсии:
s12
_ (38,20 - 37,95)2 + (38,00 - 37,95)2 + (37,66 - 37,95)2 _ 0 07453
3-1
2 _ (37,90 - 37,63)2 + (37,65 - 37,63)2 + (37,55 - 37,63)2 _ θ 00583
s2
3 - 1
Вычислим критерий Фишера (9.3):
F3κcn _ s2 _ 0,07453 _ 12,78.
эксп s22	0,00583
179

Для сравнения Дисперсий сопоставим значение 1:эксп с Fma6n (табл. 10
приложения) при Р = 0,95 и f1 = f2 = 2. Значение F0,95; 2; 2 = 19,00, т. е.
Fma6n > F3καb ^edoeamenbHo, расхождение межДу Дисперсиями не¬
значимо и воспроизвоДимо^ь рeзуnьmamoв, πonучeнных по Двум
мemoДикaм, оДинакова.
Показав незначимость расхождения дисперсий, можно провести
сравнение средних. Для этого рассчитаем среднее взвешенное двух
дисперсий (9.4):
S 2
(n∣ -1) ■ s12 + (n2 -1) ■ s22 = 2 ■ 0,07453 + 2 ■ 0,00583
П1 + n - 2	3 + 3 - 2
= 0,04018
и с помощью t-критерия (9.5) оценим расхождение между средними
x1 и x2 двух методик:
t
n1 ■n2
эксп
n1 + n2
37,95-37,63 ∕~3×3^
√0,04018 V3 + 3
=1,96.
Сопоставляем полученное значение ^ксп с табличным t0,95; 4 = 2,776
(при Р = 0,95 и f = 3 + 3 - 2 = 4). Так как ^ксп < 10,95;4 , то различие
между x1 и x2 незначимо. Следовательно, все результаты обоих ме¬
тодов отражают истинное содержание CuO в минерале. Поэтому
данные анализа по двум методикам могут быть объединены и пред¬
ставлены в виде:
x ±
tP,fs
= x ± С,
где x - среднее из всех n1 + n2 результатов.
x = 38,20 + 38,00 + 37,66 + 37,70 + 37,65 + 37,55 = 37 79.
x	3 /,/ .
6
s = 0,25. t P,f = 2,571.
0,25
Результат анализа: w(CuO),% = 37,79 ± 2,571^- = 37,79 ± 0,26
√6	’
СneДуem зaмemиmь, чmo сравнение Двух вы6орок мemoДa-
ми мameмamичecкoй cmamиcmики рeкoмeнДуemcя прoвoДиmь
180

при п1 и п2 более 10. Поэтому пример 9.7, скорее, иллюстриру -
ет схему расчета .
9.3.	Суммирование погрешностей
В химических методах количественного химического анализа -
гравиметрии и тириметрии в расчетах используют в основном сум¬
мы, разности, произведения и частные измеренных величин, опреде¬
ление каждой из которых содержит свою погрешность. Возникает
задача вычисления суммарной погрешности, решение которой зави¬
сит от вида погрешностей и выполняемых арифметических действий
с полученными значениями. В данном пособии рассмотрим сумми¬
рование погрешностей только для перечисленных арифметических
действий. Правила суммирования представлены в табл. 9.1.
Таблица 9.1
Правила суммирования погрешностей
Функция
Вид
Систематические
погрешности
Случайные
погрешности
1
2
x = a + b
Абсолютные
Dx = Da + Db
Dx = ∣Dα∣ + ∣Db∣
sx = J sα + sb
x = a - b
Dx = Da - Db
D√=Da+Da
I 2 , 2
sx = √ Sa + sb
x = a ×b
Относительные
Dx Da + Db
xab
D x
x
=
D a
a
+
D b
b
Sx =
x
< S >
d a
I a J
2
+
(s λ
d b
< b J
2
x = a/b
Dx Da Db
Dx
x
=
Da
a
+
Db
b
Sx =
x
(S
Ia J
2
+
< S A
Sd
<b j
2
xab
Примечание: суммарную систематическую погрешность рас¬
считывают по формулам столбца 1, если известны и величина, и
181

знаки отдельных составляющих; если знаки неизвестны, расчет
проводят по формулам столбца 2. Определив абсолютную погреш¬
ность, можно рассчитать относительную и наоборот.
Пример 9.8. Вычислите абсолютную и относительную систе¬
матические погрешности взвешивания гравиметрической формы
BaSO4, если масса тигля с прокаленным осадком т1=12,3383 г, а
пустого тигля т2 = 12,0112 г. Соответствующие систематические
погрешности взвешивания с использованием аналитических разно¬
весов составили Dm1= + 0,0124 и Dm2 = + 0,0122 г.
Решение. Массу гравиметрической формы вычисляем по
разности взвешиваний:
m (BaSO4) = m1 - m2 = 12,3383 - 12,0112 = 0,3271 г.
Используя правило сложения систематических погрешностей для
разности при известном знаке составляющих (колонка 1 табл. 9.1),
получаем:
Dm = Dm1 - Dm2 = 12,4 - 12,2 = 0,2 мг.
Следует обратить внимание на то, что при использовании од¬
них и тех же гирь при взвешивании тигля с осадком и без него сис¬
тематическая погрешность уменьшается.
Найдем относительную погрешность определения массы гра¬
виметрической формы:
Dm/m = 0,2/327,1 = 6,1×10-4 или 6,1×10-2 %.
Пример 9.9. Рассчитайте систематическую погрешность (аб¬
солютную и относительную) концентрации с(1/2 I2) при приготов¬
лении 250,0 мл раствора иода из навески m 1,2634 г. Систематиче¬
ская погрешность массы навески +0,4 мг, измерения объема мерной
колбой -0,2 мл.
Решение. Концентрацию раствора рассчитываем по формуле:
m(I )	1,2634
с(1/2 I2) _	—	_	—	_ 0,03982 моль/л.
1	1/2 M (I2) -Vmk	126,9045 · 0,2500
В соответствии с законом распространения систематических по¬
грешностей относительная погрешность частного при известных
знаках определяется равна разности относительных погрешностей
делимого и делителя, а произведения - сумме (табл. 9.1, колонка 1):
182

Dc = Dm _ fDM + DV"
c m M V у
Поскольку погрешность определения молярной массы мала по
сравнению с другими погрешностями, ее вкладом пренебрегаем.
Найдем относительную погрешность величины концентрации:
Dc = Dm DV = 4 -10 ’1
с mV 1,2634
Абсолютная погрешность концентрации составляет:
DC =	m(I2)
1/2M(I2) × Vmk
(_ 0,2'
250j
= 3,2 - 10 4 + 8,0 × И)4 = 1,1 × 10_3 (0,1 %).
Dc
— = 0,03982 ·1,1 -10 _3 = 4 -10 _5 моль/л.
c
Пример 9.10. Рассчитайте максимально допустимое относи¬
тельное стандартное отклонение при определении массовой доли
серы в пересчете на SO3 весовым методом, если методика предпо¬
лагает: из навески пробы около 1 г после разложения и окисления
серы до SO4 остаток перевести в мерную колбу вместимостью
100 мл, осаждение провести из аликвоты 20 мл и получить массу
гравиметрической формы 0,4 г (см. гл. 7). Использована посуда
второго класса (табл. 11 приложения).
Решение. При осаждении BaSO4 из аликвоты результаты
весового анализа могут быть рассчитаны по формуле:
) = W(BaSO1) f vmk
ma	v, ’
где mα _ масса пробы, F = ^(SOз)/М(BaSO4) _ гравиметрический
фактор.
С учетом правила суммирования случайных погрешностей для
произведения и частного (табл. 9.1) относительное стандартное от¬
клонение результата можно выразить формулой:
(
n,(SO3)	m(BaSO4)
sw
Sm
4) J
2
SV
мк
∖ Vmk J
(s Ί
V
n
Vn J
( Ϋ
Sm_
l ma j
. (9.6)
2
+
+
+
При этом пренебрегаем погрешностью гравиметрического фактора F.
Масса гравиметрической формы m(BaSO4) получается как
разность двух взвешиваний на аналитических весах:
m(BaSO4) = m1 _ m2,
183

где m1 - суммарная масса тигля и BaSO4; m2 - масса пустого тигля.
Аналогично берут навеску пробы. Погрешность взвешивания при¬
мерно одинакова в обоих случаях: sm1 » sm2. Вычислим абсолютную
случайную погрешность определения массы BaSO4 как погреш-
ность разности:
s
m
+ s 2
m2
При взвешивании тигля до постоянной массы
взвешивания составляет 2×10-4 г. Тогда абсолютная
погрешность
погрешность
определения массы:
Sm,в.ф. = √(2 × 10~4)2 + (2 × 10 4I' = 3 × 10~4 г.
Абсолютная погрешность взятия навески иода на аналитических
весах:
sm ,12 = J (1 ×10 - 4)2 + (1 ×10 - 4)2 = 1,4 -10 -4 г.
Из табл. 11 приложения берем соответствующие допуски мер¬
ной посуды и подставляя в формулу (9,6) вычисляем максимально
возможное относительное стандартное отклонение результата:
s,l =
HSO3)
4 Ί2
J+
43-10
0,4 J
0,2 j2
1100 J
' 1,4 -10-4J2
1 J
=3,7×10-3 (0,37 %).
+
'0,06 Л
I 20 J
+
Пример 9.11. Рассчитайте максимальную допустимую по¬
грешность (абсолютную и относительную) концентрации c(1∕2I2)
при приготовлении 250 мл раствора иода из навески m 1,2634 г.
Решение. Вычисление проводим с учетом примера 9.9, где
найдена концентрация с(1/2 I2)= 0,03982 моль/л, используя форму¬
лу, подобную (9.6) и рассуждения примера 9.10. Основной вклад в
суммарную погрешность концентрации иода вносят погрешность
измерения объема и массы:
4	Л2	4 s Л2
SC =	Sm	l	V,:,	=
C(I2)	Vlm(I2) J	I Vmk J	\
1,4 -10-4 Л
l 1,2634 J
22
4 0,2 Л2
+ ’	= 8,1 -10-4 (0,08 %)
250 J
Очевидно, что измерение объема вносит больший вклад в погрешность.
Вычислим максимально допустимую абсолютную погрешность:
184

sc = -s- × c(I2) = 8,1 × 10-4 × 0,03982 = 0,00003 моль/л.
c(I2)
Пример 9.12. Определите относительную и абсолютную по¬
грешность концентрации раствора тиосульфата, если она устанав¬
ливалась по раствору иода, приготовленному как в примере 9.11, по
результатам одного титрования аликвоты иода тиосульфатом (рас¬
ход тиосульфата V) и трех параллельных титрований. Соответст¬
вующие данные (с указанием в скобках стандартных отклонений):
для иода:	для тиосульфата:
Vmk = 250,0 (±0,2/3) мл,	V = 12,80 (±0,05 мл),
V∏ = 25,00 (±0,1/3) мл,
т =	1,2634 г.
Решение . Концентрацию тиосульфата вычисляем по форму¬
ле (гл. 8):
cNa2S2O3
m(12)-Vn (I2)-1000
Vmk ∙Mς∖∕^I2)-V(Na2S2O3)
1,2634- 25,00 -1000
250,0 -126,9045-12,80
= 0,07778 моль/л.
Расчет относительной погрешности проводим с учетом вклада всех
измеряемых составляющих, упуская малую погрешность молярной
массы:
s =
c 1!
( s,
C λ2
SVn
к Vn )
C s
•^г
мк
к V мк J
(
sV
к V ( мк J
■ λ2
m
к m J
2
2
+
+
+
C 1,4 -10-4 λ2
C 0,1/3
К 1,2634 )
к 25,00 J
λ2
)+
C0,2/3
к 250,0 J
λ2
)+
C 0,05
к 12,80 J
= 4,1 ×10-3.
+
2
Из расчета следует, что наибольший вклад в погрешность вно¬
сит объем титранта, и с его увеличением погрешность уменьшается.
Если титрование повторять n раз с новой аликвотой относительная
погрешность концентрации уменьшится в Vn раз, т. е. при трех
параллельных титрованиях:
Sc = 4,1 -10-3
с-Vn	√3^
= 2,4×10-3.
Абсолютная случайная погрешность определения
Na2S2O3 при однократном титровании:
концентрации
185

sc = 4,1-10-3-0,07778 = 0,00003 моль/л.
Пример 9.13. Проведите расчет погрешности результата ана¬
лиза образца на содержание Cu(II), проведенного иодометрическим
титрованием по заместителю согласно реакциям:
2Cu2+ + 4I- = Cu2I2^ + I2 , I2 + 2Na2S2O3 = 2NaI + Na2S4θ6.
Навеску образца 0,7500 (±1,4-10-4) г перевели в мерную кол¬
бу вместимостью 200,0 (±0,2/3) мл. На титрование брали три али¬
квоты по 20,00 (±0,06/3) мл, расход тиосульфата с концентрацией
0,07778 (±3-10-5) моль/л составил: 10,00; 10,05; 10,07; 10,03
(V = 10,04) мл.
Решение. Рассчитаем стандартное отклонение объема тио¬
сульфата:
sV
SV-V )2
(10,07-10,04)2 + (10,03-10,04)2 + (1Q7QQ -10,04)2 + (10,05-10,04)2
4-1
=0,03.
\	4-1	V
Массовую долю меди вычислим по формуле:
w(Cu) =
с(Na1 S2O3) × V(Na1 S2O3)- M(Cu) × Vmk · 100
ma ×Vn×1000
0,07778 × 10,04 × 63,546 × 200 × 100
0,7500 - 25,00 - 1000
= 52,93 %.
С учетом погрешностей входящих в формулу величин рассчи-
таем относительную погрешность содержания меди:
sw
w
-5 Ϋ
+
ί 0,03 V ί 0,08 V
' 1,4 -10
k 0,7500 J
ί 3-10
0,07778 J
= 10-4 -√14,9 + 893 +16 + 3,5 + 256 = 3,4 -10-3.
0,04 Y
< 25,00 j
110,04 J
+
< 200,0 J
+
- 4 Y
	 	 +
3
Абсолютная погрешность: sw = —- w = 3,4-10 -52,93 = 0,18.
w
Тогда можно представить результат определения массовой
доли меди как 53,27±0,18 (%).
Задачи для самоконтроля
1.	При определении кальция гравиметрическим методом получили сле¬
дующее содержание СаО (%): 12,86; 12,90; 12,93; 12,84. Вычислите стан¬
дартное отклонение в определении содержания кальция. Ответ: 0,04.
2.	В серебряной монете при анализе параллельных проб получили сле¬
дующее содержание серебра (%): 90,04; 90,12; 89,92; 89,94; 90,08; 90,02.
186

Вычислите стандартное отклонение единичного определения и доверитель¬
ный интервал среднего значения (для Р= 0,95).	Ответ: 0,08; 0,08.
3.	При анализе апатита получили следующие данные о содержании в нем
Р2О5 (%): 35,11; 34,14; 35,18; 35,21; 35,42. Установите, является ли последний
результат грубой погрешностью.	Ответ: Да.
4.	При определении концентрации c(1/5 KMnO4) тремя студентами по¬
лучены следующие результаты (моль/л): а) 0,1013; 0,1012; 0,1012; 0,1014;
б) 0,1015; 0,1012; 0,1012; 0,1013; в) 0,1013; 0,1015; 0,1015; 0,1013. Вычис¬
лите стандартное отклонение единичного определения и доверительный
интервал среднего значения (для Р = 0,95). Ответ: 1,2×10-4; 0,8×10-4.
5.	Содержание марганца в четырех образцах ферромарганца по результа¬
там анализов составляет (%): а) 21,34; 21,32; 21,31; 21,35; б) 34,45; 34,41;
34,42; 34,43; в) 50,17; 50,14; 50,13; 50,16; г) 65,57; 65,56; 65,59; 65,60. Вычис¬
лите стандартное отклонение при анализе марганца. Ответ: 0,02.
6.	Имеется ли систематическая погрешность в определении платины новым
методом, если при анализе стандартного образца платиновой руды, содержащего
85,97 % Pt, были получены следующие результаты Pt (%): 85,97; 85,71; 85,84;
85,79.	Ответ: Нет.
7.	Содержание активного хлора в хлорной извести составляет (%): 37,11;
37,18; 37,23; 37,15. Среднее значение генеральной совокупности (n = 50)
37,02. Установите, существует ли значимое различие между выборочным
средним и средним генеральной совокупности. Ответ: да, при Р = 0,95.
8.	При анализе стали получили следующее содержание марганца: 48,35 и
48,00 %. Установите, сколько параллельных проб необходимо для определе¬
ния марганца с доверительным интервалом ±0,48?	Ответ: 4 пробы.
9.	Содержание Fe2O3 в руде определили методами перманганатометрии и
комплексонометрии. При этом получили следующие результаты (%):
а) 60,12; 61,00; 61,25; б) 58,75; 58,90; 59,50. Существует ли статистически
значимое различие между результатами анализа этими методами?
Ответ: различие дисперсий незначимо; средних - значимо.
10.	Рассчитайте абсолютную погрешность результата вычислений (в скоб¬
ках приведены значения абсолютных систематических погрешностей):
4,10(-0,002) ×0,0050(+0,0001)
у = —— 		— 	-— 		 = 0,010406 .	Ответ: +0,0004.
1,97(-0,04)
11.	Вычислите максимальную допустимую относительную погрешность
приготовления раствора дихромата калия с концентрацией c(1/6 K2Cr2O7), ес¬
ли раствор готовили из навески 4,9032 г K2Cr2O7 в мерной колбе вместимо¬
стью 1000 мл.	Ответ: 0,06 %.
187

ГЛАВА 10. РАСЧЕТЫ В ИОНООБМЕННОЙ
ХРОМАТОГРАФИИ
Ионный обмен - это обратимая реакция, в ходе которой про¬
исходит обмен ионами между твердым веществом (ионитом) и рас¬
твором электролита. Между катионообменником и раствором про¬
исходит обмен катионами, между анионообменником и раствором -
обмен анионами. Катионообменники представляют собой специ¬
ально синтезированные полимерные нерастворимые в воде вещест¬
ва, содержащие в своей структуре ионогенные группы кислотного
характера: -SO3¾ -COOH, -OH, -PO3H2, -AsO3H2 и др. Химиче¬
ские формулы катионообменников схематически можно изобразить
следующим образом: RSO3H; RSO3Na или просто R-H, R-Na. В
первом случае катионообменник находится в H-форме, во втором -
в Na-форме; R - полимерная матрица. Катионообменные реакции
записываются как обычные гетерогенные реакции:
RH + Na+ = RNa + H+
Анионообменники содержат в своей структуре анионогенные
группы основного характера: -N(CH3)3; =NH; -NH2; ≡N и др. Их
химические формулы могут быть изображены как RN(CH3)3OH,
RN(CH3)3Cl или R-OH, R-Cl. В первом случае анионообменник на¬
ходится в OH-форме, во втором - в Cl-форме. Анионообменную ре¬
акцию можно записать следующим образом:
ROH + Cl- = RCl + OH-
Важной количественной характеристикой ионитов, опреде¬
ляющих их сорбционную способность, является число функцио¬
нальных групп, участвующих в обмене ионами, приходящееся на
единицу массы или объема ионита. Эта величина называется полной
обменной емкостью (ПОЕ). Емкость относят к единице массы или
объема и обычно выражают в миллимоль-эквивалентах (ммоль-экв.)
или миллимолях (ммоль) на 1 г сухого или 1 мл набухшего ионооб-
менника в Н-форме или Cl-форме. Для разных марок ионитов она
находится в пределах от 1 до 10 ммоль Н+/г сухого вещества.
На емкость ионитов оказывает влияние ионная сила анализи¬
руемых растворов и элюентов, для слабокислотных и слабоосновных
- рН растворов.
188

Наряду с ПОЕ емкость ионитов характеризуется другой вели¬
чиной, называемой рабочей или динамической обменной емкостью
(ДОЕ). ДОЕ - емкость ионитов, определяемая в динамических усло¬
виях по количеству поглощенных ионов до появления последних в
фильтрате (элюате) на выходе из колонки. Для характеристики рабо¬
ты слоя ионита в динамических условиях используют также величи¬
ну полной динамической обменной емкости (ПДОЕ), не всегда сов¬
падающую с ПОЕ и показывающую количество поглощенных в дан¬
ных условиях элюирования ионов до прекращения сорбции, т.е. на¬
сыщения слоя ионообменника. ДОЕ и ПДОЕ зависят от скорости
элюирования, параметров слоя (высоты, поперечного сечения), гра¬
нулометрического состава ионита, концентрации пропускаемого
раствора и других условий. Величины емкости для выпускаемых
промышленных марок регламентируются ГОСТ.
Пример 10.1. Навеску воздушно-сухого катионита (m =
= 1,2500 г) поместили в 50,0 мл раствора СаС12 с концентрацией
с(1/2СаС12) = 0,1000 моль/л. После отделения катионита на титро¬
вание 25,0 мл фильтрата затрачено 12,0 мл 0,1000 моль/л раствора
NaOH. Влажность катионита 0,10 % масс. Вычислить статическую
обменную емкость катионита.
Решение. В основе ионообменной хроматографии находит¬
ся реакция обмена между ионами раствора и ионообменника (орга¬
ническая смола или минерал). Каждый ионит способен поглощать
лишь определенное количество ионов (емкость ионита). Емкость
показывает, какую массу (мг) или количество вещества эквивалента
иона (ммоль) сорбирует 1 мл или 1 г ионита.
На катионите (RH) протекает реакция катионного обмена:
2RH + Са2+ = R2Ca + 2Н+,
выделившуюся хлористоводородную кислоту оттитровывают
раствором NaOH. При этом количество эквивалентов вещества НС1
равно количеству эквивалентов вещества NaOH и количеству экви¬
валентов вещества Са2+, сорбированному на катионите n (1/2Ca2+)
n(HCl) = n(NaOH) = n(1/2Ca2+) = 12 × 0,1000 = 1,20 ммоль.
189

Учитывают, что на титрование отобрали 25 мл раствора из
50 мл:
n0(1/2Ca2+)=1,20-2= 2,40ммоль.
Рассчитывают количество эквивалентов Са2+, сорбированное
1 г абсолютно сухого катионита (статическая обменная емкость):
2,4	100
СОЕ = (1 / 2Ca2+) = —	= 1,92 ммоль / г.
1,25 100- 0,1
Пример 10.2. Рассчитать объем раствора СаС12 с молярной
концентрацией эквивалента 0,05 моль/л, который можно пропус-
2+
тить через 50 мл набухшего катионита КУ-2 до проскока Са . Пол¬
ная динамическая обменная емкость катионита ПДОЕ (1/2Са2+) =
1,2 ммоль/мл.
Решение. Рассчитывают количество эквивалентов вещества
Са2+, которое может поглотиться 50 мл набухшего катионита:
1,2 ммоль поглотятся 1 мл катионита,
х моль - 50 мл катионита;
х = 60 ммоль.
Вычисляют объем раствора, содержащий 60,0 ммоль эквива¬
лентов Са2+:
в 1000 мл содержится 0,05 · 1000 = 50 ммоль эквивалентов
Са2+,
в v мл - 60 ммоль эквивалентов Са2+;
v = 1200 мл.
Пример 10.3. Через колонку, содержащую 5,0 г катионита,
пропустили 250,0 мл 0,050 М ZnSO4. Вытекающий из колонки рас¬
твор собирали порциями по 50,0 мл, в каждой порции определяли
содержание ионов цинка и получили следующие значения концен¬
трации (моль/л): 1 - 0,008; 2 - 0,029; 3 - 0,038; 4 - 0,050; 5 - 0,050.
Определить полную динамическую обменную емкость (ммоль/г)
катионита.
Решение. Вычисляем количество эквивалентов Zn2+, по¬
глощенное катионитом из каждой порции раствора, принимая мо¬
лярную массу эквивалента равной М (1/2Zn2+):
190

(0,050 - 0,008) - 2 - 50 -1000 = 4 20
1.
n(1/2Zn2+) =
2.
n(1/2Zn2+) =
1000
(0,050 - 0,029) - 2 - 50 -1000 = 2 10
ммоль.
3.
n(1/2Zn2+)=
1000
(0,050 - 0,038)×2×50×1000
v , = 1,20
ммоль.
ммоль.
1000
c zizπ,72^	(0,050 - 0,050) - 2 - 50-1000 λ
и 5. n(1∕2Zn ) =-			= 0 ммоль.
1000
Всего в пяти порциях раствора поглощено:
Sn(1/2Zn2+) = 4,20+2,10+1,20 = 7,50ммоль.
Отсюда полная динамическая обменная емкость катионита
для ионов цинка равна:
4
m
2+	Sn(1/ 2Zn2+ ) 7,50
ПДОЕ(1/ 2Zn2+) =	= _ θ = 1,50ммоль / г.
Задачи для самоконтроля
1.	Какая масса сухого (г) и какой объём (мл) набухшего катионита в H+-
форме потребуется для выделения ионов натрия из 1 л 0,2 М раствора хлори¬
да натрия, если СОЕ = 4,8 ммоль/г. Удельный объём набухшего катионита -
3,0 мл/г.
Ответ: 42 г, 126 мл.
2.	Какую навеску катионита в Н+-форме следует взять, чтобы сорбировать
Са2+ из 5 л раствора хлорида кальция с молярной концентрацией 0,05 моль/л?
Обменная емкость катионита 3,2 ммоль/г.
Ответ: 156 г.
3.	При обработке 5,0 г анионита в ОН--форме 100 мл 0,2 моль/л раствором
хлорида натрия собрали 250 мл раствора и промывных вод. На титрование
10,00 мл полученного раствора израсходовали 15,50 мл 0,04 моль/л раствора
НС1. Рассчитать обменную емкость анионита.
Ответ: 0,9 ммоль/г.
4.	Навеска воздушно-сухого катионита в Н+-форме (m = 1,050 г) с влажно¬
стью 0,05% мас. поместили в 100 мл раствора СаС12 с концентрацией 0,0500
моль/л. После достижения сорбционного равновесия и отделения катионита
на титрование 25,0 мл раствора затратили 12,2 мл 0,09850 моль/л раствора
NaOH. Рассчитать объемную емкость катионита.
Ответ: 4,95 ммоль/г.
5.	Динамическая объемная емкость катионита КУ-2 равна 1,5 ммоль/мл.
Какой объем раствора хлорида кальция с концентрацией с(1/2СаО2) = 0,07
моль/л можно пропустить через колонку, заполненную 100 мл набухшего ка¬
тионита, до начала проскока ионов Са2+?
Ответ: 2143 мл
191

6.	Колонку заполнили 100 мл набухшего катионита. Статическая обменная
емкость сухого катионита 4,6 ммоль/г, удельный объем 2,9 мл/г. Рассчитать
количество эквивалентов Са2+, которое может быть сорбировано катионитом.
Ответ: 0,32 моль-экв.
7.	К навеске природного ионита (m = 2,0 г) в Са2+-форме добавили 25,0 мл
0,100 моль/л раствора NaOH. После установления равновесия раствор оттит¬
ровали 15,7 мл 0,0800 моль/л раствора НС1. Вычислить обменную емкость
природного ионита.
8.	Навеску катионита (т = 1,025 г) с влажностью 0,05% мае. поместили в
100 мл 0,1 моль/л раствора NaC1. На титрование 25,0 мл полученного раство¬
ра затратили 11,4 мл 0,1 моль/л раствора NaOH. Вычислить обменную ем¬
кость катионита.
Ответ: 5,3 ммоль/г.
9.	Какая масса кобальта останется в растворе, если через колонку, запол¬
ненную 5,0 г катионита, пропустили 200 мл раствора CoSO4 с концентрацией
0,05 моль/л. Полная динамическая емкость в условиях разделения равна 1,6
2+
ммоль/г (молярная масса эквивалента равна М(1/2Со2+)).
Ответ: 0,24 г.
10.	Для определения концентрации сульфата никеля 10,00 мл анализируе¬
мого раствора поместили в мерную колбу вместимостью 100,0 мл, довели
водой до метки; 10,00 мл этого раствора пропустили через колонку с катио¬
нитом в Н+-форме. Элюат и промывные воды собрали в стакан и оттитровали
потенциометрически на автотитраторе 0,1000 М раствором NaOH, затратив
1,67 мл раствора титранта. Рассчитать концентрацию электролита (г/л).
Ответ: 12,9 г /л.
11.	Вытяжку из мясного фарша, содержащего нитрит натрия, пропустили
через колонку, заполненную сильноосновным анионитом АВ-17 в ОН--
форме. Колонку промыли дистиллированной водой до нейтральной среды по
фенолфталеину. Элюат и промывные воды собрали в коническую колбу. На
титрование полученного раствора затратили 5,00 мл раствора HC1 с концен¬
трацией 0,01000 моль/л. Составить уравнения реакций и найти массу NO2- в
исходной вытяжке из фарша.
Ответ: 2,3 мг
12.Через колонку, заполненную 10 г катионита, пропустили 250 мл раство¬
ра Си2+ с концентрацией 0,08 моль/л. На выходе из колонки собрали 5 порций
элюата по 50,0 мл, добавили раствор иодида калия и в присутствии серной ки¬
слоты выделившейся йод оттитровали 0,0100 моль/л раствором тиосульфата
натрия. В первой порции иод не выделился. На титрование 2, 3, 4 и 5 порций
израсходовали соответственно 12,0; 25,0; 39,2 и 39,2 мл раствора тиосульфата
натрия. Построить график зависимости концентрации Си2+ в элюате от объема
элюата и рассчитать полную динамическую обменную емкость.
Ответ: 1,66 ммоль/г.
192

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1.	Лурье, Ю. Ю. Справочник по аналитической химии /
Ю. Ю. Лурье. - М.: Химия, 1980. - 480 с.
2.	Основы аналитической химии: в 2 кн. - Кн. 1: Общие вопро¬
сы. Методы разделения: учебник для вузов / Ю. А. Золотов,
Е. Н. Дорохова, В. И. Фадеева [и др.]; под ред. Ю. А. Золотова.
-	М.: Высш. шк., 2004. - 361 с.; Кн. 2: Методы химического
анализа. - М.: Высш. шк., 2004. - 503 с.
3.	Скуг, Д. Основы аналитической химии. - Т. 1 /
Д. Скуг, Д. Уэст; пер. с англ.- М.: Мир, 1979. - 480 с.
4.	Основы аналитической химии. Задачи и вопросы: учеб. посо¬
бие для вузов / В. И. Фадеева, Ю. А. Барбалат, А. В. Гармаш [и
др.]; под ред. Ю. А. Золотова. - М.: Высш. шк., 2002. - 412 с.
5.	Дорохова, Е. Н. Задачи и вопросы по аналитической химии /
Е. Н. Дорохова, Г. В. Прохорова. - М.: Мир, 2001. - 267 с.
6.	Васильев, В. П. Аналитическая химия: в 2 кн. - Кн. 1: Титри-
метрические и гравиметрический методы анализа: учеб.для
студ. вузов / В. П. Васильев. - М.: Дрофа, 2002. - 368 с.
7.	Васильев, В. П. Аналитическая химия. Сборник вопросов, уп¬
ражнений и задач: пособие для вузов / В. П. Васильев,
Л. А. Кочергина, Т. Д. Орлова; под ред. В. П. Васильева. - М.:
Дрофа, 2003. - 320 с.
8.	Дорохова, Е. Н. Задачи и вопросы по аналитической химии:
практ. пособие / Е. Н. Дорохова, Г. В. Прохорова. - М.: Изд-во
МГУ, 1984. - 216 с.
9.	Сборник задач по аналитической химии.	- Ч.	2	/
A.	М. Васильев [и др.]; Казань: Изд-во Казанского ун-та, 1971.
-	121 с.
10.	Сборник вопросов и задач по аналитической химии / под ред.
B.	П. Васильева. - М.: Высшая школа, 1976. - 216 с.
11.	Сборник задач и упражнений по аналитической химии /
A.	Г. Воскресенский [и др.]. - М.: Просвещ., 1985. - 174 с.
12.	Задачник по аналитической химии / Н. Ф. Клещев [и др.] - М.:
Химия, 1993. - 224 с.
13.	Толстоусов, В. Н. Задачник по количественному анализу /
B.	Н. Толстоусов, С. М. Эфрос. - Л.: Химия, 1986. - 160 с.
193

14.	Харитонов, Ю. А. Аналитическая химия (аналитика): в 2 кн. -
Кн.1: Общие теоретические основы. Качественный анализ:
учеб. для вузов / Ю. Я. Харитонов. - М.: Высш. шк., 2001. -
615 с.; Кн. 2: Количественный анализ. Физико-химические
(инструментальные) методы анализа. - М.: Высш. шк., 2003. -
559 с.
15.	Цитович, И. К. Курс аналитической химии / И. К. Цитович. -
М.: Высш. шк., 1994. - 495 с.
16.	Бончев, П. Р. Введение в аналитическую химию / П. Р. Бончев.
- Л.: Химия, 1978. - 487 с.
17.	Дерффель, К. Статистика в аналитической химии / К. Дерф-
фель, пер. с нем. - М.: Мир, 1994. - 247 с.
18.	Чарыков, А. К. Математическая обработка результатов хими¬
ческого анализа / А. К. Чарыков. - М.: Химия, 1984. - 167 с.
194

ПРИЛОЖЕНИЕ
Таблица 1
Коэффициенты активности ионов при различных
значениях ионной силы раствора
Ионная сила
раствора, I
Значения коэффициентов активности (g)
для ионов с разными зарядами
Z = 1
Z = 2
Z = 3
0,0005
0,97
0,90
0,80
0,001
0,96
0,86
0,74
0,0025
0,95
0,80
0,63
0,005
0,93
0,74
0,54
0,01
0,91
0,67
0,44
0,02
0,88
0,55
0,32
0,03
0,88
0,54
0,28
0,04
0,87
0,48
0,24
0,05
0,86
0,47
0,21
0,06
0,85
0,46
0,20
0,07
0,85
0,46
0,19
0,08
0,83
0,45
0,18
0,09
0,82
0,44
0,17
0,10
0,81
0,43
0,16
0,12
0,81
0,42
0,15
0,15
0,80
0,41
0,15
0,20
0,80
0,40
0,14
0,30
0,81
0,42
0,15
0,40
0,82
0,45
0,17
0,50
0,84
0,50
0,21
0,60
0,86
0,56
0,27
0,70
0,89
0,63
0,36
0,80
0,92
0,72
0,48
0,90
0,96
0,83
0,66
1,00
0,99
0,96
0,91
195

Таблица 2
Термодинамические константы кислотности некоторых кислот в водном
растворе
Название
Формула
Ка
pKa=-lgKa
Азотистая
HNO2
6,9×10-4
3,16
Kal
7,1×10-10
9,15
Борная (орто)
Ka2
H3BO3
1,8×10-13
12,74
Ka3
1,6×10-14
13,80
Бромноватая
HBrO3
2,0×10-1
0,70
Иодноватая
HIO3
1,7×10-1
0,77
Масляная (норм)
CH3CH2CH2COOH
1,5×10-5
4,82
Масляная (изо)
(CH3)2CHCOOH
1,4×10-5
4,86
Муравьиная
HCOOH
1,8×10-4
3,75
Kal
5,6×10-3
2,25
Мышьяковая
Ka2
H3AsO4
1,7×10-7
6,77
Ka3
2,95×10-12
11,53
Мышьяковистая
H3AsO3
5,9×10-10
9,23
Пропионовая
CH3CH2COOH
1,3×10-5
4,87
Серная
Ka2
H2SO4
1,15×10-2
1,94
Ka1
1 4×10-2
1,85
Сернистая
Ka2
H2SO3
6,2×10-8
7,20
Ka1
1 0×10-7
6,99
Сероводородная
a
Ka2
H2S
2,5×10-13
12,60
Циановодородная
HCN
5,0××10-10
9,30
Ka1
4 5×10-7
6,35
Угольная
Ka2
H2CO3
4,8×10-11
10,32
Уксусная
CH3COOH
1,74×10-5
4,76
Фенол
C6H5OH
1,0×10-10
10,0
Ka1
3 1·10-2
1 51
Фосфористая
a1
Ka2
H3PO3
1,6∙10-7
6,79
Kal
7,1×10-3
2,15
Фосфорная
Ka2
H3PO4
6,2×10-8
7,21
Ka3
5,0×10-13
12,3
Фтороводородная
HF
6,2×10-4
3,21
Хлористая
HClO2
1,1×10-2
1,97
Хлороуксусная
ClCH2COOH
1,4∙10-3
2,86
Хлорноватистая
HClO
2,95∙10-8
7,53
Ka1
5 6·10-2
1 25
Щавелевая
a1
Ka2
H2C2O4
5,4∙10-5
4,27
196

Таблица 3
Термодинамические константы основности некоторых оснований
в водном растворе
Название
Формула
Кь
pKb=-lgKb
Аммония гидроксид
NH4OH (NH3H2O)
1,76∙10-5
4,755
Анилин
C6H5NH2+H2O
4,3-10'1°
9,37
Гидразин
N2H4+H2O
9,3∙10-7
6,03
Диметиламин
(СHз)⅛NH.H2O
5,4∙10-4
3,27
Метиламин
CH3NH2H2O
4,6-10^3
3,34
Этаноламин
NH2CH2CH2OH∙H2O
1,8∙10-5
4,75
Таблица 4
Константы устойчивости комплексных ионов
Комплексы с аммиаком (L=NH3)
Центральный ион
lgb
⅛b
lgJb
⅛b
⅛b
bb
Ag+
3,32
7,23
Cd2+
2,51
4,47
5,77
6,56
-
-
Co3+
7,3
14,0
20,1
25,7
30,8
35,21
Cu2+
3,99
7,33
10,06
12,03
-
-
Hg2+
8,8
17,5
18,5
19,3
-
-
Ni2+
2,67
4,79
6,40
7,47
8,10
8,01
Zn2+
2,18
4,43
6,74
8,70
-
-
Гидроксокомплексы (L=OH-)
Центральный
ион
Igbi
Igb
⅛b
⅛b
⅛b
lgb
Al3+
8,9
17,8
26,0
33,0
Bi3+
12,4
15,8
-
35,2
Cr3+
10,1
17,8
-
29,9
Pb2+
7,52
10,54
13,95
-
Sn2+
11,93
20,94
25,40
-
Sn4+
-
-
-
-
63,0
Zn2+
6,31
11,19
14,31
17,70
-
Иодидные комплексы (L= I)
Центральный
ион
Igb
Igb
Igb
Igb
Igb
Igb
Ag+
6,58
11,74
13,68
13,10
-
-
Cd2+
2,17
3,67
4,34
5,35
5,15
-
Hg2+
12,87
23,82
27,60
29,83
-
-
Pb2+
1,26
2,80
3,42
3,92
-
-
197

Окончание табл. 4
Фторидные комплексы (L=F )
Центральный
ион
lgβι
lgβ2
lgβ3
lgβ4
lgβ5
⅛b
Al3+
7,10
11,98
15,83
18,53
20,20
20,67
Fe3+
6,04
10,74
13,74
15,74
16,10
16,10
Роданидные (тиоцианатные) комплексы (L= SCN )
Центральный ион
lgβι
⅛b
lgβ3
lgβ4
Ag+
4,75
8,23
9,45
9,67
Co3+
1,72
1,6
1,8
-
Cu2+
2,30
3,65
5,19
6,52
Hg2+
-
17,60
20,40
21,20
Fe3+
3,03
4,33
4,63
4,53
Хло
ридные комплексы (L=Cl-)
Центральный ион
lgβι
lgβ2
lgβ3
lgβ4
lgβ5
lgβ6
Ag+
3,04
5,04
5,04
5,30
-
-
Au3+
-
-
16,96
21,30
-
-
Hg2+
6,74
13,22
14,17
15,22
-
-
Pb2+
6,1
10,5
12,9
15,5
13,4
11,3
Цианидные комплексы (L=CN-)
Центральный
ион
lgβι
lgβ2
lgβ3
lgβ4
lgβ5
lgβ6
Ag+
-
19,85
20,55
19,42
-
-
Cd2+
5,18
9,60
13,92
17,11
-
-
Fe3+
-
-
-
-
-
43,9
Fe2+
-
-
-
-
18,6
36,9
Hg2+
17,00
32,75
36,31
38,97
39,83
40,62
Ni2+
-
-
22,2
31,0
30,3
-
Zn2+
-
11,07
16,05
19,62
-
-
Комплексы с ЭДТА (L=Y4)
Центр.
ион
Ag+
Al3+
Ba2+
Ca2+
Cd2+
Co2+
Cr3+
Cu2+
Fe2+
lgβ
7,31
16,5
7,78
10,59
16,46
16,33
23,40
18,80
14,20
Центр.
ион
Fe3+
Hg2+
Mg2+
Mn2+
Ni2+
Pb2+
Sr2+
Tl+
Zn2+
lgβ
24,23
21,8
9,12
14,04
18,62
18,04
8,80
6,53
16,26
198

Таблица 5
Стандартные окислительно-восстановительные потенциалы (Е0) при 25 0С
Элемент
Полуреакция восстановления
E0, В
Ag
Ag+ + e = Ag0
0,7994
Al
Al3+ + 3e = Al0
-1,66
As
AsO43^ + 2H+ + 2e = AsOs3' + H2O
+0,57
Br
Вг2(ж) + 2e = 2Br -
HBrO + H+ + 2e = Br - + H2O
2BrO3- + 12H+ + 10e = Br2 + 6H2O
2BrO3- + 6H+ + 6e = Br - + 3H2O
+1,07
+1,59
+1,52
+1,45
C
2CO2 + 2H+ = H2C2O4
-0,49
Cd
Cd2+ + 2e = Cd0
-0,403
Ce
Ce4+ (Се^дЪ2- ) + e = Ce3+ + (3SO42-)
+1,44
Cl
Cl2 + 2e = 2Cl-
HClO + H+ + 2e = Cl- + H2O
2HClO + 2H+ + 2e = Cl2 + 2H2O
ClO3- + 6H+ + 6e = Cl- + 3H2O
2ClO3- + 12H+ + 10e = Cl2 + 6H2O
+1,359
+1,50
+1,63
+1,45
+1,47
Cr
Cr3+ + 3e = Cr0
Cr2O72- + 14H+ + 6e = 2Cr3+ + 7H2O
CrO/' + 4H2O + 3e = Cr(OH)3 + 5OH-
-0,74
+1,33
-0,13
Fe
Fe3+ + e = Fe2+
Fe2+ + 2e = Fe0
+0,771
-0,473
H
H2O2 + 2H+ + 2e = 2H2O
O2 + 2H+ + 2e = H2O2
H2O2+ 2e = 2ОН-
+1,77
+0,682
+0,88
Hg
2Hg2+ + 2e = Hg22+
Hg2+ + 2e = I Ig0( ж)
Hg22+ + 2e = 2Hg'0(>ι<)
Hg2Cl2 + 2e = 21 Ig0( ж) + 2Cl
Hg2SO4 + 2e = 21 Ig0( ж) + SO42-
+0,907
+0,850
+0,792
+0,2682
+0,615
I
I2 + 2e = 2I-
HIO + H+ + 2e = I- + H2O
2HIO + 2H+ + 2e = I2 + 2H2O
IO3- + 6H+ + 6e = I- + 3H2O
2IO3- + 12H+ + 10e = I2 + 6H2O
+0,536
+0,99
+1,45
+1,08
+1,19
Mn
Mn3+ + e = Mn2+
MnO2 + 4H+ + 2e = Mn2++ 2H2O
MnO4- + 4H+ + 3e = MnO2 + 2H2O
MnO4- + 8H+ + 5e = Mn2+ + 4H2O
MnO4- + 2H2O + 3e = MnO2 + 4OH-
MnO4- + e = MnO42-
+1,51
+1,23
+1,69
+1,51
+0,60
+0,558
199

Окончание табл. 5
N
NO3- + 3H+ + 2e = HNO2 + H2O
NO3- + H2O + 2e = NO2- + 2OH-
NO3- + 2H+ + e = NO2 + H2O
NO3- + 4H+ + 3e = NO + 2H2O
NO3- + 10H+ + 8e = NH4+ + 3H2O
+0,94
+0,01
+0,80
+0,96
+0,87
Ni
Ni2+ + 2e = Ni0
-0,228
P
H3PO4 + 2H+ + 2e = H3PO3 + H2O
-0,276
Pb
Pb2+ + 2e = Pb0
Pb4+ + 2e = Pb2+
PbO + 2H+ + 2e = Pb0+ H2O
PbO2 + 4H+ + 2e = Pb2++ 2H2O
-0,126
+1,66
+0,25
+1,455
S
S+ 2H+ + 2e = H2S
SO42- + 4H+ + 2e = H2SO3 + H2O
SO42- + H2O + 2e = SO32- + 2OH-
S2O82- + 2e = 2SO42-
S4O62- + 2e = 2S2O32-
SO32- + 6H+ + 4e = S + 3H2O
+0,14
+0,17
-0,93
+2,01
+0,09
+0,45
Sn
Sn2+ + 2e = Sn0
Sn4+ + 2e = Sn2+
HSnO3- + H2O + 2e = Sn + 3OH-
-0,14
+0,15
-0,91
Ti
Ti4+ + e = Ti3+
+0,092
Tl
Tl3+ + 2e =Tl+
+1,28
V
VO2+ + e = VO+
VO2+ + 2H+ + e = VO2+ + H2O
-0,044
+0,9996
Zn
Zn2+ + 2e = Zn0
-0,764
Таблица 6
Константы растворимости важнейших малорастворимых веществ
Элемент
Формула вещества
Ks0 (ПРт)
AgBr
5,3·10-13
Ag2CO3
1,2·10-12
AgCl
1,78·10-10
Ag
Ag2CrO4
1,1·10-12
AgI
8,3·10-17
Ag3PO4
1,3·10-20
Ag2S
2,0·10-50
Δ1
AlPO4
5,75·10-19
Al
Al(OH)3 (Al3+, 3OH-)
1,0·10-32
200

Продолжение табл. 6
Элемент
Формула вещества
Ks0 (ПРт)
Ba
ВаСОз
BaCrO4
BaSO4
4,0·10-10
1,2·10-10
1,1-10'10
Ca
СаСОз
CaC2O4
CaCrO4
CaF2
CaHPO4 (Ca2+, HPO4-)
Ca(OH)2 (Ca2+, 2OH-)
Ca3(PO4)2
CaSO4
3,8·10-9
2,3·10-9
7,1·10-4
4,0·10-11
2,7·10-7
5,5·10-6
2,0·10-29
2,5·10-5
Cd
CdS
1,6·10-28
Cr
Cr(OH)3 (Cr3+, 3OH-)
6,3·10-31
Cu
CuBr
CuI
CuCl
CuS
Cu2S
5,25·10-9
1,2·10-6
1,1·10-12
6,3·10-36
2,5·10-48
Fe
Fe(OH)3 (Fe3+, 3OH-)
FeS
6,3·10-38
5,0·10-18
Hg
Hg2Cl2
HgS (черный)
HgS (красный)
Hg2S
Hg2SO4
1,3·10-18
1,6·10-52
4,0·10-53
1,0·10-47
6,8·10-7
Mg
MgCO3
MgF2
MgNH4PO4
Mg(OH)2
2,1·10-5
6,5·10-9
2,5·10-13
6,0·10-10
Mn
Mn(OH)2 (Mn2+, 2OH-)
MnS (телесного цвета)
1,9·10-13
2,5·10-10
Ni
Ni(OH)2
NiS a
NiS b
NiS g
2,0·10-15
3,2·10-19
1,0·10-24
2,0·10-26
201

Окончание табл. 6
Элемент
Формула вещества
Ks0 (ПР)
PbCO3
7,5∙10-14
PbCl2
1,6×10-5
PbCrO4
1,8×10-14
Pb
PbI2
1,1×10-9
PbS
2,5×10-27
PbSO4
1,6∙10^8
Sn(OH)2 (Sn2+, 2OH-)
6,3∙10^27
Sn(OH)2 (SnOH+, OH-)
4,6×10-15
Sn
Sn(OH)2 (H+, HSnO2-)
1,3×10-15
Sn(OH)4
1,0×10-57
SnS
2,5∙10-27
SrCO3
1,1×10^1°
SrCrO4
3,6×10-5
Sr
Sr(OH)2
3,2×10-4
SrSO4
3,2∙10-7
Tl
TlI
5,75∙10-8
ZnCO3
1,45∙10-11
Zn(OH)2 (Zn2+, 2OH-)
1,2×10-17
Zn
Zn(OH)2 (ZnOH+, OH-)
3,0×10-13
ZnS сфалерит
1,6 × 10-24
ZnS вюрцит
2,5∙10-22
Таблица 7
Молярные доли свободных ионов Y4- (aY4-)
для этилендиаминтетрауксусной кислоты в растворах с различными
значениями рН
рН
aγ4-
рН
aγ4-
1,0
2,1∙10-18
7,0
4,8∙10-4
2,0
3,7∙ 10-14
8,0
5,4∙10-3
3,0
2,5∙10-11
9,0
5,2∙10-2
4,0
3,6∙10-9
10,0
3,5∙10-1
5,0
3,5∙10-7
11,0
8,5∙10-1
6,0
2,2∙10-5
12,0
9,8∙10-1
202

Таблица 8
Коэффициенты Стьюдента t для различной
доверительной вероятности
Число
степеней
свободы f
Доверительная вероятность Р
0,90
0,95
0,98
0,99
1
6,31
12,71
31,82
63,66
2
2,92
4,30
6,97
9,92
3
2,35
3,18
4,54
5,84
4
2,13
2,78
3,75
4,60
5
2,01
2,57
3,37
4,03
6
1,94
2,45
3,14
3,71
7
1,89
2,36
3,00
3,50
8
1,86
2,31
2,90
3,36
9
1,83
2,26
2,82
3,25
10
1,81
2,23
2,76
3,17
11
1,80
2,20
2,72
3,11
12
1,78
2,18
2,68
3,05
13
1,77
2,16
2,65
3,01
14
1,76
2,14
2,62
2,98
15
1,75
2,13
2,60
2,95
16
1,75
2,12
2,58
2,92
17
1,74
2,11
2,57
2,90
18
1,73
2,10
2,55
2,88
19
1,73
2,09
2,54
2,86
20
1,73
2,09
2,53
2,85
30
1,70
2,04
2,46
2,75
40
1,68
2,02
2,42
2,70
60
1,67
2,00
2,39
2,66
¥
1,64
1,96
2,33
2,58
Таблица 9
Значения ^-критерия
п
Р
п
Р
0,90
0,95
0,99
0,90
0,95
0,99
3
0,89
0,94
0,99
7
0,43
0,51
0,64
4
0,68
0,77
0,89
8
0,40
0,47
0,58
5
0,56
0,64
0,76
9
0,37
0,44
0,53
6
0,48
0,56
0,70
10
0,34
0,41
0,48
203

Численные значения критерия Фишера F
при доверительной вероятности Р = 0,95
Таблица 10
f1
f2 ∖
1
2
3
4
5
6
8
12
24
¥
1
164,4
199,5
215,7
224,6
230,2
234,0
239,0
244,9
244,0
254,3
2
18,5
19,2
19,2
19,3
19,3
19,3
19,4
19,4
19,5
19,5
3
10,1
9,6
9,3
9,1
9,0
8,9
8,8
8,7
8,6
8,5
4
7,7
6,9
6,6
6,4
6,3
6,2
6,0
5,9
5,8
5,6
5
6,6
5,8
5,4
5,2
5,1
5,0
4,82
4,7
4,5
4,4
6
6,0
5,1
4,7
4,5
4,4
4,3
4,2
4,0
3,8
3,7
7
5,6
4,7
4,4
4,1
4,0
3,9
3,7
3,6
3,4
3,2
8
5,3
4,5
4,1
3,8
3,7
3,6
3,4
3,3
3,1
2,9
9
5,1
4,3
3,9
3,6
3,5
3,4
3,2
3,1
2,9
2,7
10
5,0
4,1
3,7
3,5
3,3
3,2
3,1
2,9
2,8
2,5
11
4,8
4,0
3,6
3,4
3,2
3,1
3,0
2,8
2,6
2,4
12
4,8
3,9
3,5
3,3
3,1
3,0
2,9
2,7
2,5
2,3
13
4,7
3,8
3,4
3,2
3,0
2,9
2,8
2,6
2,4
2,2
14
4,6
3,7
3,3
3,1
3,0
2,9
2,7
2,5
2,3
2,1
20
4,4
3,5
3,1
2,9
2,7
2,6
2,5
2,3
2,1
1,8
¥
3,8
3,0
2,6
2,4
2,2
2,1
2,0
1,8
1,5
1,0
Таблица 11
Максимально допустимые абсолютные погрешности (мл)
мерной посуды 2 класса ( мл )
Бюретки
Мерные кол¬
бы
Пипетки
Номиналь¬
ный
объем
±V
Номинальный
объем
±V
Номинальный
объем
±V
Мора
«Две
метки»
100
0,2
2000
1,0
100
0,16
0,20
50
0,1
1000
0,6
50
0,12
0,16
25
0,06
500
0,3
25
0,10
0,10
1
0,015
250
0,2
20
0,06
0,08
0,5
0,015
200
0,2
10
0,04
0,06
100
0,2
5
0,03
0,04
50
0,1
2
0,015
0,02
25
0,06
1
0,015
0,02
204

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ	 з
ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ И РЕКОМЕНДАЦИИ	 5
1.1.	Условные обозначения и размерности величин	 5
1.2.	Правила вычисления. Условие значимости цифр	 6
1.3.	Чувствительность аналитических реакций	 10
Задачи для самоконтроля	 12
ГЛАВА 2. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В РЕАЛЬНЫХ
СИСТЕМАХ	 14
2.1.	Влияние электростатических взаимодействий на поведение
ионов в растворе. Ионная сила раствора. Коэффициент активности	15
2.2.	Влияние химических факторов на равновесие.
Молярная доля компонента в растворе	 18
2.3.	Направление химических реакций. Способы выражения
констант равновесия. Ступенчатые и общие константы равновесия	22
Задачи для самоконтроля	 25
ГЛАВА 3. КИСЛОТНО-ОСНОВНОЕ (ПРОТОЛИТИЧЕСКОЕ)
РАВНОВЕСИЕ	 26
3.1.	Расчет [H+], [OH-], рН, рОН в растворах сильных и слабых
кислот и оснований	 26
3.2.	Буферные растворы	 з5
3.3.	Расчеты при приготовлении растворов протолитов
с заданным значением рН	 з9
Задачи для самоконтроля	 4з
ГЛАВА 4. РАВНОВЕСИЕ В РАСТВОРАХ КОМПЛЕКСНЫХ
СОЕДИНЕНИЙ	 44
Задачи для самоконтроля	 50
ГЛАВА 5. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНОЕ
РАВНОВЕСИЕ	 52
5.1.	Оценка окислительно-восстановительной способности веществ
и направления окислительно-восстановительной реакции	 52
5.1.1.	Расчет стандартного потенциала полуреакции, являющейся
сочетанием двух полуреакций	 55
5.2.	Вычисление потенциала в реальных условиях. Уравнение
Нернста	 57
5.3.	Влияние электростатических и химических взаимодействий
на величину потенциала. Формальный потенциал	 58
5.3.1.	Влияние ионной силы на потенциал	 59
5.3.2.	Влияние рН раствора на величину потенциала	 60
5.3.3.	Влияние комплексообразования на величину потенциала 	61
5.3.4.	Влияние образования малорастворимых соединений на
потенциал	 6з
205

5.4.	Расчеты с использованием константы равновесия
окислительно-восстановительной реакции	 66
5.4.1.	Расчет константы равновесия по стандартным
и формальным потенциалам	 66
5.4.2.	Вычисление равновесных концентраций
по величине константы	 68
5.4.3.	Вычисление растворимости веществ
в окислительно-восстановительной реакции	 70
5.5.	Расчеты с использованием ЭДС гальванического элемента		72
Задачи для самоконтроля	 76
ГЛАВА 6. ГЕТЕРОГЕННОЕ РАВНОВЕСИЕ В СИСТЕМЕ
ОСАДОК - РАСТВОР	 78
6.1.	Определение условий выпадения осадка
и разделения ионов	 79
6.2.	Вычисление растворимости малорастворимого электролита		83
6.2.1.	Влияние ионной силы раствора на растворимость	 86
6.2.2.	Влияние одноименного иона на растворимость осадка		87
6.2.3.	Влияние конкурирующих реакций на растворимость	 89
6.2.4.	Вклад молекулярной растворимости
в общую растворимость	 93
Задачи для самоконтроля	 96
ГЛАВА 7. РАСЧЕТЫ В ГРАВИМЕТРИИ	 97
7.1.	Гравиметрический фактор и его значение	 99
7.2.	Расчет величины навески анализируемой пробы	 101
7.3.	Расчет количества осадителя	 102
7.4.	Расчет потерь при промывании осадка	 105
7.5.	Расчет результатов анализа в гравиметрии	 109
Задачи для самоконтроля	 111
ГЛАВА 8. РАСЧЕТЫ В ТИТРИМЕТРИИ	 113
8.1.	Сущность титриметрии	 113
8.2.	Методы, приемы и способы титрования	 114
8.3.	Способы выражения концентрации растворов в титриметрии		118
8.3.1.	Вычисление молярной массы эквивалента	 119
8.3.2.	Способы выражения концентрации растворов	 120
8.3.3.	Расчеты при приготовлении рабочих растворов
и установлении их концентрации	 122
Задачи для самоконтроля	 125
8.4.	Расчеты результатов анализа в титриметрии	 126
Задачи для самоконтроля	 131
8.5.	Построение кривых титрования	 133
8.5.1.	Расчет кривых кислотно-основного титрования	 135
8.5.2.	Расчет кривых окислительно-восстановительного
титрования	 146
206

8.5.3.	Расчет кривых титрования в методах осаждения	 152
8.5.4.	Расчет кривых титрования в методе комплексонометрии		15з
Задачи для самоконтроля	 157
8.6.	Индикаторные погрешности титрования	 158
Задачи для самоконтроля	 168
ГЛАВА 9. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
КОЛИЧЕСТВЕННОГО АНАЛИЗА	 170
9.1.	Классификация и оценка погрешностей количественного
анализа	 170
9.2.	Сравнение результатов двух методов количественного анализа..	177
9.3.	Суммирование погрешностей	 181
Задачи для самоконтроля	 186
ГЛАВА 10. РАСЧЕТЫ В ИОНООБМЕННОЙ
ХРОМАТОГРАФИИ	 188
Задачи для самоконтроля	 191
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА	 19з
ПРИЛОЖЕНИЕ	 195
207

Учебное издание
Шрайбман Галина Николаевна
Халфина Полина Даниловна
Булгакова Ольга Николаевна
Иванова Наталья Владимировна
РЕШЕНИЕ ЗАДАЧ
ПО АНАЛИТИЧЕСКОЙ ХИМИИ
Редактор З. А. Кунашева
Технический редактор В. П. Долгих
Подписано в печать г. Формат 60x84 1/16.
Печать офсетная. Бумага офсетная № 1. Печ. л. 1з.
Тираж 100 экз. Заказ № 55.

Кемеровский государственный университет,
650043, г. Кемерово, ул. Красная, 6.

Отпечатано в типографии ООО Студия Рекламы «Реформа», 650002,
г. Кемерово, ул. Институтская, 12-16,
тел. 8(3842)90-09-02, 65-72-72, 961-729-2829.


                

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)