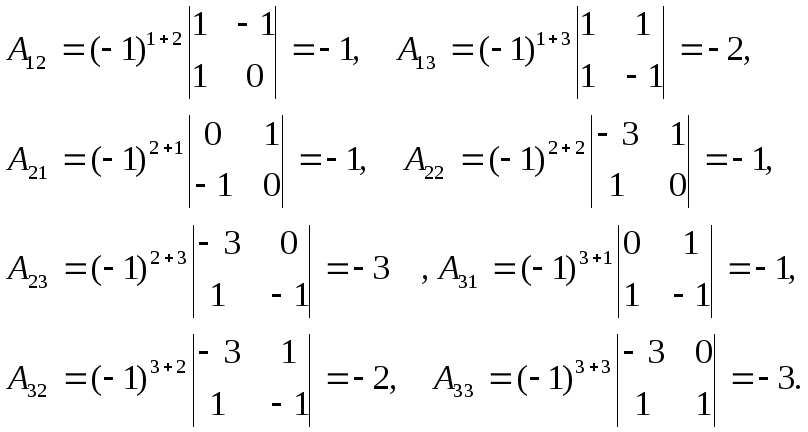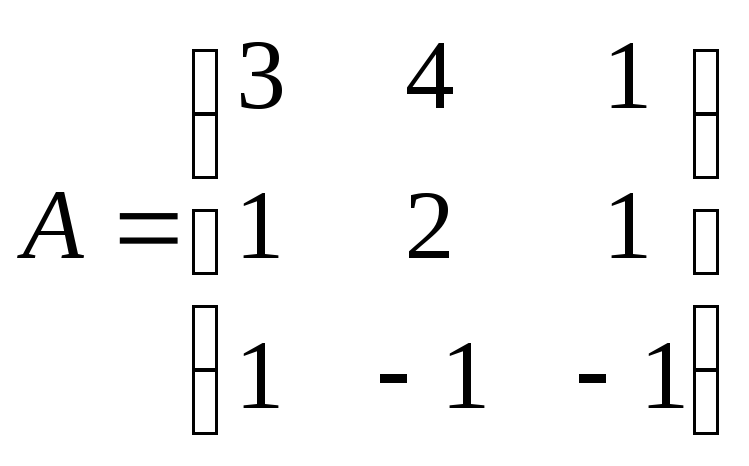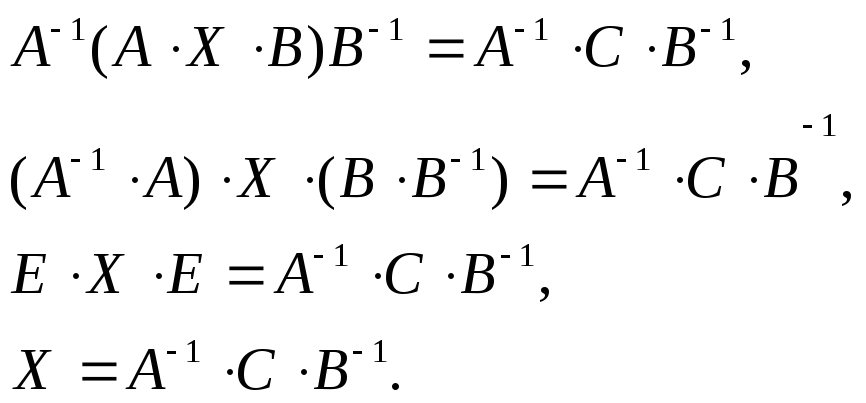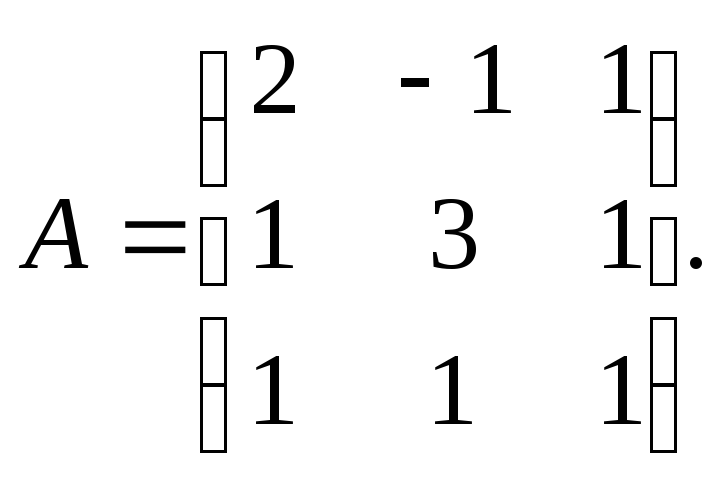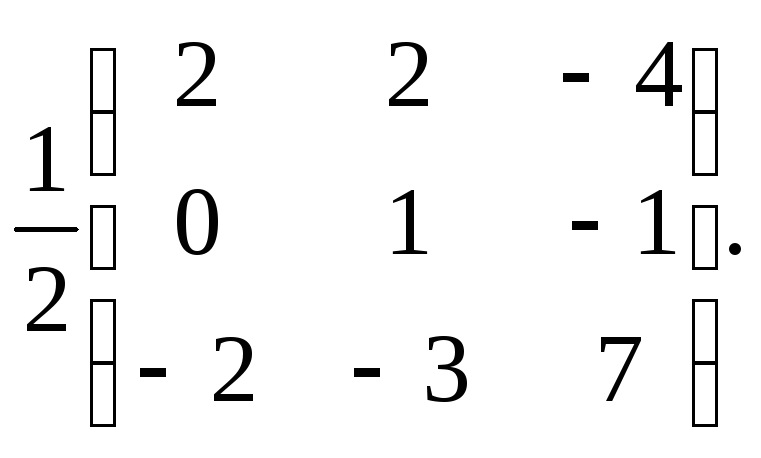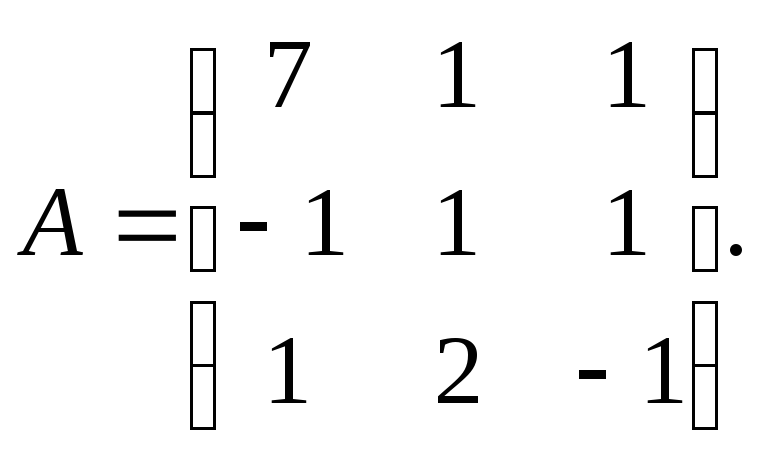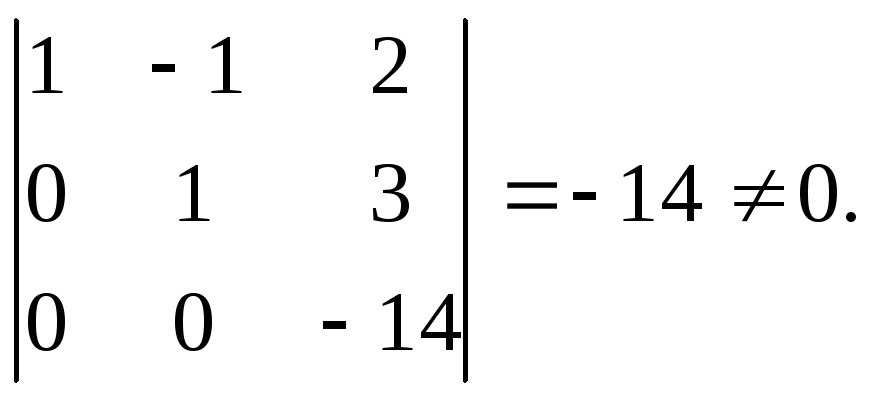Обратная матрица примеры с решением 3х3 пошаговая инструкция - Большая энциклопедия инструкций и руководств

Загрузить PDF

Как правило, обратные операции используются для упрощения сложных алгебраических выражений. Например, если в задаче присутствует операция деления на дробь, можно заменить ее операцией умножения на обратную дробь, что является обратной операцией. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.

1
Проверьте определитель матрицы. Сначала вычислите определитель матрицы. Если определитель равен 0, то обратную матрицу вычислить нельзя. Определитель матрицы М обозначается как det(М).^[1]
- В случае матрицы размером 3х3 сначала обязательно вычислите определитель.
- Чтобы получить подробную информацию, прочитайте статью Как найти определитель матрицы 3х3.
2
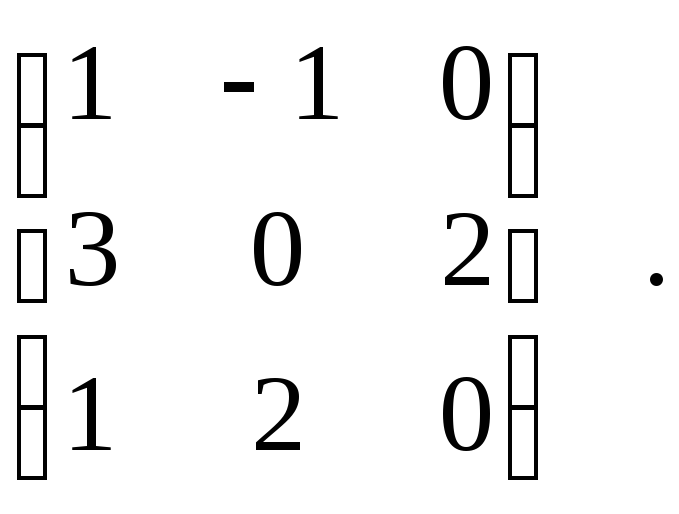
Транспонируйте исходную матрицу. Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.^[2]
- Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.
3
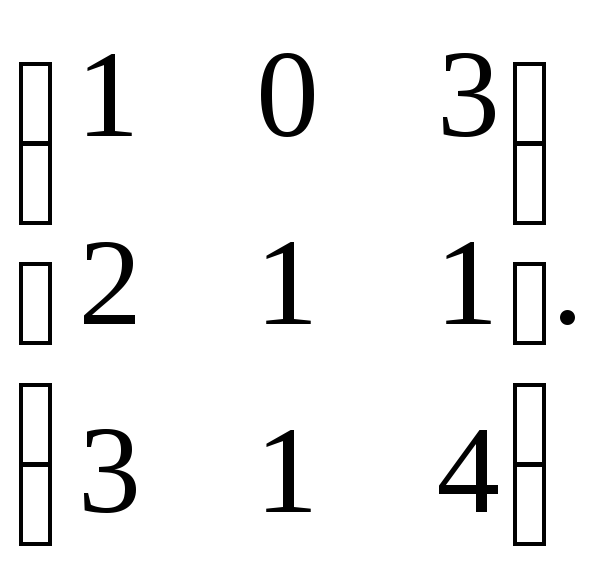
Найдите определить каждой матрицы размером 2х2. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.^[3]
- Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
- Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
- Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.
4
Создайте матрицу кофакторов. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.^[4]
- Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
- Подробную информацию о матрицах кофакторов можно найти в интернете.
- Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).
5
Разделите каждый элемент присоединенной матрицы на определитель. Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель. Результат каждой операции деления запишите там, где находится соответствующий элемент. Так вы найдете матрицу, обратную исходной.^[5]
- Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
- В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.
Реклама

1
Единичную матрицу напишите рядом с исходной матрицей. Запишите исходную матрицу М, справа от нее нарисуйте вертикальную черту, а затем справа от черты запишите единичную матрицу. Получится матрица с тремя строками и шестью столбцами (большая матрица).^[6]
- Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Подробную информацию о единичных матрицах можно найти в интернете.
2
Выполните элементарные преобразования, чтобы из исходной матрицы получить единичную. Наша цель заключается в том, чтобы создать единичную матрицу на левой половине большой матрицы. Элементарные преобразования, выполняемые на левой половине большой матрицы, нужно выполнять и на ее правой половине (напомним, что правой половиной большой матрицы является единичная матрица).^[7]
- Помните, что элементарные преобразования включают в себя операции скалярного умножения, а также сложения и вычитания строк, чтобы обособить определенные элементы. Подробную информацию об элементарных преобразованиях матриц можно найти в интернете.
3

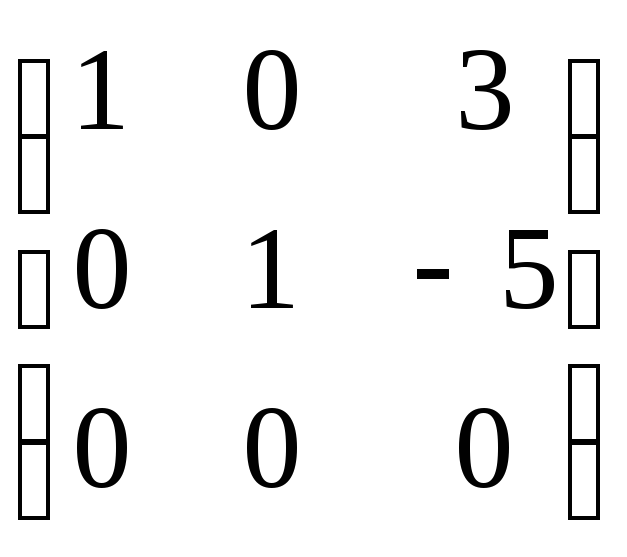
Продолжайте преобразовывать большую матрицу до тех пор, пока ее левая половина (то есть исходная матрица) не превратится в единичную матрицу. Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Когда исходная матрица станет единичной, на правой половине большой матрицы вы получите матрицу, обратную исходной.^[8]
4

Запишите обратную матрицу. Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.^[9]

Реклама

1

Выберите калькулятор, который работает с матрицами. С помощью простых калькуляторов нельзя найти обратную матрицу, но это можно сделать на хорошем графическом калькуляторе, таком как Texas Instruments TI-83 или TI-86.^[10]
2

Введите исходную матрицу в память калькулятора. Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2^nd и Matrix.
3

Выберите меню Edit (Редактирование). Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).^[11]
4

Введите обозначение матрицы. Большинство графических калькуляторов умеет работать с 3-10 матрицами, которые можно обозначить буквами А-J. Как правило, просто выберите [A], чтобы обозначить исходную матрицу. Затем нажмите кнопку Enter (Ввод).^[12]
5

Введите размер матрицы. В данной статье говорится о матрицах 3х3. Но графические калькуляторы умеют работать с матрицами больших размеров. Введите количество строк, нажмите кнопку Enter, затем введите количество столбцов и еще раз нажмите кнопку Enter.^[13]
6
Введите каждый элемент матрицы. На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.^[14]
- Чтобы ввести отрицательное значение элемента, нажмите специальную кнопку со знаком «минус», а не кнопку операции вычитания; в противном случае калькулятор не сможет правильно обработать это число.
- Чтобы перейти к определенному элементу матрицы, воспользуйтесь кнопками со стрелками.
7

Выйдите из режима введения матрицы. Введя значения всех элементов матрицы, нажмите кнопку Quit (Выход). (Или, если необходимо, нажмите кнопки 2^nd и Quit.) Так вы выйдете из режима введения матрицы и перейдете на основной экран калькулятора.^[15]
8
Воспользуйтесь специальной кнопкой, чтобы найти обратную матрицу. Во-первых, войдите в режим ввода матрицы (нажмите кнопку Matrix) и нажмите кнопку Names (Обозначения), чтобы выбрать обозначение матрицы, которое вы указали ранее (скорее всего, [A]). Затем нажмите кнопку выполнения обратной операции, которая помечена как $x^{{-1}}$ (возможно, сначала придется нажать кнопку 2^nd). На экране отобразится $A^{{-1}}$ . Нажмите Enter, чтобы вывести на экран обратную матрицу.^[16]
- Не пользуйтесь кнопкой ^ (кнопка для возведения в степень), чтобы ввести A^-1 посредством нажатия нескольких клавиш. Калькулятор не поймет эту операцию.
- Если после нажатия на кнопку обратной операции на экране отобразилось сообщение об ошибке, скорее всего, обратная матрица не существует. Чтобы убедиться в этом, вычислите определить матрицы.
9
Преобразуйте значения элементов обратной матрицы в обыкновенные дроби. По умолчанию калькулятор отображает значения элементов обратной матрицы в виде десятичных дробей; в большинстве случаев такую матрицу нельзя записать в ответе. Поэтому десятичные значения элементов обратной матрицы необходимо преобразовать в обыкновенные дроби (в редчайших случаях все элементы обратной матрицы будут целыми числами).^[17]
- Во многих графических калькуляторах есть кнопка, позволяющая преобразовывать десятичные дроби в обыкновенные. Например, на калькуляторе TI-86 нажмите Math (Математика), выберите Misc (Другое), затем выберите Frac (Дробь) и нажмите Enter. Десятичные дроби будут автоматически преобразованы в обыкновенные.
Реклама

Советы

Описанные методы можно применять к матрицам, элементами которых являются не только числа, но и переменные, неизвестные и даже алгебраические выражения.
Вычисления записывайте на бумаге, так как найти обратную матрицу в уме крайне сложно.
Существуют компьютерные программы, которые умеют работать с любыми матрицами^[18], включая матрицы 30х30.
Проверьте ответ, полученный с помощью любого из описанных в этой статье методов. Для этого перемножьте исходную (М) и обратную (М¹) матрицы. Помните, что М*М¹ = М¹*М = 1. Единичная матрица – это матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Если результат перемножения не равен 1, проверьте ваши вычисления.

Предупреждения

Не все матрицы 3×3 обратимы. Если определитель матрицы равен 0, обратная матрица не существует. (Обратите внимание, что в вычислениях присутствует деление на определитель, а на 0 делить нельзя.)

Об этой статье

Эту страницу просматривали 92 650 раз.

Была ли эта статья полезной?

Источник

Download Article

Struggling with a tough algebra problem? Finding the inverse of a matrix is key to solving systems of linear equations. Plus, inverse operations provide an easy way to simplify difficult problems in general. For example, if a problem asks you to divide by a fraction, you can more easily multiply by its reciprocal. That’s a basic inverse operation! Similarly, since there’s no division operator for matrices, you need to multiply by the inverse matrix. We’ve put together a step-by-step guide to calculating the inverse of a 3×3 matrix by hand, using determinants and linear row reduction. Then, we’ll even teach you how to find the inverse with an advanced graphing calculator.

1
Check the determinant of the matrix. You need to calculate the determinant of the matrix as an initial step. If the determinant is 0, then your work is finished, because the matrix has no inverse. The determinant of matrix M can be represented symbolically as det(M).^[1]
- For a 3×3 matrix, find the determinant by first
2
Transpose the original matrix. Transposing means reflecting the matrix about the main diagonal, or equivalently, swapping the (i,j)th element and the (j,i)th. When you transpose the terms of the matrix, you should see that the main diagonal (from upper left to lower right) is unchanged.^[2]
- Another way to think of transposing is that you rewrite the first row as the first column, the middle row becomes the middle column, and the third row becomes the third column. Notice the colored elements in the diagram above and see where the numbers have changed position.
Advertisement
3
Find the determinant of each of the 2×2 minor matrices. Every item of the newly transposed 3×3 matrix is associated with a corresponding 2×2 “minor” matrix.^[3] To find the right minor matrix for each term, first highlight the row and column of the term you begin with. This should include five terms of the matrix. The remaining four terms make up the minor matrix.^[4]
- In the example shown above, if you want the minor matrix of the term in the second row, first column, you highlight the five terms that are in the second row and the first column. The remaining four terms are the corresponding minor matrix.
- Find the determinant of each minor matrix by cross-multiplying the diagonals and subtracting, as shown.
- For more on minor matrices and their uses, see Understand the Basics of Matrices.
4
Create the matrix of cofactors. Place the results of the previous step into a new matrix of cofactors by aligning each minor matrix determinant with the corresponding position in the original matrix. Thus, the determinant that you calculated from item (1,1) of the original matrix goes in position (1,1). You must then reverse the sign of alternating terms of this new matrix, following the “checkerboard” pattern shown.^[5]
- When assigning signs, the first element of the first row keeps its original sign. The second element is reversed. The third element keeps its original sign. Continue on with the rest of the matrix in this fashion. Note that the (+) or (-) signs in the checkerboard diagram do not suggest that the final term should be positive or negative. They are indicators of keeping (+) or reversing (-) whatever sign the number originally had.
- The final result of this step is called the adjugate matrix of the original. This is sometimes referred to as the adjoint matrix. The adjugate matrix is noted as Adj(M).
5
Divide each term of the adjugate matrix by the determinant. Recall the determinant of M that you calculated in the first step (to check that the inverse was possible). You now divide every term of the matrix by that value. Place the result of each calculation into the spot of the original term. The result is the inverse of the original matrix.^[6]
- For the sample matrix shown in the diagram, the determinant is 1. Therefore, dividing every term of the adjugate matrix results in the adjugate matrix itself. (You won’t always be so lucky.)
- Instead of dividing, some sources represent this step as multiplying each term of M by 1/det(M). Mathematically, these are equivalent.

1
Adjoin the identity matrix to the original matrix. Write out the original matrix M, draw a vertical line to the right of it, and then write the identity matrix to the right of that.^[7] You should now have what appears to be a matrix with three rows of six columns each.^[8]
- Recall that the identity matrix is a special matrix with 1s in each position of the main diagonal from upper left to lower right, and 0s in all other positions.
2
Perform linear row reduction operations. Your objective is to create the identity matrix on the left side of this newly augmented matrix. As you perform row reduction steps on the left, you must consistently perform the same operations on the right, which began as your identity matrix.^[9]
- Remember that row reductions are performed as a combination of scalar multiplication and row addition or subtraction, in order to isolate individual terms of the matrix. For a more complete review, see Row-Reduce Matrices.
3

Continue until you form the identity matrix. Keep repeating linear row reduction operations until the left side of your augmented matrix displays the identity matrix (diagonal of 1s, with other terms 0). When you have reached this point, the right side of your vertical divider will be the inverse of your original matrix.^[10]
4

Write out the inverse matrix. Copy the elements now appearing on the right side of the vertical divider as the inverse matrix.^[11]

1

Select a calculator with matrix capabilities. Simple 4-function calculators will not be able to help you directly find the inverse. However, due to the repetitive nature of the calculations, an advanced graphing calculator, such as the Texas Instruments TI-83 or TI-86, can greatly reduce the work.^[12]
2

Enter your matrix into the calculator. First, enter your calculator’s Matrix function by pressing the Matrix key, if you have one. On the Texas Instruments calculators, you may need to press 2^nd Matrix.^[13]
3

Select the Edit submenu. To reach the submenu, you may need to use the arrow buttons or choose the appropriate function key at the top of your calculator’s keypad, depending on the layout of your calculator.^[14]
4

Select a name for your matrix. Most calculators are equipped to work with anywhere from 3 to 10 matrices, labeled with letters A through J. Typically, just choose [A] to work with. Hit the Enter key after making your selection.^[15]
5

Enter the dimensions of your matrix. This article is focusing on 3×3 matrices. However, the calculator can handle larger sizes. Enter the number of rows, then press Enter, and then the number of columns, and Enter.^[16]
6
Enter each element of the matrix. The calculator screen will show a matrix. If you previously were working with the matrix function, the prior matrix will appear on the screen. The cursor will highlight the first element of the matrix. Type in the value of the matrix you wish to solve, and then Enter. The cursor will move automatically to the next element of the matrix, overwriting any previous numbers.^[17]
- If you wish to enter a negative number, use your calculator’s negative button (-) and not the minus key. The matrix function will not read the number properly.
- If necessary, you can use your calculator’s arrow keys to jump around the matrix.
7

Quit the Matrix function. After you have entered all values of the matrix, press the Quit key (or 2^nd Quit, if necessary). This will exit you from the Matrix function and return you to the main display screen of your calculator.^[18]
8
Use the inverse key to find the inverse matrix. First, reopen the Matrix function and use the Names button to select the matrix label that you used to define your matrix (probably [A]). Then, press your calculator’s inverse key, $x^{{-1}}$ . This may require using the 2^nd button, depending on your calculator. Your screen display should show $A^{{-1}}$ . Press Enter, and the inverse matrix should appear on your screen.^[19]
- Do not use the ^ button on your calculator to try entering A^-1 as separate keystrokes. The calculator will not understand this operation.
- If you receive an error message when you enter the inverse key, chances are that your original matrix does not have an inverse. You may want to go back and calculate the determinant to find out.
9
Convert your inverse matrix to exact answers. The first calculation that the calculator will give you is in decimal form. This is not considered “exact” for most purposes. You should convert the decimal answers to fractional form, as necessary. (If you are very lucky, all your results will be integers, but this is rare.)^[20]
- Your calculator probably has a function that will automatically convert the decimals to fractions. For example, using the TI-86, enter the Math function, then select Misc, and then Frac, and Enter. The decimals will automatically appear as fractions.
10

Most graphing calculators also have square bracket keys (on TI-84 it’s 2nd + x and 2nd + -) which can be used to type in a matrix without using the matrix function. Note: The calculator will not format the matrix until after the enter/equals key has been used (i.e. everything will be one line and not pretty).

Practice Problems and Answers

Add New Question

Question

How do you use elementary row operations to get the inverse of a matrix?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics

Expert Answer

Begin by setting up the system [A | I] where I is the identity matrix. Then, use elementary row operations to make the left hand side of the system reduce to I. The resulting system will be [I | A⁻¹] where A⁻¹ is the inverse of A.
Question

How do I evaluate the inverse of the matrix {1 2 -4}{0 -2 3}{5 0 4}?

Find the determinant, then determine the co-factor matrix. Find the adj of the co-factor matrix, then divide through each term by the determinant.
Question

Are there any shortcuts for finding the inverse of a 3×3 matrix?

The methods shown in the article is as simple as it gets unfortunately; you can do drills and make up your own 3×3 matrices to find the inverse of in order to remember the steps.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Write down all your steps as it is extremely difficult to find the inverse of a 3×3 matrix in your head.
You can follow these steps to find the inverse of a matrix that contains not only numbers but also variables, unknowns or even algebraic expressions.
Computer programs exist that work out the inverses of matrices for you, up to and including the size of 30×30 matrices.

Show More Tips

Not all 3×3 matrices have inverses. If the determinant of the matrix is equal to 0, then it does not have an inverse. (Notice that in the formula we divide by det(M). Division by zero is not defined.)

References

About This Article

Article SummaryX

To find the inverse of a 3×3 matrix, first calculate the determinant of the matrix. If the determinant is 0, the matrix has no inverse. Next, transpose the matrix by rewriting the first row as the first column, the middle row as the middle column, and the third row as the third column. Find the determinant of each of the 2×2 minor matrices, then create a matrix of cofactors using the results of the previous step. Divide each term of the adjugate matrix by the determinant to get the inverse. If you want to learn how to find the inverse using the functions on a scientific calculator, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 4,346,260 times.

Reader Success Stories

Kathleen Magana

Mar 13, 2019

«Studying for a CSET in math and have to review matrices. No calculator, but I’m getting it, thanks to…» more

Did this article help you?

Источник

Пример нахождения обратной матрицы 3×3

Данное решение сделано калькулятором, представленным на сайте.

Найдем матрицу A^-1, обратную исходной:

A =		4	3	2
2	1	-1
3	3	2

Запишем формулу для нахождения обратной матрицы:

A^-1 = 1 / det A *		A₁₁	A₂₁	A₃₁
A₁₂	A₂₂	A₃₂
A₁₃	A₂₃	A₃₃

A₁₁ … A₃₃ — это числа (алгебраические дополнения), которые будут найдены позже.

На ноль делить нельзя. Поэтому если det A равен нулю, то найти обратную матрицу невозможно.

Вычислим det A.

det A =		4	3	2	=
2	1	-1
3	3	2

К элементам строки 1 прибавляем соответствующие элементы строки 3, умноженные на -1. подробнее

	4 + 3 * ( -1)	3 + 3 * ( -1)	2 + 2 * ( -1)
2	1	-1
3	3	2

Данное элементарное преобразование не изменит значение определителя.

=		1	0	0	=
2	1	-1
3	3	2

Разложим определитель по элементам строки 1. подробнее

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 1

Элемент

Строку 1 и столбец 1
вычеркнули

( -1) ^{1 + 1}

		1	-1
3	2

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 2

Элемент

Строку 1 и столбец 2
вычеркнули

( -1) ^{1 + 2}

		2	-1
3	2

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 3

Элемент

Строку 1 и столбец 3
вычеркнули

( -1) ^{1 + 3}

		2	1
3	3

Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.

= ( -1) ^{1 + 1} * 1 *		1	-1		=
3	2

= 5

det A не равен нулю. Следовательно, найти обратную матрицу возможно.

Вычислим числа (алгебраические дополнения) A₁₁ … A₃₃

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 1

Строку 1 и столбец 1
вычеркнули

A₁₁

( -1) ^{1 + 1}

		1	-1		=
3	2

= 1 * 2 — ( -1) * 3 = 2 + 3 = 5

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 2

Строку 1 и столбец 2
вычеркнули

A₁₂

( -1) ^{1 + 2}

		2	-1		=
3	2

= — ( 2 * 2 — ( -1) * 3 ) = — (4 + 3) = -7

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 3

Строку 1 и столбец 3
вычеркнули

A₁₃

( -1) ^{1 + 3}

		2	1		=
3	3

= 2 * 3 — 1 * 3 = 6 — 3 = 3

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 1

Строку 2 и столбец 1
вычеркнули

A₂₁

( -1) ^{2 + 1}

		3	2		=
3	2

= — ( 3 * 2 — 2 * 3 ) = — (6 — 6) = 0

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 2

Строку 2 и столбец 2
вычеркнули

A₂₂

( -1) ^{2 + 2}

		4	2		=
3	2

= 4 * 2 — 2 * 3 = 8 — 6 = 2

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 3

Строку 2 и столбец 3
вычеркнули

A₂₃

( -1) ^{2 + 3}

		4	3		=
3	3

= — ( 4 * 3 — 3 * 3 ) = — (12 — 9) = -3

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 1

Строку 3 и столбец 1
вычеркнули

A₃₁

( -1) ^{3 + 1}

		3	2		=
1	-1

= 3 * ( -1) — 2 * 1 = -3 — 2 = -5

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 2

Строку 3 и столбец 2
вычеркнули

A₃₂

( -1) ^{3 + 2}

		4	2		=
2	-1

= — ( 4 * ( -1) — 2 * 2 ) = — (-4 — 4) = 8

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 3

Строку 3 и столбец 3
вычеркнули

A₃₃

( -1) ^{3 + 3}

		4	3		=
2	1

= 4 * 1 — 3 * 2 = 4 — 6 = -2

Ответ:

A^-1 = 1 / det A *		A₁₁	A₂₁	A₃₁
A₁₂	A₂₂	A₃₂
A₁₃	A₂₃	A₃₃

A^-1 = 1 / 5 *		5	0	-5
-7	2	8
3	-3	-2

A^-1 =		1	0	-1
-7/5	2/5	8/5
3/5	-3/5	-2/5

Необходимо проверить, что выполняется условие: A^-1 * A = E.

Мы будем использовать предпоследнюю форму записи обратной матрицы A^-1.
Это позволит нам избежать вычислений с дробями.

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	b₁₁	b₁₂	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₁ = 5 * 4 + 0 * 2 + ( -5) * 3 =
20 + 0 — 15 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	b₁₂	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₂ = 5 * 3 + 0 * 1 + ( -5) * 3 =
15 + 0 — 15 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₃ = 5 * 2 + 0 * ( -1) + ( -5) * 2 =
10 + 0 — 10 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₂₁ = -7 * 4 + 2 * 2 + 8 * 3 =
-28 + 4 + 24 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₂₂ = -7 * 3 + 2 * 1 + 8 * 3 =
-21 + 2 + 24 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	b₂₃
b₃₁	b₃₂	b₃₃

b₂₃ = -7 * 2 + 2 * ( -1) + 8 * 2 =
-14 — 2 + 16 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
b₃₁	b₃₂	b₃₃

b₃₁ = 3 * 4 + ( -3) * 2 + ( -2) * 3 =
12 — 6 — 6 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	b₃₂	b₃₃

b₃₂ = 3 * 3 + ( -3) * 1 + ( -2) * 3 =
9 — 3 — 6 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	0	b₃₃

b₃₃ = 3 * 2 + ( -3) * ( -1) + ( -2) * 2 =
6 + 3 — 4 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	0	5

Необходимо умножить получившуюся матрицу на 1/5

1/5 *		5	0	0
0	5	0
0	0	5

	1	0	0
0	1	0
0	0	1

= E

Таким образом, найденная матрица A^-1 является обратной для исходной матрицы A.

Пожалуйста, не забудьте поддержать сайт ссылкой.

2023 All rights reserved
matematika1974@yandex.ru
site partners

Источник

Данное решение сделано калькулятором, представленным на сайте.

Найдем матрицу A^-1, обратную исходной:

A =		4	3	2
2	1	-1
3	3	2

Запишем формулу для нахождения обратной матрицы:

A^-1 = 1 / det A *		A₁₁	A₂₁	A₃₁
A₁₂	A₂₂	A₃₂
A₁₃	A₂₃	A₃₃

A₁₁ … A₃₃ — это числа (алгебраические дополнения), которые будут найдены позже.

На ноль делить нельзя. Поэтому если det A равен нулю, то найти обратную матрицу невозможно.

Вычислим det A.

det A =		4	3	2	=
2	1	-1
3	3	2

К элементам строки 1 прибавляем соответствующие элементы строки 3, умноженные на -1. подробнее

	4 + 3 * ( -1)	3 + 3 * ( -1)	2 + 2 * ( -1)
2	1	-1
3	3	2

Данное элементарное преобразование не изменит значение определителя.

=		1	0	0	=
2	1	-1
3	3	2

Разложим определитель по элементам строки 1. подробнее

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 1

Элемент

Строку 1 и столбец 1
вычеркнули

( -1) ^{1 + 1}

		1	-1
3	2

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 2

Элемент

Строку 1 и столбец 2
вычеркнули

( -1) ^{1 + 2}

		2	-1
3	2

	1	0	0
2	1	-1
3	3	2

Номер строки 1
Номер столбца 3

Элемент

Строку 1 и столбец 3
вычеркнули

( -1) ^{1 + 3}

		2	1
3	3

Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.

= ( -1) ^{1 + 1} * 1 *		1	-1		=
3	2

= 5

det A не равен нулю. Следовательно, найти обратную матрицу возможно.

Вычислим числа (алгебраические дополнения) A₁₁ … A₃₃

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 1

Строку 1 и столбец 1
вычеркнули

A₁₁

( -1) ^{1 + 1}

		1	-1		=
3	2

= 1 * 2 — ( -1) * 3 = 2 + 3 = 5

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 2

Строку 1 и столбец 2
вычеркнули

A₁₂

( -1) ^{1 + 2}

		2	-1		=
3	2

= — ( 2 * 2 — ( -1) * 3 ) = — (4 + 3) = -7

	4	3	2
2	1	-1
3	3	2

Номер строки 1
Номер столбца 3

Строку 1 и столбец 3
вычеркнули

A₁₃

( -1) ^{1 + 3}

		2	1		=
3	3

= 2 * 3 — 1 * 3 = 6 — 3 = 3

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 1

Строку 2 и столбец 1
вычеркнули

A₂₁

( -1) ^{2 + 1}

		3	2		=
3	2

= — ( 3 * 2 — 2 * 3 ) = — (6 — 6) = 0

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 2

Строку 2 и столбец 2
вычеркнули

A₂₂

( -1) ^{2 + 2}

		4	2		=
3	2

= 4 * 2 — 2 * 3 = 8 — 6 = 2

	4	3	2
2	1	-1
3	3	2

Номер строки 2
Номер столбца 3

Строку 2 и столбец 3
вычеркнули

A₂₃

( -1) ^{2 + 3}

		4	3		=
3	3

= — ( 4 * 3 — 3 * 3 ) = — (12 — 9) = -3

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 1

Строку 3 и столбец 1
вычеркнули

A₃₁

( -1) ^{3 + 1}

		3	2		=
1	-1

= 3 * ( -1) — 2 * 1 = -3 — 2 = -5

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 2

Строку 3 и столбец 2
вычеркнули

A₃₂

( -1) ^{3 + 2}

		4	2		=
2	-1

= — ( 4 * ( -1) — 2 * 2 ) = — (-4 — 4) = 8

	4	3	2
2	1	-1
3	3	2

Номер строки 3
Номер столбца 3

Строку 3 и столбец 3
вычеркнули

A₃₃

( -1) ^{3 + 3}

		4	3		=
2	1

= 4 * 1 — 3 * 2 = 4 — 6 = -2

Ответ:

A^-1 = 1 / det A *		A₁₁	A₂₁	A₃₁
A₁₂	A₂₂	A₃₂
A₁₃	A₂₃	A₃₃

A^-1 = 1 / 5 *		5	0	-5
-7	2	8
3	-3	-2

A^-1 =		1	0	-1
-7/5	2/5	8/5
3/5	-3/5	-2/5

Необходимо проверить, что выполняется условие: A^-1 * A = E.

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	b₁₁	b₁₂	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₁ = 5 * 4 + 0 * 2 + ( -5) * 3 =
20 + 0 — 15 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	b₁₂	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₂ = 5 * 3 + 0 * 1 + ( -5) * 3 =
15 + 0 — 15 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	b₁₃
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₁₃ = 5 * 2 + 0 * ( -1) + ( -5) * 2 =
10 + 0 — 10 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
b₂₁	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₂₁ = -7 * 4 + 2 * 2 + 8 * 3 =
-28 + 4 + 24 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	b₂₂	b₂₃
b₃₁	b₃₂	b₃₃

b₂₂ = -7 * 3 + 2 * 1 + 8 * 3 =
-21 + 2 + 24 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	b₂₃
b₃₁	b₃₂	b₃₃

b₂₃ = -7 * 2 + 2 * ( -1) + 8 * 2 =
-14 — 2 + 16 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
b₃₁	b₃₂	b₃₃

b₃₁ = 3 * 4 + ( -3) * 2 + ( -2) * 3 =
12 — 6 — 6 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	b₃₂	b₃₃

b₃₂ = 3 * 3 + ( -3) * 1 + ( -2) * 3 =
9 — 3 — 6 = 0

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	0	b₃₃

b₃₃ = 3 * 2 + ( -3) * ( -1) + ( -2) * 2 =
6 + 3 — 4 = 5

	5	0	-5
-7	2	8
3	-3	-2

	4	3	2
2	1	-1
3	3	2

	5	0	0
0	5	0
0	0	5

Необходимо умножить получившуюся матрицу на 1/5

1/5 *		5	0	0
0	5	0
0	0	5

	1	0	0
0	1	0
0	0	1

= E

Таким образом, найденная матрица A^-1 является обратной для исходной матрицы A.

2022 All rights reserved
matematika1974@yandex.ru
site partners

Загрузить PDF

1
Проверьте определитель матрицы. Сначала вычислите определитель матрицы. Если определитель равен 0, то обратную матрицу вычислить нельзя. Определитель матрицы М обозначается как det(М).^[1]
- В случае матрицы размером 3х3 сначала обязательно вычислите определитель.
- Чтобы получить подробную информацию, прочитайте статью Как найти определитель матрицы 3х3.
2
Транспонируйте исходную матрицу. Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.^[2]
- Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.
3
Найдите определить каждой матрицы размером 2х2. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.^[3]
- Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
- Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
- Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.
4
Создайте матрицу кофакторов. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.^[4]
- Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
- Подробную информацию о матрицах кофакторов можно найти в интернете.
- Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).
5
Разделите каждый элемент присоединенной матрицы на определитель. Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель. Результат каждой операции деления запишите там, где находится соответствующий элемент. Так вы найдете матрицу, обратную исходной.^[5]
- Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
- В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.
Реклама

1
Единичную матрицу напишите рядом с исходной матрицей. Запишите исходную матрицу М, справа от нее нарисуйте вертикальную черту, а затем справа от черты запишите единичную матрицу. Получится матрица с тремя строками и шестью столбцами (большая матрица).^[6]
- Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Подробную информацию о единичных матрицах можно найти в интернете.
2
Выполните элементарные преобразования, чтобы из исходной матрицы получить единичную. Наша цель заключается в том, чтобы создать единичную матрицу на левой половине большой матрицы. Элементарные преобразования, выполняемые на левой половине большой матрицы, нужно выполнять и на ее правой половине (напомним, что правой половиной большой матрицы является единичная матрица).^[7]
- Помните, что элементарные преобразования включают в себя операции скалярного умножения, а также сложения и вычитания строк, чтобы обособить определенные элементы. Подробную информацию об элементарных преобразованиях матриц можно найти в интернете.
3

Продолжайте преобразовывать большую матрицу до тех пор, пока ее левая половина (то есть исходная матрица) не превратится в единичную матрицу. Напомним, что единичной матрицей является матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Когда исходная матрица станет единичной, на правой половине большой матрицы вы получите матрицу, обратную исходной.^[8]
4

Запишите обратную матрицу. Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.^[9]

Реклама

1

Выберите калькулятор, который работает с матрицами. С помощью простых калькуляторов нельзя найти обратную матрицу, но это можно сделать на хорошем графическом калькуляторе, таком как Texas Instruments TI-83 или TI-86.^[10]
2

Введите исходную матрицу в память калькулятора. Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2^nd и Matrix.
3

Выберите меню Edit (Редактирование). Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).^[11]
4

Введите обозначение матрицы. Большинство графических калькуляторов умеет работать с 3-10 матрицами, которые можно обозначить буквами А-J. Как правило, просто выберите [A], чтобы обозначить исходную матрицу. Затем нажмите кнопку Enter (Ввод).^[12]
5

Введите размер матрицы. В данной статье говорится о матрицах 3х3. Но графические калькуляторы умеют работать с матрицами больших размеров. Введите количество строк, нажмите кнопку Enter, затем введите количество столбцов и еще раз нажмите кнопку Enter.^[13]
6
Введите каждый элемент матрицы. На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.^[14]
- Чтобы ввести отрицательное значение элемента, нажмите специальную кнопку со знаком «минус», а не кнопку операции вычитания; в противном случае калькулятор не сможет правильно обработать это число.
- Чтобы перейти к определенному элементу матрицы, воспользуйтесь кнопками со стрелками.
7

Выйдите из режима введения матрицы. Введя значения всех элементов матрицы, нажмите кнопку Quit (Выход). (Или, если необходимо, нажмите кнопки 2^nd и Quit.) Так вы выйдете из режима введения матрицы и перейдете на основной экран калькулятора.^[15]
8
Воспользуйтесь специальной кнопкой, чтобы найти обратную матрицу. Во-первых, войдите в режим ввода матрицы (нажмите кнопку Matrix) и нажмите кнопку Names (Обозначения), чтобы выбрать обозначение матрицы, которое вы указали ранее (скорее всего, [A]). Затем нажмите кнопку выполнения обратной операции, которая помечена как $x^{{-1}}$ (возможно, сначала придется нажать кнопку 2^nd). На экране отобразится $A^{{-1}}$ . Нажмите Enter, чтобы вывести на экран обратную матрицу.^[16]
- Не пользуйтесь кнопкой ^ (кнопка для возведения в степень), чтобы ввести A^-1 посредством нажатия нескольких клавиш. Калькулятор не поймет эту операцию.
- Если после нажатия на кнопку обратной операции на экране отобразилось сообщение об ошибке, скорее всего, обратная матрица не существует. Чтобы убедиться в этом, вычислите определить матрицы.
9
Преобразуйте значения элементов обратной матрицы в обыкновенные дроби. По умолчанию калькулятор отображает значения элементов обратной матрицы в виде десятичных дробей; в большинстве случаев такую матрицу нельзя записать в ответе. Поэтому десятичные значения элементов обратной матрицы необходимо преобразовать в обыкновенные дроби (в редчайших случаях все элементы обратной матрицы будут целыми числами).^[17]
- Во многих графических калькуляторах есть кнопка, позволяющая преобразовывать десятичные дроби в обыкновенные. Например, на калькуляторе TI-86 нажмите Math (Математика), выберите Misc (Другое), затем выберите Frac (Дробь) и нажмите Enter. Десятичные дроби будут автоматически преобразованы в обыкновенные.
Реклама

Советы

Описанные методы можно применять к матрицам, элементами которых являются не только числа, но и переменные, неизвестные и даже алгебраические выражения.
Вычисления записывайте на бумаге, так как найти обратную матрицу в уме крайне сложно.
Существуют компьютерные программы, которые умеют работать с любыми матрицами^[18], включая матрицы 30х30.
Проверьте ответ, полученный с помощью любого из описанных в этой статье методов. Для этого перемножьте исходную (М) и обратную (М¹) матрицы. Помните, что М*М¹ = М¹*М = 1. Единичная матрица – это матрица, где элементами главной диагонали являются единицы, а остальными элементами являются нули. Если результат перемножения не равен 1, проверьте ваши вычисления.

Предупреждения

Не все матрицы 3×3 обратимы. Если определитель матрицы равен 0, обратная матрица не существует. (Обратите внимание, что в вычислениях присутствует деление на определитель, а на 0 делить нельзя.)

Об этой статье

Эту страницу просматривали 89 400 раз.

Была ли эта статья полезной?

Download Article

1
Check the determinant of the matrix. You need to calculate the determinant of the matrix as an initial step. If the determinant is 0, then your work is finished, because the matrix has no inverse. The determinant of matrix M can be represented symbolically as det(M).^[1]
- For a 3×3 matrix, find the determinant by first
2
Transpose the original matrix. Transposing means reflecting the matrix about the main diagonal, or equivalently, swapping the (i,j)th element and the (j,i)th. When you transpose the terms of the matrix, you should see that the main diagonal (from upper left to lower right) is unchanged.^[2]
- Another way to think of transposing is that you rewrite the first row as the first column, the middle row becomes the middle column, and the third row becomes the third column. Notice the colored elements in the diagram above and see where the numbers have changed position.
Advertisement
3
Find the determinant of each of the 2×2 minor matrices. Every item of the newly transposed 3×3 matrix is associated with a corresponding 2×2 “minor” matrix. To find the right minor matrix for each term, first highlight the row and column of the term you begin with. This should include five terms of the matrix. The remaining four terms make up the minor matrix.^[3]
- In the example shown above, if you want the minor matrix of the term in the second row, first column, you highlight the five terms that are in the second row and the first column. The remaining four terms are the corresponding minor matrix.
- Find the determinant of each minor matrix by cross-multiplying the diagonals and subtracting, as shown.
- For more on minor matrices and their uses, see Understand the Basics of Matrices.
4
Create the matrix of cofactors. Place the results of the previous step into a new matrix of cofactors by aligning each minor matrix determinant with the corresponding position in the original matrix. Thus, the determinant that you calculated from item (1,1) of the original matrix goes in position (1,1). You must then reverse the sign of alternating terms of this new matrix, following the “checkerboard” pattern shown.^[4]
- When assigning signs, the first element of the first row keeps its original sign. The second element is reversed. The third element keeps its original sign. Continue on with the rest of the matrix in this fashion. Note that the (+) or (-) signs in the checkerboard diagram do not suggest that the final term should be positive or negative. They are indicators of keeping (+) or reversing (-) whatever sign the number originally had.
- The final result of this step is called the adjugate matrix of the original. This is sometimes referred to as the adjoint matrix. The adjugate matrix is noted as Adj(M).
5
Divide each term of the adjugate matrix by the determinant. Recall the determinant of M that you calculated in the first step (to check that the inverse was possible). You now divide every term of the matrix by that value. Place the result of each calculation into the spot of the original term. The result is the inverse of the original matrix.^[5]
- For the sample matrix shown in the diagram, the determinant is 1. Therefore, dividing every term of the adjugate matrix results in the adjugate matrix itself. (You won’t always be so lucky.)
- Instead of dividing, some sources represent this step as multiplying each term of M by 1/det(M). Mathematically, these are equivalent.

1
Adjoin the identity matrix to the original matrix. Write out the original matrix M, draw a vertical line to the right of it, and then write the identity matrix to the right of that.^[6] You should now have what appears to be a matrix with three rows of six columns each.^[7]
- Recall that the identity matrix is a special matrix with 1s in each position of the main diagonal from upper left to lower right, and 0s in all other positions.
2
Perform linear row reduction operations. Your objective is to create the identity matrix on the left side of this newly augmented matrix. As you perform row reduction steps on the left, you must consistently perform the same operations on the right, which began as your identity matrix.^[8]
- Remember that row reductions are performed as a combination of scalar multiplication and row addition or subtraction, in order to isolate individual terms of the matrix. For a more complete review, see Row-Reduce Matrices.
3

Continue until you form the identity matrix. Keep repeating linear row reduction operations until the left side of your augmented matrix displays the identity matrix (diagonal of 1s, with other terms 0). When you have reached this point, the right side of your vertical divider will be the inverse of your original matrix.^[9]
4

Write out the inverse matrix. Copy the elements now appearing on the right side of the vertical divider as the inverse matrix.^[10]

1

Select a calculator with matrix capabilities. Simple 4-function calculators will not be able to help you directly find the inverse. However, due to the repetitive nature of the calculations, an advanced graphing calculator, such as the Texas Instruments TI-83 or TI-86, can greatly reduce the work.^[11]
2

Enter your matrix into the calculator. First, enter your calculator’s Matrix function by pressing the Matrix key, if you have one. On the Texas Instruments calculators, you may need to press 2^nd Matrix.
3

Select the Edit submenu. To reach the submenu, you may need to use the arrow buttons or choose the appropriate function key at the top of your calculator’s keypad, depending on the layout of your calculator.^[12]
4

Select a name for your matrix. Most calculators are equipped to work with anywhere from 3 to 10 matrices, labeled with letters A through J. Typically, just choose [A] to work with. Hit the Enter key after making your selection.^[13]
5

Enter the dimensions of your matrix. This article is focusing on 3×3 matrices. However, the calculator can handle larger sizes. Enter the number of rows, then press Enter, and then the number of columns, and Enter.^[14]
6
Enter each element of the matrix. The calculator screen will show a matrix. If you previously were working with the matrix function, the prior matrix will appear on the screen. The cursor will highlight the first element of the matrix. Type in the value of the matrix you wish to solve, and then Enter. The cursor will move automatically to the next element of the matrix, overwriting any previous numbers.^[15]
- If you wish to enter a negative number, use your calculator’s negative button (-) and not the minus key. The matrix function will not read the number properly.
- If necessary, you can use your calculator’s arrow keys to jump around the matrix.
7

Quit the Matrix function. After you have entered all values of the matrix, press the Quit key (or 2^nd Quit, if necessary). This will exit you from the Matrix function and return you to the main display screen of your calculator.^[16]
8
Use the inverse key to find the inverse matrix. First, reopen the Matrix function and use the Names button to select the matrix label that you used to define your matrix (probably [A]). Then, press your calculator’s inverse key, $x^{{-1}}$ . This may require using the 2^nd button, depending on your calculator. Your screen display should show $A^{{-1}}$ . Press Enter, and the inverse matrix should appear on your screen.^[17]
- Do not use the ^ button on your calculator to try entering A^-1 as separate keystrokes. The calculator will not understand this operation.
- If you receive an error message when you enter the inverse key, chances are that your original matrix does not have an inverse. You may want to go back and calculate the determinant to find out.
9
Convert your inverse matrix to exact answers. The first calculation that the calculator will give you is in decimal form. This is not considered “exact” for most purposes. You should convert the decimal answers to fractional form, as necessary. (If you are very lucky, all your results will be integers, but this is rare.)^[18]
- Your calculator probably has a function that will automatically convert the decimals to fractions. For example, using the TI-86, enter the Math function, then select Misc, and then Frac, and Enter. The decimals will automatically appear as fractions.
10

Most graphing calculators also have square bracket keys (on TI-84 it’s 2nd + x and 2nd + -) which can be used to type in a matrix without using the matrix function. Note: The calculator will not format the matrix until after the enter/equals key has been used (i.e. everything will be one line and not pretty).

Practice Problems and Answers

Add New Question

Question

How do you use elementary row operations to get the inverse of a matrix?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics

Expert Answer

Support wikiHow by
unlocking this expert answer.

Begin by setting up the system [A | I] where I is the identity matrix. Then, use elementary row operations to make the left hand side of the system reduce to I. The resulting system will be [I | A⁻¹] where A⁻¹ is the inverse of A.
Question

How do I evaluate the inverse of the matrix {1 2 -4}{0 -2 3}{5 0 4}?

Find the determinant, then determine the co-factor matrix. Find the adj of the co-factor matrix, then divide through each term by the determinant.
Question

Are there any shortcuts for finding the inverse of a 3×3 matrix?

The methods shown in the article is as simple as it gets unfortunately; you can do drills and make up your own 3×3 matrices to find the inverse of in order to remember the steps.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Write down all your steps as it is extremely difficult to find the inverse of a 3×3 matrix in your head.
Computer programs exist that work out the inverses of matrices for you, up to and including the size of 30×30 matrices.
You can follow these steps to find the inverse of a matrix that contains not only numbers but also variables, unknowns or even algebraic expressions.

Show More Tips

Not all 3×3 matrices have inverses. If the determinant of the matrix is equal to 0, then it does not have an inverse. (Notice that in the formula we divide by det(M). Division by zero is not defined.)

References

About This Article

Article SummaryX

Did this summary help you?

Thanks to all authors for creating a page that has been read 4,241,598 times.

Reader Success Stories

Kathleen Magana

Mar 13, 2019

«Studying for a CSET in math and have to review matrices. No calculator, but I’m getting it, thanks to step-by-step…» more

Did this article help you?

Как найти обратную матрицу

Быстрый способ для матриц $2 times 2$
1. Пример 1
2. Пример 2
Нахождение с помощью метода Гаусса
1. Пример 3
2. Пример 4
Метод союзной матрицы(алгебраические дополнения)
1. Пример 5

Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.

Быстрый способ для матриц $2 times 2$

Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$

Пример 1

Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$.

Решение

Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$

Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$

Ответ

$$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$

Пример 2

Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$.

Решение

Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$

Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$

Ответ

$$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$

Нахождение с помощью метода Гаусса

На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.

$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$

Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:

$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$

$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$

Пример 3

Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$

Решение

Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$

Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$

Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу.

Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$

Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$

Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$

Пример 4

Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$

Решение

Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$

Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$

Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу.

Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$

Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$

Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$

Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$

Ответ

$$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$

Метод союзной матрицы(алгебраические дополнения)

Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом

$$A^{-1} = frac{1}{|A|} (A^*)^T. $$

Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:

$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$

$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.

Пример 5

Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$

Решение

Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $

Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю:

$$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$

Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление.

Вычеркиваем первую строку и первый столбец:

$$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$

Убираем первую строку и второй столбец:

$$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$

Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя.

$$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$

$$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$

$$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$

$$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$

$$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$

$$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$

$$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$

Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений:

$$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$

Транспонируем её и обозначаем $ (A^*)^T $:

$$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

В итоге находим обратную матрицу $ A^{-1} $:

$$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$

Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$

Ответ

$$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$

Обратной матрицей называют такую
матрицу, для которой выполняется условие

.
Тогда

обозначает обратную матрицу.

существует тогда, когда det(A)0,
=det(A)-определитель
квадратной матрицы А. Для вычисления
обратной матрицы без доказательства
приводим формулу

, где

— алгебраические дополнения элементов

матрицы А.

Рассмотрим квадратную матрицу
размерности 3х3
,
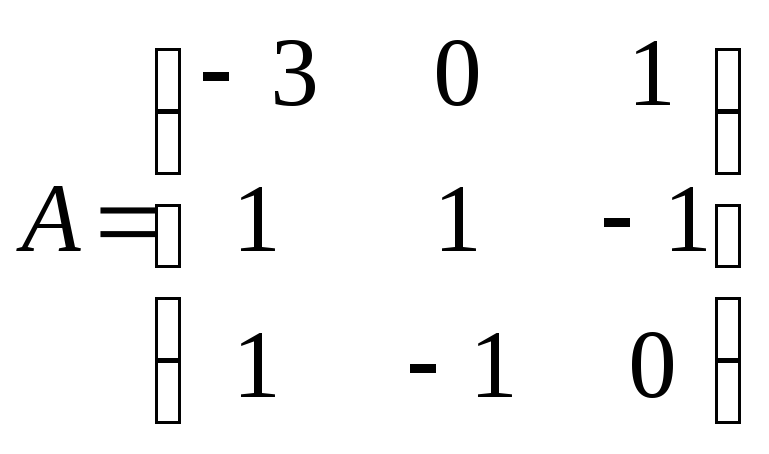
на примере которой объясним построение
обратной матрицы. Вычислим det(A)
с помощью любого известного правила,
получим det(A)=

Вычислим алгебраические дополнения
каждого элемента матрицы

т.е. алгебраическое дополнение является
произведением (-1) в степени, равной сумме
индексов элемента, на определитель той
матрицы, которая останется, если
вычеркнуть из заданной матрицы А первую
строку и первый столбец. По этому
правилу

Теперь вычислим
в
соответствии с формулой:

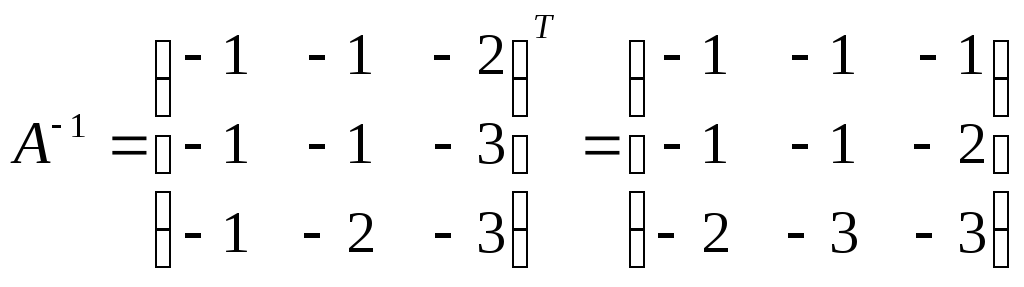
Проверим наши вычисления, используя
определение обратной матрицы, т.е.


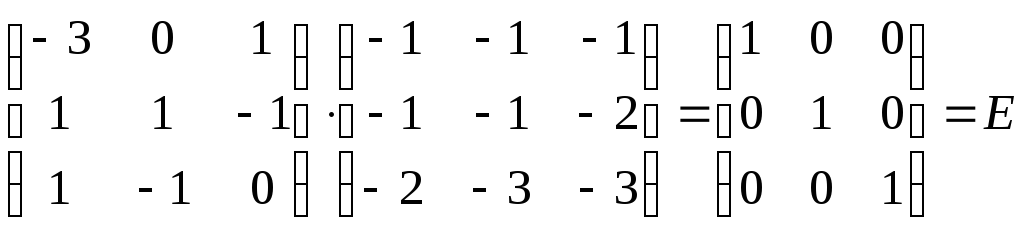
Обратная матрица вычислена верно.

Самостоятельно получите обратную
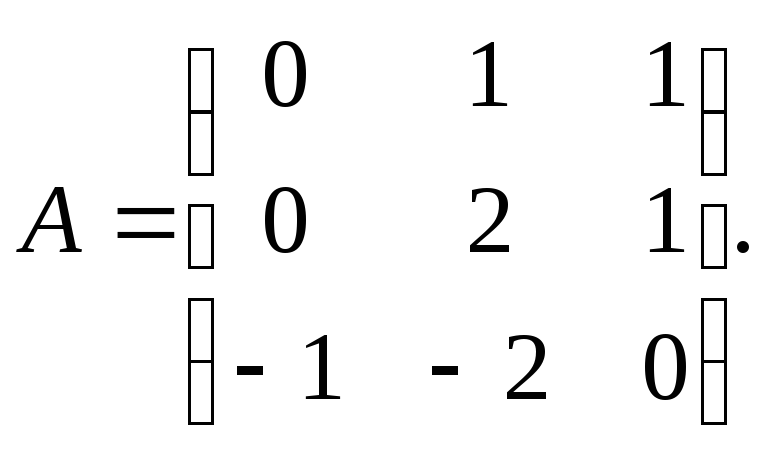
матрицу к матрице

и проверьте свои расчеты. Ниже приведено
решение этой задачи.

Решение
Вычислим определитель матрицы А: detA=2.

Так как det(A)0,
то вычислим алгебраические дополнения
каждого элемента матрицы А:

Построим

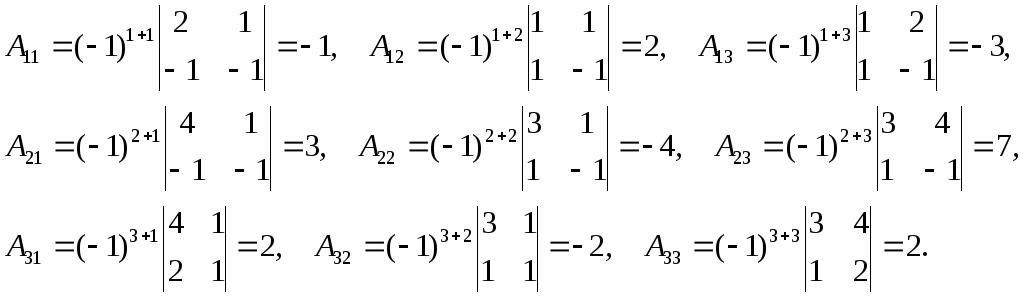
в соответствии с теоремой о существовании
обратной матрицы

Проверим полученную матрицу. По
определению
.
Умножим А на полученную матрицу


1.4. Решение простейших матричных уравнений

Пусть требуется решить уравнение
АХ=В , где А, В, Х – матрицы. Если А такая,
что det(A)0
, то у нее существует
.
Тогда произведем тождественное
преобразование уравнения, умножив левую
и правую часть на матрицу
.
Каждый раз размещаем множитель

слева от сомножителей. Получим
.
По определению матрицы
,
а Е· Таким
образом, левая часть уравнения
преобразуется следующим образом
.
Неизвестная матрица найдена Х=.

Аналогично решается уравнение Х·А=В.
Приведем окончательный ответ Х=В·.

Для решения уравнения А··С
придется дважды домножать уравнение,
размещая множитель

слева от группы матриц, а множитель

справа, что приводит к следующим
преобразованиям 

Такое решение возможно, если det(A)0
и det(B)0.

Пример. Решить уравнение А··С,
если

А=
Решение..
Вычислим определитель матрицы А
det(A)=-
det(B)=
Cформируем обратную
матрицу к А и В

Теперь матрица Х вычисляется по формуле

Проверка решения
подставим найденную матрицу Х в исходное
уравнение

следовательно
.

Упражнения для самостоятельного
решения

Построить обратную матрицу для следующих
матриц:

1.

Ответ А^-1=

2.

Ответ А^-1=

3.

Ответ А^-1=

Решить матричное уравнение АХВ=С,
если

Ответ Х=

Решить матричное уравнение АХ=В,
если

Ответ Х=

Решить матричное уравнение ХА=В,
если

Ответ Х=

1.5. Ранг матрицы

Пусть задана произвольная матрица

А=

Из элементов матрицы, расположенных на
пересечении некоторых к строк и
к столбцов, можно образовать
определитель к-го порядка, который
называется минором к-го порядка
этой матрицы. Например,

миноры второго порядка,

минор третьего порядка. Очевидно, что
порядок образуемого минора меньше или
равен наименьшему из чисел m,
n.

Пример. Дана матрица А=
Написать минор самого большого порядка.

Решение. Самый большой порядок
минора для данной матрицы к=3. Одним из
миноров 3-го порядка является минор
образованный
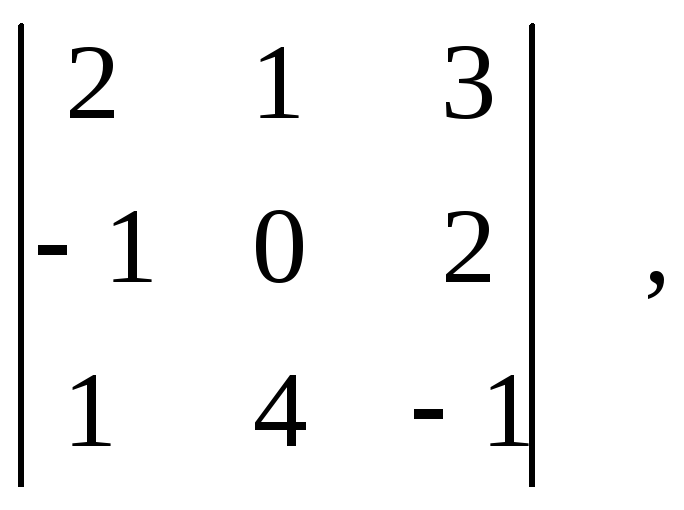
элементами первых трех строк. Вообще
же можно написать 4 минора 3-го порядка,
последовательно вычеркивая по одной
строке.

Определение. Если в матрице среди
миноров порядка r имеется
хотя бы один, отличный от нуля, а все
миноры порядка kr
равны нулю, то число r
называется рангом матрицы.

Если матрица квадратная и ее детерминант
не равен нулю, то ранг матрицы равен ее
порядку. Например , пусть А- матрица
3-го порядка А=
Det(A)=
По определению ранг r=3.

Пример. Определить ранг матрицы А=

Решение.
Очевидно, что в качестве минора 2-ого
порядка, отличного от нуля, можно взять
минор

Все миноры 3-его порядка равны нулю, так
как третья строка пропорциональна
первой. Значит r=2.

Вычисление
ранга матрицы непосредственно по
определению является громоздким и
поэтому рассмотрим прием, основанный
на элементарных преобразованиях матрицы.

Элементарными
преобразованиями матрицы называют
следующие операции

Умножение
всех элементов некоторой строки
(столбца) матрицы на число 
Прибавление
к элементам некоторой строки (столбца)
матрицы соответствующих элементов
другой строки (столбца) , умноженных на
одно и то же число .
Перемена
местами строк ( столбцов ) матрицы.

Матрицы, полученные одна из другой при
помощи конечного числа элементарных
преобразований, называются эквивалентными.
Для эквивалентных матриц выполняется
теорема, которую приводим без
доказательства.

Теорема. Эквивалентные матрицы
имеют один и тот же ранг.

Построение
эквивалентных матриц и применение этой
теоремы позволяет использовать для
вычисления ранга матрицы следующее
правило с помощью
элементарных преобразований привести
исходную матрицу к треугольному виду,
число ненулевых строк которой будет
равно рангу данной матрицы.

Пример.
Найти ранг матрицы А=
Решение. Умножим первую строку на
два и вычтем из второй строки, затем
умножим первую строку на три и вычтем
из третьей строки, получим эквивалентную
матрицу , в которой из третьей строки
вычтем вторую А~~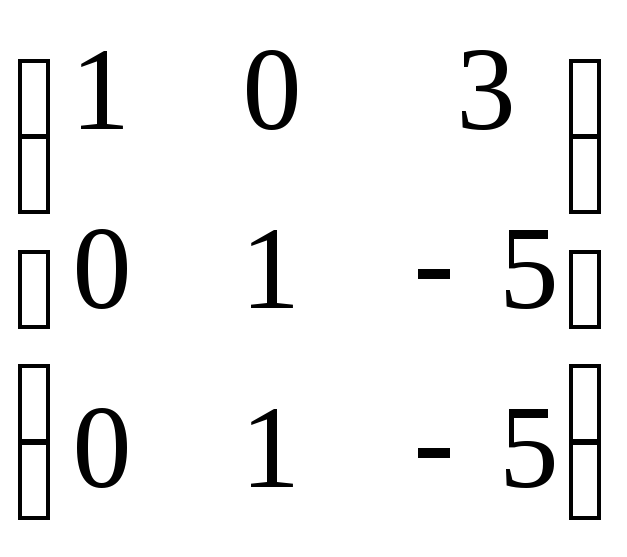
Ранг последней матрицы, а, значит и
данной, равен 2.

Пример.
Найти ранг матрицы А=

Решение.
Первую строку прибавим ко второй строке,
умножив на 3 вычтем из третьей строки,
умножив на 2, вычтем из четвертой строки.
Получим следующую матрицу, эквивалентную
данной: А~
В этой матрице вторую строку умножим
на 3 и вычтем из третьей
А~
Из последней матрицы ясно, что минор
третьего порядка

Все же миноры четвертого порядка равны
0, поэтому ранг данной матрицы равен 3.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.

Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.

Онлайн-калькулятор

Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.

Важно

В том случае, если обратная матрица может существовать, то она будет единственной.

Формула для вычисления обратной матрицы

Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:

A−1=1det⁡A⋅A∗A^{-1}=frac{1}{det A}cdot A^*

det⁡Adet A — определитель матрицы A,A,

A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.

Задача 1

Нужно найти обратную матрицу для следующей матрицы:

A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}

Решение

Вычислим детерминант:

det⁡A=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} — (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8

Так как det⁡A≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.

Посчитаем алгебраические дополнение:

A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,

A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,

A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,

A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,

A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,

A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,

A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,

A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,

A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.

Обратная матрица:

A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}

Важно

Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.

Задача 2

Найдите обратную матрицу для матрицы:

A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}

Решение

det⁡A=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.

A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,

A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,

A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,

A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.

Ответ:

A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}

Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.

Метод элементарных преобразований

Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:

перестановка местами любых двух рядов (строк или столбцов) матрицы;
умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.

Рассмотрим алгоритм нахождения обратной матрицы данным методом.

Алгоритм нахождения обратной матрицы методом элементарных преобразований

Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
Выписать обратную матрицу, которая находится справа от черты.

Задача 1

Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.

Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:

(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №3, умноженную на -3:

(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Задача 2

Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.

Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:

(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Произведем элементарные преобразования расширенной матрицы.

Прибавим к строке №1 строку №2, умноженную на -1:

(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.

Прибавим к строке №3 строку №2, умноженную на -3:

(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.

Умножим строку №3 на 13frac{1}{3}:

(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.

Слева получили единичную матрицу.

Выпишем обратную матрицу:

F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.

Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.

F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.

Значит, обратная матрица найдена правильно.

Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!

Содержание:

Нахождение обратной матрицы с помощью присоединённой матрицы
Нахождение обратной матрицы с помощью союзной матрицы
Облегченный способ для матрицы второго порядка

Обратную матрицу
можно найти с помощью двух ниже описанных методов.

Нахождение обратной матрицы с помощью присоединённой матрицы

Пример

Задание. Для матрицы $ A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right) $
найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице
справа
единичную матрицу второго порядка:

$$ Aleft|E=left( begin{array}{cc|cc}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right. $$

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

$$ Aleft|E = left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right. $$

От второй строки отнимаем две первых:

$$ Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right. $$

Первую и вторую строки меняем местами:

$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right. $$

От второй строки отнимаем две первых:

$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right. $$

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

$$ Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right. $$

Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $

Ответ. $ A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right) $

Замечание

Если на некотором этапе в «левой» матрице получается
нулевая строка, то это
означает, что исходная матрица обратной не имеет.

Облегченный способ для матрицы второго порядка

Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:

Шаг 1. Находим определитель $ Delta $ заданной матрицы,
если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.

Шаг 2. Элементы, стоящие на
главной диагонали меняем местами, а у элементов
побочной диагонали меняем знак на противоположный.

Шаг 3. Делим все элементы на $ Delta $ и получаем обратную матрицу.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти обратную матрицу для
$ A=left( begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right) $

Решение. Шаг 1. $ Delta=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=4-4=0 $ ,
тогда обратной матрицы не существует.

Ответ. Так как
определитель матрицы $A$ равен нулю,
то она не имеет обратной.

Пример

Задание. Найти обратную матрицу для $ A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right) $

Решение. Шаг 1. Находим определитель: $ Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0 $

Шаг 2. $ A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $

Шаг 3. $ A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $

Ответ. $ A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right) $

Нахождение обратной матрицы с помощью союзной матрицы

Определение

Матрица $ tilde{A} $ называется lt strong>союзной lt /strong> к квадратной матрице $A$ ,
если элементы матрицы $ tilde{A} $ равны
алгебраическим дополнениям соответствующих
элементов матрицы $A$ .

$$ A=left( begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right) Rightarrow tilde{A}=left( begin{array}{ccc}{A_{11}} & {A_{12}} & {A_{13}} \ {A_{21}} & {A_{22}} & {A_{23}} \ {A_{31}} & {A_{32}} & {A_{33}}end{array}right) $$

Имеет место следующее свойство: $ A cdot widetilde{A}^{T}=|A| cdot E $

Тогда, если $ |A| neq 0 $ , то
$ A cdot tilde{A}^{T} cdot frac{1}{|A|}=E $ , а тогда
$ A^{-1}=frac{1}{|A|} cdot tilde{A}^{T} $

Таким образом, матрица имеет союзную тогда и только тогда, когда она
невырожденная.

Пример

Задание. Найти обратную матрицу к матрице $ A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right) $

Решение. Вычисляем определитель матрицы:

$$ Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1- $$

$$ -1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0 $$

Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:

$$ A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T} $$

Найдем союзную матрицу $ tilde{A} $ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :

$$ A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2 $$

$$ A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3 $$

$$ A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7 $$

$$ A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6 $$

$$ A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3 $$

$$ A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3 $$

$$ A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2 $$

$$ A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3 $$

$$ A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1 $$

Таким образом, $ tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right) $

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

$$ widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $$

Итак, $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $

Ответ. $ A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right) $

Читать дальше: линейно зависимые и линейно независимые строки.

Источник

Как найти обратную матрицу

Быстрый способ для матриц $2 \times 2$
1. Пример 1
2. Пример 2
Нахождение с помощью метода Гаусса
1. Пример 3
2. Пример 4
Метод союзной матрицы(алгебраические дополнения)
1. Пример 5

Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A \neq 0 $.

Быстрый способ для матриц $2 \times 2$

Пусть задана матрица $A = \begin{pmatrix} a&b\\c&d \end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = \frac{1}{det A} \begin{pmatrix} d&-b \\ -c&a \end{pmatrix} = \frac{1}{ad-bc} \begin{pmatrix} d&-b \\ -c&a \end{pmatrix}.$$

Пример 1

Найти обратную матрицу для $A = \begin{pmatrix} 3&4 \\ 5&9 \end{pmatrix}$.

Решение

Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = \begin{vmatrix} 3&4 \\ 5&9 \end{vmatrix} = 3\cdot9 — 4\cdot5 = 27 — 20 = 7.$$

Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = \frac{1}{7} \begin{pmatrix} 9&-4 \\ -5&3 \end{pmatrix} = \begin{pmatrix} \frac{9}{7}&\frac{-4}{7} \\ \frac{-5}{7}&\frac{3}{7} \end{pmatrix}.$$

Ответ

$$A^{-1} = \begin{pmatrix} \frac{9}{7}&\frac{-4}{7} \\ \frac{-5}{7}&\frac{3}{7} \end{pmatrix}$$

Пример 2

Вычислить обратную матрицу для $A = \begin{pmatrix} 2&-1 \\ 4&-6 \end{pmatrix}$.

Решение

Находим определитель $$det A = \begin{vmatrix} 2&-1 \\ 4&-6 \end{vmatrix} = 2\cdot(-6) — 4\cdot(-1) = -12 + 4 = -8.$$

Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = \frac{1}{-8} \begin{pmatrix} -6&1 \\ -4&2 \end{pmatrix} = \begin{pmatrix} \frac{-6}{-8}&\frac{1}{-8} \\ \frac{-4}{-8}&\frac{2}{-8} \end{pmatrix} = \begin{pmatrix} \frac{3}{4}&-\frac{1}{8} \\ \frac{1}{2}&-\frac{1}{4} \end{pmatrix}$$

Ответ

$$A^{-1} = \begin{pmatrix} \frac{3}{4}&-\frac{1}{8} \\ \frac{1}{2}&-\frac{1}{4} \end{pmatrix}$$

Нахождение с помощью метода Гаусса

$$ \Bigg (\begin{matrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{matrix} \Bigg | \begin{matrix} 1&0&0\\0&1&0\\0&0&1 \end{matrix} \Bigg ) $$

$$ \Bigg (\begin{matrix} 1&0&0\\0&1&0\\0&0&1 \end{matrix} \Bigg | \begin{matrix} b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33} \end{matrix} \Bigg ) $$

$$A^{-1} = \begin{pmatrix} b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33} \end{pmatrix}$$

Пример 3

Найти обратную матрицу элементарными преобразованиями $$A = \begin{pmatrix} 2&-1&0 \\ 0&2&-1 \\ -1&-1&1 \end{pmatrix}.$$

Решение

Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = \begin{vmatrix} 2&-1&0 \\ 0&2&-1 \\ -1&-1&1 \end{vmatrix} = 4-1+0-0-2-0=1 \neq 0.$$

Выписываем основную матрицу и добавляем справа единичную матрицу. $$\begin{pmatrix} 2&-1&0 &|& 1&0&0 \\ 0&2&-1 &|& 0&1&0 \\ -1&-1&1 &|& 0&0&1 \end{pmatrix}$$

Умножаем третью строку на 2 и прибавляем первую. $$\begin{pmatrix} 2&-1&0 &|& 1&0&0 \\ 0&2&-1 &|& 0&1&0 \\ 0&-3&2 &|& 1&0&2 \end{pmatrix}$$

Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$\begin{pmatrix} 2&-1&0 &|& 1&0&0 \\ 0&2&-1 &|& 0&1&0 \\ 0&0&1 &|& 2&3&4 \end{pmatrix}$$

Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$\begin{pmatrix} 2&-1&0 &|& 1&0&0 \\ 0&2&0 &|& 2&4&4 \\ 0&0&1 &|& 2&3&4 \end{pmatrix}$$

Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$\begin{pmatrix} 4&0&0 &|& 4&4&4 \\ 0&2&0 &|& 2&4&4 \\ 0&0&1 &|& 2&3&4 \end{pmatrix}$$

Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$\begin{pmatrix} 1&0&0 &|& 1&1&1 \\ 0&1&0 &|& 1&2&2 \\ 0&0&1 &|& 2&3&4 \end{pmatrix}$$

Справа как видим получилась обратная матрица $$A^{-1} = \begin{pmatrix} 1&1&1 \\ 1&2&2 \\ 2&3&4 \end{pmatrix}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$A^{-1} = \begin{pmatrix} 1&1&1 \\ 1&2&2 \\ 2&3&4 \end{pmatrix}$$

Пример 4

Дана матрица, найти обратную $$A = \begin{pmatrix} 3&2&1 \\ 1&0&2 \\ 4&1&3 \end{pmatrix}.$$

Решение

Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = \begin{vmatrix} 3&2&1 \\ 1&0&2 \\ 4&1&3 \end{vmatrix} = 0+16+1-0-6-6=5.$$

Теперь справа от матрицы дописываем единичную матрицу $$\begin{pmatrix} 3&2&1 &|& 1&0&0 \\ 1&0&2 &|& 0&1&0 \\ 4&1&3 &|& 0&0&1 \end{pmatrix}.$$

Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$\begin{pmatrix} 3&2&1 &|& 1&0&0 \\ 0&-2&5 &|& -1&3&0 \\ 0&-5&5 &|& -4&0&3 \end{pmatrix}$$

Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$\begin{pmatrix} 3&2&1 &|& 1&0&0 \\ 0&-2&5 &|& -1&3&0 \\ 0&0&-15 &|& -3&-15&6 \end{pmatrix}$$

Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$\begin{pmatrix} 3&2&1 &|& 1&0&0 \\ 0&-2&5 &|& -1&3&0 \\ 0&0&-5 &|& -1&-5&2 \end{pmatrix}$$

Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$\begin{pmatrix} 15&10&0 &|& 4&-5&2 \\ 0&-2&0 &|& -2&-2&2 \\ 0&0&-5 &|& -1&-5&2 \end{pmatrix}$$

К первой строке прибавляем вторую, умноженную на 5. $$\begin{pmatrix} 15&0&0 &|& -6&-15&12 \\ 0&-2&0 &|& -2&-2&2 \\ 0&0&-5 &|& -1&-5&2 \end{pmatrix}$$

Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$\begin{pmatrix} 1&0&0 &|& -\frac{2}{5}&-1&\frac{4}{5} \\ 0&1&0 &|& 1&1&-1 \\ 0&0&1 &|& \frac{1}{5}&1&-\frac{2}{5} \end{pmatrix}$$

Ответ

$$\begin{pmatrix} 1&0&0 &|& -\frac{2}{5}&-1&\frac{4}{5} \\ 0&1&0 &|& 1&1&-1 \\ 0&0&1 &|& \frac{1}{5}&1&-\frac{2}{5} \end{pmatrix}$$

Метод союзной матрицы(алгебраические дополнения)

Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом

$$A^{-1} = \frac{1}{|A|} (A^*)^T. $$

$$ A^* = \begin{pmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{22}&A_{33} \end{pmatrix}, \text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$

Пример 5

Найти обратную матрицу методом алгебраических дополнений $$ A = \begin{pmatrix} 3&1&2\\-1&3&-2\\0&-1&4 \end{pmatrix} $$

Решение

Итак, пользуемся формулой $ A^{-1} = \frac{1}{|A|} (A^*)^T $

$$ |A| = \begin{vmatrix} 3&1&2\\-1&3&-2\\0&-1&4 \end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 \neq 0 $$

Вычеркиваем первую строку и первый столбец:

$$ A_{11} = (-1)^{1+1} \cdot \begin{vmatrix} 3&-2\\-1&4 \end{vmatrix} = 12 — 2 = 10 $$

Убираем первую строку и второй столбец:

$$ A_{12} = (-1)^{1+2} \cdot \begin{vmatrix} -1&-2\\0&4 \end{vmatrix} = -(-4 — 0) = 4 $$

Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя.

$$ A_{13} = (-1)^{1+3} \cdot \begin{vmatrix} -1&3\\0&-1 \end{vmatrix} = 1 — 0 = 1 $$

$$ A_{21} = (-1)^{2+1} \cdot \begin{vmatrix} 1&2\\-1&4 \end{vmatrix} = -(4 + 2) = -6 $$

$$ A_{22} = (-1)^{2+2} \cdot \begin{vmatrix} 3&2\\0&4 \end{vmatrix} = 12 — 0 = 12 $$

$$ A_{23} = (-1)^{2+3} \cdot \begin{vmatrix} 3&1\\0&-1 \end{vmatrix} = -(-3 — 0) = 3 $$

$$ A_{31} = (-1)^{3+1} \cdot \begin{vmatrix} 1&2\\3&-2 \end{vmatrix} = -2 — 6 = -8 $$

$$ A_{32} = (-1)^{3+2} \cdot \begin{vmatrix} 3&2\\-1&-2 \end{vmatrix} = -(-6 + 2) = 4 $$

$$ A_{33} = (-1)^{3+3} \cdot \begin{vmatrix} 3&1\\-1&3 \end{vmatrix} = 9+1 = 10 $$

Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений:

$$ A^* = \begin{pmatrix} 10&4&1\\-6&12&3\\-8&4&10 \end{pmatrix}. $$

Транспонируем её и обозначаем $ (A^*)^T $:

$$ (A^*)^T = \begin{pmatrix} 10&-6&-8\\4&12&4\\1&3&10 \end{pmatrix} $$

В итоге находим обратную матрицу $ A^{-1} $:

$$ A^{-1} = \frac{1}{36} \begin{pmatrix} 10&-6&-8\\4&12&4\\1&3&10 \end{pmatrix} $$

Делим каждый элемент матрицы на 36 и получаем следующее: $$\begin{pmatrix} \frac{5}{18}&-\frac{1}{6}&-\frac{2}{9}\\ \frac{1}{9}&\frac{1}{3}&\frac{1}{9}\\\frac{1}{36}&\frac{1}{12}&\frac{5}{18} \end{pmatrix}.$$

Ответ

$$A^{-1} =\begin{pmatrix} \frac{5}{18}&-\frac{1}{6}&-\frac{2}{9}\\ \frac{1}{9}&\frac{1}{3}&\frac{1}{9}\\\frac{1}{36}&\frac{1}{12}&\frac{5}{18} \end{pmatrix}$$

Источник