Научим создавать свои игры, сайты и приложения
Начать учиться
Алгоритм: понятие в информатике и его свойства
Новое
Алгоритм — ключевое понятие в информатике и программировании. Он играет важную роль в понимании того, как компьютеры обрабатывают информацию и выполняют задачи. Давайте рассмотрим, что такое алгоритм и какими свойствами он обладает.
Материал на этой странице не был проверен методистами Skysmart и может содержать ошибки. Если вы заметили неточность, напишите нам на skysmart.blog@skyeng.ru.
Алгоритм — это чётко определенная последовательность действий или инструкций, предназначенная для решения определённой задачи или класса задач. Понятие алгоритма не ограничивается только информатикой; оно используется в различных областях, начиная от математики и заканчивая кулинарией.
Основные свойства алгоритма
-
Определённость. Каждый шаг алгоритма должен быть чётко определён, без каких-либо двусмысленностей.
-
Конечность. Алгоритм должен завершиться после конечного числа шагов. Это не означает, что алгоритм короткий, но гарантирует, что он не будет выполняться вечно.
-
Массовость. Алгоритм должен быть применим к широкому классу задач, а не только к одной конкретной задаче.
-
Результативность. После завершения алгоритма нужно получить результат, который соответствует цели, для которой алгоритм был разработан.
-
Эффективность. Хотя это свойство не является обязательным, хорошие алгоритмы обычно оптимизированы таким образом, чтобы они были как можно более эффективными в плане использования ресурсов и времени выполнения.
Стартуй в программировании прямо сейчас
Реши свою первую настоящую задачу на JavaScript и поделись крутым результатом с друзьями
Пример алгоритма
Рассмотрим простой пример — алгоритм приготовления чая:
-
Налить в чайник воду.
-
Включить чайник.
-
Дождаться, пока вода закипит.
-
Налить кипяток в чашку.
-
Положить в чашку пакетик чая.
-
Дать чаю завариться в течение 2–5 минут.
-
Добавить сахар или лимон по вкусу.
Данный алгоритм удовлетворяет основным свойствам: он чётко определён, конечен, результативен и может быть применён к любой задаче заваривания чая.
Алгоритмы — это фундаментальная часть информатики. Они позволяют нам формализовать процессы и действия, которые компьютеры выполняют для достижения конкретных целей. Понимание алгоритмов и их свойств является ключом к успешному программированию и разработке высокоэффективных решений.
Поможем детям и подросткам стать успешными IT-специалистами в будущем
Научим основам программирования, поможем создать реальный проект и выплатим деньги за первый заказ
Статья расскажет о происхождении термина «Алгоритм» и о том, какими свойствами он обладает.
Алгоритмом называют определенную конечную последовательность действий (набор инструкций), выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). В литературе по информатике, как и на просторах глобальной сети, можно найти множество общей теоретической информации относительно понятия и решения алгоритма. Достаточно запомнить основную мысль: достижение алгоритмического результата обеспечивается выполнением определенной последовательности действий (чаще всего, действий арифметических или логических).
История возникновения термина
Сегодня это понятие является фундаментальным и в математике, и в информатике. Однако сам термин возник задолго до появления компьютеров и прочих электронных средств вычислительной техники. Впервые об алгоритме заговорили в средние века — именно тогда европейские ученые ознакомились с методами вычисления арифметических действий, производимых в десятичной системе счисления азиатским математиком по имени Мухаммед ибн Муса аль-Хорезми (от имени этого математика и сформировался термин Algorithm). Сочинение аль-Хорезми перевели, а в последующие столетия появилось много трудов, посвященных вопросу обучения искусству счёта посредством цифр. Можно вспомнить описание алгоритма в европейской науке в те годы:
Также значение слова «алгоритм» сегодня нередко связывают со значениями таких слов, как «рецепт», «метод», «процесс», «инструкция».
Исполнитель и программа
Судя по историческим справкам, изначально речь шла о способе выполнения арифметических действий над десятичными числами. Прошли годы. Понятие стали применять при обозначении любой последовательности действий, которая приводит к получению требуемого результата. Причем алгоритмы существуют не сами по себе — они предназначаются для конкретного исполнителя. Кто может выступать таким исполнителем:
— человек;
— роботизированное/автоматизированное устройство, механизм;
— компьютер;
— язык программирования и т. д.
Отличительная черта исполнителя — способность выполнять команды, которые включены в алгоритм. Это становится возможным, благодаря описанию последнего на формальном языке, который исключает неоднозначность толкования. Множество команд задано изначально строго и является конечным. Действия, которые должен выполнить исполнитель, называют элементарными действиями, а сама запись алгоритмической последовательности на формальном языке — это программа. Разработка алгоритма в целях решения задачи — это алгоритмизация.
Главные характеристики
Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.
Основные виды алгоритмов
В информатике и программировании выделяют много видов алгоритмов. Основные из них:
— линейные (команды выполняются последовательно, одна за одной);
— разветвляющиеся (есть условие, при проверке которого возможно разветвление на несколько параллельных ветвей);
— циклические (предусматривается многократное повторение одних и тех же действий).
Источники:
• https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf;
• https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/materialy-1.
-
Понятие алгоритма и его свойства
«Алгоритм»
является базовым основополагающим
понятием информатики, а алгоритмизация
и программирование – основным разделом
курса информатики (ядром курса). Понятие
алгоритма, как и понятие информации,
даётся множеством самых разнообразных
определений – от «наивно-интуитивных»
(«алгоритм – это план решения задачи»)
до «строго формализованных» (нормальные
алгоритмы Маркова). Понятие алгоритма,
являющееся фундаментальным в математике
и информатике, возникло задолго до
появления средств вычислительной
техники.
Термин
«алгоритм (алгорифм)» появился в Средние
века, когда европейцы знакомились со
способами выполнения арифметических
действий в десятичной системе счисления
по книге узбекского математика Абу
Джафара Муххамада ибн Мусы аль-Хорезми
(783–850 г.) «Арифметика индусскими цифрами»,
получившей широкую известность. Слово
«алгоритм» есть результат европейского
произношения слов «аль-Хорезми»
(«аль-Хорезми» – человек из города
Хорезми; в настоящее время город Хива
в Хорезмской области Узбекистана).
Единого
определения понятия алгоритма нет.
Первоначально под алгоритмом понимали
способ выполнения арифметических
действий над десятичными числами. В
дальнейшем алгоритмом стали называть
точное предписание, определяющее порядок
действий, обеспечивающий получение
требуемого результата из исходных
данных за конечное число шагов.
Алгоритм (по
Д. Э. Кнуту)
– это конечный набор правил, который
определяет последовательность операций
для решения конкретного множества задач
и обладает пятью важными чертами:
конечность, определённость, ввод, вывод,
эффективность.
Алгоритм (по
А.
Н. Колмогорову) – это система вычислений,
выполняемых по строго определённым
правилам, которая после какого-либо
числа шагов заведомо приводит к решению
поставленной задачи.
Алгоритм (по
А. А.
Маркову) – это точное предписание,
определяющее вычислительный процесс,
идущий от варьируемых исходных данных
к искомому результату.
Алгоритм
может быть предназначен для выполнения
его человеком или автоматическим
устройством.
Применительно
к ЭВМ алгоритм определяет вычислительный
процесс, начинающийся с обработки
некоторой совокупности возможных
исходных данных и направленный на
получение определенных этими исходными
данными результатов. Термин «вычислительный
процесс» распространяется и на обработку
других видов информации, например,
символьной, графической или звуковой.
Алгоритм должен обладать
следующими свойствами:
-
дискретностью;
-
массовостью;
-
определённостью;
-
результативностью;
-
формальностью.
Дискретность
(разрывность,
раздельность). Каждый
алгоритм состоит из отдельных законченных
действий, т.е. делится
на шаги.
Массовость
– применимость
алгоритма ко всем задачам некоторого
класса, различающимся
только исходными данными.
При этом исходные данные могут
выбираться из некоторой области, которая
называется областью применимости
алгоритма.
Определённость
(детерминированность, точность) –
свойство алгоритма, указывающее на то,
что каждый шаг алгоритма должен быть
строго определён и не должен допускать
произвола в толковании. Также строго
должен быть определён порядок выполнения
отдельных шагов. Благодаря этому
свойству многократное выполнение
алгоритма при одних и тех же исходных
данных даёт один и тот же результат.
Результативность
(конечность)– свойство,
состоящее в том, что любой алгоритм
должен приводить к правильному
решению задачи за конечное(может
быть очень большое) число шагов,
либо подавать сигнал о том, что данный
алгоритм неприменим для решения
поставленной задачи.
Формальность
– это свойство
указывает на то, что любой исполнитель,
незнакомый с содержанием алгоритма,
но способный воспринимать и выполнять
инструкции алгоритма, действуя формально,
т.е. отвлекаясь от содержания поставленной
задачи и лишь строго выполняя инструкции,
получает необходимый результат. Думать
о том, какие действия и в какой
последовательности нужно выполнить,
должен разработчик алгоритма, а
исполнитель формально (не думая,
механически) поочерёдно исполняет
предложенные команды и получает
необходимый результат.
Соседние файлы в папке Информатика_ЗФ
- #
- #
- #
- #
- #
- #
Алгоритм и свойства алгоритма¶
- Алгоритм:
-
точное предписание, которое задается вычислительному процессу и представляет собой конечную последовательность обычных элементарных действий, четко определяющую процесс преобразования исходных данных в искомый результат
Свойства алгоритма¶
-
Конечность. Должен заканчиваться за конечное число шагов.
-
Элементарность (понятность). Каждый шаг алгоритма должен быть простым, чтобы устройство, выполняющее операции,могло выполнить его одним действием
-
Дискретность. Процесс решения задачи представляется конечной последовательностью отдельных шагов, и каждый шаг алгоритма выполняется за конечное (не обязательно единичное) время.
-
Детерминированность (определенность). Каждый шаг алгоритма должен быть однозначно и недвусмысленно определен и не должен допускать произвольной трактовки. После каждого шага либо указывается, какой шаг делать дальше, либо дается команда остановки, после чего работа алгоритма считается законченной.
-
Результативность. Алгоритм имеет некоторое число входных величин — аргументов. Цель выполнения алгоритма состоит в получении конкретного результата, имеющего отношение к исходным данным.
-
Массовость. Алгоритм должен быть применим для некоторого класса задач, различающихся лишь исходными данными.
-
Эффективность. Необходимо приводить алгоритм к состоянию, чтобы он состоял из минимального числа шагов и при этом решение удовлетворяло бы условию точности и требовало минимальных затрат других ресурсов.
Типы алгоритмических моделей¶
-
Вычислительный алгоритм
-
Устройство, выполняющее примитивные операции
-
Формальные алгоритмы
Запись алгоритма на некотором языке представляет собой программу. Если программа написана на специальном алгоритмическом языке (например, на ПАСКАЛе или С++), то говорят об исходной программе. Программа, написанная на языке, который непосредственно понимает компьютер (как правило, это двоичные коды), называется машинной, или двоичной.
Основные способы записи алгоритмов¶
-
вербальный — алгоритм описывается на человеческом языке;
-
символьный — алгоритм описывается с помощью набора символов;
-
графический — алгоритм описывается с помощью набора графических изображений.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т. п.) соответствует геометрическая фигура. Блоки соединяются линиями переходов, определяющими очередность выполнения действий.
Основные блоки
Базовые алгоритмические структуры¶
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов. Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
Следование – действия выполняются строго в том порядке, в котором записаны. Образуется последовательностью действий, следующих одно за другим.
Ветвление¶
- Ветвление:
-
Форма организации действий, при которой в зависимости от справедливости проверяемого условия алгоритм может пойти по одной из двух возможных ветвей. Происходит выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран
-
Неполная форма ветвления (если…то, if…then)
-
Полная форма ветвления (если…то…иначе, if…then…else)
-
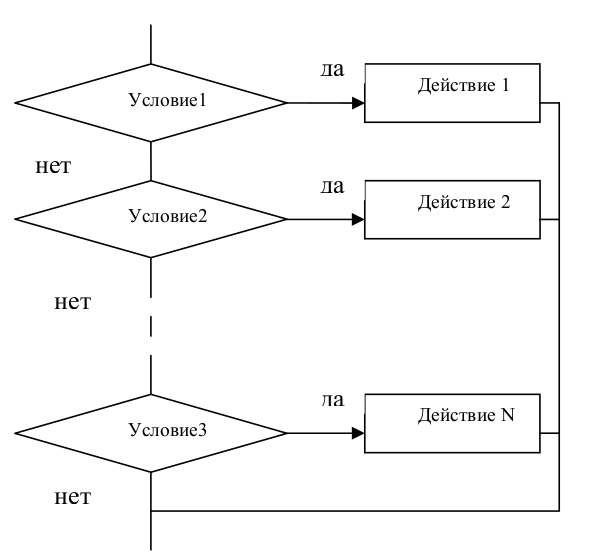
Выбор (select case)
Цикл¶
- Цикл:
-
Форма организации действий, при которой одна и та же последовательность шагов алгоритма выполняется несколько раз или ни разу в зависимости от проверяемого условия
-
Цикл с параметром (for) – тело цикла выполняется для всех значений некоторой переменной (параметра цикла) в заданном диапазоне;
-
Цикл с предусловием (while) – тело цикла выполняется до тех пор, пока выполняется условие;
-
Цикл с постусловием (repeat…until) – тело цикла выполняется до тех пор, пока условие не выполняется;
-
Вложенные циклы
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
Примечание
При использовании такой структуры необходимо помнить, что параметр внутреннего цикла меняется быстрее параметра внешнего, при одном значении параметра внешнего цикла параметр внутреннего пробегает все свои возможные значения
Данные и величины¶
В программировании изучаются методы программного управления работой компьютера, который выступает в качестве исполнителя. Компьютер работает с величинами — различными информационными объектами: числами, символами, кодами и др., поэтому алгоритмы, предназначенные для управления компьютером, называются алгоритмами работы с величинами.
- Данные:
-
Совокупность величин, с которыми работает компьютер.
По отношению к программе различают исходные, окончательные (результаты) и промежуточные данные, которые получают в процессе вычислений.
Величина имеет три основных свойства: имя, значение и тип. На уровне команд процессора величина идентифицируется при помощи адреса ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные
Костанта — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, k, true и т.д.
Переменная может изменять свои значения в ходе выполнения программы и представляется символическим именем — идентификатором, например: X, S2, cod 15.
Тип данных
- Тип данных:
-
определяет множество значений, которые может принимать переменная и множество допустимых опе:раций
В любой язык входит минимально необходимый набор основных типов данных, к которому относятся: целый, вещественный, логический и символьный типы
Примеры алгоритмов¶
Линейный вычислительный алгоритм¶
- Пример:
-
Создать алгоритм деления обыкновенных дробей.
Математическая модель:
-
Числитель первой дроби умножить на знаменатель второй дроби.
-
Знаменатель первой дроби умножить на числитель второй дроби.
-
Записать дробь, числитель которой есть результат выполнения пункта 1, а знаменатель — результат выполнения пункта 2.
Алгебраическая форма:
Блок — схема и текст на алгоритмическом языке (псевдокоде) выглядят следующим образом:
Данный алгоритм имеет линейную структуру. В нем все команды выполняются в строго однозначной последовательности, каждая по одному разу. Линейный алгоритм составляется из команд присваивания, ввода, вывода. При описании алгоритмов в блок-схемах типы, как правило,не указываются (но подразумеваются).
В алгоритмах на АЯ для всех переменных типы указываются явно. Описание типов переменных производится сразу после заголовка алгоритма. В них используются следующие обозначения типов: цел — целый тип, вещ — вещественный тип, лит — символьный (литерный) тип, лог — логический тип. В алгоритме для деления дробей для всех переменных указан целый тип.
Ветвление¶
Составить алгоритм решения квадратного уравнения ax2+ bx + c = 0
Математическая модель
Решением в общем случае будут два корня x1, и x2 , которые вычисляются по формуле:
Блок-схема алгоритма представлена на рисунке
Псевдокод
Циклы¶
Дано целое положительное число п. Требуется вычислить n! (n-факториал).
Математическая модель
- Таблица трассировки:
-
Метод, используемый для тестирования алгоритмов, чтобы убедиться, что во время обработки вычислений не возникает логических ошибок. Таблица обычно имеет форму многоколоночной таблицы с несколькими строками; В каждом столбце показана переменная, а в каждой строке-каждое число, введенное в алгоритм, и последующие значения переменных.
Блок-схема
В алгоритме используются три переменные целого типа: n — аргумент; i—промежуточнаяпеременная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица.
Псевдокод
В алгоритме использована структурная команда цикл-пока, или цикл с предусловием. Общий вид команды цикл-пока в блок-схемах и в алгоритмических языках следующий:
Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова нц и кц обозначают начало цикла и конец цикла соответственно.
Вспомогательные алгоритмы¶
- Вспомогательный алгоритм:
-
Алгоритм, целиком используемый в составе другого алгоритма.
Составить алгоритм вычисления степенной функции с целым показателем у = хk, где к — целое число, не равное 0
Математическая модель
Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень.
Основной алгоритм будет выглядеть следующим образом:
Дважды используется команда обращения к вспомогательному алгоритму с именем СТЕПЕНЬ. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами.
Вспомогательные алгоритмы оформляются в виде процедур. Процедура СТЕПЕНЬ будет выглядеть так:
а и k — формальные параметры-аргументы, z — параметр-результат.
Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия:
* по количеству (сколько формальных, столько и фактических параметров);
* по последовательности (первому формальному соответствует первый фактический параметр, второму — второй и т.д.);
* по типам (типы соответствующих формальных и фактических параметров должны совпадать)
Обращение к процедуре инициирует следующие действия:
-
Значения параметров-аргументов присваиваются соответствующим формальным параметрам.
-
Выполняется тело процедуры (команды внутри процедуры).
-
Значение результата передается соответствующему фактическому параметру, и происходит переход к выполнению следующей команды основного алгоритма.
Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации
asd \(a^2 + b^2 = c^2\)
\[ \begin{align}\begin{aligned}(a + b)^2 = a^2 + 2ab + b^2\\\frac{3}{4}\end{aligned}\end{align} \]
Продолжение следует…