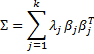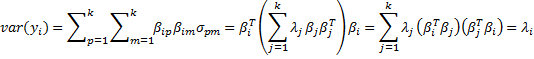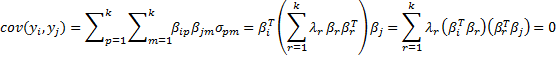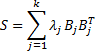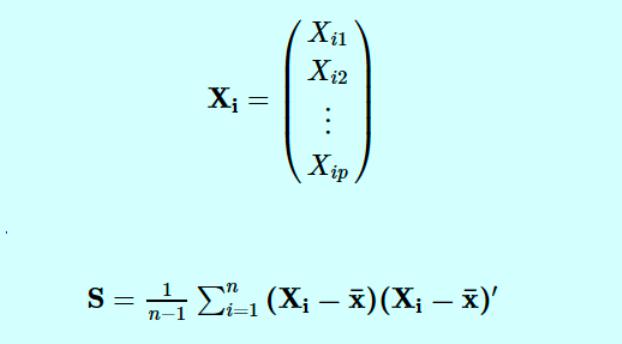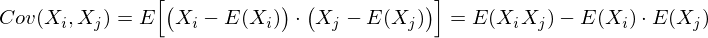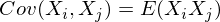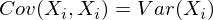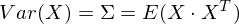Метод главных компонент в excel инструкция - Большая энциклопедия инструкций и руководств

Principal component analysis is a statistical technique that is used to analyze the interrelationships among a large number of variables and to explain these variables in terms of a smaller number of variables, called principal components, with a minimum loss of information.

Definition 1: Let X = [x_i] be any k × 1 random vector. We now define a k × 1 vector Y = [y_i], where for each i the ith principal component of X is

for some regression coefficients β_ij. Since each y_iis a linear combination of the x_j, Y is a random vector.

Now define the k × k coefficient matrix β = [β_ij] whose rows are the 1 × k vectors $\beta^T X$ = [β_ij]. Thus,

y_i = $\beta_i^T X$ Y = $\beta^T X$

For reasons that will be become apparent shortly, we choose to view the rows of β as column vectors β_i, and so the rows themselves are the transpose $\beta_i^T X$ .

Observation: Let Σ = [σ_ij] be the k × k population covariance matrix for X. Then the covariance matrix for Y is given by

Σ_Y = β^TΣ β

i.e. population variances and covariances of the y_i are given by

Observation: Our objective is to choose values for the regression coefficients β_ij so as to maximize var(y_i) subject to the constraint that cov(y_i, y_j) = 0 for all i ≠ j. We find such coefficients β_ij using the Spectral Decomposition Theorem (Theorem 1 of Linear Algebra Background). Since the covariance matrix is symmetric, by Theorem 1 of Symmetric Matrices, it follows that

Σ = β D β^T

where β is a k × k matrix whose columns are unit eigenvectors β₁, …, β_k corresponding to the eigenvalues λ₁, …, λ_k of Σ and D is the k × k diagonal matrix whose main diagonal consists of λ₁, …, λ_k. Alternatively, the spectral theorem can be expressed as

Property 1: If λ₁ ≥ … ≥ λ_k are the eigenvalues of Σ with corresponding unit eigenvectors β₁, …, β_k, then

and furthermore, for all i and j ≠ i

var(y_i) = λ_i cov(y_i, y_j) = 0

Proof: The first statement results from Theorem 1 Symmetric Matrices as explained above. Since the column vectors β_j are orthonormal, β_i · β_j = $\beta_i^T \beta_j$ = 0 if j ≠ i and $\beta_i^T \beta_j$ = 1 if j = i. Thus

Property 2:

Proof: By definition of the covariance matrix, the main diagonal of Σ contains the values $\sigma_1^2$ , …, $\sigma_k^2$ , and so trace(Σ) = $\sum_{i=1}^k \sigma_i^2$ . But by Property 1 of Eigenvalues and Eigenvectors, trace(Σ) = $\sum_{i=1}^k \lambda_i$ .

Observation: Thus the total variance $\sum_{i=1}^k \sigma_i^2$ for X can be expressed as trace(Σ) = $\sum_{i=1}^k \lambda_i$ , but by Property 1, this is also the total variance for Y.

Thus the portion of the total variance (of X or Y) explained by the ith principal component y_i is λ_i/ $\sum_{i=1}^k \lambda_i$ . Assuming that λ₁ ≥ … ≥ λ_k the portion of the total variance explained by the first m principal components is therefore $\sum_{i=1}^m \lambda_i$ / $\sum_{i=1}^k \lambda_i$ .

Our goal is to find a reduced number of principal components that can explain most of the total variance, i.e. we seek a value of m that is as low as possible but such that the ratio $\sum_{i=1}^m \lambda_i$ / $\sum_{i=1}^k \lambda_i$ is close to 1.

Observation: Since the population covariance Σ is unknown, we will use the sample covariance matrix S as an estimate and proceed as above using S in place of Σ. Recall that S is given by the formula:

where we now consider X = [x_ij] to be a k × n matrix such that for each i, {x_ij: 1 ≤ j ≤ n} is a random sample for random variable x_i. Since the sample covariance matrix is symmetric, there is a similar spectral decomposition

where the B_j = [b_ij] are the unit eigenvectors of S corresponding to the eigenvalues λ_j of S (actually this is a bit of an abuse of notation since these λ_j are not the same as the eigenvalues of Σ).

We now use b_ij as the regression coefficients and so have

and as above, for all i and j ≠ i

var(y_i) = λ_i cov(y_i, y_j) = 0

As before, assuming that λ₁ ≥ … ≥ λ_k, we want to find a value of m so that $\sum_{i=1}^m \lambda_i$ explains as much of the total variance as possible. In this way we reduce the number of principal components needed to explain most of the variance.

Example 1: The school system of a major city wanted to determine the characteristics of a great teacher, and so they asked 120 students to rate the importance of each of the following 9 criteria using a Likert scale of 1 to 10 with 10 representing that a particular characteristic is extremely important and 1 representing that the characteristic is not important.

Setting high expectations for the students
Entertaining
Able to communicate effectively
Having expertise in their subject
Able to motivate
Caring
Charismatic
Having a passion for teaching
Friendly and easy-going

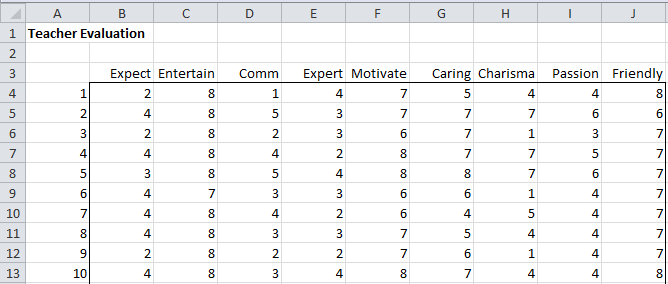
Figure 1 shows the scores from the first 10 students in the sample and Figure 2 shows some descriptive statistics about the entire 120 person sample.

Figure 1 – Teacher evaluation scores

Figure 2 – Descriptive statistics for teacher evaluations

The sample covariance matrix S is shown in Figure 3 and can be calculated directly as

=MMULT(TRANSPOSE(B4:J123-B126:J126),B4:J123-B126;J126)/(COUNT(B4:B123)-1)

Here B4:J123 is the range containing all the evaluation scores and B126:J126 is the range containing the means for each criterion. Alternatively, we can simply use the Real Statistics formula COV(B4:J123) to produce the same result.

Figure 3 – Covariance Matrix

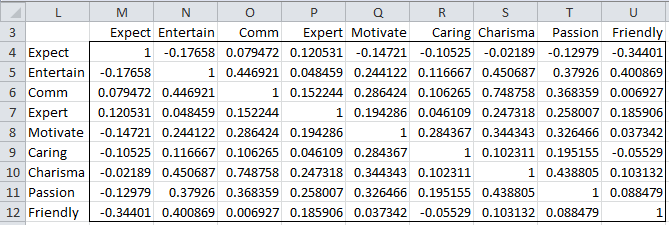
In practice, we usually prefer to standardize the sample scores. This will make the weights of the nine criteria equal. This is equivalent to using the correlation matrix. Let R = [r_ij] where r_ij is the correlation between x_i and x_j, i.e.

The sample correlation matrix R is shown in Figure 4 and can be calculated directly as

=MMULT(TRANSPOSE((B4:J123-B126:J126)/B127:J127),(B4:J123-B126:J126)/B127:J127)/(COUNT(B4:B123)-1)

Here B127:J127 is the range containing the standard deviations for each criterion. Alternatively, we can simply use the Real Statistics function CORR(B4:J123) to produce the same result.

Figure 4 – Correlation Matrix

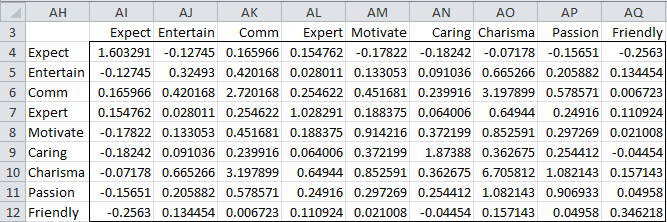
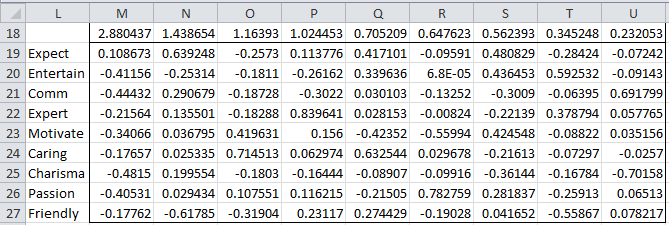
Note that all the values on the main diagonal are 1, as we would expect since the variances have been standardized. We next calculate the eigenvalues for the correlation matrix using the Real Statistics eigVECTSym(M4:U12) formula, as described in Linear Algebra Background. The result appears in range M18:U27 of Figure 5.

Figure 5 – Eigenvalues and eigenvectors of the correlation matrix

The first row in Figure 5 contains the eigenvalues for the correlation matrix in Figure 4. Below each eigenvalue is a corresponding unit eigenvector. E.g. the largest eigenvalue is λ₁ = 2.880437. Corresponding to this eigenvalue is the 9 × 1 column eigenvector B₁ whose elements are 0.108673, -0.41156, etc.

As we described above, coefficients of the eigenvectors serve as the regression coefficients of the 9 principal components. For example, the first principal component can be expressed by

This can also be expressed as

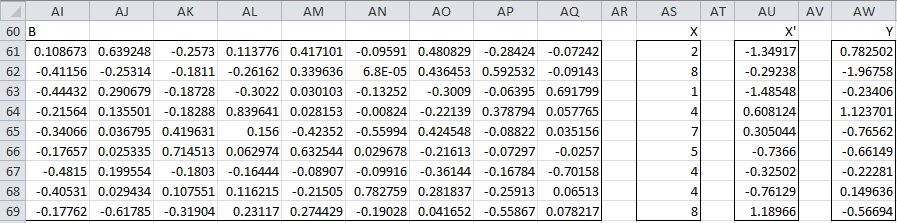
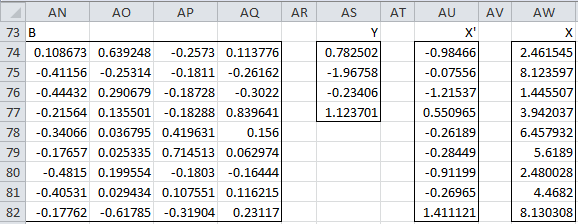
Thus for any set of scores (for the x_j) you can calculate each of the corresponding principal components. Keep in mind that you need to standardize the values of the x_j first since this is how the correlation matrix was obtained. For the first sample (row 4 of Figure 1), we can calculate the nine principal components using the matrix equation Y = BX′ as shown in Figure 6.

Figure 6 – Calculation of PC1 for first sample

Here B (range AI61:AQ69) is the set of eigenvectors from Figure 5, X (range AS61:AS69) is simply the transpose of row 4 from Figure 1, X′ (range AU61:AU69) standardizes the scores in X (e.g. cell AU61 contains the formula =STANDARDIZE(AS61, B126, B127), referring to Figure 2) and Y (range AW61:AW69) is calculated by the formula

=MMULT(TRANSPOSE(AI61:AQ69),AU61:AU69)

Thus the principal component values corresponding to the first sample are 0.782502 (PC1), -1.9758 (PC2), etc.

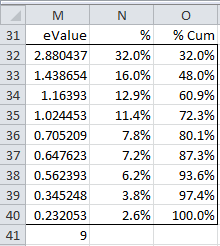
As observed previously, the total variance for the nine random variables is 9 (since the variance was standardized to 1 in the correlation matrix), which is, as expected, equal to the sum of the nine eigenvalues listed in Figure 5. In fact, in Figure 7 we list the eigenvalues in decreasing order and show the percentage of the total variance accounted for by that eigenvalue.

Figure 7 – Variance accounted for by each eigenvalue

The values in column M are simply the eigenvalues listed in the first row of Figure 5, with cell M41 containing the formula =SUM(M32:M40) and producing the value 9 as expected. Each cell in column N contains the percentage of the variance accounted for by the corresponding eigenvalue. E.g. cell N32 contains the formula =M32/M41, and so we see that 32% of the total variance is accounted for by the largest eigenvalue. Column O simply contains the cumulative weights, and so we see that the first four eigenvalues account for 72.3% of the variance.

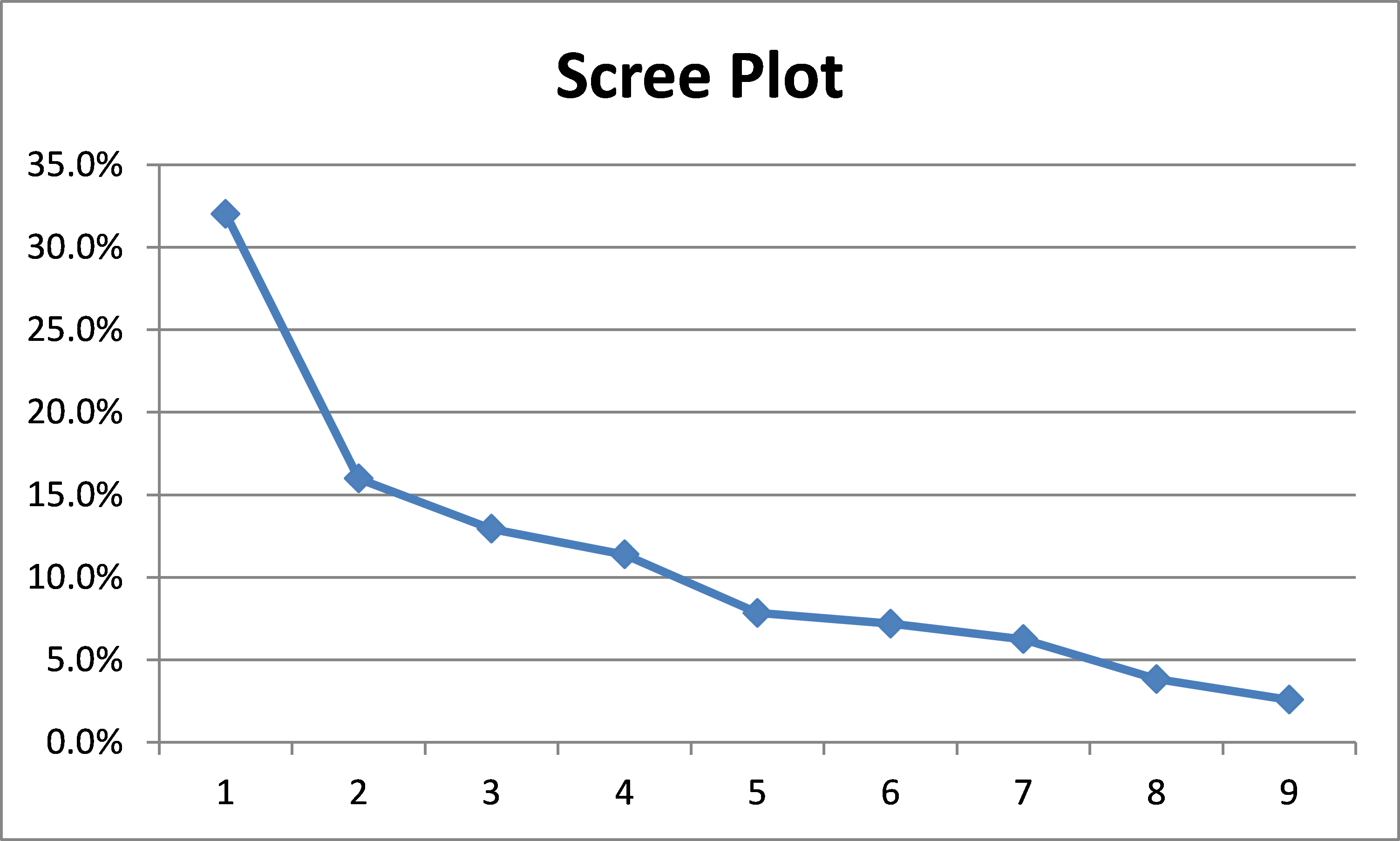
Using Excel’s charting capability, we can plot the values in column N of Figure 7 to obtain a graphical representation, called a scree plot.

Figure 8 – Scree Plot

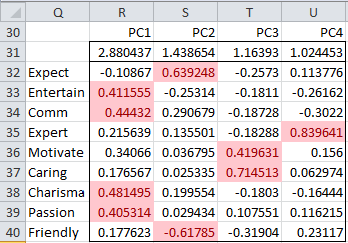
We decide to retain the first four eigenvalues, which explain 72.3% of the variance. In section Basic Concepts of Factor Analysis we will explain in more detail how to determine how many eigenvalues to retain. The portion of Figure 5 that refers to these eigenvalues is shown in Figure 9. Since all but the Expect value for PC1 is negative, we first decide to negate all the values. This is not a problem since the negative of a unit eigenvector is also a unit eigenvector.

Figure 9 – Principal component coefficients (Reduced Model)

Those values that are sufficiently large, i.e. the values that show a high correlation between the principal components and the (standardized) original variables, are highlighted. We use a threshold of ±0.4 for this purpose.

This is done by highlighting the range R32:U40 and selecting Home > Styles|Conditional Formatting and then choosing Highlight Cell Rules > Greater Than and inserting the value .4 and then selecting Home > Styles|Conditional Formatting and then choosing Highlight Cell Rules > Less Than and inserting the value -.4.

Note that Entertainment, Communications, Charisma and Passion are highly correlated with PC1, Motivation and Caring are highly correlated with PC3 and Expertise is highly correlated with PC4. Also, Expectation is highly positively correlated with PC2 while Friendly is negatively correlated with PC2.

Ideally, we would like to see that each variable is highly correlated with only one principal component. As we can see from Figure 9, this is the case in our example. Usually, this is not the case, however, and we will show what to do about this in the Basic Concepts of Factor Analysis when we discuss rotation in Factor Analysis.

In our analysis, we retain 4 of the 9 principal factors. As noted previously, each of the principal components can be calculated by

i.e. Y= B^TX′, where Y is a k × 1 vector of principal components, B is a k x k matrix (whose columns are the unit eigenvectors) and X′ is a k × 1 vector of the standardized scores for the original variables.

If we retain only m principal components, then Y = B^TX where Y is an m × 1 vector, B is a k × m matrix (consisting of the m unit eigenvectors corresponding to the m largest eigenvalues) and X′ is the k × 1 vector of standardized scores as before. The interesting thing is that if Y is known we can calculate estimates for standardized values for X using the fact that X′ = BB^TX’ = B(B^TX′) = BY (since B is an orthogonal matrix, and so, BB^T = I). From X′ it is then easy to calculate X.

Figure 10 – Estimate of original scores using reduced model

In Figure 10 we show how this is done using the four principal components that we calculated from the first sample in Figure 6. B (range AN74;AQ82) is the reduced set of coefficients (Figure 9), Y (range AS74:AS77) are the principal components as calculated in Figure 6, X′ are the estimated standardized values for the first sample (range AU74:AU82) using the formula =MMULT(AN74:AQ82,AS74:AS77) and finally, X are the estimated scores in the first sample (range AW74:AW82) using the formula =AU74:AU82*TRANSPOSE(B127:J127)+TRANSPOSE(B126:J126).

As you can see the values for X in Figure 10 are similar, but not exactly the same as the values for X in Figure 6, demonstrating both the effectiveness as well as the limitations of the reduced principal component model (at least for this sample data).

Источник

Метод главных компонентов (английский — principal component analysis, PCA) упрощает сложность высокоразмерных данных, сохраняя тенденции и шаблоны. Он делает это, преобразуя данные в меньшие размеры, которые действуют, как резюме функций. Такие данные очень распространены в разных отраслях науки и техники, и возникают, когда для каждого образца измеряются несколько признаков, например, таких как экспрессия многих видов. Подобный тип данных представляет проблемы, вызванные повышенной частотой ошибок из-за множественной коррекции данных.

Метод похож на кластеризацию — находит шаблоны без ссылок и анализирует их, проверяя, взяты ли образцы из разных групп исследования, и имеют ли они существенные различия. Как и во всех статистических методах, его можно применить неправильно. Масштабирование переменных может привести к разным результатам анализа, и очень важно, чтобы оно не корректировалось, на предмет соответствия предыдущему значению данных.

Цели анализа компонентов

Основная цель метода — обнаружить и уменьшить размерность набора данных, определить новые значимые базовые переменные. Для этого предлагается использовать специальные инструменты, например, собрать многомерные данные в матрице данных TableOfReal, в которой строки связаны со случаями и столбцами переменных. Поэтому TableOfReal интерпретируется как векторы данных numberOfRows, каждый вектор которых имеет число элементов Columns.

Традиционно метод главных компонентов выполняется по ковариационной матрице или по корреляционной матрице, которые можно вычислить из матрицы данных. Ковариационная матрица содержит масштабированные суммы квадратов и кросс-произведений. Корреляционная матрица подобна ковариационной матрице, но в ней сначала переменные, то есть столбцы, были стандартизованы. Вначале придется стандартизировать данные, если дисперсии или единицы измерения переменных сильно отличаются. Чтобы выполнить анализ, выбирают матрицу данных TabelOfReal в списке объектов и даже нажимают перейти.

Это приведет к появлению нового объекта в списке объектов по методу главных компонент. Теперь можно составить график кривых собственных значений, чтобы получить представление о важности каждого. И также программа может предложить действие: получить долю дисперсии или проверить равенство числа собственных значений и получить их равенство. Поскольку компоненты получены путем решения конкретной задачи оптимизации, у них есть некоторые «встроенные» свойства, например, максимальная изменчивость. Кроме того, существует ряд других их свойств, которые могут обеспечить факторный анализ:

дисперсию каждого, при этом доля полной дисперсии исходных переменных задается собственными значениями;
вычисления оценки, которые иллюстрируют значение каждого компонента при наблюдении;
получение нагрузок, которые описывают корреляцию между каждым компонентом и каждой переменной;
корреляцию между исходными переменными, воспроизведенными с помощью р–компонента;
воспроизведения исходных данных могут быть воспроизведены с р–компонентов;
«поворот» компонентов, чтобы повысить их интерпретируемость.

Выбор количества точек хранения

Существует два способа выбрать необходимое количество компонентов для хранения. Оба метода основаны на отношениях между собственными значениями. Для этого рекомендуется построить график значений. Если точки на графике имеют тенденцию выравниваться и достаточно близки к нулю, то их можно игнорировать. Ограничивают количество компонентов до числа, на которое приходится определенная доля общей дисперсии. Например, если пользователя удовлетворяет 95% от общей дисперсии — получают количество компонентов (VAF) 0.95.

Основные компоненты получают проектированием многомерного статистического анализа метода главных компонентов datavectors на пространстве собственных векторов. Это можно сделать двумя способами — непосредственно из TableOfReal без предварительного формирования PCA объекта и затем можно отобразить конфигурацию или ее номера. Выбрать объект и TableOfReal вместе и «Конфигурация», таким образом, выполняется анализ в собственном окружении компонентов.

Если стартовая точка оказывается симметричной матрицей, например, ковариационной, сначала выполняют сокращение до формы, а затем алгоритм QL с неявными сдвигами. Если же наоборот и отправная точка является матрица данных, то нельзя формировать матрицу с суммами квадратов. Вместо этого, переходят от численно более стабильного способа, и образуют разложения по сингулярным значениям. Тогда матрица будет содержать собственные векторы, а квадратные диагональные элементы — собственные значения.

Виды линейных комбинаций

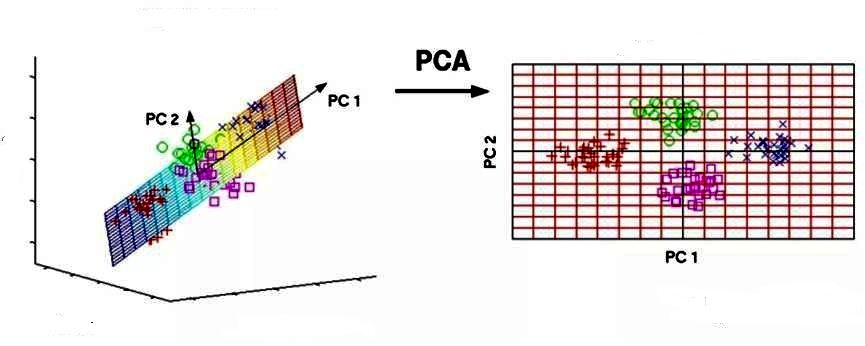
Основным компонентом является нормализованная линейная комбинация исходных предикторов в наборе данных по методу главных компонент для чайников. На изображении выше PC1 и PC2 являются основными компонентами. Допустим, есть ряд предикторов, как X1, X2…,Xp.

Основной компонент можно записать в виде: Z1 = 11X1 + 21X2 + 31X3 + …. + p1Xp

где:

Z1 — является первым главным компонентом;
p1 — является вектором нагрузки, состоящим из нагрузок (1, 2.) первого основного компонента.

Нагрузки ограничены суммой квадрата равного 1. Это связано с тем, что большая величина нагрузок может привести к большой дисперсии. Он также определяет направление основной компоненты (Z1), по которой данные больше всего различаются. Это приводит к тому, что линия в пространстве р-мер, ближе всего к n-наблюдениям.

Близость измеряется с использованием среднеквадратичного евклидова расстояния. X1..Xp являются нормированными предикторами. Нормализованные предикторы имеют среднее значение, равное нулю, а стандартное отклонение равно единице. Следовательно, первый главный компонент — это линейная комбинация исходных предикторных переменных, которая фиксирует максимальную дисперсию в наборе данных. Он определяет направление наибольшей изменчивости в данных. Чем больше изменчивость, зафиксированная в первом компоненте, тем больше информация, полученная им. Ни один другой не может иметь изменчивость выше первого основного.

Первый основной компонент приводит к строке, которая ближе всего к данным и сводит к минимуму сумму квадрата расстояния между точкой данных и линией. Второй главный компонент (Z2) также представляет собой линейную комбинацию исходных предикторов, которая фиксирует оставшуюся дисперсию в наборе данных и некоррелирована Z1. Другими словами, корреляция между первым и вторым компонентами должна равняться нулю. Он может быть представлен как: Z2 = 12X1 + 22X2 + 32X3 + …. + p2Xp.

Если они некоррелированы, их направления должны быть ортогональными.

Процесс прогнозирования тестовых данных

После того как вычислены главные компоненты начинают процесс прогнозирования тестовых данных с их использованием. Процесс метода главных компонент для чайников прост.

Например, необходимо сделать преобразование в тестовый набор, включая функцию центра и масштабирования в языке R (вер.3.4.2) и его библиотеке rvest. R — свободный язык программирования для статистических вычислений и графики. Он был реконструирован в 1992 году для решения статистических задач пользователями. Это полный процесс моделирования после извлечения PCA.

Набор данных Python:

Для реализации PCA в python импортируют данные из библиотеки sklearn. Интерпретация остается такой же, как и пользователей R. Только набор данных, используемый для Python, представляет собой очищенную версию, в которой отсутствуют вмененные недостающие значения, а категориальные переменные преобразуются в числовые. Процесс моделирования остается таким же, как описано выше для пользователей R. Метод главных компонент, пример расчета:

Спектральное разложение

Идея метода основного компонента заключается в приближении этого выражения для выполнения факторного анализа. Вместо суммирования от 1 до p теперь суммируются от 1 до m, игнорируя последние p-m членов в сумме и получая третье выражение. Можно переписать это, как показано в выражении, которое используется для определения матрицы факторных нагрузок L, что дает окончательное выражение в матричной нотации. Если используются стандартизованные измерения, заменяют S на матрицу корреляционной выборки R.

Это формирует матрицу L фактор-нагрузки в факторном анализе и сопровождается транспонированной L. Для оценки конкретных дисперсий фактор-модель для матрицы дисперсии-ковариации.

Σ = L L’+ Ψ

Теперь будет равна матрице дисперсии-ковариации минус LL ‘ .

Ψ = Σ — L L’

Основные компоненты определяются по формуле

Где:

Xi — вектор наблюдений для i-го субъекта.
S обозначает нашу выборочную дисперсионно-ковариационную матрицу.

Тогда p собственные значения для этой матрицы ковариации дисперсии, а также соответствующих собственных векторов для этой матрицы.

Собственные значения S:λ^1, λ^2, … , λ^п.

Собственные векторы S:е^1, e^2, … , e^п.

Анализ Excel в биоинформатике

Анализ PCA — это мощный и популярный метод многомерного анализа, который позволяет исследовать многомерные наборы данных с количественными переменными. По этой методике широко используется метод главных компонент в биоинформатике, маркетинге, социологии и многих других областях. XLSTAT предоставляет полную и гибкую функцию для изучения данных непосредственно в Excel и предлагает несколько стандартных и расширенных опций, которые позволят получить глубокое представление о пользовательских данных.

Можно запустить программу на необработанных данных или на матрицах различий, добавить дополнительные переменные или наблюдения, отфильтровать переменные в соответствии с различными критериями для оптимизации чтения карт. Кроме того, можно выполнять повороты. Легко настраивать корреляционный круг, график наблюдений в качестве стандартных диаграмм Excel. Достаточно перенести данные из отчета о результатах, чтобы использовать их в анализе.

XLSTAT предлагает несколько методов обработки данных, которые будут использоваться на входных данных до вычислений основного компонента:

Pearson, классический PCA, который автоматически стандартизирует данные для вычислений, чтобы избежать раздутого влияния переменных с большими отклонениями от результата.
Ковариация, которая работает с нестандартными отклонениями.
Полихорические, для порядковых данных.

Примеры анализа данных размерностей

Можно рассмотреть метод главных компонентов на примере выполнения симметричной корреляционной или ковариационной матрицы. Это означает, что матрица должна быть числовой и иметь стандартизованные данные. Допустим, есть набор данных размерностью 300 (n) × 50 (p). Где n — представляет количество наблюдений, а p — число предикторов.

Поскольку имеется большой p = 50, может быть p(p-1)/2 диаграмма рассеяния. В этом случае было бы хорошим подходом выбрать подмножество предиктора p (p<< 50), который фиксирует количество информации. Затем следует составление графика наблюдения в полученном низкоразмерном пространстве. Не следует забывать, что каждое измерение является линейной комбинацией р-функций.

Пример для матрицы с двумя переменными. В этом примере метода главных компонентов создается набор данных с двумя переменными (большая длина и диагональная длина) с использованием искусственных данных Дэвиса.

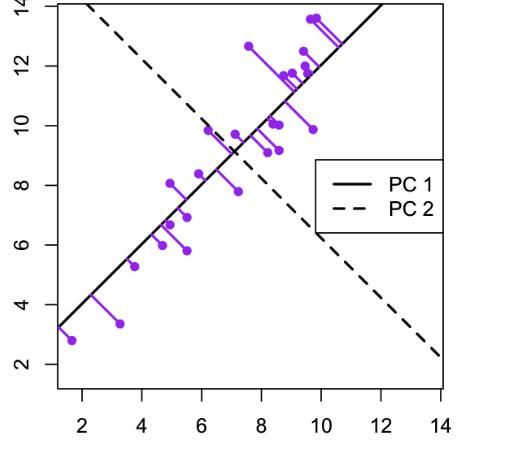
Компоненты можно нарисовать на диаграмме рассеяния следующим образом.

Этот график иллюстрирует идею первого или главного компонента, обеспечивающего оптимальную сводку данных — никакая другая линия, нарисованная на таком графике рассеяния, не создаст набор прогнозируемых значений точек данных на линии с меньшей дисперсией.

Первый компонент также имеет приложение в регрессии с уменьшенной главной осью (RMA), в которой предполагается, что как x-, так и y-переменные имеют ошибки или неопределенности или, где нет четкого различия между предсказателем и ответом.

Эконометрические модели прогнозирования

Метод главных компонентов в эконометрике — это анализ переменных, таких как ВНП, инфляция, обменные курсы и т. д. Их уравнения затем оцениваются по имеющимся данным, главным образом совокупным временным рядам. Однако эконометрические модели могут использоваться для многих приложений, а не для макроэкономических. Таким образом, эконометрика означает экономическое измерение.

Применение статистических методов к соответствующей эконометрике данных показывает взаимосвязь между экономическими переменными. Простой пример эконометрической модели. Предполагается, что ежемесячные расходы потребителей линейно зависят от доходов потребителей в предыдущем месяце. Тогда модель будет состоять из уравнения

Задачей эконометрика является получение оценок параметров a и b. Эти оценочные значения параметров, если они используются в уравнении модели, позволяют прогнозировать будущие значения потребления, которые будут зависеть от дохода предыдущего месяца. При разработке этих видов моделей необходимо учитывать несколько моментов:

характер вероятностного процесса, который генерирует данные;
уровень знаний об этом;
размер системы;
форма анализа;
горизонт прогноза;
математическая сложность системы.

Все эти предпосылки важны, потому что от них зависят источники ошибок, вытекающих из модели. Кроме того, для решения этих проблем необходимо определить метод прогнозирования. Его можно привести к линейной модели, даже если имеется только небольшая выборка. Этот тип является одним из самых общих, для которого можно создать прогнозный анализ.

Непараметрическая статистика

Метод главных компонент для непараметрических данных относится к методам измерения, в которых данные извлекаются из определенного распределения. Непараметрические статистические методы широко используются в различных типах исследований. На практике, когда предположение о нормальности измерений не выполняется, параметрические статистические методы могут приводить к вводящим в заблуждение результатам. Напротив, непараметрические методы делают гораздо менее строгие предположения о распределении по измерениям.

Они являются достоверными независимо от лежащих в их основе распределений наблюдений. Из-за этого привлекательного преимущества для анализа различных типов экспериментальных конструкций было разработано много разных типов непараметрических тестов. Такие проекты охватывают дизайн с одной выборкой, дизайн с двумя образцами, дизайн рандомизированных блоков. В настоящее время непараметрический байесовский подход с применением метода главных компонентов используется для упрощения анализа надежности железнодорожных систем.

Железнодорожная система представляет собой типичную крупномасштабную сложную систему с взаимосвязанными подсистемами, которые содержат многочисленные компоненты. Надежность системы сохраняется за счет соответствующих мер по техническому обслуживанию, а экономичное управление активами требует точной оценки надежности на самом низком уровне. Однако данные реальной надежности на уровне компонентов железнодорожной системы не всегда доступны на практике, не говоря уже о завершении. Распределение жизненных циклов компонентов от производителей часто скрывается и усложняется фактическим использованием и рабочей средой. Таким образом, анализ надежности требует подходящей методологии для оценки времени жизни компонента в условиях отсутствия данных об отказах.

Метод главных компонент в общественных науках используется для выполнения двух главных задач:

анализа по данным социологических исследований;
построения моделей общественных явлений.

Алгоритмы расчета моделей

Алгоритмы метода главных компонент дают другое представление о структуре модели и ее интерпретации. Они являются отражением того, как PCA используется в разных дисциплинах. Алгоритм нелинейного итеративного частичного наименьшего квадрата NIPALS представляет собой последовательный метод вычисления компонентов. Вычисление может быть прекращено досрочно, когда пользователь считает, что их достаточно. Большинство компьютерных пакетов имеют тенденцию использовать алгоритм NIPALS, поскольку он имеет два основных преимущества:

он обрабатывает отсутствующие данные;
последовательно вычисляет компоненты.

Цель рассмотрения этого алгоритма:

дает дополнительное представление о том, что означают нагрузки и оценки;
показывает, как каждый компонент не зависит ортогонально от других компонентов;
показывает, как алгоритм может обрабатывать недостающие данные.

Алгоритм последовательно извлекает каждый компонент, начиная с первого направления наибольшей дисперсии, а затем второго и т. д. NIPALS вычисляет один компонент за раз. Вычисленный первый эквивалентен t1t1, а также p1p1 векторов, которые были бы найдены из собственного значения или разложения по сингулярным значениям, может обрабатывать недостающие данные в XX. Он всегда сходится, но сходимость иногда может быть медленной. И также известен, как алгоритм мощности для вычисления собственных векторов и собственных значений и отлично работает для очень больших наборов данных. Google использовал этот алгоритм для ранних версий своей поисковой системы.

Алгоритм NIPALS показан на фото ниже.

Оценки коэффициента матрицы Т затем вычисляется как T=XW и в частичной мере коэффициентов регрессии квадратов B из Y на X, вычисляются, как B = WQ. Альтернативный метод оценки для частей регрессии частичных наименьших квадратов можно описать следующим образом.

Метод главных компонентов — это инструмент для определения основных осей дисперсии в наборе данных и позволяет легко исследовать ключевые переменные данных. Правильно примененный метод является одним из самых мощных в наборе инструментов анализа данных.

В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.

Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.

В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.

К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величиные разные, но на самом деле они строго зависят друг от друга. В миле 1600км, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.

Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.

Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.

Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.

Шаг 1. Подготовка данных

Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.

Сгенерируем выборку:

X = np.arange(1,11)
y = 2 * x + np.random.randn(10)*2
X = np.vstack((x,y))
print X
OUT:
[[ 1. 2. 3. 4. 5.
6. 7. 8. 9. 10. ]
[ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444
12.09865079 13.78706794 13.85301221 15.29003911 18.0998018 ]]

В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!

Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер.

Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.

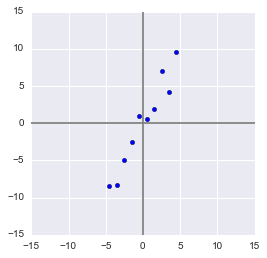
Xcentered = (X — x.mean(), X — y.mean())
m = (x.mean(), y.mean())
print Xcentered
print «Mean vector: «, m
OUT:
(array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]),
array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247,
0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658]))
Mean vector: (5.5, 10.314393916)

Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.

Шаг 2. Ковариационная матрица

В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!

Для описания формы случайного вектора необходима ковариационная матрица.

Это матрица, у которой (i,j)
-элемент является корреляцией признаков (X i , X j). Вспомним формулу ковариации:

В нашем случае она упрощается, так как E(X i) = E(X j) = 0:

Заметим, что когда X i = X j:

и это справедливо для любых случайных величин.

Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.

Замечание:
Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.

И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).

Итак, сформируем ковариационную матрицу Σ
для нашей выборки. Для этого посчитаем дисперсии X i и X j , а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X)
. Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)

Covmat = np.cov(Xcentered)
print covmat, «n»
print «Variance of X: «, np.cov(Xcentered)
print «Variance of Y: «, np.cov(Xcentered)
print «Covariance X and Y: «, np.cov(Xcentered)
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124

Шаг 3. Собственные вектора и значения (айгенпары)

О»кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X 1 и X 2), а также примерную форму на плоскости. Теперь надо надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.

Замечание:
Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.

Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна v T X. Дисперсия проекции на вектор будет соответственно равна Var(v T X). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:

Соответственно, дисперсия проекции:

Легко заметить, что дисперсия максимизируется при максимальном значении v T Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:

Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).

Кстати, в английском языке собственные значения и векторы именуются eigenvalues
и eigenvectors
соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.

Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором имеющим максимальное собственное значение, равное величине этой дисперсии
.

И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.

Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.

В библиотеке numpy реализована функция numpy.linalg.eig(X)
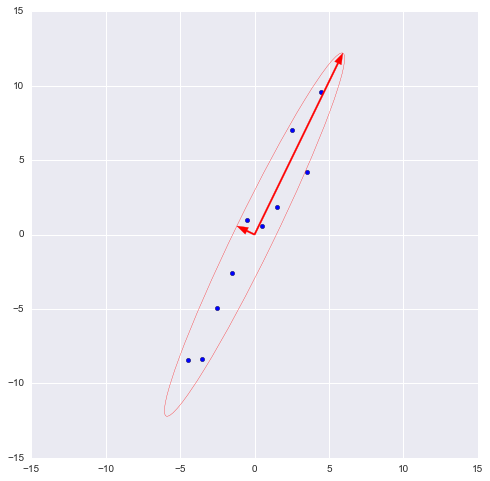
, где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.

На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т.е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.

Шаг 4. Снижение размерности (проекция)

Наибольший вектор имеет направление, схожее с линией регрессии и спроецировав на него нашу выборку мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.

Замечание:
диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).

Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!

Замечание:
На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.

Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию v T X (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора v T берем матрицу базисных векторов V T . Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.

V = (-vecs, -vecs)
Xnew = dot(v,Xcentered)
print Xnew
OUT:
[ -9.56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]

dot(X,Y)
— почленное произведение (так мы перемножаем векторы и матрицы в Python)

Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.

Шаг 5. Восстановление данных

С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.

Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выбоки: X T v T +m

Xrestored = dot(Xnew,v) + m
print «Restored: «, Xrestored
print «Original: «, X[:,9]
OUT:
Restored: [ 10.13864361 19.84190935]
Original: [ 10. 19.9094105]

Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.

Вместо заключения – проверка алгоритма

Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.

From sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XPCAreduced = pca.fit_transform(transpose(X))

Параметр n_components
указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:

Print «Our reduced X: n», Xnew
print «Sklearn reduced X: n», XPCAreduced
OUT:
Our reduced X:
[ -9.56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]

Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.

В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.

Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:

Вектор средних: mean_

— Вектор(матрица) проекции: components_

— Дисперсии осей проекции (выборочная): explained_variance_

— Доля информации (доля от общей дисперсии): explained_variance_ratio_

Замечание:
explained_variance_ показывает выборочную
дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные
дисперсии!

Сравним полученные нами значения со значениями библиотечной функции.

Print «Mean vector: «, pca.mean_, m
print «Projection: «, pca.components_, v
print «Explained variance ratio: «, pca.explained_variance_ratio_, l/sum(l)
OUT:
Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916)
Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594)
Explained variance: [ 41.39455058] 45.9939450918
Explained variance ratio: [ 0.99058588] 0.990585881238

Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.

Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).

Замечание:
библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.

Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!

P.S.:
Просьба не ругать автора за возможные неточности. Автор сам в процессе знакомства с дата-анализом и хочет помочь таким же как он в процессе освоения этой удивительной области знаний! Но конструктивная критика и разнообразный опыт всячески приветствуются!

Компонентный анализ относится к многомерным методам снижения размерности. Он содержит один метод — метод главных компонент. Главные компоненты представляют собой ортогональную систему координат, в которой дисперсии компонент характеризуют их статистические свойства.

Учитывая, что объекты исследования в экономике характеризуются большим, но конечным количеством признаков, влияние которых подвергается воздействию большого количества случайных причин.

Вычисление главных компонент

Первой главной компонентой Z1 исследуемой системы признаков Х1, Х2, Х3 , Х4 ,…, Хn называется такая центрировано — нормированная линейная комбинация этих признаков, которая среди прочих центрировано — нормированных линейных комбинаций этих признаков, имеет дисперсию наиболее изменчивую.

В качестве второй главной компоненты Z2 мы будем брать такую центрировано — нормированную комбинацию этих признаков, которая:

не коррелированна с первой главной компонентой,

не коррелированны с первой главной компонентой, эта комбинация имеет наибольшую дисперсию.

K-ой главной компонентой Zk (k=1…m) мы будем называть такую центрировано — нормированную комбинацию признаков, которая:

не коррелированна с к-1 предыдущими главными компонентами,

среди всех возможных комбинаций исходных признаков, которые не

не коррелированны с к-1 предыдущими главными компонентами, эта комбинация имеет наибольшую дисперсию.

Введём ортогональную матрицу U и перейдём от переменных Х к переменным Z, причём

Вектор выбирается т. о., чтобы дисперсия была максимальной. После получения выбирается т. о., чтобы дисперсия была максимальной при условии, что не коррелированно с и т. д.

Так как признаки измерены в несопоставимых величинах, то удобнее будет перейти к центрированно-нормированным величинам. Матрицу исходных центрированно-нормированных значений признаков найдем из соотношения:

где — несмещенная, состоятельная и эффективная оценка математического ожидания,

Несмещенная, состоятельная и эффективная оценка дисперсии.

Матрица наблюденных значений исходных признаков приведена в Приложении.

Центрирование и нормирование произведено с помощью программы»Stadia».

Так как признаки центрированы и нормированы, то оценку корреляционной матрицы можно произвести по формуле:

Перед тем как проводить компонентный анализ, проведем анализ независимости исходных признаков.

Проверка значимости матрицы парных корреляций с помощью критерия Уилкса.

Выдвигаем гипотезу:

Н0: незначима

Н1: значима

125,7; (0,05;3,3) = 7,8

т.к > , то гипотеза Н0 отвергается и матрица является значимой, следовательно, имеет смысл проводить компонентный анализ.

Проверим гипотезу о диагональности ковариационной матрицы

Выдвигаем гипотезу:

Строим статистику, распределена по закону с степенями свободы.

123,21, (0,05;10) =18,307

т.к >, то гипотеза Н0 отвергается и имеет смысл проводить компонентный анализ.

Для построения матрицы факторных нагрузок необходимо найти собственные числа матрицы, решив уравнение.

Используем для этой операции функцию eigenvals системы MathCAD, которая возвращает собственные числа матрицы:

Т.к. исходные данные представляют собой выборку из генеральной совокупности, то мы получили не собственные числа и собственные вектора матрицы, а их оценки. Нас будет интересовать на сколько “хорошо” со статистической точки зрения выборочные характеристики описывают соответствующие параметры для генеральной совокупности.

Доверительный интервал для i-го собственного числа ищется по формуле:

Доверительные интервалы для собственных чисел в итоге принимают вид:

Оценка значения нескольких собственных чисел попадает в доверительный интервал других собственных чисел. Необходимо проверить гипотезу о кратности собственных чисел.

Проверка кратности производится с помощью статистики

где r-количество кратных корней.

Данная статистика в случае справедливости распределена по закону с числом степеней свободы. Выдвинем гипотезы:

Так как, то гипотеза отвергается, то есть собственные числа и не кратны.

Необходимо выделить главные компоненты на уровне информативности 0,85. Мера информативности показывает какую часть или какую долю дисперсии исходных признаков составляют k-первых главных компонент. Мерой информативности будем называть величину:

На заданном уровне информативности выделено три главных компоненты.

Запишем матрицу =

Для получения нормализованного вектора перехода от исходных признаков к главным компонентам необходимо решить систему уравнений: , где — соответствующее собственное число. После получения решения системы необходимо затем нормировать полученный вектор.

Для решения данной задачи воспользуемся функцией eigenvec системы MathCAD, которая возвращает нормированный вектор для соответствующего собственного числа.

В нашем случае первых четырех главных компонент достаточно для достижения заданного уровня информативности, поэтому матрица U (матрица перехода от исходного базиса к базису из собственных векторов)

Строим матрицу U, столбцами которой являются собственные вектора:

Матрица весовых коэффициентов:

Коэффициенты матрицы А являются коэффициентами корреляции между центрировано — нормированными исходными признаками и ненормированными главными компонентами, и показывают наличие, силу и направление линейной связи между соответствующими исходными признаками и соответствующими главными компонентами.

Метод главных
компонент – это метод, который переводит
большое количество связанных между
собой (зависимых, коррелирующих)
переменных в меньшее количество
независимых переменных, так как большое
количество переменных часто затрудняет
анализ и интерпретацию информации.
Строго говоря, этот метод не относится
к факторному анализу, хотя и имеет с ним
много общего. Специфическим является,
во-первых, то, что в ходе вычислительных
процедур одновременно получают все
главные компоненты и их число первоначально
равно числу исходных переменных;
во-вторых, постулируется возможность
полного разложения дисперсии всех
исходных переменных, т.е. ее полное
объяснение через латентные факторы
(обобщенные признаки).

Например,
представим, что мы провели исследование,
в котором измерили у студентов интеллект
по тесту Векслера, тесту Айзенка, тесту
Равена, а также успеваемость по социальной,
когнитивной и общей психологии. Вполне
возможно, что показатели различных
тестов на интеллект будут коррелировать
между собой, так как они, в конце концов,
измеряют одну характеристику испытуемого
– его интеллектуальные способности,
хотя и по-разному. Если переменных в
исследовании слишком много (x
1
,
x
2
,
…,
x
p
)
,
а некоторые из них взаимосвязаны, то у
исследователя иногда возникает желание
уменьшить сложность данных, сократив
количество переменных. Для этого и
служит метод главных компонент, который
создает несколько новых переменных y
1
,
y
2
,
…,
y
p
,
каждая из которых является линейной
комбинацией первоначальных переменных
x
1
,
x
2
,
…,
x
p
:

y 1 =a 11 x 1 +a 12 x 2 +…+a 1p x p

y 2 =a 21 x 1 +a 22 x 2 +…+a 2p x p

… (1)

y p =a p1 x 1 +a p2 x 2 +…+a pp x p

Переменные
y
1
,
y
2
,
…,
y
p

называются главными компонентами или
факторами. Таким образом, фактор
– это искусственный статистический
показатель, возникающий в результате
специальных преобразований корреляционной
матрицы
.

Процедура извлечения факторов называется
факторизацией матрицы. В результате
факторизации из корреляционной матрицы
может быть извлечено разное количество
факторов вплоть до числа, равного
количеству исходных переменных. Однако
факторы, определяемые в результате
факторизации, как правило, не равноценны
по своему значению.

Коэффициенты
a
ij
,
определяющие новую переменную, выбираются
таким образом, чтобы новые переменные
(главные компоненты, факторы) описывали
максимальное количество вариативности
данных и не коррелировали между собой.
Часто полезно представить коэффициенты
a
ij

таким образом,
чтобы они представляли собой коэффициент
корреляции между исходной переменной
и новой переменной (фактором). Это
достигается умножением a
ij

на стандартное отклонение фактора. В
большинстве статистических пакетов
так и делается (в программе STATISTICA
тоже). Коэффициенты
a

ij

Обычно они представляются в виде таблицы,
где факторы располагаются в виде
столбцов, а переменные в виде строк:

Такая
таблица называется таблицей (матрицей)
факторных нагрузок. Числа, приведенные
в ней, являются коэффициентами a
ij
.Число
0,86 означает, что корреляция между первым
фактором и значением по тесту Векслера
равна 0,86. Чем выше факторная нагрузка
по абсолютной величине, тем сильнее
связь переменной с фактором.

ПРИМЕНЕНИЕ МЕТОДА ГЛАВНЫХ КОМПОНЕНТ

ДЛЯ ОБРАБОТКИ МНОГОМЕРНЫХ СТАТИСТИЧЕСКИХ ДАННЫХ

Рассмотрены вопросы обработки многомерных статистических данных рейтинговой оценки студентов на основе применения метода главных компонент.

Ключевые слова: многомерный анализ данных, снижение размерности, метод главных компонент, рейтинг.

На практике часто приходится сталкиваться с ситуацией, когда объект исследования характеризуется множеством разнообразных параметров, каждый из которых измеряется или оценивается. Анализ полученного в результате исследования нескольких однотипных объектов массива исходных данных представляет собой практически нерешаемую задачу. Поэтому исследователю необходимо проанализировать связи и взаимозависимости между исходными параметрами, с тем чтобы отбросить часть из них или заменить их меньшим числом каких-либо функций от них, сохранив при этом по возможности всю заключенную в них информацию.

В связи с этим встают задачиснижения размерности, т. е. перехода от исходного массива данных к существенно меньшему количеству показателей, отобранных из числа исходных или полученных путем некоторого их преобразования (с наименьшей потерей информации, содержащейся в исходном массиве), и классификации – разделения рассматриваемой совокупности объектов на однородные (в некотором смысле) группы. Если по большому числу разнотипных и стохастически взаимосвязанных показателей были получены результаты статистического обследования целой совокупности объектов, то для решения задач классификации и снижения размерности следует использовать инструментарий многомерного статистического анализа, в частности метод главных компонент .

В статье предлагается методика применения метода главных компонент для обработки многомерных статистических данных. В качестве примера приводится решение задачи статистической обработки многомерных результатов рейтинговой оценки студентов.

1.
Определение и вычисление главных компонент
..png» height=»22 src=»> признаков. В результате получаем многомерные наблюдения, каждое из которых можно представить в виде векторного наблюдения

где https://pandia.ru/text/79/206/images/image005.png» height=»22 src=»>.png» height=»22 src=»>– символ операции транспонирования.

Полученные многомерные наблюдения необходимо подвергнуть статистической обработке..png» height=»22 src=»>.png» height=»22 src=»>.png» width=»132″ height=»25 src=»>.png» width=»33″ height=»22 src=»> допустимых преобразований исследуемых признаков 0 » style=»border-collapse:collapse»>

	– условие нормировки;
	– условие ортогональности

Полученные подобным преобразованием https://pandia.ru/text/79/206/images/image018.png» width=»79″ height=»23 src=»> и представляют собой главные компоненты. Из нихпри дальнейшем анализеисключают переменные с минимальной дисперсией , т. е..png» width=»131″ height=»22 src=»> в преобразовании (2)..png» width=»13″ height=»22 src=»> этой матрицы равны дисперсиям главных компонент .

Таким образом, первой главной компонентой https://pandia.ru/text/79/206/images/image013.png» width=»80″ height=»23 src=»>называется такая нормированно-центрированная линейная комбинация этих показателей, которая среди всех прочих подобных комбинаций обладает наибольшей дисперсией..png» width=»12″ height=»22 src=»> –
собственный вектор матрицы https://pandia.ru/text/79/206/images/image025.png» width=»15″ height=»22 src=»>.png» width=»80″ height=»23 src=»> называется такая нормированно-центрированная линейная комбинация этих показателей, которая не коррелирована с https://pandia.ru/text/79/206/images/image013.png» width=»80″ height=»23 src=»>.png» width=»80″ height=»23 src=»> измеряются в различных единицах, то результаты исследования с помощью главных компонент будут существенно зависеть от выбора масштаба и природы единиц измерения , а полученные линейные комбинации исходных переменных будет трудно интерпретировать. В связи с этим при различных единицах измерения исходных признаков DIV_ADBLOCK310″>

https://pandia.ru/text/79/206/images/image030.png» width=»17″ height=»22 src=»>.png» width=»56″ height=»23 src=»>. После подобного преобразования проводят анализ главных компонент относительно величин https://pandia.ru/text/79/206/images/image033.png» width=»17″ height=»22 src=»>,
которая является одновременно корреляционной матрицей https://pandia.ru/text/79/206/images/image035.png» width=»162″ height=»22 src=»>.png» width=»13″ height=»22 src=»> на i
—
й исходный признак ..png» width=»14″ height=»22 src=»>.png» width=»10″ height=»22 src=»> равна дисперсии v
—
й главной компонентыhttps://pandia.ru/text/79/206/images/image038.png» width=»10″ height=»22 src=»> используются при содержательной интерпретации главных компонент..png» width=»20″ height=»22 src=»>.png» width=»251″ height=»25 src=»>

Для проведения расчетов векторные наблюдения агрегируем в выборочную матрицу, в которой строки соответствуют контролируемым признакам, а столбцы – объектам исследования (размерность матрицы – https://pandia.ru/text/79/206/images/image043.png» width=»348″ height=»67 src=»>

После центрирования исходных данных находим выборочную корреляционную матрицу по формуле

https://pandia.ru/text/79/206/images/image045.png» width=»204″ height=»69 src=»>

Диагональные элементы матрицы https://pandia.ru/text/79/206/images/image047.png» width=»206″ height=»68 src=»>

Недиагональные элементы этой матрицы представляют собой выборочные оценки коэффициентов корреляции между соответствующей парой признаков.

Составляем характеристическое уравнение для матрицы 0 » style=»margin-left:5.4pt;border-collapse:collapse»>

Находим все его корни:

Теперь для нахождения компонент главных векторов подставляем последовательно численные значения https://pandia.ru/text/79/206/images/image065.png» width=»16″ height=»22 src=»>.png» width=»102″ height=»24 src=»>

Например, при https://pandia.ru/text/79/206/images/image069.png» width=»262″ height=»70 src=»>

Очевидно, что полученная система уравнений совместна ввиду однородности и неопределенна, т. е. имеет бесконечное множество решений. Для нахождения единственного интересующего нас решения воспользуемся следующими положениями:

1. Для корней системы может быть записано соотношение

https://pandia.ru/text/79/206/images/image071.png» width=»20″ height=»23 src=»> – алгебраическое дополнение j
-го элемента любой i
-й строки матрицы системы.

2. Наличие условия нормировки (2) обеспечивает единственность решения рассматриваемой системы уравнений..png» width=»13″ height=»22 src=»>, определяются однозначно, за исключением того, что все они могут одновременно изменить знак. Однако знаки компонентов собственных векторов не играют существенной роли, так как их смена не влияет на результат анализа. Они могут служить только для индикации противоположных тенденций на соответствующей главной компоненте .

Таким образом, получаем собственный вектор https://pandia.ru/text/79/206/images/image025.png» width=»15″ height=»22 src=»>:

https://pandia.ru/text/79/206/images/image024.png» width=»12″ height=»22 src=»> проверяем по равенству

https://pandia.ru/text/79/206/images/image076.png» width=»503″ height=»22″>

… … … … … … … … …

https://pandia.ru/text/79/206/images/image078.png» width=»595″ height=»22 src=»>

https://pandia.ru/text/79/206/images/image080.png» width=»589″ height=»22 src=»>

где https://pandia.ru/text/79/206/images/image082.png» width=»16″ height=»22 src=»>.png» width=»23″ height=»22 src=»> – стандартизированные значения соответствующих исходных признаков.

Составляем ортогональную матрицу линейного преобразования https://pandia.ru/text/79/206/images/image086.png» width=»94″ height=»22 src=»>

Так как в соответствии со свойствами главных компонент сумма дисперсий исходных признаков равна сумме дисперсий всех главных компонент, то с учетом того, что мы рассматривали нормированные исходные признаки, можно оценить, какую часть общей изменчивости исходных признаков объясняет каждая из главных компонент. Например, для первых двух главных компонент имеем:

Таким образом, в соответствии с критерием информативности, используемым для главных компонент, найденных по корреляционной матрице, семьпервых главных компонент объясняют 88,97% общей изменчивости пятнадцати исходных признаков.

Используя матрицу линейного преобразования https://pandia.ru/text/79/206/images/image038.png» width=»10″ height=»22 src=»> (для семи первых главных компонент):

https://pandia.ru/text/79/206/images/image090.png» width=»16″ height=»22 src=»> – число дипломов, полученных в конкурсе научных и дипломных работ ; https://pandia.ru/text/79/206/images/image092.png» width=»16″ height=»22 src=»>.png» width=»22″ height=»22 src=»>.png» width=»22″ height=»22 src=»>.png» width=»22″ height=»22 src=»> – награды и призовые места, занятые на региональных, областных и городских спортивных соревнованиях.

3..png» width=»16″ height=»22 src=»>(число грамот по результатам участия в конкурсах научных и дипломных работ).

4..png» width=»22″ height=»22 src=»>(награды и призовые места, занятые на вузовских соревнованиях).

6. Шестая главная компонента положительно коррелирована с показателем DIV_ADBLOCK311″>

4. Третья главная компонента – активность студентов в учебном процессе.

5. Четвертая и шестая компоненты – прилежность студентов в течение весеннего и осеннего семестров соответственно.

6. Пятая главная компонента – степень участия в спортивных соревнованиях университета.

В дальнейшем для проведения всех необходимых расчетов при выделении главных компонент предлагается использовать специализированные статистические программные комплексы, например STATISTICA, что существенно облегчит процесс анализа.

Описанный в данной статье процесс выделения главных компонент на примере рейтинговой оценки студентов предлагается использовать для аттестации бакалавров и магистров.

СПИСОК ЛИТЕРАТУРЫ

1. Прикладная статистика: Классификация и снижение размерности: справ. изд. / , ; под ред. . – М.: Финансы и статистика, 1989. – 607 с.

2. Справочник по прикладной статистике:в 2 т.: [пер. с англ.] / под ред. Э. Ллойда, У. Ледермана, . – М.:Финансы и статистика, 1990. – Т. 2. – 526 c.

3. Прикладная статистика. Основы эконометрики . В 2 т. Т.1. Теория вероятностей и прикладная статистика: учеб. для вузов / , B. C. Мхитарян. – 2-е изд., испр.– М: ЮНИТИ-ДАНА, 2001. – 656 с.

4. Афифи, А. Статистический анализ: подход с использованием ЭВМ: [пер. с англ.] / А. Афифи, С. Эйзен.– М.: Мир, 1982. – 488 с.

5. Дронов, статистический анализ: учеб. пособие / . – Барна3. – 213 с.

6. Андерсон, Т. Введение в многомерный статистический анализ / Т. Андерсон; пер. с англ. [и др.]; под ред. . – М.: Гос. изд-во физ.-мат. лит., 1963. – 500 с.

7. Лоули, Д. Факторный анализ как статистический метод / Д. Лоули, А. Максвелл; пер. с англ. . – М.: Мир, 1967. – 144 с.

8. Дубров, статистические методы: учебник / , . – М.: Финансы и статистика, 2003. – 352 с.

9. Кендалл, М. Многомерный статистический анализ и временные ряды / М. Кендалл, А. Стьюарт;пер. с англ. , ; под ред. , . – М.: Наука,1976. – 736 с.

10. Белоглазов, анализ в задачах квалиметрии образования / // Изв. РАН. Теория и системы управления. – 2006. – №6. – С. 39 – 52.

Материал поступил в редколлегию 8.11.11.

Работа выполнена в рамках реализации федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 гг. (государственный контракт № П770).

Цели анализа компонентов

дисперсию каждого, при этом доля полной дисперсии исходных переменных задается собственными значениями;
вычисления оценки, которые иллюстрируют значение каждого компонента при наблюдении;
получение нагрузок, которые описывают корреляцию между каждым компонентом и каждой переменной;
корреляцию между исходными переменными, воспроизведенными с помощью р-компонента;
воспроизведения исходных данных могут быть воспроизведены с р-компонентов;
«поворот» компонентов, чтобы повысить их интерпретируемость.

Выбор количества точек хранения

Основной компонент можно записать в виде: Z1 = 11X1 + 21X2 + 31X3 + …. + p1Xp

Z1 — является первым главным компонентом;
p1 — является вектором нагрузки, состоящим из нагрузок (1, 2.) первого основного компонента.

Если они некоррелированы, их направления должны быть ортогональными.

Теперь будет равна матрице дисперсии-ковариации минус LL » .

Xi — вектор наблюдений для i-го субъекта.
S обозначает нашу выборочную дисперсионно-ковариационную матрицу.

Собственные значения S:λ^1, λ^2, … , λ^п.

Собственные векторы S:е^1, e^2, … , e^п.

Pearson, классический PCA, который автоматически стандартизирует данные для вычислений, чтобы избежать раздутого влияния переменных с большими отклонениями от результата.
Ковариация, которая работает с нестандартными отклонениями.
Полихорические, для порядковых данных.

Примеры анализа данных размерностей

Компоненты можно нарисовать на диаграмме рассеяния следующим образом.

характер вероятностного процесса, который генерирует данные;
уровень знаний об этом;
размер системы;
форма анализа;
горизонт прогноза;
математическая сложность системы.

Непараметрическая статистика

Метод главных компонент в общественных науках используется для выполнения двух главных задач:

анализа по данным социологических исследований;
построения моделей общественных явлений.

Алгоритмы расчета моделей

он обрабатывает отсутствующие данные;
последовательно вычисляет компоненты.

Цель рассмотрения этого алгоритма:

дает дополнительное представление о том, что означают нагрузки и оценки;
показывает, как каждый компонент не зависит ортогонально от других компонентов;
показывает, как алгоритм может обрабатывать недостающие данные.

Алгоритм NIPALS показан на фото ниже.

Время на прочтение
10 мин

Количество просмотров 222K

К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.

Шаг 1. Подготовка данных

Сгенерируем выборку:

x = np.arange(1,11)
y = 2 * x + np.random.randn(10)*2
X = np.vstack((x,y))
print X

OUT:
[[  1.           2.           3.           4.           5.          
    6.           7.           8.           9.          10.        ]
 [  2.73446908   4.35122722   7.21132988  11.24872601   9.58103444   
  12.09865079  13.78706794  13.85301221  15.29003911  18.0998018 ]]

Xcentered = (X[0] - x.mean(), X[1] - y.mean())
m = (x.mean(), y.mean())
print Xcentered
print "Mean vector: ", m

OUT:
(array([-4.5, -3.5, -2.5, -1.5, -0.5,  0.5,  1.5,  2.5,  3.5,  4.5]),
 array([-8.44644233, -8.32845585, -4.93314426, -2.56723136,  1.01013247,
         0.58413394,  1.86599939,  7.00558491,  4.21440647,  9.59501658]))
Mean vector:  (5.5, 10.314393916)

Шаг 2. Ковариационная матрица

Для описания формы случайного вектора необходима ковариационная матрица.

Это матрица, у которой (i,j)-элемент является корреляцией признаков (X_i, X_j). Вспомним формулу ковариации:

В нашем случае она упрощается, так как

E(X_i) = E(X_j) = 0:

Заметим, что когда X_i = X_j:

и это справедливо для любых случайных величин.

Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.

Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии X_i и X_j, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)

covmat = np.cov(Xcentered)
print covmat, "n"
print "Variance of X: ", np.cov(Xcentered)[0,0]
print "Variance of Y: ", np.cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]

OUT:
[[  9.16666667  17.93002811]
 [ 17.93002811  37.26438587]] 

Variance of X:  9.16666666667
Variance of Y:  37.2643858743
Covariance X and Y:  17.9300281124

Шаг 3. Собственные вектора и значения (айгенпары)

О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X₁ и X₂), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.

Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.

Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна v^TX. Дисперсия проекции на вектор будет соответственно равна Var(v^TX). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:

Соответственно, дисперсия проекции:

Легко заметить, что дисперсия максимизируется при максимальном значении v^T Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:

Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.

Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии.

Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.

В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.

Шаг 4. Снижение размерности (проекция)

Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.

Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).

Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.

Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию v^TX (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора v^T берем матрицу базисных векторов V^T. Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.

_, vecs = np.linalg.eig(covmat)
v = -vecs[:,1])
Xnew = dot(v,Xcentered)
print Xnew

OUT:
[ -9.56404107  -9.02021624  -5.52974822  -2.96481262   0.68933859
   0.74406645   2.33433492   7.39307974   5.3212742   10.59672425]

dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)

Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.

Шаг 5. Восстановление данных

n = 9     #номер элемента случайной величины
Xrestored = dot(Xnew[n],v) + m
print 'Restored: ', Xrestored
print 'Original: ', X[:,n]

OUT:
Restored:  [ 10.13864361  19.84190935]
Original:  [ 10.         19.9094105]

Вместо заключения – проверка алгоритма

from sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XPCAreduced = pca.fit_transform(transpose(X))

Параметр n_components указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:

print 'Our reduced X: n', Xnew
print 'Sklearn reduced X: n', XPCAreduced

OUT:
Our reduced X: 
[ -9.56404106  -9.02021625  -5.52974822  -2.96481262   0.68933859
   0.74406645   2.33433492   7.39307974   5.3212742   10.59672425]
Sklearn reduced X: 
[[ -9.56404106]
 [ -9.02021625]
 [ -5.52974822]
 [ -2.96481262]
 [  0.68933859]
 [  0.74406645]
 [  2.33433492]
 [  7.39307974]
 [  5.3212742 ]
 [ 10.59672425]]

— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_

Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!

Сравним полученные нами значения со значениями библиотечной функции.

print 'Mean vector: ', pca.mean_, m
print 'Projection: ', pca.components_, v
print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l)

OUT: 
Mean vector:  [  5.5         10.31439392] (5.5, 10.314393916)
Projection:  [[ 0.43774316  0.89910006]] (0.43774316434772387, 0.89910006232167594)
Explained variance:  [ 41.39455058] 45.9939450918
Explained variance ratio:  [ 0.99058588] 0.990585881238

Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.

Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!

P.S.: Просьба не ругать автора за возможные неточности. Автор сам в процессе знакомства с дата-анализом и хочет помочь таким же как он в процессе освоения этой удивительной области знаний! Но конструктивная критика и разнообразный опыт всячески приветствуются!

Источник

We decided to write a series of posts on a very useful statistical technique called Principal Component Analysis (PCA). In the current post we give a brief explanation of the technique and its implementation in excel. In practice it is less important to know the computations behind PCA than it is to understand the intuition behind the results. For those who are interested to know the mathematics behind this technique we recommend any multivariate statics book. One book which we really like is Carol Alexander’s Market Risk Analysis Volume 1. This book comes with a free excel addin Matrix.xla that can be used to implement PCA in excel. Alternatively the reader can download this excellent addin for free from http://excellaneous.com/Downloads.html.

The idea of PCA is to find a set of linear combinations of variables that describe most of the variation in the entire data set. For example, we may have a time series of daily changes in interest rate swap rates for the past year. We consider changes in 2y, 3y, 4y, 5y, 7y, 10y, 15y, 20y, 30y swap tenors. Our data set has nine variables in total. With so many variables it may be easier to consider a smaller number of combinations of this original data rather than consider the full data set. This is often called a reduction in the data set’s dimension. Having set the goal of reducing dimension of our data set to a smaller number of factors a simple choice would be to use the average. In our case this would be Average = 1/9*2y+1/9*3y+1/9*4y+1/9*5y+1/9*7y+1/9*10y+1/9*15y+1/9*20y+1/9*30y. Our vector of coefficients C=[1/9, 1/9, 1/9, 1/9, 1/9, 1/9, 1/9, 1/9, 1/9] is called a linear combination. Linear combinations where the sum of squared coefficients equal to 1 are called a standardized linear combinations. PCA finds a set of standardized linear combinations where each individual factor is orthogonal (meaning not correlated). There are as many principal components as there are variables in the original data set but they are ordered in such a way that only a few factors explain most of the original data. The orthogonal factors are computed from the correlation or covariance matrix of the original (sometimes standardized) data.

Let’s walk through an example to gain a better understanding. We start out with daily changes in US swap rates for abovementioned tenors.

Shot1

We would like to reduce the dimension to as few factors as possible that describe the variability in the data. To run PCA on the data we need to generate a correlation or covariance matrix. We choose to use a covariance matrix in this example.

Shot2

To make the calculations of a covariance matrix easier we use below custom array function that will loop through each data column and calculate pair wise covariance using excels built in COVAR function

VBA

We can then use =MEigenvecPow(OurCovarianceMatrix,TRUE) function from the Matrix.xla addin to generate the eigenvector of the covariance matrix. These values are often called loadings. Below are the results for our example.

Shot3

Now it is time for the interpretation of the results. The loading for each factor give us the sensitivity of a particular variable to a 1 unit change in a given factor (principal component). For example, in the above, if the first principal component goes up by 1 then the 2yr swap rate will change by .17 bps, the 5yr will go up but .36bps, and 30yr swap will increase by.35 bps (this is the first column of the matrix). The second column gives us the loadings for the second factor (principal component). In this case, when the second principal component increases by 1, the short end of the curve will increase while the longer end will decrease. This just means that the curve flattens as the second principal component increases. Finally, when the third principal component increases, the short and long end of the curve increases while the middle points of the curve decrease.

When we plot the loadings we can see the data better.

Shot4

This shows us that the first component captures mostly parallel yield curve moves, the second captures the slope, while the third captures the curvature (butterfly).

So far we spoke about changes in principal components. We would like to know what value they actually take. This is easy; each principal component is a linear combination of the original data and the loadings. So for example, using above data, on 26 Jun2015 the first principal component is equal to 14.70 [.17*4.18 +.25*2.67+.32*3.47 +.36*4.28+.38*5.18+ .38*5.48 +.37*6.02+.36*6.05+.35*6.34]. Calculating a time series of the first three principal components we can see that they are indeed uncorrelated (orthogonal)

Shot5

Now we would like to answer the obvious question, why did we stop at three principal components in our discussion above. The answer is that three components account for 99.7% of the variation in the data. How can we compute that number? We can use the eigenvalues of our covariance/correlation matrix. To compute these we use MEigenvalPow(OurCovarianceMatrix) from the matrix.xla addin. Below (green row) presents our results.

Shot6

To assign meaning to these values and compute the percentage of variation that each principal component explains we need to do the following; Take the sum of all eigenvalues. In our example the sum across the green row is 155.41. We can now divide the first eigenvalue by 155.41 to get 90.4%. This means the first principal component explains 90.4% of the variation in the data. The second component captures 8.7% [13.57/155.41]. We can see that in total the first three principal components explain approximately 99.7% of the variation in the data. Adding more factors doesn’t add to our understanding of the data.

We wish to come back to our main point that we mentioned at the start. PCA is used to represent the original data as a function of a reduced number of factors. In our case that means each change in yield for a chosen swap tenor is a function of three factors. So, for example, on any given day the change in 30yr swap is a given by its loadings times the principal components. On 26 June 2015 the first principal component was 14.70, the second principal component was -1.65 and the third was 1.71. From above table of loadings we see that the loadings of 30yr tenor for the first three principal components are .35, -.45, .35. Taking the sum of products we get 6.48 [(14.7*.35)+(-1.65*-.45)+.(1.71*.35)]. This means that we can expect the 30yr swap rate to increase by 6.48 bps given the change in the first three principal components that we witnessed. The actual change on June 26 2015 was 6.34bps.

In this post we tried to present an intuitive explanation of Principal Component Analysis. In follow up posts we will discuss the many uses of PCA in managing risk, modelling asset prices, and trading.

Some useful resources:

1) Market Risk Analysis Volume 1 by Carol Alexander: http://www.amazon.com/Market-Analysis-Quantitative-Methods-Finance/dp/0470998008/ref=sr_1_2?s=books&ie=UTF8&qid=1435483909&sr=1-2&keywords=market+risk+analysis

Источник

Метод главных компонент, или PCA (Principal Component Analysis) – это математическая процедура, которая используется для снижения размерности данных. Она помогает найти наиболее важные признаки в наборе данных и преобразовать их в новые переменные, называемые главными компонентами.

Главные компоненты представляют собой линейные комбинации исходных переменных и выбираются таким образом, чтобы они объясняли как можно большую часть дисперсии в данных. Таким образом, PCA позволяет сократить количество переменных в наборе данных, сохраняя важную информацию.

В Excel можно использовать метод главных компонент для анализа данных, идентификации скрытых корреляций и снижения размерности данных. Для этого необходимо воспользоваться инструментами анализа данных, предоставляемыми Excel.

Например, чтобы использовать PCA в Excel, нужно выбрать на вкладке «Данные» соответствующую функцию или анализ данных, загрузить или ввести данные, а затем настроить параметры анализа. Excel вычислит главные компоненты и предоставит вам результаты, которые можно использовать для дальнейшего анализа данных или визуализации.

Содержание

Понятие метода главных компонент в Excel
Зачем нужен метод главных компонент
Как работает метод главных компонент в Excel
Достоинства метода главных компонент
Ограничения метода главных компонент
Примеры использования метода главных компонент в Excel
Выводы

Понятие метода главных компонент в Excel

При использовании метода главных компонент в Excel, первый шаг — это подготовка данных. Для этого необходимо выделить числовые переменные, удалить нулевые значения и стандартизировать данные. Затем можно приступать к применению PCA.

Процесс PCA в Excel включает следующие шаги:

Шаг	Описание
1	Выделение числовых переменных
2	Удаление нулевых значений
3	Стандартизация данных
4	Вычисление ковариационной матрицы
5	Вычисление собственных значений и собственных векторов
6	Выбор главных компонент
7	Проекция данных на новое пространство

Метод главных компонент в Excel может использоваться для различных задач, таких как кластеризация данных, снижение размерности для визуализации данных или выделение наиболее информативных признаков. Он позволяет получить новое представление данных, которое может быть полезным для анализа и принятия решений.

Использование метода главных компонент в Excel может быть достаточно простым и удобным способом работы с данными. Однако, для достижения оптимальных результатов необходимо тщательно выбирать параметры и правильно интерпретировать полученные результаты.

Зачем нужен метод главных компонент

Главная цель метода главных компонент заключается в сокращении размерности данных, то есть преобразовании исходных переменных в новые, которые лучше представляют вариацию исходной информации. Это позволяет упростить структуру данных, избавиться от лишней информации и снизить избыточность.

Основной принцип метода заключается в том, чтобы найти линейные комбинации исходных переменных (главные компоненты), которые объясняют наибольшую часть вариации данных. Главные компоненты строятся таким образом, чтобы первая компонента объясняла максимальную долю вариации, вторая компонента — максимальную долю оставшейся вариации, и так далее.

Преимущества использования метода главных компонент включают:

Снижение размерности данных, что упрощает их визуализацию и позволяет работать с меньшим количеством информации;
Устранение мультиколлинеарности (высокой корреляции) между исходными переменными, что позволяет обойти проблемы, связанные с мультиколлинеарностью в регрессионном анализе;
Упрощение моделей, что позволяет облегчить интерпретацию и повысить качество прогнозирования;
Выделение главных факторов или признаков, которые наиболее влияют на исследуемую переменную;
Обработка данных с пропущенными значениями и выбросами, исключение из анализа наиболее нетипичных случаев.

Таким образом, метод главных компонент является мощным инструментом для анализа данных и может быть полезен в различных ситуациях, где необходимо сжать информацию и выявить наиболее важные переменные или факторы.

Как работает метод главных компонент в Excel

Процесс работы метода главных компонент в Excel осуществляется в несколько шагов:

1. Нормализация данных. Это первый шаг перед применением PCA. Нормализация позволяет привести все переменные к одинаковой шкале и избежать их доминирования в процессе анализа.

2. Расчет ковариационной матрицы. Ковариационная матрица показывает зависимость между переменными и позволяет определить, какие из них вносят наибольший вклад в общую дисперсию данных.

3. Расчет собственных значений и собственных векторов. Собственные значения и собственные векторы ковариационной матрицы позволяют определить главные компоненты. Главные компоненты являются линейными комбинациями исходных переменных и ортогональны друг другу.

4. Отбор главных компонент. Метод главных компонент позволяет определить, сколько главных компонент охватывает большую часть дисперсии данных. Обычно выбираются главные компоненты с наибольшими собственными значениями.

5. Проецирование данных. После выбора главных компонент можно проецировать исходные данные на новое пространство, состоящее из главных компонент. Это позволяет сократить размерность данных и визуализировать их в удобном виде.

Использование метода главных компонент в Excel позволяет сократить избыточность данных, выявить основные факторы, которые влияют на изменения в данных, и сократить время анализа данных. Этот метод широко применяется в разных областях, таких как финансы, медицина, маркетинг и многих других.

Достоинства метода главных компонент

Уменьшение размерности данных: PCA позволяет существенно сократить размерность исходных данных, сохраняя при этом основные характеристики набора данных. Это особенно полезно, когда имеется большой набор признаков или столбцов, и вы хотите упростить анализ данных.
Устранение мультиколлинеарности: Если в данных присутствуют сильно коррелирующие признаки, PCA может помочь избавиться от мультиколлинеарности. Это позволяет устранить проблему, когда признаки избыточно повторяют информацию, чтобы алгоритмы анализа данных работали более эффективно.
Визуализация данных: PCA позволяет проецировать многомерные данные на двухмерную или трехмерную плоскость, что облегчает визуальное представление данных. Такая визуализация может помочь выявить паттерны и взаимосвязи в данных, которые может быть сложно заметить в исходном наборе данных.
Улучшение производительности моделей: Уменьшение размерности данных с помощью PCA может привести к улучшению производительности моделей машинного обучения. Модели могут обучаться быстрее и давать более точные прогнозы при использовании сжатых представлений данных.
Обеспечение анонимности данных: Если данные содержат конфиденциальные или личные сведения, PCA может использоваться для представления данных в виде анонимных компонентов, сохраняя важные характеристики данных.

Совокупность этих преимуществ делает метод главных компонент мощным инструментом в области анализа данных и машинного обучения.

Ограничения метода главных компонент

1. Линейность

Метод главных компонент основан на предположении о линейных взаимосвязях между переменными. Если взаимосвязи являются нелинейными, то PCA может дать неправильные результаты.

2. Чувствительность к выбросам

PCA может быть чувствительным к выбросам в данных. Одно аномальное значение может существенно искажать результаты PCA и приводить к неправильным выводам.

3. Потеря интерпретируемости

После применения PCA и сокращения размерности данных, исходные переменные теряют свою исходную интерпретируемость. Появление новых главных компонент делает интерпретацию результатов более сложной.

4. Выбор числа компонент

Определение оптимального числа главных компонент является сложной задачей. Неверный выбор числа компонент может привести либо к недостаточному объяснению дисперсии данных, либо к переобъяснению с большим числом компонент.

5. Нормировка данных

PCA требует, чтобы данные были нормированы, чтобы избежать проблем с переменными различной шкалы. Отсутствие нормировки данных может привести к искаженным результатам и неправильным выводам.

Несмотря на эти ограничения, метод главных компонент остается ценным инструментом в анализе данных и может быть использован для сокращения размерности и выявления скрытых закономерностей.

Примеры использования метода главных компонент в Excel

В Excel можно использовать адд-ин «Анализ данных» для применения метода главных компонент. Для этого нужно установить адд-ин, выбрать данные, на которые хотите применить PCA, и выбрать соответствующую опцию в меню «Анализ данных». После этого следуйте инструкциям адд-ина для настройки параметров анализа.

Вот несколько примеров, как можно использовать метод главных компонент в Excel:

Пример	Описание
Анализ многомерных данных	PCA может помочь в исследовании сложных многомерных данных, таких как результаты опросов, экономические показатели или результаты экспериментов. Он позволяет выявить основные факторы, влияющие на данные, и определить взаимосвязи между переменными.
Визуализация данных	PCA позволяет снизить размерность данных и отобразить их в пространстве меньшей размерности. Это может быть полезно для визуализации данных на графиках или диаграммах.
Удаление шума и выбросов	PCA может использоваться для удаления шума и выбросов из данных. Он позволяет идентифицировать главные компоненты и исключить из них выбросы или случайные шумы.
Поиск главных факторов	PCA может использоваться для поиска главных факторов, влияющих на данные. Это может быть полезно, например, в маркетинговых исследованиях для определения ключевых факторов успеха продукта.

Применение метода главных компонент в Excel позволяет сделать данные более понятными и интерпретируемыми, а также выявить важные связи и зависимости.

Выводы

В данной статье мы рассмотрели основные принципы работы метода главных компонент и его применение в программе Excel. Мы узнали, как провести данное анализ данных, как интерпретировать полученные результаты и как использовать их для принятия решений.

Важно отметить, что результаты при использовании метода главных компонент могут быть зависимы от выбора начальных данных и предположений. Поэтому рекомендуется проводить несколько итераций, проверять результаты и вносить необходимые коррективы.

В целом, метод главных компонент является мощным инструментом для анализа и визуализации данных. Он позволяет сжать информацию, выявить основные закономерности и упростить их интерпретацию. Этот метод может быть полезен для решения широкого круга задач и может помочь в принятии более обоснованных решений.

Источник

Анализ главных компонентов (PCA) – это мощный статистический метод, который позволяет сократить размерность данных, представленных в многомерном пространстве, и выделять наиболее важные факторы в данных. Этот метод основывается на преобразовании исходных переменных в новые, так называемые главные компоненты. Анализ главных компонентов широко применяется в различных областях, таких как экономика, финансы, биология, социология и др.

В данной статье мы рассмотрим, как провести анализ главных компонентов в Excel с помощью встроенных функций и советов. Мы покажем, как подготовить данные для анализа, как провести сам анализ и как интерпретировать результаты. Мы также расскажем о некоторых ключевых моментах, которые важно учесть при использовании этого метода. Наша цель – помочь вам освоить анализ главных компонентов в Excel и научиться использовать его для вашей конкретной задачи.

Важно отметить, что для проведения анализа главных компонентов в Excel необходимо иметь набор данных, в котором имеются хотя бы две переменные. Идеально, если эти переменные будут коррелировать между собой. Если вы еще не имеете подходящий набор данных, вы можете использовать открытые источники данных или создать собственную выборку.

Для тех, кто только начинает знакомиться с анализом главных компонентов, это может показаться сложным и непонятным процессом. Однако, с помощью Excel и нашей инструкции, мы надеемся, что вы сможете освоить этот метод и использовать его для анализа и интерпретации вашего собственного набора данных.

Содержание

Метод анализа главных компонентов
Использование Excel для анализа главных компонентов
Подготовка данных для анализа главных компонентов в Excel
Шаги анализа главных компонентов в Excel
Интерпретация результатов анализа главных компонентов в Excel
Преимущества и ограничения анализа главных компонентов в Excel
Советы по проведению анализа главных компонентов в Excel

Метод анализа главных компонентов

Главные компоненты представляют собой линейные комбинации исходных переменных и обладают следующими свойствами:

Максимальная дисперсия: Первая главная компонента (PC1) объясняет наибольшую часть дисперсии в данных. Вторая главная компонента (PC2) объясняет максимально возможную дисперсию, не зависимую от PC1, и так далее.
Ортогональность: Главные компоненты ортогональны друг другу, что означает, что они не коррелированы.
Содержат всю информацию: Сумма дисперсий всех главных компонентов равна общей дисперсии исходных данных, что означает, что главные компоненты сохраняют всю информацию из исходного набора данных.

Процесс анализа главных компонентов включает несколько шагов:

Стандартизация данных: Исходные данные стандартизируются путем вычитания среднего значения и деления на стандартное отклонение. Это необходимо для обеспечения всех переменных сравнимыми масштабами.
Вычисление ковариационной матрицы или корреляционной матрицы: Ковариационная матрица используется, если переменные имеют разные единицы измерения, а корреляционная матрица — если переменные измеряются в одной и той же шкале.
Вычисление собственных значений и собственных векторов: Собственные значения представляют собой меру важности каждой главной компоненты, а собственные векторы — их направление в пространстве исходных переменных.
Выбор главных компонент: Главные компоненты выбираются на основе собственных значений. Обычно выбираются главные компоненты с наибольшими собственными значениями, чтобы сохранить наибольшую часть информации из исходных данных.
Проекция исходных данных на главные компоненты: Исходные данные проецируются на главные компоненты, чтобы получить новые наборы переменных, состоящие из главных компонент.

Метод анализа главных компонентов широко используется в многих областях, таких как финансы, биоинформатика, маркетинг и др. Он позволяет сократить размерность данных, выявить скрытые связи между переменными и улучшить понимание данных в целом.

Использование Excel для анализа главных компонентов

Для проведения анализа главных компонентов в Excel необходимо следовать нескольким шагам:

Подготовить данные. Необходимо иметь подготовленный набор данных, в котором все переменные должны быть числового типа. Для этого можно использовать функции Excel, такие как SUM, AVERAGE, STDEV и др., чтобы получить числовые значения для каждой переменной.
Создать корреляционную матрицу. В Excel можно использовать функцию CORREL для вычисления корреляции между переменными в наборе данных. Для этого необходимо выбрать диапазон ячеек, в которых находятся переменные, и применить функцию CORREL для каждой комбинации переменных.
Выполнить анализ главных компонентов. В Excel для анализа главных компонентов можно использовать функцию PCAResults. Эта функция вычисляет главные компоненты и их вклад в переменные набора данных. Результаты анализа главных компонентов можно сохранить в новый лист или диапазон ячеек.
Интерпретировать результаты. После проведения анализа главных компонентов необходимо проанализировать результаты и интерпретировать главные компоненты, их значимость и влияние на переменные набора данных. Для этого можно использовать графики и статистические методики, доступные в Excel.

Использование Excel для анализа главных компонентов дает возможность проводить разнообразные манипуляции с данными и получать информацию о главных факторах, влияющих на данные. Этот метод анализа позволяет сократить размерность данных и выявить основные факторы, которые объясняют большую часть изменчивости в наборе данных.

Подготовка данных для анализа главных компонентов в Excel

1. Очистка данных: Прежде чем приступить к анализу, необходимо выполнить очистку данных от выбросов, пропущенных значений и других ошибок. Это позволит получить более точные результаты и избежать искажения результатов из-за ошибок в данных.

2. Нормализация данных: Если переменные в вашем наборе данных имеют различные шкалы измерения или единицы измерения, необходимо выполнить их нормализацию. Нормализация данных позволит уравнять значимость переменных в анализе главных компонентов.

3. Выбор переменных: Перед проведением анализа главных компонентов необходимо выбрать только те переменные, которые являются релевантными для вашего анализа. Исключение нерелевантных переменных поможет улучшить качество результатов и снизить вычислительную сложность.

4. Подготовка данных: В Excel необходимо организовать данные в табличной форме, где каждый столбец представляет собой переменную, а каждая строка — наблюдение. Убедитесь, что в каждой ячейке содержится одно значение и что в первой строке указаны имена переменных.

5. Применение анализа главных компонентов: После подготовки данных, можно приступить к применению анализа главных компонентов в Excel. Воспользуйтесь соответствующими инструментами и функциями, доступными в программе, чтобы провести анализ и получить результаты.

6. Интерпретация результатов: Полученные результаты анализа главных компонентов нужно проанализировать и проинтерпретировать. Основные компоненты (главные компоненты) могут быть интерпретированы как новые переменные, объясняющие различие в данных. Они могут быть использованы для визуализации данных и выявления основных паттернов.

Подготовка данных для анализа главных компонентов в Excel является важным этапом, который влияет на точность и качество полученных результатов. Правильная подготовка данных гарантирует достоверность и интерпретируемость полученных главных компонентов.

Шаги анализа главных компонентов в Excel

1. Подготовка данных: перед началом анализа необходимо подготовить данные. Важно убедиться, что все переменные находятся в численном формате и не содержат пропущенных значений. Также рекомендуется провести масштабирование данных, чтобы избежать влияния разных единиц измерения.

2. Создание корреляционной матрицы: следующим шагом является создание корреляционной матрицы для оценки степени взаимосвязи между переменными. В Excel можно использовать функцию КОРРЕЛ для расчета коэффициентов корреляции между парами переменных.

3. Расчет собственных значений и собственных векторов: далее необходимо вычислить собственные значения и собственные векторы на основе корреляционной матрицы. В Excel это можно сделать с помощью функции СОВПР. Результатом будут собственные значения и собственные векторы, которые представляют собой главные компоненты.

4. Отбор компонент: для дальнейшего анализа можно выбрать определенное количество главных компонент, которые объясняют наибольшую долю дисперсии данных. Для этого можно рассчитать долю дисперсии, объясняемую каждой компонентой, и выбрать компоненты с наибольшими значениями собственных значений.

5. Визуализация данных: после отбора компонент можно приступать к визуализации данных. Это можно сделать с помощью графиков рассеяния или биографов, которые отображают отношения между переменными и главными компонентами. В Excel можно использовать графические инструменты, такие как графики рассеяния или диаграммы рассеяния с хвостовиками.

6. Интерпретация результатов: наконец, анализ главных компонентов позволяет интерпретировать результаты и выявить главные факторы, которые вносят наибольший вклад в данные. Обычно главные компоненты можно описать с помощью факторных нагрузок, которые показывают, какие переменные наиболее сильно коррелируют с каждой компонентой.

В заключение, анализ главных компонентов в Excel является эффективным способом снижения размерности и визуализации многомерных данных. Следуя описанным выше шагам, вы сможете провести анализ главных компонентов в Excel и получить ценные инсайты из ваших данных.

Интерпретация результатов анализа главных компонентов в Excel

После проведения анализа главных компонентов в Excel, полученные результаты требуется правильно интерпретировать. Важно понимать, что каждая главная компонента объясняет определенную долю дисперсии в данных, которая указывается в столбце «Доля дисперсии». Чем выше значение доли дисперсии, тем больше информации содержит соответствующая компонента.

Еще одним важным аспектом интерпретации результатов PCA является анализ главных нагрузок (loadings). Главные нагрузки отображают вклад каждой переменной в каждую главную компоненту. Положительные и отрицательные значения нагрузок указывают на направление и силу влияния переменных на каждую компоненту. Чем выше по модулю значение нагрузки, тем сильнее переменная связана с данной компонентой.

Также стоит обратить внимание на скриптграфик (scree plot), который отображает доли дисперсии для каждой главной компоненты. Этот график помогает определить количество компонент, которые достаточно для объяснения основной части дисперсии в данных. Обычно сохраняются только те компоненты, доля дисперсии которых составляет более 1-5%.

Интерпретация результатов анализа главных компонентов в Excel помогает выявить наиболее значимые переменные и упростить сложные данные. Это позволяет сделать более точные выводы и принимать обоснованные решения на основе фактических данных.

Преимущества и ограничения анализа главных компонентов в Excel

Одним из главных преимуществ анализа главных компонентов в Excel является его простота использования. Excel имеет интуитивно понятный интерфейс и множество встроенных функций, позволяющих реализовать PCA без особого технического опыта. Это полезно для непрофессионалов, которым требуется быстро провести анализ данных и извлечь наиболее важные компоненты.

Еще одним преимуществом анализа главных компонентов в Excel является его способность обеспечить линейную комбинацию исходных переменных, которая объясняет наибольшую часть дисперсии данных. Это позволяет увидеть общие закономерности и основные факторы, влияющие на исследуемую проблему. Такой подход позволяет сократить количество переменных и облегчить дальнейшую интерпретацию данных.

Однако также необходимо учитывать ограничения анализа главных компонентов в Excel. Во-первых, Excel имеет ограничения на размер входных данных. Если вам нужно обработать большое количество данных, возможно потребуется использование других программ или языков программирования. Во-вторых, Excel не предоставляет много гибкости при настройке процедуры PCA. Он использует стандартные настройки, и вы не можете изменять внутренние параметры анализа.

Таким образом, анализ главных компонентов в Excel имеет свои преимущества и ограничения. Он является простым и доступным инструментом для анализа данных, но ограничен по размеру и настройкам. При выборе метода анализа главных компонентов необходимо учитывать конкретную задачу и объем данных, с которыми вы работаете.

Советы по проведению анализа главных компонентов в Excel

Подготовьте данные: Перед проведением анализа главных компонентов важно убедиться, что ваши данные соответствуют требованиям метода. Убедитесь, что данные представлены в виде таблицы, где каждый столбец представляет собой переменную, а каждая строка — наблюдение.
Стандартизируйте данные: Чтобы анализ главных компонентов был эффективным, рекомендуется стандартизировать данные. Это позволяет уравнять вклад различных переменных и избежать преобладания переменных с большими значениями.
Выберите число компонент: Определение оптимального числа компонент является важной задачей при проведении анализа главных компонентов. Для этого можно использовать метод «локтя», график собственных значений или установить пороговое значение объясняемой дисперсии.
Интерпретируйте результаты: После проведения анализа главных компонентов не забудьте проанализировать полученные результаты. Интерпретация главных компонент позволяет понять, какие переменные оказывают наибольшее влияние на каждую компоненту и как они взаимосвязаны друг с другом.
Используйте визуализацию: Визуализация может значительно облегчить понимание результатов анализа главных компонентов. Примените диаграммы рассеяния, графики суммарной дисперсии или biplot для наглядного представления компонент и их взаимосвязи.
Проверьте стабильность: Анализ главных компонентов может быть чувствителен к выбросам и изменениям в данных. Чтобы убедиться в стабильности результатов, рекомендуется провести анализ на нескольких подвыборках данных или сделать перекрестную проверку.

Следуя этим советам, вы сможете провести анализ главных компонентов в Excel более эффективно и получить содержательные результаты, которые помогут вам при работе с данными.

Источник