9. Кластерный анализ
Кластерный анализ — позволяет выявить группы (кластеры) объектов по заданным переменным. Программа при этом автоматически определяет количество существующих кластеров.
Задача кластерного анализа состоит в формировании групп:
- однородных внутри, объекты схожи между собой (условие внутренней гомогенности);
- отличных от объектов в других группах (условие внешней гетерогенности) [2].
С помощью кластерного анализа в маркетинге выявляются целевые группы потребителей, для которых необходимо разработать уникальный комплекс инструментов маркетинга.
Пример. Необходимо разделить всех курящих по возрасту и уровню дохода на однородные группы (кластеры) (рисунок 9.1).
На рисунке 9.1. вариант В не выявлено однородных кластеров, все курильщики представляют единю группу, следовательно, разработка уникальных торговых предложений не имеет смысла.
На рисунке 9.1. вариант А выявлены два однородных кластера курящих: “старые и бедные”, “молодые и богатые”. Данные группы могут быть представлены, как две целевые группы потребителей табачных
изделий. Следовательно. Для каждой из них необходимо разработать уникальные торговые предложения по цене, качеству, особым свойствам, дизайну упаковки, особенностям продвижения, системе распределения
товара.
Рисунок 9.1 — Кластерный анализ [2]
В процессе выполнения кластерного анализа выявляются статистические связи между анализируемыми переменными, которые указывают на схожесть переменных и, затем объединение выявленных факторов в
группы на основе уровня различий между ними. Количество кластеров зависит от задаваемых параметров схожести переменных, объединяемых в один кластер.
Основные термины, применяемые в кластерном анализе
Евклидово расстояние — расстояние между объектами, равное сумме квадратов разностей между значениями одноименных переменных объектов.
Иерархическая кластеризация — метод, при котором строится иерархическая или древовидная структура. Позволяет детально исследовать различия между объектами, выбрать оптимальное число кластеров.
Агломеративная или объединяющая кластеризация — иерархический метод формирования кластеров, при котором каждый объект сначала находится в отдельном кластере, затем объекты группируются в значительно
более крупные кластеры.
Разделяющая или дивизиональная кластеризация — иерархический метод формирования кластеров, при котором один общий большой все кластер делится на более мелкие для создания однородных кластеров.
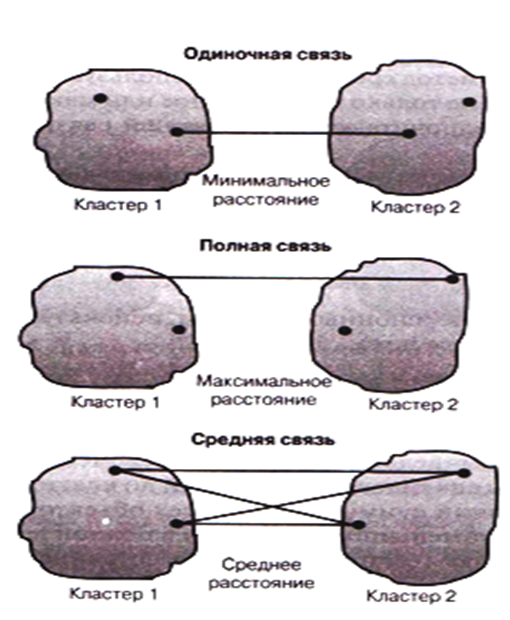
Методы связи — методы формирования кластеров, при которых объекты объединяются в группу на основе рассчитанного между ними расстояния (рисунок 9.2).
Метод одиночной связи — или правило ближайшего соседа — в основе лежит выбор переменных, расстояние между которыми минимально.
Метод полной связи — или правило дальнего соседа — в основе лежит выбор переменных, расстояние между которыми максимально.
Метод средней связи — в основе лежит среднее значение расстояния между переменными разных кластеров.
Рисунок 9.2 — Методы связи
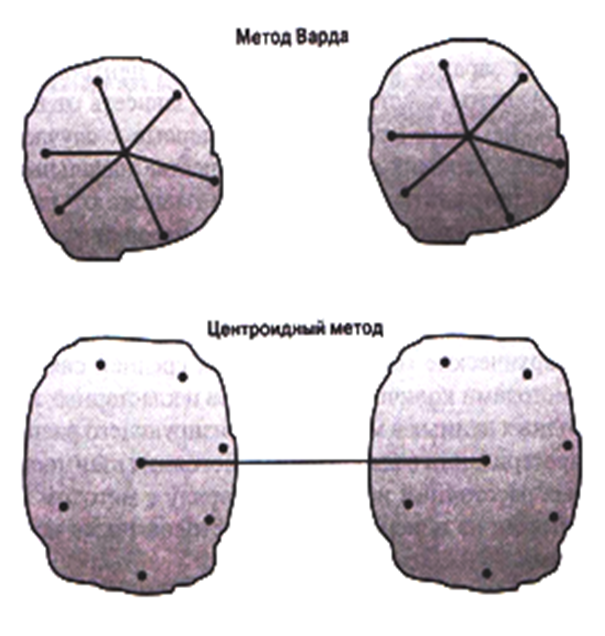
Дисперсионные методы — Метод Варда и Центроидный метод (Рисунок 9.3).
Метод Варда — в качестве меры используется квадрат евклидового расстояния, который должен быть минимальным.
Центроидный метод — оценивается расстояние между центроидами (средними) групп переменных.
Рисунок 9.3 — Дисперсионные методы
Метод к — средних — переменные группируются в кластер в пределах порогового значения, которое задается исходя из определенного центра кластера.
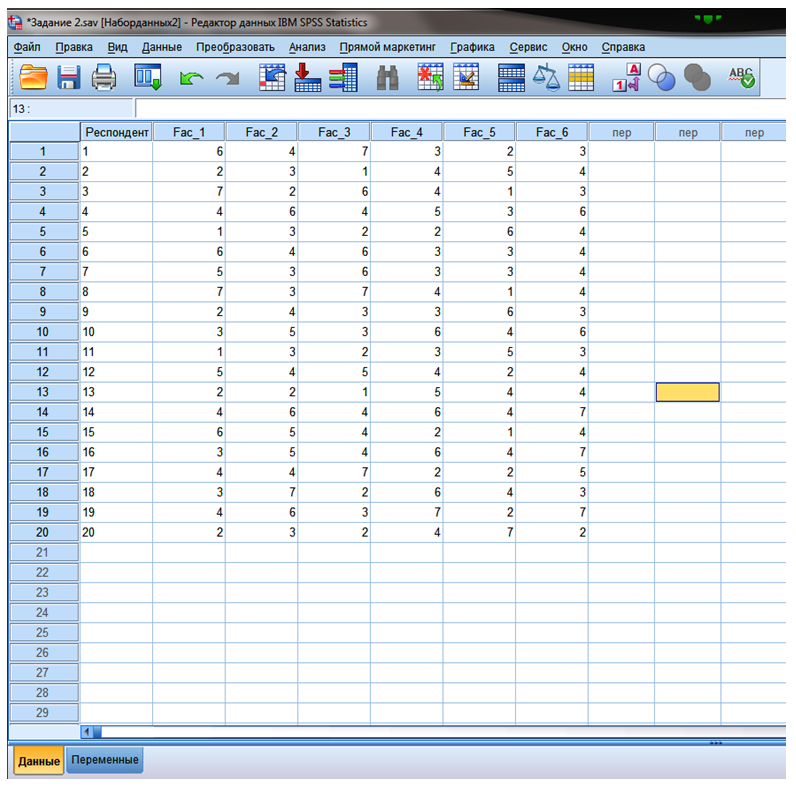
Пример. 20 респондентов попросили выразить свое отношение к посещению торговых центров для приобретения товаров. Выделили шесть утверждений, степень согласия с которыми респондентов попросили
выразить на основе семибалльной шкалы (1 — совсем не согласен, 7 — абсолютно согласен).
Fac_1 — Считаю посещение торговых центром приятным процессом.
Fac_2 — Посещение торговых центров подрывает бюджет моей семьи.
Fac_3 — Мне нравиться обедать и ужинать в торговых центрах.
Fac_4 — В торговых центрах мне нравиться делать хорошие покупки.
Fac_5 — Меня очень раздражает посещение торговых центров.
Fac_6 — Посещая разные магазины, можно сравнивать цены и выбирать более дешевый товар.
Рисунок 9.4 — Данные для кластеризации
Вверх
Пошаговая инструкция
ШАГ 1. Подготовить данные для анализа в SPSS.
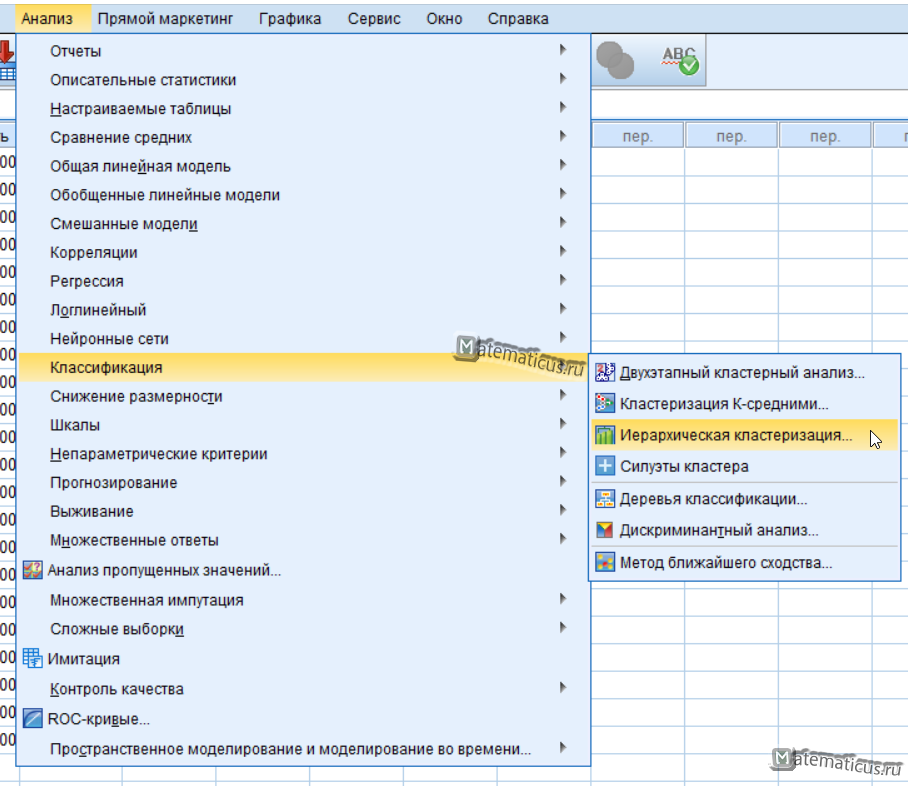
ШАГ 2. “Анализ” — выбрать “Классификация”. В рассматриваемом примере применяется иерархический кластерный анализ.
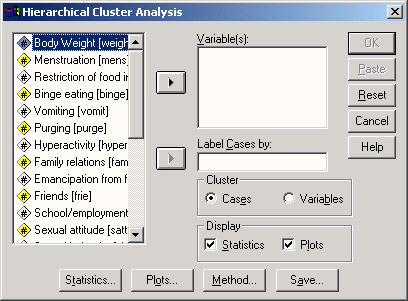
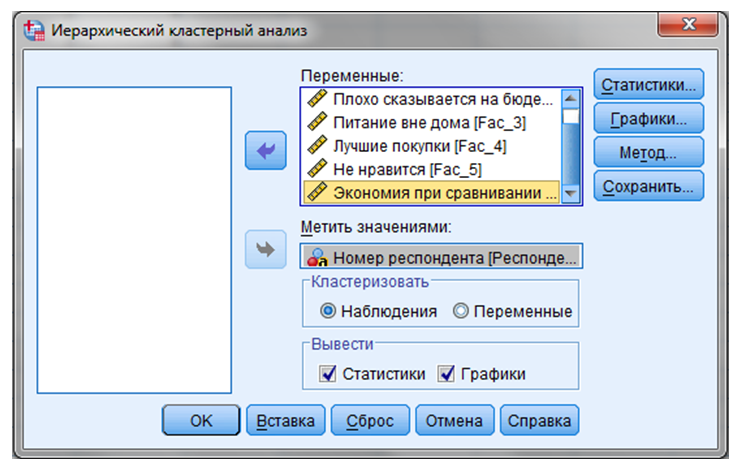
ШАГ 3. Анализ — Классификация — Иерархическая кластеризация — “Иерархический кластерный анализ” (Рисунок 9.5).
Рисунок 9.5 — Иерархический кластерный анализ
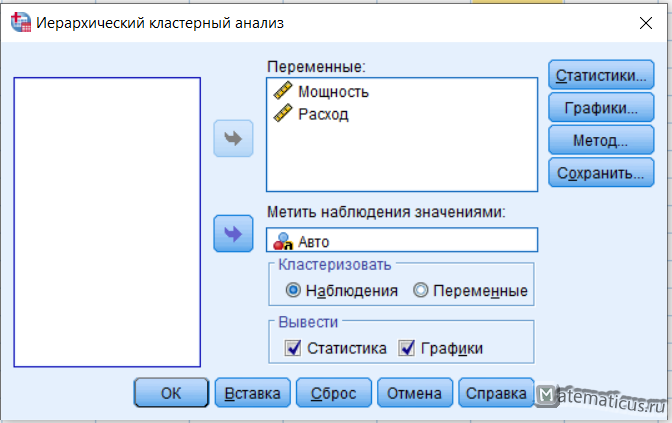
Выбираем все шесть факторов, отражающих отношение респондентов к посещению торговых центров, и переносим их в поле “Переменные”.
В поле “Метить значениями” необходимо перенести переменную “Номер респондента”. В данном случае могут использоваться только поле текстовые переменные, поэтому в столбце
“Тип переменной” необходимо выбрать “Текстовая”.
В поле “Кластеризовать” выбрать один из двух предлагаемых вариантов: “Наблюдения” или “Переменные”. В нашем примере выбирается вариант “Наблюдения”,
в ходе кластерного анализа будут собираться в кластеры потребители, а не характеристики их отношения.
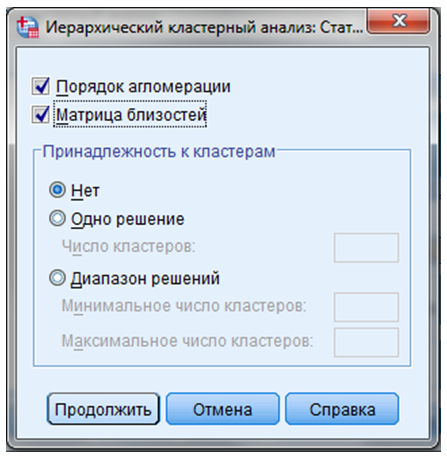
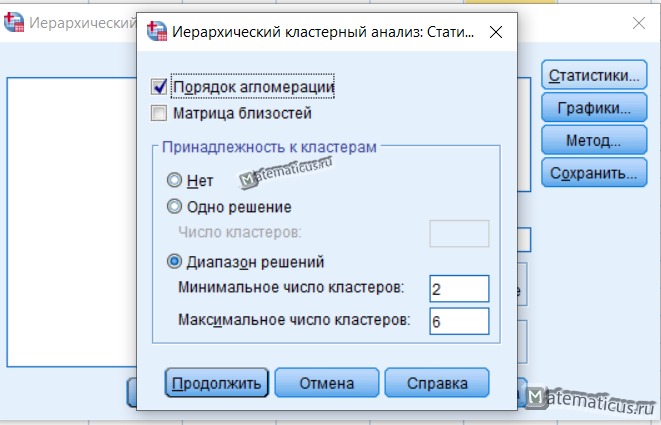
ШАГ 4. Нажать кнопку “Статистики” — диалоговое окно “Статистические показатели”.
В окне “Статистические показатели” отметить команды “Порядок агломерации” и “Матрица близостей” (Рисунок 9.6).
Рисунок 9.6 — Диалоговое окно “Статистические показатели”
В группе “Принадлежность к кластерам” можно выбрать три варианта:
- “Нет” — в результаты анализа включаются все кластеры.
- “Одно решение” — задается точное количество кластеров.
- “Диапазон решений” — дает возможность получить несколько решений с разным количеством кластеров.
Кнопка “Продолжить” — возвращаемся в основное диалоговое окно.
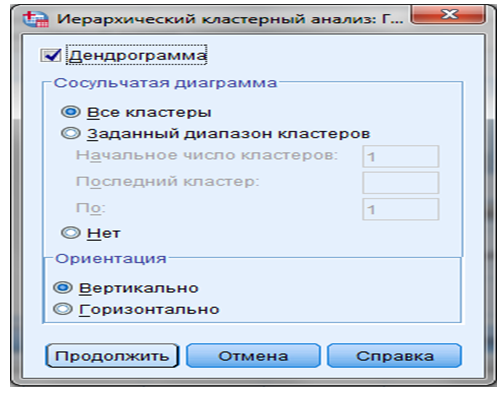
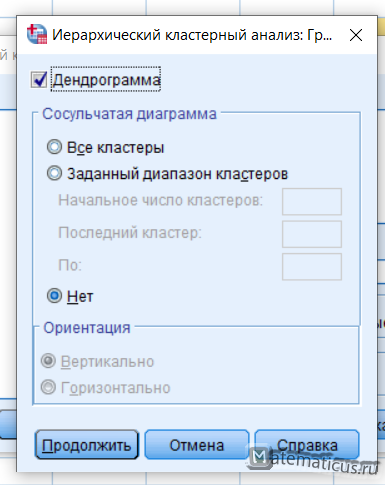
ШАГ 5. Кнопка “Графики” — на экране появляется вспомогательное диалоговое окно “Графики” (Рисунок 9.7).
Рисунок 9.7 — Диалоговое окно “Графики”
В данном окне можно выбрать в качестве выводимых результатов анализа сосульчатую диаграмму, которая демонстрирует процесс формирования кластеров на основе величины разности между переменными.
Далее выбираем “Продолжить” — “Иерархический кластерный анализ”.
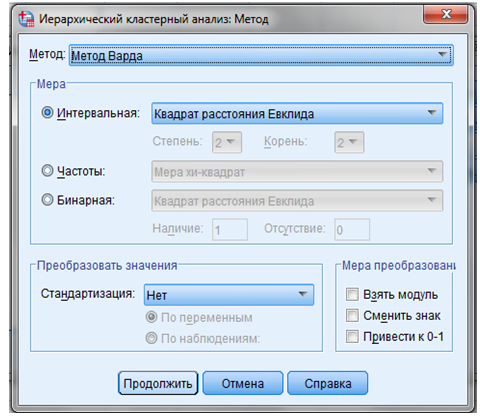
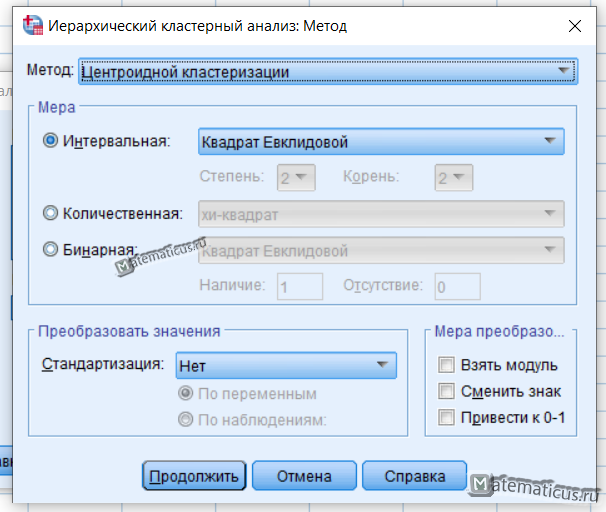
ШАГ 6. Кнопка “Метод” — позволяет нам работать с функциями окна “Методы” (Рисунок 9.8).
Рисунок 9.8 — Методы кластерного анализа
В поле “Метод” — выбрать метод “Варда”.
В поле “Мера” — выбрать интервальный показатель, по которому совокупность объектов исследования разделяется на кластеры.
Из предлагаемых программой интервальных показателей выбираем квадрат расстояния Евклида.
Кнопка “Продолжить” — “Иерархический кластерный анализ”.
ШАГ 7. Кнопка “Сохранить” — диалоговое окно “Сохранить”. В данном окне выбираем вариант сохранения результатов анализа в исходной базе данных. Выбираем кнопку “Диапазон решений”
и устанавливаем диапазон от 3 до 5. В результате в конце списка переменных базы данных появятся новые переменные, которые были созданы в результате кластеризации. Данным переменным можно дать имена,
которые соответствуют их общим характеристикам.
ШАГ 8. Кнопка “ОК”.
Интерпретация результатов
В таблице 9.2 “Шаги агломерации” показаны номера кластеров, которые объединяются на каждом этапе. В колонке “Коэффициенты” показаны эвклидовы расстояния между кластерами. В колонке “Следующий
этап” показан шаг, на котором впервые был создан данный кластер.
С помощью данной таблицы можно провести предварительную оценку количества создаваемых кластеров, определив на каком этапе, резко возрастает евклидово расстояние между переменными.
| Этап | Кластер объединен с | Коэффициенты | Этап первого появления кластера | Следующий этап | ||
|---|---|---|---|---|---|---|
| Кластер 1 | Кластер 2 | Кластер 1 | Кластер 2 | |||
| 1 | 14 | 16 | 1,000 | 0 | 0 | 6 |
| 2 | 6 | 7 | 2,000 | 0 | 0 | 7 |
| 3 | 2 | 13 | 3,5000 | 0 | 0 | 15 |
| 4 | 5 | 11 | 5,000 | 0 | 0 | 11 |
| 5 | 3 | 8 | 6,500 | 0 | 0 | 16 |
| 6 | 10 | 14 | 8,167 | 0 | 1 | 9 |
| 7 | 6 | 12 | 10,500 | 2 | 0 | 10 |
| 8 | 9 | 20 | 13,000 | 0 | 0 | 11 |
| 9 | 4 | 10 | 15,583 | 0 | 6 | 12 |
| 10 | 1 | 6 | 18,500 | 0 | 7 | 13 |
| 11 | 5 | 9 | 23,000 | 4 | 8 | 15 |
| 12 | 4 | 19 | 27,750 | 9 | 0 | 17 |
| 13 | 1 | 17 | 33,100 | 10 | 0 | 14 |
| 14 | 1 | 15 | 41,333 | 13 | 0 | 16 |
| 15 | 2 | 5 | 51,833 | 3 | 11 | 18 |
| 16 | 1 | 3 | 64,500 | 14 | 5 | 19 |
| 17 | 4 | 18 | 79,667 | 12 | 0 | 18 |
| 18 | 2 | 4 | 172,667 | 15 | 17 | 19 |
| 19 | 1 | 2 | 328,600 | 16 | 18 | 0 |
Таблица 9.2 — Шаги агломерации
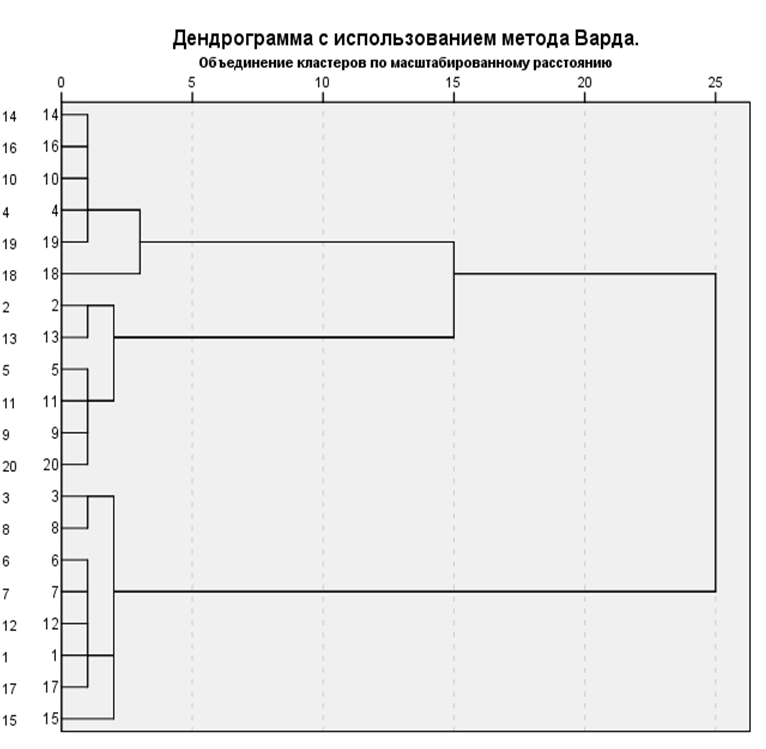
Следующим элементов окна вывода является древовидная диаграмма (рисунок 9.9). Данная диаграмма позволяет оценить расстояние между объектами и их принадлежность к кластерам на любом уровне.
Читать древовидную диаграмму нужно слева направо. Кластеры, которые объединяются в группу соединены вертикальными линиями. Шкала расстояний от 0 до 25 показывает величину квадрата расстояния
Евклида, при которой кластеры объединяются. 0 — наименьшее расстояние первого этапа, 25 — наибольшее расстояние последнего этапа.
Рисунок 9.9 — Древовидная диаграмма
Для определения количества кластеров можно руководствоваться следующим:
- теоретическими и практическими соображениями.
- этапом, на котором резко возрастает евклидово расстояние между переменными. В данном случае в два раза увеличивается расстояние между шагами 17 и 18. Следовательно, из общих 20
переменных вычитаем 17, получаем 3. Можно остановиться на 3 кластерах. - размеры кластеров должны быть существенными, включать достаточное количество переменных.
Подсчитав частоты кластерной принадлежности, видно, что выбор трех кластеров приводит к кластерам, содержащим 8, 6 и 6 элементов, если же перейти к 4 — то размеры кластеров будут 8,
6, 5, 1.
| Ward Method | Приятный процесс | Подрывает бюджет | Питание вне дома | Хорошие покупки | Раздражение | Экономия при сравнивании цен | |
|---|---|---|---|---|---|---|---|
| 1 | Среднее | 5,75 | 3,63 | 6,00 | 3,13 | 1,88 | 3,88 |
| N | 8 | 8 | 8 | 8 | 8 | 8 | |
| Стд.Отклонение | 1,035 | ,916 | 1,069 | ,835 | ,835 | ,641 | |
| 2 | Среднее | 1,67 | 3,00 | 1,83 | 3,50 | 5,50 | 3,33 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | |
| Стд.Отклонение | ,516 | ,632 | ,753 | 1,049 | 1,049 | ,816 | |
| 3 | Среднее | 3,50 | 5,83 | 3,33 | 6,00 | 3,50 | 6,00 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | |
| Стд.Отклонение | ,548 | ,753 | ,816 | ,632 | ,837 | 1,549 | |
| Итого | Среднее | 3,85 | 4,10 | 3,95 | 4,10 | 3,45 | 4,35 |
| N | 20 | 20 | 20 | 20 | 20 | 20 | |
| Стд.Отклонение | 1,899 | 1,410 | 2,012 | 1,518 | 1,761 | 1,496 |
Таблица 9.3 — Результаты кластерного анализа
В таблице “Результаты кластерного анализа” выбираем переменные, включаемые в каждый из трех кластеров. В кластер 1 могут попасть респонденты, предпочитающие питаться вне дома и ответившие,
что им нравиться посещать магазины (среднее 6,00 и 5,75). Следовательно, данный кластер можно назвать “любители торговых центров”. В данный кластер попадают переменные: 1, 3, 6, 7, 8, 12, 15 и 17.
В кластер 2 попадают случаи 2, 5, 9, 11, 13 и 20, которые соответствуют варианту ответов, связанных с раздражением от торговых центров. Назовем его “раздраженные покупатели”. Кластер 3 можно назвать
“экономные покупатели”, так как он имеет высокие средние показатели по факторам 2 (Подрывает бюджет), 4 (Хорошие покупки), 6 (Экономия при сравнивании цен).
Иерархический кластерный анализ в SPSS
Рассмотрим процедуру иерархического кластерного анализа в пакете SPSS (SPSS). Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов) [54]. Можно считать, что в последнем случае роль объектов играют строки, а роль переменных — столбцы.
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, в ходе алгоритма они объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования зависит от способов вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные подходы. С учетом этого в SPSS предусмотрены следующие методы:
- Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.
- Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров (Within-groups linkage).
- Расстояние между ближайшими соседями — ближайшими объектами кластеров (Nearest neighbor).
- Расстояние между самыми далекими соседями (Furthest neighbor).
- Расстояние между центрами кластеров (Centroid clustering) или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
- Метод медиан — тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
- Метод Варда.
Пример иерархического кластерного анализа
Порядок агломерации (протокол объединения кластеров) представленных ранее данных приведен в таблице 13.2. В протоколе указаны такие позиции:
- Stage — стадии объединения (шаг);
- Cluster Combined — объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров);
- Coefficients — коэффициенты.
| Cluster Combined | Coefficients | ||
|---|---|---|---|
| Cluster 1 | Cluster 2 | ||
| 1 | 9 | 10 | ,000 |
| 2 | 2 | 14 | 1,461E-02 |
| 3 | 3 | 9 | 1,461E-02 |
| 4 | 5 | 8 | 1,461E-02 |
| 5 | 6 | 7 | 1,461E-02 |
| 6 | 3 | 13 | 3,490E-02 |
| 7 | 2 | 11 | 3,651E-02 |
| 8 | 4 | 5 | 4,144E-02 |
| 9 | 2 | 6 | 5,118E-02 |
| 10 | 4 | 12 | ,105 |
| 11 | 1 | 3 | ,120 |
| 12 | 1 | 4 | 1,217 |
| 13 | 1 | 2 | 7,516 |
Так, в колонке Cluster Combined можно увидеть порядок объединения в кластеры: на первом шаге были объединены наблюдения 9 и 10, они образовывают кластер под номером 9, кластер 10 в обзорной таблице больше не появляется. На следующем шаге происходит объединение кластеров 2 и 14, далее 3 и 9, и т.д.
В колонке Coefficients приведено количество кластеров, которое следовало бы считать оптимальным; под значением этого показателя подразумевается расстояние между двумя кластерами, определенное на основании выбранной меры расстояния. В нашем случае это квадрат евклидова расстояния, определенный с использованием стандартизированных значений. Процедура стандартизации используется для исключения вероятности того, что классификацию будут определять переменные, имеющие наибольший разброс значений. В SPSS применяются следующие виды стандартизации:
- Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
- Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
- Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
- Максимум 1. Значения переменных делятся на их максимум.
- Среднее 1. Значения переменных делятся на их среднее.
- Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Определение количества кластеров
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в процессе агломерации/разделения множества объектов.
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е. Скачкообразное увеличение значения критерия Е можно определить как характеристику числа кластеров, которые действительно существуют в исследуемом наборе данных. Таким образом, этот способ сводится к определению скачкообразного увеличения некоторого коэффициента, который характеризует переход от сильно связанного к слабо связанному состоянию объектов.
В таблице 13.2 мы видим, что значение поля Coefficients увеличивается скачкообразно, следовательно, объединение в кластеры следует остановить, иначе будет происходить объединение кластеров, находящихся на относительно большом расстоянии друг от друга.
В нашем примере это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества наблюдений (14) и количества шагов до скачкообразного увеличения коэффициента (12).
Следовательно, после создания двух кластеров объединений больше производить не следует, хотя визуально мы ожидали появления трех кластеров.
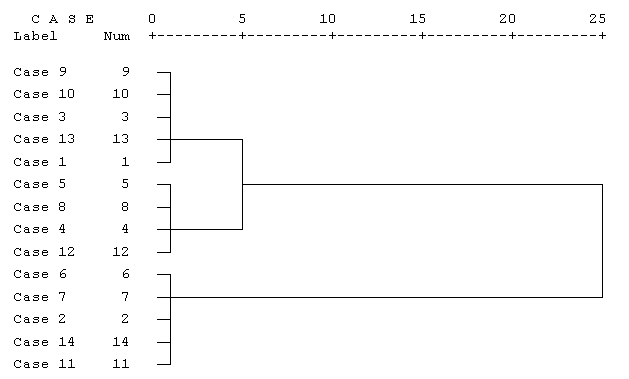
Агрегирование данных может быть представлено графически в виде дендрограммы. Она определяет объединенные кластеры и значения коэффициентов на каждом шаге агломерации (отображены значения коэффициентов, приведенные к шкале от 0 до 25).
Дендрограмма для нашего примера приведена на рис. 13.5. Разрез дерева агрегирования вертикальной чертой дал нам два кластера, состоящих из 9 и 5 объектов.
На верхней линии по горизонтали отмечены номера шагов алгоритма, всего алгоритму потребовалось 25 шагов для объединения всех объектов в один кластер.
Рис.
13.5.
Дендрограмма процесса слияния
Невзвешенный центроидный метод (метод невзвешенного попарного центроидного усреднения — unweighted pair-group method using the centroid average (Sneath and Sokal, 1973)).
В качестве расстояния между двумя кластерами в этом методе берется расстояние между их центрами тяжести.
Взвешенный центроидный метод (метод взвешенного попарного центроидного усреднения — weighted pair-group method using the centroid average, WPGMC (Sneath, Sokal 1973)). Этот метод похож на предыдущий, разница состоит в том, что для учета разницы между размерами кластеров (числе объектов в них), используются веса. Этот метод предпочтительно использовать в случаях, если имеются предположения относительно существенных отличий в размерах кластеров.
Рассмотрим процедуру иерархического кластерного анализа в пакете SPSS (SPSS). Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов) [54]. Можно считать, что в последнем случае роль объектов играют переменные, а роль переменных — столбцы.
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, в ходе алгоритма они объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования зависит от
способов вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные подходы. С учетом этого в SPSS предусмотрены следующие методы:
∙Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.
∙Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров (Within-groups linkage).
∙Расстояние между ближайшими соседями — ближайшими объектами кластеров (Nearest neighbor).
∙Расстояние между самыми далекими соседями (Furthest neighbor).
∙Расстояние между центрами кластеров (Centroid clustering) или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
∙Метод медиан — тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
∙Метод Варда.
155

Пример иерархического кластерного анализа
Порядок агломерации (протокол объединения кластеров) представленных ранее данных приведен в таблице 13.2. В протоколе указаны такие позиции:
∙Stage — стадии объединения (шаг);
∙Cluster Combined — объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров);
∙Coefficients — коэффициенты.
Таблица 13.2. Порядок агломерации
|
Cluster Combined |
Coefficients |
||
|
Cluster 1 |
Cluster 2 |
||
|
1 |
9 |
10 |
,000 |
|
2 |
2 |
14 |
1,461E-02 |
|
3 |
3 |
9 |
1,461E-02 |
|
4 |
5 |
8 |
1,461E-02 |
|
5 |
6 |
7 |
1,461E-02 |
|
6 |
3 |
13 |
3,490E-02 |
|
7 |
2 |
11 |
3,651E-02 |
|
8 |
4 |
5 |
4,144E-02 |
|
9 |
2 |
6 |
5,118E-02 |
|
10 |
4 |
12 |
,105 |
|
11 |
1 |
3 |
,120 |
|
12 |
1 |
4 |
1,217 |
|
13 |
1 |
2 |
7,516 |
Так, в колонке Cluster Combined можно увидеть порядок объединения в кластеры: на первом шаге были объединены наблюдения 9 и 10, они образовывают кластер под номером 9, кластер 10 в обзорной таблице больше не появляется. На следующем шаге происходит объединение кластеров 2 и 14, далее 3 и 9, и т.д.
В колонке Coefficients приведено количество кластеров, которое следовало бы считать оптимальным; под значением этого показателя подразумевается расстояние между двумя кластерами, определенное на основании выбранной меры расстояния. В нашем случае это квадрат евклидова расстояния, определенный с использованием стандартизированных
156
значений. Процедура стандартизации используется для исключения вероятности того, что классификацию будут определять переменные, имеющие наибольший разброс значений.
ВSPSS применяются следующие виды стандартизации:
∙Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
∙Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
∙Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
∙Максимум 1. Значения переменных делятся на их максимум.
∙Среднее 1. Значения переменных делятся на их среднее.
∙Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Определение количества кластеров
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в процессе агломерации/разделения множества объектов.
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е. Скачкообразное увеличение значения критерия Е можно определить как характеристику числа кластеров, которые действительно существуют в исследуемом наборе данных. Таким образом, этот способ сводится к определению скачкообразного увеличения некоторого коэффициента, который характеризует переход от сильно связанного к слабо связанному состоянию объектов.
Втаблице 13.2 мы видим, что значение поля Coefficients увеличивается скачкообразно, следовательно, объединение в кластеры следует остановить, иначе будет происходить объединение кластеров, находящихся на относительно большом расстоянии друг от друга.
Внашем примере это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества наблюдений (14) и количества шагов до скачкообразного увеличения коэффициента (12).
Следовательно, после создания двух кластеров объединений больше производить не следует, хотя визуально мы ожидали появления трех кластеров.
Агрегирование данных может быть представлено графически в виде дендрограммы. Она определяет объединенные кластеры и значения коэффициентов на каждом шаге агломерации (отображены значения коэффициентов, приведенные к шкале от 0 до 25).
Дендрограмма для нашего примера приведена на рис. 13.5. Разрез дерева агрегирования вертикальной чертой дал нам два кластера, состоящих из 9 и 5 объектов.
157
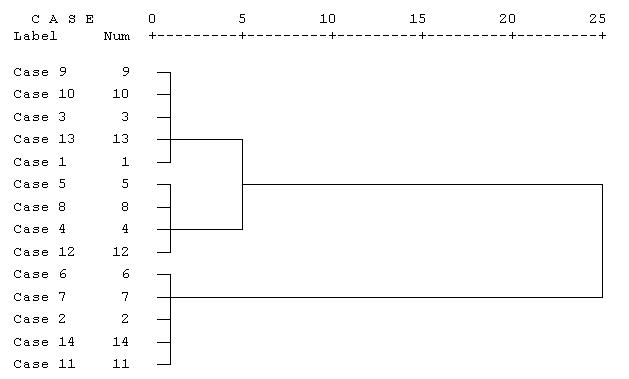
На верхней линии по горизонтали отмечены номера шагов алгоритма, всего алгоритму потребовалось 25 шагов для объединения всех объектов в один кластер.
Рис. 13.5. Дендрограмма процесса слияния
158
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
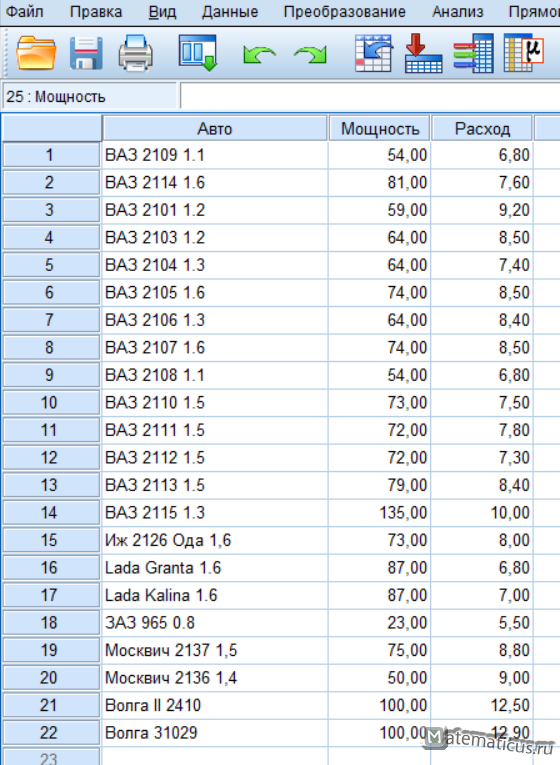
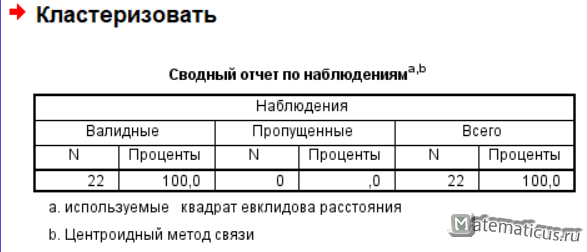
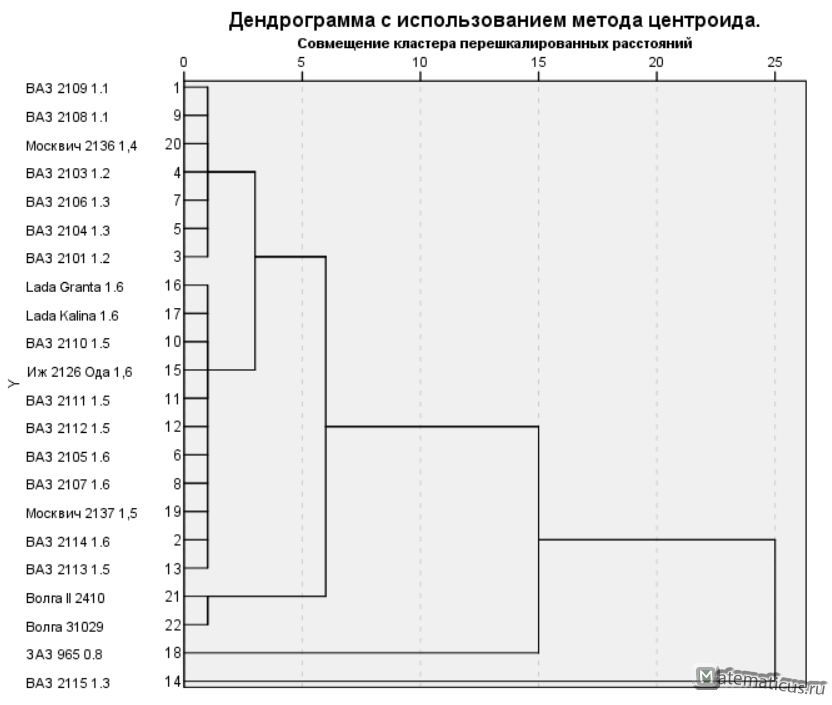
В целях реализации иерархической кластеризации в SPSS Statistics возьмем в качестве примера данные о некоторых приближенных характеристиках автомобилей – средний расход топлива и мощность двигателя в л.с.
Вводим три переменные, Авто — Мера номинальная, Мощность – Мера Шкалы, Расход – Мера Шкалы
Переходим Анализ -> Классификация -> Иерархическая кластеризация
Появится окно — иерархический кластерный анализ.
В поле переменные вставляем Мощность и Расход. В поле метить наблюдения значениями вставляем Авто, ставим галочки вывести Статистика, Графики.
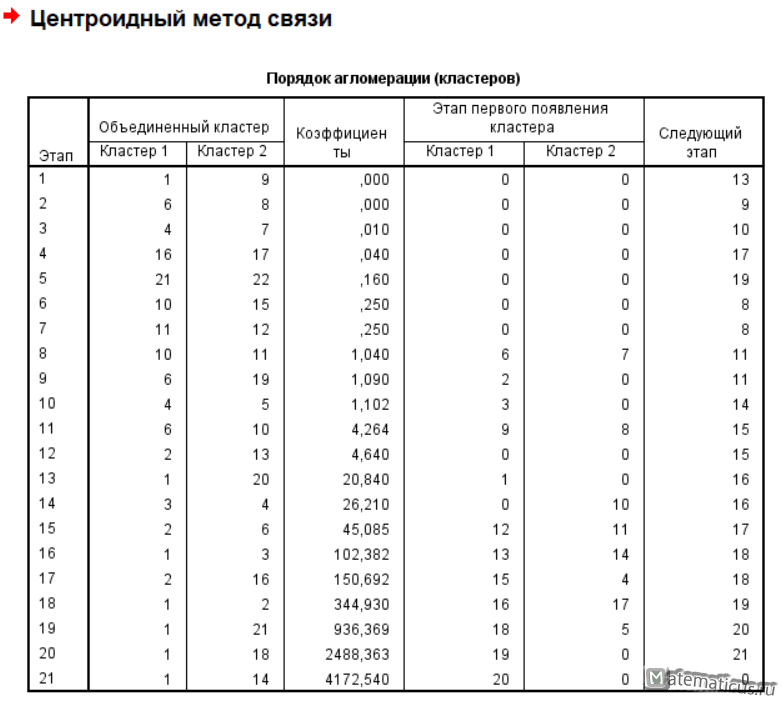
Нажимаем на кнопку Статистики, появляется соответствующее окно, ставим галку порядок агломерации в диапазоне решений указываем минимальное и максимальное число кластеров и жмем Продолжить.
Нажимаем на кнопку Графики, появляется окно, ставим галку Дендрограмма и диаграмма — нет, далее жмем Продолжить.
Нажимаем на кнопку Метод, появляется окно Метод, выбираем метод Центроидной кластеризации, мера – интервальная квадрат и жмем Продолжить.
Нажимаем Ок и SPSS Statistics выполняет расчет и получаем результаты иерархического кластерного анализа в SPSS
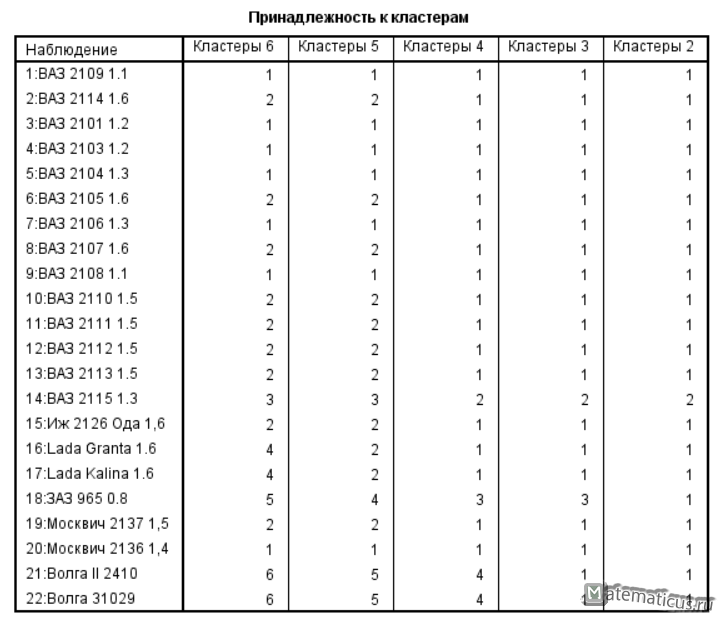
Принадлежность к кластерам
Дендрограмма с использованием метода центроида
2509
9. Кластерный анализ
Кластерный анализ — позволяет выявить группы (кластеры) объектов по заданным переменным. Программа при этом автоматически определяет количество существующих кластеров.
Задача кластерного анализа состоит в формировании групп:
- однородных внутри, объекты схожи между собой (условие внутренней гомогенности);
- отличных от объектов в других группах (условие внешней гетерогенности) [2].
С помощью кластерного анализа в маркетинге выявляются целевые группы потребителей, для которых необходимо разработать уникальный комплекс инструментов маркетинга.
Пример. Необходимо разделить всех курящих по возрасту и уровню дохода на однородные группы (кластеры) (рисунок 9.1).
На рисунке 9.1. вариант В не выявлено однородных кластеров, все курильщики представляют единю группу, следовательно, разработка уникальных торговых предложений не имеет смысла.
На рисунке 9.1. вариант А выявлены два однородных кластера курящих: “старые и бедные”, “молодые и богатые”. Данные группы могут быть представлены, как две целевые группы потребителей табачных
изделий. Следовательно. Для каждой из них необходимо разработать уникальные торговые предложения по цене, качеству, особым свойствам, дизайну упаковки, особенностям продвижения, системе распределения
товара.
Рисунок 9.1 — Кластерный анализ [2]
В процессе выполнения кластерного анализа выявляются статистические связи между анализируемыми переменными, которые указывают на схожесть переменных и, затем объединение выявленных факторов в
группы на основе уровня различий между ними. Количество кластеров зависит от задаваемых параметров схожести переменных, объединяемых в один кластер.
Основные термины, применяемые в кластерном анализе
Евклидово расстояние — расстояние между объектами, равное сумме квадратов разностей между значениями одноименных переменных объектов.
Иерархическая кластеризация — метод, при котором строится иерархическая или древовидная структура. Позволяет детально исследовать различия между объектами, выбрать оптимальное число кластеров.
Агломеративная или объединяющая кластеризация — иерархический метод формирования кластеров, при котором каждый объект сначала находится в отдельном кластере, затем объекты группируются в значительно
более крупные кластеры.
Разделяющая или дивизиональная кластеризация — иерархический метод формирования кластеров, при котором один общий большой все кластер делится на более мелкие для создания однородных кластеров.
Методы связи — методы формирования кластеров, при которых объекты объединяются в группу на основе рассчитанного между ними расстояния (рисунок 9.2).
Метод одиночной связи — или правило ближайшего соседа — в основе лежит выбор переменных, расстояние между которыми минимально.
Метод полной связи — или правило дальнего соседа — в основе лежит выбор переменных, расстояние между которыми максимально.
Метод средней связи — в основе лежит среднее значение расстояния между переменными разных кластеров.
Рисунок 9.2 — Методы связи
Дисперсионные методы — Метод Варда и Центроидный метод (Рисунок 9.3).
Метод Варда — в качестве меры используется квадрат евклидового расстояния, который должен быть минимальным.
Центроидный метод — оценивается расстояние между центроидами (средними) групп переменных.
Рисунок 9.3 — Дисперсионные методы
Метод к — средних — переменные группируются в кластер в пределах порогового значения, которое задается исходя из определенного центра кластера.
Пример. 20 респондентов попросили выразить свое отношение к посещению торговых центров для приобретения товаров. Выделили шесть утверждений, степень согласия с которыми респондентов попросили
выразить на основе семибалльной шкалы (1 — совсем не согласен, 7 — абсолютно согласен).
Fac_1 — Считаю посещение торговых центром приятным процессом.
Fac_2 — Посещение торговых центров подрывает бюджет моей семьи.
Fac_3 — Мне нравиться обедать и ужинать в торговых центрах.
Fac_4 — В торговых центрах мне нравиться делать хорошие покупки.
Fac_5 — Меня очень раздражает посещение торговых центров.
Fac_6 — Посещая разные магазины, можно сравнивать цены и выбирать более дешевый товар.
Рисунок 9.4 — Данные для кластеризации
Вверх
Пошаговая инструкция
ШАГ 1. Подготовить данные для анализа в SPSS.
ШАГ 2. “Анализ” — выбрать “Классификация”. В рассматриваемом примере применяется иерархический кластерный анализ.
ШАГ 3. Анализ — Классификация — Иерархическая кластеризация — “Иерархический кластерный анализ” (Рисунок 9.5).
Рисунок 9.5 — Иерархический кластерный анализ
Выбираем все шесть факторов, отражающих отношение респондентов к посещению торговых центров, и переносим их в поле “Переменные”.
В поле “Метить значениями” необходимо перенести переменную “Номер респондента”. В данном случае могут использоваться только поле текстовые переменные, поэтому в столбце
“Тип переменной” необходимо выбрать “Текстовая”.
В поле “Кластеризовать” выбрать один из двух предлагаемых вариантов: “Наблюдения” или “Переменные”. В нашем примере выбирается вариант “Наблюдения”,
в ходе кластерного анализа будут собираться в кластеры потребители, а не характеристики их отношения.
ШАГ 4. Нажать кнопку “Статистики” — диалоговое окно “Статистические показатели”.
В окне “Статистические показатели” отметить команды “Порядок агломерации” и “Матрица близостей” (Рисунок 9.6).
Рисунок 9.6 — Диалоговое окно “Статистические показатели”
В группе “Принадлежность к кластерам” можно выбрать три варианта:
- “Нет” — в результаты анализа включаются все кластеры.
- “Одно решение” — задается точное количество кластеров.
- “Диапазон решений” — дает возможность получить несколько решений с разным количеством кластеров.
Кнопка “Продолжить” — возвращаемся в основное диалоговое окно.
ШАГ 5. Кнопка “Графики” — на экране появляется вспомогательное диалоговое окно “Графики” (Рисунок 9.7).
Рисунок 9.7 — Диалоговое окно “Графики”
В данном окне можно выбрать в качестве выводимых результатов анализа сосульчатую диаграмму, которая демонстрирует процесс формирования кластеров на основе величины разности между переменными.
Далее выбираем “Продолжить” — “Иерархический кластерный анализ”.
ШАГ 6. Кнопка “Метод” — позволяет нам работать с функциями окна “Методы” (Рисунок 9.8).
Рисунок 9.8 — Методы кластерного анализа
В поле “Метод” — выбрать метод “Варда”.
В поле “Мера” — выбрать интервальный показатель, по которому совокупность объектов исследования разделяется на кластеры.
Из предлагаемых программой интервальных показателей выбираем квадрат расстояния Евклида.
Кнопка “Продолжить” — “Иерархический кластерный анализ”.
ШАГ 7. Кнопка “Сохранить” — диалоговое окно “Сохранить”. В данном окне выбираем вариант сохранения результатов анализа в исходной базе данных. Выбираем кнопку “Диапазон решений”
и устанавливаем диапазон от 3 до 5. В результате в конце списка переменных базы данных появятся новые переменные, которые были созданы в результате кластеризации. Данным переменным можно дать имена,
которые соответствуют их общим характеристикам.
ШАГ 8. Кнопка “ОК”.
Интерпретация результатов
В таблице 9.2 “Шаги агломерации” показаны номера кластеров, которые объединяются на каждом этапе. В колонке “Коэффициенты” показаны эвклидовы расстояния между кластерами. В колонке “Следующий
этап” показан шаг, на котором впервые был создан данный кластер.
С помощью данной таблицы можно провести предварительную оценку количества создаваемых кластеров, определив на каком этапе, резко возрастает евклидово расстояние между переменными.
| Этап | Кластер объединен с | Коэффициенты | Этап первого появления кластера | Следующий этап | ||
|---|---|---|---|---|---|---|
| Кластер 1 | Кластер 2 | Кластер 1 | Кластер 2 | |||
| 1 | 14 | 16 | 1,000 | 0 | 0 | 6 |
| 2 | 6 | 7 | 2,000 | 0 | 0 | 7 |
| 3 | 2 | 13 | 3,5000 | 0 | 0 | 15 |
| 4 | 5 | 11 | 5,000 | 0 | 0 | 11 |
| 5 | 3 | 8 | 6,500 | 0 | 0 | 16 |
| 6 | 10 | 14 | 8,167 | 0 | 1 | 9 |
| 7 | 6 | 12 | 10,500 | 2 | 0 | 10 |
| 8 | 9 | 20 | 13,000 | 0 | 0 | 11 |
| 9 | 4 | 10 | 15,583 | 0 | 6 | 12 |
| 10 | 1 | 6 | 18,500 | 0 | 7 | 13 |
| 11 | 5 | 9 | 23,000 | 4 | 8 | 15 |
| 12 | 4 | 19 | 27,750 | 9 | 0 | 17 |
| 13 | 1 | 17 | 33,100 | 10 | 0 | 14 |
| 14 | 1 | 15 | 41,333 | 13 | 0 | 16 |
| 15 | 2 | 5 | 51,833 | 3 | 11 | 18 |
| 16 | 1 | 3 | 64,500 | 14 | 5 | 19 |
| 17 | 4 | 18 | 79,667 | 12 | 0 | 18 |
| 18 | 2 | 4 | 172,667 | 15 | 17 | 19 |
| 19 | 1 | 2 | 328,600 | 16 | 18 | 0 |
Таблица 9.2 — Шаги агломерации
Следующим элементов окна вывода является древовидная диаграмма (рисунок 9.9). Данная диаграмма позволяет оценить расстояние между объектами и их принадлежность к кластерам на любом уровне.
Читать древовидную диаграмму нужно слева направо. Кластеры, которые объединяются в группу соединены вертикальными линиями. Шкала расстояний от 0 до 25 показывает величину квадрата расстояния
Евклида, при которой кластеры объединяются. 0 — наименьшее расстояние первого этапа, 25 — наибольшее расстояние последнего этапа.
Рисунок 9.9 — Древовидная диаграмма
Для определения количества кластеров можно руководствоваться следующим:
- теоретическими и практическими соображениями.
- этапом, на котором резко возрастает евклидово расстояние между переменными. В данном случае в два раза увеличивается расстояние между шагами 17 и 18. Следовательно, из общих 20
переменных вычитаем 17, получаем 3. Можно остановиться на 3 кластерах. - размеры кластеров должны быть существенными, включать достаточное количество переменных.
Подсчитав частоты кластерной принадлежности, видно, что выбор трех кластеров приводит к кластерам, содержащим 8, 6 и 6 элементов, если же перейти к 4 — то размеры кластеров будут 8,
6, 5, 1.
| Ward Method | Приятный процесс | Подрывает бюджет | Питание вне дома | Хорошие покупки | Раздражение | Экономия при сравнивании цен | |
|---|---|---|---|---|---|---|---|
| 1 | Среднее | 5,75 | 3,63 | 6,00 | 3,13 | 1,88 | 3,88 |
| N | 8 | 8 | 8 | 8 | 8 | 8 | |
| Стд.Отклонение | 1,035 | ,916 | 1,069 | ,835 | ,835 | ,641 | |
| 2 | Среднее | 1,67 | 3,00 | 1,83 | 3,50 | 5,50 | 3,33 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | |
| Стд.Отклонение | ,516 | ,632 | ,753 | 1,049 | 1,049 | ,816 | |
| 3 | Среднее | 3,50 | 5,83 | 3,33 | 6,00 | 3,50 | 6,00 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | |
| Стд.Отклонение | ,548 | ,753 | ,816 | ,632 | ,837 | 1,549 | |
| Итого | Среднее | 3,85 | 4,10 | 3,95 | 4,10 | 3,45 | 4,35 |
| N | 20 | 20 | 20 | 20 | 20 | 20 | |
| Стд.Отклонение | 1,899 | 1,410 | 2,012 | 1,518 | 1,761 | 1,496 |
Таблица 9.3 — Результаты кластерного анализа
В таблице “Результаты кластерного анализа” выбираем переменные, включаемые в каждый из трех кластеров. В кластер 1 могут попасть респонденты, предпочитающие питаться вне дома и ответившие,
что им нравиться посещать магазины (среднее 6,00 и 5,75). Следовательно, данный кластер можно назвать “любители торговых центров”. В данный кластер попадают переменные: 1, 3, 6, 7, 8, 12, 15 и 17.
В кластер 2 попадают случаи 2, 5, 9, 11, 13 и 20, которые соответствуют варианту ответов, связанных с раздражением от торговых центров. Назовем его “раздраженные покупатели”. Кластер 3 можно назвать
“экономные покупатели”, так как он имеет высокие средние показатели по факторам 2 (Подрывает бюджет), 4 (Хорошие покупки), 6 (Экономия при сравнивании цен).
Иерархический кластерный анализ в SPSS
Рассмотрим процедуру иерархического кластерного анализа в пакете SPSS (SPSS). Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов) [54]. Можно считать, что в последнем случае роль объектов играют строки, а роль переменных — столбцы.
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, в ходе алгоритма они объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования зависит от способов вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные подходы. С учетом этого в SPSS предусмотрены следующие методы:
- Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.
- Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров (Within-groups linkage).
- Расстояние между ближайшими соседями — ближайшими объектами кластеров (Nearest neighbor).
- Расстояние между самыми далекими соседями (Furthest neighbor).
- Расстояние между центрами кластеров (Centroid clustering) или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
- Метод медиан — тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
- Метод Варда.
Пример иерархического кластерного анализа
Порядок агломерации (протокол объединения кластеров) представленных ранее данных приведен в таблице 13.2. В протоколе указаны такие позиции:
- Stage — стадии объединения (шаг);
- Cluster Combined — объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров);
- Coefficients — коэффициенты.
Таблица
13.2.
Порядок агломерации
| Cluster Combined | Coefficients | ||
|---|---|---|---|
| Cluster 1 | Cluster 2 | ||
| 1 | 9 | 10 | ,000 |
| 2 | 2 | 14 | 1,461E-02 |
| 3 | 3 | 9 | 1,461E-02 |
| 4 | 5 | 8 | 1,461E-02 |
| 5 | 6 | 7 | 1,461E-02 |
| 6 | 3 | 13 | 3,490E-02 |
| 7 | 2 | 11 | 3,651E-02 |
| 8 | 4 | 5 | 4,144E-02 |
| 9 | 2 | 6 | 5,118E-02 |
| 10 | 4 | 12 | ,105 |
| 11 | 1 | 3 | ,120 |
| 12 | 1 | 4 | 1,217 |
| 13 | 1 | 2 | 7,516 |
Так, в колонке Cluster Combined можно увидеть порядок объединения в кластеры: на первом шаге были объединены наблюдения 9 и 10, они образовывают кластер под номером 9, кластер 10 в обзорной таблице больше не появляется. На следующем шаге происходит объединение кластеров 2 и 14, далее 3 и 9, и т.д.
В колонке Coefficients приведено количество кластеров, которое следовало бы считать оптимальным; под значением этого показателя подразумевается расстояние между двумя кластерами, определенное на основании выбранной меры расстояния. В нашем случае это квадрат евклидова расстояния, определенный с использованием стандартизированных значений. Процедура стандартизации используется для исключения вероятности того, что классификацию будут определять переменные, имеющие наибольший разброс значений. В SPSS применяются следующие виды стандартизации:
- Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
- Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
- Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
- Максимум 1. Значения переменных делятся на их максимум.
- Среднее 1. Значения переменных делятся на их среднее.
- Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Определение количества кластеров
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в процессе агломерации/разделения множества объектов.
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е. Скачкообразное увеличение значения критерия Е можно определить как характеристику числа кластеров, которые действительно существуют в исследуемом наборе данных. Таким образом, этот способ сводится к определению скачкообразного увеличения некоторого коэффициента, который характеризует переход от сильно связанного к слабо связанному состоянию объектов.
В таблице 13.2 мы видим, что значение поля Coefficients увеличивается скачкообразно, следовательно, объединение в кластеры следует остановить, иначе будет происходить объединение кластеров, находящихся на относительно большом расстоянии друг от друга.
В нашем примере это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества наблюдений (14) и количества шагов до скачкообразного увеличения коэффициента (12).
Следовательно, после создания двух кластеров объединений больше производить не следует, хотя визуально мы ожидали появления трех кластеров.
Агрегирование данных может быть представлено графически в виде дендрограммы. Она определяет объединенные кластеры и значения коэффициентов на каждом шаге агломерации (отображены значения коэффициентов, приведенные к шкале от 0 до 25).
Дендрограмма для нашего примера приведена на рис. 13.5. Разрез дерева агрегирования вертикальной чертой дал нам два кластера, состоящих из 9 и 5 объектов.
На верхней линии по горизонтали отмечены номера шагов алгоритма, всего алгоритму потребовалось 25 шагов для объединения всех объектов в один кластер.
Рис.
13.5.
Дендрограмма процесса слияния
В целях реализации иерархической кластеризации в SPSS Statistics возьмем в качестве примера данные о некоторых приближенных характеристиках автомобилей – средний расход топлива и мощность двигателя в л.с.
Вводим три переменные, Авто — Мера номинальная, Мощность – Мера Шкалы, Расход – Мера Шкалы
Переходим Анализ -> Классификация -> Иерархическая кластеризация
Появится окно — иерархический кластерный анализ.
В поле переменные вставляем Мощность и Расход. В поле метить наблюдения значениями вставляем Авто, ставим галочки вывести Статистика, Графики.
Нажимаем на кнопку Статистики, появляется соответствующее окно, ставим галку порядок агломерации в диапазоне решений указываем минимальное и максимальное число кластеров и жмем Продолжить.
Нажимаем на кнопку Графики, появляется окно, ставим галку Дендрограмма и диаграмма — нет, далее жмем Продолжить.
Нажимаем на кнопку Метод, появляется окно Метод, выбираем метод Центроидной кластеризации, мера – интервальная квадрат и жмем Продолжить.
Нажимаем Ок и SPSS Statistics выполняет расчет и получаем результаты иерархического кластерного анализа в SPSS
Принадлежность к кластерам
Дендрограмма с использованием метода центроида
2117
Невзвешенный центроидный метод (метод невзвешенного попарного центроидного усреднения — unweighted pair-group method using the centroid average (Sneath and Sokal, 1973)).
В качестве расстояния между двумя кластерами в этом методе берется расстояние между их центрами тяжести.
Взвешенный центроидный метод (метод взвешенного попарного центроидного усреднения — weighted pair-group method using the centroid average, WPGMC (Sneath, Sokal 1973)). Этот метод похож на предыдущий, разница состоит в том, что для учета разницы между размерами кластеров (числе объектов в них), используются веса. Этот метод предпочтительно использовать в случаях, если имеются предположения относительно существенных отличий в размерах кластеров.
Рассмотрим процедуру иерархического кластерного анализа в пакете SPSS (SPSS). Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов) [54]. Можно считать, что в последнем случае роль объектов играют переменные, а роль переменных — столбцы.
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, в ходе алгоритма они объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования зависит от
способов вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные подходы. С учетом этого в SPSS предусмотрены следующие методы:
∙Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.
∙Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров (Within-groups linkage).
∙Расстояние между ближайшими соседями — ближайшими объектами кластеров (Nearest neighbor).
∙Расстояние между самыми далекими соседями (Furthest neighbor).
∙Расстояние между центрами кластеров (Centroid clustering) или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
∙Метод медиан — тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
∙Метод Варда.
155

Пример иерархического кластерного анализа
Порядок агломерации (протокол объединения кластеров) представленных ранее данных приведен в таблице 13.2. В протоколе указаны такие позиции:
∙Stage — стадии объединения (шаг);
∙Cluster Combined — объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров);
∙Coefficients — коэффициенты.
Таблица 13.2. Порядок агломерации
|
Cluster Combined |
Coefficients |
||
|
Cluster 1 |
Cluster 2 |
||
|
1 |
9 |
10 |
,000 |
|
2 |
2 |
14 |
1,461E-02 |
|
3 |
3 |
9 |
1,461E-02 |
|
4 |
5 |
8 |
1,461E-02 |
|
5 |
6 |
7 |
1,461E-02 |
|
6 |
3 |
13 |
3,490E-02 |
|
7 |
2 |
11 |
3,651E-02 |
|
8 |
4 |
5 |
4,144E-02 |
|
9 |
2 |
6 |
5,118E-02 |
|
10 |
4 |
12 |
,105 |
|
11 |
1 |
3 |
,120 |
|
12 |
1 |
4 |
1,217 |
|
13 |
1 |
2 |
7,516 |
Так, в колонке Cluster Combined можно увидеть порядок объединения в кластеры: на первом шаге были объединены наблюдения 9 и 10, они образовывают кластер под номером 9, кластер 10 в обзорной таблице больше не появляется. На следующем шаге происходит объединение кластеров 2 и 14, далее 3 и 9, и т.д.
В колонке Coefficients приведено количество кластеров, которое следовало бы считать оптимальным; под значением этого показателя подразумевается расстояние между двумя кластерами, определенное на основании выбранной меры расстояния. В нашем случае это квадрат евклидова расстояния, определенный с использованием стандартизированных
156
значений. Процедура стандартизации используется для исключения вероятности того, что классификацию будут определять переменные, имеющие наибольший разброс значений.
ВSPSS применяются следующие виды стандартизации:
∙Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
∙Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
∙Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
∙Максимум 1. Значения переменных делятся на их максимум.
∙Среднее 1. Значения переменных делятся на их среднее.
∙Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Определение количества кластеров
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в процессе агломерации/разделения множества объектов.
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е. Скачкообразное увеличение значения критерия Е можно определить как характеристику числа кластеров, которые действительно существуют в исследуемом наборе данных. Таким образом, этот способ сводится к определению скачкообразного увеличения некоторого коэффициента, который характеризует переход от сильно связанного к слабо связанному состоянию объектов.
Втаблице 13.2 мы видим, что значение поля Coefficients увеличивается скачкообразно, следовательно, объединение в кластеры следует остановить, иначе будет происходить объединение кластеров, находящихся на относительно большом расстоянии друг от друга.
Внашем примере это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества наблюдений (14) и количества шагов до скачкообразного увеличения коэффициента (12).
Следовательно, после создания двух кластеров объединений больше производить не следует, хотя визуально мы ожидали появления трех кластеров.
Агрегирование данных может быть представлено графически в виде дендрограммы. Она определяет объединенные кластеры и значения коэффициентов на каждом шаге агломерации (отображены значения коэффициентов, приведенные к шкале от 0 до 25).
Дендрограмма для нашего примера приведена на рис. 13.5. Разрез дерева агрегирования вертикальной чертой дал нам два кластера, состоящих из 9 и 5 объектов.
157

На верхней линии по горизонтали отмечены номера шагов алгоритма, всего алгоритму потребовалось 25 шагов для объединения всех объектов в один кластер.
Рис. 13.5. Дендрограмма процесса слияния
158
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
20.2. Иерархический кластерный анализ
В иерархических методах каждое наблюдение образовывает сначала свой отдельный кластер. На первом шаге два соседних кластера объединяются в один; этот процесс может продолжаться до тех пор,
пока не останутся только два кластера. В методе, который в SPSS установлен по умолчанию (Between-groups linkage (Межгрупповые связи)), расстояние между кластерами является средним значением
всех расстояний между всеми возможными парами точек из обоих кластеров.
Иерархический кластерный анализ с двумя переменными
Соберём заданные 17 сортов пива в кластеры при помощи параметров kalorien (калории) и kosten (расходы).
-
Выберите в меню Analyze (Анализ) ► Classify (Классифицировать) ► Hierarchical Cluster… (Иерархический кластерный анализ). Вы увидите диалоговое окно Hierarchical Cluster Analysis (Иерархический кластерный анализ) (см. рис. 20.3).
-
Переменные каlorien (калории) и kosten (расходы) поместите в поле тестируемых переменных, а текстовую переменную bier (пиво) в поле с именем Label cases by: (Наименования наблюдений:).
-
Щелчком по выключателю Statistics… (Статистики) откройте диалоговое окно Hierarchical Cluster Analysis: Statistics (Иерархический кластерный анализ: Статистики)
и наряду с выводом последовательности слияния (Agglomeration schedule) активируйте вывод показателя принадлежности к кластеру для каждого наблюдения.
Хотя на основании графического представления на диаграмме рассеяния (см. рис. 20.2) и ожидается результат в виде четырёх кластеров, но не можем быть полностью уверены в достижении этого результата.
Поэтому, для верности активируйте Range of solutions: (Область решений) и введите числа 2 и 5 в качестве границ области. -
Вернувшись в главное диалоговое окно, щёлкните по выключателю Plots… (Диаграммы). Активируйте опцию вывода древовидной диаграммы (Dendrogram) и посредством опции None (Нет)
отмените вывод накопительной диаграммы. -
С помощью кнопки Method… (Метод) Вы получаете возможность выбрать метод образования кластеров, а также метод расчета дистанционной меры и меры подобия соответственно.
SPSS предлагает, в общей сложности, семь различных методов объединения, которые будут рассмотрены в главе 20.8.
Метод Between-groups linkage (Межгрупповые связи) устанавливается по умолчанию.
Рис. 20.3: Диалоговое окно Hierarchical Cluster Analysis (Иерархический кластерный анализ)
Дистанционные меры и меры подобия зависят от вида переменных, участвующих в анализе, то есть выбор меры зависит от типа переменной и
вида шкалы, к которой она относится: интервальная переменная, частоты или бинарные (дихотомические) данные.
В рассматриваемом примере фигурируют данные, относящиеся к интервальной шкале, для которых по умолчанию в качестве дистанционной меры устанавливается Квадрат Евклидового расстояния
(Squared Euclidean distance). Некоторые дистанционные меры и меры подобия будут рассмотрены в главе 20.5.
-
Оставьте предварительные установки и в поле Transform Values (Преобразовывать значения) установите z-преобразование (стандартизацию) значений;
необходимость этой опции была уже рассмотрена в предыдущей главе. Другие предлагаемые возможности стандартизации играют скорее второстепенную роль. -
Вернитесь назад в главное диалоговое окно и начните расчёт нажатием ОК.
После обычной обшей статистической сводки итогов по наблюдениям, в окне просмотра сначала приводится обзор принадлежности, из которого можно выяснить очерёдность построения кластеров,
а также их оптимальное количество. По двум колонкам, расположенным под общей шапкой Cluster Combined (Объединение в кластеры), можно увидеть, что на первом шаге были объединены наблюдения 5 и 12
(т.е. Heineken и Becks). Эти две марки максимально похожи друг на друга и отдалены друг от друга очень малое расстояние. Эти два наблюдения образовывают кластер с номером 5,
в то время как кластер 12 в обзорной таблице больше не появляется. На следующем шаге происходит объединение наблюдений 10 и 17 (Coors Light и Schlitz Light), затем 2 и 3 (Lowenbrau и Michelob) и т.д.
Agglomeration Schedule (Порядок агломерации)
| Stage (Шаг) | Cluster Combined (Объединение в кластеры) |
Coefficients (Коэффициенты) | Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) | Next Stage (Следующий шаг) | ||
| Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | |||
| 1 | 5 | 12 | 8.508Е-03 | 0 | 0 | 9 |
| 2 | 10 | 17 | 2.880Е-02 | 0 | 0 | 4 |
| 3 | 2 | 3 | 4.273Е-02 | 0 | 0 | 13 |
| 4 | 8 | 10 | 6.432Е-02 | 0 | 2 | 7 |
| 5 | 7 | 13 | 8.040Е-02 | 0 | 0 | 8 |
| 6 | 1 | 15 | ,117 | 0 | 0 | 8 |
| 7 | 8 | 9 | ,206 | 4 | 0 | 14 |
| 8 | 1 | 7 | ,219 | 6 | 5 | 12 |
| 9 | 5 | 11 | ,233 | 1 | 0 | 11 |
| 10 | 14 | 16 | ,313 | 0 | 0 | 14 |
| 11 | 4 | 5 | ,487 | 0 | 9 | 16 |
| 12 | 1 | 6 | ,534 | 8 | 0 | 13 |
| 13 | 1 | 2 | ,820 | 12 | 3 | 15 |
| 14 | 8 | 14 | 1,205 | 7 | 70 | 15 |
| 15 | 1 | 8 | 4,017 | 13 | 14 | 16 |
| 16 | 1 | 4 | 6,753 | 15 | 11 | 0 |
Для определения, какое количество кластеров следовало бы считать оптимальным, решающее значение имеет показатель, выводимый под заголовком «Coefficients». По этим коэффициентом
подразумевается расстояние между двумя кластерами, определенное на основании выбранной дистанционной меры с учётом предусмотренного преобразования значений.
В нашем случае это квадрат евклидового расстояния, определенный с использованием стандартизованных значений. На этом этапе, где эта мера расстояния между двумя кластерами увеличивается скачкообразно,
процесс объединения в новые кластеры необходимо остановить, так как в противном случае были бы объединены уже кластеры, находящиеся на относительно большом расстоянии друг от друга.
В приведенном примере — это скачок с 1,205 до 4,017. Это означает, что после образования трёх кластеров мы больше не должны производить никаких последующих объединений,
а результат с тремя кластерами является оптимальным. Визуально же мы ожидали результат с четырьмя кластерами. Оптимальным считается число кластеров равное разности количества наблюдений (здесь: 17)
и количества шагов, после которого коэффициент увеличивается скачкообразно (здесь: 14).
В пояснении нуждаются ещё и три последние колонки вышеприведенной таблицы, отражающей порядок агломерации; для этого в качестве примера мы рассмотрим строку, соответствующую 14 шагу.
Здесь объединяются кластеры 8 и 14. Перед этим кластер 8 уже участвовал в объединениях на шагах 4 и 7, последний раз, стало быть, на шаге 7. Строго говоря,
название колонки Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) можно считать ошибочным и вместо этого её следовало назвать Cluster Last Appears
(Последнее появление кластера). Кластер 14 последний раз участвовал в объединении кластеров на шаге 10. Новый кластер 8 затем примет участие в объединении кластеров на шаге 15
(колонка: Next Stage (Следующий шаг)).
Далее по отдельности для результатов расчёта содержащих 5, 4, 3 и 2 кластеров, приводится таблица с информацией о принадлежности каждого наблюдения к кластеру.
Cluster Membership (Принадлежность к кластеру)
| Case (Случай) | 5 Clusters (5 кластеров) |
4 Clusters (4 кластера) |
3 Clusters (3 кластера) |
2 Clusters (2 кластера) |
| 1:Budweiser | 1 | 1 | 1 | 1 |
| 2:Lowenbrau | 2 | 1 | 1 | 1 |
| 3:Michelob | 2 | 1 | 1 | 1 |
| 4:Kronenbourg | 3 | 2 | 2 | 2 |
| 5:Heineken | 3 | 2 | 2 | 2 |
| 6:Schmidts | 1 | 1 | 1 | 1 |
| 7:Pabst Blue Ribbon | 1 | 1 | 1 | 1 |
| 8:Miller Light | 4 | 4 | 3 | 1 |
| 9:Budweiser Light | 4 | 3 | 3 | 1 |
| 10:Coors Light | 4 | 3 | 3 | 1 |
| 11:Dos Equis | 3 | 2 | 2 | 2 |
| 12:Becks | 3 | 2 | 2 | 2 |
| 13:Rolling Rock | 1 | 1 | 1 | 1 |
| 14:Pabst Extra Light | 5 | 4 | 3 | 1 |
| 15:Tuborg | 1 | 1 | 1 | 1 |
| 16:Olympia Gold Light | 5 | 4 | 3 | 1 |
| 17:Schlitz Light | 4 | 3 | 3 | 1 |
Таблица показывает, что два наблюдения 14 и 16 (Pabst Extra Light и Olympia Gold Light) при переходе к 3-х кластерному решению были включены в кластеры, соседствующие на диаграмме рассеяния;
эти марки пива при оптимальном кластерном решении рассматриваются как принадлежащие к одному кластеру. Если посмотреть на 2-х кластерное решение, то оно группирует наблюдения 4, 5, 11 и 12
(Kronenbourg, Heineken, Dos Equis, Becks), то есть марки верхних правых кластеров диаграммы рассеяния; это марки иностранного производства.
В заключение приводится затребованная нами дендрограмма, которая визуализирует процесс слияния, приведенный в обзорной таблице порядка агломерации.
Она идентифицирует объединённые кластеры и значения коэффициентов на каждом шаге. При этом отображаются не исходные значения коэффициентов, а значения приведенные к шкале от 0 до 25.
Кластеры, получающиеся в результате слияния, отображаются горизонтальными пунктирными линиями.
В то время как дендрограмма годится только для графического представления процесса слияния, по диаграмме накопления можно проследить деление кластеров.
Так как начиная с 7 версии SPSS графическое представление диаграммы накопления оставляет желать лучшего, мы отказались от активирования ее вывода.
Для вводного рассмотрения мы выбрали довольно простой пример, включающий только две переменных. В этом случае конфигурация кластеров поддается представлению в графическом виде.

![Рисунок 9.1 — Кластерный анализ [2]](https://meu.usue.ru/lessons/images/901.png)

![Рисунок 9.1 — Кластерный анализ [2]](http://meu.usue.ru/lessons/images/901.png)