Какое свойство алгоритма определяет однозначность исполнения инструкций

Алгоритм –
это точное предписание, определяющее
вычислительный процесс, ведущий от
варьируемых начальных данных к искомому
результату. Это конечный набор правил,
однозначно раскрывающих содержание и
последовательность выполнения операций
для систематического решения определенного
класса задач за конечное число шагов.

Любой
алгоритм обладает следующими свойствами:

1детерминированность,
2массовость, 3результативность,
4дискретность.

Детерминированность (определенность)
означает, что набор указаний алгоритма
должен быть однозначно понят любым
исполнителем. Это свойство определяет
однозначность результата работы
алгоритма при заданных исходных
данных. Массовость алгоритма
предполагает возможность варьирования
исходных данных в некоторых пределах.
Это свойство определяет пригодность
использования алгоритма для решения
множества конкретных задач определенного
класса. Результативность алгоритма
означает, что для любых допустимых
исходных данных он должен через конечное
число шагов (или итераций)  завершить
свою работу. Дискретность алгоритма
означает возможность разбиения
определенного алгоритмического процесса
на отдельные элементарные этапы,
возможность реализации которых человеком
или компьютером не вызывает сомнения,
а результат выполнения каждого
элементарного этапа вполне определен
и понятен.

Таким
образом, алгоритм дает возможность
чисто механически решать любую конкретную
задачу из некоторого класса однотипных
задач. Существует несколько способов
описания алгоритмов:

         словесный,

         формально-словесный,

         графический
и др.

Словесный способ
описания алгоритма отражает содержание
выполняемых действий средствами
естественного языка. К достоинствам
этого способа описания следует отнести
его общедоступность, а также возможность
описывать алгоритм с любой степенью
детализации. К главным недостаткам
этого способа следует отнести достаточно
громоздкое описание, отсутствие строгой
формализации вследствие неоднозначности
восприятия естественного языка.

Формально-словесный способ
описания алгоритма основан на записи
содержания выполняемых действий с
использованием изобразительных
возможностей языка математики,
дополненного с целью указания необходимых
пояснений средствами естественного
языка. Данный способ, обладая всеми
достоинствами словесного способа,
вместе с тем более лаконичен, а значит,
и более нагляден, имеет большую
формализацию, однако тоже не является
строго формальным.

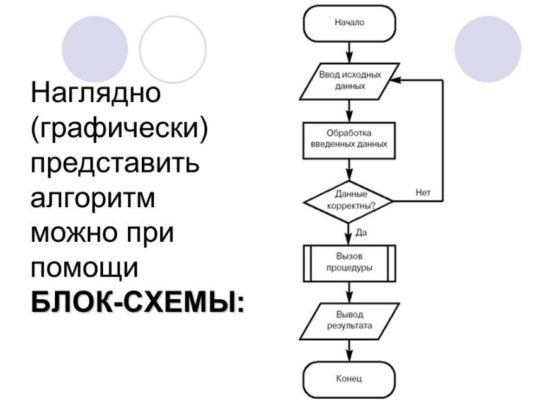
Графический способ
описания алгоритмов представляет собой
изображение логико-математической
структуры алгоритма, при котором все
этапы процесса обработки данных
представляются с помощью определенного
набора геометрических фигур (блоков),
имеющих строго определенную конфигурацию
в соответствии с характером выполняемых
действий. (см. рис.1)

 

—          начало,
конец

—          
вычисления

—          
ввод / вывод

 

                                 проверка
условия                         модификация                        подпрограмма

Рис.
Основные графические обозначения блоков
программ.

Все
блоки в схеме располагаются в
последовательности сверху вниз и слева
направо, объединяясь между собой линиями
потока.

АЛГОРИТМИЧЕСКИЕ
ЯЗЫКИ ДЛЯ ПК. Алгоритмические
языки представляют собой  средства
описания данных и алгоритмов решения
задач, они разработаны для составления
программы пользователем.

Класс
машинно зависимых языков
представлен ассемблером. Язык ассемблера
делает доступными все программно-управляемые
компоненты компьютера, поэтому он
применяется для написания программ,
использующих специфику конкретной
аппаратуры. Ассемблер – это наиболее
трудоемкий язык программирования, и
из-за его низкого уровня не удается
построить средства отладки, которые
существенно снизили бы трудоемкость
разработки программ. К
классу машинно-ориентированных языков
можно отнести языки группы С, С⁺⁺,
Турбо С. Эти языки являются результатом
попытки объединить возможности ассемблера
со встроенными структурами данных.

Класс
универсальных языков
программирования представлен наиболее
широко (Бейсик, Фортран, Паскаль и др.).
Версия Паскаля для ПК – Турбо-Паскаль
– характеризуется такими важными
особенностями, как полноэкранное
редактирование и управление, графика,
звуковое сопровождение и развитые связи
с DOS.
Система программирования на Турбо-Паскале
является резидентной программой. Это
позволяет пользователю вводить тексты
программ и немедленно их выполнять, не
тратя времени на компилирование.  Язык
Кобол был разработан специально для
решения экономических задач. Он дает
возможность составлять наиболее
удобочитаемые программы, которые понятны
и непрограммисту. В обработке данных
сложной структуры Кобол бывает эффективнее
Паскаля. Класс
проблемно-ориентированных языков
программирования представлен языками
Лого, РПГ и системой программирования
GPSS. Лого – диалоговый процедурный язык,
реализованный на основе интерпретатора
с возможностью работы со списками и на
их основе с текстами, оснащенными
развитыми графическими средствами,
которые доступны для детского восприятия.
Этот язык реализован в большинстве ПК,
применяемых в школах. РПГ, или генератор
отчетов, представляет собой язык,
включающий многие понятия и выражения,
которые связаны с машинными методами
составления отчетов и проектирования
форм выходных документов. Язык используется
главным образом для печати отчетов,
записанных в одном или нескольких файлах
баз данных.

1.      В
последние годы
развивается объектно-ориентированный подход
к программированию. Наиболее полно он
реализован в языках форт и смолток. Форт
сочетает в себе свойства операционной
системы, интерпретатора и компилятора
одновременно. Основной чертой языка
является его открытость. Форт позволяет
поддерживать многозадачный режим
работы, использует принцип одновременного
доступа программ. К функциональным языкам
программирования можно отнести языки
лиеп, пролог и снобол. Лиеп является
инструментальным средством для построения
программ с использованием методов
искусственного интеллекта. Особенность
этого языка заключается в удобстве
динамического создания новых объектов.
В качестве объектов могут выступать и
сами исходные объекты. В настоящее время
для лиепа определились две сферы
активного применения: проектирование
систем искусственного интеллекта и
анализ текстов на естественном языке.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Цель занятия: познакомить учащихся
с понятием алгоритма, исполнителями алгоритмов,
примерами алгоритмов в жизни, алгоритмическим
способом решения задач, закрепить полученные
знания с помощью электронного теста, развивать
навыки самоконтроля.

Ход урока

1. Организационный момент.
2. Подготовка к изучению нового материала.
   (ознакомление с планом и целью занятия) .
3. Изучение нового материала. (просмотр
   электронного урока с использованием мультимедиа
   проектора) . Слайды + текст лекции.
4. По ходу урока учащиеся конспектируют
   определения и отвечают на вопросы.
5. Закрепление темы занятия (работа уч-ся на
   компьютере) . Электронный тест с последующей
   самопроверкой. Решение алгоритмических задач.
6. Подведение итогов. Выставление оценок с учетом
   процентного выполнения теста.
7. Задание на дом. (выучить определения, привести
   примеры алгоритмов из жизненной практики.)

Изучение нового материала.

Один из важнейших этапов решения задач на
ЭВМ – составление алгоритма. О том, что такое
алгоритмы, какими общими свойствами они обладают
и как исполняются, мы и поговорим на этом уроке.

В 1983 году отмечалось 1200-летие со дня рождения
одного из величайших ученых Средней Азии и
средневекового Востока Мухамада ибн Мусы
аль-Хорезми. Он написал ряд трактатов по
арифметике и алгебре, в том числе книгу
«Арифметика индусскими цифрами» – о
счете с помощью десяти цифр и правилах
арифметических действий с числами.

Имя ученого аль-Хорезми превратилось в понятие
algorithmi, первоначально обозначавшее десятичную
систему исчисления и правила арифметических
действий в этой системе. Отсюда и возник
современный научный термин «алгоритм».

Каждый из нас ежедневно использует различные
алгоритмы: инструкции, правила, рецепты и т.п.
Обычно мы это делаем не задумываясь. Например,
открывая дверь ключом, никто не размышляет над
тем, в какой последовательности выполнять
действия. Однако чтобы научить кого-нибудь
открывать дверь, придется четко указать и сами
действия, и порядок их выполнения. То же
потребуется и при указании маршрута поездки.

Сравним эти алгоритмы. На первый взгляд, между
ними нет ничего общего. Одно дело – открывать
дверь, другое – ехать в гости. Но если
приглядеться внимательно, можно заметить
существенное сходство между ними. Прежде всего,
это строгий порядок выполнения действий.

Демонстрация слайда 1.
/Приложение/

Мы можем теперь сказать, что алгоритм – это
организованная последовательность действий.
Данную формулировку, конечно, нельзя считать
определением алгоритма. Например, мы не
объяснили, что означают слова
«организованная» и «действия». Скажем
сразу: абсолютно строгого определения алгоритма
не существует. Алгоритм – это одно из тех
основных понятий (категорий) математики, которые
не обладают формальным определением в терминах
более простых понятий, а абстрагируются
непосредственно из опыта.

На слайде еще одно задание. Выполните его,
используя для записи ответа любой текстовый
редактор или бумагу и карандаш.

Демонстрация слайда 2. /Приложение/

Сравните свой ответ с правильным.

Правильный алгоритм:

1. Налить в чайник воду.
2. Зажечь спичку.
3. Открыть кран газовой горелки.
4. Поднести спичку к горелке.
5. Поставить чайник на плиту.
6. Ждать, пока вода закипит.
7. Выключить газ.

Демонстрация слайда 3. /Приложение/

Рассмотренные нами алгоритмы составлены для
исполнения человеком. Но человек далеко не
единственный возможный исполнитель алгоритмов.
Все живые существа и даже отдельные клетки
исполняют различные алгоритмы. Способны на это и
созданные человеком устройства –
роботы-манипуляторы и станки с программным
управлением. Но прежде чем составлять алгоритм
решения задачи, нужно узнать, какие действия
предполагаемый исполнитель способен выполнить.

Поясним сказанное на примере. Допустим, нужно
решить квадратное уравнение.

Десятикласснику требуется минимум инструкций,
потому что он уже знает способ решения.

Восьмикласснику понадобятся намного более
сложные инструкции, потому что он этого еще не
проходил.

Теперь мы можем уточнить понятие алгоритма: это
организованная последовательность действий,
допустимых для некоторого исполнителя.

Рассмотрим информационный процесс
редактирования текста. При работе с текстом
возможны различные операции: удаление,
копирование, перемещение или замена его
фрагментов. Что необходимо для того, чтобы
преобразовать текст?

• Первое. Требуется исполнитель.
• Второе. Процесс должен быть разбит на этапы,
  понятные исполнителю.
• Третье. Должно быть определено начальное
  состояние текста и его требуемое конечное
  состояние.

Теория алгоритмов имеет большое практическое
значение. Алгоритмический тип деятельности
важен не только как одна из эффективных форм
труда человека. Через алгоритмизацию, через
расчленение сложных действий на всё более
простые, на действия, выполнение которых
доступно машинам, пролегает путь к автоматизации
различных процессов.

Далее под алгоритмом будет пониматься конечная
последовательность указаний, адресованных
исполнителю, четко и однозначно задающая процесс
решения задач какого-либо типа во всех деталях и
позволяющая получить за конечное число шагов
результат, однозначно определяемый исходными
данными.

Такое свойство алгоритма, как однозначность
результата при заданных исходных данных,
называется определенностью
(детерминированностью) .

Заметим, что большинство алгоритмов могут
выполняться при достаточно разнообразных
наборах исходных данных, то есть использоваться
для решения не какой-либо одной задачи, а целого
класса подобных задач. Это свойство алгоритма
называется массовостью.

С алгоритмами человек встречается на каждом
шагу.

Пример 1. Дан угол. Необходимо провести
биссектрису. (Есть способ, как, пользуясь
линейкой и циркулем, можно решить эту задачу.)

Пример 2. Даны два целых числа. Необходимо
найти их разность. (Имеется правило, в котором
ясно изложен весь порядок действий с цифрами
данных чисел.)

В приведенных примерах речь идет о том, как
сложную работу представить в виде
последовательности простых действий. Вычитание
многоразрядных чисел сводится к действиям с
цифрами. При делении угла пополам выполняются
несложные построения линейкой и циркулем.

Однако высказанные соображения следует
дополнить. Ведь правила вычитания формулируются
для любых многоразрядных чисел, а не для каких-то
конкретных двух. Инструкция проведения
биссектрисы тоже такова, что, пользуясь ею, можно
разделить пополам любой угол. То есть каждому
алгоритму присуща массовость –
пригодность для решения не какой-либо одной, а
целого класса задач.

Далее под алгоритмом будет пониматься конечная
последовательность указаний, адресованных
исполнителю, четко и однозначно задающая процесс
решения задач какого-либо типа во всех деталях и
позволяющая получить за конечное число шагов
результат, однозначно определяемый исходными
данными.

Такое свойство алгоритма, как однозначность
результата при заданных исходных данных,
называется определенностью
(детерминированностью) .На этом занятии мы
познакомились с такими важнейшими понятиями, как
алгоритм, исполнитель, система команд
исполнителя, узнали основные свойства
алгоритма.

Закрепление темы:

Алгоритмические задачи

№1. Старик должен переправить на лодке через
реку волка, козу и капусту. Лодка может выдержать
только старика и одного “пассажира”. В каком
порядке старик перевезет пассажиров? Не забудь,
что волк может съесть козу, а коза – капусту.
Найди 2 варианта решения.

Алгоритм решения задачи:

1 вариант	2 вариант
1) __________________________	1) _________________________
2) _________________________	2) _________________________
3) __________________________	3) _________________________

и т.д.

№2 Два мальчика и двое взрослых должны
переправиться на другую сторону реки на плоту,
который выдерживает либо двух мальчиков, либо
одного мальчика и одного взрослого. Как
осуществить переправу? Найди несколько способов
решения этой задачи.

Алгоритм решения задачи:

	1 способ	2 способ	3 способ
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг

Обозначения: 1м- один мальчик, 2м – два мальчика,
1в – один взрослый.

1. Практикум по решению задач

Злоумышленник поменял местами действия в
алгоритме вычисления среднего арифметического
из квадратного корня трёх чисел:

Присвоить а значение (а²+в²+с²)
/3.

Вести а,в,с

Сообщить “Среднее арифметическое квадратов
равно”

Сообщить а.

Восстановите правильный порядок действий.

2. Исправьте следующий алгоритм решения
уравнения (х-2) (х+2) =0:

Присвоить х значение +-2.

Сообщить “Корни уравнения равны”.

Сообщить первое значение х.

Сообщить второе значение х.

3. Автомобиль проехал три участка пути разной
длины с разными скоростями. Составьте алгоритм
нахождения средней скорости автомобиля.

4. Проснувшись утром, школьник почувствовал
недомогание. Находившийся рядом злоумышленник
тут же составил для него следующий алгоритм:

Измерить температуру.

Если температура выше 37⁰, то:

Вызвать врача.

Пойти в школу.

Несмотря на недомогание, школьник исправил
этот алгоритм, добавив всего две строки. Какие
строки добавил школьник?

5. Запишите в виде алгоритмов правила
определения знака:

А) произведения двух действительных чисел;

Б) суммы двух действительных чисел.

6. В записи алгоритма вычисления значения
выражения (х²— 5х+5) / (х⁶— 4х²+3)

Злоумышленник одно действие поставил не на
свое место. Вот как стал выглядеть алгоритм:

1. ввести х
2. если х⁶— 4х² + 3=0, то:
3. сообщить “При таком х значение выражения не
   определено”.
4. иначе:
5. присвоить у значение (х²— 5х +5) /(х⁶—
   4х²+3) .
6. конец ветвления.
7. сообщить у.

Верните действие на свое место.

Электронный тест

1.Которые из документов являются алгоритмами?

а) Правило правописания приставок,
оканчивающихся на з,с(да)

б) Программа телепередач

в) Кулинарный рецепт приготовления блюда

г) Инструкция по сборке проданного в
разобранном виде шкафа

2. В каких случаях правильно заканчивается
предложение: Алгоритм – это

а) конечная последовательность действий,
приводящая к искомому результату при любых
допустимых исходных данных

б) указание на выполнение действий

в) конечный набор понятных некоторому
исполнителю команд, выполнение которых приводит
к однозначному решению поставленной задачи

г) программа в машинных кодах

3. Расчлененность алгоритма на отдельные
элементарные действия – это

а) Дискретность

б) Определенность

в) Массовость

г) Детерминированность

4. Которые из документов являются алгоритмами?

А) Каталог книг в библиотеке

Б) Порядок набора международного телефонного
номера

В) Рецепт приготовления клея

Г) Настенный календарь на текущий год

Подведение итогов. Выставление оценок с учетом
процентного выполнения теста.

Задание на дом. (выучить определения, привести
примеры алгоритмов из жизненной практики.)

Свойства алгоритма

Алгоритм — это понятное и точное предписание
исполнителю совершить последовательность действий, направленных на
решение поставленной задачи или достижение указанной цели.

Термин имеет интересное историческое происхождение.
В IХ веке великий узбекский математик аль-Хорезми разработал правила-
арифметических действий над десятичными числами. Совокупность этих
правил в Европе стали называть «алгоризм”. Впоследствии слово
трансформировалось до известного нам сейчас вида. Алгоритмом — стали
называть любую последовательность действий, которая приводит к решению
той или иной задачи. Можно сказать, что понятие вышло за рамки
математики и стало применяться в самых различных областях.

Свойства алгоритма

•  Дискретность — разделение информационного процесса в алгоритме на
отдельные команды.

•   Однозначность (детерминированность, определенность) — каждая команда алгоритма
однозначно определяет действие исполнителя;

•    Понятность — в алгоритме используются только система команд
исполнителя (СКИ).

•    Результативность (конечность) — т. е. алгоритм должен приводить к
решению задачи за конечное число шагов;

•     Массовость (универсальность) — т. е. алгоритм должен выполняться
для любого набора исходных данных, удовлетворяющих условию задачи;   

• Дискретность — процесс
решения задачи должен быть разбит на последовательность отдельных шагов,
каждый из которых называется командой.

•  Однозначность (детерминированность)
— команды, образующие алгоритм (или, можно
сказать, входящие в СКИ), должны быть предельно четкими и однозначными.
Их результат не может зависеть от какой-либо дополнительной информации
извне алгоритма. Сколько бы раз вы не запускали программу, для одних и
тех же исходных данных всегда будет получаться один и тот же результат.

При наличии ошибок в алгоритме последнее
сформулированное свойство может иногда нарушаться.

Определенность также предполагает, что данные,
необходимые для выполнения очередной команды алгоритма, получены на
одном из предыдущих шагов алгоритма.

•  Понятность — каждая
команда алгоритма должна быть понятна тому, кто исполняет алгоритм.

•  Результативность (Конечность) — результат
выполнения алгоритма должен быть обязательно получен, т.е. правильный
алгоритм не может обрываться безрезультатно из-за какого-либо
непреодолимого препятствия в ходе выполнения. Кроме того, любой алгоритм
должен завершиться за конечное число шагов, Большинство алгоритмов
данным требованиям удовлетворяют, но при наличии ошибок возможны
нарушения результативности.

•   Корректность — любой
алгоритм создан для решения той или иной задачи, поэтому нам необходима
уверенность, что это решение будет правильным для любых допустимых
исходных данных. Как показывает опыт, грамотная и всесторонняя отладка
для сложных алгоритмов часто требует значительно больших усилий, чем
собственно разработка этих алгоритмов. При этом важно не столько
количество проверенных сочетаний входных данных, сколько количество их
типов. Например, можно сделать сколько угодно проверок для положительных
значений аргумента алгоритма, но это никак не будет гарантировать
корректную его работу в случае отрицательной величины аргумента.

•   Массовость — алгоритм
имеет смысл разрабатывать только в том случае, когда он будет
применяться многократно для различных наборов исходных данных. Например,
если составляется алгоритм обработки текстов, то вряд ли целесообразно
ограничивать его возможности только русскими буквами — стоит
предусмотреть также латинский алфавит, цифры, знаки препинания и т.п.
Тем более что такое обобщение особых трудностей не вызывает.

Алгоритм — формальная вычислительная процедура, получающая исходные данные, называемые так же входом алгоритма или его аргументом, выдающая результат вычислений на выход, и обладающая свойствами:

• Массовость Возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.

• Определенность На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.

• Конечность(результативность) Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике. Например, алгоритм работы системы сбора метеорологических данных состоит в непрерывном повторении последовательности действий («измерить температуру воздуха», «определить атмосферное давление»), выполняемых с определенной частотой (через минуту, час) во все время существования данной системы.

• Детерминированность При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.

Алгоритмы строятся для решеня тех или иных вычислительных задач. Формулировка задачи описывает, каким требованиям должно удовлетворять решение задачи, а алгоритм, решающий эту задачу, находит объект, этим требованиям удовлетворяющий.

Принято различать два вида алгоритмов:

• Комбинаторным(нечисленным) алгоритмом называется алгоритм, объектом обработки которого являются комбинаторные объекты, построенные из элементов конечного множества. К данному виду алгоритмов относится алгоритмы генерации комбинаторных объектов, графовые алгоритмы, потоковые алгоритмы, алгоритмы кодирования и т.д. .

• Численным алгоритмом называется алгоритм, объектом обработки которого служат числа. В данный класс относят различные вычислитеьные алгоритмы, алгоритмы численного решения дифференциальных уравнений и т.д. .

Проблема определения понятия «алгоритм»[]

На протяжении многих веков понятие алгоритма связывалось с числами и относительно простыми действиями над ними, да и сама математика была, по большей части, наукой о вычислениях, наукой прикладной. Чаще всего алгоритмы представлялись в виде математических формул. Порядок элементарных шагов алгоритма задавался расстановкой скобок, а сами шаги заключались в выполнении арифметических операций и операций отношения (проверки равенства, неравенства и т.д.). Часто вычисления были громоздкими, а вычисления вручную – трудоемкими, но суть самого вычислительного процесса оставалась очевидной. У математиков не возникала потребность в осознании и строгом определении понятия алгоритма, в его обобщении. Но с развитием математики появлялись новые объекты, которыми приходилось оперировать: векторы, графы, матрицы, множества и др. Как определить для них однозначность или как установить конечность алгоритма, какие шаги считать элементарными? В 1920-х задача точного определения понятия алгоритма стала одной из центральных проблем математики. В то время существовало две точки зрения на математические проблемы: «Все проблемы алгоритмически разрешимы, но для некоторых алгоритм еще не найден, поскольку еще не развиты соответствующие разделы математики» и «Есть проблемы, для которых алгоритм вообще не может существовать».

Идея о существовании алгоритмически неразрешимых проблем оказалась верной, но для того, чтобы ее обосновать, необходимо было дать точное определение алгоритма. Попытки выработать такое определение привели к возникновению теории алгоритмов, в которую вошли труды многих известных математиков – К.Гедель, К.Черч, С.Клини, А.Тьюринг, Э.Пост, А.Марков, А.Колмогоров и многие другие. Точное определение понятия алгоритма дало возможность доказать алгоритмическую неразрешимость многих математических проблем.

Приведем классические алгоритмически неразрешимые задачи:

• Десятая проблема Гильберта. Докакзано что не существует алгоритма, который по многочлену от нескольких переменных с целыми коэффициентами определял, есть ли у него целочисленные корни.
• Неразрешимость элементарной теории арифметики. Не существует алгоритма, который по утверждению о натуральных числах выдавал ответ на вопрос: истино оно или ложно?

Анализ алгоритмов и их порядок роста[]

Для алгоритмов существует два основных критерия: Правильность и Сложность(трудоемкость).

Алгоритм считается правильным если он дает верный результат для решаемой задачи.

Что касается трудоемкости алгоритмов, то она составляется из четырех позиций:

• Логическая сложность оценивается числом человеко-месяцев, затраченных на выполнение алгоритма. Основной недостаток — человеческий фактор.
• Статическая сложность это длинна описания алгоритма, измеряемая числом операторов языка программирования.
• Временная сложность это математическое время выполнения алгоритма, измеряемое в условных единицах времени.
• Емкостная сложность это число условных едениц памяти, необходимых для выполнения алгоритма.

Важно отметить, что временная и емкостная сложности не привязываются к конкретным языкам программироания и к конкретным компьютерам, и поэтому является основными критериями в оценке алгоритмов и заключаются в построении функиций сложности и ассимптотической оценке этих функций.

Функции временной и емкостной сложностей строятся по аналогии. Так как для современной машины время выполнения алгоритма наиболее важно нежели занимаемая память при его работе, то разберем на примере алгоритма сортировки вствками построение его функции временной сложности.

Сортировка вставками наиболее удобна для сортировки коротких постедовательностей и заключается в том, что к уже имеющейся отсортированной последовательности вставляется в нужное место новый элемент, пробегая последовательность справа налево. после выполнения процедуры имеется отсортированна последовательность по возрастанию.

Очевидно, что время работы процедуры будет зависеть от начальных данных. Условимся, что псевдокод будет написан на языке Delthi. изобразим условно код программы:

  Procedure Sort(A);

  var key,j,i

  begin

1. For j:= 2 to length(A) do

2. __key:=A[j]

3. __{ добавить A[j] к отсортированной части A[1..j-1] }

4. __i:=i-1

5. __while i>0 and A[i]>0 do

6. ____A[i+1]:=A[i]

7. ____i:=i-1

8. __A[i+1]:=key

Где отступ от левого края указывает уровень вложенности, т.е. в цикле «for» содержится цикл «while». Отметим каждую сторку стоимостью(чистом операций): пусть i-ая строка имеет стоимость _i

Далее, отметим сколько раз повторяется каждая сторка:

Где n это размер последовательности, а t_j это колличество повторений строки 5.

Строка стоимости числом повторений m дает вклад m в общее число операций.

Сложив вклады всех строк получаем функцию временной сложности алгоритма:

T(n)=₁n + ₂(n-1) + ₃(n-1) + ₄(n-1) + ₅t_j + ₆(t_j-1) + ₇(t_j-1) + ₃(n-1);

время работы процедуры булет зависеть не только конкретного значения n, но и от того какая последовательность подана на вход, если же последовательность подана отсортированная, то 5 строка будет повторяться единственный раз, т.е. t_j=1 и функция времени будет линейной функцией, а если же на вход будет подана отсортированная последовательность в обратном порядке, то t_j=jи функция времени будет квадратичная.

Ясно, что под временем работы алгоритма понимается время его работы в худшем-в нашем примере втором-случае. Это обуславливается, тем что именно за это время функция времени гарантирует получене результата.

Порядком роста алгоритма или его ассимтотической сложностью называется О-оценка функции временной или емкостной сложности в худшем случае(при самых плохих исходных данных). Говорят, что функция f(n)=O(q(n)) если =C, где С>0. Таким образом порядок роста нашего алгоритма сортировки есть O(n²).

Алгоритм с меньшим порядком роста времени обычно предпочтителен, если, скажем, один алгоритм имеет время работы О(n²), а другой О(n³), то первый более эффективен.

разделяют два класса алгоритмов по их порядку роста. Все алгоритмы, имеющие порядок роста меньший чем О(n^k) называют полиномиальные алгоритмы, алгоритмы имеющие порядок роста выше-экспонициальные(трудноразрешимые) алгоритмы

См.также[]

• Алгоритм

Литература[]

• Т.Кормен, Ч.Лейзер «Алгоритмы: построение и анализ»
• В.В.Быкова «Практика на ЭВМ»