-
Вы здесь:
- Главная
- Правильные призмы
Правильные призмы
Призма — это многогранник, две грани которого, многоугольники по форме, являются основаниями, остальные грани (боковые грани) имеют форму параллелограмма.
Правильной призмой — является призма, у которой в основаниях правильные многоугольники, а боковые грани равные прямоугольники.
Высота призмы — это отрезок, перпендикулярный основаниям призмы.
Бумажная развёртка призмы — это плоская геометрическая фигура, которая полностью повторяет поверхность тела и при изгибании и склеивании позволяет воссоздать геометрическое тело.
В зависимости от числа углов основания, правильные призмы различают:
— треугольные или трехгранные призмы;
— четырехугольные или четырехгранные призмы;
и т.д.
Призмы
основание — правильный треугольник
основание — правильный четырёхугольник (квадрат)
основание — правильный пятиугольник
основание — правильный шестиугольник
основание — правильный семиугольник
основание — правильный восьмиугольник
основание — правильный девятиугольник
основание — правильный n-угольник
Правильная n-угольная призма
Популярное
Люстра из многогранника
Подвесной потолочный светильник или по-простому — люстра, ещё никогда не был так близок к точным математическим формам.
Головоломка звёздчатый октаэдр
Это новый, весьма необычный способ создать модель Звёздчатого многогранника открытого 1619 году немецким математиком и астрономом Иоганном Кеплером.
Платоновы тела. Платоновы многогранники
Именем Древнегреческого ученого — Платона названа группа из пяти геометрических тел. Пять многогранников, которые математики называют — правильные, мы чаще всего в…
Самая прочная конструкция
Какое из известных нам геометрических тел обладает наибольшей прочностью? Наиболее устойчиво к внешним деформациям?
На чтение 11 мин Просмотров 86 Опубликовано Обновлено
Содержание
- Как сделать призму из бумаги?
- Правильная шестиугольная призма
- Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
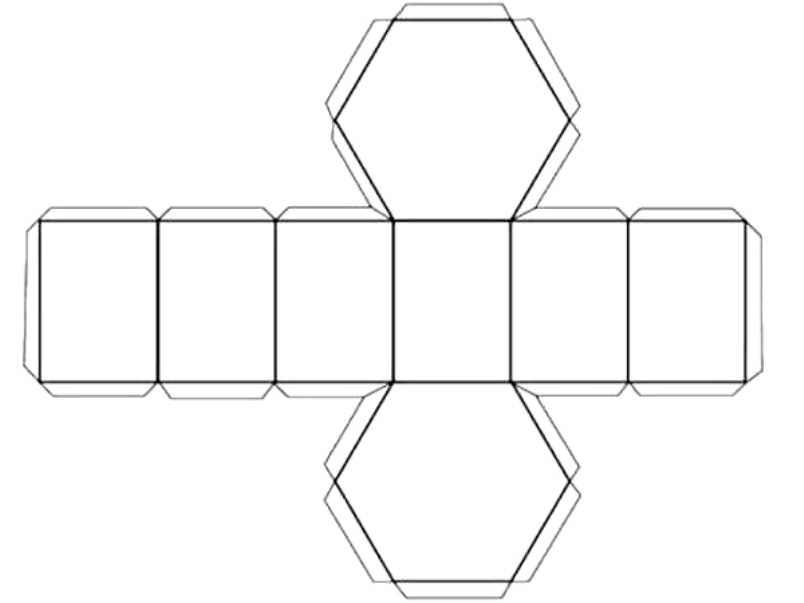
- Построение развертки шестиугольной призмы
- Призма Треугольная Из Картона скачать с mp4 mp3 flv
- Как сделать призму из бумаги
- Видео
- Элементы правильной четырехугольной призмы
- Правильная треугольная призма
- Поделки из бумаги!
- Примеры задач с решениями
- Площадь поверхности и объём
- Построение развертки призмы
- Как сделать треугольную призму
Как сделать призму из бумаги?
В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.
Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники. Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Продумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой — равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка. 
По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.
Пример заготовки для пятигранной призмы представлен на рисунке. 
Наклонная призма из бумаги представлена на этом рисунке. 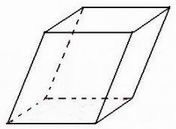

Источник
Правильная шестиугольная призма
Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Правильная шестиугольная призма — это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными шестиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности шестиугольной призмы:
Источник
Построение развертки шестиугольной призмы
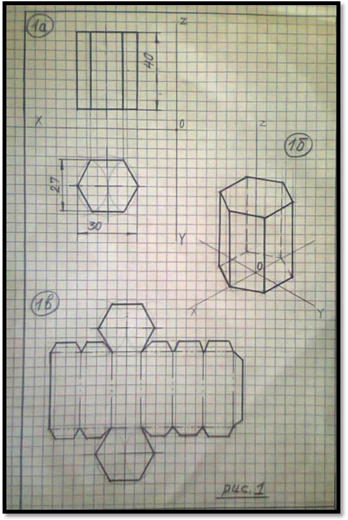
Проекции шестиугольной призмы. Развертка.
На рис. 1 даны ортогональные ( 3 вида: спереди, сверху, слева ( рис 1а)), аксонометрическая ( прямоугольная изометрическая (рис.1б)) проекции шестиугольной призмы и развертка (рис.1в).
Построение изометрической проекции шестиугольной призмы начинается с построения основания, которое располагается ближе к нулевой отметке (см. рис 1а). Основание призмы дано без искажения на виде сверху. Именно на этом виде внутри шестиугольника условно задаются оси координат ,по которым в дальнейшем строится изометрическая проекция нижнего основания ( подробнее построение шестиугольника по заданному виду в изометрической проекции смотри в конспекте урока на тему: « Ортогональные и аксонометрические проекции шестиугольника » ).
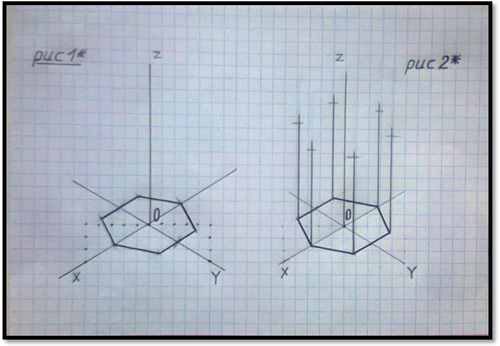
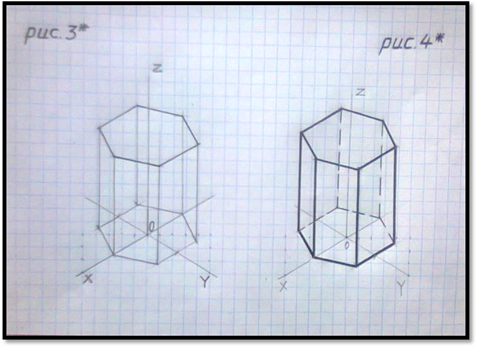
После того, как основание шестиугольной призмы в изометрической проекции будет построено (см. рис.1*), надо из каждой вершины этого основания провести боковые рёбра в виде прямых линий, которые определяют высоту этого геометрического тела , а именно, посмотрев на вид спереди определить какой оси координат параллельны эти боковые рёбра. В нашем случае они параллельны оси координат z , следовательно, из каждой вершины основания 1; 2 и 3 в изометрической проекции надо провести линии параллельные оси координат z и по ним отмерить высоту (( 40 мм) см. рис. 2*). Полученные точки между собой соединяем ( см. рис.3*). Обводим сплошными толстыми линиями видимый контур данного геометрического тела. Невидимые рёбра изображаем штриховыми линиями ( см. рис.4*).
Построение развертки шестиугольной призмы
Геометрическое тело – шестиугольная призма состоит из шести боковых граней в виде прямоугольников и двух оснований в виде шестиугольников ( см. рис.2 ).
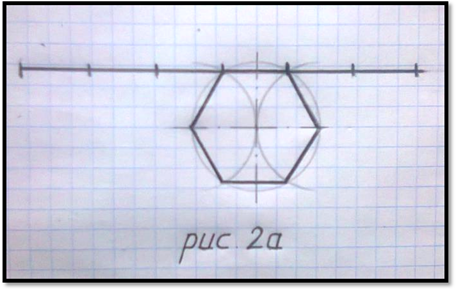
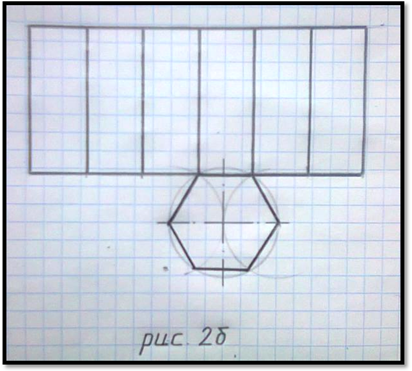
При построении развертки этого геометрического тела сначала надо изобразить нужное основание в виде шестиугольника, затем через одну из его сторон провести горизонтальную линию. На ней надо отметить ширину шести боковых граней шестиугольной призмы ( см. рис.2а ). Ширина каждой из этих граней равна стороне шестиугольника.
Из каждой точки на горизонтальной линии проводятся вертикальные линии и по ним отмечается высота шестиугольной призмы – 40 мм. Соединив полученные точки, мы получаем вторую горизонтальную линию и шесть боковых граней в виде прямоугольников ( см. рис.2б ).
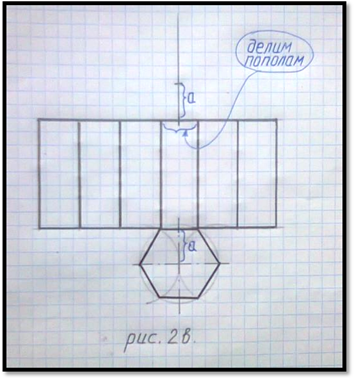
Относительно верхней горизонтальной линии достраиваем второе основание шестиугольной призмы. Для этого сторону боковой грани, к которой прикреплено нижнее основание – шестиугольник, делим на две равные части и ставим точку. Из этой точки наверх проводим вертикальную линию и по ней откладываем расстояние до центра будущего шестиугольника ( см. фигурные скобки с буквой ана рис. 2в ).
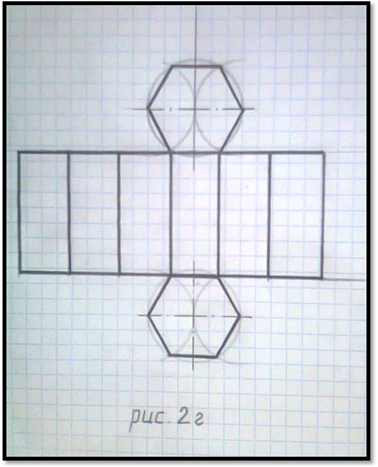
Из найденной точки, как из центра изображаем окружность диаметром 30 мм и встраиваем в не равносторонний шестиугольник ( см. рис.2г ).
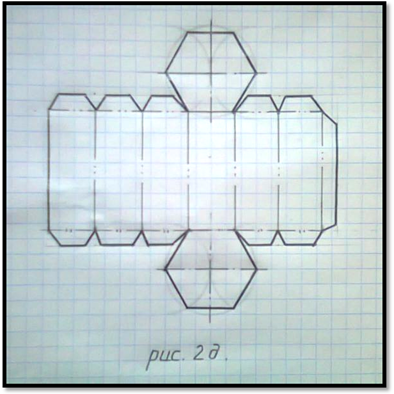
В завершении построения развертки нужно изобразить припуски ( примерно 5 мм ) около боковых граней для удобства склеивания модели ( см. рис.2д ).
Внешний контур построенной развертки на чертеже обводится сплошной основной толстой линией, линии сгиба – штрихпунктирными с двумя точками линиями.
Источник
Призма Треугольная Из Картона скачать с mp4 mp3 flv
Как сделать призму из бумаги
Сразу условимся, что делать мы будем прямую призму, то есть призму, у которой боковые ребра будут перпендикулярны основаниям. Сделать же наклонную призму из бумаги весьма проблематично (подобные макеты обычно выполняются из проволоки).
Мы уже знаем, что в основаниях призмы лежат два одинаковых многоугольника. Поэтому нашу работу начнем именно с них. Простейший из многоугольников – треугольник. Значит, и призму сначала будем делать треугольную.
Видео
Элементы правильной четырехугольной призмы
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:
- Основания ABCD и A 1 B 1 C 1 D 1 равны и параллельны друг другу
- Боковые грани AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C и CC 1 D 1 D, каждая из которых является прямоугольником
- Боковая поверхность — сумма площадей всех боковых граней призмы
- Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA 1 , BB 1 , CC 1 и DD 1 .
- Диагональ B 1 D
- Диагональ основания BD
- Диагональное сечение BB 1 D 1 D
- Перпендикулярное сечение A 2 B 2 C 2 D 2 .
Правильная треугольная призма
Выше была рассмотрена треугольная призма общего типа. Она будет называться правильной, если выполняются следующих два обязательных условия:
- Ее основание должно представлять правильный треугольник, то есть все его углы и стороны должны быть одинаковыми (равносторонний).
- Угол между каждой боковой гранью и основанием должен быть прямым, то есть составлять 90 o .
На фото выше изображена рассматриваемая фигура.
Для правильной треугольной призмы удобно выполнять расчеты длины ее диагоналей и высоты, объема и площади поверхности.
Поделки из бумаги!
Благодаря искусству оригами можно создать и пирамиду.
Такие структуры есть по всему миру (в Мексике, Китае и прочих местах).
1. Согните квадрат по вертикали и разогните, по горизонтали и разогните, по диагоналям и разомните.
Все это делается, чтобы наметить линии. Все уголки согните к центру. 8.
Примеры задач с решениями
Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.
В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?
Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a . В таком случае для первой коробки объём вещества составит:
Для второй коробки длина основания составляет 2a , но неизвестна высота уровня песка:
Поскольку V₁ = V₂ , можно приравнять выражения:
После сокращения обеих частей уравнения на a² получается:
В результате новый уровень песка составит h = 10 / 4 = 2,5 см.
ABCDA₁B₁C₁D₁ — правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.
Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.
Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.
Длина любого ребра определяется через известную диагональ:
Площадь полной поверхности находится по формуле для куба:
В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?
Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.
Длина комнаты составляет a = √9 = 3 м.
Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м² .
Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.
Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.
Площадь поверхности и объём
Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:
Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:
Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:
С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:
Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:
Применительно к четырёхугольной правильной призме формула имеет вид:
Для площади поверхности куба:
Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.
Построение развертки призмы
Построение развертки прямой призмы облегчается тем, что все размеры для развертки берутся с эпюр и нам не надо находить натуральные величины ребер призмы. Так как дана прямая призма, то боковые ребра призмы проецируются на фронтальную плоскость проекций в натуральную величину. Ребра оснований прямой призмы параллельны горизонтальной плоскости проекций и проецируются на нее также в натуральную величину.
Как сделать треугольную призму
Нам понадобится плотная белая бумага для черчения, карандаш, транспортир, циркуль, линейка, ножницы и клей.
Чертим треугольник, можно любой, но чтобы наша призма получилась особенно красивой, треугольник сделаем равносторонний. Такая призма в геометрии называется «правильная». Выбираем на свое усмотрение величину стороны треугольника, допустим 10 см. Линейкой откладываем этот отрезок на бумаге и транспортиром отмеряем угол в 60 ∗ от одного конца нашего отрезка.
Проводим наклонную линию. На ней при помощи линейки откладываем 10 см от конца отрезка. Таким образом, мы нашли третью вершину треугольника. Соединяем эту точку с концами начального отрезка и равносторонний треугольник готов. Его можно вырезать. Аналогично делаем второй треугольник, или аккуратно обводим на бумаге контуры первого. Ну вот, два основания у нас уже есть.
Делаем боковые грани. Решаем, какая у призмы будет высота. Допустим, 20 см. Чертим прямоугольник, у которого величина одной стороны это высота призмы (в нашем случае – 20 см), а вторая сторона равна величине стороны основания, умноженной на количество этих сторон (у нас: 10 см х 3 = 30 см).
На длинных сторонах делаем отметки через каждые 10 см. Соединяем противоположные отметки прямыми линиями. По ним потом надо будет аккуратно согнуть бумагу. Это — боковые ребра нашей призмы. Намечаем узкие припуски для склеивания по двум длинным и одной короткой стороне прямоугольника (достаточно полосок шириной 1 см). Вырезаем прямоугольник вместе с припусками, аккуратно отгибаем их по разметке. Сгибаем ребра.
Начинаем сборку. Склеиваем прямоугольник по боковой грани в трубу треугольного сечения. Сверху и снизу на отогнутые припуски наклеиваем треугольники-основания. Призма готова.
Вдаваться в подробности вопроса как сделать призму из картона, пожалуй, не стоит. Весь алгоритм сборки остается таким же, только бумагу замените тонким картоном. Меняя количество сторон у многоугольников основания, вы теперь самостоятельно сможете сделать и пяти- и шестиугольную призму.
Источник
Главная
/
Рукоделие
-
- Пожаловаться
visit-petersburg.com
04.09.2017, 7:49:06
Сохранено в Коробочки .упаковки
Рукоделие
Елена Рудякова
64 подписчика
-
Вы здесь:
- Главная
- Правильная шестиугольная призма
Правильная шестиугольная призма
Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Правильная шестиугольная призма — это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными шестиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности шестиугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной шестиугольной призмы:
Правильная шестиугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной шестиугольной призмы:
Двойственным многогранником прямой призмы является бипирамида.
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Геометрические размеры готовой призмы (мм):
Длина = 90
Ширина = 78
Высота = 45
Геометрические размеры готовой призмы (мм):
Длина = 73
Ширина = 64
Высота = 73
Геометрические размеры готовой призмы (мм):
Длина = 62
Ширина = 54
Высота = 93
посмотреть другие призмы
Популярное
Призмы, которые спасли Мир
Сюжет фантастического блокбастера «Пятый элемент», построен на легенде, что существуют пять элементов, которые способны защитить мир от угрозы Абсолютного Зла.
Живой мир внутри многогранника
С приходом весны, все растения вокруг оживают, появляется листва, всё зеленеет, и распускаются цветы. Но для домашних растений лето продолжается круглый год, конечно при…
Ссылки на видеоматериал
1. Вы хотели бы увидеть, как можно преобразовать развертку обычного куба? Если да, то следующий…
Звезда Кеплера
Монумент «Звезда Кеплера» (норв. Keplerstjernen), высотой 45 метров, расположен недалеко от города Осло (Норвегия) в окрестностях аэропорта…
Многогранники для Хэллоуина
Если ты не любишь математику, опасайся хэллоуина! Злые силы придут за тобой в хэллоуин! Создай двух стражей, которые будут оберегать тебя от злых сил! Ну, или,…
Как сделать призму из бумаги?
В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.
Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники. Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Треугольная призма
Продумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой — равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка.
Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму.
По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.
Шестиугольная призма
Пример заготовки для пятигранной призмы представлен на рисунке.
Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник.
Наклонная призма
Наклонная призма из бумаги представлена на этом рисунке.
Ее боковые грани находятся под углом к основанию. Такую призму можно изготовить по шаблону-развертке.
Освоив изготовление призмы, можно приступать к следующим геометрическим фигурами: пирамиде, параллелепипеду и более сложному икосаэдру из бумаги.
Статьи по теме:

Бумага — благодатный материал для детского творчества, позволяющий воплощать любые задумки юного творца. Одной из поделок, которую можно смастерить к Рождеству, просто на подарок или для украшения комнаты — ангелочек. |
Тетраэдр является простейшим многогранником, четыре грани которого представляют собой равносторонние треугольники. Для более наглядного ознакомления с фигурой ее можно смастерить из бумаги. А мы подскажем, как это сделать. |

Создание поделок из спичек — очень увлекательное развивающее занятие для ребенка. Причем создавать из них можно практически все, что вы захотите. Предлагаем вам мастер-класс кораблика из спичек, сделать который не так сложно. |

Гадание на бумажной гадалке, сложенной особым образом — развлечение, которым были увлечены дети лет 20 назад. Но и сейчас интерес к ней велик. В нашей статье мы напомним вам, как сделать такую гадалку. |
Как сделать шестиугольную призму
Призма – объемная фигура, многогранник, видов которого очень много: правильные и неправильные, прямые и наклонные. По фигуре, лежащей в основании, призма бывает от треугольной до многоугольной. Проще всего сделать прямую призму, а вот над наклонной нужно немного больше потрудиться.

Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — ножницы;
- — клей;
- — бумага или картон.
Инструкция
Начертите основания призмы, в данном случае это будут 2 шестиугольника. Для того, чтобы начертить правильный шестиугольник воспользуйтесь циркулем. Нарисуйте им круг, и с помощью этого же радиуса разделите окружность на шесть частей (у правильного шестиугольника стороны равны радиусу описанной окружности). Получившаяся фигура напоминает ячейку пчелиной соты. Неправильный шестиугольник начертите произвольно, но с помощью линейки.
Теперь приступайте к проектированию «выкройки». Стенками призмы являются параллелограммы, и вам нужно их начертить. В прямой модели параллелограммом будет простой прямоугольник. И его ширина будет всегда равна стороне шестиугольника, лежащего в основании призмы. При правильной фигуре в основании, все грани призмы будут равны между собой. При неправильной – каждой стороне шестиугольника будет соответствовать только один параллелограмм (одна боковая грань), подходящий по размеру. При этом следите за последовательностью размеров граней.
На горизонтальной прямой последовательно отложите 6 отрезков, равных стороне основания шестиугольника. Из полученных точек проведите перпендикулярные линии нужной высоты. Концы перпендикуляров соедините второй горизонтальной линией. У вас получилось 6 прямоугольников, соединенных вместе.
Пристройте к нижней и верхней стороне одного из прямоугольников 2 сконструированных ранее шестиугольника. К любому основанию, если он правильный, и к соответствующему по длине, если шестиугольник неправильный. Обведите контур сплошной линией, а линии сгиба внутри фигуры – пунктирной. У вас получилась развертка поверхности прямой призмы.
Для создания наклонной призмы основания оставьте такими же. Начертите сторону-параллелограмм, которая будет являться одной из граней. Таких граней должно быть шесть, как вы помните. Чтобы теперь начертить развертку наклонной призмы, нужно расположить шесть параллелограммов в следующем порядке: три по возрастанию, так, чтобы их косые стороны образовали одну линию, далее три по убыванию с тем же условием. Крутизна получившейся линии прямо пропорциональна градусу наклона призмы.
К пяти прямоугольникам в развертке пририсуйте небольшие трапециевидные захлесты на коротких сторонах для склеивания фигуры, а также на одной свободной длинной стороне. Вырежете заготовку для призмы вместе с захлестами и склейте модель.
Обратите внимание
В развертке наклонной призмы не чертите ее грани под слишком большим углом, иначе модель будет неустойчивой.
Источники:
- развертка наклонной призмы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Мы этого не замечаем, но вокруг нас существует огромное количество объемных геометрических фигур. Практически все технические устройства, дома, мебель и автомобили созданы с их применением. Именно поэтому знакомство с многогранниками начинается еще в школе. Представление тел в 3D — измерении лишь только кажется сложным и скучным. Рассмотрим доступные инструкции, как сделать из бумаги объемные фигуры геометрической формы, а также интересные примеры поделок из них.
Содержание
- 1. Как правильно сделать объемные фигуры из бумаги и картона
- 2. Развертки простых объемных геометрических фигур
- 2.1. Шаблон для склеивания параллелепипеда
- 2.2. Правильная четырехгранная пирамида
- 2.3. Правильна многогранная пирамида
- 2.4. Непростая развертка усеченной пирамиды
- 2.5. Развертка шестигранной призмы
- 2.6. Как правильно сделать круглый конус
- 2.7. Развертка цилиндра
- 3. Шаблоны и схемы правильных выпуклых многогранников
- 3.1. Тетраэдр или фигура из четырех равносторонних треугольников
- 3.2. Куб или гексаэдр, то есть фигура из шести квадратов
- 3.3. Фигура октаэдра состоит из 8 равносторонних треугольников
- 3.4. Додекаэдр, то есть фигура из 12 правильных пятиугольников
- 3.5. Икосаэдр, то есть фигура из 20 равносторонних треугольников
- 4. Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
- 5. Комментарии посетителей по теме статьи
Как правильно сделать объемные фигуры из бумаги и картона
Удобнее всего выполнить задание, используя плотную бумагу или картон. Разумеется, необходимо знать, как выглядит требуемая фигура в 3D – формате. Кроме того, необходимо начертить или распечатать схему развертки многогранника. Чаще всего макет склеивают, и для этого чертеж должен иметь соответствующие припуски материала. Впрочем, многие геометрические фигуры дети могут сделать своими руками в технике оригами из нескольких листов бумаги, то есть без клея.
Имея навыки черчения, схему несложно начертить на бумаге самостоятельно. Грани фигур состоят из треугольника, квадрата, ромба, круга, трапеции или другого многоугольника. При этом ребра многогранников должны иметь точный одинаковый размер, иначе фигуру не получится собрать. В случае одинаковых граней можно подготовить шаблон одной из них, а затем его обвести, формируя полный чертеж развертки.
Чтобы грани были аккуратными, ровными, рекомендуется подготовить линии изгибов, прочертив их тупой стороной иглы по металлической линейке. Таким образом, в общей сложности для работы потребуются:
- тонкий картон или плотная бумага;
- карандаш и линейка;
- клей для бумаги и канцелярские ножницы.
Из цветного материала получится веселая и привлекательная фигурка. Лучший вариант клея – ПВА.
Развертки простых объемных геометрических фигур
Грани объемных фигур вовсе не обязаны быть одинаковыми. Получается большое разнообразие возможных вариантов, и мы рассмотрим основные из них.
Шаблон для склеивания параллелепипеда
Тривиальный параллелепипед встречается повсюду. Фигура имеет шесть граней в виде параллелограммов. Если его грани прямоугольные, значит и параллелепипед – прямоугольный.
При вычерчивании шаблона для изготовления фигуры необходимо обеспечить углы 90°, а прямоугольники должны быть попарно одинаковые. В следующем примере грани фигуры образуют ромбы, а не параллелограммы. Удобно изготовить шаблон одного из них, а затем обвести 6 раз.
Это видео поможет изготовить параллелепипед из бумаги или картона.
Правильная четырехгранная пирамида
Такая пирамида называется правильной не потому, что хорошо себя ведет, а потому, что в ее основании — равносторонняя геометрическая фигура. В данном случае это квадрат. Чертеж выполнить очень просто: сначала изображаем квадрат, а к нему пристыковываем 4 одинаковых треугольника. К ним добавляем 4 припуска на склейку.
Можно распечатать шаблон с формулами расчета параметров фигуры. Очень поможет на уроке!
Это видео поможет изготовить пирамиду из бумаги.
Кстати, из правильной четырехгранной пирамиды получается оригинальная коробочка для подарка. Ее лучше изготовить из плотной цветной бумаги. Другой вариант – сделать упаковку из картона и оклеить бумагой с рисунком. В верхней части треугольников нужно пробить отверстия дыроколом и пропустить через низ красивый шнурок с бантом.
Правильна многогранная пирамида
Непростая развертка усеченной пирамиды
Шаблон усеченной пирамиды — не самый простой. Его чертеж достаточно точно можно выполнить с помощью циркуля и линейки.
Для склейки фигуры следует оставить припуски в соответствии с рисунком.
Чертеж шаблона с конкретными размерам представлен на следующем фото.
Это видео поможет изготовить четырехгранную усеченную пирамиду своими руками.
Развертка шестигранной призмы
Это видео поможет изготовить четырехгранную призму своими руками.
Как правильно сделать круглый конус
Проще всего шаблон для изготовления круглого конуса распечатать на принтере.
Припуски на склейку можно предусмотреть либо на круглом основании, либо на боковой поверхности конуса.
Это видео поможет правильно вырезать шаблон и склеить конус.
Развертка цилиндра
Добавляем припуски на склейку и получаем полноценный шаблон для изготовления цилиндра. Следующее видео поможет правильно вырезать шаблон и склеить цилиндр.
Шаблоны и схемы правильных выпуклых многогранников
Тетраэдр или фигура из четырех равносторонних треугольников
Другой вариант разметки шаблона – разделить пополам две противоположные стороны параллелограмма.
Грани тетраэдра можно раскрасить в разные цвета. Фигура станет веселее и поможет ребенку запомнить названия цветов.
Еще один вариант оформления тетраэдра – наклеить на его грани веселые детские картинки.
Грани тетраэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Это видео поможет правильно вырезать и склеить тетраэдр.
Это видео поможет собрать 3D — фигуру в технике оригами, то есть без клея.
Куб или гексаэдр, то есть фигура из шести квадратов
Его развертку можно построить из квадратов, добавим припуски на склейку.
Грани гексаэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Куб небольших размеров превращается в игральный кубик, если на его грани нанести маркером соответствующее количество точек.
Это видео поможет правильно вырезать и склеить куб.
Фигура октаэдра состоит из 8 равносторонних треугольников
Составляем параллелограмм из 3-х ромбов с углами 60° и добавляем короткие диагонали. Достраиваем снизу и сверху по треугольнику, а также добавляем припуски на склейку. Получаем шаблон для вырезания октаэдра.
Грани поделки можно оклеить веселыми картинками для детей.
Еще один вариант оформления – распечатать шаблон с формулами расчета параметров фигуры. Это поможет на уроке!
Далее видео изготовления звездчатого октаэдра.
Додекаэдр, то есть фигура из 12 правильных пятиугольников
Развертка додекаэдра состоит из 2-х одинаковых групп пятиугольников.
Грани фигуры можно украсить занимательными детскими картинками.
Это видео поможет собрать 3D — фигуру додекаэдра в технике оригами, то есть без клея.
Икосаэдр, то есть фигура из 20 равносторонних треугольников
Составляем параллелограмм из 5-ти ромбов с углами 60° и проводим короткие диагонали. Достраиваем снизу и сверху по 5 треугольников, а также добавляем припуски на склейку. Получаем шаблон для вырезания икосаэдра.
Есть еще один вариант шаблона, который удобен для вырезания из квадратного листа бумаги.
Возможно, такая схема шаблона покажется более понятной.
Это видео поможет правильно вырезать шаблон и склеить икосаэдр.
Если по заданию учителя изготовить не один, а два икосаэдра, можно собрать композицию снеговика и гарантированно рассчитывать на 5 баллов!
Один икосаэдр должен быть чуть больше другого. Склеиваем их вместе и подрисовываем фломастерами глаза, щеки и пуговички у снеговика. Нос – маленькая пятигранная пирамида, которую нужно сделать из красной бумаги.
Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
Освоив изготовление объемных геометрических фигур по заданию учителя, самое время сделать теперь что-то повеселее. Используя полученные навыки, можно создать своими руками 3Д — фигурки животных и героев мультфильмов, коробочки для подарков, сами праздничные подарки, элементы украшения комнаты и прочие поделки для детей. Рассмотрим наиболее интересные пошаговые инструкции для учащихся и дошкольников.
Так, шестигранная призма превращается в карандаш, если ее увенчать шестигранной же пирамидой. Шаблон следует раскрасить в соответствии с фото, и тогда получится полная аналогия.
Дети очень любят фигурки животных. Используя приведенную выкройку, можно изготовить очаровательную таксу.
С помощью такого шаблона можно изготовить игрушечный домик. В следующем видео Вы найдете еще один вариант домика из бумаги.
Таким образом из объемных геометрических фигурок можно построить целый город.
Как известно, из цветной бумаги делают самые разные цветы. При этом, даже если бутоны представляют из себя объемные геометрические фигуры, из них можно сформировать очаровательный букет.
Один из вариантов сборки красочных бутонов представлен в следующем мастер-классе. Шаблон представляет из себя восьмиконечную звезду.
В итоге получаются вот такие фигуры. Их собирают с помощью клея ПВА.
Объемные геометрические фигуры, изготовленные из цветной бумаги и картона, удивительным образом подходят для оформления интерьера.
Достаточно подвесить их на нитях к потолку, и необычное оформление комнаты к празднику обеспечено.
Впрочем, и на столе они произведут неизгладимое впечатление. Подобные украшения легко изготовить к празднику, так же просто и выбросить их после окончания торжества.
Как Вам такая вазочка с набором желаний, которые размещены внутри уже знакомых фигур? Просто и со вкусом.
Собирайте своими руками объемные геометрические фигуры и радуйтесь их прямой и правильной красоте!
Мастер-класс: как сделать модель шестигранной призмы из бумаги
Шестигранная призма – это геометрическая фигура, которая состоит из шести равных граней и двух оснований в форме шестиугольника. Создание модели шестигранной призмы из бумаги – интересный и увлекательный процесс для детей и взрослых. В этой статье мы расскажем, как сделать такую модель своими руками.
Для начала необходимо подготовить все необходимые материалы:
— 6 листов бумаги формата А4
— ножницы
— клей
— линейка
— карандаш
— цветная бумага (по желанию)
Шаг 1. Нарисуйте на листе бумаги два шестиугольника, которые будут служить основаниями призмы. Стороны шестиугольников должны быть равны между собой. Вырежьте оба шестиугольника ножницами.
Шаг 2. Определите высоту призмы и нарисуйте на белой бумаге 6 прямоугольников, высотой равной предварительно выбранной высоте, а шириной равными сторонам шестиугольников.
Шаг 3. Вырежьте все шестиугольники и прямоугольники.
Шаг 4. При помощи клея соедините все прямоугольники между собой, чтобы получить из них ровные, бесшовные грани призмы. Затем, наложите на одну грань шестиугольник-основание и соедините его с примыкающими гранями.
Шаг 5. Повторите шаг 4 для всех граней призмы.
Шаг 6. Оставшуюся часть шестиугольников можно использовать для создания крышки на модели. Оберните шестиугольник цветной бумагой, при помощи клея закрепите края и приклейте к вершине призмы.
И вот ваша модель шестигранной призмы готова! Теперь ее можно украсить, например, нарисовать цветные орнаменты или использовать стикеры. Также можно экспериментировать с размерами и использовать разные цвета бумаги для создания более сложных и креативных композиций.
Создание модели шестиугольной призмы из бумаги – это не только увлекательное занятие, но и прекрасный способ изучения геометрии и опыта в работе с материалами. Такой проект можно использовать для школьных презентаций, выставок или просто как украшение для дома. Попробуйте сами и получите позитивные эмоции от процесса творчества!