Вопросы
для подготовки к экзамену по дисциплине
«Информатика»
Наша учеба, работа, личные дела — это
каждодневное, ежечасное решение различных
задач. Каждая задача требует для своего
решения выполнения определенных
действий. Многократно решая задачи,
можно заметьть, что необходимые действия
должны выполняться в строго определенном
порядке. В таких случаях принято говорить
об алгоритме решения задач. Понятие
алгоритма считается одним из древнейших.
Оно возникло задолго до появления ЭВМ,
но с развитием вычислительной техники
его роль значительно возросла.
Происхождение понятия алгоритма связано
с именем великого среднеазиатского
ученого Аль Хорезми, жившего в 9 веке
н.э. Им были сформулированы впервые
правила выполнения четырех арифметических
действий.
Алгоритм — это точная инструкция, а
инструкции встречаются во всех областях
человеческой деятельности. Однако не
всякую инструкцию можно назвать
алгоритмом. Решая задачу, человек часто
не задумывается над тем, как он это
делает, и порой, затрудняется записать
последовательность выполняемых действий.
Но для того, чтобы поручить решение
задачи автоматическому устройству
необходимо составить алгоритм с четким
указанием последовательности действий.
Чтобы автоматическое устройство могло
решить задачу в соответствии с алгоритмом,
оно должно понимать каждое указание
алгоритма. Алгоритм применяется к
искомому набору исходных величин,
называемых аргументами. Цель исполнения
алгоритма получение определенного
результата, если в результате исполнения
алгоритма не достигнута определенная
цель, значит алгоритм либо неверен, либо
не завершен.
Алгоритмом называется точная инструкция
исполнителю в понятной для него форме,
определяющая процесс достижения
поставленной цели на основе имеющихся
исходных данных за конечное число шагов.
Основными свойствами алгоритмов
являются:
1. Универсальность (массовость)
— применимость алгоритма к различным
наборам исходных данных.
2. Дискретность — процесс решения
задачи по алгоритму разбит на отдельные
действия.
3. Однозначность — правила и порядок
выполнения действий алгоритма имеют
единственное толкование.
4. Конечность — каждое из действий и
весь алгоритм в целом обязательно
завершаются.
5. Результативность — по завершении
выполнения алгоритма обязательно
получается конечный результат.
6. Выполнимость — результата алгоритма
достигается за конечное число шагов.
Алгоритм считается правильным, если
его выполнение дает правильный результат.
Соответственно алгоритм содержит
ошибки, если можно указать такие
допустимые исходные данные или условия,
при которых выполнение алгоритма либо
не завершится вообще, либо не будет
получено никаких результатов, либо
полученные результаты окажутся
неправильными.
Выделяют три крупных класса алгоритмов:
— вычислительные алгоритмы, работающие
со сравнительно простыми видами данных,
такими как числа и матрицы, хотя сам
процесс вычисления может быть долгим
и сложным;
— информационные алгоритмы,
представляющие собой набор сравнительно
простых процедур, работающих с большими
объемами информации (алгоритмы баз
данных);
— управляющие алгоритмы, генерирующие
различные управляющие воздействия на
основе данных, полученных от внешних
процессов, которыми алгоритмы управляют.
Для записи алгоритмов используют самые
разнообразные средства. Выбор средства
определяется типом исполняемого
алгоритма. Выделяют следующие основные
способы записи алгоритмов:
— вербальный, когда алгоритм описывается
на человеческом языке;
— символьный, когда алгоритм описывается
с помощью набора символов;
— графический, когда алгоритм
описывается с помощью набора графических
изображений.
Общепринятыми способами записи являются
графическая запись с помощью блок-схем
и символьная запись с помощью какого-либо
алгоритмического языка.
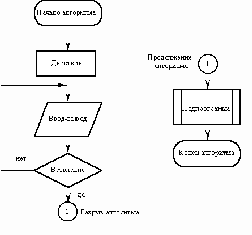
Описание алгоритма с помощью блок схем
осуществляется рисованием последовательности
геометрических фигур, каждая из которых
подразумевает выполнение определенного
действия алгоритма. Порядок выполнения
действий указывается стрелками. Написание
алгоритмов с помощью блок-схем
регламентируется ГОСТом. Внешний вид
основных блоков, применяемых при
написании блок схем, приведен на рисунке:
В зависимости от последовательности
выполнения действий в алгоритме выделяют
алгоритмы линейной, разветвленной и
циклической структуры.
В алгоритмах линейной структуры действия
выполняются последовательно одно за
другим:
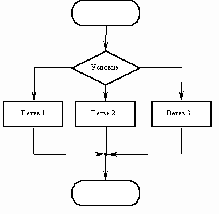
В алгоритмах разветвленной структуры в
зависимости от выполнения или невыполнения
какого-либо условия производятся
различные последовательности действий.
Каждая такая последовательность действий
называется ветвью алгоритма.
В алгоритмах циклической структуры в
зависимости от выполнения или невыполнения
какого-либо условия выполняется
повторяющаяся последовательность
действий, называющаяся телом
цикла. Вложенным называется цикл,
находящийся внутри тела другого цикла.
Различают циклы с предусловием и послеусловием:
Итерационным называется цикл, число
повторений которого не задается, а
определяется в ходе выполнения цикла.
В этом случае одно повторение цикла
называется итерацией.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цели урока:
- познакомить с понятием алгоритма, исполнителем
алгоритма, видами исполнителя, средой, СКИ и
системой отказов исполнителя, свойствами
алгоритма, показать среду, СКИ и систему отказов
для конкретного исполнителя, - развивать умение работать самостоятельно,
творчески. - воспитывать нравственное отношение к труду.
ХОД УРОКА
Презентация 1
В течение всей жизни каждый человек постоянно
пользуется набором всевозможных алгоритмов —
правил, которые заложены природой, даны
воспитанием, обучением, тренировкой, выработаны
на основе собственного опыта. Инструкции, в
которых указано, как пользоваться лифтом,
телефоном, различными автоматами и бытовыми
приборами, правила перехода улицы, оказания
первой медицинской помощи, распорядок дня,
кулинарные рецепты, порядок проведения
химического опыта, правила вычислений, методы
решения алгебраических и геометрических задач —
все это можно считать алгоритмами. Таким образом,
все мы живем в мире алгоритмов. Алгоритмы
экономят силы и время человека, так как однажды
усвоенным правилом (алгоритмом) он может
пользоваться всю жизнь.
Приведите пример алгоритма перехода дороги с
светофором, и без светофора.
Ваш мозг постоянно занят работой, поиском
решений. Говорят, что человек составляет
алгоритм.
Тема нашего сегодняшнего урока. Алгоритм.
Свойства алгоритма.
Учащиеся записывают тему урока (с
презентации).
На экране вы видите команды, необходимо
составить алгоритм заваривания чая.
Работа идет со всем классом, учащиеся
обсуждают о выборе последовательности команд,
учитель на доске регистрирует их ответ.
- размешать сахар ложечкой;
- добавить кипятку;
- налить в чашку заварку;
- вскипятить воду;
- положить сахар.
У вас должен был получиться такой алгоритм:
- вскипятить воду;
- налить в чашку заварку;
- добавить кипятку;
- положить сахар;
- размешать сахар ложечкой;
В природе все взаимосвязано, все на все влияет и
все зависит друг от друга. Складываются сложные
цепочки событий. Если вынуть хоть одно звено, вся
цепочка разорвется.
Как вы думаете, что будет если убрать из рецепта
вторую команду? А четвертую?
Надо научится выстраивать в нужном порядке все
звенья какой-нибудь жизненной или
математической задачи. Эти умения нужны и при
обработке информации. Информацию следует
обрабатывать по определенным правилам, которые
выполняются в определенном порядке.
Итак, давайте с вами, попробуем дать
определения понятию алгоритм.
Учащиеся формулируют и записывают с доски.
Алгоритм – понятное и точное
предписание исполнителю совершить
последовательность действий, направленных на
достижение указанной цели или на решение
поставленной задачи.
Учащиеся записывают в тетрадь определение.
Синонимы слова «алгоритм»:
- план;
- инструкция;
- рецепт;
- предписание.
Происхождение термина «алгоритм» связывают с
именем великого узбекского математика и
астронома аль-Хорезми (жившего в IX в.). Абу
Абдуллах Мухаммад ибн Муса аль-Хорезми (ок. 783,
Хива , Хорезм — ок. 850, Багдад) — один из
крупнейших средневековых ученых (математик,
астроном, географ и историк) IX века, основатель
классической алгебры.
Ал-Хорезми известен прежде всего своей «Книгой о
восполнении и противопоставлении» («Аль-китаб
аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»),
которая сыграла важнейшую роль в истории
математики. От названия этой книги произошло
слово «алгебра».
В своих трудах по арифметике и алгебре он
разработал, в частности, правила выполнения
четырех арифметических операций над
многозначными десятичными числами. Эти правила
определяют последовательность действий, которые
необходимо выполнить, чтобы получить сумму
чисел, произведение и т. д. Почти в таком же виде
эти правила изучаются всеми школьниками в
начальных классах.
Латинский перевод книги начинается словами
«Dixit Algorizmi» (сказал Алгоризми). Так как сочинение
об арифметике было очень популярно в Европе, имя
автора (Algorizmi или Algorizmus) стало нарицательным и
средневековые математики так называли
арифметику, основанную на десятичной
позиционной системе счисления. Позднее
европейские математики стали называть так
всякую систему вычислений по определенному
правилу. В настоящее время термин «алгоритм»
означает набор инструкций, описывающих порядок
действий исполнителя для достижения результата
решения задачи за конечное число действий.
Затем понятие алгоритма переместилось в
область логики, где появилась теория алгоритмов,
изучавшая процесс доказательств или
разрешимость и неразрешимость математических
задач. В 1937 году, когда английский
математик Алан Тьюринг доказал
теоретически возможность построения устройства,
осуществляющего алгоритм. Такое абстрактное
устройство получило название МАШИНА ТЬЮРИНГА.
Аналогичный, но более простой исполнитель
алгоритма – МАШИНА ПОСТА. Когда же были
созданы первые ЭВМ, понятие алгоритма и теория
алгоритмов переместились в новую науку,
связанную с этими вычислительными устройствами
– информатику.
Приведите примеры алгоритмов.
А теперь скажите кто может выполнить данный
алгоритм?
Приведите пример алгоритмов с разными
исполнителями.
Получается, всякий алгоритм составляется в
расчете на определенного исполнителя. Им может
быть человек, робот, компьютер и др. Чтобы
составить алгоритм для исполнителя, нужно знать,
какие команды исполнитель может понять и
исполнить, а какие нет.
Исполнитель – объект, который будет выполнять
алгоритм.
Приведите примеры исполнителей и что они
могут делать.
В классе исполнителей выделяют два типа:
формальные, неформальные. Формальный
исполнитель одну и ту же команду всегда выполнит
одинаково, неформальный может выполнять команду
по-разному. Неформальный исполнитель – человек,
формальный – технические устройства.
У каждого исполнителя можно выделить: среду
исполнителя, систему команд исполнителя, систему
отказов.
Среда – обстановка, в которой
работает исполнитель.
Система команд исполнителя (СКИ) –
совокупность команд, которую исполнитель умеет
выполнять.
Система отказов – ситуации сбоя
работы исполнителя, которые возникают, если
команда вызывается пpи недопустимом для нее
состоянии сpеды («не понимаю», «не могу»).
«Не понимаю» – возникает тогда, когда
исполнителю дается команда не входящая в его СКИ,
«не могу» – когда команда из СКИ не может быть
выполнена в конкретных условиях среды.
Укажите для данных примеров среду, ски,
систему отказов.
Свойства алгоритмов
1. Как мы уже знаем, алгоритм задает полную
последовательность действий, которые необходимо
выполнять для решения задачи. При этом, как
правило, для выполнения этих действий их
расчленяют (разбивают) в определенной
последовательности на простые шаги. Возникает
упорядоченная запись совокупности четко
разделенных предписаний (директив, команд),
образующих прерывную (или, как говорят,
дискретную) структуру алгоритма. Выполнить
действия следующего предписания можно лишь
выполнив действия предыдущего.
Под ДИСКРЕТНОСТЬЮ понимают возможность
разбиения алгоритма на отдельные элементарные
действия, выполнение которых человеком или
машиной не вызывает сомнения.
Пример по алгоритму заваривая чая
2. Чтобы исполнитель сумел решить поставленную
перед ним задачу, используя алгоритм, он должен
уметь выполнить каждое его указание. Иными
словами, он должен понимать суть управления. То
есть при составлении алгоритма нужно
обязательно учитывать «правила игры», т.е.
систему предписаний (или систему команд), которые
понимает ЭВМ. Мы будем говорить в данном случае о
«понятности» алгоритма.
Под «ПОНЯТНОСТЬЮ» алгоритмов понимают
указания, которые понятны исполнителю.
Пример по пришиванию пуговицы.
3. Будучи понятным, алгоритм не должен все же
содержать предписаний, смысл которых может
восприниматься неоднозначно. Этими свойствами
часто не обладают предписания и инструкции,
которые составляются для людей.
Например, вспомним известную всем притчу о
царской воле. Царь приказал подчиненным
выполнить такой указ: «Казнить нельзя
помиловать». Он забыл в указе поставить
запятую, а подчиненные не знали, что им делать.
Указание «казнить нельзя, помиловать» и
«казнить, нельзя помиловать» задают совсем
разные действия, от которых зависит жизнь
человека.
Кроме того, в алгоритмах недопустимы такие
ситуации, когда после выполнения очередного
предписания алгоритма исполнителю неясно, какое
из них должно выполняться на следующем шаге.
Под ОДНОЗНАЧНОСТЬЮ алгоритмов понимается
единственность толкования правил выполнения
действий и порядка их выполнения.
Пример, фрагмент мультфильма «Стран
невыученных уроков».
4. Очень важно, чтобы составленный алгоритм
обеспечивал решение не одной частной задачи, а
мог выполнять решение широкого класса задач
данного типа.
Алгоритм можно использовать для любого
квадратного у равнения. Такой алгоритм будет
МАССОВЫЙ.
Пример с чайниками, обогревателями.
5. Под КОНЕЧНОСТЬЮ алгоритмов понимают
завершение работы алгоритма в целом за конечное
число шагов.
Пример с ловлей рыбы.
6. Еще к желательным свойствам алгоритмов нужно
отнести РЕЗУЛЬТАТИВНОСТЬ, она предполагает, что
выполнение алгоритмов должно завершаться
получением определенных результатов.
Подобные ситуации в информатике возникают, когда
какие-либо действия невозможно выполнить. В
математике такие ситуации называют
неопределенностью. Например, деление числа на
ноль, извлечение квадратного корня из
отрицательного числа, да и само понятие
бесконечности неопределенно. Поэтому, если
алгоритм задает бесконечную последовательность
действий, то в этом случае он также считается
результатом неопределенным.
Но можно действовать по-другому. А именно:
указать причину неопределенного результата. В
таком случае, пояснения типа «на ноль делить
нельзя», «компьютер выполнить такое не в
состоянии» и т.п. можно считать результатом
выполнение алгоритма.
Таким образом, свойство результативности
состоит в том, что во всех» случаях можно
указать, что мы понимаем под результатом
выполнения алгоритма.
Пример с нахождением стрелы Ивана Царевича у
лягушки.
7. И последнее общее свойство алгоритмов – их
правильность.
Мы говорим, что алгоритм ПРАВИЛЬНЫЙ, если его
выполнение дает правильные результаты решения
поставленных задач.
Соответственно мы говорим, что алгоритм СОДЕРЖИТ
ОШИБКИ, если можно указать такие допустимые
исходные данные или условия, при которых
выполнение алгоритма либо не завершится вообще,
либо не будет получено никаких результатов, либо
полученные результаты окажутся неправильными.
Пример с арифметическим выражением.
Вывод:
Основные свойства алгоритмов:
- дискретность;
- понятность;
- однозначность;
- массовость;
- результативность;
- конечность;
- правильность.
Учащиеся записывают в тетрадь свойства.
Решение задач на определение свойств.
Обсуждение свойств с классом.
Задание 1.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция по варке манной каши
Молоко вскипятить добавить соль, сахар, засыпать
тонкой струйкой, непрерывно помешивая манную
крупу, довести до кипения, прокипятить минут 5-7,
добавить масло и дать остыть.
Нет понятности: какое количество (в граммах)
брать продуктов.
Возможный исправленный вариант
- Включить плиту
- Влить в кастрюлю 1,5 литра молока
- Добавить 5 грамм соли, 15 грамм сахара
- Довести молоко до кипения
- 8 столовых ложек манной крупы засыпать тонкой
струйкой, непрерывно помешивая молоко - Довести до кипения
- Кипятить 5 минут
- Добавить 20 грамм сливочного масла
- Выключить плиту, снять с плиты кастрюлю.
Задание 2.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция нахождения большего из двух данных
чисел.
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше
Нет результативности. Что делать в том случае,
если А=В?
Возможный исправленный вариант
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше - Если получился ноль, сообщить, что числа равны
Задание 3.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция покраски забора
- Покрасить первую доску.
- Переместиться к следующей доске.
- Перейти к действию 1.
Нет конечности. Что делать в том случае, когда
доски закончились?
Возможный исправленный вариант
- Покрасить первую доску.
- Если есть еще доска, переместиться к следующей
доске. - Перейти к действию 1.
- Если доски закончились, завершить работу.
Практическая работа в парах (5 мин.)
Приложение 1
Задание 1. Исправьте алгоритм
«Получения кипятка», чтобы предотвратить
несчастный случай.
Задание 2. Используя представленные
команды, составить алгоритм покраски мяча
Задание 3. Составить инструкцию, в
которой не выполняется хотя бы одно свойство
алгоритма. Записать какие изменения нужно в нее
внести, чтобы получить алгоритм.
Тест самопроверкой (5 мин.)
1. Алгоритм – это:
А) Указание на выполнение действий,
Б) Система правил, описывающая
последовательность действий, которые необходимо
выполнить для решения задачи,
В) Процесс выполнения вычислений, приводящих к
решению задачи
2. Свойство алгоритма – дискретность, выражает,
что:
А) Команды должны следовать последовательно
друг за другом,
Б) Каждая команда должна быть описана в расчете
на конкретного исполнителя,
В) Разбиение алгоритма на конечное число команд
3. Среда исполнителя – это:
А) Обстановка, в которой работает исполнитель.
Б) Объект, который будет выполнять алгоритм
В) Совокупность команд, которую исполнитель
умеет выполнять.
4. В расчете на кого должен строиться алгоритм:
А) В расчете на ЭВМ,
Б) В расчете на умственные способности товарища,
В) В расчете на конкретного исполнителя
5. Какое из перечисленных свойств относится к
свойствам алгоритма:
А) Визуальность,
Б) Совокупность,
В) Понятность
6. Исполнитель «человек» – это
А) Формальный исполнитель
Б) Неформальный исполнитель
В) Нормальный исполнитель
Проверка теста.
Подведение итогов (5 мин.)
Домашнее задание:
1. Выучить теоретический материал
2. Привести 3 примера алгоритмов для различных
исполнителей.
3. Составить 2 инструкции, в которых не
выполняется хотя бы одно свойство алгоритма.
Записать какие изменения нужно в них внести,
чтобы получить алгоритм.
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
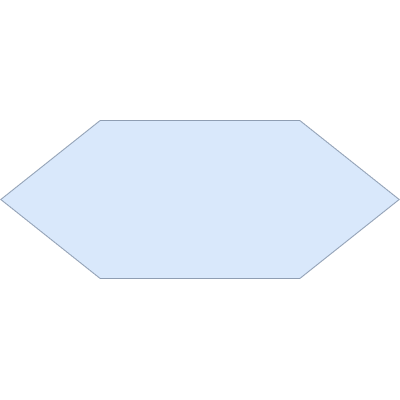
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
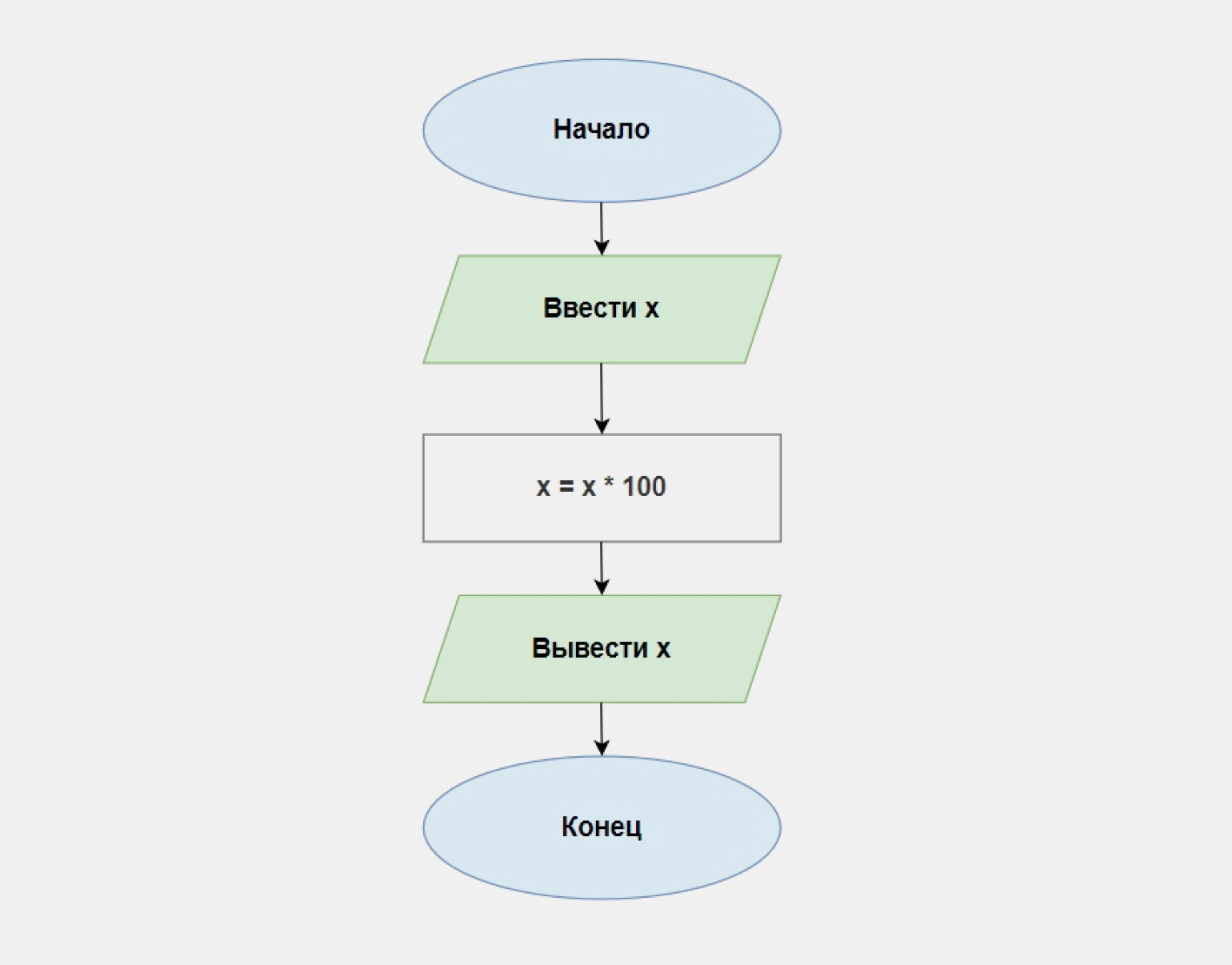
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
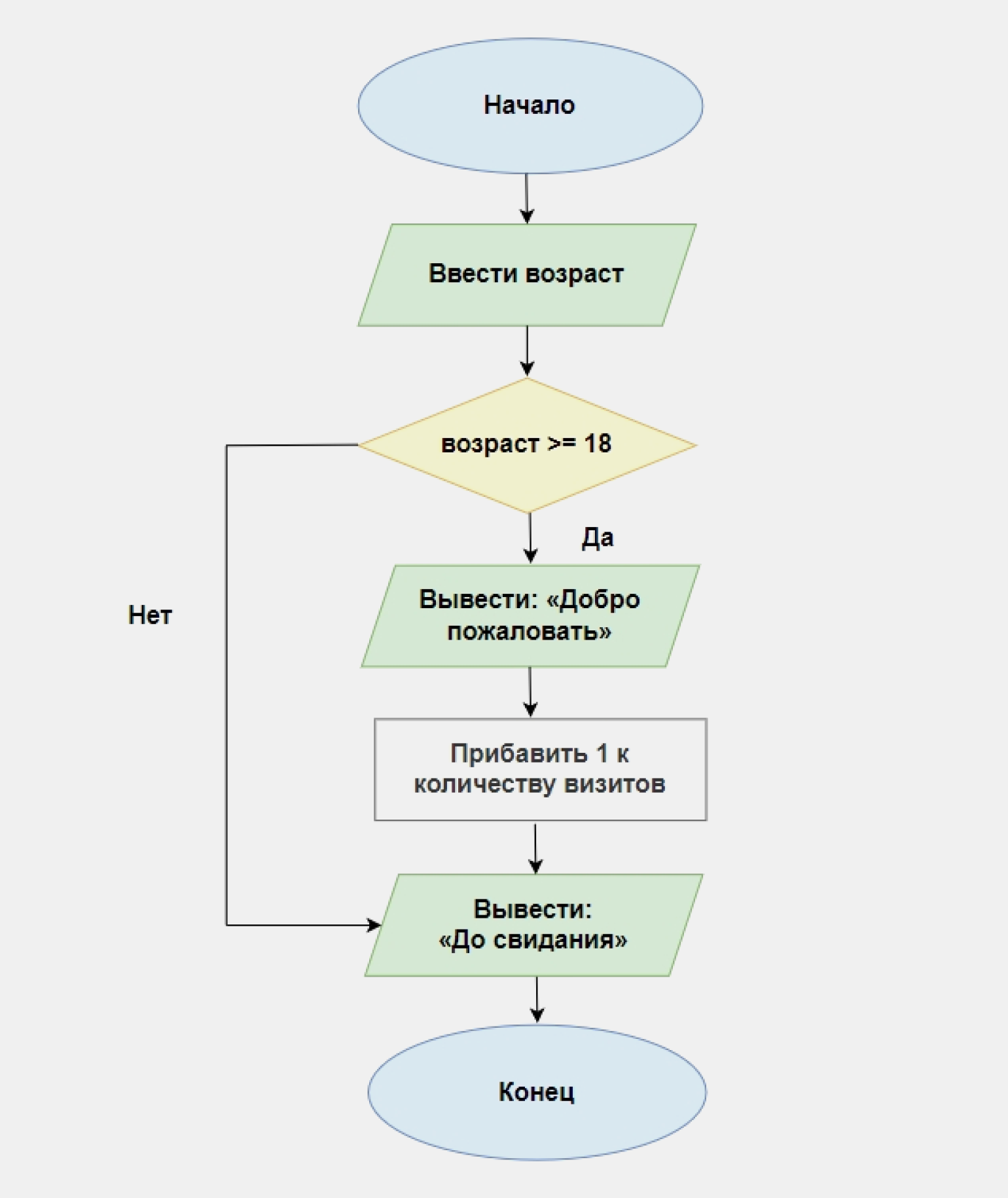
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
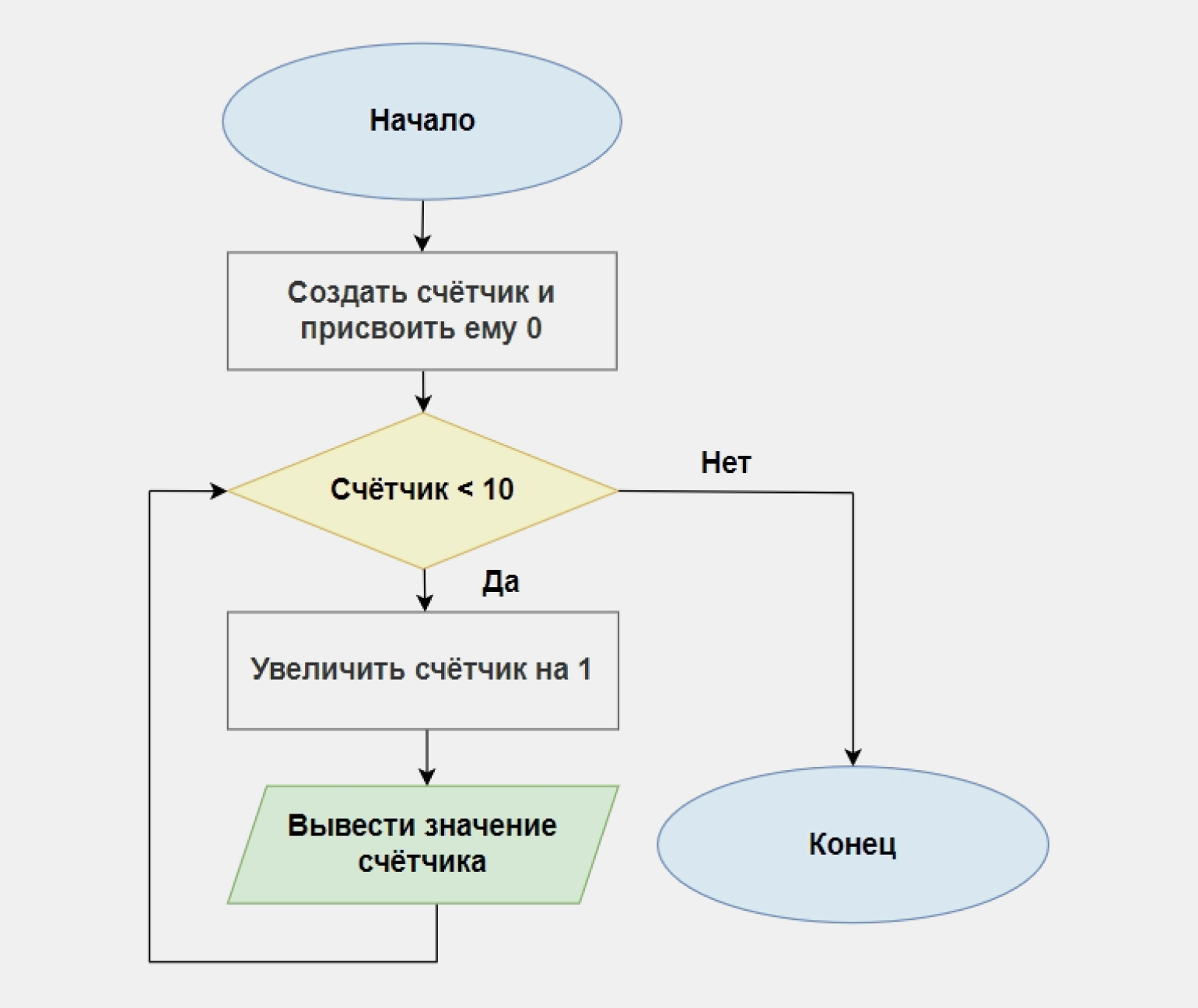
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
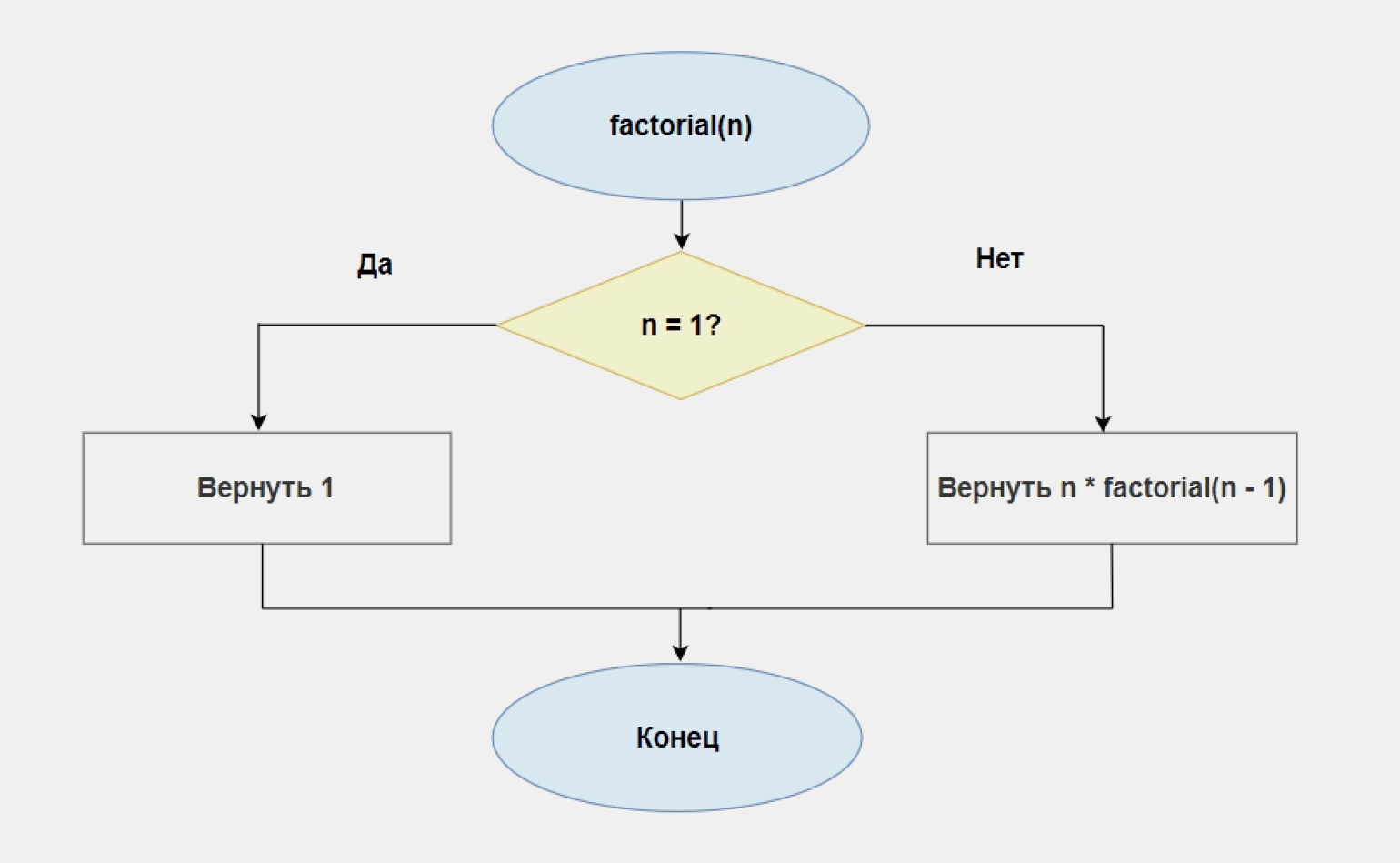
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.
Нейросети вам помогут.
Большой вебинар по нейросетям. 15 экспертов, 7 топ-нейросетей. Научитесь использовать ИИ в своей работе и повысьте эффективность.
Узнать больше
Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.
Ранее часто писали «алгорифм», сейчас такое написание используется редко, но, тем не менее, имеет место (например, Нормальный алгорифм Маркова).
Часто в качестве исполнителя выступает некоторый механизм (компьютер, токарный станок, швейная машина), но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек.
Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако, в явном виде понятие алгоритма сформировалось лишь в начале XX века.
Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений[1] или «эффективного метода»[2]; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга. В методологии алгоритм является базисным понятием и получает качественно новое понятие как оптимальности по мере приближения к прогнозируемому абсолюту. В современном мире алгоритм в формализованном выражении составляет основу образования на примерах, по подобию. На основе сходства алгоритмов различных сфер деятельности была сформирована концепция (теория) экспертных систем.
Содержание
- 1 История термина
- 2 Определения алгоритма
- 2.1 Формальное определение
- 2.1.1 Машина Тьюринга
- 2.1.2 Рекурсивные функции
- 2.1.3 Нормальный алгоритм Маркова
- 2.2 Стохастические алгоритмы
- 2.3 Другие формализации
- 2.1 Формальное определение
- 3 Формальные свойства алгоритмов
- 4 Виды алгоритмов
- 5 Нумерация алгоритмов
- 6 Алгоритмически неразрешимые задачи
- 7 Анализ алгоритмов
- 7.1 Время работы
- 8 Наличие исходных данных и некоторого результата
- 9 Представление алгоритмов
- 10 Эффективность алгоритмов
- 11 Пример
- 12 См. также
- 13 Примечания
- 14 Литература
- 15 Ссылки
История термина
Страница из «Алгебры» аль-Хорезми — хорезмского математика, от имени которого происходит слово алгоритм.
Современное формальное определение алгоритма было дано в 30—50-е годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.
Само слово «алгоритм» происходит от имени хорезмского учёного Абу Абдуллах Мухаммеда ибн Муса аль-Хорезми (алгоритм — аль-Хорезми). Около 825 года он написал сочинение, в котором впервые дал описание придуманной в Индии позиционной десятичной системы счисления. К сожалению, персидский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (её индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритмы о счёте индийском»). По-арабски же книга именовалась Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»). Из оригинального названия книги происходит слово Алгебра (алгебра — аль-джебр — восполнение).
Таким образом, мы видим, что латинизированное имя среднеазиатского учёного было вынесено в заглавие книги, и сегодня считается, что слово «алгоритм» попало в европейские языки именно благодаря этому сочинению. Однако вопрос о его смысле длительное время вызывал ожесточённые споры. На протяжении многих веков происхождению слова давались самые разные объяснения.
Одни выводили algorism из греческих algiros (больной) и arithmos (число). Из такого объяснения не очень ясно, почему числа именно «больные». Или же лингвистам больными казались люди, имеющие несчастье заниматься вычислениями? Своё объяснение предлагал и энциклопедический словарь Брокгауза и Ефрона. В нём алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень». Разумеется, эти объяснения вряд ли можно счесть убедительными.
Упомянутый выше перевод сочинения аль-Хорезми стал первой ласточкой, и в течение нескольких следующих столетий появилось множество других трудов, посвящённых всё тому же вопросу — обучению искусству счёта с помощью цифр. И все они в названии имели слово algoritmi или algorismi.
Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), всё ещё связывали это слово с именем конкретного человека. Очень распространённой была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:
Алгоризм был придуман в Греции. Это часть арифметики. Придуман он был мастером по имени Алгоризм, который дал ему своё имя. И поскольку его звали Алгоризм, Он назвал свою книгу «Алгоризм».
Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счёте мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.
«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счётного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюблённые. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счётчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.
Впрочем, греческая версия была не единственной. Мифический АлГор (Algor) именовался то королём Кастилии (Rex quodam Castelliae), то индийским королём, то арабским мудрецом (philosophus Algus nomine Arabicus), то египетским божеством. Соответственно АлГорРитм — это ритм (порядок) бога Гора (АлГора).
Баронесса Ада Лавлейс, которую считают первым программистом.
Однако со временем такие объяснения всё менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г.
Алгоритм — это искусство счёта с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчёмного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.
Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и учёные. Достоинства вычислений на счётной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счёта окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).
Итак, сочинения по искусству счёта назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).
Постепенно значение слова расширялось. Учёные начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошёл к идее логарифмов. Когда же на смену абаку пришёл так называемый счёт на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счёта на линиях.
Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.
В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.
В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus всё ещё объясняется как понятие о четырёх арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена ещё только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.
Однако потребовалось ещё почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.
Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счётная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к ещё более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по еллински и по гречески арифметика, а по немецки алгоризма, а по русски цифирная счётная мудрость».
Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырёх арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определённым правилам, и это объяснение также даётся в следующих изданиях БСЭ.
Алгоритмы становились предметом всё более пристального внимания учёных, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далёких, то к началу сороковых годов это слово они могли услышать разве что во время учёбы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм всё ещё воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объёмных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.
Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров. Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они ещё не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далёкого будущего. Соответственно и алгоритмы ни разу не упоминаются на её страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ». За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится всё более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живёт, обогащаясь всё новыми значениями и смысловыми оттенками.
Определения алгоритма
Формальное определение
Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.
Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Чёрча — Тьюринга)[3]
Машина Тьюринга
Схематическая иллюстрация работы машины Тьюринга.
Основная идея, лежащая в основе машины Тьюринга, очень проста. Машина Тьюринга — это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шагу машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом, машина может изменить свое состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево.[4]
На основе исследования этих машин был выдвинут тезис Тьюринга (основная гипотеза алгоритмов):
Этот тезис является аксиомой, постулатом, и не может быть доказан математическими методами, поскольку алгоритм не является точным математическим понятием.
Рекурсивные функции
С каждым алгоритмом можно сопоставить функцию, которую он вычисляет. Однако возникает вопрос, можно ли произвольной функции сопоставить машину Тьюринга, а если нет, то для каких функций существует алгоритм? Исследования этих вопросов привели к созданию в 1930-х годах теории рекурсивных функций[5].
Класс вычислимых функций был записан в образ, напоминающий построение некоторой аксиоматической теории на базе системы аксиом. Сначала были выбраны простейшие функции, вычисление которых очевидно. Затем были сформулированы правила (операторы) построения новых функций на основе уже существующих. Необходимый класс функций состоит из всех функций, которые можно получить из простейших применением операторов.
Подобно тезису Тьюринга в теории вычислительных функций была выдвинута гипотеза, которая называется тезис Чёрча:
Доказательство того, что класс вычислимых функций совпадает с исчисляемыми по Тьюрингу, происходит в два шага: сначала доказывают вычисление простейших функций на машине Тьюринга, а затем — вычисление функций, полученных в результате применения операторов.
Таким образом, неформально алгоритм можно определить как четкую систему инструкций, определяющих дискретный детерминированный процесс, который ведет от начальных данных (на входе) к искомому результату (на выходе), если он существует, за конечное число шагов; если искомого результата не существует, алгоритм или никогда не завершает работу, либо заходит в тупик.
Нормальный алгоритм Маркова
Нормальный алгоритм Маркова — это система последовательных применений подстановок, которые реализуют определенные процедуры получения новых слов из базовых, построенных из символов некоторого алфавита. Как и машина Тьюринга, нормальные алгоритмы не выполняют самих вычислений: они лишь выполняют преобразование слов путем замены букв по заданным правилам[6].
Нормально вычислимой называют функцию, которую можно реализовать нормальным алгоритмом. То есть, алгоритмом, который каждое слово из множества допустимых данных функции превращает в ее исходные значения[7]..
Создатель теории нормальных алгоритмов А. А. Марков выдвинул гипотезу, которая получила название принцип нормализации Маркова:
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не может быть доказан математическими средствами.
Стохастические алгоритмы
Однако, приведенное выше формальное определение алгоритма в некоторых случаях может быть слишком строгим. Иногда возникает потребность в использовании случайных величин[8]. Алгоритм, работа которого определяется не только исходными данными, но и значениями, полученными из генератора случайных чисел, называют стохастическим (или рандомизированным, от англ. randomized algorithm)[9]. Формально, такие алгоритмы нельзя называть алгоритмами, поскольку существует вероятность (близкая к нулю), что они не остановятся. Однако, стохастические алгоритмы часто бывают эффективнее детерминированных, а в отдельных случаях — единственным способом решить задачу[8].
На практике вместо генератора случайных чисел используют генератор псевдослучайных чисел.
Однако следует отличать стохастические алгоритмы и методы, которые дают с высокой вероятностью правильный результат. В отличие от метода, алгоритм дает корректные результаты даже после продолжительной работы.
Некоторые исследователи допускают возможность того, что стохастический алгоритм даст с некоторой заранее известной вероятностью неправильный результат. Тогда стохастические алгоритмы можно разделить на два типа[10]:
- алгоритмы типа Лас-Вегас всегда дают корректный результат, но время их работы не определено.
- алгоритмы типа Монте-Карло, в отличие от предыдущих, могут давать неправильные результаты с известной вероятностью (их часто называют методами Монте-Карло).
Другие формализации
Для некоторых задач названные выше формализации могут затруднять поиск решений и осуществление исследований. Для преодоления препятствий были разработаны как модификации «классических» схем, так и созданы новые модели алгоритма. В частности, можно назвать:
- многоленточная и недетерминированная машины Тьюринга;
- регистровая и РАМ машина — прототип современных компьютеров и виртуальных машин;
- конечные и клеточные автоматы
и другие.
Формальные свойства алгоритмов
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
- Дискретность — алгоритм должен представлять процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.
- Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа. Однако при включении метода генерации случайных чисел в список «исходных данных», вероятностный алгоритм становится подвидом обычного.
- Понятность — алгоритм должен включать только те команды, которые доступны исполнителю и входят в его систему команд.
- Завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов.[источник не указан 713 дней] С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.
- Массовость (универсальность). Алгоритм должен быть применим к разным наборам исходных данных.
- Результативность — завершение алгоритма определёнными результатами.
- Алгоритм содержит ошибки, если приводит к получению неправильных результатов либо не даёт результатов вовсе.
- Алгоритм не содержит ошибок, если он даёт правильные результаты для любых допустимых исходных данных.
Виды алгоритмов
Особую роль выполняют прикладные алгоритмы, предназначенные для решения определённых прикладных задач. Алгоритм считается правильным, если он отвечает требованиям задачи (например, даёт физически правдоподобный результат). Алгоритм (программа) содержит ошибки, если для некоторых исходных данных он даёт неправильные результаты, сбои, отказы или не даёт никаких результатов вообще. Последний тезис используется в олимпиадах по алгоритмическому программированию, чтобы оценить составленные участниками программы.
Важную роль играют рекурсивные алгоритмы (алгоритмы, вызывающие сами себя до тех пор, пока не будет достигнуто некоторое условие возвращения). Начиная с конца XX — начала XXI века активно разрабатываются параллельные алгоритмы, предназначенные для вычислительных машин, способных выполнять несколько операций одновременно.
Нумерация алгоритмов
Нумерация алгоритмов играет важную роль в их исследовании и анализе[11]. Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счётное, то множество всех алгоритмов также счётное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.
Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.
Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.
Алгоритмически неразрешимые задачи
Формализация понятия алгоритма позволила исследовать существование задач, для которых не существует алгоритмов поиска решений. Впоследствии была доказана невозможность алгоритмического вычисления решений ряда задач, что делает невозможным их решение на любом вычислительном устройстве. Функцию 


Случай, когда результатом вычисления функции 

Важно точно указывать допустимое множество входных данных, поскольку задача может быть решаемой для одного множества и нерешаемой для другого.
Одной из первых задач, для которой была доказана нерешаемость, является проблема остановки. Формулируется она следующим образом:
Доказательство неразрешимости проблемы остановки важно тем, что к ней можно свести другие задачи. Например, простую проблему остановки можно свести к задаче остановки на пустой строке (когда нужно определить для заданной машины Тьюринга, остановится ли она, будучи запущенной на пустой строке), доказав тем самым неразрешимость последней. [12].
Анализ алгоритмов
Вместе с распространением информационных технологий увеличился риск программных сбоев. Одним из способов избежания ошибок в алгоритмах и их реализациях служат доказательства корректности систем математическими средствами.
Использование математического аппарата для анализа алгоритмов и их реализаций называют формальными методами. Формальные методы предусматривают применение формальных спецификаций и, обычно, набора инструментов для синтаксического анализа и доказательства свойств спецификаций. Абстрагирование от деталей реализации позволяет установить свойства системы независимо от ее реализации. Кроме того, точность и однозначность математических утверждений позволяет избежать многозначности и неточности естественных языков[14].
По гипотезе Ричарда Мейса, «избежание ошибок лучше устранения ошибок»[15]. По гипотезе Хоара, «доказательство программ решает проблему корректности, документации и совместимости»[16]. Доказательство корректности программ позволяет выявлять их свойства по отношению ко всему диапазону входных данных. Для этого понятие корректности было разделено на два типа:
- Частичная корректность — программа дает правильный результат для тех случаев, когда она завершается.
- Полная корректность — программа завершает работу и выдает правильный результат для всех элементов из диапазона входных данных.
Во время доказательства корректности сравнивают текст программы со спецификацией желаемого соотношения входных-выходных данных. Для доказательств типа Хоара эта спецификация имеет вид утверждений, которые называют предусловиями и постусловиями. В совокупности с самой программой, их еще называют тройкой Хоара. Эти утверждения записывают
- P{Q}R
где P — это предусловие, что должно выполняться перед запуском программы Q, а R — постусловие, правильное после завершения работы программы.
Формальные методы были успешно применены для широкого круга задач, в частности: разработке электронных схем, искусственного интеллекта, автоматических систем на железной дороге, верификации микропроцессоров, спецификации стандартов и спецификации и верификации программ[17].
Время работы
Графики функций, приведенных в таблице ниже.
Распространенным критерием оценки алгоритмов является время работы и порядок роста продолжительности работы в зависимости от объема входных данных.[18]
Для каждой конкретной задачи составляют некоторое число, которое называют ее размером. Например, размером задачи вычисления произведения матриц может быть наибольший размер матриц-множителей, для задач на графах размером может быть количество ребер графа.
Время, которое тратит алгоритм как функция от размера задачи 
Именно асимптотическая сложность определяет размер задач, которые алгоритм способен обработать. Например, если алгоритм обрабатывает входные данные размером 
Часто, во время разработки алгоритма пытаются уменьшить асимптотическую временную сложность для наихудших случаев. На практике же бывают случаи, когда достаточным является алгоритм, который «обычно» работает быстро.
Грубо говоря, анализ средней асимптотической временной сложности можно разделить на два типа: аналитический и статистический. Аналитический метод дает более точные результаты, но сложен в использовании на практике. Зато статистический метод позволяет быстрее осуществлять анализ сложных задач[19].
В следующей таблице приведены распространенные асимптотические сложности с комментариями[20].
| Сложность | Комментарий | Примеры |
|---|---|---|
| O(1) | Устойчивое время работы не зависит от размера задачи | Ожидаемое время поиска в в хеш-таблице |
| O(log log n) | Очень медленный рост необходимого времени | Ожидаемое время работы интерполирующего поиска n элементов |
| O(log n) | Логарифмический рост — удвоение размера задачи увеличивает время работы на постоянную величину | Вычисление xn; Двоичный поиск в массиве из n элементов |
| O(n) | Линейный рост — удвоение размера задачи удвоит и необходимое время | Сложение/вычитание чисел из n цифр; Линейный поиск в массиве из n элементов |
| O(n log n) | Линеаритмичный рост — удвоение размера задачи увеличит необходимое время чуть более чем вдвое | Сортировка слиянием или кучей n элементов; нижняя граница сортировки сопоставлением n элементов |
| O(n²) | Квадратичный рост — удвоение размера задачи увеличивает необходимое время в четыре раза | Элементарные алгоритмы сортировки |
| O(n³) | Кубичный рост — удвоение размера задачи увеличивает необходимое время в восемь раз | Обычное умножение матриц |
| O(cn) | Экспоненциальный рост — увеличение размера задачи на 1 приводит к c-кратному увеличению необходимого времени; удвоение размера задачи увеличивает необходимое время в квадрат | Некоторые задачи коммивояжёра, алгоритмы поиска полным перебором |
Наличие исходных данных и некоторого результата
Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание, исполнительно совершить последовательность действий, направленных на достижение цели.
Представление алгоритмов
Формы записи алгоритма:
- словесная или вербальная (языковая, формульно-словесная);
- дракон-схема;
- псевдокод (формальные алгоритмические языки);
- схематическая:
- структурограммы (схемы Насси-Шнайдермана);
- графическая (блок-схемы).
Обычно сначала (на уровне идеи) алгоритм описывается словами, но по мере приближения к реализации он обретает всё более формальные очертания и формулировку на языке, понятном исполнителю (например, машинный код).
Эффективность алгоритмов
Хотя в определении алгоритма требуется лишь конечность числа шагов, требуемых для достижения результата, на практике выполнение даже хотя бы миллиарда шагов является слишком медленным. Также обычно есть другие ограничения (на размер программы, на допустимые действия). В связи с этим вводят такие понятия как сложность алгоритма (временна́я, по размеру программы, вычислительная и др.).
Для каждой задачи может существовать множество алгоритмов, приводящих к цели. Увеличение эффективности алгоритмов составляет одну из задач современной информатики. В 50-х гг. XX века появилась даже отдельная её область — быстрые алгоритмы. В частности, в известной всем с детства задаче об умножении десятичных чисел обнаружился ряд алгоритмов, позволяющих существенно (в асимптотическом смысле) ускорить нахождение произведения. См. быстрое умножение
Ярким примером является алгоритм Чудновского для вычисления числа 
Пример
В качестве примера можно привести алгоритм Евклида.
Алгоритм Евклида — эффективный метод вычисления наибольшего общего делителя (НОД). Назван в честь греческого математика Евклида; один из древнейших алгоритмов, который используют до сих пор[21].
Описан в «Началах» Евклида (примерно 300 до н. э.), а именно в книгах VII и X. В седьмой книге описан алгоритм для целых чисел, а в десятой — для длин отрезков.
Существует несколько вариантов алгоритма, ниже записанный в псевдокоде рекурсивный вариант:
функция нод(a, b)
если b = 0
возврат a
иначе
возврат нод(b, a mod b)
Иллюстрация выполнения алгоритма Евклида для вычисления НОД чисел 1599 и 650.
НОД чисел 1599 и 650:
| Шаг 1 | 1599 = 650*2 + 299 |
| Шаг 2 | 650 = 299*2 + 52 |
| Шаг 3 | 299 = 52*5 + 39 |
| Шаг 4 | 52 = 39*1 + 13 |
| Шаг 5 | 39 = 13*3 + 0 |
См. также
- Список алгоритмов
- Адаптивный алгоритм
- Метаалгоритм
- Теория алгоритмов
Примечания
- ↑ Kleene 1943 in Davis 1965:274
- ↑ Rosser 1939 in Davis 1965:225
- ↑ (Игошин, с. 317)
- ↑ Basics: The Turing Machine (with an interpreter!. Good Math, Bad Math (9 февраля 2007). Архивировано из первоисточника 2 февраля 2012.
- ↑ (Игошин, раздел 33)
- ↑ Энциклопедия кибернетики, т. 2, c. 90-91.
- ↑ (Игошин, раздел 34)
- ↑ 1 2 «Probabilistic algorithms should not be mistaken with methods (which I refuse to call algorithms), which produce a result which has a high probability of being correct. It is essential that an algorithm produces correct results (discounting human or computer errors), even if this happens after a very long time.» Henri Cohen A Course in Computational Algebraic Number Theory. — Springer-Verlag, 1996. — P. 2. — ISBN 3-540-55640-0
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rives’t, Clifford Stein . — ISBN 0-262-03293-7
- ↑ (Раздел 12, с. 12-22 в Atallah, 2010)
- ↑ (Игошин, раздел 36)
- ↑ 1 2 3 Peter Linz An Introduction to Formal Languages and Automata. — Jones and Bartlett Publishers, 2000. — ISBN 0-7637-1422-4
- ↑ «computability and complexity», Encyclopedia of computer Science and Technology, Facts On File, 2009, ISBN 978-0-8160-6382-6
- ↑ (O’Regan, раздел 4.5)
- ↑ (раздел 5.3.6 в Enders, 2003)
- ↑ (раздел 5.3.7 в Enders, 2003)
- ↑ (O’Regan, с. 119)
- ↑ А. Ахо, Дж. Хопкрофт, Дж. Ульман Построение и анализ вычислительных алгоритмов = The Design and Analysis of Computer Algorithms. — «Мир», 1979.
- ↑ (раздел 11 в Atallah, 2010)
- ↑ (раздел 1 в Atallah, 2010)
- ↑ Knuth D The Art of Computer Programming, Volume 2: Seminumerical Algorithms. — 3rd. — Addison–Wesley, 1997. — ISBN 0201896842
Литература
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Порублев Илья Николаевич, Ставровский Андрей Борисович. Алгоритмы и программы. Решение олимпиадных задач. — М.: «Вильямс», 2007. — С. 480. — ISBN 978-5-8459-1244-2
- Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стер.. — М.: ИЦ «Академия», 2008. — 448 с. — ISBN 5-7695-1363-2
Ссылки
| алгоритм в Викисловаре? | |
| Что такое алгоритм в Викиучебнике? |
- «Слово „алгоритм“: происхождение и развитие», В. В. Шилов, Журнал «Потенциал» — источник исторических сведений.
- Алгоритмы, методы, исходники — сайт по алгоритмам и методам программирования
- Дискретная математика: Алгоритмы — список алгоритмов
- Юрий Лифшиц. Курс лекций Алгоритмы для Интернета
- Геометрические алгоритмы
- об алгоритме в энциклопедии «Кругосвет»
- Сборник алгоритмов на сайте e-maxx.ru
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation.[1] Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning), achieving automation eventually. Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as «memory», «search» and «stimulus».[2]
In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result.[3]
As an effective method, an algorithm can be expressed within a finite amount of space and time[4] and in a well-defined formal language[5] for calculating a function.[6] Starting from an initial state and initial input (perhaps empty),[7] the instructions describe a computation that, when executed, proceeds through a finite[8] number of well-defined successive states, eventually producing «output»[9] and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.[10]
History[edit]
Ancient algorithms[edit]
Since antiquity, step-by-step procedures for solving mathematical problems have been attested. This includes Babylonian mathematics (around 2500 BC),[11] Egyptian mathematics (around 1550 BC),[11] Indian mathematics (around 800 BC and later; e.g. Shulba Sutras, Kerala School, and Brāhmasphuṭasiddhānta),[12][13] The Ifa Oracle (around 500 BC), Greek mathematics (around 240 BC, e.g. sieve of Eratosthenes and Euclidean algorithm),[14] and Arabic mathematics (9th century, e.g. cryptographic algorithms for code-breaking based on frequency analysis).[15]
Al-khwarizmi and the term algorithm[edit]
Around 825, Muhammad ibn Musa al-Khwarizmi wrote kitāb al-ḥisāb al-hindī («Book of Indian computation») and kitab al-jam’ wa’l-tafriq al-ḥisāb al-hindī («Addition and subtraction in Indian arithmetic»). Both of these texts are lost in the original Arabic at this time. (However, his other book on algebra remains.)[16]
In the early 12th century, Latin translations of said al-Khwarizmi texts involving the Hindu–Arabic numeral system and arithmetic appeared: Liber Alghoarismi de practica arismetrice (attributed to John of Seville) and Liber Algorismi de numero Indorum (attributed to Adelard of Bath).[17] Hereby, alghoarismi or algorismi is the Latinization of Al-Khwarizmi’s name; the text starts with the phrase Dixit Algorismi («Thus spoke Al-Khwarizmi»).[18]
In 1240, Alexander of Villedieu writes a Latin text titled Carmen de Algorismo. It begins with:
Haec algorismus ars praesens dicitur, in qua / Talibus Indorum fruimur bis quinque figuris.
which translates to:
Algorism is the art by which at present we use those Indian figures, which number two times five.
The poem is a few hundred lines long and summarizes the art of calculating with the new styled Indian dice (Tali Indorum), or Hindu numerals.[19]
English evolution of the word[edit]
Around 1230, the English word algorism is attested and then by Chaucer in 1391. English adopted the French term.[20][21]
In the 15th century, under the influence of the Greek word ἀριθμός (arithmos, «number»; cf. «arithmetic»), the Latin word was altered to algorithmus.
In 1656, in the English dictionary Glossographia, it says:[22]
Algorism ([Latin] algorismus) the Art or use of Cyphers, or of numbering by Cyphers; skill in accounting.
Augrime ([Latin] algorithmus) skil in accounting or numbring.
In 1658, in the first edition of The New World of English Words, it says:[23]
Algorithme, (a word compounded of Arabick and Spanish,) the art of reckoning by Cyphers.
In 1706, in the sixth edition of The New World of English Words, it says:[24]
Algorithm, the Art of computing or reckoning by numbers, which contains the five principle Rules of Arithmetick, viz. Numeration, Addition, Subtraction, Multiplication and Division; to which may be added Extraction of Roots: It is also call’d Logistica Numeralis.
Algorism, the practical Operation in the several Parts of Specious Arithmetick or Algebra; sometimes it is taken for the Practice of Common Arithmetick by the ten Numeral Figures.
In 1751, in the Young Algebraist’s Companion, Daniel Fenning contrasts the terms algorism and algorithm as follows:[25]
Algorithm signifies the first Principles, and Algorism the practical Part, or knowing how to put the Algorithm in Practice.
Since at least 1811, the term algorithm is attested to mean a «step-by-step procedure» in English.[26][27]
In 1842, in the Dictionary of Science, Literature and Art, it says:
ALGORITHM, signifies the art of computing in reference to some particular subject, or in some particular way; as the algorithm of numbers; the algorithm of the differential calculus.[28]
Machine usage[edit]
In 1928, a partial formalization of the modern concept of algorithms began with attempts to solve the Entscheidungsproblem (decision problem) posed by David Hilbert. Later formalizations were framed as attempts to define «effective calculability»[29] or «effective method».[30] Those formalizations included the Gödel–Herbrand–Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church’s lambda calculus of 1936, Emil Post’s Formulation 1 of 1936, and Alan Turing’s Turing machines of 1936–37 and 1939.
Informal definition[edit]
For a detailed presentation of the various points of view on the definition of «algorithm», see Algorithm characterizations.
One informal definition is «a set of rules that precisely defines a sequence of operations»,[31][need quotation to verify] which would include all computer programs (including programs that do not perform numeric calculations), and (for example) any prescribed bureaucratic procedure[32]
or cook-book recipe.[33]
In general, a program is an algorithm only if it stops eventually[34]—even though infinite loops may sometimes prove desirable.
A prototypical example of an algorithm is the Euclidean algorithm, which is used to determine the maximum common divisor of two integers; an example (there are others) is described by the flowchart above and as an example in a later section.
Boolos, Jeffrey & 1974, 1999 offer an informal meaning of the word «algorithm» in the following quotation:
No human being can write fast enough, or long enough, or small enough† ( †»smaller and smaller without limit … you’d be trying to write on molecules, on atoms, on electrons») to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols.[35]
An «enumerably infinite set» is one whose elements can be put into one-to-one correspondence with the integers. Thus Boolos and Jeffrey are saying that an algorithm implies instructions for a process that «creates» output integers from an arbitrary «input» integer or integers that, in theory, can be arbitrarily large. For example, an algorithm can be an algebraic equation such as y = m + n (i.e., two arbitrary «input variables» m and n that produce an output y), but various authors’ attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
- Precise instructions (in a language understood by «the computer»)[36] for a fast, efficient, «good»[37] process that specifies the «moves» of «the computer» (machine or human, equipped with the necessary internally contained information and capabilities)[38] to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = … and «effectively»[39] produce, in a «reasonable» time,[40] output-integer y at a specified place and in a specified format.
The concept of algorithm is also used to define the notion of decidability—a notion that is central for explaining how formal systems come into being starting from a small set of axioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related to the customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.
Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brain implementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device.
Formalization[edit]
Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform—in a specific order—to carry out a specified task, such as calculating employees’ paychecks or printing students’ report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by a Turing-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987), and Gurevich (2000):
Minsky: «But we will also maintain, with Turing … that any procedure which could «naturally» be called effective, can, in fact, be realized by a (simple) machine. Although this may seem extreme, the arguments … in its favor are hard to refute».[41]
Gurevich: «… Turing’s informal argument in favor of his thesis justifies a stronger thesis: every algorithm can be simulated by a Turing machine … according to Savage [1987], an algorithm is a computational process defined by a Turing machine».[42]
Turing machines can define computational processes that do not terminate. The informal definitions of algorithms generally require that the algorithm always terminates. This requirement renders the task of deciding whether a formal procedure is an algorithm impossible in the general case—due to a major theorem of computability theory known as the halting problem.
Typically, when an algorithm is associated with processing information, data can be read from an input source, written to an output device and stored for further processing. Stored data are regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.
For some of these computational processes, the algorithm must be rigorously defined: and specified in the way it applies in all possible circumstances that could arise. This means that any conditional steps must be systematically dealt with, case by case; the criteria for each case must be clear (and computable).
Because an algorithm is a precise list of precise steps, the order of computation is always crucial to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting «from the top» and going «down to the bottom»—an idea that is described more formally by flow of control.
So far, the discussion on the formalization of an algorithm has assumed the premises of imperative programming. This is the most common conception—one which attempts to describe a task in discrete, «mechanical» means. Unique to this conception of formalized algorithms is the assignment operation, which sets the value of a variable. It derives from the intuition of «memory» as a scratchpad. An example of such an assignment can be found below.
For some alternate conceptions of what constitutes an algorithm, see functional programming and logic programming.
Expressing algorithms[edit]
Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, drakon-charts, programming languages or control tables (processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts, drakon-charts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in the statements based on natural language. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are also often used as a way to define or document algorithms.
There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see finite-state machine, state transition table and control table for more), as flowcharts and drakon-charts (see state diagram for more), or as a form of rudimentary machine code or assembly code called «sets of quadruples» (see Turing machine for more).
Representations of algorithms can be classed into three accepted levels of Turing machine description, as follows:[43]
- 1 High-level description
- «…prose to describe an algorithm, ignoring the implementation details. At this level, we do not need to mention how the machine manages its tape or head.»
- 2 Implementation description
- «…prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level, we do not give details of states or transition function.»
- 3 Formal description
- Most detailed, «lowest level», gives the Turing machine’s «state table».
For an example of the simple algorithm «Add m+n» described in all three levels, see Examples.
Design[edit]
See also: Algorithm § By design paradigm
Algorithm design refers to a method or a mathematical process for problem-solving and engineering algorithms. The design of algorithms is part of many solution theories, such as divide-and-conquer or dynamic programming within operation research. Techniques for designing and implementing algorithm designs are also called algorithm design patterns,[44] with examples including the template method pattern and the decorator pattern.
One of the most important aspects of algorithm design is resource (run-time, memory usage) efficiency; the big O notation is used to describe e.g. an algorithm’s run-time growth as the size of its input increases.
Typical steps in the development of algorithms:
- Problem definition
- Development of a model
- Specification of the algorithm
- Designing an algorithm
- Checking the correctness of the algorithm
- Analysis of algorithm
- Implementation of algorithm
- Program testing
- Documentation preparation[clarification needed]
Computer algorithms[edit]
IF test THEN GOTO step xxx, shown as diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks results in complex diagrams (cf. Tausworthe 1977:100, 114).
«Elegant» (compact) programs, «good» (fast) programs : The notion of «simplicity and elegance» appears informally in Knuth and precisely in Chaitin:
- Knuth: » … we want good algorithms in some loosely defined aesthetic sense. One criterion … is the length of time taken to perform the algorithm …. Other criteria are adaptability of the algorithm to computers, its simplicity, and elegance, etc.»[45]
- Chaitin: » … a program is ‘elegant,’ by which I mean that it’s the smallest possible program for producing the output that it does»[46]
Chaitin prefaces his definition with: «I’ll show you can’t prove that a program is ‘elegant‘«—such a proof would solve the Halting problem (ibid).
Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This is true, even without expanding the available instruction set available to the programmer. Rogers observes that «It is … important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms».[47]
Unfortunately, there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example that uses Euclid’s algorithm appears below.
Computers (and computors), models of computation: A computer (or human «computer»[48]) is a restricted type of machine, a «discrete deterministic mechanical device»[49] that blindly follows its instructions.[50] Melzak’s and Lambek’s primitive models[51] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[52] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[53]
Minsky describes a more congenial variation of Lambek’s «abacus» model in his «Very Simple Bases for Computability».[54] Minsky’s machine proceeds sequentially through its five (or six, depending on how one counts) instructions unless either a conditional IF-THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky’s machine includes three assignment (replacement, substitution)[55] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[56] Rarely must a programmer write «code» with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing complete with only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT. However, a few different assignment instructions (e.g. DECREMENT, INCREMENT, and ZERO/CLEAR/EMPTY for a Minsky machine) are also required for Turing-completeness; their exact specification is somewhat up to the designer. The unconditional GOTO is convenient; it can be constructed by initializing a dedicated location to zero e.g. the instruction » Z ← 0 «; thereafter the instruction IF Z=0 THEN GOTO xxx is unconditional.
Simulation of an algorithm: computer (computor) language: Knuth advises the reader that «the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example».[57] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectively execute. Stone gives an example of this: when computing the roots of a quadratic equation the computer must know how to take a square root. If they do not, then the algorithm, to be effective, must provide a set of rules for extracting a square root.[58]
This means that the programmer must know a «language» that is effective relative to the target computing agent (computer/computor).
But what model should be used for the simulation? Van Emde Boas observes «even if we base complexity theory on abstract instead of concrete machines, the arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters».[59] When speed is being measured, the instruction set matters. For example, the subprogram in Euclid’s algorithm to compute the remainder would execute much faster if the programmer had a «modulus» instruction available rather than just subtraction (or worse: just Minsky’s «decrement»).
Structured programming, canonical structures: Per the Church–Turing thesis, any algorithm can be computed by a model known to be Turing complete, and per Minsky’s demonstrations, Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that, while «undisciplined» use of unconditional GOTOs and conditional IF-THEN GOTOs can result in «spaghetti code», a programmer can write structured programs using only these instructions; on the other hand «it is also possible, and not too hard, to write badly structured programs in a structured language».[60] Tausworthe augments the three Böhm-Jacopini canonical structures:[61] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[62] An additional benefit of a structured program is that it lends itself to proofs of correctness using mathematical induction.[63]
Canonical flowchart symbols[64]: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program corresponding to it). Like the program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only four: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm–Jacopini canonical structures are made of these primitive shapes. Sub-structures can «nest» in rectangles, but only if a single exit occurs from the superstructure. The symbols and their use to build the canonical structures are shown in the diagram.
Examples[edit]
Algorithm example[edit]
One of the simplest algorithms is to find the largest number in a list of numbers of random order. Finding the solution requires looking at every number in the list. From this follows a simple algorithm, which can be stated in a high-level description in English prose, as:
High-level description:
- If there are no numbers in the set, then there is no highest number.
- Assume the first number in the set is the largest number in the set.
- For each remaining number in the set: if this number is larger than the current largest number, consider this number to be the largest number in the set.
- When there are no numbers left in the set to iterate over, consider the current largest number to be the largest number of the set.
(Quasi-)formal description:
Written in prose but much closer to the high-level language of a computer program, the following is the more formal coding of the algorithm in pseudocode or pidgin code:
Algorithm LargestNumber Input: A list of numbers L. Output: The largest number in the list L.
if L.size = 0 return null
largest ← L[0]
for each item in L, do
if item > largest, then
largest ← item
return largest
- «←» denotes assignment. For instance, «largest ← item» means that the value of largest changes to the value of item.
- «return» terminates the algorithm and outputs the following value.
Euclid’s algorithm[edit]
In mathematics, the Euclidean algorithm or Euclid’s algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).[65] It is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
Euclid poses the problem thus: «Given two numbers not prime to one another, to find their greatest common measure». He defines «A number [to be] a multitude composed of units»: a counting number, a positive integer not including zero. To «measure» is to place a shorter measuring length s successively (q times) along longer length l until the remaining portion r is less than the shorter length s.[66] In modern words, remainder r = l − q×s, q being the quotient, or remainder r is the «modulus», the integer-fractional part left over after the division.[67]
For Euclid’s method to succeed, the starting lengths must satisfy two requirements: (i) the lengths must not be zero, AND (ii) the subtraction must be «proper»; i.e., a test must guarantee that the smaller of the two numbers is subtracted from the larger (or the two can be equal so their subtraction yields zero).
Euclid’s original proof adds a third requirement: the two lengths must not be prime to one another. Euclid stipulated this so that he could construct a reductio ad absurdum proof that the two numbers’ common measure is in fact the greatest.[68] While Nicomachus’ algorithm is the same as Euclid’s, when the numbers are prime to one another, it yields the number «1» for their common measure. So, to be precise, the following is really Nicomachus’ algorithm.
1599 = 650×2 + 299 650 = 299×2 + 52 299 = 52×5 + 39 52 = 39×1 + 13 39 = 13×3 + 0
Computer language for Euclid’s algorithm[edit]
Only a few instruction types are required to execute Euclid’s algorithm—some logical tests (conditional GOTO), unconditional GOTO, assignment (replacement), and subtraction.
- A location is symbolized by upper case letter(s), e.g. S, A, etc.
- The varying quantity (number) in a location is written in lower case letter(s) and (usually) associated with the location’s name. For example, location L at the start might contain the number l = 3009.
An inelegant program for Euclid’s algorithm[edit]
The following algorithm is framed as Knuth’s four-step version of Euclid’s and Nicomachus’, but, rather than using division to find the remainder, it uses successive subtractions of the shorter length s from the remaining length r until r is less than s. The high-level description, shown in boldface, is adapted from Knuth 1973:2–4:
INPUT:
1 [Into two locations L and S put the numbers l and s that represent the two lengths]: INPUT L, S 2 [Initialize R: make the remaining length r equal to the starting/initial/input length l]: R ← L
E0: [Ensure r ≥ s.]
3 [Ensure the smaller of the two numbers is in S and the larger in R]: IF R > S THEN the contents of L is the larger number so skip over the exchange-steps 4, 5 and 6: GOTO step 7 ELSE swap the contents of R and S. 4 L ← R (this first step is redundant, but is useful for later discussion). 5 R ← S 6 S ← L
E1: [Find remainder]: Until the remaining length r in R is less than the shorter length s in S, repeatedly subtract the measuring number s in S from the remaining length r in R.
7 IF S > R THEN done measuring so GOTO 10 ELSE measure again, 8 R ← R − S 9 [Remainder-loop]: GOTO 7.
E2: [Is the remainder zero?]: EITHER (i) the last measure was exact, the remainder in R is zero, and the program can halt, OR (ii) the algorithm must continue: the last measure left a remainder in R less than measuring number in S.
10 IF R = 0 THEN
done so
GOTO step 15
ELSE
CONTINUE TO step 11,
E3: [Interchange s and r]: The nut of Euclid’s algorithm. Use remainder r to measure what was previously smaller number s; L serves as a temporary location.
11 L ← R 12 R ← S 13 S ← L 14 [Repeat the measuring process]: GOTO 7
OUTPUT:
15 [Done. S contains the greatest common divisor]:
PRINT S
DONE:
16 HALT, END, STOP.
An elegant program for Euclid’s algorithm[edit]
The following version of Euclid’s algorithm requires only six core instructions to do what thirteen are required to do by «Inelegant»; worse, «Inelegant» requires more types of instructions.[clarify] The flowchart of «Elegant» can be found at the top of this article. In the (unstructured) Basic language, the steps are numbered, and the instruction LET [] = [] is the assignment instruction symbolized by ←.
5 REM Euclid's algorithm for greatest common divisor 6 PRINT "Type two integers greater than 0" 10 INPUT A,B 20 IF B=0 THEN GOTO 80 30 IF A > B THEN GOTO 60 40 LET B=B-A 50 GOTO 20 60 LET A=A-B 70 GOTO 20 80 PRINT A 90 END
How «Elegant» works: In place of an outer «Euclid loop», «Elegant» shifts back and forth between two «co-loops», an A > B loop that computes A ← A − B, and a B ≤ A loop that computes B ← B − A. This works because, when at last the minuend M is less than or equal to the subtrahend S (Difference = Minuend − Subtrahend), the minuend can become s (the new measuring length) and the subtrahend can become the new r (the length to be measured); in other words the «sense» of the subtraction reverses.
The following version can be used with programming languages from the C-family:
// Euclid's algorithm for greatest common divisor int euclidAlgorithm (int A, int B) { A = abs(A); B = abs(B); while (B != 0) { while (A > B) { A = A-B; } B = B-A; } return A; }
Testing the Euclid algorithms[edit]
Does an algorithm do what its author wants it to do? A few test cases usually give some confidence in the core functionality. But tests are not enough. For test cases, one source[69] uses 3009 and 884. Knuth suggested 40902, 24140. Another interesting case is the two relatively prime numbers 14157 and 5950.
But «exceptional cases»[70] must be identified and tested. Will «Inelegant» perform properly when R > S, S > R, R = S? Ditto for «Elegant»: B > A, A > B, A = B? (Yes to all). What happens when one number is zero, both numbers are zero? («Inelegant» computes forever in all cases; «Elegant» computes forever when A = 0.) What happens if negative numbers are entered? Fractional numbers? If the input numbers, i.e. the domain of the function computed by the algorithm/program, is to include only positive integers including zero, then the failures at zero indicate that the algorithm (and the program that instantiates it) is a partial function rather than a total function. A notable failure due to exceptions is the Ariane 5 Flight 501 rocket failure (June 4, 1996).
Proof of program correctness by use of mathematical induction: Knuth demonstrates the application of mathematical induction to an «extended» version of Euclid’s algorithm, and he proposes «a general method applicable to proving the validity of any algorithm».[71] Tausworthe proposes that a measure of the complexity of a program be the length of its correctness proof.[72]
Measuring and improving the Euclid algorithms[edit]
Elegance (compactness) versus goodness (speed): With only six core instructions, «Elegant» is the clear winner, compared to «Inelegant» at thirteen instructions. However, «Inelegant» is faster (it arrives at HALT in fewer steps). Algorithm analysis[73] indicates why this is the case: «Elegant» does two conditional tests in every subtraction loop, whereas «Inelegant» only does one. As the algorithm (usually) requires many loop-throughs, on average much time is wasted doing a «B = 0?» test that is needed only after the remainder is computed.
Can the algorithms be improved?: Once the programmer judges a program «fit» and «effective»—that is, it computes the function intended by its author—then the question becomes, can it be improved?
The compactness of «Inelegant» can be improved by the elimination of five steps. But Chaitin proved that compacting an algorithm cannot be automated by a generalized algorithm;[74] rather, it can only be done heuristically; i.e., by exhaustive search (examples to be found at Busy beaver), trial and error, cleverness, insight, application of inductive reasoning, etc. Observe that steps 4, 5 and 6 are repeated in steps 11, 12 and 13. Comparison with «Elegant» provides a hint that these steps, together with steps 2 and 3, can be eliminated. This reduces the number of core instructions from thirteen to eight, which makes it «more elegant» than «Elegant», at nine steps.
The speed of «Elegant» can be improved by moving the «B=0?» test outside of the two subtraction loops. This change calls for the addition of three instructions (B = 0?, A = 0?, GOTO). Now «Elegant» computes the example-numbers faster; whether this is always the case for any given A, B, and R, S would require a detailed analysis.
Algorithmic analysis[edit]
It is frequently important to know how much of a particular resource (such as time or storage) is theoretically required for a given algorithm. Methods have been developed for the analysis of algorithms to obtain such quantitative answers (estimates); for example, an algorithm which adds up the elements of a list of n numbers would have a time requirement of 


Different algorithms may complete the same task with a different set of instructions in less or more time, space, or ‘effort’ than others. For example, a binary search algorithm (with cost 

Formal versus empirical[edit]
The analysis, and study of algorithms is a discipline of computer science, and is often practiced abstractly without the use of a specific programming language or implementation. In this sense, algorithm analysis resembles other mathematical disciplines in that it focuses on the underlying properties of the algorithm and not on the specifics of any particular implementation. Usually pseudocode is used for analysis as it is the simplest and most general representation. However, ultimately, most algorithms are usually implemented on particular hardware/software platforms and their algorithmic efficiency is eventually put to the test using real code. For the solution of a «one off» problem, the efficiency of a particular algorithm may not have significant consequences (unless n is extremely large) but for algorithms designed for fast interactive, commercial or long life scientific usage it may be critical. Scaling from small n to large n frequently exposes inefficient algorithms that are otherwise benign.
Empirical testing is useful because it may uncover unexpected interactions that affect performance. Benchmarks may be used to compare before/after potential improvements to an algorithm after program optimization.
Empirical tests cannot replace formal analysis, though, and are not trivial to perform in a fair manner.[75]
Execution efficiency[edit]
To illustrate the potential improvements possible even in well-established algorithms, a recent significant innovation, relating to FFT algorithms (used heavily in the field of image processing), can decrease processing time up to 1,000 times for applications like medical imaging.[76] In general, speed improvements depend on special properties of the problem, which are very common in practical applications.[77] Speedups of this magnitude enable computing devices that make extensive use of image processing (like digital cameras and medical equipment) to consume less power.
Classification[edit]
There are various ways to classify algorithms, each with its own merits.
By implementation[edit]
One way to classify algorithms is by implementation means.
int gcd(int A, int B) { if (B == 0) return A; else if (A > B) return gcd(A-B,B); else return gcd(A,B-A); } |
| Recursive C implementation of Euclid’s algorithm from the above flowchart |
- Recursion
- A recursive algorithm is one that invokes (makes reference to) itself repeatedly until a certain condition (also known as termination condition) matches, which is a method common to functional programming. Iterative algorithms use repetitive constructs like loops and sometimes additional data structures like stacks to solve the given problems. Some problems are naturally suited for one implementation or the other. For example, towers of Hanoi is well understood using recursive implementation. Every recursive version has an equivalent (but possibly more or less complex) iterative version, and vice versa.
- Serial, parallel or distributed
- Algorithms are usually discussed with the assumption that computers execute one instruction of an algorithm at a time. Those computers are sometimes called serial computers. An algorithm designed for such an environment is called a serial algorithm, as opposed to parallel algorithms or distributed algorithms. Parallel algorithms are algorithms that take advantage of computer architectures where multiple processors can work on a problem at the same time. Distributed algorithms are algorithms that use multiple machines connected with a computer network. Parallel and distributed algorithms divide the problem into more symmetrical or asymmetrical subproblems and collect the results back together. For example, a CPU would be an example of a parallel algorithm. The resource consumption in such algorithms is not only processor cycles on each processor but also the communication overhead between the processors. Some sorting algorithms can be parallelized efficiently, but their communication overhead is expensive. Iterative algorithms are generally parallelizable, but some problems have no parallel algorithms and are called inherently serial problems.
- Deterministic or non-deterministic
- Deterministic algorithms solve the problem with exact decision at every step of the algorithm whereas non-deterministic algorithms solve problems via guessing although typical guesses are made more accurate through the use of heuristics.
- Exact or approximate
- While many algorithms reach an exact solution, approximation algorithms seek an approximation that is closer to the true solution. The approximation can be reached by either using a deterministic or a random strategy. Such algorithms have practical value for many hard problems. One of the examples of an approximate algorithm is the Knapsack problem, where there is a set of given items. Its goal is to pack the knapsack to get the maximum total value. Each item has some weight and some value. Total weight that can be carried is no more than some fixed number X. So, the solution must consider weights of items as well as their value.[78]
- Quantum algorithm
- They run on a realistic model of quantum computation. The term is usually used for those algorithms which seem inherently quantum, or use some essential feature of Quantum computing such as quantum superposition or quantum entanglement.
By design paradigm[edit]
Another way of classifying algorithms is by their design methodology or paradigm. There is a certain number of paradigms, each different from the other. Furthermore, each of these categories includes many different types of algorithms. Some common paradigms are:
- Brute-force or exhaustive search
- Brute force is a method of problem-solving that involves systematically trying every possible option until the optimal solution is found. This approach can be very time consuming, as it requires going through every possible combination of variables. However, it is often used when other methods are not available or too complex. Brute force can be used to solve a variety of problems, including finding the shortest path between two points and cracking passwords.
- Divide and conquer
- A divide-and-conquer algorithm repeatedly reduces an instance of a problem to one or more smaller instances of the same problem (usually recursively) until the instances are small enough to solve easily. One such example of divide and conquer is merge sorting. Sorting can be done on each segment of data after dividing data into segments and sorting of entire data can be obtained in the conquer phase by merging the segments. A simpler variant of divide and conquer is called a decrease-and-conquer algorithm, which solves an identical subproblem and uses the solution of this subproblem to solve the bigger problem. Divide and conquer divides the problem into multiple subproblems and so the conquer stage is more complex than decrease and conquer algorithms. An example of a decrease and conquer algorithm is the binary search algorithm.
- Search and enumeration
- Many problems (such as playing chess) can be modeled as problems on graphs. A graph exploration algorithm specifies rules for moving around a graph and is useful for such problems. This category also includes search algorithms, branch and bound enumeration and backtracking.
- Randomized algorithm
- Such algorithms make some choices randomly (or pseudo-randomly). They can be very useful in finding approximate solutions for problems where finding exact solutions can be impractical (see heuristic method below). For some of these problems, it is known that the fastest approximations must involve some randomness.[79] Whether randomized algorithms with polynomial time complexity can be the fastest algorithms for some problems is an open question known as the P versus NP problem. There are two large classes of such algorithms:
- Monte Carlo algorithms return a correct answer with high-probability. E.g. RP is the subclass of these that run in polynomial time.
- Las Vegas algorithms always return the correct answer, but their running time is only probabilistically bound, e.g. ZPP.
- Reduction of complexity
- This technique involves solving a difficult problem by transforming it into a better-known problem for which we have (hopefully) asymptotically optimal algorithms. The goal is to find a reducing algorithm whose complexity is not dominated by the resulting reduced algorithm’s. For example, one selection algorithm for finding the median in an unsorted list involves first sorting the list (the expensive portion) and then pulling out the middle element in the sorted list (the cheap portion). This technique is also known as transform and conquer.
- Back tracking
- In this approach, multiple solutions are built incrementally and abandoned when it is determined that they cannot lead to a valid full solution.
Optimization problems[edit]
For optimization problems there is a more specific classification of algorithms; an algorithm for such problems may fall into one or more of the general categories described above as well as into one of the following:
- Linear programming
- When searching for optimal solutions to a linear function bound to linear equality and inequality constraints, the constraints of the problem can be used directly in producing the optimal solutions. There are algorithms that can solve any problem in this category, such as the popular simplex algorithm.[80] Problems that can be solved with linear programming include the maximum flow problem for directed graphs. If a problem additionally requires that one or more of the unknowns must be an integer then it is classified in integer programming. A linear programming algorithm can solve such a problem if it can be proved that all restrictions for integer values are superficial, i.e., the solutions satisfy these restrictions anyway. In the general case, a specialized algorithm or an algorithm that finds approximate solutions is used, depending on the difficulty of the problem.
- Dynamic programming
- When a problem shows optimal substructures—meaning the optimal solution to a problem can be constructed from optimal solutions to subproblems—and overlapping subproblems, meaning the same subproblems are used to solve many different problem instances, a quicker approach called dynamic programming avoids recomputing solutions that have already been computed. For example, Floyd–Warshall algorithm, the shortest path to a goal from a vertex in a weighted graph can be found by using the shortest path to the goal from all adjacent vertices. Dynamic programming and memoization go together. The main difference between dynamic programming and divide and conquer is that subproblems are more or less independent in divide and conquer, whereas subproblems overlap in dynamic programming. The difference between dynamic programming and straightforward recursion is in caching or memoization of recursive calls. When subproblems are independent and there is no repetition, memoization does not help; hence dynamic programming is not a solution for all complex problems. By using memoization or maintaining a table of subproblems already solved, dynamic programming reduces the exponential nature of many problems to polynomial complexity.
- The greedy method
- A greedy algorithm is similar to a dynamic programming algorithm in that it works by examining substructures, in this case not of the problem but of a given solution. Such algorithms start with some solution, which may be given or have been constructed in some way, and improve it by making small modifications. For some problems they can find the optimal solution while for others they stop at local optima, that is, at solutions that cannot be improved by the algorithm but are not optimum. The most popular use of greedy algorithms is for finding the minimal spanning tree where finding the optimal solution is possible with this method. Huffman Tree, Kruskal, Prim, Sollin are greedy algorithms that can solve this optimization problem.
- The heuristic method
- In optimization problems, heuristic algorithms can be used to find a solution close to the optimal solution in cases where finding the optimal solution is impractical. These algorithms work by getting closer and closer to the optimal solution as they progress. In principle, if run for an infinite amount of time, they will find the optimal solution. Their merit is that they can find a solution very close to the optimal solution in a relatively short time. Such algorithms include local search, tabu search, simulated annealing, and genetic algorithms. Some of them, like simulated annealing, are non-deterministic algorithms while others, like tabu search, are deterministic. When a bound on the error of the non-optimal solution is known, the algorithm is further categorized as an approximation algorithm.
By field of study[edit]
Every field of science has its own problems and needs efficient algorithms. Related problems in one field are often studied together. Some example classes are search algorithms, sorting algorithms, merge algorithms, numerical algorithms, graph algorithms, string algorithms, computational geometric algorithms, combinatorial algorithms, medical algorithms, machine learning, cryptography, data compression algorithms and parsing techniques.
Fields tend to overlap with each other, and algorithm advances in one field may improve those of other, sometimes completely unrelated, fields. For example, dynamic programming was invented for optimization of resource consumption in industry but is now used in solving a broad range of problems in many fields.
By complexity[edit]
Algorithms can be classified by the amount of time they need to complete compared to their input size:
- Constant time: if the time needed by the algorithm is the same, regardless of the input size. E.g. an access to an array element.
- Logarithmic time: if the time is a logarithmic function of the input size. E.g. binary search algorithm.
- Linear time: if the time is proportional to the input size. E.g. the traverse of a list.
- Polynomial time: if the time is a power of the input size. E.g. the bubble sort algorithm has quadratic time complexity.
- Exponential time: if the time is an exponential function of the input size. E.g. Brute-force search.
Some problems may have multiple algorithms of differing complexity, while other problems might have no algorithms or no known efficient algorithms. There are also mappings from some problems to other problems. Owing to this, it was found to be more suitable to classify the problems themselves instead of the algorithms into equivalence classes based on the complexity of the best possible algorithms for them.
Continuous algorithms[edit]
The adjective «continuous» when applied to the word «algorithm» can mean:
- An algorithm operating on data that represents continuous quantities, even though this data is represented by discrete approximations—such algorithms are studied in numerical analysis; or
- An algorithm in the form of a differential equation that operates continuously on the data, running on an analog computer.[81]
Algorithm = Logic + Control[edit]
In logic programming, algorithms are viewed as having both «a logic component, which specifies the knowledge to be used in solving problems, and a control component, which determines the problem-solving strategies by means of which that knowledge is used.»[82]
The Euclidean algorithm illustrates this view of an algorithm. [83][84] Here is a logic programming representation, using :- to represent «if», and the relation gcd(A, B, C) to represent the function gcd(A, B) = C:
gcd(A, A, A). gcd(A, B, C) :- A > B, gcd(A-B, B, C). gcd(A, B, C) :- B > A, gcd(A, B-A, C).
In the logic programming language Ciao the gcd relation can be represented directly in functional notation:
gcd(A, A) := A. gcd(A, B) := gcd(A-B, B) :- A > B. gcd(A, B) := gcd(A, B-A) :- B > A.
The Ciao implementation translates the functional notation into a relational representation in Prolog, extracting the embedded subtractions, A-B and B-A, as separate conditions:
gcd(A, A, A). gcd(A, B, C) :- A > B, A' is A-B, gcd(A', B, C). gcd(A, B, C) :- B > A, B' is B-A, gcd(A, B, C).
The resulting program has a purely logical (and «declarative») reading, as a recursive (or inductive) definition, which is independent of how the logic is used to solve problems:
The gcd of A and A is A. The gcd of A and B is C, if A > B and A' is A-B and the gcd of A' and B is C. The gcd of A and B is C, if B > A and B' is B-A and the gcd of A and B' is C.
Different problem-solving strategies turn the logic into different algorithms. In theory, given a pair of integers A and B, forward (or «bottom-up») reasoning could be used to generate all instances of the gcd relation, terminating when the desired gcd of A and B is generated. Of course, forward reasoning is entirely useless in this case. But in other cases, such as the definition of the Fibonacci sequence[82] and Datalog, forward reasoning can be an efficient problem solving strategy.
In contrast with the inefficiency of forward reasoning in this example, backward (or «top-down») reasoning using SLD resolution turns the logic into the Euclidean algorithm:
To find the gcd C of two given numbers A and B: If A = B, then C = A. If A > B, then let A' = A-B and find the gcd of A' and B, which is C. If B > A, then let B' = B-A and find the gcd of A and B', which is C.
One of the advantages of the logic programming representation of the algorithm is that its purely logical reading makes it easier to verify that the algorithm is correct relative to the standard non-recursive definition of gcd.[83] Here is the standard definition written in Prolog:
gcd(A, B, C) :- divides(C, A), divides(C, B), forall((divides(D, A), divides(D, B)), D =< C). divides(C, Number) :- between(1, Number, C), 0 is Number mod C.
This definition, which is the specification of the Euclidean algorithm, is also executable in Prolog: Backward reasoning treats the specification as the brute-force algorithm that iterates through all of the integers C between 1 and A, checking whether C divides both A and B, and then for each such C iterates again through all of the integers D between 1 and A, until it finds a C such that C is greater than or equal to all of the D that also divide both A and B. Although this algorithm is hopelessly inefficient, it shows that formal specifications can often be written in logic programming form, and they can be executed by Prolog, to check that they correctly represent informal requirements.
Legal issues[edit]
Algorithms, by themselves, are not usually patentable. In the United States, a claim consisting solely of simple manipulations of abstract concepts, numbers, or signals does not constitute «processes» (USPTO 2006), and hence algorithms are not patentable (as in Gottschalk v. Benson). However practical applications of algorithms are sometimes patentable. For example, in Diamond v. Diehr, the application of a simple feedback algorithm to aid in the curing of synthetic rubber was deemed patentable. The patenting of software is highly controversial, and there are highly criticized patents involving algorithms, especially data compression algorithms, such as Unisys’ LZW patent.
Additionally, some cryptographic algorithms have export restrictions (see export of cryptography).
History: Development of the notion of «algorithm»[edit]
Ancient Near East[edit]
The earliest evidence of algorithms is found in the Babylonian mathematics of ancient Mesopotamia (modern Iraq). A Sumerian clay tablet found in Shuruppak near Baghdad and dated to c. 2500 BC described the earliest division algorithm.[11] During the Hammurabi dynasty c. 1800 – c. 1600 BC, Babylonian clay tablets described algorithms for computing formulas.[85] Algorithms were also used in Babylonian astronomy. Babylonian clay tablets describe and employ algorithmic procedures to compute the time and place of significant astronomical events.[86]
Algorithms for arithmetic are also found in ancient Egyptian mathematics, dating back to the Rhind Mathematical Papyrus c. 1550 BC.[11] Algorithms were later used in ancient Hellenistic mathematics. Two examples are the Sieve of Eratosthenes, which was described in the Introduction to Arithmetic by Nicomachus,[87][14]: Ch 9.2 and the Euclidean algorithm, which was first described in Euclid’s Elements (c. 300 BC).[14]: Ch 9.1
Discrete and distinguishable symbols[edit]
Tally-marks: To keep track of their flocks, their sacks of grain and their money the ancients used tallying: accumulating stones or marks scratched on sticks or making discrete symbols in clay. Through the Babylonian and Egyptian use of marks and symbols, eventually Roman numerals and the abacus evolved (Dilson, p. 16–41). Tally marks appear prominently in unary numeral system arithmetic used in Turing machine and Post–Turing machine computations.
Manipulation of symbols as «place holders» for numbers: algebra[edit]
Muhammad ibn Mūsā al-Khwārizmī, a Persian mathematician, wrote the Al-jabr in the 9th century. The terms «algorism» and «algorithm» are derived from the name al-Khwārizmī, while the term «algebra» is derived from the book Al-jabr. In Europe, the word «algorithm» was originally used to refer to the sets of rules and techniques used by Al-Khwarizmi to solve algebraic equations, before later being generalized to refer to any set of rules or techniques.[88] This eventually culminated in Leibniz’s notion of the calculus ratiocinator (c. 1680):
A good century and a half ahead of his time, Leibniz proposed an algebra of logic, an algebra that would specify the rules for manipulating logical concepts in the manner that ordinary algebra specifies the rules for manipulating numbers.[89]
Cryptographic algorithms[edit]
The first cryptographic algorithm for deciphering encrypted code was developed by Al-Kindi, a 9th-century Arab mathematician, in A Manuscript On Deciphering Cryptographic Messages. He gave the first description of cryptanalysis by frequency analysis, the earliest codebreaking algorithm.[15]
Mechanical contrivances with discrete states[edit]
The clock: Bolter credits the invention of the weight-driven clock as «The key invention [of Europe in the Middle Ages]», in particular, the verge escapement[90] that provides us with the tick and tock of a mechanical clock. «The accurate automatic machine»[91] led immediately to «mechanical automata» beginning in the 13th century and finally to «computational machines»—the difference engine and analytical engines of Charles Babbage and Countess Ada Lovelace, mid-19th century.[92] Lovelace is credited with the first creation of an algorithm intended for processing on a computer—Babbage’s analytical engine, the first device considered a real Turing-complete computer instead of just a calculator—and is sometimes called «history’s first programmer» as a result, though a full implementation of Babbage’s second device would not be realized until decades after her lifetime.
Logical machines 1870 – Stanley Jevons’ «logical abacus» and «logical machine»: The technical problem was to reduce Boolean equations when presented in a form similar to what is now known as Karnaugh maps. Jevons (1880) describes first a simple «abacus» of «slips of wood furnished with pins, contrived so that any part or class of the [logical] combinations can be picked out mechanically … More recently, however, I have reduced the system to a completely mechanical form, and have thus embodied the whole of the indirect process of inference in what may be called a Logical Machine» His machine came equipped with «certain moveable wooden rods» and «at the foot are 21 keys like those of a piano [etc.] …». With this machine he could analyze a «syllogism or any other simple logical argument».[93]
This machine he displayed in 1870 before the Fellows of the Royal Society.[94] Another logician John Venn, however, in his 1881 Symbolic Logic, turned a jaundiced eye to this effort: «I have no high estimate myself of the interest or importance of what are sometimes called logical machines … it does not seem to me that any contrivances at present known or likely to be discovered really deserve the name of logical machines»; see more at Algorithm characterizations. But not to be outdone he too presented «a plan somewhat analogous, I apprehend, to Prof. Jevon’s abacus … [And] [a]gain, corresponding to Prof. Jevons’s logical machine, the following contrivance may be described. I prefer to call it merely a logical-diagram machine … but I suppose that it could do very completely all that can be rationally expected of any logical machine».[95]
Jacquard loom, Hollerith punch cards, telegraphy and telephony – the electromechanical relay: Bell and Newell (1971) indicate that the Jacquard loom (1801), precursor to Hollerith cards (punch cards, 1887), and «telephone switching technologies» were the roots of a tree leading to the development of the first computers.[96] By the mid-19th century the telegraph, the precursor of the telephone, was in use throughout the world, its discrete and distinguishable encoding of letters as «dots and dashes» a common sound. By the late 19th century the ticker tape (c. 1870s) was in use, as was the use of Hollerith cards in the 1890 U.S. census. Then came the teleprinter (c. 1910) with its punched-paper use of Baudot code on tape.
Telephone-switching networks of electromechanical relays (invented 1835) was behind the work of George Stibitz (1937), the inventor of the digital adding device. As he worked in Bell Laboratories, he observed the «burdensome’ use of mechanical calculators with gears. «He went home one evening in 1937 intending to test his idea… When the tinkering was over, Stibitz had constructed a binary adding device».[97]
The mathematician Martin Davis observes the particular importance of the electromechanical relay (with its two «binary states» open and closed):
- It was only with the development, beginning in the 1930s, of electromechanical calculators using electrical relays, that machines were built having the scope Babbage had envisioned.»[98]
Mathematics during the 19th century up to the mid-20th century[edit]
Symbols and rules: In rapid succession, the mathematics of George Boole (1847, 1854), Gottlob Frege (1879), and Giuseppe Peano (1888–1889) reduced arithmetic to a sequence of symbols manipulated by rules. Peano’s The principles of arithmetic, presented by a new method (1888) was «the first attempt at an axiomatization of mathematics in a symbolic language».[99]
But Heijenoort gives Frege (1879) this kudos: Frege’s is «perhaps the most important single work ever written in logic. … in which we see a «‘formula language’, that is a lingua characterica, a language written with special symbols, «for pure thought», that is, free from rhetorical embellishments … constructed from specific symbols that are manipulated according to definite rules».[100] The work of Frege was further simplified and amplified by Alfred North Whitehead and Bertrand Russell in their Principia Mathematica (1910–1913).
The paradoxes: At the same time a number of disturbing paradoxes appeared in the literature, in particular, the Burali-Forti paradox (1897), the Russell paradox (1902–03), and the Richard Paradox.[101] The resultant considerations led to Kurt Gödel’s paper (1931)—he specifically cites the paradox of the liar—that completely reduces rules of recursion to numbers.
Effective calculability: In an effort to solve the Entscheidungsproblem defined precisely by Hilbert in 1928, mathematicians first set about to define what was meant by an «effective method» or «effective calculation» or «effective calculability» (i.e., a calculation that would succeed). In rapid succession the following appeared: Alonzo Church, Stephen Kleene and J.B. Rosser’s λ-calculus[102] a finely honed definition of «general recursion» from the work of Gödel acting on suggestions of Jacques Herbrand (cf. Gödel’s Princeton lectures of 1934) and subsequent simplifications by Kleene.[103] Church’s proof[104] that the Entscheidungsproblem was unsolvable, Emil Post’s definition of effective calculability as a worker mindlessly following a list of instructions to move left or right through a sequence of rooms and while there either mark or erase a paper or observe the paper and make a yes-no decision about the next instruction.[105] Alan Turing’s proof of that the Entscheidungsproblem was unsolvable by use of his «a- [automatic-] machine»[106]—in effect almost identical to Post’s «formulation», J. Barkley Rosser’s definition of «effective method» in terms of «a machine».[107] Kleene’s proposal of a precursor to «Church thesis» that he called «Thesis I»,[108] and a few years later Kleene’s renaming his Thesis «Church’s Thesis»[109] and proposing «Turing’s Thesis».[110]
Emil Post (1936) and Alan Turing (1936–37, 1939)[edit]
Emil Post (1936) described the actions of a «computer» (human being) as follows:
- «…two concepts are involved: that of a symbol space in which the work leading from problem to answer is to be carried out, and a fixed unalterable set of directions.
His symbol space would be
- «a two-way infinite sequence of spaces or boxes … The problem solver or worker is to move and work in this symbol space, being capable of being in, and operating in but one box at a time. … a box is to admit of but two possible conditions, i.e., being empty or unmarked, and having a single mark in it, say a vertical stroke.
- «One box is to be singled out and called the starting point. … a specific problem is to be given in symbolic form by a finite number of boxes [i.e., INPUT] being marked with a stroke. Likewise, the answer [i.e., OUTPUT] is to be given in symbolic form by such a configuration of marked boxes…
- «A set of directions applicable to a general problem sets up a deterministic process when applied to each specific problem. This process terminates only when it comes to the direction of type (C ) [i.e., STOP]».[111] See more at Post–Turing machine
Alan Turing’s work[112] preceded that of Stibitz (1937); it is unknown whether Stibitz knew of the work of Turing. Turing’s biographer believed that Turing’s use of a typewriter-like model derived from a youthful interest: «Alan had dreamt of inventing typewriters as a boy; Mrs. Turing had a typewriter, and he could well have begun by asking himself what was meant by calling a typewriter ‘mechanical‘«.[113] Given the prevalence at the time of Morse code, telegraphy, ticker tape machines, and teletypewriters, it is quite possible that all were influences on Turing during his youth.
Turing—his model of computation is now called a Turing machine—begins, as did Post, with an analysis of a human computer that he whittles down to a simple set of basic motions and «states of mind». But he continues a step further and creates a machine as a model of computation of numbers.[114]
- «Computing is normally done by writing certain symbols on paper. We may suppose this paper is divided into squares like a child’s arithmetic book…I assume then that the computation is carried out on one-dimensional paper, i.e., on a tape divided into squares. I shall also suppose that the number of symbols which may be printed is finite…
- «The behavior of the computer at any moment is determined by the symbols which he is observing, and his «state of mind» at that moment. We may suppose that there is a bound B to the number of symbols or squares that the computer can observe at one moment. If he wishes to observe more, he must use successive observations. We will also suppose that the number of states of mind which need be taken into account is finite…
- «Let us imagine that the operations performed by the computer to be split up into ‘simple operations’ which are so elementary that it is not easy to imagine them further divided.»[115]
Turing’s reduction yields the following:
- «The simple operations must therefore include:
- «(a) Changes of the symbol on one of the observed squares
- «(b) Changes of one of the squares observed to another square within L squares of one of the previously observed squares.
«It may be that some of these change necessarily invoke a change of state of mind. The most general single operation must, therefore, be taken to be one of the following:
-
- «(A) A possible change (a) of symbol together with a possible change of state of mind.
- «(B) A possible change (b) of observed squares, together with a possible change of state of mind»
- «We may now construct a machine to do the work of this computer.»[115]
A few years later, Turing expanded his analysis (thesis, definition) with this forceful expression of it:
- «A function is said to be «effectively calculable» if its values can be found by some purely mechanical process. Though it is fairly easy to get an intuitive grasp of this idea, it is nevertheless desirable to have some more definite, mathematical expressible definition … [he discusses the history of the definition pretty much as presented above with respect to Gödel, Herbrand, Kleene, Church, Turing, and Post] … We may take this statement literally, understanding by a purely mechanical process one which could be carried out by a machine. It is possible to give a mathematical description, in a certain normal form, of the structures of these machines. The development of these ideas leads to the author’s definition of a computable function, and to an identification of computability † with effective calculability…
- «† We shall use the expression «computable function» to mean a function calculable by a machine, and we let «effectively calculable» refer to the intuitive idea without particular identification with any one of these definitions».[116]
J. B. Rosser (1939) and S. C. Kleene (1943)[edit]
J. Barkley Rosser defined an «effective [mathematical] method» in the following manner (italicization added):
- «‘Effective method’ is used here in the rather special sense of a method each step of which is precisely determined and which is certain to produce the answer in a finite number of steps. With this special meaning, three different precise definitions have been given to date. [his footnote #5; see discussion immediately below]. The simplest of these to state (due to Post and Turing) says essentially that an effective method of solving certain sets of problems exists if one can build a machine which will then solve any problem of the set with no human intervention beyond inserting the question and (later) reading the answer. All three definitions are equivalent, so it doesn’t matter which one is used. Moreover, the fact that all three are equivalent is a very strong argument for the correctness of any one.» (Rosser 1939:225–226)
Rosser’s footnote No. 5 references the work of (1) Church and Kleene and their definition of λ-definability, in particular, Church’s use of it in his An Unsolvable Problem of Elementary Number Theory (1936); (2) Herbrand and Gödel and their use of recursion, in particular, Gödel’s use in his famous paper On Formally Undecidable Propositions of Principia Mathematica and Related Systems I (1931); and (3) Post (1936) and Turing (1936–37) in their mechanism-models of computation.
Stephen C. Kleene defined as his now-famous «Thesis I» known as the Church–Turing thesis. But he did this in the following context (boldface in original):
- «12. Algorithmic theories… In setting up a complete algorithmic theory, what we do is to describe a procedure, performable for each set of values of the independent variables, which procedure necessarily terminates and in such manner that from the outcome we can read a definite answer, «yes» or «no,» to the question, «is the predicate value true?»» (Kleene 1943:273)
History after 1950[edit]
A number of efforts have been directed toward further refinement of the definition of «algorithm», and activity is on-going because of issues surrounding, in particular, foundations of mathematics (especially the Church–Turing thesis) and philosophy of mind (especially arguments about artificial intelligence). For more, see Algorithm characterizations.
See also[edit]
- Abstract machine
- ALGOL
- Algorithm engineering
- Algorithm characterizations
- Algorithmic bias
- Algorithmic composition
- Algorithmic entities
- Algorithmic synthesis
- Algorithmic technique
- Algorithmic topology
- Garbage in, garbage out
- Introduction to Algorithms (textbook)
- Government by algorithm
- List of algorithms
- List of algorithm general topics
- Regulation of algorithms
- Theory of computation
- Computability theory
- Computational complexity theory
- Computational mathematics
Notes[edit]
- ^ «Definition of ALGORITHM». Merriam-Webster Online Dictionary. Archived from the original on February 14, 2020. Retrieved November 14, 2019.
- ^ Blair, Ann, Duguid, Paul, Goeing, Anja-Silvia and Grafton, Anthony. Information: A Historical Companion, Princeton: Princeton University Press, 2021. p. 247
- ^ David A. Grossman, Ophir Frieder, Information Retrieval: Algorithms and Heuristics, 2nd edition, 2004, ISBN 1402030045
- ^ «Any classical mathematical algorithm, for example, can be described in a finite number of English words» (Rogers 1987:2).
- ^ Well defined with respect to the agent that executes the algorithm: «There is a computing agent, usually human, which can react to the instructions and carry out the computations» (Rogers 1987:2).
- ^ «an algorithm is a procedure for computing a function (with respect to some chosen notation for integers) … this limitation (to numerical functions) results in no loss of generality», (Rogers 1987:1).
- ^ «An algorithm has zero or more inputs, i.e., quantities which are given to it initially before the algorithm begins» (Knuth 1973:5).
- ^ «A procedure which has all the characteristics of an algorithm except that it possibly lacks finiteness may be called a ‘computational method‘» (Knuth 1973:5).
- ^ «An algorithm has one or more outputs, i.e. quantities which have a specified relation to the inputs» (Knuth 1973:5).
- ^ Whether or not a process with random interior processes (not including the input) is an algorithm is debatable. Rogers opines that: «a computation is carried out in a discrete stepwise fashion, without the use of continuous methods or analogue devices … carried forward deterministically, without resort to random methods or devices, e.g., dice» (Rogers 1987:2).
- ^ a b c d Chabert, Jean-Luc (2012). A History of Algorithms: From the Pebble to the Microchip. Springer Science & Business Media. pp. 7–8. ISBN 9783642181924.
- ^ Sriram, M. S. (2005). «Algorithms in Indian Mathematics». In Emch, Gerard G.; Sridharan, R.; Srinivas, M. D. (eds.). Contributions to the History of Indian Mathematics. Springer. p. 153. ISBN 978-93-86279-25-5.
- ^ Hayashi, T. (2023, January 1). Brahmagupta. Encyclopedia Britannica. https://www.britannica.com/biography/Brahmagupta
- ^ a b c Cooke, Roger L. (2005). The History of Mathematics: A Brief Course. John Wiley & Sons. ISBN 978-1-118-46029-0.
- ^ a b Dooley, John F. (2013). A Brief History of Cryptology and Cryptographic Algorithms. Springer Science & Business Media. pp. 12–3. ISBN 9783319016283.
- ^ Burnett, Charles (2017). «Arabic Numerals». In Thomas F. Glick (ed.). Routledge Revivals: Medieval Science, Technology and Medicine (2006): An Encyclopedia. Taylor & Francis. p. 39. ISBN 978-1-351-67617-5. Archived from the original on March 28, 2023. Retrieved May 5, 2019.
- ^ «algorism». Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ Brezina, Corona (2006). Al-Khwarizmi: The Inventor Of Algebra. The Rosen Publishing Group. ISBN 978-1-4042-0513-0.
- ^ «Abu Jafar Muhammad ibn Musa al-Khwarizmi». members.peak.org. Archived from the original on August 21, 2019. Retrieved November 14, 2019.
- ^ Mehri, Bahman (2017). «From Al-Khwarizmi to Algorithm». Olympiads in Informatics. 11 (2): 71–74. doi:10.15388/ioi.2017.special.11.
- ^ «algorismic». The Free Dictionary. Archived from the original on December 21, 2019. Retrieved November 14, 2019.
- ^ Blount, Thomas (1656). Glossographia or a Dictionary… London: Humphrey Moseley and George Sawbridge.
- ^ Phillips, Edward (1658). The new world of English words, or, A general dictionary containing the interpretations of such hard words as are derived from other languages…
- ^ Phillips, Edward; Kersey, John (1706). The new world of words: or, Universal English dictionary. Containing an account of the original or proper sense, and various significations of all hard words derived from other languages … Together with a brief and plain explication of all terms relating to any of the arts and sciences … to which is added, the interpretation of proper names. Printed for J. Phillips etc.
- ^ Fenning, Daniel (1751). The young algebraist’s companion, or, A new & easy guide to algebra; introduced by the doctrine of vulgar fractions: designed for the use of schools … illustrated with variety of numerical & literal examples … Printed for G. Keith & J. Robinson. p. xi.
- ^ The Electric Review 1811-07: Vol 7. Open Court Publishing Co. July 1811. p. [1].
Yet it wants a new algorithm, a compendious method by which the theorems may be established without ambiguity and circumlocution, […]
- ^ «algorithm». Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ Already 1684, in Nova Methodus pro Maximis et Minimis, Leibnitz used the Latin term «algorithmo».
- ^ Kleene 1943 in Davis 1965:274
- ^ Rosser 1939 in Davis 1965:225
- ^ Stone 1973:4
- ^
Simanowski, Roberto (2018). The Death Algorithm and Other Digital Dilemmas. Untimely Meditations. Vol. 14. Translated by Chase, Jefferson. Cambridge, Massachusetts: MIT Press. p. 147. ISBN 9780262536370. Archived from the original on December 22, 2019. Retrieved May 27, 2019.[…] the next level of abstraction of central bureaucracy: globally operating algorithms.
- ^
Dietrich, Eric (1999). «Algorithm». In Wilson, Robert Andrew; Keil, Frank C. (eds.). The MIT Encyclopedia of the Cognitive Sciences. MIT Cognet library. Cambridge, Massachusetts: MIT Press (published 2001). p. 11. ISBN 9780262731447. Retrieved July 22, 2020.An algorithm is a recipe, method, or technique for doing something.
- ^ Stone requires that «it must terminate in a finite number of steps» (Stone 1973:7–8).
- ^ Boolos and Jeffrey 1974,1999:19
- ^ cf Stone 1972:5
- ^ Knuth 1973:7 states: «In practice, we not only want algorithms, but we also want good algorithms … one criterion of goodness is the length of time taken to perform the algorithm … other criteria are the adaptability of the algorithm to computers, its simplicity, and elegance, etc.»
- ^ cf Stone 1973:6
- ^
Stone 1973:7–8 states that there must be, «…a procedure that a robot [i.e., computer] can follow in order to determine precisely how to obey the instruction». Stone adds finiteness of the process, and definiteness (having no ambiguity in the instructions) to this definition. - ^ Knuth, loc. cit
- ^ Minsky 1967, p. 105
- ^ Gurevich 2000:1, 3
- ^ Sipser 2006:157
- ^ Goodrich, Michael T.; Tamassia, Roberto (2002). Algorithm Design: Foundations, Analysis, and Internet Examples. John Wiley & Sons, Inc. ISBN 978-0-471-38365-9. Archived from the original on April 28, 2015. Retrieved June 14, 2018.
- ^ Knuth 1973:7
- ^ Chaitin 2005:32
- ^ Rogers 1987:1–2
- ^ In his essay «Calculations by Man and Machine: Conceptual Analysis» Seig 2002:390 credits this distinction to Robin Gandy, cf Wilfred Seig, et al., 2002 Reflections on the foundations of mathematics: Essays in honor of Solomon Feferman, Association for Symbolic Logic, A.K. Peters Ltd, Natick, MA.
- ^ cf Gandy 1980:126, Robin Gandy Church’s Thesis and Principles for Mechanisms appearing on pp. 123–148 in J. Barwise et al. 1980 The Kleene Symposium, North-Holland Publishing Company.
- ^ A «robot»: «A computer is a robot that performs any task that can be described as a sequence of instructions.» cf Stone 1972:3
- ^ Lambek’s «abacus» is a «countably infinite number of locations (holes, wires, etc.) together with an unlimited supply of counters (pebbles, beads, etc.). The locations are distinguishable, the counters are not». The holes have unlimited capacity, and standing by is an agent who understands and is able to carry out the list of instructions» (Lambek 1961:295). Lambek references Melzak who defines his Q-machine as «an indefinitely large number of locations … an indefinitely large supply of counters distributed among these locations, a program, and an operator whose sole purpose is to carry out the program» (Melzak 1961:283). B-B-J (loc. cit.) add the stipulation that the holes are «capable of holding any number of stones» (p. 46). Both Melzak and Lambek appear in The Canadian Mathematical Bulletin, vol. 4, no. 3, September 1961.
- ^ If no confusion results, the word «counters» can be dropped, and a location can be said to contain a single «number».
- ^ «We say that an instruction is effective if there is a procedure that the robot can follow in order to determine precisely how to obey the instruction.» (Stone 1972:6)
- ^ cf Minsky 1967: Chapter 11 «Computer models» and Chapter 14 «Very Simple Bases for Computability» pp. 255–281, in particular,
- ^ cf Knuth 1973:3.
- ^ But always preceded by IF-THEN to avoid improper subtraction.
- ^ Knuth 1973:4
- ^ Stone 1972:5. Methods for extracting roots are not trivial: see Methods of computing square roots.
- ^ Leeuwen, Jan (1990). Handbook of Theoretical Computer Science: Algorithms and complexity. Volume A. Elsevier. p. 85. ISBN 978-0-444-88071-0.
- ^ John G. Kemeny and Thomas E. Kurtz 1985 Back to Basic: The History, Corruption, and Future of the Language, Addison-Wesley Publishing Company, Inc. Reading, MA, ISBN 0-201-13433-0.
- ^ Tausworthe 1977:101
- ^ Tausworthe 1977:142
- ^ Knuth 1973 section 1.2.1, expanded by Tausworthe 1977 at pages 100ff and Chapter 9.1
- ^ cf Tausworthe 1977
- ^ Heath 1908:300; Hawking’s Dover 2005 edition derives from Heath.
- ^ » ‘Let CD, measuring BF, leave FA less than itself.’ This is a neat abbreviation for saying, measure along BA successive lengths equal to CD until a point F is reached such that the length FA remaining is less than CD; in other words, let BF be the largest exact multiple of CD contained in BA» (Heath 1908:297)
- ^ For modern treatments using division in the algorithm, see Hardy and Wright 1979:180, Knuth 1973:2 (Volume 1), plus more discussion of Euclid’s algorithm in Knuth 1969:293–297 (Volume 2).
- ^ Euclid covers this question in his Proposition 1.
- ^ «Euclid’s Elements, Book VII, Proposition 2». Aleph0.clarku.edu. Archived from the original on May 24, 2012. Retrieved May 20, 2012.
- ^ While this notion is in widespread use, it cannot be defined precisely.
- ^ Knuth 1973:13–18. He credits «the formulation of algorithm-proving in terms of assertions and induction» to R W. Floyd, Peter Naur, C.A.R. Hoare, H.H. Goldstine and J. von Neumann. Tausworth 1977 borrows Knuth’s Euclid example and extends Knuth’s method in section 9.1 Formal Proofs (pp. 288–298).
- ^ Tausworthe 1997:294
- ^ cf Knuth 1973:7 (Vol. I), and his more-detailed analyses on pp. 1969:294–313 (Vol II).
- ^ Breakdown occurs when an algorithm tries to compact itself. Success would solve the Halting problem.
- ^ Kriegel, Hans-Peter; Schubert, Erich; Zimek, Arthur (2016). «The (black) art of run-time evaluation: Are we comparing algorithms or implementations?». Knowledge and Information Systems. 52 (2): 341–378. doi:10.1007/s10115-016-1004-2. ISSN 0219-1377. S2CID 40772241.
- ^ Gillian Conahan (January 2013). «Better Math Makes Faster Data Networks». discovermagazine.com. Archived from the original on May 13, 2014. Retrieved May 13, 2014.
- ^ Haitham Hassanieh, Piotr Indyk, Dina Katabi, and Eric Price, «ACM-SIAM Symposium On Discrete Algorithms (SODA) Archived July 4, 2013, at the Wayback Machine, Kyoto, January 2012. See also the sFFT Web Page Archived February 21, 2012, at the Wayback Machine.
- ^ Kellerer, Hans; Pferschy, Ulrich; Pisinger, David (2004). Knapsack Problems | Hans Kellerer | Springer. Springer. doi:10.1007/978-3-540-24777-7. ISBN 978-3-540-40286-2. S2CID 28836720. Archived from the original on October 18, 2017. Retrieved September 19, 2017.
- ^ For instance, the volume of a convex polytope (described using a membership oracle) can be approximated to high accuracy by a randomized polynomial time algorithm, but not by a deterministic one: see Dyer, Martin; Frieze, Alan; Kannan, Ravi (January 1991). «A Random Polynomial-time Algorithm for Approximating the Volume of Convex Bodies». J. ACM. 38 (1): 1–17. CiteSeerX 10.1.1.145.4600. doi:10.1145/102782.102783. S2CID 13268711.
- ^
George B. Dantzig and Mukund N. Thapa. 2003. Linear Programming 2: Theory and Extensions. Springer-Verlag. - ^ Tsypkin (1971). Adaptation and learning in automatic systems. Academic Press. p. 54. ISBN 978-0-08-095582-7.
- ^ a b Kowalski, Robert (1979). «Algorithm=Logic+Control». Communications of the ACM. 22 (7): 424–436. doi:10.1145/359131.359136. S2CID 2509896.
- ^ a b Warren, D.S., 2023. Writing correct prolog programs. In Prolog: The Next 50 Years (pp. 62-70). Cham: Springer Nature Switzerland.
- ^ Kowalski, R., Dávila, J., Sartor, G. and Calejo, M., 2023. Logical English for law and education. In Prolog: The Next 50 Years (pp. 287–299). Cham: Springer Nature Switzerland.
- ^ Knuth, Donald E. (1972). «Ancient Babylonian Algorithms» (PDF). Commun. ACM. 15 (7): 671–677. doi:10.1145/361454.361514. ISSN 0001-0782. S2CID 7829945. Archived from the original (PDF) on December 24, 2012.
- ^ Aaboe, Asger (2001). Episodes from the Early History of Astronomy. New York: Springer. pp. 40–62. ISBN 978-0-387-95136-2.
- ^ Ast, Courtney. «Eratosthenes». Wichita State University: Department of Mathematics and Statistics. Archived from the original on February 27, 2015. Retrieved February 27, 2015.
- ^ Chabert, Jean-Luc (2012). A History of Algorithms: From the Pebble to the Microchip. Springer Science & Business Media. p. 2. ISBN 9783642181924.
- ^ Davis 2000:18
- ^ Bolter 1984:24
- ^ Bolter 1984:26
- ^ Bolter 1984:33–34, 204–206.
- ^ All quotes from W. Stanley Jevons 1880 Elementary Lessons in Logic: Deductive and Inductive, Macmillan and Co., London and New York. Republished as a googlebook; cf Jevons 1880:199–201. Louis Couturat 1914 the Algebra of Logic, The Open Court Publishing Company, Chicago and London. Republished as a googlebook; cf Couturat 1914 in:75–76 gives a few more details; he compares this to a typewriter as well as a piano. Jevons states that the account is to be found at January 20, 1870 The Proceedings of the Royal Society.
- ^ Jevons 1880:199–200
- ^ All quotes from John Venn 1881 Symbolic Logic, Macmillan and Co., London. Republished as a googlebook. cf Venn 1881:120–125. The interested reader can find a deeper explanation in those pages.
- ^ Bell and Newell diagram 1971:39, cf. Davis 2000
- ^ * Melina Hill, Valley News Correspondent, A Tinkerer Gets a Place in History, Valley News West Lebanon NH, Thursday, March 31, 1983, p. 13.
- ^ Davis 2000:14
- ^ van Heijenoort 1967:81ff
- ^ van Heijenoort’s commentary on Frege’s Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought in van Heijenoort 1967:1
- ^ Dixon 1906, cf. Kleene 1952:36–40
- ^ cf. footnote in Alonzo Church 1936a in Davis 1965:90 and 1936b in Davis 1965:110
- ^ Kleene 1935–6 in Davis 1965:237ff, Kleene 1943 in Davis 1965:255ff
- ^ Church 1936 in Davis 1965:88ff
- ^ cf. «Finite Combinatory Processes – formulation 1», Post 1936 in Davis 1965:289–290
- ^ Turing 1936–37 in Davis 1965:116ff
- ^ Rosser 1939 in Davis 1965:226
- ^ Kleene 1943 in Davis 1965:273–274
- ^ Kleene 1952:300, 317
- ^ Kleene 1952:376
- ^ Turing 1936–37 in Davis 1965:289–290
- ^ Turing 1936 in Davis 1965, Turing 1939 in Davis 1965:160
- ^ Hodges, p. 96
- ^ Turing 1936–37:116
- ^ a b Turing 1936–37 in Davis 1965:136
- ^ Turing 1939 in Davis 1965:160
Bibliography[edit]
- Axt, P (1959). «On a Subrecursive Hierarchy and Primitive Recursive Degrees». Transactions of the American Mathematical Society. 92 (1): 85–105. doi:10.2307/1993169. JSTOR 1993169.
- Bell, C. Gordon and Newell, Allen (1971), Computer Structures: Readings and Examples, McGraw–Hill Book Company, New York. ISBN 0-07-004357-4.
- Blass, Andreas; Gurevich, Yuri (2003). «Algorithms: A Quest for Absolute Definitions» (PDF). Bulletin of European Association for Theoretical Computer Science. 81. Archived (PDF) from the original on October 9, 2022. Includes a bibliography of 56 references.
- Bolter, David J. (1984). Turing’s Man: Western Culture in the Computer Age (1984 ed.). Chapel Hill, NC: The University of North Carolina Press. ISBN 978-0-8078-1564-9., ISBN 0-8078-4108-0
- Boolos, George; Jeffrey, Richard (1999) [1974]. Computability and Logic (4th ed.). Cambridge University Press, London. ISBN 978-0-521-20402-6.: cf. Chapter 3 Turing machines where they discuss «certain enumerable sets not effectively (mechanically) enumerable».
- Burgin, Mark (2004). Super-Recursive Algorithms. Springer. ISBN 978-0-387-95569-8.
- Campagnolo, M.L., Moore, C., and Costa, J.F. (2000) An analog characterization of the subrecursive functions. In Proc. of the 4th Conference on Real Numbers and Computers, Odense University, pp. 91–109
- Church, Alonzo (1936). «An Unsolvable Problem of Elementary Number Theory». The American Journal of Mathematics. 58 (2): 345–363. doi:10.2307/2371045. JSTOR 2371045. Reprinted in The Undecidable, p. 89ff. The first expression of «Church’s Thesis». See in particular page 100 (The Undecidable) where he defines the notion of «effective calculability» in terms of «an algorithm», and he uses the word «terminates», etc.
- Church, Alonzo (1936). «A Note on the Entscheidungsproblem». The Journal of Symbolic Logic. 1 (1): 40–41. doi:10.2307/2269326. JSTOR 2269326. S2CID 42323521. Church, Alonzo (1936). «Correction to a Note on the Entscheidungsproblem». The Journal of Symbolic Logic. 1 (3): 101–102. doi:10.2307/2269030. JSTOR 2269030. S2CID 5557237. Reprinted in The Undecidable, p. 110ff. Church shows that the Entscheidungsproblem is unsolvable in about 3 pages of text and 3 pages of footnotes.
- Daffa’, Ali Abdullah al- (1977). The Muslim contribution to mathematics. London: Croom Helm. ISBN 978-0-85664-464-1.
- Davis, Martin (1965). The Undecidable: Basic Papers On Undecidable Propositions, Unsolvable Problems and Computable Functions. New York: Raven Press. ISBN 978-0-486-43228-1. Davis gives commentary before each article. Papers of Gödel, Alonzo Church, Turing, Rosser, Kleene, and Emil Post are included; those cited in the article are listed here by author’s name.
- Davis, Martin (2000). Engines of Logic: Mathematicians and the Origin of the Computer. New York: W.W. Nortion. ISBN 978-0-393-32229-3. Davis offers concise biographies of Leibniz, Boole, Frege, Cantor, Hilbert, Gödel and Turing with von Neumann as the show-stealing villain. Very brief bios of Joseph-Marie Jacquard, Babbage, Ada Lovelace, Claude Shannon, Howard Aiken, etc.
This article incorporates public domain material from Paul E. Black. «algorithm». Dictionary of Algorithms and Data Structures. NIST.
- Dean, Tim (2012). «Evolution and moral diversity». Baltic International Yearbook of Cognition, Logic and Communication. 7. doi:10.4148/biyclc.v7i0.1775.
- Dennett, Daniel (1995). Darwin’s Dangerous Idea. pp. 32–36. Bibcode:1996Cmplx…2a..32M. doi:10.1002/(SICI)1099-0526(199609/10)2:1<32::AID-CPLX8>3.0.CO;2-H. ISBN 978-0-684-80290-9.
- Dilson, Jesse (2007). The Abacus ((1968, 1994) ed.). St. Martin’s Press, NY. ISBN 978-0-312-10409-2., ISBN 0-312-10409-X
- Yuri Gurevich, Sequential Abstract State Machines Capture Sequential Algorithms, ACM Transactions on Computational Logic, Vol 1, no 1 (July 2000), pp. 77–111. Includes bibliography of 33 sources.
- van Heijenoort, Jean (2001). From Frege to Gödel, A Source Book in Mathematical Logic, 1879–1931 ((1967) ed.). Harvard University Press, Cambridge. ISBN 978-0-674-32449-7., 3rd edition 1976[?], ISBN 0-674-32449-8 (pbk.)
- Hodges, Andrew (1983). Alan Turing: The Enigma. pp. 107–108. Bibcode:1984PhT….37k.107H. doi:10.1063/1.2915935. ISBN 978-0-671-49207-6. , ISBN 0-671-49207-1. Cf. Chapter «The Spirit of Truth» for a history leading to, and a discussion of, his proof.
- Kleene, Stephen C. (1936). «General Recursive Functions of Natural Numbers». Mathematische Annalen. 112 (5): 727–742. doi:10.1007/BF01565439. S2CID 120517999. Archived from the original on September 3, 2014. Retrieved September 30, 2013. Presented to the American Mathematical Society, September 1935. Reprinted in The Undecidable, p. 237ff. Kleene’s definition of «general recursion» (known now as mu-recursion) was used by Church in his 1935 paper An Unsolvable Problem of Elementary Number Theory that proved the «decision problem» to be «undecidable» (i.e., a negative result).
- Kleene, Stephen C. (1943). «Recursive Predicates and Quantifiers». Transactions of the American Mathematical Society. 53 (1): 41–73. doi:10.2307/1990131. JSTOR 1990131. Reprinted in The Undecidable, p. 255ff. Kleene refined his definition of «general recursion» and proceeded in his chapter «12. Algorithmic theories» to posit «Thesis I» (p. 274); he would later repeat this thesis (in Kleene 1952:300) and name it «Church’s Thesis»(Kleene 1952:317) (i.e., the Church thesis).
- Kleene, Stephen C. (1991) [1952]. Introduction to Metamathematics (Tenth ed.). North-Holland Publishing Company. ISBN 978-0-7204-2103-3.
- Knuth, Donald (1997). Fundamental Algorithms, Third Edition. Reading, Massachusetts: Addison–Wesley. ISBN 978-0-201-89683-1.
- Knuth, Donald (1969). Volume 2/Seminumerical Algorithms, The Art of Computer Programming First Edition. Reading, Massachusetts: Addison–Wesley.
- Kosovsky, N.K. Elements of Mathematical Logic and its Application to the theory of Subrecursive Algorithms, LSU Publ., Leningrad, 1981
- Kowalski, Robert (1979). «Algorithm=Logic+Control». Communications of the ACM. 22 (7): 424–436. doi:10.1145/359131.359136. S2CID 2509896.
- A.A. Markov (1954) Theory of algorithms. [Translated by Jacques J. Schorr-Kon and PST staff] Imprint Moscow, Academy of Sciences of the USSR, 1954 [i.e., Jerusalem, Israel Program for Scientific Translations, 1961; available from the Office of Technical Services, U.S. Dept. of Commerce, Washington] Description 444 p. 28 cm. Added t.p. in Russian Translation of Works of the Mathematical Institute, Academy of Sciences of the USSR, v. 42. Original title: Teoriya algerifmov. [QA248.M2943 Dartmouth College library. U.S. Dept. of Commerce, Office of Technical Services, number OTS 60-51085.]
- Minsky, Marvin (1967). Computation: Finite and Infinite Machines (First ed.). Prentice-Hall, Englewood Cliffs, NJ. ISBN 978-0-13-165449-5. Minsky expands his «…idea of an algorithm – an effective procedure…» in chapter 5.1 Computability, Effective Procedures and Algorithms. Infinite machines.
- Post, Emil (1936). «Finite Combinatory Processes, Formulation I». The Journal of Symbolic Logic. 1 (3): 103–105. doi:10.2307/2269031. JSTOR 2269031. S2CID 40284503. Reprinted in The Undecidable, pp. 289ff. Post defines a simple algorithmic-like process of a man writing marks or erasing marks and going from box to box and eventually halting, as he follows a list of simple instructions. This is cited by Kleene as one source of his «Thesis I», the so-called Church–Turing thesis.
- Rogers, Hartley Jr. (1987). Theory of Recursive Functions and Effective Computability. The MIT Press. ISBN 978-0-262-68052-3.
- Rosser, J.B. (1939). «An Informal Exposition of Proofs of Godel’s Theorem and Church’s Theorem». Journal of Symbolic Logic. 4 (2): 53–60. doi:10.2307/2269059. JSTOR 2269059. S2CID 39499392. Reprinted in The Undecidable, p. 223ff. Herein is Rosser’s famous definition of «effective method»: «…a method each step of which is precisely predetermined and which is certain to produce the answer in a finite number of steps… a machine which will then solve any problem of the set with no human intervention beyond inserting the question and (later) reading the answer» (p. 225–226, The Undecidable)
- Santos-Lang, Christopher (2015). «Moral Ecology Approaches to Machine Ethics» (PDF). In van Rysewyk, Simon; Pontier, Matthijs (eds.). Machine Medical Ethics. Intelligent Systems, Control and Automation: Science and Engineering. Vol. 74. Switzerland: Springer. pp. 111–127. doi:10.1007/978-3-319-08108-3_8. ISBN 978-3-319-08107-6. Archived (PDF) from the original on October 9, 2022.
- Scott, Michael L. (2009). Programming Language Pragmatics (3rd ed.). Morgan Kaufmann Publishers/Elsevier. ISBN 978-0-12-374514-9.
- Sipser, Michael (2006). Introduction to the Theory of Computation. PWS Publishing Company. ISBN 978-0-534-94728-6.
- Sober, Elliott; Wilson, David Sloan (1998). Unto Others: The Evolution and Psychology of Unselfish Behavior. Cambridge: Harvard University Press. ISBN 9780674930469.
- Stone, Harold S. (1972). Introduction to Computer Organization and Data Structures (1972 ed.). McGraw-Hill, New York. ISBN 978-0-07-061726-1. Cf. in particular the first chapter titled: Algorithms, Turing Machines, and Programs. His succinct informal definition: «…any sequence of instructions that can be obeyed by a robot, is called an algorithm» (p. 4).
- Tausworthe, Robert C (1977). Standardized Development of Computer Software Part 1 Methods. Englewood Cliffs NJ: Prentice–Hall, Inc. ISBN 978-0-13-842195-3.
- Turing, Alan M. (1936–37). «On Computable Numbers, With An Application to the Entscheidungsproblem». Proceedings of the London Mathematical Society. Series 2. 42: 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712.. Corrections, ibid, vol. 43(1937) pp. 544–546. Reprinted in The Undecidable, p. 116ff. Turing’s famous paper completed as a Master’s dissertation while at King’s College Cambridge UK.
- Turing, Alan M. (1939). «Systems of Logic Based on Ordinals». Proceedings of the London Mathematical Society. 45: 161–228. doi:10.1112/plms/s2-45.1.161. hdl:21.11116/0000-0001-91CE-3. Reprinted in The Undecidable, pp. 155ff. Turing’s paper that defined «the oracle» was his PhD thesis while at Princeton.
- United States Patent and Trademark Office (2006), 2106.02 **>Mathematical Algorithms: 2100 Patentability, Manual of Patent Examining Procedure (MPEP). Latest revision August 2006
- Zaslavsky, C. (1970). Mathematics of the Yoruba People and of Their Neighbors in Southern Nigeria. The Two-Year College Mathematics Journal, 1(2), 76–99. https://doi.org/10.2307/3027363
Further reading[edit]
- Bellah, Robert Neelly (1985). Habits of the Heart: Individualism and Commitment in American Life. Berkeley: University of California Press. ISBN 978-0-520-25419-0.
- Berlinski, David (2001). The Advent of the Algorithm: The 300-Year Journey from an Idea to the Computer. Harvest Books. ISBN 978-0-15-601391-8.
- Chabert, Jean-Luc (1999). A History of Algorithms: From the Pebble to the Microchip. Springer Verlag. ISBN 978-3-540-63369-3.
- Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2009). Introduction To Algorithms (3rd ed.). MIT Press. ISBN 978-0-262-03384-8.
- Harel, David; Feldman, Yishai (2004). Algorithmics: The Spirit of Computing. Addison-Wesley. ISBN 978-0-321-11784-7.
- Hertzke, Allen D.; McRorie, Chris (1998). «The Concept of Moral Ecology». In Lawler, Peter Augustine; McConkey, Dale (eds.). Community and Political Thought Today. Westport, CT: Praeger.
- Knuth, Donald E. (2000). Selected Papers on Analysis of Algorithms. Stanford, California: Center for the Study of Language and Information.
- Knuth, Donald E. (2010). Selected Papers on Design of Algorithms. Stanford, California: Center for the Study of Language and Information.
- Wallach, Wendell; Allen, Colin (November 2008). Moral Machines: Teaching Robots Right from Wrong. US: Oxford University Press. ISBN 978-0-19-537404-9.
- Bleakley, Chris (2020). Poems that Solve Puzzles: The History and Science of Algorithms. Oxford University Press. ISBN 978-0-19-885373-2.
External links[edit]
Look up algorithm in Wiktionary, the free dictionary.
Wikimedia Commons has media related to Algorithms.
- «Algorithm». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- Algorithms at Curlie
- Weisstein, Eric W. «Algorithm». MathWorld.
- Dictionary of Algorithms and Data Structures – National Institute of Standards and Technology
- Algorithm repositories
- The Stony Brook Algorithm Repository – State University of New York at Stony Brook
- Collected Algorithms of the ACM – Associations for Computing Machinery
- The Stanford GraphBase – Stanford University
Вопросы
для подготовки к экзамену по дисциплине
«Информатика»
Наша учеба, работа, личные дела — это
каждодневное, ежечасное решение различных
задач. Каждая задача требует для своего
решения выполнения определенных
действий. Многократно решая задачи,
можно заметьть, что необходимые действия
должны выполняться в строго определенном
порядке. В таких случаях принято говорить
об алгоритме решения задач. Понятие
алгоритма считается одним из древнейших.
Оно возникло задолго до появления ЭВМ,
но с развитием вычислительной техники
его роль значительно возросла.
Происхождение понятия алгоритма связано
с именем великого среднеазиатского
ученого Аль Хорезми, жившего в 9 веке
н.э. Им были сформулированы впервые
правила выполнения четырех арифметических
действий.
Алгоритм — это точная инструкция, а
инструкции встречаются во всех областях
человеческой деятельности. Однако не
всякую инструкцию можно назвать
алгоритмом. Решая задачу, человек часто
не задумывается над тем, как он это
делает, и порой, затрудняется записать
последовательность выполняемых действий.
Но для того, чтобы поручить решение
задачи автоматическому устройству
необходимо составить алгоритм с четким
указанием последовательности действий.
Чтобы автоматическое устройство могло
решить задачу в соответствии с алгоритмом,
оно должно понимать каждое указание
алгоритма. Алгоритм применяется к
искомому набору исходных величин,
называемых аргументами. Цель исполнения
алгоритма получение определенного
результата, если в результате исполнения
алгоритма не достигнута определенная
цель, значит алгоритм либо неверен, либо
не завершен.
Алгоритмом называется точная инструкция
исполнителю в понятной для него форме,
определяющая процесс достижения
поставленной цели на основе имеющихся
исходных данных за конечное число шагов.
Основными свойствами алгоритмов
являются:
1. Универсальность (массовость)
— применимость алгоритма к различным
наборам исходных данных.
2. Дискретность — процесс решения
задачи по алгоритму разбит на отдельные
действия.
3. Однозначность — правила и порядок
выполнения действий алгоритма имеют
единственное толкование.
4. Конечность — каждое из действий и
весь алгоритм в целом обязательно
завершаются.
5. Результативность — по завершении
выполнения алгоритма обязательно
получается конечный результат.
6. Выполнимость — результата алгоритма
достигается за конечное число шагов.
Алгоритм считается правильным, если
его выполнение дает правильный результат.
Соответственно алгоритм содержит
ошибки, если можно указать такие
допустимые исходные данные или условия,
при которых выполнение алгоритма либо
не завершится вообще, либо не будет
получено никаких результатов, либо
полученные результаты окажутся
неправильными.
Выделяют три крупных класса алгоритмов:
— вычислительные алгоритмы, работающие
со сравнительно простыми видами данных,
такими как числа и матрицы, хотя сам
процесс вычисления может быть долгим
и сложным;
— информационные алгоритмы,
представляющие собой набор сравнительно
простых процедур, работающих с большими
объемами информации (алгоритмы баз
данных);
— управляющие алгоритмы, генерирующие
различные управляющие воздействия на
основе данных, полученных от внешних
процессов, которыми алгоритмы управляют.
Для записи алгоритмов используют самые
разнообразные средства. Выбор средства
определяется типом исполняемого
алгоритма. Выделяют следующие основные
способы записи алгоритмов:
— вербальный, когда алгоритм описывается
на человеческом языке;
— символьный, когда алгоритм описывается
с помощью набора символов;
— графический, когда алгоритм
описывается с помощью набора графических
изображений.
Общепринятыми способами записи являются
графическая запись с помощью блок-схем
и символьная запись с помощью какого-либо
алгоритмического языка.
Описание алгоритма с помощью блок схем
осуществляется рисованием последовательности
геометрических фигур, каждая из которых
подразумевает выполнение определенного
действия алгоритма. Порядок выполнения
действий указывается стрелками. Написание
алгоритмов с помощью блок-схем
регламентируется ГОСТом. Внешний вид
основных блоков, применяемых при
написании блок схем, приведен на рисунке:
В зависимости от последовательности
выполнения действий в алгоритме выделяют
алгоритмы линейной, разветвленной и
циклической структуры.
В алгоритмах линейной структуры действия
выполняются последовательно одно за
другим:
В алгоритмах разветвленной структуры в
зависимости от выполнения или невыполнения
какого-либо условия производятся
различные последовательности действий.
Каждая такая последовательность действий
называется ветвью алгоритма.
В алгоритмах циклической структуры в
зависимости от выполнения или невыполнения
какого-либо условия выполняется
повторяющаяся последовательность
действий, называющаяся телом
цикла. Вложенным называется цикл,
находящийся внутри тела другого цикла.
Различают циклы с предусловием и послеусловием:
Итерационным называется цикл, число
повторений которого не задается, а
определяется в ходе выполнения цикла.
В этом случае одно повторение цикла
называется итерацией.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Научитесь: Профессия Python-разработчик
Узнать больше
Что такое алгоритм?
Алгоритм — это последовательность указаний, которые нужно исполнить, чтобы решить чётко сформулированную задачу. Мы описываем задачи исходя из ввода и вывода, и алгоритм становится способом превращения ввода в вывод. При этом формулировка задачи должна быть точной и недвусмысленной — это помогает избежать неверной интерпретации.
Когда вы закончили проектировать алгоритм, необходимо ответить на два важных вопроса: «Правильно ли он работает?» и «Сколько времени занимает выполнение?». Разумеется, вас не устроит алгоритм, который выдаёт правильный результат лишь в половине случаев или требует $1,000$ лет для поиска ответа.
Псевдокод
Чтобы понять, как работает алгоритм, нам необходимо перечислить шаги, которые он выполняет. Для этого мы будем использовать псевдокод — язык, которым пользуются разработчики для описания алгоритмов. Он игнорирует многие детали, необходимые в языках программирования, но он более точен, чем рецепт из кулинарной книги.
Задача и экземпляр задачи
Задача описывает класс возможных входных данных. Экземпляр задачи — это один конкретный ввод такого класса. Чтобы продемонстрировать понятия задачи и экземпляра задачи, рассмотрим следующий пример. Вы оказались в книжном магазине и собираетесь купить книгу за $4,23$$, расплатившись купюрой в $5$$. Вам должны вернуть $77$ центов в качестве сдачи. Теперь кассир принимает решение, как именно это сделать. Согласитесь, неприятно получить горсть из $77$ пенни или $15$ никелей и $2$ пенни. Возникает вопрос: как выдать сдачу, не расстроив клиента? Большинство кассиров стараются уместить сумму сдачи в наименьшее количество монет.
💡 Остановитесь и подумайте:
Каково минимальное количество монет номиналом $(25, 10, 5, 1)$, необходимо для сдачи в $77$ центов?
Пример с $77$ центами представляет собой экземпляр задачи Размен. Предполагается, что есть $d$ номиналов, которые представлены массивом $c = (c_1, c_2, dotsc, c_d)$. Для упрощения будем считать, что номиналы даны в порядке убывания. Например, $c = (25, 10, 5, 1)$ для монет, используемых в США.
Задача "Размен"
Переведите определенное количество денег в данные номиналы, используя как можно меньше монет.
- Входные данные: Целое число $money$ и массив из $d$ номиналов $c = (c_1, c_2, dotsc, c_d)$ в порядке убывания ( $c_1 > c_2 > dotsb > c_d$ ).
- Выходные данные: Список из $d$ целых чисел $i_1, i_2, dotsc , i_d$, в котором $c_1cdot i_1+c_2 cdot i_2+dotsm+ c_d cdot i_d = money$ и $i_1 + i_2 +dotsm +i_d$ как можно меньше.
Кассиры по всему миру решают эту проблему с помощью простого алгоритма:
Change(money, c, d):
while money > 0:
coin = ... // монета с самым большим номиналом, который не превышает money
// дать монету с номиналом coin клиенту
money = money - coin
Вот быстрая версия Change:
Change(money, c, d):
for k in range(1, d + 1)
i_k = floor(money / c[k]) // наибольшее количество монет номинала c[k]
// дать i_k монет с номиналом c_k клиенту
money = money - c[k] * i_k
Корректные и некорректные алгоритмы
Мы называем алгоритм корректным, если на каждый получаемый ввод он делает правильный вывод. Алгоритм считается некорректным, если хотя бы один ввод приводит к неправильному выводу.
💡 Остановитесь и подумайте:
Каково минимальное количество монет номиналами $(25, 20, 10, 5, 1)$, необходимое для сдачи в $40$ центов?
Change — это некорректный алгоритм! Представьте сдачу в 40 центов, выданную в номиналах $c_1 = 25$, $c_2 = 20$, $c_3 = 10$, $c_4 = 5$ и $c_5 = 1$. Change привел бы к неправильному результату: он выдал бы 1 четвертак (25 центов), 1 дайм (10 центов) и 1 никель (5 центов) вместо 2 монет по двадцать центов. Хоть это и может выглядеть надуманно, в 1875 году в США существовала монета в двадцать центов. Насколько мы можем быть уверены, что Change выдаст минимальное количество монет в современных номиналах Соединенных Штатов или любой другой страны?
Чтобы исправить алгоритм Change, нам нужно рассмотреть все возможные комбинации монет с номиналами $c_1, c_2, dotsc , c_d$, которые дают в сумме $money$, и выдать комбинацию с минимальным количеством монет. Мы рассматриваем только комбинации, в которых $i_1 le money/c_1$ и $i_2 le money/c_2$ (в целом, величина $i_k$ не должна превышать $money/c_k$), в ином случае мы вернем большее количество денег, чем $money$. В псевдокоде, приведенном ниже, используется символ $sum$. Он обозначает суммирование: $sum^m_{i=1} a_i = a_1 + a_2 + dotsm + a_m$. Псевдокод также использует концепт «бесконечность» (обозначается $infty$) в качестве начального значения для $smallestNumberOfCoins$. Реализация описанного подхода на реальных языках программирования может различаться, но сейчас подробности для нас не важны.
BruteForceChange(money, c, d):
smallestNumberOfCoins = ∞
for each combinations of coins (i_1,...,i_d)
// от (0,...,0) до (money/c[1],...,money/c[d])
valueOfCoins = ∑ i_k*c_k // сумма по всем k от 1 до d
if valueOfCoins = M:
numberOfCoins = ∑ i_k // суммарное количество монет
if numberOfCoins < smallestNumberOfCoins:
smallestNumberOfCoins = numberOfCoins
change = (i_1, i_2, ... ,i_d)
return change
Вторая строка повторяется с каждой возможной комбинацией $(i_1, dotsc, i_d)$ из $d$ индексов и останавливается, когда достигает
$$
left(frac{money}{c_1}, dotsc, frac{money}{c_d}right),
$$
Как мы можем узнать, что BruteForceChange не содержит ту же проблему, что и Change, — неверный результат при каком-то вводе? Раз BruteForceChange рассматривает все возможные комбинации номиналов, рано или поздно алгоритм придёт к оптимальному решению и запишет его в массив $change$. В любой комбинации монет, которая даёт в сумме $M$, должно быть как минимум столько же монет, сколько и в оптимальной. Таким образом, BruteForceChange никогда не завершит работу с неоптимальным набором $change$.
На данный момент мы ответили только на один из двух важных вопросов об алгоритмах: «Работает ли он?». Однако мы не ответили на вопрос: «Сколько времени занимает выполнение?».
💡 Остановитесь и подумайте:
Сколько примерно итераций цикла for выполняет BruteForceChange?
- money
- $money^d$
- $d$
Быстрые и медленные алгоритмы
Настоящие компьютеры требуют определенное количество времени на выполнение таких операций, как сложение, вычитание или проверка условий цикла while. Суперкомпьютер может выполнить сложение за $10^{-10}$ секунды, а калькулятор — за $10^{-5}$. Представьте, что у вас есть компьютер, которому требуется $10^{-10}$ секунды на выполнение простой операции (например, сложения), и вы знаете, сколько операций выполняет какой-то конкретный алгоритм. Вы могли бы рассчитать время выполнения алгоритма, просто взяв произведение количества операций и времени, которое занимает одна операция. Однако компьютеры постоянно улучшаются, благодаря чему им требуется меньше времени на операцию. Так, ваше представление о времени выполнения быстро стало бы устаревшим. Вместо того, чтобы рассчитывать время выполнения на каждом компьютере, мы описываем время выполнения через общее количество операций, необходимых алгоритму, — это характеристика самого алгоритма, а не компьютера, который вы используете.
К сожалению, нам не всегда легко определить, сколько операций выполнит алгоритм. Однако если мы можем рассчитать количество базовых операций, выполняемых алгоритмом, то это позволит сравнить его с другим алгоритмом, решающим ту же задачу. Чтобы мучительно не подсчитывать каждое умножение и сложение, можно сравнивать только те участки кода, которые при увеличении размера ввода потребуют больше операций.
Представьте, что алгоритм $A$ выполняет $n^2$ операций при вводе размера $n$, и алгоритм $B$ решает ту же задачу за $3n+2$ операций. Какой алгоритм быстрее: $A$ или $B$? Хотя $A$ и может быть быстрее, чем $B$, при более малом значении $n$ (например, при $n$ между 1 и 3), $B$ будет быстрее при больших значениях $n$ (например, $n >4$). См. рис.. Так как $f(n)=n^2$ — это, в каком-то смысле, более «быстрорастущая» функция относительно $n$, чем $g(n)=n$. При этом константы 3 и 2 в $3n+2$ не влияют на конкуренцию между двумя алгоритмами при больших значениях $n$. Мы называем $A$ квадратичным алгоритмом и $B$ — линейным. $A$ менее эффективен, чем $B$, потому что он выполняет больше операций для решения задачи, когда значение $n$ большое. Так, иногда мы будем допускать неточности при подсчете операций алгоритма: поведение алгоритма при маленьком вводе неважно.
Рассчитаем примерное количество операций, которое потребуется для BruteForceChange при вводе из $M$ центов и номиналов $(c_1, c_2, dotsc, c_d)$. Чтобы рассчитать общее количество операций в цикле for, нам необходимо взять примерное число операций, выполняемое при каждой итерации, и умножить его на общее количество итераций. Так как в нашем случае около
$$
frac{money}{c_1} times frac{money}{c_2} times dotsm times frac{money}{c_d}
$$
Такой тип алгоритмов называется экспоненциальным в противоположность квадратичным, кубическим или другим полиномиальным алгоритмам. Выражение времени выполнения экспоненциального алгоритма использует $n^d$, где $n$ и $d$ — это параметры задачи (например, $n$ и $d$ можно произвольно сделать большими, изменив ввод для алгоритма). Время выполнения полиномиального алгоритма ограничено $n^k$, где $k$ — это константа, не связанная с величиной параметров задачи.
Например, алгоритм с временем выполнения $n^1$ (линейный), $n^2$ (квадратичный), $n^3$ (кубический) или даже $n^{2018}$ будет полиномиальным. Конечно, алгоритм с временем выполнения $n^{2018}$ не очень практичен. Возможно, даже менее практичен, чем некоторые экспоненциальные алгоритмы. Впрочем, разработчики тратят много усилий, чтобы проектировать всё более и более быстрые полиномиальные алгоритмы. Раз значение $d$ может быть большим при вызове алгоритма с большим количеством номиналов (например, $c = (1, 2, 3, 4, 5, dotsc , 100)$), мы видим, что выполнение BruteForceChange может потребовать много времени.
Цели урока:
- познакомить с понятием алгоритма, исполнителем
алгоритма, видами исполнителя, средой, СКИ и
системой отказов исполнителя, свойствами
алгоритма, показать среду, СКИ и систему отказов
для конкретного исполнителя, - развивать умение работать самостоятельно,
творчески. - воспитывать нравственное отношение к труду.
ХОД УРОКА
Презентация 1
В течение всей жизни каждый человек постоянно
пользуется набором всевозможных алгоритмов —
правил, которые заложены природой, даны
воспитанием, обучением, тренировкой, выработаны
на основе собственного опыта. Инструкции, в
которых указано, как пользоваться лифтом,
телефоном, различными автоматами и бытовыми
приборами, правила перехода улицы, оказания
первой медицинской помощи, распорядок дня,
кулинарные рецепты, порядок проведения
химического опыта, правила вычислений, методы
решения алгебраических и геометрических задач —
все это можно считать алгоритмами. Таким образом,
все мы живем в мире алгоритмов. Алгоритмы
экономят силы и время человека, так как однажды
усвоенным правилом (алгоритмом) он может
пользоваться всю жизнь.
Приведите пример алгоритма перехода дороги с
светофором, и без светофора.
Ваш мозг постоянно занят работой, поиском
решений. Говорят, что человек составляет
алгоритм.
Тема нашего сегодняшнего урока. Алгоритм.
Свойства алгоритма.
Учащиеся записывают тему урока (с
презентации).
На экране вы видите команды, необходимо
составить алгоритм заваривания чая.
Работа идет со всем классом, учащиеся
обсуждают о выборе последовательности команд,
учитель на доске регистрирует их ответ.
- размешать сахар ложечкой;
- добавить кипятку;
- налить в чашку заварку;
- вскипятить воду;
- положить сахар.
У вас должен был получиться такой алгоритм:
- вскипятить воду;
- налить в чашку заварку;
- добавить кипятку;
- положить сахар;
- размешать сахар ложечкой;
В природе все взаимосвязано, все на все влияет и
все зависит друг от друга. Складываются сложные
цепочки событий. Если вынуть хоть одно звено, вся
цепочка разорвется.
Как вы думаете, что будет если убрать из рецепта
вторую команду? А четвертую?
Надо научится выстраивать в нужном порядке все
звенья какой-нибудь жизненной или
математической задачи. Эти умения нужны и при
обработке информации. Информацию следует
обрабатывать по определенным правилам, которые
выполняются в определенном порядке.
Итак, давайте с вами, попробуем дать
определения понятию алгоритм.
Учащиеся формулируют и записывают с доски.
Алгоритм – понятное и точное
предписание исполнителю совершить
последовательность действий, направленных на
достижение указанной цели или на решение
поставленной задачи.
Учащиеся записывают в тетрадь определение.
Синонимы слова «алгоритм»:
- план;
- инструкция;
- рецепт;
- предписание.
Происхождение термина «алгоритм» связывают с
именем великого узбекского математика и
астронома аль-Хорезми (жившего в IX в.). Абу
Абдуллах Мухаммад ибн Муса аль-Хорезми (ок. 783,
Хива , Хорезм — ок. 850, Багдад) — один из
крупнейших средневековых ученых (математик,
астроном, географ и историк) IX века, основатель
классической алгебры.
Ал-Хорезми известен прежде всего своей «Книгой о
восполнении и противопоставлении» («Аль-китаб
аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»),
которая сыграла важнейшую роль в истории
математики. От названия этой книги произошло
слово «алгебра».
В своих трудах по арифметике и алгебре он
разработал, в частности, правила выполнения
четырех арифметических операций над
многозначными десятичными числами. Эти правила
определяют последовательность действий, которые
необходимо выполнить, чтобы получить сумму
чисел, произведение и т. д. Почти в таком же виде
эти правила изучаются всеми школьниками в
начальных классах.
Латинский перевод книги начинается словами
«Dixit Algorizmi» (сказал Алгоризми). Так как сочинение
об арифметике было очень популярно в Европе, имя
автора (Algorizmi или Algorizmus) стало нарицательным и
средневековые математики так называли
арифметику, основанную на десятичной
позиционной системе счисления. Позднее
европейские математики стали называть так
всякую систему вычислений по определенному
правилу. В настоящее время термин «алгоритм»
означает набор инструкций, описывающих порядок
действий исполнителя для достижения результата
решения задачи за конечное число действий.
Затем понятие алгоритма переместилось в
область логики, где появилась теория алгоритмов,
изучавшая процесс доказательств или
разрешимость и неразрешимость математических
задач. В 1937 году, когда английский
математик Алан Тьюринг доказал
теоретически возможность построения устройства,
осуществляющего алгоритм. Такое абстрактное
устройство получило название МАШИНА ТЬЮРИНГА.
Аналогичный, но более простой исполнитель
алгоритма – МАШИНА ПОСТА. Когда же были
созданы первые ЭВМ, понятие алгоритма и теория
алгоритмов переместились в новую науку,
связанную с этими вычислительными устройствами
– информатику.
Приведите примеры алгоритмов.
А теперь скажите кто может выполнить данный
алгоритм?
Приведите пример алгоритмов с разными
исполнителями.
Получается, всякий алгоритм составляется в
расчете на определенного исполнителя. Им может
быть человек, робот, компьютер и др. Чтобы
составить алгоритм для исполнителя, нужно знать,
какие команды исполнитель может понять и
исполнить, а какие нет.
Исполнитель – объект, который будет выполнять
алгоритм.
Приведите примеры исполнителей и что они
могут делать.
В классе исполнителей выделяют два типа:
формальные, неформальные. Формальный
исполнитель одну и ту же команду всегда выполнит
одинаково, неформальный может выполнять команду
по-разному. Неформальный исполнитель – человек,
формальный – технические устройства.
У каждого исполнителя можно выделить: среду
исполнителя, систему команд исполнителя, систему
отказов.
Среда – обстановка, в которой
работает исполнитель.
Система команд исполнителя (СКИ) –
совокупность команд, которую исполнитель умеет
выполнять.
Система отказов – ситуации сбоя
работы исполнителя, которые возникают, если
команда вызывается пpи недопустимом для нее
состоянии сpеды («не понимаю», «не могу»).
«Не понимаю» – возникает тогда, когда
исполнителю дается команда не входящая в его СКИ,
«не могу» – когда команда из СКИ не может быть
выполнена в конкретных условиях среды.
Укажите для данных примеров среду, ски,
систему отказов.
Свойства алгоритмов
1. Как мы уже знаем, алгоритм задает полную
последовательность действий, которые необходимо
выполнять для решения задачи. При этом, как
правило, для выполнения этих действий их
расчленяют (разбивают) в определенной
последовательности на простые шаги. Возникает
упорядоченная запись совокупности четко
разделенных предписаний (директив, команд),
образующих прерывную (или, как говорят,
дискретную) структуру алгоритма. Выполнить
действия следующего предписания можно лишь
выполнив действия предыдущего.
Под ДИСКРЕТНОСТЬЮ понимают возможность
разбиения алгоритма на отдельные элементарные
действия, выполнение которых человеком или
машиной не вызывает сомнения.
Пример по алгоритму заваривая чая
2. Чтобы исполнитель сумел решить поставленную
перед ним задачу, используя алгоритм, он должен
уметь выполнить каждое его указание. Иными
словами, он должен понимать суть управления. То
есть при составлении алгоритма нужно
обязательно учитывать «правила игры», т.е.
систему предписаний (или систему команд), которые
понимает ЭВМ. Мы будем говорить в данном случае о
«понятности» алгоритма.
Под «ПОНЯТНОСТЬЮ» алгоритмов понимают
указания, которые понятны исполнителю.
Пример по пришиванию пуговицы.
3. Будучи понятным, алгоритм не должен все же
содержать предписаний, смысл которых может
восприниматься неоднозначно. Этими свойствами
часто не обладают предписания и инструкции,
которые составляются для людей.
Например, вспомним известную всем притчу о
царской воле. Царь приказал подчиненным
выполнить такой указ: «Казнить нельзя
помиловать». Он забыл в указе поставить
запятую, а подчиненные не знали, что им делать.
Указание «казнить нельзя, помиловать» и
«казнить, нельзя помиловать» задают совсем
разные действия, от которых зависит жизнь
человека.
Кроме того, в алгоритмах недопустимы такие
ситуации, когда после выполнения очередного
предписания алгоритма исполнителю неясно, какое
из них должно выполняться на следующем шаге.
Под ОДНОЗНАЧНОСТЬЮ алгоритмов понимается
единственность толкования правил выполнения
действий и порядка их выполнения.
Пример, фрагмент мультфильма «Стран
невыученных уроков».
4. Очень важно, чтобы составленный алгоритм
обеспечивал решение не одной частной задачи, а
мог выполнять решение широкого класса задач
данного типа.
Алгоритм можно использовать для любого
квадратного у равнения. Такой алгоритм будет
МАССОВЫЙ.
Пример с чайниками, обогревателями.
5. Под КОНЕЧНОСТЬЮ алгоритмов понимают
завершение работы алгоритма в целом за конечное
число шагов.
Пример с ловлей рыбы.
6. Еще к желательным свойствам алгоритмов нужно
отнести РЕЗУЛЬТАТИВНОСТЬ, она предполагает, что
выполнение алгоритмов должно завершаться
получением определенных результатов.
Подобные ситуации в информатике возникают, когда
какие-либо действия невозможно выполнить. В
математике такие ситуации называют
неопределенностью. Например, деление числа на
ноль, извлечение квадратного корня из
отрицательного числа, да и само понятие
бесконечности неопределенно. Поэтому, если
алгоритм задает бесконечную последовательность
действий, то в этом случае он также считается
результатом неопределенным.
Но можно действовать по-другому. А именно:
указать причину неопределенного результата. В
таком случае, пояснения типа «на ноль делить
нельзя», «компьютер выполнить такое не в
состоянии» и т.п. можно считать результатом
выполнение алгоритма.
Таким образом, свойство результативности
состоит в том, что во всех» случаях можно
указать, что мы понимаем под результатом
выполнения алгоритма.
Пример с нахождением стрелы Ивана Царевича у
лягушки.
7. И последнее общее свойство алгоритмов – их
правильность.
Мы говорим, что алгоритм ПРАВИЛЬНЫЙ, если его
выполнение дает правильные результаты решения
поставленных задач.
Соответственно мы говорим, что алгоритм СОДЕРЖИТ
ОШИБКИ, если можно указать такие допустимые
исходные данные или условия, при которых
выполнение алгоритма либо не завершится вообще,
либо не будет получено никаких результатов, либо
полученные результаты окажутся неправильными.
Пример с арифметическим выражением.
Вывод:
Основные свойства алгоритмов:
- дискретность;
- понятность;
- однозначность;
- массовость;
- результативность;
- конечность;
- правильность.
Учащиеся записывают в тетрадь свойства.
Решение задач на определение свойств.
Обсуждение свойств с классом.
Задание 1.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция по варке манной каши
Молоко вскипятить добавить соль, сахар, засыпать
тонкой струйкой, непрерывно помешивая манную
крупу, довести до кипения, прокипятить минут 5-7,
добавить масло и дать остыть.
Нет понятности: какое количество (в граммах)
брать продуктов.
Возможный исправленный вариант
- Включить плиту
- Влить в кастрюлю 1,5 литра молока
- Добавить 5 грамм соли, 15 грамм сахара
- Довести молоко до кипения
- 8 столовых ложек манной крупы засыпать тонкой
струйкой, непрерывно помешивая молоко - Довести до кипения
- Кипятить 5 минут
- Добавить 20 грамм сливочного масла
- Выключить плиту, снять с плиты кастрюлю.
Задание 2.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция нахождения большего из двух данных
чисел.
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше
Нет результативности. Что делать в том случае,
если А=В?
Возможный исправленный вариант
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше - Если получился ноль, сообщить, что числа равны
Задание 3.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция покраски забора
- Покрасить первую доску.
- Переместиться к следующей доске.
- Перейти к действию 1.
Нет конечности. Что делать в том случае, когда
доски закончились?
Возможный исправленный вариант
- Покрасить первую доску.
- Если есть еще доска, переместиться к следующей
доске. - Перейти к действию 1.
- Если доски закончились, завершить работу.
Практическая работа в парах (5 мин.)
Приложение 1
Задание 1. Исправьте алгоритм
«Получения кипятка», чтобы предотвратить
несчастный случай.
Задание 2. Используя представленные
команды, составить алгоритм покраски мяча
Задание 3. Составить инструкцию, в
которой не выполняется хотя бы одно свойство
алгоритма. Записать какие изменения нужно в нее
внести, чтобы получить алгоритм.
Тест самопроверкой (5 мин.)
1. Алгоритм – это:
А) Указание на выполнение действий,
Б) Система правил, описывающая
последовательность действий, которые необходимо
выполнить для решения задачи,
В) Процесс выполнения вычислений, приводящих к
решению задачи
2. Свойство алгоритма – дискретность, выражает,
что:
А) Команды должны следовать последовательно
друг за другом,
Б) Каждая команда должна быть описана в расчете
на конкретного исполнителя,
В) Разбиение алгоритма на конечное число команд
3. Среда исполнителя – это:
А) Обстановка, в которой работает исполнитель.
Б) Объект, который будет выполнять алгоритм
В) Совокупность команд, которую исполнитель
умеет выполнять.
4. В расчете на кого должен строиться алгоритм:
А) В расчете на ЭВМ,
Б) В расчете на умственные способности товарища,
В) В расчете на конкретного исполнителя
5. Какое из перечисленных свойств относится к
свойствам алгоритма:
А) Визуальность,
Б) Совокупность,
В) Понятность
6. Исполнитель «человек» – это
А) Формальный исполнитель
Б) Неформальный исполнитель
В) Нормальный исполнитель
Проверка теста.
Подведение итогов (5 мин.)
Домашнее задание:
1. Выучить теоретический материал
2. Привести 3 примера алгоритмов для различных
исполнителей.
3. Составить 2 инструкции, в которых не
выполняется хотя бы одно свойство алгоритма.
Записать какие изменения нужно в них внести,
чтобы получить алгоритм.
#статьи
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Как зарабатывать больше с помощью нейросетей?
Бесплатный вебинар: 15 экспертов, 7 топ-нейросетей. Научитесь использовать ИИ в своей работе и увеличьте доход.
Узнать больше