Квантовомеханические расчеты молекул с использованием программного комплекса GAUSSIAN
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное агентство по образованию
Государственное образовательное
учреждение
высшего профессионального образования
“ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ”
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ФИЗИКИ
Методическое пособие:
“Квантовомеханические расчеты молекул
с использованием программного комплекса GAUSSIAN”
для студентов, бакалавров, магистров
и аспирантов
физического и химического факультетов
Исполнитель:
стажер-исследователь ОРС НИИФ Власенко Е.В.
Координатор проекта:
д-р физ.-мат. наук, проф. Ведринский Р.В.
2007 год
ОГЛАВЛЕНИЕ
Введение
. Основные положения квантовой химии
.1 Метод Хартри-Фока-Слейтера
.2 Приближение линейных комбинаций атомных орбиталей (МО
ЛКАО)
.3 Анализ заселенностей орбиталей
.4 Методы теории функционала плотности
.5 Корреляционные поправки
.6 Полуэмпирические методы
.7 Методы оптимизации (молекулярное моделирование)
. Квантовомеханические расчеты при помощи программы
.1 Основные возможности пакета GAUSSIAN-03
.2 Принцип работы программ GAUSSIAN
.3 Задание расчета и структура входного файла
.4 Структура Input File
.5 Проведение расчета и структура выходного файла
Заключение
ВОПРОСЫ И ЗАДАНИЯ
Литература
Введение
атомный орбиталь
молекулярный gaussian
Использование квантомеханических расчетов для предсказания
геометрического строения, энергии, термодинамических характеристик и др. для
известных и предполагаемых молекул является, в настоящее время, одним из важных
и быстроразвивающихся методов химических исследований. Особую ценность этот
метод приобретает в случае предсказания свойств неизвестных соединений, синтез
которых может являться достаточно сложной процедурой, требующей больших затрат
времени и материальных ресурсов исследователей. К тому же, на современном этапе
развития компьютерной техники и создания высокопроизводительных и универсальных
программ для квантовой химии, существует возможность расчета химических свойств
соединений с очень высокой точностью и надежностью. Одной из таких программ по
расчету структуры и свойств молекул является программа GAUSSIAN [1-11]. Со времени своего появления
в 1970 г. вышло несколько версий этой программ, в каждую из которых были
включены все достижения развития квантовой химии и программирования на
определенном этапе. Последняя существующая версия в настоящий момент есть GAUSSIAN-03. Описание работы GAUSSIAN различных версий можно найти не
только в авторских инструкциях для пользователей, но и в некоторых монографиях
по квантовой химии [12]. Широкое использование, в настоящее время, программы GAUSSIAN не только для
научно-исследовательских работ, но и в учебном процессе требует создания
специализированного методического пособия по работе с этой программой для
студентов и аспирантов. Настоящее методическое пособие предназначено для начального
ознакомления с принципами работы программы GAUSSIAN и дает возможность приступить к
расчетам на основании конкретных примеров построения расчетного задания и
интерпретировать полученные результаты. Методическое пособие
«Квантовомеханические расчеты молекул с использованием программного комплекса GAUSSIAN» предназначено для студентов,
обучающихся по специальностям 020100- химия, магистров, аспирантов и научных
работников.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ХИМИИ
Квантовая механика позволяют получить достаточно точное математическое
описание любых экспериментально наблюдаемых молекулярных взаимодействий. Однако
для реализации этих возможностей необходимо располагать достаточно мощными ЭВМ
и достаточно точными вычислительными методами. За последние годы в этих
областях был достигнут значительный прогресс. Быстрое развитие вычислительной
техники и программного обеспечения наряду с разработкой эффективных и точных
полуэмпирических и неэмпирических (ab initio) вариантов
расчетов позволили, в настоящее время, сделать квантовую химию одним из
наиболее важных инструментов физико-химических исследований [13-16].
В основе современной квантовой химии лежит уравнение Шредингера для
стационарных состояний. Обычно используют адиабатическое приближение
(приближение Борна-Оппенгеймера), согласно которому ядра неподвижны и можно
решать уравнения только для движения электронов. Однако даже в этом случае
точно решить уравнение Шредингера можно только для одноэлектронных систем.
Поэтому в квантовохимических расчетах используют различные приближенные методы,
наиболее распространенным из которых является метод самосогласованного поля
(ССП) или метод Хартри-Фока. Для систем, подобных водородному атому, возможно
точное аналитическое решение уравнения Шредингера. Для систем с малым
количеством электронов, типа гелия, «многоэлектронная» проблема может
быть решена более или менее точно (в настоящее время нерелятивистская энергия
стандартного состояния гелия известна с точность до пятнадцатого знака). В
общем случае — электронные системы нельзя рассмотреть с такой точностью.
Большинство элементов в периодической таблице — многоэлектронные системы, где
движение каждого электрона зависит от движения всех других электронов, так же
как и ядер. Чтобы изучать такие системы, необходимы некоторые методы
последовательных приближений.
.1 Метод Хартри-Фока-Слейтера
Один из широко используемых методов последовательных приближений — метод
Хартри-Фока. Он базируется на довольно естественном приближении, что каждый
электрон перемещается в потенциале, созданном ядром и средним потенциалом всех
других электронов атома. Это приводит к модели независимой частицы, которая
позволяет перейти от многоэлектронной проблемы к проблеме решения множества
взаимосвязанных одноэлектронных уравнений.
Одноэлектронные уравнения вычисляются, пока выбранный уровень точности не
достигнут. Хартри сделал первое вычисление, основанное на этих идеях, вручную в
1928. Приближение Хартри-Фока — быстрый и надежный метод для расчета атомных
систем, но это — только первое приближение.
Еще одним приближением является приближение Слейтера при решении
уравнений Хартри-Фока. Начнем рассмотрение с формализма Хартри, представляя
многоэлектронный гамильтониан для атомной системы как сумму одноэлектронных
гамильтонианов:
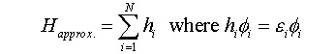
где
N — число электронов в системе. Каждый электрон независимо взаимодействует с
атомным ядром и для него можно получить решение независимо от других
электронов. Для потенциальной энергии гамильтониана, берется приближение
Борна-Оппенгеймера, когда игнорируется межъядерные взаимодействия, которые
предполагаются постоянными. Это предположение обосновывается тем, что ядра
совершают медленные колебания в узловых точках, в то время как электронная
подсистема распределена по всей молекуле или кристаллу.
В
самой простой форме, можно также предполагать, что электроны также
невзаимодействуют. В этом случае строится гамильтониан Happrox. без
учета электрон-электронного взаимодействия и точная волновая функция будет
иметь вид:
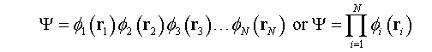
где
индексы 1, 2, 3…, N определяют, в каком квантовом состоянии находятся
одноэлектронные волновые функции. Любая перестановка одноэлектронных функций,
которые можно назвать спин-орбиталями, будет также приводить к волновым функциям
для Happrox..
В
полном методе Хартри, электрон-электронные взаимодействия включены в
гамильтониан в виде дополнительного члена потенциальной энергии. Этот
дополнительный член представляет собой возмущение простого решения для
невзаимодействующих электронов. Этот более полный гамильтониан является
стартовой точкой для расчетов методом Хартри-Фока.
(3)
Поскольку
электроны являются фермионами, полная волновая функция должна быть
антисимметрична относительно обмена любыми двумя из электронов (принцип Паули).
Такие волновые функции могут быть представлены в матричном виде:

Это
представление полной волновой функции в виде детерминанта Слейтера. Детерминант
будет нулевой, если любой i = j.
Как
простой пример рассмотрим атом гелия с его двумя электронами в конфигурации
основного состояния. Антисимметричная волновая функция тогда будет:
(5)
где
спин-орбитальные индексы были заменены определенными квантовыми уровнями
электронов. Обратим внимание, что набор всех возможных детерминантов Слейтера
порядка N формирует полный набор для описания системы. Для случая гелия, мы
можем также иметь вклады от отдельных возбужденных состояний с 1s-3s или
2s-3s; с уменьшающимся вкладом от более высоко возбужденных
состояний.
Величина
полной энергии для состояния, представленного детерминантом Слейтера
определяется величиной полного гамильтониана. «Лучшим» детерминантом
для стандартного состояния должен быть тот, который минимизирует величину H;
(6)
Это
приводит к уравнениям Хартри-Фока.

Как
и прежде, i и j обозначаем квантовые числа, необходимые для
определения отдельного электронного состояния. Сумма по j
выполняется по всем занятым состояниям. Каждая спин-орбиталь φi(rm)
характеризуется своим значением εi которое
является собственным значением оператора Фока (гамильтониан, включающий
усредненное электрон-электронное отталкивание и учитывающий принцип Паули).
(8)
где
h — упрощенный гамильтониан Хартри для невзаимодействующих электронов и
дополнительный потенциал Хартри-Фока (в квадратных скобках), который включает
электрон-электронные взаимодействия с антисимметричной волновой функцией.
Потенциал Хартри-Фока имеет два члена. Первый член Vee — средняя
потенциальная энергия кулоновского отталкивания. Второй член Vex —
обменная энергия взаимодействия. Эта поправка Хартри-Фока, приводит к понижению
полной энергии взаимодействия, и связана со спиновой корреляцией.
В
одноэлектронном гамильтониане кулоновский и электрон-электронный компоненты оба
являются локальными операторами. Они оперируют i-спин-орбиталью
в положении rm. Обменный член Vex —
нелокальный оператор.
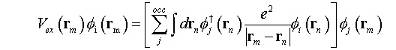
Для
i-спин-орбитали в положении rm, он
функционирует в положении rn. Обменный член обусловлен принципом Паули. Это может
быть более понятно, если рассматривать спин-орбитальные волновые функции
раздельно в виде спиновой и пространственной компонент. Спиновые компоненты
дают дельта-функцию между i и j волновыми функциями. Таким образом, только
подобные спин-электроны соответствуют этому члену. Это создает то, что называют
обменной дыркой.
В
общем случае, уравнения Хартри-Фока (7) трудно решить. На практике несколько
других ограничений накладываются на спин-орбитали при их рассмотрении. Первое
ограничение — требование, чтобы каждая спин-орбиталь имела различные спиновые и
пространственные значения. Второе ограничение — то, что мы предполагаем, что
спин-орбиталь является решением в сферически симметричном потенциале. Это
последнее ограничение называют центральным полевым приближением, и это делает
возможным разделение орбитального компонента волновой функции на радиальную и
угловую части.
Для
системы с закрытой оболочкой, где полный спин и угловой момент являются
нулевыми, система действительно сферически симметрична, и это ограничение
автоматически выполнено. Мы можем написать спин-орбиталь в rn
как:
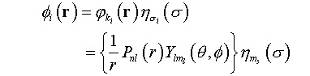
Yl m. —
обычная сферическая гармоника, и уравнения Хартри-Фока могут быть упрощены к
радиальным уравнениям Хартри-Фока:
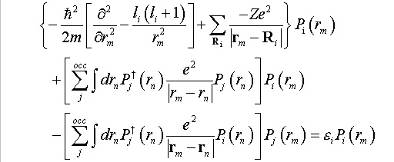
радиальные
функции Pi могут быть вычислены.
Как
можно видеть из уравнений (11), Pi зависит от радиальных функций всех других joccupied электронов. Из-за этой зависимости уравнения Хартри-Фока могут быть
решены, используя итерационный метод. Исходная точка расчета — приблизительное
описание одночастичной функции, P(r). Это может быть водородоподобные функции,
но обычно используется различное приближение. С этими стартовыми функциями
создается потенциал Хартри-Фока и находятся собственные значения уравнение
(11). Полученный новый набор одночастичных функций применяется для создания
нового потенциала Хартри-Фока и находятся новые собственные решения. Такая
операция проводится много раз, пока радиальные функции и собственные значения
энергии не становятся устойчивыми.
.2
Приближение линейных комбинаций атомных орбиталей (МО ЛКАО)
Для
нахождения одноэлектронных функций МО для молекул при использовании метода
Хартри-Фока возможно получение таблиц их числовых значений как и при
аналогичных атомных расчетах. Однако, кроме отсутствия аналитического решения,
существуют большие математические трудности, обусловленные отсутствием
центральной симметрии. Для молекул МО должны обладать теми же элементами
симметрии, какими обладают сами молекулы. Наилучшим приближением для построения
МО оказалось приближение ЛКАО. В этом приближении каждая МО записывается в виде
линейной комбинации АО атомов, образующих молекулу:
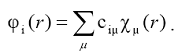
Коэффициенты сiμ, принимающие как положительные, так и отрицательные
значения, определяют вклад каждой атомной орбитали (АО) χμ(r)
в МО ϕi (r). Одна и
та же АО по-разному входит в разные МО, поэтому коэффициенты ciμ
при АО χμ
для каждой МО различны.
МО и АО есть одноэлектронные функции (орбитали), которые приближенно
описывают поведение каждого из электронов в молекулах и атомах, соответственно.
Приближение МО ЛКАО (11) опирается на принцип суперпозиции и отражает волновую
природу электронов. Поэтому можно заключить, что МО (11) формируются в
результате взаимного проникновения или интерференции АО, причем эта
интерференция может носить как конструктивный (взаимодействие АО происходит в
фазе, т.е. коэффициенты ciμ имеют одинаковые знаки), так и
деструктивный (взаимодействие АО происходит в противофазе и коэффициенты ciμ
имеют разные знаки)
характер. Соответственно, образуются связывающие МО, обладающие более низкой
энергией, и антисвязывающие (или разрыхляющие) МО, энергия которых выше. Если
интерференция очень мала, МО формируются преимущественно из орбиталей атомного
характера: такие МО называются несвязывающими: они описывают, например,
остовные электроны и неподеленные электронные пары. Возможное число и тип МО в
системе определяется принципом Паули.
Электронная плотность молекулы в приближении МО ЛКАО записывается
следующим образом:
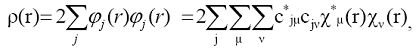
т.е. ЭП есть сумма вкладов, связанных с плотностью электронов на атомных
орбиталях и интерференцией АО. Степень и характер взаимного проникновения АО
количественно характеризуют с помощью интегралов перекрывания
Выбор базисных функций в разложении ЛКАО является важной задачей, так как
этим определяется точность аппроксимации молекулярных орбиталей Хартри-Фока.
Базисные функции должны удовлетворять трем основным критериям:
1. Базисные функции должны давать хорошее приближение к истинной
волновой функции (возле ядер и на больших расстояниях от них).
2. Базисные функции должны допускать аналитическое вычисление
нужных интегралов.
. Полное число базисных функций не должно быть очень большим.
Приближение MO ЛКАО состоит в аппроксимации МО суммой AO, центрированных
на всех ядрах. AO есть решения уравнений Хартри-Фока для атома, т. е.
одноэлектронные атомные волновые функции, рассчитанные для среднего потенциала,
созданного другими электронами и ядром. Использование аналитических АО
позволяет значительно упростить вычисления. Угловые части АО хорошо известны —
это сферические гармоники. Рассмотрим аналитические приближения к радиальным
частям AO: именно они обычно определяют тип базиса.
В принципе, в качестве базисных можно использовать любые функции, которые
в достаточной степени охватывают пространство электронного распределения.
Оптимальный выбор состоит в том, чтобы аналитическая функция была максимально
близкой к радиальной составляющей точной водородоподобной AO. Такие функции
известны как орбитали слейтеровского типа (STO или ОСТ). OСТ отвечают
потенциалу центрального поля
V( r ) = — ζn/r + [n(n-1) — l(l+1)]/2r2 (14)
(n и l — главное и орбитальное квантовые числа, l = 0, 1, 2,… , n-1) и
удовлетворяют асимптотическому поведению точной волновой функции как вблизи
ядра, так и на больших расстояниях от него.
В сферических координатах ϕ,θ,r ОСТ имеют вид:
(15)
где N — нормировочный множитель, — сферическая гармоника, m —
магнитное квантовое число.
При l = -1 ОСТ переходит в АО водородоподобного атома с экспоненциальным
фактором ζ = Z/n, поэтому ОСТ обеспечивают правильное поведение AO ОСТ с l >
1 являются безузловыми; ОСТ с одинаковыми l, но разными n, не-ортогональны.
К сожалению, ОСT не подходят для быстрого вычисления двухцентровых
кулоновских и обменных интегралов. Вычисление этих интегралов очень упрощается
при использовании в качестве базисных функций орбиталей гауссова типа (ОГТ).
Эти базисные функции обладают следующим важным свойством: произведение двух
гауссиан, центрированных в точках А(Аx, Аy, Аz) и В ( Вx, Вy, Вz ), есть
гауссиан, центрированный в точке P =(α1A + α2B) /
(α1+α2), лежащей
на линии АВ:
exp(-α1rA2) exp(-α2rB2)=
exp[-(α1α2rAB2)/( α1+α2)] exp[(-α1+α2)rР2)]. (16)
ОГТ отвечают потенциалу центрального поля
V(r) = 2α2/r2+ [n(n-1) —
l(l+1)]/2r2. (17)
ОГТ на данном центре с одинаковыми l, но разными n, как и ОСТ, не
ортогональны. Недостатком индивидуальных ОГТ является то, что их радиальное
поведение вблизи и вдали от ядра, отличается от такового у точных волновых
функций.
Форма ХФ АО легко аппроксимируется линейной комбинацией ОГT с различными
экспонентами и весовыми коэффициентами χ = ΣсiGi (хотя, чтобы обеспечить
правильное поведение АО в непосредственной близости от ядра, приходится
дополнять ОГТ функциями, имеющими радиальную зависимость типа ). Использование даже десяти ОГT для
аппроксимации АО позволяет вычислять интегралы намного быстрее, чем при
использовании одной ОСТ. Поэтому сейчас в квантово-химических расчетах
используются, как правило, базисные наборы, составленные из ОГT.
Особенно удобны в расчетах так называемые декартовы ОГT, которые в координатах
x, y, z имеют вид
(18)
где N — нормировочный множитель, α — орбитальный экспоненциальный
множитель, r2= x2 + y2 + z2. Числа n, l, m в декартовой ОГT не являются
обычными квантовыми числами: их сумма (n+l+m), аналогичная орбитальному
квантовому числу для атомов, определяет вид угловой части ОГТ в декартовых
координатах. Строго говоря, отдельные декартовы ОГT даже не являются
приближениями к АО: это лишь простые и удобные математические функции,
ускоряющие вычисление интегралов; их даже часто называют гауссовыми
примитивами.
Самые первые базисные наборы строились из ОГТ так, чтобы наилучшим
образом описывать ОСТ. Сейчас базисные наборы строят из линейных комбинаций ОГT
или, иначе из сгруппированных (их также называют контрактированными или
сжатыми) ОГT (СОГТ):
(19)
Минимальный ЛКАО базис для расчета МО двухатомных молекул, состоящих из
атомов второго ряда, состоит из 1s, 2s и 2р атомных орбиталей. На каждый атом
приходится по пять АО, а полное число АО равно десяти. Чтобы найти коэффициенты
ciμ
разложения МО по АО
(11), необходимо решить уравнения Хартри-Фока-Рутана. С формальной точки зрения
задача сводится к решению секулярного уравнения десятого порядка, в результате
чего получают 10 различных МО.
Номенклатура базисных наборов. На первых порах СОГТ получали методом
наименьших квадратов подгонкой под единственную ОСТ с экспоненциальным фактором
ζ
= 1.0. Затем экспоненты
в ОГТ умножали на величину ζ2 (этого требует специальная теорема
преобразования масштаба радиальной функции). Величины ζ
определяли путем
усреднения результатов оптимизации для близких по строению молекул.
Соответствующие базисы обозначали STO-nG, (n — число гауссиан в СОГТ).
Экспоненты гауссиан брались одинаковыми для базисных функций, описывающих
орбитали с тем же самым главным квантовым числом (например, одни и те же
гауссианы использовались для 2s и 2p функций). На этой стадии и возникла
терминология, в основном используемая в настоящее время.
Минимальный атомный базисный набор. Минимальный атомный базисный набор
включает только одну функцию на каждую АО атомного остова, занятую парой
электронов, и одну функцию на каждую валентную орбиталь каждого атома в
основном состоянии, в число которых входят все орбитали частично занятых
подоболочек. Минимальный базисный набор для водорода состоит из 1 функции
(например, единственной СОГТ). Для всех элементов второго периода периодической
системы такой базис описывает функции s- и p-типа: 1s, 2s, 2px, 2py, 2pz. Для
атомов от Na до Ar используют 9 функций, от K до Ca — 13 функций и т.д.
Минимальный базисный набор называют также одноэкспонен-циальным (или единичным
зета-набором (сокращение — SZ), где Z означает экспоненциальный множитель в
ОСТ).
Расширенные атомные базисные наборы. Параметры СОГТ находят оптимизацией,
добиваясь минимума энергии свободного атома или атома в молекуле. Чтобы
добиться лучшего описания АО, каждую атомную орбиталь описывают большим
количеством функций: двумя, тремя и т.д. Параметры базисных функций также ищут
с помощью вариационного принципа. Соответственно, различают базисы двух- (DZ),
трехэкспоненциальный (TZ) и т.д.
Поляризационные и диффузные функции. При описании химической связи наборы
СОГТ, полученные расчетом отдельных атомов по Хартри-Фоку, часто дополняются
другими функциями. Чаще всего используют поляризационные и диффузные функции.
Поляризационные функции помогают лучше описать межатомные взаимодействия
и химическую связь. Эти функции имеют более высокие значения орбитального
квантового числа l, чем у занятой электронами атомной орбитали соответствующего
атома в основном состоянии. Экспоненты для них нельзя получить из атомных
вычислений по Хартри-Фоку, так как в основном состоянии эти АО не заселены
электронами. Поэтому параметры поляризационных функций определяют при расчетах
молекул.терминология применяется и для поляризационных функций. Так, DZP
означает двухэкспоненциальный базис, в который дополнительно включены
поляризационные функции, TZP — трехэкспоненциальный базис плюс поляризационные
функции и т.д. Иногда указывают число наборов поляризационных функций: ТZDP
(или TZ2P) означает трех-экспоненциальный Z-базис плюс два набора
поляризационных функций. Для молекул, включающих атомы от Li до F, в качестве
поляризационных функций обычно используют шесть d-ОГТ, для атома водорода — три
р-ОГТ.
Диффузные функции важны для правильного описания анионов и слабых связей
(например, водородных), для вычислений дипольного момента, поляризуемости и
т.д. Это обычно гауссианы s- и p-типа с очень маленькими экспонеци-альными
множителями, медленно спадающие с увеличением расстояния от ядра.
Базисные наборы Попла. Иное соглашение было принято Дж. Поплом с
сотрудниками, внесшими огромный вклад в развитие неэмпирических расчетов.
Структура базисного набора дается для целой молекулы, а не для отдельных
атомов, как по Фудзинаге и Даннингу. Обозначения n-ijG или n-ijkG
расшифровываются так: n — число ОГТ для внутренних оболочек; ij или ijk — число
ОГТ для СОГТ в валентных оболочках; ij обозначения описывают валентные DZ
наборы, ijk — валентные TZ наборы. Последние называются также
валентно-расщепленными базисными наборами.
В базисных наборах Попла число гауссиан s- и p-типа для той же самой
sp-электронной подоболочки одинаково, и они имеют одинаковые экспоненты. Однако
коэффициенты разложения для СОГТ s- и p-типа различны. Базисные наборы Попла
могут также быть расширены за счет включения поляризационных функций d-типа для
неводородных атомов (n-ijG* или n-ijkG*) и p-функций для атомов водорода
(n-ijG** или n-ijkG**). Так, в молекуле метана СН4 базис 4-31G** предполагает
наличие 4-х ОГТ для единственной остовной 1s-АО углерода, 3-х и 1-й ОГТ для
каждой из двух функций, аппроксимирующей валентные (2s, 2px, 2py, 2pz) АО
углерода (DZ базис), плюс 6 поляризационных 3d-АО на атоме С. Каждый атом Н
описывается двумя s-функциями и тремя поляризационными функциями р-типа. Полное
число базисных функций равно:
{1 (1s) + 2*[1 (2s) + 3 (2p)] + 6 (3d)} + 4*[2 (1s) + 3 (2p)] = 35.
При введении диффузных функций используются следующие обозначения:
n-ij+G, или n-ijk+G. Это означает, что к стандартному базисному набору для
неводородных атомов добавлен диффузный гауссиан s-типа и 3-й гауссиан p-типа:
все они имеют одинаковые экспоненты. Наборы n-ij++G, или n-ijk++G получены из
предыдущих добавлением 3-х диффузных гауссиан p-типа для атома водорода.
Таблица 1. Некоторые базисные наборы Попла для молекул, содержащих атомы
от Н до F
1.3 Анализ заселенностей орбиталей
Химическую связь можно охарактеризовать количественно, оценивая вклады
различных АО в МО. Используя приближение МО ЛКАО, удобно ввести матрицу
плотности или матрицу зарядов-порядков связей P c элементами
(20)
(суммирование ведется по занятым МО). Электронная часть энергии молекулы
с закрытыми оболочками записывается с помощью этой матрицы весьма компактно:
(21)
Где hμν — одноэлектронные интегралы, описывающие кинетические энергии
электронов и потенциальные энергии их притяжения к ядрам, — интегралы электрон-электронного
взаимодействия, <μλ|νσ> — обменные интегралы.
Матрица плотности описывает распределение электронной плотности по
молекуле в орбитальном приближении следующим образом (закрытые оболочки):
(22)
Перепишем выражение (22) таким образом, чтобы выделить вклады АО атомов А
и В:
(23)
Индексы I и J в выражении (23) нумеруют атомы, а α
и β
— АО, принадлежащие этим
атомам. Интегрируя левую и правую части выражения (23), имеем:
(24)
(интеграл перекрывания Sαβ(I,J)=1, если α=β,
I=J). Таким образом,
полное число электронов молекулы N в приближении МО ЛКАО оказывается формально
распределенным по атомам и связям между ними. Величина 2Рαα(I,I)
есть электронная
заселенность орбитали α, центрированной на атоме А, а величина 2Рαβ(I,J)Sαβ(I,J)
есть электронная
заселенность перекрывания орбиталей α и β, центрированных на атомах I и J.
Малликен предложил оценивать электронные заселенности атомов, деля
заселенности перекрывания орбиталей между каждой рассматриваемой парой атомов
поровну. Тогда полная электронная заселенность атомной орбитали равна
, а полное число электронов,
приписываемых атому I, определяется соотношением
(25)
В результате, эффективный заряд атома qI в единицах «число электронов»,
определяется как разность qI = ZI — QI , где ZI — атомный номер атома А.
Полная межатомная электронная заселенность связи
(26)
характеризует прочность связи между парами атомов I и J в молекуле.
Описанный анализ электронных заселенностей орбиталей по Малликену дает лишь
приближенную оценку распределения заряда по молекуле: получаемые величины
зависят от используемых при расчете метода и базиса, а деление электронов между
атомами без учета природы последних неправомочно. Кроме того, в ортогональном
базисе все электроны оказываются формально распределенными только между
атомами: в этом случае говорят об анализе электронных заселенностей по Лёвдину.
Тем не менее, анализ заселенностей орбиталей по Малликену проводится всеми
современными квантово-химическими программами и используется вместе с другими
результатами расчета.
Величины 2Рαα, следуя Коулсону, называют
орбитальными зарядами, а 2Рαβ — орбитальными порядками связей: отсюда
и происходит название матрицы Р. Знак 2Рαβ определяет конструктивная или
деструктивная интерференция имеет место при взаимодействии данной пары АО.
Полный порядок связи между атомами находят как сумму вкладов от перекрывания
соответствующих АО.
.4 Методы теории функционала плотности
Многоэлектронная волновая функция Ψ очень просто связана с электронной
плотностью ρ(r) соотношением
ρ(r) = ∫ ψ
(r)ψ(r)dV′
(27)
Электронная энергия системы зависит от электронной плотности основного
состояния следующим образом:
(28)
где — потенциал ядер. Теорема Хоэнберга-Кона утверждает, что
существует одинаковый для всех многоэлектронных систем (универсальный)
функционал электронной плотности G(ρ). Он представляет собой сумму
кинетической энергии и неклассической энергии электрон-электронного взаимодействия,
включая обмен и корреляцию электронов. Причем, точная электронная плотность
основного состояния обеспечивает минимум этого функционала. Теория, которая
изучает способы расчета электронной структуры молекул и кристаллов, основываясь
на минимизации функционала, называется теорией функционала (электронной)
плотности.
Принимают, что электронная плотность основного состояния
взаимодействующих электронов такая же, как и невзаимодействующих. Выражение для
кинетической энергии электронов одинаково для всех систем. Тогда минимизация
функционала относительно одноэлектронных функций ϕi(r) при условии их
ортонормировки и постоянства числа электронов в системе дает уравнения
Кона-Шэма:
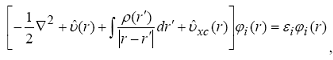
где — обменно-корреляционный потенциал, Exc(ρ)
— зависящая от
электронной плотности обменно-корреляционная энергия. Система уравнений (30)
заменяет в теории функционала плотности стандартные уравнения Хартри-Фока. Они
решаются самосогласованно, причем все приближения связаны с аппроксимацией
обменно-корреляционного потенциала υxc. Все сказанное ранее в отношении
использования и выбора базисных функций в неэмпирических квантово-химических
методах справедливо и в теории функционала плотности.
Энергии одноэлектронных состояний в теории функционала плотности равны
εi(ТФП)= δE(ρ)/δni
, (30)
где ni -электронная заселенность состояния i. В методе Хартри-Фока они
равны разности энергий двух состояний с электронными заселенностями,
отличающимися на единицу:
εi(ХФ) = EХФ[ni = 1] — EХФ[ni = 0]. (31)
Это означает, что одноэлектронные функции ϕi(r), вообще говоря,
отличны от молекулярных орбиталей ϕi(r). Это иногда дает преимущество
теории функционала плотности. Например, разложив (31) в ряд Тейлора и приняв во
внимание соотношение (30), можно получить для потенциала ионизации весьма
точное выражение:
≈ — εi(ni = 1/2). (32)
Можно сказать, что потенциал ионизации может быть вычислен с помощью
некоего переходного состояния с наполовину уменьшенной электронной заселенностью
ВЗМО. Аналогичным образом концепция переходного состояния используется и при
расчетах спектров. Это особенно важно для координационных соединений, где
требуется высокий уровень вычислений методом ХФ, чтобы результаты могли быть
применены для соотнесения переходов.
Простым, но эффективным вариантом теории функционала плотности является
метод Хартри-Фока-Слейтера. Корреляцией электронов здесь, как и в методе
Хартри-Фока, пренебрегают, а обменный потенциал представляется в виде
vx(r) = -3α[(3/8π)ρ(r
)]1/3. (33)
Величина α лежит в пределах 0,7-1,0 (этот метод часто называют
также Xα-методом).
.5 Корреляционные поправки
Электроны с однонаправленными спинами не могут находиться в одной точке
пространства и стараются избегать друг друга. Такое движение электронов
называется коррелированным. Энергия корреляции может достигать 5% от полной
электронной энергии молекулы. Учет корреляционной поправки дополняет расчеты по
методу ССП и приводит к понижению полной энергии молекулы. Осуществляется эта
процедура методом конфигурационного взаимодействия (КВ) или методами,
основанными на теории возмущений Рэлея-Шредингера. Процедура расчета
корреляционной энергии разработана Поплом и соавторами на основе варианта
теории возмущений для молекулярных систем, развитого в работеах Мёллера и
Плессета. В неэмпирическом расчете предусмотрена возможность вычисления
корреляционных поправок второго, третьего и четвертого порядка теории
возмущений («МР2», «МРЗ» или «МР4»).
Значения корреляционных поправок зависят от качества базисного набора, в
котором выполняется процедура ССП, т. е. от способа описания виртуальных
орбиталей в исходной волновой функции. Так, например, базис 3-31ГФ в расчетах
по Мёллеру-Плессету обычно не используются. Вычисление корреляционной энергии,
проводят, как правило, в достаточно широких базисах. Метод Мёллера-Плессета
(МР) не дает возможности определить полное значение корреляционной энергии
(корреляционная поправка МР2 обычно составляет приблизительно половину этого
значения), однако он требует значительно меньше машинного времени по сравнению
с обычным конфигурационным взаимодействием и, как показывает практика, хорошо
воспроизводит энергетические эффекты электронной корреляции при сравнительных
расчетах молекул.
В целях экономии машинного времени и памяти в расчетах по методу МР
остовные орбитали обычно не включаются. В более ранних расчетах по методу МР2
энергию рассчитывали на полном пространстве занятых МО. В ряде задач требуется
оптимизация геометрии с учетом корреляционной поправки второго порядка теории
возмущений. Такой расчет можно провести как по методу BERNY, так и по методу
Мэтага-Сержента, но в этих случаях в расчете по методу МР2 учитываются все
заполненные МО, а не только валентные. Вообще для получения надежных
результатов при оптимизации геометрии в расчетах по методу МР2 следует
применять базисный набор с включением поляризационных фрагментов.
Существенным недостатком метода Мёллера-Плессета и других методов учета
электронной корреляции является то, что они не дают иной информации, кроме
корреляционной поправки к полной энергии молекулы.
.6 Полуэмпирические методы
На практике обычно пользуются как неэмпирическими (ab initio) , так и
полуэмпирическими методами. Они отличаются методикой вычисления матричных
элементов, описывающих электрон-электронные и электрон-ядерные взаимодействия в
системе. В полуэмпирических методах для этой цели используют приближенные
эмпирические формулы и известные из экспериментов параметры атомов. В
неэмпирических методах проводится непосредственный аналитический расчет
матричных элементов.
Принципиальное отличие полуэмпирических методов состоит в полном или
частичном отказе от вычисления одноэлектронных и двухэлектронных интегралов,
фигурирующих в методе ХФ. Вместо точного оператора Фока используется приближенный,
элементы которого получают из эмпирических данных. Соответствующие параметры
подбирают для каждого атома (иногда с учетом конкретного окружения) и для пар
атомов: они либо являются фиксированными, либо зависят от расстояния между
атомами. При этом часто предполагается, что многоэлектронная волновая функция
является однодетерминантной, базис минимальным, а базисные функции — симметричными ортогональными
комбинациями ОСТ χj. Такие комбинации легко получить из исходных ОСТ χj
с помощью преобразования
(34)
где Sij — матрица интегралов перекрывания (эта процедура называется
ортогонализацией функции по Левдину). Расчет МО проводится обычным итерационным
путем.
Полуэмпирические методы работают на несколько порядков быстрее, чем
неэмпирические. Они применимы к большим (и очень большим, например,
биологическим) системам и для некоторых классов соединений дают более точные
результаты. Однако следует понимать, что это достигается за счет специально
подобранных параметров, справедливых лишь в пределах узкого класса соединений.
При переносе на другие соединения те же методы могут дать абсолютно неверные
результаты. Кроме того, параметры часто подбираются таким образом, чтобы
воспроизводить те или иные молекулярные свойства, поэтому придавать физический
смысл отдельным параметрам не следует.
Основные приближения, используемые в полуэмпирических методах, следующие.
) Рассматриваются только валентные электроны: считают, что электроны
атомных остовов лишь экранируют ядра, поэтому эти электроны учитывают в
функциях, описывающих энергию остов-остовного отталкивания (в которое
включается ядер-ядерное отталкивание). Поляризацией остовов пренебрегают.
) В МО учитывают только АО с главным квантовым числом, соответствующим
высшим заселенным электронами орбиталям изолированных атомов (минимальный
базис), причем считают, что базисные функции образуют набор ортонормированных
АО.
) Для двухэлектронных кулоновских и обменных интегралов вводят
приближение нулевого дифференциального перекрывания (НДП):
(35)
Считают, что из-за экспоненциальной зависимости радиальной части АО от
расстояния можно пренебречь двухэлектронными кулоновскими и обменными
интегралами, содержащими произведения разных атомных орбиталей, зависящих от
одного аргумента:
(36)
Это приближение резко уменьшает число вычисляемых двухэлектронных
интегралов, поэтому оно в том или ином виде используется во всех
полуэмпирических методах.
Расширенный метод Хюккеля (Extended Huckel) (РМХ) предназначен для
вычислений молекулярных орбиталей и не позволяет оптимизировать геометрию и
проводить молекулярно-динамические расчеты. В нем используется приближение
невзаимодействующих электронов и в нем не используется приближение ССП.
Метод CNDO (Complete Neglect of Differential Overlap, полное
пренебрежение дифференциальным перекрыванием) является простейшим методом ССП.
Он используется для расчетов основного состояния электронных характеристик систем
с открытой и закрытой оболочками, оптимизации геометрии и полной энергии.
Метод INDO (Intermediate Neglect of Differential Overlap, частичное
пренебрежение дифференциальным перекрыванием) улучшает метод CNDO за счет учета
расталкивания электронов на одном атомном центре. Позволяет проводить расчет
основного состояния систем с открытой и закрытой оболочками, оптимизации
геометрии и полной энергии с использованием ССП.
Метод MINDO3 (Modified INDO, version 3, улучшенный метод INDO, версия 3)
является дальнейшим развитием и расширением метода INDO. Для многих
взаимодействий в нем используются эмпирические параметры вместо соответствующих
вычислений. Этот метод позволяет получать хорошие результаты для больших
органических молекул при расчетах основного состояния систем с открытой и
закрытой оболочками, оптимизации геометрии и полной энергии. Это ССП метод.
Метод MNDO является дальнейшим развитием метода MINDO3, в котором
исправлен ряд ошибок последнего. Позволяет проводить качественные расчеты
электронной и атомной структур органических молекул, содержащих атомы 1-й и 2-й
главных подгрупп (но не атомов переходных элементов). Этот метод позволяет
получать хорошие результаты для больших органических молекул при расчетах
электронных характеристик системы и теплот образования. ССП метод.
Метод AM1 является улучшением метода MNDO. Один из наиболее точных
методов. Используется для органических молекул, содержащих элементы из главных
подгрупп 1 и 2 групп периодической системы. Возможно, этот метод позволяет
получать более качественные результаты, по сравнению с методом MNDO, для
молекул, содержащих как азот, так и кислород. Вычисляет электронную структуру,
оптимизирует геометрию, рассчитывает полную энергию и теплоты образования. ССП
метод.
Метод PM3 является версией метода AM1. PM3 отличается от AM1 только
величинами параметров. Параметры для PM3 были получены сравнением большого
числа и вида экспериментов с результатами расчетов. Как правило, нековалентные
взаимодействия в методе PM3 являются менее расталкивающими, нежели чем в AM1.
PM3 первоначально предназначался для расчета для органических молекул, но потом
он был также параметризован и для ряда других групп элементов, в частности — и
для переходных металлов. ССП метод.
Метод ZINDO/1 является вариантом метода INDO, адаптированного для
проведения расчетов молекул, включающих атомы переходных элементов.
Эквивалентен последней версии метода INDO/1, который отличается от оригинала
использованием постоянных орбитальных экспонент. ZINDO/1 позволяет вычислять
энергетику и геометрию молекул, содержащих переходные металлы.
Метод ZINDO/S является версией метода INDO, параметризованного для
воспроизведения УФ и видимых оптических переходов при расчетах
конфигурационного взаимодействия (CI) с одночастичными возбуждениями. Полезен
для прогнозирования УФ и видимых спектров, но не пригоден для оптимизации
геометрии или молекулярной динамики.
.7 Методы оптимизации (молекулярное моделирование)
Метод молекулярной механики. Простейшим инструментом молекулярного
моделирования многоатомных систем, является метод молекулярной механики (ММ).
Методы молекулярной механики позволяют использовать классический Ньютоновский
метод вычислений энергии одной точки, равновесной геометрии и молекулярной
динамики объектов вместо квантово-механического подхода (одного из
полуэмпирических методов или неэмпирического метода Хартри-Фока (ab initio)).
В методе молекулярной механики атомы рассматриваются как ньютоновские
частицы, которые взаимодействуют друг с другом посредством неких потенциальных
полей, задаваемых эмпирически. Потенциальная энергия взаимодействия зависит от
длины связей, углов связи, торсионных углов и нековалентных взаимодействий (в
т.ч. сил Ван-дер-Ваальса, электростатических взаимодействий и водородных
связей). В этих расчетах силы, действующие на атомы, представляются в виде
функций координат атомов.
Можно назвать четырех наиболее распространенных метода ММ (MM+, AMBER,
BIO+, OPLS).
Метод MM+ разрабатывался для органических молекул. Он учитывает
потенциальные поля, формируемыми всеми атомами рассчитываемой системы и
позволяет гибко модифицировать параметры расчета в зависимости от конкретной
задачи, что делает его, с одной стороны, наиболее общим, а с другой — резко
увеличивает необходимые ресурсы по сравнению с другими методами молекулярной
механики.
Метод AMBER разрабатывался для белков и нуклеиновых кислот. В нем
существует возможность выбрать опцию либо учета всех атомов по отдельности,
либо опцию объединенного атома, под которым подразумевается группа
эквивалентных атомов с одинаковыми свойствами. В последнем случае несколько
атомов, либо их групп, обрабатываются как один атом с одним типом.+
разрабатывался для биологических макромолекул и во многом повторяет
AMBER.разработан для белков и нуклеиновых кислот. Он подобен AMBER, но более точно
обрабатывает нековалентные взаимодействия.
Метод молекулярной динамики. В настоящее время для теоретического
исследования влияния температуры, в частности, и динамики атомного остова,
вообще (например, во время различного рода атомных перегруппировок и пр.)
широкое применение нашел метод неэмпирической молекулярной динамики, который не
требует введения эмпирических межмолекулярных и межатомных потенциалов для
расчетов.
В подходе неэмпирической молекулярной динамики электронная система
описывается набором волновых функций , которые принадлежат основному
состоянию потенциальной поверхности Борна-Оппенгеймера в любой момент времени,
что позволяет описать совместное движение электронов и ядер, которые
описываются набором координат {Rl}.
При этом фиктивная кинетическая энергия электронов остается малой по сравнению
с кинетической энергией ионов, что позволяет рассчитывать силы, действующие на
ядра в любой момент времени по теореме Гельмана-Феймана для электронных систем,
соответствующих мгновенным ядерным конфигурациям.
Фиктивную электронную динамику, ионную динамику и влияние внешних
условий, например — температуры, описывают уравнения движения Эйлера-Лагранжа:
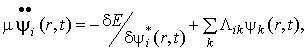
(38)
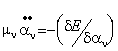
где — функционал полной энергии, получаемый в любом
квантово-химическом методе, набор — любые возможные внешние условия —
температура, давление, объем и пр., — фиктивная масса для электронной
динамики, — произвольный параметр соответствующей размерности. Матрица
является набором множителей
Лагранжа, которые обеспечивают ортонормированность .
Неэмпирическая молекулярная динамика удовлетворяет приближению
Борна-Оппенгеймера только при определенных условиях. Для систем, в которых щель
мала, ионы и электроны сильно взаимодействуют. Это приводит к тепловому
равновесию между ионами и электронами и к отходу от условий применимости
Борна-Оппенгеймера. Для того чтобы преодолеть эти трудности, в неэмпирической
молекулярной динамики используется алгоритм термостатов, один для ионов, другой
— для электронов:
, (40)
где fi- число заполнения.
(41)
Переменные термостата h и x определяются
уравнениями:
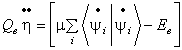
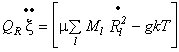
где и
— массы термостатов для электронной и ионных частей
соответственно, и
— необходимые из условий задачи кинетическая энергия
электронов и ионная температура, — число степеней свободы ионов.
Температурные флюктуации, зависящие от времени, включены в уравнения
электронного и ионного термостатов, а динамика всей системы подчиняется
принципу минимума термодинамического потенциала.
В методе неэмпирической молекулярной динамики выполняется закон
сохранения энергии во всей системе (термодинамический потенциал), включающей в
себя электронный и ионный термостаты, который записывается в следующем виде:
, (44)
тогда как энергия электронно-ядерной системы без термостатов из-за
температурных флюктуаций не сохраняется. Следовательно, для систем с нежестким
атомным остовом возможны ситуации, когда из-за невыполнения закона сохранения
энергии температурные условия будут влиять на электронную структуру.
2. КВАНТОВОМЕХАНИЧЕСКИЕ РАСЧЕТЫ ПРИ ПОМОЩИ ПРОГРАММЫ GAUSSIAN
Программа GAUSSIAN,
является, вероятно, самым популярным средством выполнения квантово-химических
расчетов среди основной массы химиков. Основные причины этого — широта охвата
реализованных квантово-химических методик, высокая эффективность и удобный
интерфейс пользователя. Этот пакет моделирования электронных структур
используется для разработок в области химии и биохимии, физике и других
известных и развивающихся областях, связанных с химическими процессами.
Методология моделирования, используемая в пакетах Gaussian, была отмечена
Нобелевской Премией в области химии 1998 года.
Основываясь на фундаментальных законах квантовой механики, Gaussian
позволяет предсказывать энергии, молекулярные структуры и колебательные частоты
молекулярных систем, на ряду со многими другими многочисленными свойствами
молекул, производными от этих базовых характеристик. Пакет может быть
использован для изучения молекул при широком наборе условий, включая устойчивые
виды молекул, которые трудно или невозможно наблюдать в экспериментальных
условиях, например, короткоживущие промежуточные соединения и переходные
структуры. К тому же, к настоящему времени эта программа написана для
нескольких операционных систем и может быть использована для широкого круга
различных ЭВМ.
Недавно появмвшаяся версия GAUSSIAN-03 отличается от предыдущих версий в первую очередь расширением спектра
поддерживаемых квантово-химических методов и их модификаций.
2.1 Основные возможности пакета GAUSSIAN-03
Комплекс программ GAUSSIAN позволяет рассчитывать энергию, структуры молекул, частоты их колебаний,
а также разнообразные свойства молекул в газовой фазе и в растворе, как в
основном, так и в возбужденных состояниях.
Основное направление, в котором развивалась версия GAUSSIAN-03 после G98, это развитие методов
расчета сверхбольших молекулярных систем. Это вызвано, в частности, большим
интересом к расчетам больших биомолекул, и в т.ч. потребностями задач
конструирования лекарств. Среди таких методов можно отметить:
) Методику парционирования молекул ONIOM, развитую проф. Морокума и др.,
в которой вся молекула разбивается на 3 области, которые рассматриваются с
разной степенью точности. Такой подход эффективен, в частности, и для
биомолекул. Например, «активное место» лекарства можно рассчитать с
максимально высокой степенью точности, на наиболее высоком квантово-химическом
уровне; непосредственное окружение активной части можно считать можно посчитать
менее точно, а дальнее атомы — наоброт, учесть максимально приближенно. Метод
ONIOM применим к большим молекулам в различных областях моделирования, включая
моделирование энзимов и механизмов реакций в органических системах,
исследование кластерных моделей поверхностей и поверхностных реакций,
фотохимических реакций органических соединений, замещающих эффектов химической
активности органических и органометаллических соединений, а также гомогенный
катализ.
) Быстрый метод мультиполей (FMM) в схеме DFT в сочетании с
использованием технологии разреженных матриц, реализованный в G98, позволяет,
по мнению разработчиков, достигнуть линеаризации «вычислительной
стоимости», что делает возможным применять DFT для молекул большего
размера, в т.ч. в расчетах частот.
3) В GAUSSIAN-03 получила дальнейшее развитие
методика оптимизации геометрии. В результате стало возможным проводить
неэмпирические расчеты молекулярных систем, содержащих много тяжелых атомов, с
оптимизацией геометрии. Также возможно моделирование периодических систем,
таких как полимеры и кристаллы, посредством использования периодических
граничных условий. Например, GAUSSIAN-03 позволяет предсказать равновесные геометрии и переходные структуры
полимеров, изучать их реактивность посредством предсказания энергии
изомеризации, моделировать запрещенные энергетические зоны веществ.
) Моделирование очень широкого диапазона спектров и спектроскопических
свойств молекул. GAUSSIAN-03
позволяет вычислять многие тензоры, вносящие вклад в сверхтонкий спектр
молекул, позволяя исследовать нелинейные молекулы так же легко, как и линейные.
) Использование Модели Поляризуемого Континуума (Polarizable Continuum
Model, PCM) для моделирования систем в растворах, для которой характерно
представление растворителя как поляризуемого континуума и помещение
растворяемого вещества в полость внутри растворителя. поддержку SCRF PCM
поддерживается в широком спектре методов (ХФ, DFT, MP2/3/4(SDQ), QCISD, CCD,
CID, CISD)
В программах GAUSSIAN-03, как и
в предыдущей версии G98 существуют возможности расчета свойств:
· тензоров экранирования и химсдвигов ЯМР на уровне MP2 (ранее
поддерживались методы XФ, DFT);
· VCD — интенсивности на уровне XФ и DFT;
· рамановские интенсивности на уровне DFT и MP2 (ранее их
расчеты поддерживались на уровне ХФ).
· методы расчета возбужденных состояний: ZINDO для расчетов
сверхбольших молекул и время-зависимые методы RBA на уровне ХФ и DFT, которые
дополняют имеющиеся ранее вохможности CIS.
· внедрены новые функционалы плотности в методе DFT. улучшены
схемы определения пути реакции;
· реализован метод IRCMax для более точного определения
структуры переходного состояния;
· cделаны доработки в реализации псевдопотенциальных методик;
так, полулокальные ECP стали доступны с проекторами для любых угловых моментов,
и достигнута возможность аналитического расчета вторых производных; добавлены
новые схемы параметризации ECP;
· добавлены новые встроенные базисные наборы гауссовских
функций, в т.ч. Midi!, сс-pV6Z, cc-pVDZ, cc-pVTZ и др., включены новые базисы
EPR-II и EPR-III, эффективные для расчетов констант сверхтонкого взаимодействия
в методе DFT
GAUSSIAN-03 позволяет выполнять вычисления на высокопроизволительных
вычислительных кластерах посредством использования пакета TCPLinda.
Использование параллельных систем для вычислений основано на параллельной
реализации части методов, используемых в GAUSSIAN-03. Методы HF, CIS=Direct и DFT
являются распараллеленными, вычисления TDDFT и MP2 энергий является также
распараллеленным. Использование этих методов в моделировании позволяет
распараллеливать процесс решения автоматически, используя лишь настройки
исходной задачи.
Линейно масштабируемые (FMM) алгоритмы, используемые в GAUSSIAN-03 по умолчанию для молекул с
количеством атомов более 65, не являются параллельными. Для получения реального
преимущества использования параллельных вычислений в GAUSSIAN-03, количество атомов в моделируемых
молекулах должны превышать 300.
2.2 Принцип работы программ GAUSSIAN
Начиная с G80 программы
серии GAUSSIAN построены по одному принципу, тело
программы состоит из серии линков, которые представляют собой отдельную
программу. Каждый линк загружается в течении расчета по мере необходимости,
запуск и обмен данными между линками осуществляется отдельной управляющей
программой. Линки обьединены группами в оверлеи по принципу выполнения сходных
функций. Каждый линк имеет свой трехзначный или четырехзначный номер. Последние
две цифры означают номер линка в оверлее, первые цифры- номер оверлея. Пример
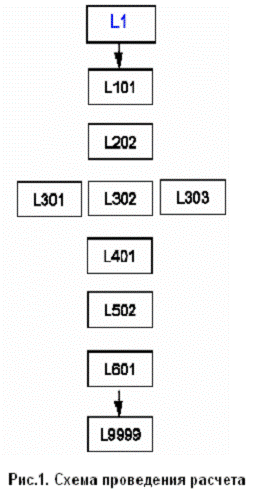
построения расчета приведен на схеме рис.
Оверлей 0 определяет набор файлов и машинных параметров, необходимых для
решения задачи и задает последовательность выполнения отдельных линков, исходя
из последовательности ключевых слов.
Оверлей 1 выполняет считывание (заголовок, заряд, мультиплетность, Z-матрица) и контроль оптимизации
геометрии. Оверлей 1 включает несколько линков, где L101 считывает задание и спецификацию молекулы, L102, L103, L105, L109 определяет выбор метода
оптимизации, соответственно, Флетчера-Пауэлла, BERNY и Метага-Сержента, Ньютон-Рапсона, L108-расчет поверхности потенциальной
энергии, L118- расчет траекторий хим. реакций, L120- контроль ONIOM расчетов и т.д.
Число Линков растет с каждой новой версией и их спецификации можно увидеть в
справке для версии программы. (L101-Reads title and molecule specification, L102-FP
optimization, L103-Berny optimizations to minima and TS, STQN transition state
searches, L105-MS optimization, L106-Numerical differentiation of
forces/dipoles to obtain polarizability/hyperpolarizability,
L107-Linear-synchronous-transit (LST) transition state search, L108-Potential
energy surface scan, L109-Newton-Raphson optimization, L110-Double numerical
differentiation of energies to produce frequencies, L111 Double num. diff. of
energies to compute polarizabilities & hyperpolarizabilities, L113-EF
optimization using analytic gradients, L114-EF numerical optimization (using
only energies), L115-Follows reaction path using the intrinsic reaction
coordinate (IRC), L116-Numerical self-consistent reaction field (SCRF),
L117-Post-SCF SCRF, L118 Trajectory calculations, L120-Controls ONIOM
calculations)
Оптимизация по методу X. Бернарда Шлегеля (BERNY) самая быстрая и
вычисляет аналитически градиенты энергии и численно приближенную матрицу
силовых постоянных, которая постоянно обновляется в процессе оптимизации, для
оценки положения минимума энергии. Однако для циклических молекул, а также для
молекул с необычными силовыми постоянными она может оказаться неэффективной:
процесс оптимизации будет проходить очень медленно или вообще результаты
окажутся неверными. Если оптимизация геометрии дает неверные результаты, то
следует обратиться к методу Мэтага-Сержента. В нем применена другая стратегия
для отыскания структуры с минимальной энергией. Он работает медленнее, чем
BERNY, но более надежно. Третий вариант оптимизации- метод Флетчера-Пауэлла. Он
предусмотрен для таких ситуаций, когда не представляется возможным вычислить
градиенты аналитически. В этих случаях метод Флетчера-Пауэлла выбирается
программой автоматически. Затем градиенты энергии оцениваются методами конечных
разностей. Эта процедура может быть использована для любых способов расчета
энергии, но она чрезвычайно медленна по сравнению с методами аналитического
расчета градиентов (сил на атомах).
Оверлей 2 содержит линк L202
осуществляющий расчет декартовых координат атомов молекулы в соответствии с Z-матрицей, определяет симметрию
молекулы, которая используется в дальнейшем при расчете интегралов, определении
симметрии МО и электронных состояний. (L202-Reorients coordinates, calculates symmetry, and
checks variables).
Оверлей
3 содержит боле10 линков, которые: L301-устанавливает набор базисных функций для каждого атома в соответствии с выбранным ключевым словом, L301, остальные линки L303- L319 рассчитывают различного типа интегралы и их первые производные (L301-Generates basis set information, L302-Calculates
overlap, kinetic, and potential integrals, L303-Calculates multipole integrals,
L308-Computes dipole velocity and Rx integrals, L309-Computes ECP integrals,
L310-Computes spdf 2-electron integrals in a primitive fashion, L311-Computes
sp 2-electron integrals, L314-Computes spdf 2-electron integrals, L316-Prints
2-electron integrals, L319-Computes 1-electron integrals for approximate spin
orbital coupling).
Оверлей
4 содержит: линк L401, который создает начальный набор МО для итерационной процедуры ССП, L402- проведение полуэмпирических расчетов и расчетов методом молекулярной механики, L405- проведение расчета
методом полного
учета взаимодействия электронных конфигураций -Complete Active Space Multiconfiguration SCF
(MC-SCF)(L401-Forms the initial MO guess, L402-Performs semi-empirical and
molecular mechanics calculations, L405-Initializes an MCSCF calculation).
Оверлей 5 в отличии от других оверлеев содержит линки, которые не имеют
общего набора опций, так как в каждой задаче используется только один из
линков. Линки оверлея 5 содержат процедуры самосогласованного расчета с
использованием различных методов: L502- метод Хартри-Фока для систем с открытыми и замкнутыми оболочками,
все прямые методы и т.д., L503-
производится расчет выбранным методом способом скорейшего спуска, L510- многоконфигурационный расчет (L502-Iteratively solves the SCF equations (conven. UHF & ROHF, all direct methods, SCRF), L503-Iteratively
solves the SCF equations using direct minimization, L506-Performs an ROHF or
GVB-PP calculation, L508-Quadratically convergent SCF program, L510-MC-SCF).
Оверлей 6 осуществляет анализ волновых функций, которые рассчитываются в
оверлее 5. Линк L601 проводит
анализ заселенностей, рассчитывает таблицу собственных значений, заселенности
перекрываний, орбитальные заселенности и дипольные моменты, L602- расчет электронных свойств, L607- проводит анализ натуральных
орбиталей, L609- анализ атомных и молекулярных
свойств (L601-Population and related analyses (including multipole moments), L602-1-electron properties (potential, field, and field gradient), L604-Evaluates MOs or density over a grid of points, L607-Performs NBO analyses, L608-Non-iterative DFT energies, L609-Atoms in Molecules properties).
Оверлей 7 рассчитывает первые и вторые производные электронных интегралов
— линки L701- L703. Эти три линка используются при оптимизации геометрии
молекулы по методу ССП при помощи сил, вычисленных аналитическим способом. Линк L716 вычисляет силы на атомах по значениям первых
производных (L701-1-electron integral
first or second derivatives, L702 2-electron integral first or second
derivatives (sp), L703-2-electron integral first or second derivatives (spdf),
L709-Forms the ECP integral derivative contribution to gradients,
L716-Processes information for optimizations and frequencies)
Оверлей
8 (L801-Initializes transformation of 2-electron integrals, L802-Performs
integral transformation (N3 in-core), L803-Complete basis set (CBS)
extrapolation, L804-Integral transformation, L811-Transforms integral
derivatives & computes their contributions to MP2 2nd derivatives) и Оверлей 9 (L901-Anti-symmetrizes
2-electron integrals, L902-Determines the stability of the Hartree-Fock
wavefunction, L903-Old in-core MP2, L905-Complex MP2, L906-Semi-direct MP2,
L908-OVGF (closed shell), L909-OVGF (open shell), L913-Calculates post-SCF
energies and gradient terms, L914-CI-Singles, RPA and Zindo excited states; SCF
stability, L915-Computes fifth order quantities (for MP5, QCISD(TQ) and
BD(TQ)), L918-Reoptimizes the wavefunction) предназначены для расчета
электронных корреляций. Линк
L901 проводит начальные расчеты для
корреляционных расчетов, Линки L903, L905, L906 выполняют корреляционные расчеты по методу
Меллера-Плессета, расчет функций Грина для систем с открытой и замкнутой
оболочками, L918 осуществляет начальное
приближение при оптимизации волновой функции, если зафиксирована ее
нестабильность.
Оверлей 10 содержит линки L1002
расчитывающие различные молекулярные свойства, включая спектральные (ЯМР),
линки L1003 и L1014 для расчета конфигурационных взаимодействий возбужденных
состояни й (L1002-Iteratively solves the CPHF equations; computes various properties (including NMR), L1003-Iteratively solves the CP-MCSCF equations, L1014-Computes analytic
CI-Singles second derivatives).
Оверлей 11 рассчитывает производные электронных интегралов- линки L1101, L1102, L1110-
L1112. Эти три линка используются при оптимизации геометрии молекулы (L1101-Computes 1-electron integral derivatives,
L1102-Computes dipole derivative integrals, L1110-2-electron integral
derivative contribution to Fx, L1111-2 PDM and post-SCF derivatives, L1112-MP2
second derivatives).
Оверлей 99-последний оверлей с линком L9999 производит разгрузку комьютера, записывают результаты
расчета в архив и заканчивают работу одной из цитат, содержащихся в тексте
программы.
.3 Задание расчета и структура входного файла
Для проведения квантовомеханических расчетов с использованием программы GAUSSIAN необходимо дать входное задание,
которое может прдставлено в виде файла определенной структуры. Это можно
осуществить в виде отдельного файла, который считывается после запуска
программы GAUSSIAN или это можно сделать с помощью
отдельной вспомогательной программы для ввода задания и визуализации
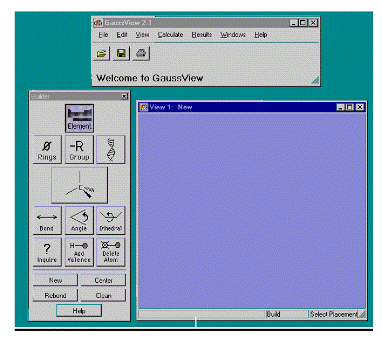
результатов расчета- GaussView. При запуске этой программы появляется три окна (i) GaussView X.Y, (ii) Builder и (iii) View1 (рис. 2 ). X.Y- номер версии
программы.
Рис.2. Окна программы GaussView после ее запуска
Из окна GaussView X.Yможно считать и
записать в память машины входной файл, из окна Builder возможна генерация геометрии молекулы с
использованием кнопок для выбора вида атома, длины связи, углов, готовых
химических группировок и т.д. Окно View служит для визуализации молекулы. Например, для построения молекулы
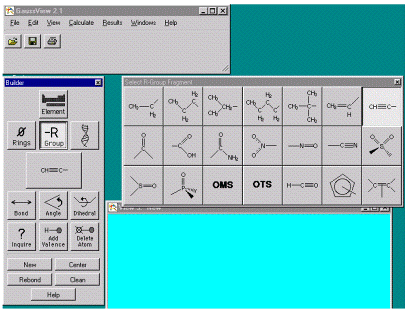
ацетилена C2H2 надо кликнуть на кнопку -R Group в окне Builder,
при этом появляется окно Select
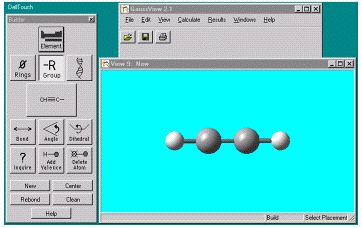
_R Group Fragment, выбрать группу CH_C__, после двойного клика в окне View появляется структура молекулы C2H2 в стиле Ball and Stick (рис. 3,4 ).
Рис.3,4. Выбор стандартного фрагмента молекулы CH_C__ и построение
В окне View структуры молекулы C2H2 в стиле Ball and Stick.
После построения молекулы переходим к заданию расчетных параметров. Для
этого кликаем на Calculate и
выбираем Gaussian (в окне GaussView), после чего появляется окно заданий
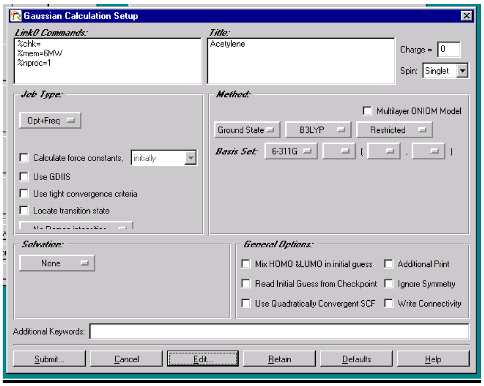
Gaussian Calculation Setup (рис.5). Заполнение различных окон и выбор методики
расчета в этом окне позволяют полностью сформировать входной файл, необходимый
для запуска программы расчета GAUSSIAN. Для выбранного нами примера ацетилена необходимо в окне Title внести комментарии для идентификации
расчета (например, Acetylene).
Выбираем заряд молекулы Charge
равный 0 и мультиплетность в окне Spin как Singlet.
Рис.5. Окно заданий
Gaussian Calculation Setup.
Кнопка Job Type позволяет выбрать тип расчета из списка реализуемых в
программе GAUSSIAN. Если нам необходимо произвести
оптимизацию геометрии молекулы с расчетом частот колебаний, то мы выбираем Opt+Freq. Выбор спецификации No Raman Intensities позволяет нам увеличить скорость
расчета, однако, если это необходимо, можно также рассчитать и интенсивности
рамановского спектра. Далее необходимо выбрать метод расчета и базисный набор.
Кнопками на панели Method выбираем
следующие спецификации расчета: Ground state, B3LYP, Restricted, базисный набор: 6-311G. В
окне Solvation выбираем none, так как расчет производим не в растворе. В окне General Options не выбираем не одного окна. Окончательно все параметры
можно записать в память ЭВМ в виде входного файла кликом Submit и выбрав имя файла и папку для
хранения на диске.
.4 Структура Input File.
Образованный входной файл, содержащий задания для расчета при помощи
программы GAUSSIAN имеет определенную структуру,
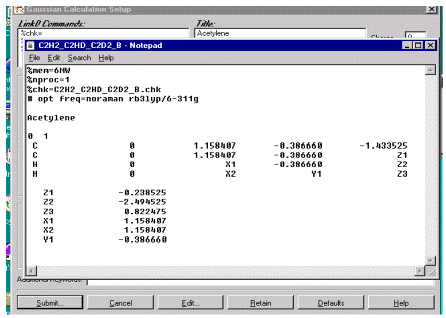
состоящую из ключевых слов и порядка их расположения. На рис.6 приведен пример
такого задания для рассматриваемого расчета оптимизации и частот колебаний
молекулы C2H2.
Рис.6. Пример задания для расчета оптимизации и частот колебаний
Первые две строки генерируются при запуске программы и указывают на
количество оперативной памяти, нобходимой для расчета и количество
задействованных процессоров. Знак % означает, что все записи после него
являются не исполняемыми, а информационными. Третья строка содержит название
автоматически создаваемого файла с результатами текущих расчетов (checkpoint file).
Символы # , #T, #р в начале
командной строки характеризуют разную степень объема выводимых результатов
расчета на печать. В последнем случае вся расчетная информация выдается на
печать.
Ключевое слово opt
указывает, что будет производиться оптимизация геометрии молекулы. Так как не
указывается спецификация процедуры оптимизации, то поиск оптимальной геометрии
будет производиться по умолчанию с помощью процедуры BERNY.
freq=noraman указывает на расчет частот колебаний
без расчета интенсивностей рамановского спектра.
Ключевое слово rb3lyp означает, что расчет будет
производиться методом теории функционала плотности с использованием
трехпараметрического функционала Becke
и учетом корреляции электронов методом Lee, Yang, Parr.
Ключевое слово 6-311G
указывает используемый базис, характеризующийся описанием орбиталей остова
шестью примитивными гауссовыми функциями, тремя и одной функцией для валентных
s- и р-орбиталей и одной функцией для d-орбиталей, которые выполняют роль диффузных функций.
Следующий набор ключевых слов разделен пустой строкой после которой идет
строка с заголовком расчета, где указывается, обычно, название молекулы и
другая информация, необходимая для идентификации конкретного расчета.
После пустой строки указывается заряд charge и multiplicity молекулы. Мультиплетность точно соответствует мультиплетности
электронного состояния: 1-синглет, 2-дублет, 3-триплет и т.д.
Далее идет Z-матрица
молекулы, в которой кроме длин связей, также могут быть указаны значения углов
между связями. Любой набор букв может служить определенными символами
переменных. Если какие-либо переменные остаются постоянными в процессе оптимизации,
то в Z-матрице приводятся их численные
значения. В конце задания геометрии приводится пустая строка.
В зависимости от расчетной задачи содержание входного файла может иметь
различное содержание, в котором меняются ключевые слова цели, методов расчета,
количества выводимой информации и т.д. В каждом конкретном случае необходимо
пользоваться инструкцией для полбзователей GAUSSIAN (Gaussian User’s Guide). Ниже приведен список ключевых слов
для методов и способов расчета.
НЕЭМПИРИЧЕСКИЕ МЕТОДЫ:- Hartree Fock (uses RHF for
singlets and UHF for others)- restricted Hartree Fock- unrestricted Hartree
Fock- spin-restricted open-shell Hartree Fock- two open shell singlet wave
function- generalized valence bond — complete active space MCSCF-
Moller-Plesset second order correlation energy correction- Moller-Plesset third
order correlation energy correction- same as MP4SDTQDQ — Moller-Plesset fourth
order correlation energy correction with double and quadruple substitutions.SDQ
— Moller-Plesset fourth order correlation energy correction with single, double
and quadruple substitutions.SDTQ — Moller-Plesset fourth order correlation
energy correction with single, double, triple and quaduple substitutions.- same
as CISD- configuration interaction with single excitations- configuration
interaction with double excitations- configuration interaction with single and
double excitations- quadratic configuration interaction with single and double
excitations(T) — quadratic configuration interaction with single and double
excitations and triples contribution to the energy
БАЗИСНЫЕ НАБОРЫ:
|
базис |
дополнение |
атомы |
|
STO-3G |
* |
H — Xe |
|
3-21G |
* ** |
H — Cl |
|
4-21G |
* ** |
|
|
4-31G |
* ** |
H — Ne |
|
6-21G |
* ** |
|
|
6-31G |
+ ++ * ** |
H — Cl |
|
LP-31G |
* ** |
|
|
LP-41G |
* ** |
|
|
6-311G |
+ ++ * ** |
H — Ar |
|
MC-311G |
H — Ar |
|
|
D95 |
+ ++ * ** |
H — Cl |
|
D95V |
+ ++ * ** |
H — Ne |
|
SEC |
+ ++ * ** |
H — Cl |
|
CEP-4G |
+ ++ * ** |
H — Cl |
|
CEP-31G |
+ ++ * ** |
H — Cl |
|
CEP-121G |
+ ++ * ** |
H — Cl |
|
LANLIMB |
H — Bi (кроме lanthanides) |
|
|
LANLIDZ |
H — Bi (кроме lanthanides) |
ПОЛУЭМПИРИЧЕСКИЕ МЕТОДЫ:
AM1 — Austin method one- complete neglect of differential
overlap- intermediate neglect of differential overlap- modified intermediate
neglect of differential overlap third modification.- modified neglect of
differential overlap
СПЕЦИФИКАЦИЯ РАСЧЕТА- distances in Angstroms- distances
in bohrs- angles in degrees- angles in radians- generate a cube file- for cube
file generation- do integrals as needed (vice in a file on the disk)- do integrals
in core memory- add a finite field to the calculation- frequency
determination=noraman — frequency determination without Raman intensities- put
basis in output file- put basis in output file in format for generalized input-
follow a reaction path- linear synchronous transit — optimize all variables-
geometry optimization- calculate polarizability and hyperpolarizability, if
possible=none — no population analysis=min — minimal printing of Mulliken
population analysis=reg — some printing of Mulliken population analysis=full —
full printing of Mulliken population analysis=bonding — bonding population
analysis=no — natural orbital analysis=noab — natural orbital analysis for
separate alpha and beta spins=grid — computes electrostatic potential=field —
computes electrostatic potential and field=EFG — computes electrostatic
potential, field and field gradients- puts various information in a separate
output file- read in masses for each atom- restart optimization from a
checkpoint file- optimization of a transition state
.5 Проведение расчета и структура выходного файла
После записи входного файла на диске ЭВМ для запуска программы расчета
необходимо или загрузить непосредственно программу GAUSSIAN, например, кликнув на
соответствующий этой программе ярлык или выйти на запуск этой прграммы
непосредственно из GaussView после
клика на Submit. В последнем случае появляется окно
с предложением установить имя входного (.gjf) и выходного файлов (.out), после чего появляется окно программы GAUSSIAN (рис. 7) и начинается процедура
счета. По оканчанию счета работа программы останавливается и запись выходного
файла происходит автоматически.
Ниже приведены результаты расчета для оптимизации и расчета частот для
молекулы ацетилена, как они представлены в выходном файле. А самом начале
указан адрес линка, запускающего расчет, далее указывается версия программы, ее
правовладелец, адреса, авторы и т.д., время запуска программы.
Entering Link 1 = C:G98Wl1.exe PID= 856.(c)
1988,1990,1992,1993,1995,1998 Gaussian, Inc.Office Park, Building 6,
Pittsburgh, PA 15106 USAthis work as:98, Revision A.9,
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,
……
*********************************************98:
x86-Win32-G98RevA.9 19-Apr-2000
06-Nov-2007
Рис.7. Окно программы GAUSSIAN.
Количество оперативной памяти, нобходимой для расчета и количество
задействованных процессоров, имя файла автоматической записи результатов (.chk).
*********************************************
%mem=6MW
%nproc=1use up to 1 processors via shared memory.
%chk=acetylene.chkroute: MaxDisk=2000MB
Повторяется строка задания со списком ключевых слов.
—————————————————
# opt freq=noraman rb3lyp/6-311g geom=connectivity
Последующий набор строк определяет алгоритм выполнения вычислений
программой, т.е. определяет порядок вызова линков из определенных оверлеев.
Каждая строка соответствует оверлею, номер которого стоит первым. Значение
чисел между двумя наклонными чертами определяют значение опций, с которыми
выполняются линки данного оверлея. Например, строка 4/7=1/1; соответствует
оверлею 4, в котором выполняется линк 401 (создается начальный набор МО для
итерационной процедуры ССП), при этом опция 7 имеет значение, равное 1. полный
список опций дан в инструкции для пограммы. Число в круглых скобках означает
переход через несколько оверлеев, например, 1/14=-1,18=20/3(1) означает, что
если оптимизация не завершена, то следующий за данной строкой оверлей будет
пропущен. Последней строкой стоит оверлей 99 окончания счета и записи
результата.
————————————————-
/9=110,17=6,18=5,40=1/2;
/5=4,6=6,11=2,25=1,30=1/1,2,3;
/7=1/1;
/5=2,38=4,42=-5/2;
/7=2,8=2,9=2,10=2,28=1/1;
//1,2,3,16;
/14=-1,18=20/3(1);
//99;
Строка с заголовком расчета
———
acetiylene
———
Строки с указанием заряда и мультиплетности и Z-матрица молекулы, в которой указаны варьируемые и постоянные
параметры.
Symbolic Z-matrix:= 0 Multiplicity = 10 3.46875 0. -1.31250
3.46875 0. Z10 X1 0. Z20 X2 Y1 Z3:-0.1175-2.37350.94353.468753.468750.
Строка с спецификацией метода оптимизации.
Berny optimization.
Таблица начальных параметров расчета длин связей и углов, необходимых для
оптимизации, а также декартовы координаты молекулы.
! Initial Parameters !
! (Angstroms and Degrees) !
———————— ————————-
! Name Definition Value Derivative Info. !
—————————————————————————-
! R1 R(1,2) 1.195 estimate D2E/DX2 !
! R2 R(1,3) 1.061 estimate D2E/DX2 !
! R3 R(2,4) 1.061 estimate D2E/DX2 !
! A1 L(2,1,3,-1,-1) 180. estimate D2E/DX2 !
! A2 L(1,2,4,-1,-1) 180. estimate D2E/DX2 !
! A3 L(2,1,3,-2,-2) 180. estimate D2E/DX2 !
! A4 L(1,2,4,-2,-2) 180. estimate D2E/DX2 !
—————————————————————————-Radius=3.00D-01
FncErr=1.00D-07 GrdErr=1.00D-06of steps in this run= 20 maximum allowed number
of steps= 100.orientation:
———————————————————————Atomic
Atomic Coordinates (Angstroms)Number Type X Y Z
———————————————————————
6 0 3.468750 0.000000 -1.312500
6 0 3.468750 0.000000 -0.117500
1 0 3.468750 0.000000 -2.373500
1 0 3.468750 0.000000 0.943500
———————————————————————
Матрица расстояний в ангстремах для действительных атомов
Distance matrix
(angstroms):
1 2 3 4
C 0.000000
C 1.195000 0.000000
3 H 1.061000 2.256000 0.000000
H
2.256000 1.061000 3.317000 0.000000
Для определения симметрии используется Z-матрица, точечная группа соответствует тем ограничениям по
симметрии, используемые при оптимизации. Симметрия исходной и оптимизированной
структур может отличаться от симметрии, полученной из Z-матрицы. В обозначении симметрии структурных элементов
указывается, какие атомы совпадают с элементами симметрии. Программа
рассчитывает также число степеней свободы молекулы в рамках данной симметрии,
т.е. количество оптимизируемых параметров. Полная точечная группа и абелевы
подгруппы применяются в других частях программы для экономии машинного времени
за счет использования симметрии, а также для определения симметрии полной
волновой функции и отдельных МО.
Stoichiometry C2H2group D*H[C*(HC.CH)]. of freedom 2point
group D*H NOp 8Abelian subgroup D2H NOp 8concise Abelian subgroup C2 NOp 2
Далее указывается стандартный базис, который приписывается каждому
атомному центру. Далее в программе, используя точечную группу молекулы,
строятся симметризованные базисные функции. Симметрия этих орбиталей обозначена
при помощи символов Малликена. В нашем случае имеются МО, свойства симметрии
которых можно определить по таблице 2.
Таблица 2. Малликеновские символы для обозначения симметрии МО
|
Символ |
Значение |
|
A(B) |
Симметрична |
|
E |
Двухкратно вырождена |
|
T |
Трехкратно вырождена |
|
1(2) |
Симметрична |
|
g(u) |
Симметрична |
|
/ (//) |
Симметрична(антисимметрична) |
Standard basis: 6-311G (5D, 7F)are 10 symmetry adapted basis
functions of AG symmetry.are 0 symmetry adapted basis functions of B1G
symmetry.are 3 symmetry adapted basis functions of B2G symmetry.are 3 symmetry
adapted basis functions of B3G symmetry.are 0 symmetry adapted basis functions
of AU symmetry.are 10 symmetry adapted basis functions of B1U symmetry.are 3
symmetry adapted basis functions of B2U symmetry.are 3 symmetry adapted basis
functions of B3U symmetry.
Ниже печатаются сообщение о применение метода Раффенти для записи и
хранения интегралов и об использовании симметрии для вычисления двухэлектронных
интегралов. Также указано количество рассчитанных интегралов.estimate of integral set expansion from redundant
integrals=1.000.buffers will be 262144 words long.2 integral format.electron
integral symmetry is turned on.
basis functions 62 primitive gaussians
alpha electrons 7 beta electrons
Расчет энергии отталкивания ядер в единицах Хартри = 27.2116 эВ
nuclear repulsion energy 24.9010884632 Hartrees.electron
integrals computed using PRISM.= 32 RedAO= T NBF= 10 0 3 3 0 10 3 3= 32
1.00D-04 NBFU= 10 0 3 3 0 10 3 3
Следующая стадия расчета- определение начального приближения для
процедуры ССП посредством метода INDO.
Печатается симметрия МО начального приближения с разделением на занятые и
свободные орбитали.
Projected INDO Guess.guess orbital symmetries:(SGG) (SGU)
(SGG) (SGU) (SGG) (PIU) (PIU)(SGU) (PIG) (PIG) (SGG) (SGU) (SGG) (SGG) (SGG)
(SGG) (SGG) (SGG) (PIG) (PIG) (PIG) (PIG) (SGU)
(SGU) (SGU) (SGU) (SGU) (SGU) (PIU) (PIU) (PIU)
(PIU)
После того как все необходимые интегралы и начальное приближение
получены, программа переходит к выполнению ССП. Критерием сходимости служит
изменение матрицы плотности на величину, меньшую чем 1.00D-05. В нашем случае сходимость
достигается за 9 итераций .
Requested convergence on RMS density matrix=1.00D-08 within 64 cycles.
Requested convergence on MAX density matrix=1.00D-06.R1 and
R2 integrals in memory in canonical form, NReq= 687310.accuracy reduced to
1.0D-05 until final iterations.convergence to 1.0D-05 achieved. Increase
integral accuracy.Done: E(RB+HF-LYP) = -77.3356007715 A.U. after 9 cycles = 0.3165D-08 -V/T = 2.0033
S**2 =
0.0000
После того как самосогласование достигнуто, печатается полная энергия
молекулы E(RB+HF-LYP) в атомных единицах (1 а.е.= 627.5
ккал/моль). Полная энергия представляет собой сумму энергии отталкивания ядер,
электронной энергии и корреляционной энергии. Приводится значениесходимости по
матрице плотности, достигнутое на последнем итерационном шаге 0.3165D-08 и вириальный коэффициент -V/T равный отношению потенциальной энергии к кинетической,
точное значение которого в соответствии с теоремой вириала равно 2.
Процедура ССП завершается малликеновским анализом заселенностей. В начале
печатаются МО с указанием типа симметрии.
*************************************************************
Population analysis using the SCF density.
*************************************************************Symmetries:(SGG)
(SGU) (SGG) (SGU) (SGG) (PIU) (PIU)(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (PIU)
(PIU)
(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (SGU) (SGG)
(SGU) (PIU) (PIU) (PIG) (PIG) (SGU) (SGG) (SGG)
(SGU)electronic state is 1-SGG.
Энергии МО приведены в Хартри
Alpha occ. eigenvalues — -10.18096 -10.17829 -0.76610
-0.57058 -0.50667occ. eigenvalues — -0.29990 -0.29990virt. eigenvalues —
0.03885 0.03885 0.06440 0.08452 0.25453virt. eigenvalues — 0.26004 0.39692
0.39692 0.52144 0.52144virt. eigenvalues — 0.56815 0.64783 0.71897 0.98990
1.08350virt. eigenvalues — 2.21541 2.28832 2.58573 2.58573 2.69182
Alpha virt. eigenvalues — 2.69182 3.16084 3.22833 23.16698
23.71859
Заселенность атома представляет собой сумму заселенностей, рассчитанных
для всех базисных функций АО. Заселенности для всех атомов сведены в таблицу.
Недиагональные элементы матрицы характеризуют степень перекрывания между
атомами. Например, видно, что перекрывания С1 — Н3 положительное и равно 2∙0.368349,
тогда как С1 — Н4 связи нет и перекрывание отрицательное. Далее приведены
распределение зарядов на атомах с учетом перекрывания, расчет дипольных,
квадрупольных и более высокого порядка моментов молекулы.
Condensed to atoms (all electrons):
2 3 4
C 4.851852 1.024059 0.368349 -0.010217
C 1.024059 4.851852 -0.010217 0.368349
H 0.368349 -0.010217 0.406674 0.001152
H -0.010217 0.368349 0.001152 0.406674atomic charges:
C -0.234042
C -0.234042
H 0.234042
H 0.234042of Mulliken charges= 0.00000charges with hydrogens
summed into heavy atoms:
C 0.000000
C 0.000000
H 0.000000
H 0.000000of Mulliken charges= 0.00000
Electronic spatial extent (au): <R**2>= 60.2656= 0.0000
electronsmoment (Debye):= 0.0000 Y= 0.0000 Z= 0.0000 Tot= 0.0000moment
(Debye-Ang):= -13.4598 YY= -13.4598 ZZ= -7.1390= 0.0000 XZ= 0.0000 YZ=
0.0000moment (Debye-Ang**2):= 0.0000 YYY= 0.0000 ZZZ= 0.0000 XYY= 0.0000=
0.0000 XXZ= 0.0000 XZZ= 0.0000 YZZ= 0.0000= 0.0000 XYZ= 0.0000moment
(Debye-Ang**3):= -15.1152 YYYY= -15.1152 ZZZZ= -37.6696 XXXY= 0.0000= 0.0000
YYYX= 0.0000 YYYZ= 0.0000 ZZZX= 0.0000= 0.0000 XXYY= -5.0384 XXZZ= -12.0664
YYZZ= -12.0664= 0.0000 YYXZ= 0.0000 ZZXY= 0.0000N= 2.490108846321D+01
E-N=-2.292404823474D+02 KE= 7.708108608436D+01
Symmetry AG KE= 3.813333457619D+01B1G KE=
0.000000000000D+00B2G KE= 2.335770561963D-33B3G KE= 6.728674288393D-34AU KE=
0.000000000000D+00B1U KE= 3.442577134687D+01
Symmetry B2U KE= 2.260990080654D+00B3U KE= 2.260990080655D+00
Далее программа приступает к оптимизации. Вычисляются первые производные
интегралы и определяются на их основе силы на атомах в системе координат
заданной ориентации Z-матрицы, которые
приведены ниже в таблице, а затем в системе внутренних координат Z-матрицы, т.е. длин связей и углов.
Программа проводит оценку матрицы вторых производных по значениям первых
производных и проверку на достижение минимума энергии. Далее программа рассчитывает
изменения, которые необходимо внести в Z-матрицу для достижения минимума энергии.
***** Axes restored to original set *****
——————————————————————Atomic
Forces (Hartrees/Bohr)Number X Y Z
——————————————————————
6 0.000000000 0.000000000 -0.016549601
6 0.000000000 0.000000000 0.016549601
1 0.000000000 0.000000000 -0.000096767
1 0.000000000 0.000000000 0.000096767
——————————————————————Forces:
Max 0.016549601 RMS 0.006756462optimization.Forces: Max 0.000010306 RMS
0.000005512for a local minimum.number 1 out of a maximum of 20quantities
printed in internal units (Hartrees-Bohrs-Radians)derivative matrix not updated
— analytic derivatives used.
Программа проводит оценку матрицы вторых производных по значениям первых
производных и проверку на достижение минимума энергии. Далее программа
рассчитывает изменения, которые необходимо внести в Z-матрицу для достижения минимума энергии.
The second derivative matrix:R2 R3 A1 A21.09115-0.01001
0.41100-0.01001 0.00030 0.411000.00000 0.00000 0.00000 0.066910.00000 0.00000
0.00000 -0.01967 0.066910.00000 0.00000 0.00000 0.00000 0.000000.00000 0.00000
0.00000 0.00000 0.00000A40.06691-0.01967 0.06691— 0.04724 0.04724 0.08659
0.08659 0.41070— 0.41101 1.09145between quadratic step and forces= 1.83
degrees.search not attempted — first point.1 RMS(Cart)= 0.00001341 RMS(Int)=
0.000000002 RMS(Cart)= 0.00000000 RMS(Int)= 0.00000000
Значения переменных в таблице, где печатаются их текущие (Old X) и новые значения (New X) и приращения (Delta X) приведены в радиусах Бора, а первая производная энергии (DE/DX) в а.е. Изменение в геометрии получается на первом шаге
осуществляется путем оценки вторых производных, поэтому единственный вклад
вносит квадратичная экстраполяция, Новое значение переменных равно сумме Old X + Delta X. Максимальные и
среднеквадратичные значения сил сравниваются с пороговыми и по достижению
предела порога оптимизация считается успешной.
Variable Old X -DE/DX Delta X Delta X Delta X New X
(Linear) (Quad) (Total)2.27316 0.00000 0.00000 0.00000
0.00000 2.273162.00562 -0.00001 0.00000 -0.00003 -0.00003 2.005602.00562
-0.00001 0.00000 -0.00003 -0.00003 2.005603.14159 0.00000 0.00000 0.00000
0.00000 3.141593.14159 0.00000 0.00000 0.00000 0.00000 3.141593.14159 0.00000
0.00000 0.00000 0.00000 3.141593.14159 0.00000 0.00000 0.00000 0.00000
3.14159Value Threshold Converged?Force 0.000010 0.000450 YESForce 0.000006
0.000300 YESDisplacement 0.000025 0.001800 YESDisplacement 0.000013 0.001200
YES
Оценка изменения энергии при переходе к новой геометрии.
Predicted change in Energy=-2.582548D-10completed.point
found.
Печатается таблица оптимизированных параметровгеометрии молекулы.
—————————-
! Optimized Parameters !
! (Angstroms and Degrees) !
———————— ————————-
! Name Definition Value Derivative Info. !
——————————————————————————
! R1 R(1,2) 1.2029 -DE/DX = 0. !
! R2 R(1,3) 1.0613 -DE/DX = 0. !
! R3 R(2,4) 1.0613 -DE/DX = 0. !
! A1 L(2,1,3,-1,-1) 180. -DE/DX = 0. !
! A2 L(1,2,4,-1,-1) 180. -DE/DX = 0. !
! A3 L(2,1,3,-2,-2) 180. -DE/DX = 0. !
! A4 L(1,2,4,-2,-2) 180. -DE/DX = 0. !
—————————————————————————-
Производится коррекция базисного набора, с расчетом симметрии и энергий
МО, а также маликеновский анализ заселенностей с учетом новой геометрии.
******************************************************************analysis
using the SCF density.
******************************************************************Symmetries:(SGG)
(SGU) (SGG) (SGU) (SGG) (PIU) (PIU)(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (PIU)
(PIU)
(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (SGU) (SGG)
(SGU) (PIU) (PIU) (PIG) (PIG) (SGU) (SGG) (SGG)
(SGU)electronic state is 1-SGG.
Alpha occ. eigenvalues — -10.18297 -10.18047 -0.76439
-0.57157 -0.50662occ. eigenvalues — -0.29867 -0.29867virt. eigenvalues —
0.03649 0.03649 0.06366 0.08430 0.25486virt. eigenvalues — 0.25756 0.39782
0.39782 0.51974 0.51974virt. eigenvalues — 0.56818 0.64781 0.71702 0.97928
1.07979virt. eigenvalues — 2.21614 2.28385 2.58313 2.58313 2.69182
Alpha virt. eigenvalues — 2.69182 3.15893 3.22897 23.16381
23.71155to atoms (all electrons):
2 3 4
C 4.858044 1.018943 0.368300 -0.010634
C 1.018943 4.858044 -0.010634 0.368300
H 0.368300 -0.010634 0.406532 0.001148
H -0.010634 0.368300 0.001148 0.406532atomic charges:
C -0.234654
C -0.234654
H 0.234654
H 0.234654of Mulliken charges= 0.00000charges with hydrogens
summed into heavy atoms:
C 0.000000
C 0.000000
H 0.000000
H 0.000000of Mulliken charges= 0.00000
Electronic spatial extent (au): <R**2>= 60.5983= 0.0000
electronsmoment (Debye):= 0.0000 Y= 0.0000 Z= 0.0000 Tot= 0.0000moment
(Debye-Ang):= -13.4937 YY= -13.4937 ZZ= -7.1092= 0.0000 XZ= 0.0000 YZ=
0.0000moment (Debye-Ang**2):= 0.0000 YYY= 0.0000 ZZZ= 0.0000 XYY= 0.0000=
0.0000 XXZ= 0.0000 XZZ= 0.0000 YZZ= 0.0000= 0.0000 XYZ= 0.0000moment
(Debye-Ang**3):= -15.1902 YYYY= -15.1902 ZZZZ= -37.8567 XXXY= 0.0000= 0.0000
YYYX= 0.0000 YYYZ= 0.0000 ZZZX= 0.0000= 0.0000 XXYY= -5.0634 XXZZ= -12.1537
YYZZ= -12.1537= 0.0000 YYXZ= 0.0000 ZZXY= 0.0000N= 2.478386021537D+01
E-N=-2.289723424465D+02 KE= 7.704465961076D+01
Symmetry AG KE= 3.810532000368D+01B1G KE=
0.000000000000D+00B2G KE= 2.326131213188D-33B3G KE= 6.649958094964D-34AU KE=
0.000000000000D+00B1U KE= 3.442881138382D+01
Symmetry B2U KE= 2.255264111628D+00B3U KE=
2.255264111629D+00polarizability: 8.533 0.000 8.533 0.000 0.000
28.731polarizability: 9.179 0.000 9.179 0.000 0.000 52.199
Производится расчет частот колебаний в молекуле.
Full mass-weighted force constant matrix:frequencies —
0.0006 0.0006 0.0010 7.7848 7.7849 711.2516frequencies — 711.2516 782.2685
782.2685frequencies (cm**-1), IR intensities (KM/Mole),scattering activities
(A**4/AMU), Raman depolarization ratios,masses (AMU), force constants (mDyne/A)
and normal coordinates:
2 3PIG PIU— 711.2515 711.2515 782.2685. masses — 1.5701
1.5701 1.0848consts — 0.4680 0.4680 0.3911Inten — 0.0000 0.0000 129.9314Activ
— 0.0000 0.0000 0.0000— 0.0000 0.0000 0.0000AN X Y Z X Y Z X Y Z
6 0.00 0.16 0.00 0.16 0.00 0.00 0.06 0.00 0.00
6 0.00 -0.16 0.00 -0.16 0.00 0.00 0.06 0.00 0.00
1 0.00 -0.69 0.00 -0.69 0.00 0.00 -0.70 0.00 0.00
1 0.00 0.69 0.00 0.69 0.00 0.00 -0.70 0.00 0.00
5 6SGG SGU— 782.2685 2043.1236 3416.5404. masses — 1.0848
3.8066 1.0848consts — 0.3911 9.3623 7.4607Inten — 129.9314 0.0000
69.6778Activ — 0.0000 0.0000 0.0000— 0.0000 0.0000 0.0000AN X Y Z X Y Z X Y Z
6 0.00 0.06 0.00 0.00 0.00 0.36 0.00 0.00 0.06
6 0.00 0.06 0.00 0.00 0.00 -0.36 0.00 0.00 0.06
1 0.00 -0.70 0.00 0.00 0.00 0.61 0.00 0.00 -0.70
1 0.00 -0.70 0.00 0.00 0.00 -0.61 0.00 0.00 -0.70
— 3522.6947. masses — 1.2302consts — 8.9945Inten —
0.0000Activ — 0.0000— 0.0000 AN X Y Z
6 0.00 0.00 -0.10
6 0.00 0.00 0.10
1 0.00 0.00 0.70
1 0.00 0.00 -0.70
Расчет термодинамических характеристик молекулы: энергии, энтальпии,
теплоемкости и т.д.
——————-
Thermochemistry —
——————298.150 Kelvin. Pressure 1.00000 Atm.1 has
atomic number 6 and mass 12.000002 has atomic number 6 and mass 12.000003 has
atomic number 1 and mass 1.007834 has atomic number 1 and mass 1.00783mass:
26.01565 amu.axes and moments of inertia in atomic units:
2 3— 0.00000 50.90478 50.904780.00000 0.74884 0.662750.00000
-0.66275 0.748841.00000 0.00000 0.00000MOLECULE IS A PROLATE SYMMETRIC
TOP.SYMMETRY NUMBER 2.TEMPERATURE (KELVIN) 1.70148CONSTANT (GHZ) 35.453277point
vibrational energy 71592.9 (Joules/Mol)
.11112 (Kcal/Mol)TEMPERATURES: 1023.33 1023.33 1125.50
1125.50 2939.58
(KELVIN) 4915.61 5068.34point correction= 0.027268
(Hartree/Particle)correction to Energy= 0.030013correction to Enthalpy=
0.030957correction to Gibbs Free Energy= 0.008335of electronic and zero-point
Energies= -77.308456of electronic and thermal Energies= -77.305711of electronic
and thermal Enthalpies= -77.304767of electronic and thermal Free Energies=
-77.327389(Thermal) CV S/MOL CAL/MOL-KELVIN CAL/MOL-KELVIN18.833 7.955
47.6120.000 0.000 0.0000.889 2.981 35.7050.592 1.987 10.876
VIBRATIONAL 17.352 2.987 1.032LOG10(Q) LN(Q)BOT 0.146601D-03
-3.833862 -8.827793
TOTAL V=0 0.511211D+09 8.708600 20.052293(BOT) 0.320810D-12
-12.493752 -28.767928(V=0) 0.111869D+01 0.048710 0.1121580.100000D+01 0.000000
0.0000000.521570D+07 6.717312 15.4671840.876149D+02 1.942578 4.472952
***** Axes restored to original set *****
——————————————————————Atomic
Forces (Hartrees/Bohr)Number X Y Z
——————————————————————
1 6 0.000000000 0.000000000 -0.000010750
6 0.000000000 0.000000000 0.000010750
1 0.000000000 0.000000000 0.000010306
1 0.000000000 0.000000000 -0.000010306
——————————————————————
Cartesian Forces: Max 0.000010750 RMS 0.000006080
Запись в архивный файл результатов расчета, который будет использоваться
в последующих расчетах.
1|1|UNPC-UNK|Freq|RB3LYP|6-311G|C2H2|PCUSER|06-Nov-2007|0||#N
GEOM=ALL
CHECK GUESS=TCHECK RB3LYP/6-311G
FREQ||acetiylene||0,1|C,0.,0.,-0.6014
|C,0.,0.,0.6014511182|H,0.,0.,-1.6627806113|H,0.,0.,1.6627806113
||Version=x86-Win32-G98RevA.9|State=1-SGG|HF=-77.3357242|RMSD=6.698e-0
|RMSF=6.080e-006|Dipole=0.,0.,0.|DipoleDeriv=-0.2489113,0.,0.,0.,-0.
,0.,0.,0.,-0.1822776,-0.2489112,0.,0.,0.,-0.2489112,0.,0.,0.,-0
.1822778,0.2489111,0.,0.,0.,0.2489111,0.,0.,0.,0.1822781,0.2489111,0.,
.,0.,0.2489111,0.,0.,0.,0.1822781|Polar=8.5333455,0.,8.5333455,-0.000
,0.,28.7307553|PG=D*H
[C*(H1C1.C1H1)]|NImag=0||0.05564345,0.,0.055
64345,0.,0.,1.52218580,-0.03411242,0.,0.,0.05564345,0.,-0.03411242,0.,
.,0.05564345,0.,0.,-1.11148433,0.,0.,1.52218580,-0.02700461,0.,0.,0.0
,0.,0.,0.01664460,0.,-0.02700461,0.,0.,0.00547358,0.,0.,0.01664
,0.,0.,-0.42101841,0.,0.,0.01031694,0.,0.,0.41100458,0.00547358,0.,
.,-0.02700461,0.,0.,0.00488643,0.,0.,0.01664460,0.,0.00547358,0.,0.,-
.02700461,0.,0.,0.00488643,0.,0.,0.01664460,0.,0.,0.01031694,0.,0.,-0
.42101841,0.,0.,-0.00030309,0.,0.,0.41100458||0.,0.,0.00001075,0.,0.,-
.00001075,0.,0.,-0.00001031,0.,0.,0.00001031|||@
Одна из многочисленных цитат, содержащихся в программе.
THE NUMBERS ARE MEANINGLESS, BUT THE TRENDS ARE IMPORTANT.
— LARRY BURGGRAF
Время работы программы.
Job cpu time: 0 days 0 hours 0 minutes 11.0 seconds.lengths
(MBytes): RWF= 10 Int= 0 D2E= 0 Chk= 6 Scr= 1
Normal termination of Gaussian 98.
Заключение
Приведенный пример оптимизации геометрии и расчета частот колебаний
молекулы ацетилена показывает только малую часть возможностей программы GAUSSIAN. Основные возможности для последней
версии программы GAUSSIAN-03 были
уже изложены выше. Однако для лучшего представления о всем наборе
вычислительных ресурсов, функционировании программы, наборе методов, базисов и
функционалов, ключевых слов, необходимых для работы следует обратиться к
инструкции для пользователей конкретной версии программы. Эти инструкции можно
найти также на сайте GAUSSIAN [17]. Следует обратить внимание на прилагаемый к программе список примеров
различных расчетов молекул, для которых составлены разработчиками готовые
входные файлы.
Выражаем искренние пожелания в успешном освоении программы GAUSSIAN и проведении с ее помощью
необходимых квантовохимических расчетов.
ВОПРОСЫ И ЗАДАНИЯ
. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ХИМИИ
. Дайте определение адиабатического приближения при решении уравнения
Шредингера.
2. Какие основные приближения использует метод Хартри-Фока?
. В чем заключается принцип Паули?
. В уравнении Хартри-Фока укажите члены, ответственные за
различные взаимодействия?
1.2. Приближение линейных комбинаций атомных орбиталей (МО ЛКАО)
. Дайте определение приближению линейных комбинаций атомных
орбиталей? Для каких объектов оно применимо?
2. Каким критериям должны отвечать базисные функции?
. Что представляют из себя орбитали Слейтеровского типа?
. Почему в качестве базисных функций можно использовать гауссовые
функции?
. Что такое минимальный базисный набор? Определите минимальный
базисный набор для атома водорода, серы, натрия.
. В каких случаях применяются поляризационные и диффузные функции
в базисном наборе?
. Как определяются базисные наборы Попла? Расшифруйте базиснй
набор Попла 4-31G** для молекулы метана СН4 .
1.3. Анализ заселенностей орбиталей
. Что такое матрица плотности?
2. Дайте определение заселенности по Малликену. Какие приближения
содержит такой метод определения заселенностей?
1.4. Методы теории функционала плотности
. Дайте определение теоремы Хоэнберга-Кона?
2. Что такое функционал электронной плотности?
. Определите члены уравнения Кона-Шема?
. Что представляет собой Xα-метод?
1.5 Корреляционные поправки
. Какую величину от полной энергии системы составляют примерно
корреляционные поправки?
. Метод Мёллера-Плессета и его приближения.
.5. Полуэмпирические методы.
. Основное отличие полуэмпирических методов от неэмпирических
методов. Какими преимуществами обладают полуэмпирические методы?
2. Основные приближения, используемые в полуэмпирических методах.
. Назовите известные полуэмпирические методы и области их
применения.
1.6. Методы оптимизации (молекулярное моделирование)
. На чем основывается метод молекулярной механики, какие он содержит
приближения?
2. Назовите основные методы молекулярной механики и их области
применения.
. Метод молекулярной динамики и его применение.
2. КВАНТОВОМЕХАНИЧЕСКИЕ РАСЧЕТЫ ПРИ ПОМОЩИ ПРОГРАММЫ GAUSSIAN
.1. Основные возможности пакета GAUSSIAN-03
. Перечислите основные возможности программного пакета GAUSSIAN-03.
2. Какие основные квантомеханические методы расчетов реализованы в
программе GAUSSIAN-03?
2.2. Принцип работы программ GAUSSIAN
1. Какой
основной принцип построения тела программ GAUSSIAN? Что такое линк и оверлей?
2. Расшифруйте номер линка.
3. Определите функции каждого оверлея.
2.3. Задание расчета и структура входного файла
. Запустите программу GaussView и опишите все открытые окна.
2. Постройте на базе библиотеки структур программы GaussView любую молекулу.
. В окне Gaussian Calculation Setup задайте расчетное задание для
построенной молекулы.
. Запомните input
файл с заданием и опишите его структуру.
2.4. Проведение расчета и структура выходного файла
1. Проведите расчет основного состояния заданной молекулы
одним из методов и с разными базисами.
2. Откройте выходной файл с рзультатами
расчета и опишите процедуру расчета по используемым линкам.
3. Переведите энергии МО в
электронвольты.
4. Рассмотрите матрицу заселенностей МО,
сделайте выводы о химической связи в молекуле.
ЛИТЕРАТУРА
1. W. J. Hehre, W. A. Lathan, R. Ditchfield, M. D.
Newton, and J. A. Pople, Gaussian 70, Quantum Chemistry Program Exchange,
Program No. 237, 1970).
J. S. Binkley, R. A. Whiteside, P. C. Hariharan, R.
Seeger, J. A. Pople, W. J. Hehre, and M. D. Newton, Gaussian 76(Carnegie-Mellon
University, Pittsburgh, PA, 1976).
J. S. Binkley, R. A. Whiteside, R. Krishnan, R.
Seeger, D. J. Defrees, H. B. Schlegel, S. Topiol, L. R. Kahn, and J. A. Pople,
Gaussian 80 (Carnegie-Mellon Quantum Chemistry Publishing Unit, Pittsburgh, PA,
1980).
J. S. Binkley, M. J. Frisch, D. J. Defrees, R.
Krishnan, R. A. Whiteside, H. B. Schlegel, E. M. Fluder, and J. A. Pople,
Gaussian 82 (Carnegie-Mellon Quantum Chemistry Publishing Unit, Pittsburgh, PA,
1982).
M. J. Frisch, J. S. Binkley, H. B. Schlegel, K. Raghavachari,
C. F. Melius, R. L. Martin, J. J. P. Stewart, F. W. Bobrowicz, C. M. Rohlfing,
L. R. Kahn, D. J. Defrees, R. Seeger, R. A. Whiteside, D. J. Fox, E. M. Fluder,
and J. A. Pople, Gaussian 86 (Gaussian, Inc., Pittsburgh, PA, 1986).
M. J. Frisch, M. Head-Gordon, H. B. Schlegel, K.
Raghavachari, J. S. Binkley, C. Gonzalez, D. J. Defrees, D. J. Fox, R. A.
Whiteside, R. Seeger, C. F. Melius, J. Baker, L. R. Kahn, J. J. P. Stewart, E.
M. Fluder, S. Topiol, and J. A. Pople, Gaussian 88 (Gaussian, Inc., Pittsburgh,
PA, 1988).
M. J. Frisch, M. Head-Gordon, G. W. Trucks, J. B.
Foresman, K. Raghavachari, H. B. Schlegel, M. Robb, J. S. Binkley, C. Gonzalez,
D. J. Defrees, D. J. Fox, R. A. Whiteside, R. Seeger, C. F. Melius, J. Baker,
L. R. Kahn, J. J. P. Stewart, E. M. Fluder, S. Topiol, and J. A. Pople,
Gaussian 90 (Gaussian, Inc., Pittsburgh, PA, 1990).
M. J. Frisch, G. W. Trucks, M. Head-Gordon, P. M. W.
Gill, M. W. Wong, J. B. Foresman, B. G. Johnson, H. B. Schlegel, M. A. Robb, E.
S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C.
Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart,
and J. A. Pople, Gaussian 92 (Gaussian, Inc., Pittsburgh, PA, 1992).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W.
Gill, B. G. Johnson, M. W. Wong, J. B. Foresman, M. A. Robb, M. Head-Gordon, E.
S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C.
Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart,
and J. A. Pople, Gaussian 92/DFT (Gaussian, Inc., Pittsburgh, PA, 1993).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W.
Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson,
J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz,
J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe,
C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R.
Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J.
P. Stewart, M. Head-Gordon, C. Gonzalez, and J. A. Pople, Gaussian 94
(Gaussian, Inc., Pittsburgh, PA, 1995).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E.
Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr.,
R. E. Stratmann, J. C. Burant, S. Dapprich, J. M.
Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, Ö. Farkas, J. Tomasi, V.
Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J.
Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, P. Salvador, J. J.
Dannenberg, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J.
Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P.
Piskorz, I. Komáromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M.
A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W.
Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle,
and J. A. Pople, Gaussian 98 (Gaussian, Inc., Pittsburgh, PA, 1998).
12. Т. Кларк. Компьютерная химия. — М.: Мир, 1990.-382с.
. Минкин В.И. Теория строения молекул 1997, 1997, 560 с.
. Цирельсон В.Г., Бобров М.Ф., Апостолова Е.С., Михайлюк А.И.
Лекции по квантовой химии. РХТУ, 1998. 350 с.
. В.И. Минкин, Б.Я. Симкин, Р.М. Миняев. Теория строения
молекул. Ростов-на-Дону «Феникс», 1998, 407 c .
. Абаренков И.В. Начала квантовой химии, 1989, 304 с.
17. http://www.gaussian.com/
Термохимия в Gaussian
2012-10-22 Квантовая химия,
Для того чтобы Gaussian рассчитал всю термохимию достаточно указать параметр freq во входном файле. При этом, дополнительно к электронной энергии, будут рассчитаны такие параметры как энергия нулевых колебаний ZPE, энтропия и термические поправки к энергии. Из этих чисел несложно получить энергию Гиббса и энтальпию, которые тоже появляются в результатах. По умолчанию расчет идет для температуры […]
Читать дальше
Gaussian, энергии
Ошибки Gaussian
2012-05-08 Зеленая Буковка Квантовая химия,
Ошибки со сходимостью Error in internal coordinate system Error termination via Lnk1e in /opt/q/g09/l103.exe at Sun Sep 16 21:42:43 2012. Command exited with non-zero status 1 В этом случае обычно помогает оптимизация с использованием декартовой системы координат Opt(Cartesian). При этом использование параметра Cartesian может приводить к осложнениям с оптимизацией геометрии и просто ухудшать сходимость, поэтому его […]
Читать дальше
Gaussian
Как бороться с мнимыми частотами
2012-05-01 Зеленая Буковка Квантовая химия,
Чем больше и несимметричнее система, с которой приходится работать, тем чаще при оптимизации появляются мнимые частоты с небольшими значениями (особенно если используются модели вроде PCM). Это неприятно, неудобно и вызывает сомнения в качестве полученных результатов. Как правило, с помощью некоторых способов, их комбинаций и такой-то матери, от частот обычно можно избавиться. Подробнее о способах: I. […]
Читать дальше
Gaussian
Учет неспецифической сольватации в Gaussian 09
2012-05-01 Зеленая Буковка Квантовая химия,
Обычный учет растворителя При неспецифическом учете растворителя, итоговая энергия включает в себя все поправки и выглядит следующим образом: SCF Done: E(RTPSS-TPSS) = -797.383911417 A.U. after 15 cycles Convg = 0.2583D-08 -V/T = 2.0032 По умолчанию Gaussian 09 не производит учет неэлектростатических взаимодействий с растворителем. Чтобы это исправить, нужно добавить параметр Read к группе SCRF: SCRF=(Solvent=Water,Read) […]
Читать дальше
Gaussian, сольватация, энергии
Изменения параметров при расчете в PCM
2012-03-28 Зеленая Буковка Квантовая химия,
Влияние величины alpha на энергетические характеристики Alpha это масштабирующий коэффициент для Ван-дер-ваальсовых сфер при расчетах в PCM. В Gaussian 09 по умолчанию равен 1.1 (в Gaussian 03 — 1.2). Изменение alpha приводит к изменениям в геометрических и энергетических характеристиках. Исключение составляет энтропия, которая или не меняется вообще, или меняется очень мало. Изменение энергии Гиббса при […]
Читать дальше
Gaussian, сольватация, энергии
Запуск Gaussian
2011-09-17 Зеленая Буковка Квантовая химия,
Небольшой перлоскрипт для запуска расчетов в Gaussian. Свойства: 1. Ест входные файлы с расширением .inp и выдает .out файлы. Оба типа можно изменить прямо в теле скрипта. Можно запускать по маске, удобнее всего *. 2. При запуске с параметром chk выдаст готовые Formatted Checkpoint файлы .fchk с названием входных файлов. Для корректной работы необходимо наличие […]
Читать дальше
bash, Gaussian
Natural Bond Orbital Analysis (NBO) в Gaussian
2011-07-08 Зеленая Буковка Квантовая химия,
Gaussian NBO Version 3.1 Чтобы он произвел расчет по умолчанию, достаточно указать pop=NBO. Если нужно задать дополнительные параметры, то нужно использовать pop=NBORead Тогда в конце входного файла можно будет задать дополнительные параметры для NBO анализа, указанные в официальной документации. Например изменить пороговое значение для вывода донорно-акцепторных взаимодействий на 5ккал/моль: $NBO E2PERT=5 $end
Читать дальше
Gaussian
Очередь заданий в Gaussian
2011-05-30 Зеленая Буковка Квантовая химия,
Пример входного файла, делающего TD-DFT расчет первых десяти возбужденных состояний для оптимизированной на первом шаге молекулы. Geom=Checkpoint и Guess=Read показывают, какую информация нужно брать из .chk файла. Аналогично можно начать расчет заново при условии наличия checkpoint. %Chk=/tmp/g09/1 #P Opt TPSSTPSS/6-311+G(d,p) Comment 0 1 6 1.097281000 0.353792000 0.000000000 7 0.000000000 1.062321000 0.000000000 —Link1— %Chk=/tmp/g09/1 #P TPSSTPSS/6-311+G(d,p) Geom=Checkpoint […]
Читать дальше
Gaussian
Расчеты спектров в УФ и видимой области
2011-05-25 Зеленая Буковка Квантовая химия,
Расчеты УФ спектров методом Time-dependent density functional theory (TDDFT) Gaussian Для получения УФ спектра нужно задать параметр TD, а NSTATES (3 по умолчанию) показывает количество состояний, которые нужно найти (число полос). Например TD=NSTATES=10 Расчет TD работает только для SP, поэтому чтобы получить спектры для конечной структуры оптимизации, их нужно задавать через очередь заданий.
Читать дальше
Gaussian
Работа с Gaussian
2011-03-08 Зеленая Буковка Квантовая химия,
Особенности задания методов учета электронной корреляции При задании гибридного метода нужно указывать как обменную, так и корреляционную части, поэтому метод TPSS будет выглядеть как TPSSTPSS, а PBE0 как PBE1PBE Вывод значений энергии Если выходные файлы открывать в Chemcraft, то будут показываться значения энергии, указанные как SCF Done, то есть не включающие ни термические поправки (даже […]
Читать дальше
Gaussian
-
surius
- Сообщения: 1485
- Зарегистрирован: Пт сен 21, 2007 11:20 am
Руководство по програмному пакету gaussian
Будьте добры, подскажите, где можно найти русифицированное руководство по пользованию GAUSSIAN
-
Nik®
- Сообщения: 92
- Зарегистрирован: Пн апр 09, 2007 11:58 pm
Сообщение
Nik® » Пт сен 21, 2007 2:58 pm
как такового руководства для гауссиана на русском, я, лично, не встречал
попадалась как то методичка из Казанского университета(название и авторов к сожалению не помню) но там только самое простое и кратко
мой вам совет пользовать оригинальный мануал + оригинальную литературу
типа: Exploring Chemistry With Electronic Structure Methods ну и про статьи не
забываем.
-
antony.stasuk
- Сообщения: 36
- Зарегистрирован: Чт июл 19, 2007 5:16 pm
- Контактная информация:
Re: Руководство по програмному пакету gaussian
Сообщение
antony.stasuk » Пн сен 24, 2007 1:22 pm
surius писал(а):Будьте добры, подскажите, где можно найти русифицированное руководство по пользованию GAUSSIAN
У меня усть та книга о которой говорил Nik®, так что если нужно- отправлю
-
1177
- Сообщения: 148
- Зарегистрирован: Пн июн 19, 2006 11:49 am
Сообщение
1177 » Сб ноя 10, 2007 8:26 pm
А можно в exchange?
-
SSR
- Сообщения: 230
- Зарегистрирован: Пн окт 01, 2007 9:06 pm
Сообщение
SSR » Ср дек 19, 2007 4:48 pm
На всякий случай:
Код: Выделить всё
http://ihtik.2x4.ru/chem_8janv2007/chem_8janv2007_150.rar (djvu 2nd text search edition)Если люди не полагают, что математика проста, то только потому, что они не понимают, как на самом деле сложна жизнь (Джон фон Нейман)
-
yureva
- Сообщения: 19
- Зарегистрирован: Вт окт 30, 2007 8:53 am
Сообщение
yureva » Пт янв 11, 2008 1:55 pm
Есть местное пособие/методичка для студентов, которое по сути является частичным переводом оригинального руководства.
-
FOX
- Сообщения: 834
- Зарегистрирован: Сб янв 12, 2008 10:50 pm
Сообщение
FOX » Вс янв 13, 2008 9:18 pm
Если не трудно пришлите и мне! А оригинальных мануалов для GAUSSIAN 03 нет,а?
-
Darth Vasya
- Сообщения: 426
- Зарегистрирован: Чт май 24, 2007 1:54 pm
Сообщение
Darth Vasya » Вс янв 13, 2008 10:29 pm
Не люблю хвалить Гауссиан, но в 03-м вполне себе очень удобная справка.
Плохо зная грамматику, сложные конструкции должны употребляться с осторожностью.
-
FOX
- Сообщения: 834
- Зарегистрирован: Сб янв 12, 2008 10:50 pm
Сообщение
FOX » Пн янв 14, 2008 7:49 pm
Однако это не снимает ряда вопросов. Поэтому я и прошу, если это возможно,поделиться мануалами
-
yureva
- Сообщения: 19
- Зарегистрирован: Вт окт 30, 2007 8:53 am
Сообщение
yureva » Ср янв 16, 2008 7:32 am
Выложила в exchenge, состоит из 2 частей. Пардон за такой формат.Сразу предупреждаю это пособие для студентов только начинающих изучать Gaussian и это перевод не всего оригинального пособия к Gaussian.
-
FOX
- Сообщения: 834
- Зарегистрирован: Сб янв 12, 2008 10:50 pm
Сообщение
FOX » Ср янв 16, 2008 6:08 pm
СПАСИБО!!!
-
FOX
- Сообщения: 834
- Зарегистрирован: Сб янв 12, 2008 10:50 pm
Сообщение
FOX » Вт фев 12, 2008 7:32 pm
Спасибо!
А кто-нибудь выходные данные этой книжки знает?
Авторы, название и др.
-
SSR
- Сообщения: 230
- Зарегистрирован: Пн окт 01, 2007 9:06 pm
Сообщение
SSR » Ср фев 13, 2008 2:37 am
В exchange pdf вариант интерактивной справки за 2003 год с возможностью поиска и внешними гиперссылками.
Последний раз редактировалось SSR Пн фев 18, 2008 12:18 am, всего редактировалось 1 раз.
Если люди не полагают, что математика проста, то только потому, что они не понимают, как на самом деле сложна жизнь (Джон фон Нейман)
-
alxyppv
- Сообщения: 560
- Зарегистрирован: Сб апр 07, 2007 11:23 am
Сообщение
alxyppv » Ср фев 13, 2008 3:06 am
SSR писал(а):В exchange pdf вариант интерактивной справки за 2003 год с возможностью поиска и работающими гиперссылками.
Спасибо, очень полезная штука, только вот… то, что ссылки все на сайт Gaussian, а не на другие страницы pdf-файла — это так и должно быть, или у меня что-то не так работает?
А.П.
-
yureva
- Сообщения: 19
- Зарегистрирован: Вт окт 30, 2007 8:53 am
Сообщение
yureva » Ср фев 13, 2008 12:52 pm
FOX писал(а):Спасибо!
А кто-нибудь выходные данные этой книжки знает?
Авторы, название и др.
Если вам нужно сослаться на эту книжку, лучше сошлитесь на оригинальное руководство по Gaussian, т.к. эта книжка фактически частичный перевод этого руководства, сделанный для студентов, начинающих изучать Gaussian. Если вы внимательно почитаете, то увидите, что там даже даются упражнения и примеры, который входят в программу. По идее такие книжки вообще нелегальны, поэтому я не думаю что на нее стоит ссылаться.
-
FOX
- Сообщения: 834
- Зарегистрирован: Сб янв 12, 2008 10:50 pm
Сообщение
FOX » Ср фев 13, 2008 10:16 pm
yureva писал(а):
FOX писал(а):Спасибо!
А кто-нибудь выходные данные этой книжки знает?
Авторы, название и др.Если вам нужно сослаться на эту книжку, лучше сошлитесь на оригинальное руководство по Gaussian, т.к. эта книжка фактически частичный перевод этого руководства, сделанный для студентов, начинающих изучать Gaussian. Если вы внимательно почитаете, то увидите, что там даже даются упражнения и примеры, который входят в программу. По идее такие книжки вообще нелегальны, поэтому я не думаю что на нее стоит ссылаться.
Мне кажется, что ссылаться в свете нового УК можно только на сайт Gaussian. Это если нет лицензионного диска. Или я ошибаюсь и можно ссылаться отдельно на руководство к программе без покупки самой программы(лицензии)?
-
helicase
- Сообщения: 472
- Зарегистрирован: Чт окт 11, 2007 7:43 am
Сообщение
helicase » Ср фев 13, 2008 11:50 pm
common sense говорит, что на само руководство, разумеется можно. и УК этому не противоречит.
-
ИСН
- Робин Гуд
- Сообщения: 8529
- Зарегистрирован: Пт окт 10, 2003 5:32 pm
- Контактная информация:
Сообщение
ИСН » Чт фев 14, 2008 12:03 am
Common sense и наш УК друг другу часто противоречат, особенно в районе статей 272 — 274 и 282. И типа ничего. А правоприменение иногда отличается даже от УК — и надо ли напоминать, в какую сторону?
Квантовомеханические расчеты молекул с использованием программного комплекса GAUSSIAN
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное агентство по образованию
Государственное образовательное
учреждение
высшего профессионального образования
“ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ”
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ФИЗИКИ
Методическое пособие:
“Квантовомеханические расчеты молекул
с использованием программного комплекса GAUSSIAN”
для студентов, бакалавров, магистров
и аспирантов
физического и химического факультетов
Исполнитель:
стажер-исследователь ОРС НИИФ Власенко Е.В.
Координатор проекта:
д-р физ.-мат. наук, проф. Ведринский Р.В.
2007 год
ОГЛАВЛЕНИЕ
Введение
. Основные положения квантовой химии
.1 Метод Хартри-Фока-Слейтера
.2 Приближение линейных комбинаций атомных орбиталей (МО
ЛКАО)
.3 Анализ заселенностей орбиталей
.4 Методы теории функционала плотности
.5 Корреляционные поправки
.6 Полуэмпирические методы
.7 Методы оптимизации (молекулярное моделирование)
. Квантовомеханические расчеты при помощи программы
.1 Основные возможности пакета GAUSSIAN-03
.2 Принцип работы программ GAUSSIAN
.3 Задание расчета и структура входного файла
.4 Структура Input File
.5 Проведение расчета и структура выходного файла
Заключение
ВОПРОСЫ И ЗАДАНИЯ
Литература
Введение
атомный орбиталь
молекулярный gaussian
Использование квантомеханических расчетов для предсказания
геометрического строения, энергии, термодинамических характеристик и др. для
известных и предполагаемых молекул является, в настоящее время, одним из важных
и быстроразвивающихся методов химических исследований. Особую ценность этот
метод приобретает в случае предсказания свойств неизвестных соединений, синтез
которых может являться достаточно сложной процедурой, требующей больших затрат
времени и материальных ресурсов исследователей. К тому же, на современном этапе
развития компьютерной техники и создания высокопроизводительных и универсальных
программ для квантовой химии, существует возможность расчета химических свойств
соединений с очень высокой точностью и надежностью. Одной из таких программ по
расчету структуры и свойств молекул является программа GAUSSIAN [1-11]. Со времени своего появления
в 1970 г. вышло несколько версий этой программ, в каждую из которых были
включены все достижения развития квантовой химии и программирования на
определенном этапе. Последняя существующая версия в настоящий момент есть GAUSSIAN-03. Описание работы GAUSSIAN различных версий можно найти не
только в авторских инструкциях для пользователей, но и в некоторых монографиях
по квантовой химии [12]. Широкое использование, в настоящее время, программы GAUSSIAN не только для
научно-исследовательских работ, но и в учебном процессе требует создания
специализированного методического пособия по работе с этой программой для
студентов и аспирантов. Настоящее методическое пособие предназначено для начального
ознакомления с принципами работы программы GAUSSIAN и дает возможность приступить к
расчетам на основании конкретных примеров построения расчетного задания и
интерпретировать полученные результаты. Методическое пособие
«Квантовомеханические расчеты молекул с использованием программного комплекса GAUSSIAN» предназначено для студентов,
обучающихся по специальностям 020100- химия, магистров, аспирантов и научных
работников.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ХИМИИ
Квантовая механика позволяют получить достаточно точное математическое
описание любых экспериментально наблюдаемых молекулярных взаимодействий. Однако
для реализации этих возможностей необходимо располагать достаточно мощными ЭВМ
и достаточно точными вычислительными методами. За последние годы в этих
областях был достигнут значительный прогресс. Быстрое развитие вычислительной
техники и программного обеспечения наряду с разработкой эффективных и точных
полуэмпирических и неэмпирических (ab initio) вариантов
расчетов позволили, в настоящее время, сделать квантовую химию одним из
наиболее важных инструментов физико-химических исследований [13-16].
В основе современной квантовой химии лежит уравнение Шредингера для
стационарных состояний. Обычно используют адиабатическое приближение
(приближение Борна-Оппенгеймера), согласно которому ядра неподвижны и можно
решать уравнения только для движения электронов. Однако даже в этом случае
точно решить уравнение Шредингера можно только для одноэлектронных систем.
Поэтому в квантовохимических расчетах используют различные приближенные методы,
наиболее распространенным из которых является метод самосогласованного поля
(ССП) или метод Хартри-Фока. Для систем, подобных водородному атому, возможно
точное аналитическое решение уравнения Шредингера. Для систем с малым
количеством электронов, типа гелия, «многоэлектронная» проблема может
быть решена более или менее точно (в настоящее время нерелятивистская энергия
стандартного состояния гелия известна с точность до пятнадцатого знака). В
общем случае — электронные системы нельзя рассмотреть с такой точностью.
Большинство элементов в периодической таблице — многоэлектронные системы, где
движение каждого электрона зависит от движения всех других электронов, так же
как и ядер. Чтобы изучать такие системы, необходимы некоторые методы
последовательных приближений.
.1 Метод Хартри-Фока-Слейтера
Один из широко используемых методов последовательных приближений — метод
Хартри-Фока. Он базируется на довольно естественном приближении, что каждый
электрон перемещается в потенциале, созданном ядром и средним потенциалом всех
других электронов атома. Это приводит к модели независимой частицы, которая
позволяет перейти от многоэлектронной проблемы к проблеме решения множества
взаимосвязанных одноэлектронных уравнений.
Одноэлектронные уравнения вычисляются, пока выбранный уровень точности не
достигнут. Хартри сделал первое вычисление, основанное на этих идеях, вручную в
1928. Приближение Хартри-Фока — быстрый и надежный метод для расчета атомных
систем, но это — только первое приближение.
Еще одним приближением является приближение Слейтера при решении
уравнений Хартри-Фока. Начнем рассмотрение с формализма Хартри, представляя
многоэлектронный гамильтониан для атомной системы как сумму одноэлектронных
гамильтонианов:
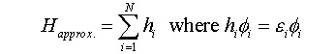
где
N — число электронов в системе. Каждый электрон независимо взаимодействует с
атомным ядром и для него можно получить решение независимо от других
электронов. Для потенциальной энергии гамильтониана, берется приближение
Борна-Оппенгеймера, когда игнорируется межъядерные взаимодействия, которые
предполагаются постоянными. Это предположение обосновывается тем, что ядра
совершают медленные колебания в узловых точках, в то время как электронная
подсистема распределена по всей молекуле или кристаллу.
В
самой простой форме, можно также предполагать, что электроны также
невзаимодействуют. В этом случае строится гамильтониан Happrox. без
учета электрон-электронного взаимодействия и точная волновая функция будет
иметь вид:
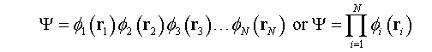
где
индексы 1, 2, 3…, N определяют, в каком квантовом состоянии находятся
одноэлектронные волновые функции. Любая перестановка одноэлектронных функций,
которые можно назвать спин-орбиталями, будет также приводить к волновым функциям
для Happrox..
В
полном методе Хартри, электрон-электронные взаимодействия включены в
гамильтониан в виде дополнительного члена потенциальной энергии. Этот
дополнительный член представляет собой возмущение простого решения для
невзаимодействующих электронов. Этот более полный гамильтониан является
стартовой точкой для расчетов методом Хартри-Фока.
(3)
Поскольку
электроны являются фермионами, полная волновая функция должна быть
антисимметрична относительно обмена любыми двумя из электронов (принцип Паули).
Такие волновые функции могут быть представлены в матричном виде:

Это
представление полной волновой функции в виде детерминанта Слейтера. Детерминант
будет нулевой, если любой i = j.
Как
простой пример рассмотрим атом гелия с его двумя электронами в конфигурации
основного состояния. Антисимметричная волновая функция тогда будет:
(5)
где
спин-орбитальные индексы были заменены определенными квантовыми уровнями
электронов. Обратим внимание, что набор всех возможных детерминантов Слейтера
порядка N формирует полный набор для описания системы. Для случая гелия, мы
можем также иметь вклады от отдельных возбужденных состояний с 1s-3s или
2s-3s; с уменьшающимся вкладом от более высоко возбужденных
состояний.
Величина
полной энергии для состояния, представленного детерминантом Слейтера
определяется величиной полного гамильтониана. «Лучшим» детерминантом
для стандартного состояния должен быть тот, который минимизирует величину H;
(6)
Это
приводит к уравнениям Хартри-Фока.

Как
и прежде, i и j обозначаем квантовые числа, необходимые для
определения отдельного электронного состояния. Сумма по j
выполняется по всем занятым состояниям. Каждая спин-орбиталь φi(rm)
характеризуется своим значением εi которое
является собственным значением оператора Фока (гамильтониан, включающий
усредненное электрон-электронное отталкивание и учитывающий принцип Паули).
(8)
где
h — упрощенный гамильтониан Хартри для невзаимодействующих электронов и
дополнительный потенциал Хартри-Фока (в квадратных скобках), который включает
электрон-электронные взаимодействия с антисимметричной волновой функцией.
Потенциал Хартри-Фока имеет два члена. Первый член Vee — средняя
потенциальная энергия кулоновского отталкивания. Второй член Vex —
обменная энергия взаимодействия. Эта поправка Хартри-Фока, приводит к понижению
полной энергии взаимодействия, и связана со спиновой корреляцией.
В
одноэлектронном гамильтониане кулоновский и электрон-электронный компоненты оба
являются локальными операторами. Они оперируют i-спин-орбиталью
в положении rm. Обменный член Vex —
нелокальный оператор.
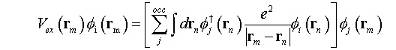
Для
i-спин-орбитали в положении rm, он
функционирует в положении rn. Обменный член обусловлен принципом Паули. Это может
быть более понятно, если рассматривать спин-орбитальные волновые функции
раздельно в виде спиновой и пространственной компонент. Спиновые компоненты
дают дельта-функцию между i и j волновыми функциями. Таким образом, только
подобные спин-электроны соответствуют этому члену. Это создает то, что называют
обменной дыркой.
В
общем случае, уравнения Хартри-Фока (7) трудно решить. На практике несколько
других ограничений накладываются на спин-орбитали при их рассмотрении. Первое
ограничение — требование, чтобы каждая спин-орбиталь имела различные спиновые и
пространственные значения. Второе ограничение — то, что мы предполагаем, что
спин-орбиталь является решением в сферически симметричном потенциале. Это
последнее ограничение называют центральным полевым приближением, и это делает
возможным разделение орбитального компонента волновой функции на радиальную и
угловую части.
Для
системы с закрытой оболочкой, где полный спин и угловой момент являются
нулевыми, система действительно сферически симметрична, и это ограничение
автоматически выполнено. Мы можем написать спин-орбиталь в rn
как:
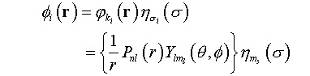
Yl m. —
обычная сферическая гармоника, и уравнения Хартри-Фока могут быть упрощены к
радиальным уравнениям Хартри-Фока:
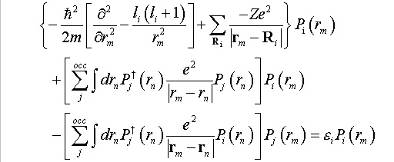
радиальные
функции Pi могут быть вычислены.
Как
можно видеть из уравнений (11), Pi зависит от радиальных функций всех других joccupied электронов. Из-за этой зависимости уравнения Хартри-Фока могут быть
решены, используя итерационный метод. Исходная точка расчета — приблизительное
описание одночастичной функции, P(r). Это может быть водородоподобные функции,
но обычно используется различное приближение. С этими стартовыми функциями
создается потенциал Хартри-Фока и находятся собственные значения уравнение
(11). Полученный новый набор одночастичных функций применяется для создания
нового потенциала Хартри-Фока и находятся новые собственные решения. Такая
операция проводится много раз, пока радиальные функции и собственные значения
энергии не становятся устойчивыми.
.2
Приближение линейных комбинаций атомных орбиталей (МО ЛКАО)
Для
нахождения одноэлектронных функций МО для молекул при использовании метода
Хартри-Фока возможно получение таблиц их числовых значений как и при
аналогичных атомных расчетах. Однако, кроме отсутствия аналитического решения,
существуют большие математические трудности, обусловленные отсутствием
центральной симметрии. Для молекул МО должны обладать теми же элементами
симметрии, какими обладают сами молекулы. Наилучшим приближением для построения
МО оказалось приближение ЛКАО. В этом приближении каждая МО записывается в виде
линейной комбинации АО атомов, образующих молекулу:
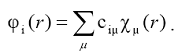
Коэффициенты сiμ, принимающие как положительные, так и отрицательные
значения, определяют вклад каждой атомной орбитали (АО) χμ(r)
в МО ϕi (r). Одна и
та же АО по-разному входит в разные МО, поэтому коэффициенты ciμ
при АО χμ
для каждой МО различны.
МО и АО есть одноэлектронные функции (орбитали), которые приближенно
описывают поведение каждого из электронов в молекулах и атомах, соответственно.
Приближение МО ЛКАО (11) опирается на принцип суперпозиции и отражает волновую
природу электронов. Поэтому можно заключить, что МО (11) формируются в
результате взаимного проникновения или интерференции АО, причем эта
интерференция может носить как конструктивный (взаимодействие АО происходит в
фазе, т.е. коэффициенты ciμ имеют одинаковые знаки), так и
деструктивный (взаимодействие АО происходит в противофазе и коэффициенты ciμ
имеют разные знаки)
характер. Соответственно, образуются связывающие МО, обладающие более низкой
энергией, и антисвязывающие (или разрыхляющие) МО, энергия которых выше. Если
интерференция очень мала, МО формируются преимущественно из орбиталей атомного
характера: такие МО называются несвязывающими: они описывают, например,
остовные электроны и неподеленные электронные пары. Возможное число и тип МО в
системе определяется принципом Паули.
Электронная плотность молекулы в приближении МО ЛКАО записывается
следующим образом:
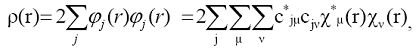
т.е. ЭП есть сумма вкладов, связанных с плотностью электронов на атомных
орбиталях и интерференцией АО. Степень и характер взаимного проникновения АО
количественно характеризуют с помощью интегралов перекрывания
Выбор базисных функций в разложении ЛКАО является важной задачей, так как
этим определяется точность аппроксимации молекулярных орбиталей Хартри-Фока.
Базисные функции должны удовлетворять трем основным критериям:
1. Базисные функции должны давать хорошее приближение к истинной
волновой функции (возле ядер и на больших расстояниях от них).
2. Базисные функции должны допускать аналитическое вычисление
нужных интегралов.
. Полное число базисных функций не должно быть очень большим.
Приближение MO ЛКАО состоит в аппроксимации МО суммой AO, центрированных
на всех ядрах. AO есть решения уравнений Хартри-Фока для атома, т. е.
одноэлектронные атомные волновые функции, рассчитанные для среднего потенциала,
созданного другими электронами и ядром. Использование аналитических АО
позволяет значительно упростить вычисления. Угловые части АО хорошо известны —
это сферические гармоники. Рассмотрим аналитические приближения к радиальным
частям AO: именно они обычно определяют тип базиса.
В принципе, в качестве базисных можно использовать любые функции, которые
в достаточной степени охватывают пространство электронного распределения.
Оптимальный выбор состоит в том, чтобы аналитическая функция была максимально
близкой к радиальной составляющей точной водородоподобной AO. Такие функции
известны как орбитали слейтеровского типа (STO или ОСТ). OСТ отвечают
потенциалу центрального поля
V( r ) = — ζn/r + [n(n-1) — l(l+1)]/2r2 (14)
(n и l — главное и орбитальное квантовые числа, l = 0, 1, 2,… , n-1) и
удовлетворяют асимптотическому поведению точной волновой функции как вблизи
ядра, так и на больших расстояниях от него.
В сферических координатах ϕ,θ,r ОСТ имеют вид:
(15)
где N — нормировочный множитель, — сферическая гармоника, m —
магнитное квантовое число.
При l = -1 ОСТ переходит в АО водородоподобного атома с экспоненциальным
фактором ζ = Z/n, поэтому ОСТ обеспечивают правильное поведение AO ОСТ с l >
1 являются безузловыми; ОСТ с одинаковыми l, но разными n, не-ортогональны.
К сожалению, ОСT не подходят для быстрого вычисления двухцентровых
кулоновских и обменных интегралов. Вычисление этих интегралов очень упрощается
при использовании в качестве базисных функций орбиталей гауссова типа (ОГТ).
Эти базисные функции обладают следующим важным свойством: произведение двух
гауссиан, центрированных в точках А(Аx, Аy, Аz) и В ( Вx, Вy, Вz ), есть
гауссиан, центрированный в точке P =(α1A + α2B) /
(α1+α2), лежащей
на линии АВ:
exp(-α1rA2) exp(-α2rB2)=
exp[-(α1α2rAB2)/( α1+α2)] exp[(-α1+α2)rР2)]. (16)
ОГТ отвечают потенциалу центрального поля
V(r) = 2α2/r2+ [n(n-1) —
l(l+1)]/2r2. (17)
ОГТ на данном центре с одинаковыми l, но разными n, как и ОСТ, не
ортогональны. Недостатком индивидуальных ОГТ является то, что их радиальное
поведение вблизи и вдали от ядра, отличается от такового у точных волновых
функций.
Форма ХФ АО легко аппроксимируется линейной комбинацией ОГT с различными
экспонентами и весовыми коэффициентами χ = ΣсiGi (хотя, чтобы обеспечить
правильное поведение АО в непосредственной близости от ядра, приходится
дополнять ОГТ функциями, имеющими радиальную зависимость типа ). Использование даже десяти ОГT для
аппроксимации АО позволяет вычислять интегралы намного быстрее, чем при
использовании одной ОСТ. Поэтому сейчас в квантово-химических расчетах
используются, как правило, базисные наборы, составленные из ОГT.
Особенно удобны в расчетах так называемые декартовы ОГT, которые в координатах
x, y, z имеют вид
(18)
где N — нормировочный множитель, α — орбитальный экспоненциальный
множитель, r2= x2 + y2 + z2. Числа n, l, m в декартовой ОГT не являются
обычными квантовыми числами: их сумма (n+l+m), аналогичная орбитальному
квантовому числу для атомов, определяет вид угловой части ОГТ в декартовых
координатах. Строго говоря, отдельные декартовы ОГT даже не являются
приближениями к АО: это лишь простые и удобные математические функции,
ускоряющие вычисление интегралов; их даже часто называют гауссовыми
примитивами.
Самые первые базисные наборы строились из ОГТ так, чтобы наилучшим
образом описывать ОСТ. Сейчас базисные наборы строят из линейных комбинаций ОГT
или, иначе из сгруппированных (их также называют контрактированными или
сжатыми) ОГT (СОГТ):
(19)
Минимальный ЛКАО базис для расчета МО двухатомных молекул, состоящих из
атомов второго ряда, состоит из 1s, 2s и 2р атомных орбиталей. На каждый атом
приходится по пять АО, а полное число АО равно десяти. Чтобы найти коэффициенты
ciμ
разложения МО по АО
(11), необходимо решить уравнения Хартри-Фока-Рутана. С формальной точки зрения
задача сводится к решению секулярного уравнения десятого порядка, в результате
чего получают 10 различных МО.
Номенклатура базисных наборов. На первых порах СОГТ получали методом
наименьших квадратов подгонкой под единственную ОСТ с экспоненциальным фактором
ζ
= 1.0. Затем экспоненты
в ОГТ умножали на величину ζ2 (этого требует специальная теорема
преобразования масштаба радиальной функции). Величины ζ
определяли путем
усреднения результатов оптимизации для близких по строению молекул.
Соответствующие базисы обозначали STO-nG, (n — число гауссиан в СОГТ).
Экспоненты гауссиан брались одинаковыми для базисных функций, описывающих
орбитали с тем же самым главным квантовым числом (например, одни и те же
гауссианы использовались для 2s и 2p функций). На этой стадии и возникла
терминология, в основном используемая в настоящее время.
Минимальный атомный базисный набор. Минимальный атомный базисный набор
включает только одну функцию на каждую АО атомного остова, занятую парой
электронов, и одну функцию на каждую валентную орбиталь каждого атома в
основном состоянии, в число которых входят все орбитали частично занятых
подоболочек. Минимальный базисный набор для водорода состоит из 1 функции
(например, единственной СОГТ). Для всех элементов второго периода периодической
системы такой базис описывает функции s- и p-типа: 1s, 2s, 2px, 2py, 2pz. Для
атомов от Na до Ar используют 9 функций, от K до Ca — 13 функций и т.д.
Минимальный базисный набор называют также одноэкспонен-циальным (или единичным
зета-набором (сокращение — SZ), где Z означает экспоненциальный множитель в
ОСТ).
Расширенные атомные базисные наборы. Параметры СОГТ находят оптимизацией,
добиваясь минимума энергии свободного атома или атома в молекуле. Чтобы
добиться лучшего описания АО, каждую атомную орбиталь описывают большим
количеством функций: двумя, тремя и т.д. Параметры базисных функций также ищут
с помощью вариационного принципа. Соответственно, различают базисы двух- (DZ),
трехэкспоненциальный (TZ) и т.д.
Поляризационные и диффузные функции. При описании химической связи наборы
СОГТ, полученные расчетом отдельных атомов по Хартри-Фоку, часто дополняются
другими функциями. Чаще всего используют поляризационные и диффузные функции.
Поляризационные функции помогают лучше описать межатомные взаимодействия
и химическую связь. Эти функции имеют более высокие значения орбитального
квантового числа l, чем у занятой электронами атомной орбитали соответствующего
атома в основном состоянии. Экспоненты для них нельзя получить из атомных
вычислений по Хартри-Фоку, так как в основном состоянии эти АО не заселены
электронами. Поэтому параметры поляризационных функций определяют при расчетах
молекул.терминология применяется и для поляризационных функций. Так, DZP
означает двухэкспоненциальный базис, в который дополнительно включены
поляризационные функции, TZP — трехэкспоненциальный базис плюс поляризационные
функции и т.д. Иногда указывают число наборов поляризационных функций: ТZDP
(или TZ2P) означает трех-экспоненциальный Z-базис плюс два набора
поляризационных функций. Для молекул, включающих атомы от Li до F, в качестве
поляризационных функций обычно используют шесть d-ОГТ, для атома водорода — три
р-ОГТ.
Диффузные функции важны для правильного описания анионов и слабых связей
(например, водородных), для вычислений дипольного момента, поляризуемости и
т.д. Это обычно гауссианы s- и p-типа с очень маленькими экспонеци-альными
множителями, медленно спадающие с увеличением расстояния от ядра.
Базисные наборы Попла. Иное соглашение было принято Дж. Поплом с
сотрудниками, внесшими огромный вклад в развитие неэмпирических расчетов.
Структура базисного набора дается для целой молекулы, а не для отдельных
атомов, как по Фудзинаге и Даннингу. Обозначения n-ijG или n-ijkG
расшифровываются так: n — число ОГТ для внутренних оболочек; ij или ijk — число
ОГТ для СОГТ в валентных оболочках; ij обозначения описывают валентные DZ
наборы, ijk — валентные TZ наборы. Последние называются также
валентно-расщепленными базисными наборами.
В базисных наборах Попла число гауссиан s- и p-типа для той же самой
sp-электронной подоболочки одинаково, и они имеют одинаковые экспоненты. Однако
коэффициенты разложения для СОГТ s- и p-типа различны. Базисные наборы Попла
могут также быть расширены за счет включения поляризационных функций d-типа для
неводородных атомов (n-ijG* или n-ijkG*) и p-функций для атомов водорода
(n-ijG** или n-ijkG**). Так, в молекуле метана СН4 базис 4-31G** предполагает
наличие 4-х ОГТ для единственной остовной 1s-АО углерода, 3-х и 1-й ОГТ для
каждой из двух функций, аппроксимирующей валентные (2s, 2px, 2py, 2pz) АО
углерода (DZ базис), плюс 6 поляризационных 3d-АО на атоме С. Каждый атом Н
описывается двумя s-функциями и тремя поляризационными функциями р-типа. Полное
число базисных функций равно:
{1 (1s) + 2*[1 (2s) + 3 (2p)] + 6 (3d)} + 4*[2 (1s) + 3 (2p)] = 35.
При введении диффузных функций используются следующие обозначения:
n-ij+G, или n-ijk+G. Это означает, что к стандартному базисному набору для
неводородных атомов добавлен диффузный гауссиан s-типа и 3-й гауссиан p-типа:
все они имеют одинаковые экспоненты. Наборы n-ij++G, или n-ijk++G получены из
предыдущих добавлением 3-х диффузных гауссиан p-типа для атома водорода.
Таблица 1. Некоторые базисные наборы Попла для молекул, содержащих атомы
от Н до F
1.3 Анализ заселенностей орбиталей
Химическую связь можно охарактеризовать количественно, оценивая вклады
различных АО в МО. Используя приближение МО ЛКАО, удобно ввести матрицу
плотности или матрицу зарядов-порядков связей P c элементами
(20)
(суммирование ведется по занятым МО). Электронная часть энергии молекулы
с закрытыми оболочками записывается с помощью этой матрицы весьма компактно:
(21)
Где hμν — одноэлектронные интегралы, описывающие кинетические энергии
электронов и потенциальные энергии их притяжения к ядрам, — интегралы электрон-электронного
взаимодействия, <μλ|νσ> — обменные интегралы.
Матрица плотности описывает распределение электронной плотности по
молекуле в орбитальном приближении следующим образом (закрытые оболочки):
(22)
Перепишем выражение (22) таким образом, чтобы выделить вклады АО атомов А
и В:
(23)
Индексы I и J в выражении (23) нумеруют атомы, а α
и β
— АО, принадлежащие этим
атомам. Интегрируя левую и правую части выражения (23), имеем:
(24)
(интеграл перекрывания Sαβ(I,J)=1, если α=β,
I=J). Таким образом,
полное число электронов молекулы N в приближении МО ЛКАО оказывается формально
распределенным по атомам и связям между ними. Величина 2Рαα(I,I)
есть электронная
заселенность орбитали α, центрированной на атоме А, а величина 2Рαβ(I,J)Sαβ(I,J)
есть электронная
заселенность перекрывания орбиталей α и β, центрированных на атомах I и J.
Малликен предложил оценивать электронные заселенности атомов, деля
заселенности перекрывания орбиталей между каждой рассматриваемой парой атомов
поровну. Тогда полная электронная заселенность атомной орбитали равна
, а полное число электронов,
приписываемых атому I, определяется соотношением
(25)
В результате, эффективный заряд атома qI в единицах «число электронов»,
определяется как разность qI = ZI — QI , где ZI — атомный номер атома А.
Полная межатомная электронная заселенность связи
(26)
характеризует прочность связи между парами атомов I и J в молекуле.
Описанный анализ электронных заселенностей орбиталей по Малликену дает лишь
приближенную оценку распределения заряда по молекуле: получаемые величины
зависят от используемых при расчете метода и базиса, а деление электронов между
атомами без учета природы последних неправомочно. Кроме того, в ортогональном
базисе все электроны оказываются формально распределенными только между
атомами: в этом случае говорят об анализе электронных заселенностей по Лёвдину.
Тем не менее, анализ заселенностей орбиталей по Малликену проводится всеми
современными квантово-химическими программами и используется вместе с другими
результатами расчета.
Величины 2Рαα, следуя Коулсону, называют
орбитальными зарядами, а 2Рαβ — орбитальными порядками связей: отсюда
и происходит название матрицы Р. Знак 2Рαβ определяет конструктивная или
деструктивная интерференция имеет место при взаимодействии данной пары АО.
Полный порядок связи между атомами находят как сумму вкладов от перекрывания
соответствующих АО.
.4 Методы теории функционала плотности
Многоэлектронная волновая функция Ψ очень просто связана с электронной
плотностью ρ(r) соотношением
ρ(r) = ∫ ψ
(r)ψ(r)dV′
(27)
Электронная энергия системы зависит от электронной плотности основного
состояния следующим образом:
(28)
где — потенциал ядер. Теорема Хоэнберга-Кона утверждает, что
существует одинаковый для всех многоэлектронных систем (универсальный)
функционал электронной плотности G(ρ). Он представляет собой сумму
кинетической энергии и неклассической энергии электрон-электронного взаимодействия,
включая обмен и корреляцию электронов. Причем, точная электронная плотность
основного состояния обеспечивает минимум этого функционала. Теория, которая
изучает способы расчета электронной структуры молекул и кристаллов, основываясь
на минимизации функционала, называется теорией функционала (электронной)
плотности.
Принимают, что электронная плотность основного состояния
взаимодействующих электронов такая же, как и невзаимодействующих. Выражение для
кинетической энергии электронов одинаково для всех систем. Тогда минимизация
функционала относительно одноэлектронных функций ϕi(r) при условии их
ортонормировки и постоянства числа электронов в системе дает уравнения
Кона-Шэма:
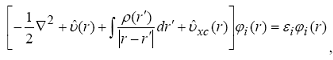
где — обменно-корреляционный потенциал, Exc(ρ)
— зависящая от
электронной плотности обменно-корреляционная энергия. Система уравнений (30)
заменяет в теории функционала плотности стандартные уравнения Хартри-Фока. Они
решаются самосогласованно, причем все приближения связаны с аппроксимацией
обменно-корреляционного потенциала υxc. Все сказанное ранее в отношении
использования и выбора базисных функций в неэмпирических квантово-химических
методах справедливо и в теории функционала плотности.
Энергии одноэлектронных состояний в теории функционала плотности равны
εi(ТФП)= δE(ρ)/δni
, (30)
где ni -электронная заселенность состояния i. В методе Хартри-Фока они
равны разности энергий двух состояний с электронными заселенностями,
отличающимися на единицу:
εi(ХФ) = EХФ[ni = 1] — EХФ[ni = 0]. (31)
Это означает, что одноэлектронные функции ϕi(r), вообще говоря,
отличны от молекулярных орбиталей ϕi(r). Это иногда дает преимущество
теории функционала плотности. Например, разложив (31) в ряд Тейлора и приняв во
внимание соотношение (30), можно получить для потенциала ионизации весьма
точное выражение:
≈ — εi(ni = 1/2). (32)
Можно сказать, что потенциал ионизации может быть вычислен с помощью
некоего переходного состояния с наполовину уменьшенной электронной заселенностью
ВЗМО. Аналогичным образом концепция переходного состояния используется и при
расчетах спектров. Это особенно важно для координационных соединений, где
требуется высокий уровень вычислений методом ХФ, чтобы результаты могли быть
применены для соотнесения переходов.
Простым, но эффективным вариантом теории функционала плотности является
метод Хартри-Фока-Слейтера. Корреляцией электронов здесь, как и в методе
Хартри-Фока, пренебрегают, а обменный потенциал представляется в виде
vx(r) = -3α[(3/8π)ρ(r
)]1/3. (33)
Величина α лежит в пределах 0,7-1,0 (этот метод часто называют
также Xα-методом).
.5 Корреляционные поправки
Электроны с однонаправленными спинами не могут находиться в одной точке
пространства и стараются избегать друг друга. Такое движение электронов
называется коррелированным. Энергия корреляции может достигать 5% от полной
электронной энергии молекулы. Учет корреляционной поправки дополняет расчеты по
методу ССП и приводит к понижению полной энергии молекулы. Осуществляется эта
процедура методом конфигурационного взаимодействия (КВ) или методами,
основанными на теории возмущений Рэлея-Шредингера. Процедура расчета
корреляционной энергии разработана Поплом и соавторами на основе варианта
теории возмущений для молекулярных систем, развитого в работеах Мёллера и
Плессета. В неэмпирическом расчете предусмотрена возможность вычисления
корреляционных поправок второго, третьего и четвертого порядка теории
возмущений («МР2», «МРЗ» или «МР4»).
Значения корреляционных поправок зависят от качества базисного набора, в
котором выполняется процедура ССП, т. е. от способа описания виртуальных
орбиталей в исходной волновой функции. Так, например, базис 3-31ГФ в расчетах
по Мёллеру-Плессету обычно не используются. Вычисление корреляционной энергии,
проводят, как правило, в достаточно широких базисах. Метод Мёллера-Плессета
(МР) не дает возможности определить полное значение корреляционной энергии
(корреляционная поправка МР2 обычно составляет приблизительно половину этого
значения), однако он требует значительно меньше машинного времени по сравнению
с обычным конфигурационным взаимодействием и, как показывает практика, хорошо
воспроизводит энергетические эффекты электронной корреляции при сравнительных
расчетах молекул.
В целях экономии машинного времени и памяти в расчетах по методу МР
остовные орбитали обычно не включаются. В более ранних расчетах по методу МР2
энергию рассчитывали на полном пространстве занятых МО. В ряде задач требуется
оптимизация геометрии с учетом корреляционной поправки второго порядка теории
возмущений. Такой расчет можно провести как по методу BERNY, так и по методу
Мэтага-Сержента, но в этих случаях в расчете по методу МР2 учитываются все
заполненные МО, а не только валентные. Вообще для получения надежных
результатов при оптимизации геометрии в расчетах по методу МР2 следует
применять базисный набор с включением поляризационных фрагментов.
Существенным недостатком метода Мёллера-Плессета и других методов учета
электронной корреляции является то, что они не дают иной информации, кроме
корреляционной поправки к полной энергии молекулы.
.6 Полуэмпирические методы
На практике обычно пользуются как неэмпирическими (ab initio) , так и
полуэмпирическими методами. Они отличаются методикой вычисления матричных
элементов, описывающих электрон-электронные и электрон-ядерные взаимодействия в
системе. В полуэмпирических методах для этой цели используют приближенные
эмпирические формулы и известные из экспериментов параметры атомов. В
неэмпирических методах проводится непосредственный аналитический расчет
матричных элементов.
Принципиальное отличие полуэмпирических методов состоит в полном или
частичном отказе от вычисления одноэлектронных и двухэлектронных интегралов,
фигурирующих в методе ХФ. Вместо точного оператора Фока используется приближенный,
элементы которого получают из эмпирических данных. Соответствующие параметры
подбирают для каждого атома (иногда с учетом конкретного окружения) и для пар
атомов: они либо являются фиксированными, либо зависят от расстояния между
атомами. При этом часто предполагается, что многоэлектронная волновая функция
является однодетерминантной, базис минимальным, а базисные функции — симметричными ортогональными
комбинациями ОСТ χj. Такие комбинации легко получить из исходных ОСТ χj
с помощью преобразования
(34)
где Sij — матрица интегралов перекрывания (эта процедура называется
ортогонализацией функции по Левдину). Расчет МО проводится обычным итерационным
путем.
Полуэмпирические методы работают на несколько порядков быстрее, чем
неэмпирические. Они применимы к большим (и очень большим, например,
биологическим) системам и для некоторых классов соединений дают более точные
результаты. Однако следует понимать, что это достигается за счет специально
подобранных параметров, справедливых лишь в пределах узкого класса соединений.
При переносе на другие соединения те же методы могут дать абсолютно неверные
результаты. Кроме того, параметры часто подбираются таким образом, чтобы
воспроизводить те или иные молекулярные свойства, поэтому придавать физический
смысл отдельным параметрам не следует.
Основные приближения, используемые в полуэмпирических методах, следующие.
) Рассматриваются только валентные электроны: считают, что электроны
атомных остовов лишь экранируют ядра, поэтому эти электроны учитывают в
функциях, описывающих энергию остов-остовного отталкивания (в которое
включается ядер-ядерное отталкивание). Поляризацией остовов пренебрегают.
) В МО учитывают только АО с главным квантовым числом, соответствующим
высшим заселенным электронами орбиталям изолированных атомов (минимальный
базис), причем считают, что базисные функции образуют набор ортонормированных
АО.
) Для двухэлектронных кулоновских и обменных интегралов вводят
приближение нулевого дифференциального перекрывания (НДП):
(35)
Считают, что из-за экспоненциальной зависимости радиальной части АО от
расстояния можно пренебречь двухэлектронными кулоновскими и обменными
интегралами, содержащими произведения разных атомных орбиталей, зависящих от
одного аргумента:
(36)
Это приближение резко уменьшает число вычисляемых двухэлектронных
интегралов, поэтому оно в том или ином виде используется во всех
полуэмпирических методах.
Расширенный метод Хюккеля (Extended Huckel) (РМХ) предназначен для
вычислений молекулярных орбиталей и не позволяет оптимизировать геометрию и
проводить молекулярно-динамические расчеты. В нем используется приближение
невзаимодействующих электронов и в нем не используется приближение ССП.
Метод CNDO (Complete Neglect of Differential Overlap, полное
пренебрежение дифференциальным перекрыванием) является простейшим методом ССП.
Он используется для расчетов основного состояния электронных характеристик систем
с открытой и закрытой оболочками, оптимизации геометрии и полной энергии.
Метод INDO (Intermediate Neglect of Differential Overlap, частичное
пренебрежение дифференциальным перекрыванием) улучшает метод CNDO за счет учета
расталкивания электронов на одном атомном центре. Позволяет проводить расчет
основного состояния систем с открытой и закрытой оболочками, оптимизации
геометрии и полной энергии с использованием ССП.
Метод MINDO3 (Modified INDO, version 3, улучшенный метод INDO, версия 3)
является дальнейшим развитием и расширением метода INDO. Для многих
взаимодействий в нем используются эмпирические параметры вместо соответствующих
вычислений. Этот метод позволяет получать хорошие результаты для больших
органических молекул при расчетах основного состояния систем с открытой и
закрытой оболочками, оптимизации геометрии и полной энергии. Это ССП метод.
Метод MNDO является дальнейшим развитием метода MINDO3, в котором
исправлен ряд ошибок последнего. Позволяет проводить качественные расчеты
электронной и атомной структур органических молекул, содержащих атомы 1-й и 2-й
главных подгрупп (но не атомов переходных элементов). Этот метод позволяет
получать хорошие результаты для больших органических молекул при расчетах
электронных характеристик системы и теплот образования. ССП метод.
Метод AM1 является улучшением метода MNDO. Один из наиболее точных
методов. Используется для органических молекул, содержащих элементы из главных
подгрупп 1 и 2 групп периодической системы. Возможно, этот метод позволяет
получать более качественные результаты, по сравнению с методом MNDO, для
молекул, содержащих как азот, так и кислород. Вычисляет электронную структуру,
оптимизирует геометрию, рассчитывает полную энергию и теплоты образования. ССП
метод.
Метод PM3 является версией метода AM1. PM3 отличается от AM1 только
величинами параметров. Параметры для PM3 были получены сравнением большого
числа и вида экспериментов с результатами расчетов. Как правило, нековалентные
взаимодействия в методе PM3 являются менее расталкивающими, нежели чем в AM1.
PM3 первоначально предназначался для расчета для органических молекул, но потом
он был также параметризован и для ряда других групп элементов, в частности — и
для переходных металлов. ССП метод.
Метод ZINDO/1 является вариантом метода INDO, адаптированного для
проведения расчетов молекул, включающих атомы переходных элементов.
Эквивалентен последней версии метода INDO/1, который отличается от оригинала
использованием постоянных орбитальных экспонент. ZINDO/1 позволяет вычислять
энергетику и геометрию молекул, содержащих переходные металлы.
Метод ZINDO/S является версией метода INDO, параметризованного для
воспроизведения УФ и видимых оптических переходов при расчетах
конфигурационного взаимодействия (CI) с одночастичными возбуждениями. Полезен
для прогнозирования УФ и видимых спектров, но не пригоден для оптимизации
геометрии или молекулярной динамики.
.7 Методы оптимизации (молекулярное моделирование)
Метод молекулярной механики. Простейшим инструментом молекулярного
моделирования многоатомных систем, является метод молекулярной механики (ММ).
Методы молекулярной механики позволяют использовать классический Ньютоновский
метод вычислений энергии одной точки, равновесной геометрии и молекулярной
динамики объектов вместо квантово-механического подхода (одного из
полуэмпирических методов или неэмпирического метода Хартри-Фока (ab initio)).
В методе молекулярной механики атомы рассматриваются как ньютоновские
частицы, которые взаимодействуют друг с другом посредством неких потенциальных
полей, задаваемых эмпирически. Потенциальная энергия взаимодействия зависит от
длины связей, углов связи, торсионных углов и нековалентных взаимодействий (в
т.ч. сил Ван-дер-Ваальса, электростатических взаимодействий и водородных
связей). В этих расчетах силы, действующие на атомы, представляются в виде
функций координат атомов.
Можно назвать четырех наиболее распространенных метода ММ (MM+, AMBER,
BIO+, OPLS).
Метод MM+ разрабатывался для органических молекул. Он учитывает
потенциальные поля, формируемыми всеми атомами рассчитываемой системы и
позволяет гибко модифицировать параметры расчета в зависимости от конкретной
задачи, что делает его, с одной стороны, наиболее общим, а с другой — резко
увеличивает необходимые ресурсы по сравнению с другими методами молекулярной
механики.
Метод AMBER разрабатывался для белков и нуклеиновых кислот. В нем
существует возможность выбрать опцию либо учета всех атомов по отдельности,
либо опцию объединенного атома, под которым подразумевается группа
эквивалентных атомов с одинаковыми свойствами. В последнем случае несколько
атомов, либо их групп, обрабатываются как один атом с одним типом.+
разрабатывался для биологических макромолекул и во многом повторяет
AMBER.разработан для белков и нуклеиновых кислот. Он подобен AMBER, но более точно
обрабатывает нековалентные взаимодействия.
Метод молекулярной динамики. В настоящее время для теоретического
исследования влияния температуры, в частности, и динамики атомного остова,
вообще (например, во время различного рода атомных перегруппировок и пр.)
широкое применение нашел метод неэмпирической молекулярной динамики, который не
требует введения эмпирических межмолекулярных и межатомных потенциалов для
расчетов.
В подходе неэмпирической молекулярной динамики электронная система
описывается набором волновых функций , которые принадлежат основному
состоянию потенциальной поверхности Борна-Оппенгеймера в любой момент времени,
что позволяет описать совместное движение электронов и ядер, которые
описываются набором координат {Rl}.
При этом фиктивная кинетическая энергия электронов остается малой по сравнению
с кинетической энергией ионов, что позволяет рассчитывать силы, действующие на
ядра в любой момент времени по теореме Гельмана-Феймана для электронных систем,
соответствующих мгновенным ядерным конфигурациям.
Фиктивную электронную динамику, ионную динамику и влияние внешних
условий, например — температуры, описывают уравнения движения Эйлера-Лагранжа:
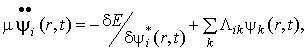
(38)
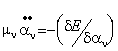
где — функционал полной энергии, получаемый в любом
квантово-химическом методе, набор — любые возможные внешние условия —
температура, давление, объем и пр., — фиктивная масса для электронной
динамики, — произвольный параметр соответствующей размерности. Матрица
является набором множителей
Лагранжа, которые обеспечивают ортонормированность .
Неэмпирическая молекулярная динамика удовлетворяет приближению
Борна-Оппенгеймера только при определенных условиях. Для систем, в которых щель
мала, ионы и электроны сильно взаимодействуют. Это приводит к тепловому
равновесию между ионами и электронами и к отходу от условий применимости
Борна-Оппенгеймера. Для того чтобы преодолеть эти трудности, в неэмпирической
молекулярной динамики используется алгоритм термостатов, один для ионов, другой
— для электронов:
, (40)
где fi- число заполнения.
(41)
Переменные термостата h и x определяются
уравнениями:
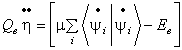
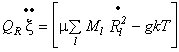
где и
— массы термостатов для электронной и ионных частей
соответственно, и
— необходимые из условий задачи кинетическая энергия
электронов и ионная температура, — число степеней свободы ионов.
Температурные флюктуации, зависящие от времени, включены в уравнения
электронного и ионного термостатов, а динамика всей системы подчиняется
принципу минимума термодинамического потенциала.
В методе неэмпирической молекулярной динамики выполняется закон
сохранения энергии во всей системе (термодинамический потенциал), включающей в
себя электронный и ионный термостаты, который записывается в следующем виде:
, (44)
тогда как энергия электронно-ядерной системы без термостатов из-за
температурных флюктуаций не сохраняется. Следовательно, для систем с нежестким
атомным остовом возможны ситуации, когда из-за невыполнения закона сохранения
энергии температурные условия будут влиять на электронную структуру.
2. КВАНТОВОМЕХАНИЧЕСКИЕ РАСЧЕТЫ ПРИ ПОМОЩИ ПРОГРАММЫ GAUSSIAN
Программа GAUSSIAN,
является, вероятно, самым популярным средством выполнения квантово-химических
расчетов среди основной массы химиков. Основные причины этого — широта охвата
реализованных квантово-химических методик, высокая эффективность и удобный
интерфейс пользователя. Этот пакет моделирования электронных структур
используется для разработок в области химии и биохимии, физике и других
известных и развивающихся областях, связанных с химическими процессами.
Методология моделирования, используемая в пакетах Gaussian, была отмечена
Нобелевской Премией в области химии 1998 года.
Основываясь на фундаментальных законах квантовой механики, Gaussian
позволяет предсказывать энергии, молекулярные структуры и колебательные частоты
молекулярных систем, на ряду со многими другими многочисленными свойствами
молекул, производными от этих базовых характеристик. Пакет может быть
использован для изучения молекул при широком наборе условий, включая устойчивые
виды молекул, которые трудно или невозможно наблюдать в экспериментальных
условиях, например, короткоживущие промежуточные соединения и переходные
структуры. К тому же, к настоящему времени эта программа написана для
нескольких операционных систем и может быть использована для широкого круга
различных ЭВМ.
Недавно появмвшаяся версия GAUSSIAN-03 отличается от предыдущих версий в первую очередь расширением спектра
поддерживаемых квантово-химических методов и их модификаций.
2.1 Основные возможности пакета GAUSSIAN-03
Комплекс программ GAUSSIAN позволяет рассчитывать энергию, структуры молекул, частоты их колебаний,
а также разнообразные свойства молекул в газовой фазе и в растворе, как в
основном, так и в возбужденных состояниях.
Основное направление, в котором развивалась версия GAUSSIAN-03 после G98, это развитие методов
расчета сверхбольших молекулярных систем. Это вызвано, в частности, большим
интересом к расчетам больших биомолекул, и в т.ч. потребностями задач
конструирования лекарств. Среди таких методов можно отметить:
) Методику парционирования молекул ONIOM, развитую проф. Морокума и др.,
в которой вся молекула разбивается на 3 области, которые рассматриваются с
разной степенью точности. Такой подход эффективен, в частности, и для
биомолекул. Например, «активное место» лекарства можно рассчитать с
максимально высокой степенью точности, на наиболее высоком квантово-химическом
уровне; непосредственное окружение активной части можно считать можно посчитать
менее точно, а дальнее атомы — наоброт, учесть максимально приближенно. Метод
ONIOM применим к большим молекулам в различных областях моделирования, включая
моделирование энзимов и механизмов реакций в органических системах,
исследование кластерных моделей поверхностей и поверхностных реакций,
фотохимических реакций органических соединений, замещающих эффектов химической
активности органических и органометаллических соединений, а также гомогенный
катализ.
) Быстрый метод мультиполей (FMM) в схеме DFT в сочетании с
использованием технологии разреженных матриц, реализованный в G98, позволяет,
по мнению разработчиков, достигнуть линеаризации «вычислительной
стоимости», что делает возможным применять DFT для молекул большего
размера, в т.ч. в расчетах частот.
3) В GAUSSIAN-03 получила дальнейшее развитие
методика оптимизации геометрии. В результате стало возможным проводить
неэмпирические расчеты молекулярных систем, содержащих много тяжелых атомов, с
оптимизацией геометрии. Также возможно моделирование периодических систем,
таких как полимеры и кристаллы, посредством использования периодических
граничных условий. Например, GAUSSIAN-03 позволяет предсказать равновесные геометрии и переходные структуры
полимеров, изучать их реактивность посредством предсказания энергии
изомеризации, моделировать запрещенные энергетические зоны веществ.
) Моделирование очень широкого диапазона спектров и спектроскопических
свойств молекул. GAUSSIAN-03
позволяет вычислять многие тензоры, вносящие вклад в сверхтонкий спектр
молекул, позволяя исследовать нелинейные молекулы так же легко, как и линейные.
) Использование Модели Поляризуемого Континуума (Polarizable Continuum
Model, PCM) для моделирования систем в растворах, для которой характерно
представление растворителя как поляризуемого континуума и помещение
растворяемого вещества в полость внутри растворителя. поддержку SCRF PCM
поддерживается в широком спектре методов (ХФ, DFT, MP2/3/4(SDQ), QCISD, CCD,
CID, CISD)
В программах GAUSSIAN-03, как и
в предыдущей версии G98 существуют возможности расчета свойств:
· тензоров экранирования и химсдвигов ЯМР на уровне MP2 (ранее
поддерживались методы XФ, DFT);
· VCD — интенсивности на уровне XФ и DFT;
· рамановские интенсивности на уровне DFT и MP2 (ранее их
расчеты поддерживались на уровне ХФ).
· методы расчета возбужденных состояний: ZINDO для расчетов
сверхбольших молекул и время-зависимые методы RBA на уровне ХФ и DFT, которые
дополняют имеющиеся ранее вохможности CIS.
· внедрены новые функционалы плотности в методе DFT. улучшены
схемы определения пути реакции;
· реализован метод IRCMax для более точного определения
структуры переходного состояния;
· cделаны доработки в реализации псевдопотенциальных методик;
так, полулокальные ECP стали доступны с проекторами для любых угловых моментов,
и достигнута возможность аналитического расчета вторых производных; добавлены
новые схемы параметризации ECP;
· добавлены новые встроенные базисные наборы гауссовских
функций, в т.ч. Midi!, сс-pV6Z, cc-pVDZ, cc-pVTZ и др., включены новые базисы
EPR-II и EPR-III, эффективные для расчетов констант сверхтонкого взаимодействия
в методе DFT
GAUSSIAN-03 позволяет выполнять вычисления на высокопроизволительных
вычислительных кластерах посредством использования пакета TCPLinda.
Использование параллельных систем для вычислений основано на параллельной
реализации части методов, используемых в GAUSSIAN-03. Методы HF, CIS=Direct и DFT
являются распараллеленными, вычисления TDDFT и MP2 энергий является также
распараллеленным. Использование этих методов в моделировании позволяет
распараллеливать процесс решения автоматически, используя лишь настройки
исходной задачи.
Линейно масштабируемые (FMM) алгоритмы, используемые в GAUSSIAN-03 по умолчанию для молекул с
количеством атомов более 65, не являются параллельными. Для получения реального
преимущества использования параллельных вычислений в GAUSSIAN-03, количество атомов в моделируемых
молекулах должны превышать 300.
2.2 Принцип работы программ GAUSSIAN
Начиная с G80 программы
серии GAUSSIAN построены по одному принципу, тело
программы состоит из серии линков, которые представляют собой отдельную
программу. Каждый линк загружается в течении расчета по мере необходимости,
запуск и обмен данными между линками осуществляется отдельной управляющей
программой. Линки обьединены группами в оверлеи по принципу выполнения сходных
функций. Каждый линк имеет свой трехзначный или четырехзначный номер. Последние
две цифры означают номер линка в оверлее, первые цифры- номер оверлея. Пример
построения расчета приведен на схеме рис.
Оверлей 0 определяет набор файлов и машинных параметров, необходимых для
решения задачи и задает последовательность выполнения отдельных линков, исходя
из последовательности ключевых слов.
Оверлей 1 выполняет считывание (заголовок, заряд, мультиплетность, Z-матрица) и контроль оптимизации
геометрии. Оверлей 1 включает несколько линков, где L101 считывает задание и спецификацию молекулы, L102, L103, L105, L109 определяет выбор метода
оптимизации, соответственно, Флетчера-Пауэлла, BERNY и Метага-Сержента, Ньютон-Рапсона, L108-расчет поверхности потенциальной
энергии, L118- расчет траекторий хим. реакций, L120- контроль ONIOM расчетов и т.д.
Число Линков растет с каждой новой версией и их спецификации можно увидеть в
справке для версии программы. (L101-Reads title and molecule specification, L102-FP
optimization, L103-Berny optimizations to minima and TS, STQN transition state
searches, L105-MS optimization, L106-Numerical differentiation of
forces/dipoles to obtain polarizability/hyperpolarizability,
L107-Linear-synchronous-transit (LST) transition state search, L108-Potential
energy surface scan, L109-Newton-Raphson optimization, L110-Double numerical
differentiation of energies to produce frequencies, L111 Double num. diff. of
energies to compute polarizabilities & hyperpolarizabilities, L113-EF
optimization using analytic gradients, L114-EF numerical optimization (using
only energies), L115-Follows reaction path using the intrinsic reaction
coordinate (IRC), L116-Numerical self-consistent reaction field (SCRF),
L117-Post-SCF SCRF, L118 Trajectory calculations, L120-Controls ONIOM
calculations)
Оптимизация по методу X. Бернарда Шлегеля (BERNY) самая быстрая и
вычисляет аналитически градиенты энергии и численно приближенную матрицу
силовых постоянных, которая постоянно обновляется в процессе оптимизации, для
оценки положения минимума энергии. Однако для циклических молекул, а также для
молекул с необычными силовыми постоянными она может оказаться неэффективной:
процесс оптимизации будет проходить очень медленно или вообще результаты
окажутся неверными. Если оптимизация геометрии дает неверные результаты, то
следует обратиться к методу Мэтага-Сержента. В нем применена другая стратегия
для отыскания структуры с минимальной энергией. Он работает медленнее, чем
BERNY, но более надежно. Третий вариант оптимизации- метод Флетчера-Пауэлла. Он
предусмотрен для таких ситуаций, когда не представляется возможным вычислить
градиенты аналитически. В этих случаях метод Флетчера-Пауэлла выбирается
программой автоматически. Затем градиенты энергии оцениваются методами конечных
разностей. Эта процедура может быть использована для любых способов расчета
энергии, но она чрезвычайно медленна по сравнению с методами аналитического
расчета градиентов (сил на атомах).
Оверлей 2 содержит линк L202
осуществляющий расчет декартовых координат атомов молекулы в соответствии с Z-матрицей, определяет симметрию
молекулы, которая используется в дальнейшем при расчете интегралов, определении
симметрии МО и электронных состояний. (L202-Reorients coordinates, calculates symmetry, and
checks variables).
Оверлей
3 содержит боле10 линков, которые: L301-устанавливает набор базисных функций для каждого атома в соответствии с выбранным ключевым словом, L301, остальные линки L303- L319 рассчитывают различного типа интегралы и их первые производные (L301-Generates basis set information, L302-Calculates
overlap, kinetic, and potential integrals, L303-Calculates multipole integrals,
L308-Computes dipole velocity and Rx integrals, L309-Computes ECP integrals,
L310-Computes spdf 2-electron integrals in a primitive fashion, L311-Computes
sp 2-electron integrals, L314-Computes spdf 2-electron integrals, L316-Prints
2-electron integrals, L319-Computes 1-electron integrals for approximate spin
orbital coupling).
Оверлей
4 содержит: линк L401, который создает начальный набор МО для итерационной процедуры ССП, L402- проведение полуэмпирических расчетов и расчетов методом молекулярной механики, L405- проведение расчета
методом полного
учета взаимодействия электронных конфигураций -Complete Active Space Multiconfiguration SCF
(MC-SCF)(L401-Forms the initial MO guess, L402-Performs semi-empirical and
molecular mechanics calculations, L405-Initializes an MCSCF calculation).
Оверлей 5 в отличии от других оверлеев содержит линки, которые не имеют
общего набора опций, так как в каждой задаче используется только один из
линков. Линки оверлея 5 содержат процедуры самосогласованного расчета с
использованием различных методов: L502- метод Хартри-Фока для систем с открытыми и замкнутыми оболочками,
все прямые методы и т.д., L503-
производится расчет выбранным методом способом скорейшего спуска, L510- многоконфигурационный расчет (L502-Iteratively solves the SCF equations (conven. UHF & ROHF, all direct methods, SCRF), L503-Iteratively
solves the SCF equations using direct minimization, L506-Performs an ROHF or
GVB-PP calculation, L508-Quadratically convergent SCF program, L510-MC-SCF).
Оверлей 6 осуществляет анализ волновых функций, которые рассчитываются в
оверлее 5. Линк L601 проводит
анализ заселенностей, рассчитывает таблицу собственных значений, заселенности
перекрываний, орбитальные заселенности и дипольные моменты, L602- расчет электронных свойств, L607- проводит анализ натуральных
орбиталей, L609- анализ атомных и молекулярных
свойств (L601-Population and related analyses (including multipole moments), L602-1-electron properties (potential, field, and field gradient), L604-Evaluates MOs or density over a grid of points, L607-Performs NBO analyses, L608-Non-iterative DFT energies, L609-Atoms in Molecules properties).
Оверлей 7 рассчитывает первые и вторые производные электронных интегралов
— линки L701- L703. Эти три линка используются при оптимизации геометрии
молекулы по методу ССП при помощи сил, вычисленных аналитическим способом. Линк L716 вычисляет силы на атомах по значениям первых
производных (L701-1-electron integral
first or second derivatives, L702 2-electron integral first or second
derivatives (sp), L703-2-electron integral first or second derivatives (spdf),
L709-Forms the ECP integral derivative contribution to gradients,
L716-Processes information for optimizations and frequencies)
Оверлей
8 (L801-Initializes transformation of 2-electron integrals, L802-Performs
integral transformation (N3 in-core), L803-Complete basis set (CBS)
extrapolation, L804-Integral transformation, L811-Transforms integral
derivatives & computes their contributions to MP2 2nd derivatives) и Оверлей 9 (L901-Anti-symmetrizes
2-electron integrals, L902-Determines the stability of the Hartree-Fock
wavefunction, L903-Old in-core MP2, L905-Complex MP2, L906-Semi-direct MP2,
L908-OVGF (closed shell), L909-OVGF (open shell), L913-Calculates post-SCF
energies and gradient terms, L914-CI-Singles, RPA and Zindo excited states; SCF
stability, L915-Computes fifth order quantities (for MP5, QCISD(TQ) and
BD(TQ)), L918-Reoptimizes the wavefunction) предназначены для расчета
электронных корреляций. Линк
L901 проводит начальные расчеты для
корреляционных расчетов, Линки L903, L905, L906 выполняют корреляционные расчеты по методу
Меллера-Плессета, расчет функций Грина для систем с открытой и замкнутой
оболочками, L918 осуществляет начальное
приближение при оптимизации волновой функции, если зафиксирована ее
нестабильность.
Оверлей 10 содержит линки L1002
расчитывающие различные молекулярные свойства, включая спектральные (ЯМР),
линки L1003 и L1014 для расчета конфигурационных взаимодействий возбужденных
состояни й (L1002-Iteratively solves the CPHF equations; computes various properties (including NMR), L1003-Iteratively solves the CP-MCSCF equations, L1014-Computes analytic
CI-Singles second derivatives).
Оверлей 11 рассчитывает производные электронных интегралов- линки L1101, L1102, L1110-
L1112. Эти три линка используются при оптимизации геометрии молекулы (L1101-Computes 1-electron integral derivatives,
L1102-Computes dipole derivative integrals, L1110-2-electron integral
derivative contribution to Fx, L1111-2 PDM and post-SCF derivatives, L1112-MP2
second derivatives).
Оверлей 99-последний оверлей с линком L9999 производит разгрузку комьютера, записывают результаты
расчета в архив и заканчивают работу одной из цитат, содержащихся в тексте
программы.
.3 Задание расчета и структура входного файла
Для проведения квантовомеханических расчетов с использованием программы GAUSSIAN необходимо дать входное задание,
которое может прдставлено в виде файла определенной структуры. Это можно
осуществить в виде отдельного файла, который считывается после запуска
программы GAUSSIAN или это можно сделать с помощью
отдельной вспомогательной программы для ввода задания и визуализации
результатов расчета- GaussView. При запуске этой программы появляется три окна (i) GaussView X.Y, (ii) Builder и (iii) View1 (рис. 2 ). X.Y- номер версии
программы.
Рис.2. Окна программы GaussView после ее запуска
Из окна GaussView X.Yможно считать и
записать в память машины входной файл, из окна Builder возможна генерация геометрии молекулы с
использованием кнопок для выбора вида атома, длины связи, углов, готовых
химических группировок и т.д. Окно View служит для визуализации молекулы. Например, для построения молекулы
ацетилена C2H2 надо кликнуть на кнопку -R Group в окне Builder,
при этом появляется окно Select
_R Group Fragment, выбрать группу CH_C__, после двойного клика в окне View появляется структура молекулы C2H2 в стиле Ball and Stick (рис. 3,4 ).
Рис.3,4. Выбор стандартного фрагмента молекулы CH_C__ и построение
В окне View структуры молекулы C2H2 в стиле Ball and Stick.
После построения молекулы переходим к заданию расчетных параметров. Для
этого кликаем на Calculate и
выбираем Gaussian (в окне GaussView), после чего появляется окно заданий
Gaussian Calculation Setup (рис.5). Заполнение различных окон и выбор методики
расчета в этом окне позволяют полностью сформировать входной файл, необходимый
для запуска программы расчета GAUSSIAN. Для выбранного нами примера ацетилена необходимо в окне Title внести комментарии для идентификации
расчета (например, Acetylene).
Выбираем заряд молекулы Charge
равный 0 и мультиплетность в окне Spin как Singlet.
Рис.5. Окно заданий
Gaussian Calculation Setup.
Кнопка Job Type позволяет выбрать тип расчета из списка реализуемых в
программе GAUSSIAN. Если нам необходимо произвести
оптимизацию геометрии молекулы с расчетом частот колебаний, то мы выбираем Opt+Freq. Выбор спецификации No Raman Intensities позволяет нам увеличить скорость
расчета, однако, если это необходимо, можно также рассчитать и интенсивности
рамановского спектра. Далее необходимо выбрать метод расчета и базисный набор.
Кнопками на панели Method выбираем
следующие спецификации расчета: Ground state, B3LYP, Restricted, базисный набор: 6-311G. В
окне Solvation выбираем none, так как расчет производим не в растворе. В окне General Options не выбираем не одного окна. Окончательно все параметры
можно записать в память ЭВМ в виде входного файла кликом Submit и выбрав имя файла и папку для
хранения на диске.
.4 Структура Input File.
Образованный входной файл, содержащий задания для расчета при помощи
программы GAUSSIAN имеет определенную структуру,
состоящую из ключевых слов и порядка их расположения. На рис.6 приведен пример
такого задания для рассматриваемого расчета оптимизации и частот колебаний
молекулы C2H2.
Рис.6. Пример задания для расчета оптимизации и частот колебаний
Первые две строки генерируются при запуске программы и указывают на
количество оперативной памяти, нобходимой для расчета и количество
задействованных процессоров. Знак % означает, что все записи после него
являются не исполняемыми, а информационными. Третья строка содержит название
автоматически создаваемого файла с результатами текущих расчетов (checkpoint file).
Символы # , #T, #р в начале
командной строки характеризуют разную степень объема выводимых результатов
расчета на печать. В последнем случае вся расчетная информация выдается на
печать.
Ключевое слово opt
указывает, что будет производиться оптимизация геометрии молекулы. Так как не
указывается спецификация процедуры оптимизации, то поиск оптимальной геометрии
будет производиться по умолчанию с помощью процедуры BERNY.
freq=noraman указывает на расчет частот колебаний
без расчета интенсивностей рамановского спектра.
Ключевое слово rb3lyp означает, что расчет будет
производиться методом теории функционала плотности с использованием
трехпараметрического функционала Becke
и учетом корреляции электронов методом Lee, Yang, Parr.
Ключевое слово 6-311G
указывает используемый базис, характеризующийся описанием орбиталей остова
шестью примитивными гауссовыми функциями, тремя и одной функцией для валентных
s- и р-орбиталей и одной функцией для d-орбиталей, которые выполняют роль диффузных функций.
Следующий набор ключевых слов разделен пустой строкой после которой идет
строка с заголовком расчета, где указывается, обычно, название молекулы и
другая информация, необходимая для идентификации конкретного расчета.
После пустой строки указывается заряд charge и multiplicity молекулы. Мультиплетность точно соответствует мультиплетности
электронного состояния: 1-синглет, 2-дублет, 3-триплет и т.д.
Далее идет Z-матрица
молекулы, в которой кроме длин связей, также могут быть указаны значения углов
между связями. Любой набор букв может служить определенными символами
переменных. Если какие-либо переменные остаются постоянными в процессе оптимизации,
то в Z-матрице приводятся их численные
значения. В конце задания геометрии приводится пустая строка.
В зависимости от расчетной задачи содержание входного файла может иметь
различное содержание, в котором меняются ключевые слова цели, методов расчета,
количества выводимой информации и т.д. В каждом конкретном случае необходимо
пользоваться инструкцией для полбзователей GAUSSIAN (Gaussian User’s Guide). Ниже приведен список ключевых слов
для методов и способов расчета.
НЕЭМПИРИЧЕСКИЕ МЕТОДЫ:- Hartree Fock (uses RHF for
singlets and UHF for others)- restricted Hartree Fock- unrestricted Hartree
Fock- spin-restricted open-shell Hartree Fock- two open shell singlet wave
function- generalized valence bond — complete active space MCSCF-
Moller-Plesset second order correlation energy correction- Moller-Plesset third
order correlation energy correction- same as MP4SDTQDQ — Moller-Plesset fourth
order correlation energy correction with double and quadruple substitutions.SDQ
— Moller-Plesset fourth order correlation energy correction with single, double
and quadruple substitutions.SDTQ — Moller-Plesset fourth order correlation
energy correction with single, double, triple and quaduple substitutions.- same
as CISD- configuration interaction with single excitations- configuration
interaction with double excitations- configuration interaction with single and
double excitations- quadratic configuration interaction with single and double
excitations(T) — quadratic configuration interaction with single and double
excitations and triples contribution to the energy
БАЗИСНЫЕ НАБОРЫ:
|
базис |
дополнение |
атомы |
|
STO-3G |
* |
H — Xe |
|
3-21G |
* ** |
H — Cl |
|
4-21G |
* ** |
|
|
4-31G |
* ** |
H — Ne |
|
6-21G |
* ** |
|
|
6-31G |
+ ++ * ** |
H — Cl |
|
LP-31G |
* ** |
|
|
LP-41G |
* ** |
|
|
6-311G |
+ ++ * ** |
H — Ar |
|
MC-311G |
H — Ar |
|
|
D95 |
+ ++ * ** |
H — Cl |
|
D95V |
+ ++ * ** |
H — Ne |
|
SEC |
+ ++ * ** |
H — Cl |
|
CEP-4G |
+ ++ * ** |
H — Cl |
|
CEP-31G |
+ ++ * ** |
H — Cl |
|
CEP-121G |
+ ++ * ** |
H — Cl |
|
LANLIMB |
H — Bi (кроме lanthanides) |
|
|
LANLIDZ |
H — Bi (кроме lanthanides) |
ПОЛУЭМПИРИЧЕСКИЕ МЕТОДЫ:
AM1 — Austin method one- complete neglect of differential
overlap- intermediate neglect of differential overlap- modified intermediate
neglect of differential overlap third modification.- modified neglect of
differential overlap
СПЕЦИФИКАЦИЯ РАСЧЕТА- distances in Angstroms- distances
in bohrs- angles in degrees- angles in radians- generate a cube file- for cube
file generation- do integrals as needed (vice in a file on the disk)- do integrals
in core memory- add a finite field to the calculation- frequency
determination=noraman — frequency determination without Raman intensities- put
basis in output file- put basis in output file in format for generalized input-
follow a reaction path- linear synchronous transit — optimize all variables-
geometry optimization- calculate polarizability and hyperpolarizability, if
possible=none — no population analysis=min — minimal printing of Mulliken
population analysis=reg — some printing of Mulliken population analysis=full —
full printing of Mulliken population analysis=bonding — bonding population
analysis=no — natural orbital analysis=noab — natural orbital analysis for
separate alpha and beta spins=grid — computes electrostatic potential=field —
computes electrostatic potential and field=EFG — computes electrostatic
potential, field and field gradients- puts various information in a separate
output file- read in masses for each atom- restart optimization from a
checkpoint file- optimization of a transition state
.5 Проведение расчета и структура выходного файла
После записи входного файла на диске ЭВМ для запуска программы расчета
необходимо или загрузить непосредственно программу GAUSSIAN, например, кликнув на
соответствующий этой программе ярлык или выйти на запуск этой прграммы
непосредственно из GaussView после
клика на Submit. В последнем случае появляется окно
с предложением установить имя входного (.gjf) и выходного файлов (.out), после чего появляется окно программы GAUSSIAN (рис. 7) и начинается процедура
счета. По оканчанию счета работа программы останавливается и запись выходного
файла происходит автоматически.
Ниже приведены результаты расчета для оптимизации и расчета частот для
молекулы ацетилена, как они представлены в выходном файле. А самом начале
указан адрес линка, запускающего расчет, далее указывается версия программы, ее
правовладелец, адреса, авторы и т.д., время запуска программы.
Entering Link 1 = C:\G98W\l1.exe PID= 856.(c)
1988,1990,1992,1993,1995,1998 Gaussian, Inc.Office Park, Building 6,
Pittsburgh, PA 15106 USAthis work as:98, Revision A.9,
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,
……
*********************************************98:
x86-Win32-G98RevA.9 19-Apr-2000
06-Nov-2007
Рис.7. Окно программы GAUSSIAN.
Количество оперативной памяти, нобходимой для расчета и количество
задействованных процессоров, имя файла автоматической записи результатов (.chk).
*********************************************
%mem=6MW
%nproc=1use up to 1 processors via shared memory.
%chk=acetylene.chkroute: MaxDisk=2000MB
Повторяется строка задания со списком ключевых слов.
—————————————————
# opt freq=noraman rb3lyp/6-311g geom=connectivity
Последующий набор строк определяет алгоритм выполнения вычислений
программой, т.е. определяет порядок вызова линков из определенных оверлеев.
Каждая строка соответствует оверлею, номер которого стоит первым. Значение
чисел между двумя наклонными чертами определяют значение опций, с которыми
выполняются линки данного оверлея. Например, строка 4/7=1/1; соответствует
оверлею 4, в котором выполняется линк 401 (создается начальный набор МО для
итерационной процедуры ССП), при этом опция 7 имеет значение, равное 1. полный
список опций дан в инструкции для пограммы. Число в круглых скобках означает
переход через несколько оверлеев, например, 1/14=-1,18=20/3(1) означает, что
если оптимизация не завершена, то следующий за данной строкой оверлей будет
пропущен. Последней строкой стоит оверлей 99 окончания счета и записи
результата.
————————————————-
/9=110,17=6,18=5,40=1/2;
/5=4,6=6,11=2,25=1,30=1/1,2,3;
/7=1/1;
/5=2,38=4,42=-5/2;
/7=2,8=2,9=2,10=2,28=1/1;
//1,2,3,16;
/14=-1,18=20/3(1);
//99;
Строка с заголовком расчета
———
acetiylene
———
Строки с указанием заряда и мультиплетности и Z-матрица молекулы, в которой указаны варьируемые и постоянные
параметры.
Symbolic Z-matrix:= 0 Multiplicity = 10 3.46875 0. -1.31250
3.46875 0. Z10 X1 0. Z20 X2 Y1 Z3:-0.1175-2.37350.94353.468753.468750.
Строка с спецификацией метода оптимизации.
Berny optimization.
Таблица начальных параметров расчета длин связей и углов, необходимых для
оптимизации, а также декартовы координаты молекулы.
! Initial Parameters !
! (Angstroms and Degrees) !
———————— ————————-
! Name Definition Value Derivative Info. !
—————————————————————————-
! R1 R(1,2) 1.195 estimate D2E/DX2 !
! R2 R(1,3) 1.061 estimate D2E/DX2 !
! R3 R(2,4) 1.061 estimate D2E/DX2 !
! A1 L(2,1,3,-1,-1) 180. estimate D2E/DX2 !
! A2 L(1,2,4,-1,-1) 180. estimate D2E/DX2 !
! A3 L(2,1,3,-2,-2) 180. estimate D2E/DX2 !
! A4 L(1,2,4,-2,-2) 180. estimate D2E/DX2 !
—————————————————————————-Radius=3.00D-01
FncErr=1.00D-07 GrdErr=1.00D-06of steps in this run= 20 maximum allowed number
of steps= 100.orientation:
———————————————————————Atomic
Atomic Coordinates (Angstroms)Number Type X Y Z
———————————————————————
6 0 3.468750 0.000000 -1.312500
6 0 3.468750 0.000000 -0.117500
1 0 3.468750 0.000000 -2.373500
1 0 3.468750 0.000000 0.943500
———————————————————————
Матрица расстояний в ангстремах для действительных атомов
Distance matrix
(angstroms):
1 2 3 4
C 0.000000
C 1.195000 0.000000
3 H 1.061000 2.256000 0.000000
H
2.256000 1.061000 3.317000 0.000000
Для определения симметрии используется Z-матрица, точечная группа соответствует тем ограничениям по
симметрии, используемые при оптимизации. Симметрия исходной и оптимизированной
структур может отличаться от симметрии, полученной из Z-матрицы. В обозначении симметрии структурных элементов
указывается, какие атомы совпадают с элементами симметрии. Программа
рассчитывает также число степеней свободы молекулы в рамках данной симметрии,
т.е. количество оптимизируемых параметров. Полная точечная группа и абелевы
подгруппы применяются в других частях программы для экономии машинного времени
за счет использования симметрии, а также для определения симметрии полной
волновой функции и отдельных МО.
Stoichiometry C2H2group D*H[C*(HC.CH)]. of freedom 2point
group D*H NOp 8Abelian subgroup D2H NOp 8concise Abelian subgroup C2 NOp 2
Далее указывается стандартный базис, который приписывается каждому
атомному центру. Далее в программе, используя точечную группу молекулы,
строятся симметризованные базисные функции. Симметрия этих орбиталей обозначена
при помощи символов Малликена. В нашем случае имеются МО, свойства симметрии
которых можно определить по таблице 2.
Таблица 2. Малликеновские символы для обозначения симметрии МО
|
Символ |
Значение |
|
A(B) |
Симметрична |
|
E |
Двухкратно вырождена |
|
T |
Трехкратно вырождена |
|
1(2) |
Симметрична |
|
g(u) |
Симметрична |
|
/ (//) |
Симметрична(антисимметрична) |
Standard basis: 6-311G (5D, 7F)are 10 symmetry adapted basis
functions of AG symmetry.are 0 symmetry adapted basis functions of B1G
symmetry.are 3 symmetry adapted basis functions of B2G symmetry.are 3 symmetry
adapted basis functions of B3G symmetry.are 0 symmetry adapted basis functions
of AU symmetry.are 10 symmetry adapted basis functions of B1U symmetry.are 3
symmetry adapted basis functions of B2U symmetry.are 3 symmetry adapted basis
functions of B3U symmetry.
Ниже печатаются сообщение о применение метода Раффенти для записи и
хранения интегралов и об использовании симметрии для вычисления двухэлектронных
интегралов. Также указано количество рассчитанных интегралов.estimate of integral set expansion from redundant
integrals=1.000.buffers will be 262144 words long.2 integral format.electron
integral symmetry is turned on.
basis functions 62 primitive gaussians
alpha electrons 7 beta electrons
Расчет энергии отталкивания ядер в единицах Хартри = 27.2116 эВ
nuclear repulsion energy 24.9010884632 Hartrees.electron
integrals computed using PRISM.= 32 RedAO= T NBF= 10 0 3 3 0 10 3 3= 32
1.00D-04 NBFU= 10 0 3 3 0 10 3 3
Следующая стадия расчета- определение начального приближения для
процедуры ССП посредством метода INDO.
Печатается симметрия МО начального приближения с разделением на занятые и
свободные орбитали.
Projected INDO Guess.guess orbital symmetries:(SGG) (SGU)
(SGG) (SGU) (SGG) (PIU) (PIU)(SGU) (PIG) (PIG) (SGG) (SGU) (SGG) (SGG) (SGG)
(SGG) (SGG) (SGG) (PIG) (PIG) (PIG) (PIG) (SGU)
(SGU) (SGU) (SGU) (SGU) (SGU) (PIU) (PIU) (PIU)
(PIU)
После того как все необходимые интегралы и начальное приближение
получены, программа переходит к выполнению ССП. Критерием сходимости служит
изменение матрицы плотности на величину, меньшую чем 1.00D-05. В нашем случае сходимость
достигается за 9 итераций .
Requested convergence on RMS density matrix=1.00D-08 within 64 cycles.
Requested convergence on MAX density matrix=1.00D-06.R1 and
R2 integrals in memory in canonical form, NReq= 687310.accuracy reduced to
1.0D-05 until final iterations.convergence to 1.0D-05 achieved. Increase
integral accuracy.Done: E(RB+HF-LYP) = -77.3356007715 A.U. after 9 cycles = 0.3165D-08 -V/T = 2.0033
S**2 =
0.0000
После того как самосогласование достигнуто, печатается полная энергия
молекулы E(RB+HF-LYP) в атомных единицах (1 а.е.= 627.5
ккал/моль). Полная энергия представляет собой сумму энергии отталкивания ядер,
электронной энергии и корреляционной энергии. Приводится значениесходимости по
матрице плотности, достигнутое на последнем итерационном шаге 0.3165D-08 и вириальный коэффициент -V/T равный отношению потенциальной энергии к кинетической,
точное значение которого в соответствии с теоремой вириала равно 2.
Процедура ССП завершается малликеновским анализом заселенностей. В начале
печатаются МО с указанием типа симметрии.
*************************************************************
Population analysis using the SCF density.
*************************************************************Symmetries:(SGG)
(SGU) (SGG) (SGU) (SGG) (PIU) (PIU)(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (PIU)
(PIU)
(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (SGU) (SGG)
(SGU) (PIU) (PIU) (PIG) (PIG) (SGU) (SGG) (SGG)
(SGU)electronic state is 1-SGG.
Энергии МО приведены в Хартри
Alpha occ. eigenvalues — -10.18096 -10.17829 -0.76610
-0.57058 -0.50667occ. eigenvalues — -0.29990 -0.29990virt. eigenvalues —
0.03885 0.03885 0.06440 0.08452 0.25453virt. eigenvalues — 0.26004 0.39692
0.39692 0.52144 0.52144virt. eigenvalues — 0.56815 0.64783 0.71897 0.98990
1.08350virt. eigenvalues — 2.21541 2.28832 2.58573 2.58573 2.69182
Alpha virt. eigenvalues — 2.69182 3.16084 3.22833 23.16698
23.71859
Заселенность атома представляет собой сумму заселенностей, рассчитанных
для всех базисных функций АО. Заселенности для всех атомов сведены в таблицу.
Недиагональные элементы матрицы характеризуют степень перекрывания между
атомами. Например, видно, что перекрывания С1 — Н3 положительное и равно 2∙0.368349,
тогда как С1 — Н4 связи нет и перекрывание отрицательное. Далее приведены
распределение зарядов на атомах с учетом перекрывания, расчет дипольных,
квадрупольных и более высокого порядка моментов молекулы.
Condensed to atoms (all electrons):
2 3 4
C 4.851852 1.024059 0.368349 -0.010217
C 1.024059 4.851852 -0.010217 0.368349
H 0.368349 -0.010217 0.406674 0.001152
H -0.010217 0.368349 0.001152 0.406674atomic charges:
C -0.234042
C -0.234042
H 0.234042
H 0.234042of Mulliken charges= 0.00000charges with hydrogens
summed into heavy atoms:
C 0.000000
C 0.000000
H 0.000000
H 0.000000of Mulliken charges= 0.00000
Electronic spatial extent (au): <R**2>= 60.2656= 0.0000
electronsmoment (Debye):= 0.0000 Y= 0.0000 Z= 0.0000 Tot= 0.0000moment
(Debye-Ang):= -13.4598 YY= -13.4598 ZZ= -7.1390= 0.0000 XZ= 0.0000 YZ=
0.0000moment (Debye-Ang**2):= 0.0000 YYY= 0.0000 ZZZ= 0.0000 XYY= 0.0000=
0.0000 XXZ= 0.0000 XZZ= 0.0000 YZZ= 0.0000= 0.0000 XYZ= 0.0000moment
(Debye-Ang**3):= -15.1152 YYYY= -15.1152 ZZZZ= -37.6696 XXXY= 0.0000= 0.0000
YYYX= 0.0000 YYYZ= 0.0000 ZZZX= 0.0000= 0.0000 XXYY= -5.0384 XXZZ= -12.0664
YYZZ= -12.0664= 0.0000 YYXZ= 0.0000 ZZXY= 0.0000N= 2.490108846321D+01
E-N=-2.292404823474D+02 KE= 7.708108608436D+01
Symmetry AG KE= 3.813333457619D+01B1G KE=
0.000000000000D+00B2G KE= 2.335770561963D-33B3G KE= 6.728674288393D-34AU KE=
0.000000000000D+00B1U KE= 3.442577134687D+01
Symmetry B2U KE= 2.260990080654D+00B3U KE= 2.260990080655D+00
Далее программа приступает к оптимизации. Вычисляются первые производные
интегралы и определяются на их основе силы на атомах в системе координат
заданной ориентации Z-матрицы, которые
приведены ниже в таблице, а затем в системе внутренних координат Z-матрицы, т.е. длин связей и углов.
Программа проводит оценку матрицы вторых производных по значениям первых
производных и проверку на достижение минимума энергии. Далее программа рассчитывает
изменения, которые необходимо внести в Z-матрицу для достижения минимума энергии.
***** Axes restored to original set *****
——————————————————————Atomic
Forces (Hartrees/Bohr)Number X Y Z
——————————————————————
6 0.000000000 0.000000000 -0.016549601
6 0.000000000 0.000000000 0.016549601
1 0.000000000 0.000000000 -0.000096767
1 0.000000000 0.000000000 0.000096767
——————————————————————Forces:
Max 0.016549601 RMS 0.006756462optimization.Forces: Max 0.000010306 RMS
0.000005512for a local minimum.number 1 out of a maximum of 20quantities
printed in internal units (Hartrees-Bohrs-Radians)derivative matrix not updated
— analytic derivatives used.
Программа проводит оценку матрицы вторых производных по значениям первых
производных и проверку на достижение минимума энергии. Далее программа
рассчитывает изменения, которые необходимо внести в Z-матрицу для достижения минимума энергии.
The second derivative matrix:R2 R3 A1 A21.09115-0.01001
0.41100-0.01001 0.00030 0.411000.00000 0.00000 0.00000 0.066910.00000 0.00000
0.00000 -0.01967 0.066910.00000 0.00000 0.00000 0.00000 0.000000.00000 0.00000
0.00000 0.00000 0.00000A40.06691-0.01967 0.06691— 0.04724 0.04724 0.08659
0.08659 0.41070— 0.41101 1.09145between quadratic step and forces= 1.83
degrees.search not attempted — first point.1 RMS(Cart)= 0.00001341 RMS(Int)=
0.000000002 RMS(Cart)= 0.00000000 RMS(Int)= 0.00000000
Значения переменных в таблице, где печатаются их текущие (Old X) и новые значения (New X) и приращения (Delta X) приведены в радиусах Бора, а первая производная энергии (DE/DX) в а.е. Изменение в геометрии получается на первом шаге
осуществляется путем оценки вторых производных, поэтому единственный вклад
вносит квадратичная экстраполяция, Новое значение переменных равно сумме Old X + Delta X. Максимальные и
среднеквадратичные значения сил сравниваются с пороговыми и по достижению
предела порога оптимизация считается успешной.
Variable Old X -DE/DX Delta X Delta X Delta X New X
(Linear) (Quad) (Total)2.27316 0.00000 0.00000 0.00000
0.00000 2.273162.00562 -0.00001 0.00000 -0.00003 -0.00003 2.005602.00562
-0.00001 0.00000 -0.00003 -0.00003 2.005603.14159 0.00000 0.00000 0.00000
0.00000 3.141593.14159 0.00000 0.00000 0.00000 0.00000 3.141593.14159 0.00000
0.00000 0.00000 0.00000 3.141593.14159 0.00000 0.00000 0.00000 0.00000
3.14159Value Threshold Converged?Force 0.000010 0.000450 YESForce 0.000006
0.000300 YESDisplacement 0.000025 0.001800 YESDisplacement 0.000013 0.001200
YES
Оценка изменения энергии при переходе к новой геометрии.
Predicted change in Energy=-2.582548D-10completed.point
found.
Печатается таблица оптимизированных параметровгеометрии молекулы.
—————————-
! Optimized Parameters !
! (Angstroms and Degrees) !
———————— ————————-
! Name Definition Value Derivative Info. !
——————————————————————————
! R1 R(1,2) 1.2029 -DE/DX = 0. !
! R2 R(1,3) 1.0613 -DE/DX = 0. !
! R3 R(2,4) 1.0613 -DE/DX = 0. !
! A1 L(2,1,3,-1,-1) 180. -DE/DX = 0. !
! A2 L(1,2,4,-1,-1) 180. -DE/DX = 0. !
! A3 L(2,1,3,-2,-2) 180. -DE/DX = 0. !
! A4 L(1,2,4,-2,-2) 180. -DE/DX = 0. !
—————————————————————————-
Производится коррекция базисного набора, с расчетом симметрии и энергий
МО, а также маликеновский анализ заселенностей с учетом новой геометрии.
******************************************************************analysis
using the SCF density.
******************************************************************Symmetries:(SGG)
(SGU) (SGG) (SGU) (SGG) (PIU) (PIU)(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (PIU)
(PIU)
(PIG) (PIG) (SGU) (SGG) (SGG) (SGU) (SGU) (SGG)
(SGU) (PIU) (PIU) (PIG) (PIG) (SGU) (SGG) (SGG)
(SGU)electronic state is 1-SGG.
Alpha occ. eigenvalues — -10.18297 -10.18047 -0.76439
-0.57157 -0.50662occ. eigenvalues — -0.29867 -0.29867virt. eigenvalues —
0.03649 0.03649 0.06366 0.08430 0.25486virt. eigenvalues — 0.25756 0.39782
0.39782 0.51974 0.51974virt. eigenvalues — 0.56818 0.64781 0.71702 0.97928
1.07979virt. eigenvalues — 2.21614 2.28385 2.58313 2.58313 2.69182
Alpha virt. eigenvalues — 2.69182 3.15893 3.22897 23.16381
23.71155to atoms (all electrons):
2 3 4
C 4.858044 1.018943 0.368300 -0.010634
C 1.018943 4.858044 -0.010634 0.368300
H 0.368300 -0.010634 0.406532 0.001148
H -0.010634 0.368300 0.001148 0.406532atomic charges:
C -0.234654
C -0.234654
H 0.234654
H 0.234654of Mulliken charges= 0.00000charges with hydrogens
summed into heavy atoms:
C 0.000000
C 0.000000
H 0.000000
H 0.000000of Mulliken charges= 0.00000
Electronic spatial extent (au): <R**2>= 60.5983= 0.0000
electronsmoment (Debye):= 0.0000 Y= 0.0000 Z= 0.0000 Tot= 0.0000moment
(Debye-Ang):= -13.4937 YY= -13.4937 ZZ= -7.1092= 0.0000 XZ= 0.0000 YZ=
0.0000moment (Debye-Ang**2):= 0.0000 YYY= 0.0000 ZZZ= 0.0000 XYY= 0.0000=
0.0000 XXZ= 0.0000 XZZ= 0.0000 YZZ= 0.0000= 0.0000 XYZ= 0.0000moment
(Debye-Ang**3):= -15.1902 YYYY= -15.1902 ZZZZ= -37.8567 XXXY= 0.0000= 0.0000
YYYX= 0.0000 YYYZ= 0.0000 ZZZX= 0.0000= 0.0000 XXYY= -5.0634 XXZZ= -12.1537
YYZZ= -12.1537= 0.0000 YYXZ= 0.0000 ZZXY= 0.0000N= 2.478386021537D+01
E-N=-2.289723424465D+02 KE= 7.704465961076D+01
Symmetry AG KE= 3.810532000368D+01B1G KE=
0.000000000000D+00B2G KE= 2.326131213188D-33B3G KE= 6.649958094964D-34AU KE=
0.000000000000D+00B1U KE= 3.442881138382D+01
Symmetry B2U KE= 2.255264111628D+00B3U KE=
2.255264111629D+00polarizability: 8.533 0.000 8.533 0.000 0.000
28.731polarizability: 9.179 0.000 9.179 0.000 0.000 52.199
Производится расчет частот колебаний в молекуле.
Full mass-weighted force constant matrix:frequencies —
0.0006 0.0006 0.0010 7.7848 7.7849 711.2516frequencies — 711.2516 782.2685
782.2685frequencies (cm**-1), IR intensities (KM/Mole),scattering activities
(A**4/AMU), Raman depolarization ratios,masses (AMU), force constants (mDyne/A)
and normal coordinates:
2 3PIG PIU— 711.2515 711.2515 782.2685. masses — 1.5701
1.5701 1.0848consts — 0.4680 0.4680 0.3911Inten — 0.0000 0.0000 129.9314Activ
— 0.0000 0.0000 0.0000— 0.0000 0.0000 0.0000AN X Y Z X Y Z X Y Z
6 0.00 0.16 0.00 0.16 0.00 0.00 0.06 0.00 0.00
6 0.00 -0.16 0.00 -0.16 0.00 0.00 0.06 0.00 0.00
1 0.00 -0.69 0.00 -0.69 0.00 0.00 -0.70 0.00 0.00
1 0.00 0.69 0.00 0.69 0.00 0.00 -0.70 0.00 0.00
5 6SGG SGU— 782.2685 2043.1236 3416.5404. masses — 1.0848
3.8066 1.0848consts — 0.3911 9.3623 7.4607Inten — 129.9314 0.0000
69.6778Activ — 0.0000 0.0000 0.0000— 0.0000 0.0000 0.0000AN X Y Z X Y Z X Y Z
6 0.00 0.06 0.00 0.00 0.00 0.36 0.00 0.00 0.06
6 0.00 0.06 0.00 0.00 0.00 -0.36 0.00 0.00 0.06
1 0.00 -0.70 0.00 0.00 0.00 0.61 0.00 0.00 -0.70
1 0.00 -0.70 0.00 0.00 0.00 -0.61 0.00 0.00 -0.70
— 3522.6947. masses — 1.2302consts — 8.9945Inten —
0.0000Activ — 0.0000— 0.0000 AN X Y Z
6 0.00 0.00 -0.10
6 0.00 0.00 0.10
1 0.00 0.00 0.70
1 0.00 0.00 -0.70
Расчет термодинамических характеристик молекулы: энергии, энтальпии,
теплоемкости и т.д.
——————-
Thermochemistry —
——————298.150 Kelvin. Pressure 1.00000 Atm.1 has
atomic number 6 and mass 12.000002 has atomic number 6 and mass 12.000003 has
atomic number 1 and mass 1.007834 has atomic number 1 and mass 1.00783mass:
26.01565 amu.axes and moments of inertia in atomic units:
2 3— 0.00000 50.90478 50.904780.00000 0.74884 0.662750.00000
-0.66275 0.748841.00000 0.00000 0.00000MOLECULE IS A PROLATE SYMMETRIC
TOP.SYMMETRY NUMBER 2.TEMPERATURE (KELVIN) 1.70148CONSTANT (GHZ) 35.453277point
vibrational energy 71592.9 (Joules/Mol)
.11112 (Kcal/Mol)TEMPERATURES: 1023.33 1023.33 1125.50
1125.50 2939.58
(KELVIN) 4915.61 5068.34point correction= 0.027268
(Hartree/Particle)correction to Energy= 0.030013correction to Enthalpy=
0.030957correction to Gibbs Free Energy= 0.008335of electronic and zero-point
Energies= -77.308456of electronic and thermal Energies= -77.305711of electronic
and thermal Enthalpies= -77.304767of electronic and thermal Free Energies=
-77.327389(Thermal) CV S/MOL CAL/MOL-KELVIN CAL/MOL-KELVIN18.833 7.955
47.6120.000 0.000 0.0000.889 2.981 35.7050.592 1.987 10.876
VIBRATIONAL 17.352 2.987 1.032LOG10(Q) LN(Q)BOT 0.146601D-03
-3.833862 -8.827793
TOTAL V=0 0.511211D+09 8.708600 20.052293(BOT) 0.320810D-12
-12.493752 -28.767928(V=0) 0.111869D+01 0.048710 0.1121580.100000D+01 0.000000
0.0000000.521570D+07 6.717312 15.4671840.876149D+02 1.942578 4.472952
***** Axes restored to original set *****
——————————————————————Atomic
Forces (Hartrees/Bohr)Number X Y Z
——————————————————————
1 6 0.000000000 0.000000000 -0.000010750
6 0.000000000 0.000000000 0.000010750
1 0.000000000 0.000000000 0.000010306
1 0.000000000 0.000000000 -0.000010306
——————————————————————
Cartesian Forces: Max 0.000010750 RMS 0.000006080
Запись в архивный файл результатов расчета, который будет использоваться
в последующих расчетах.
1|1|UNPC-UNK|Freq|RB3LYP|6-311G|C2H2|PCUSER|06-Nov-2007|0||#N
GEOM=ALL
CHECK GUESS=TCHECK RB3LYP/6-311G
FREQ||acetiylene||0,1|C,0.,0.,-0.6014
|C,0.,0.,0.6014511182|H,0.,0.,-1.6627806113|H,0.,0.,1.6627806113
||Version=x86-Win32-G98RevA.9|State=1-SGG|HF=-77.3357242|RMSD=6.698e-0
|RMSF=6.080e-006|Dipole=0.,0.,0.|DipoleDeriv=-0.2489113,0.,0.,0.,-0.
,0.,0.,0.,-0.1822776,-0.2489112,0.,0.,0.,-0.2489112,0.,0.,0.,-0
.1822778,0.2489111,0.,0.,0.,0.2489111,0.,0.,0.,0.1822781,0.2489111,0.,
.,0.,0.2489111,0.,0.,0.,0.1822781|Polar=8.5333455,0.,8.5333455,-0.000
,0.,28.7307553|PG=D*H
[C*(H1C1.C1H1)]|NImag=0||0.05564345,0.,0.055
64345,0.,0.,1.52218580,-0.03411242,0.,0.,0.05564345,0.,-0.03411242,0.,
.,0.05564345,0.,0.,-1.11148433,0.,0.,1.52218580,-0.02700461,0.,0.,0.0
,0.,0.,0.01664460,0.,-0.02700461,0.,0.,0.00547358,0.,0.,0.01664
,0.,0.,-0.42101841,0.,0.,0.01031694,0.,0.,0.41100458,0.00547358,0.,
.,-0.02700461,0.,0.,0.00488643,0.,0.,0.01664460,0.,0.00547358,0.,0.,-
.02700461,0.,0.,0.00488643,0.,0.,0.01664460,0.,0.,0.01031694,0.,0.,-0
.42101841,0.,0.,-0.00030309,0.,0.,0.41100458||0.,0.,0.00001075,0.,0.,-
.00001075,0.,0.,-0.00001031,0.,0.,0.00001031|||@
Одна из многочисленных цитат, содержащихся в программе.
THE NUMBERS ARE MEANINGLESS, BUT THE TRENDS ARE IMPORTANT.
— LARRY BURGGRAF
Время работы программы.
Job cpu time: 0 days 0 hours 0 minutes 11.0 seconds.lengths
(MBytes): RWF= 10 Int= 0 D2E= 0 Chk= 6 Scr= 1
Normal termination of Gaussian 98.
Заключение
Приведенный пример оптимизации геометрии и расчета частот колебаний
молекулы ацетилена показывает только малую часть возможностей программы GAUSSIAN. Основные возможности для последней
версии программы GAUSSIAN-03 были
уже изложены выше. Однако для лучшего представления о всем наборе
вычислительных ресурсов, функционировании программы, наборе методов, базисов и
функционалов, ключевых слов, необходимых для работы следует обратиться к
инструкции для пользователей конкретной версии программы. Эти инструкции можно
найти также на сайте GAUSSIAN [17]. Следует обратить внимание на прилагаемый к программе список примеров
различных расчетов молекул, для которых составлены разработчиками готовые
входные файлы.
Выражаем искренние пожелания в успешном освоении программы GAUSSIAN и проведении с ее помощью
необходимых квантовохимических расчетов.
ВОПРОСЫ И ЗАДАНИЯ
. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ХИМИИ
. Дайте определение адиабатического приближения при решении уравнения
Шредингера.
2. Какие основные приближения использует метод Хартри-Фока?
. В чем заключается принцип Паули?
. В уравнении Хартри-Фока укажите члены, ответственные за
различные взаимодействия?
1.2. Приближение линейных комбинаций атомных орбиталей (МО ЛКАО)
. Дайте определение приближению линейных комбинаций атомных
орбиталей? Для каких объектов оно применимо?
2. Каким критериям должны отвечать базисные функции?
. Что представляют из себя орбитали Слейтеровского типа?
. Почему в качестве базисных функций можно использовать гауссовые
функции?
. Что такое минимальный базисный набор? Определите минимальный
базисный набор для атома водорода, серы, натрия.
. В каких случаях применяются поляризационные и диффузные функции
в базисном наборе?
. Как определяются базисные наборы Попла? Расшифруйте базиснй
набор Попла 4-31G** для молекулы метана СН4 .
1.3. Анализ заселенностей орбиталей
. Что такое матрица плотности?
2. Дайте определение заселенности по Малликену. Какие приближения
содержит такой метод определения заселенностей?
1.4. Методы теории функционала плотности
. Дайте определение теоремы Хоэнберга-Кона?
2. Что такое функционал электронной плотности?
. Определите члены уравнения Кона-Шема?
. Что представляет собой Xα-метод?
1.5 Корреляционные поправки
. Какую величину от полной энергии системы составляют примерно
корреляционные поправки?
. Метод Мёллера-Плессета и его приближения.
.5. Полуэмпирические методы.
. Основное отличие полуэмпирических методов от неэмпирических
методов. Какими преимуществами обладают полуэмпирические методы?
2. Основные приближения, используемые в полуэмпирических методах.
. Назовите известные полуэмпирические методы и области их
применения.
1.6. Методы оптимизации (молекулярное моделирование)
. На чем основывается метод молекулярной механики, какие он содержит
приближения?
2. Назовите основные методы молекулярной механики и их области
применения.
. Метод молекулярной динамики и его применение.
2. КВАНТОВОМЕХАНИЧЕСКИЕ РАСЧЕТЫ ПРИ ПОМОЩИ ПРОГРАММЫ GAUSSIAN
.1. Основные возможности пакета GAUSSIAN-03
. Перечислите основные возможности программного пакета GAUSSIAN-03.
2. Какие основные квантомеханические методы расчетов реализованы в
программе GAUSSIAN-03?
2.2. Принцип работы программ GAUSSIAN
1. Какой
основной принцип построения тела программ GAUSSIAN? Что такое линк и оверлей?
2. Расшифруйте номер линка.
3. Определите функции каждого оверлея.
2.3. Задание расчета и структура входного файла
. Запустите программу GaussView и опишите все открытые окна.
2. Постройте на базе библиотеки структур программы GaussView любую молекулу.
. В окне Gaussian Calculation Setup задайте расчетное задание для
построенной молекулы.
. Запомните input
файл с заданием и опишите его структуру.
2.4. Проведение расчета и структура выходного файла
1. Проведите расчет основного состояния заданной молекулы
одним из методов и с разными базисами.
2. Откройте выходной файл с рзультатами
расчета и опишите процедуру расчета по используемым линкам.
3. Переведите энергии МО в
электронвольты.
4. Рассмотрите матрицу заселенностей МО,
сделайте выводы о химической связи в молекуле.
ЛИТЕРАТУРА
1. W. J. Hehre, W. A. Lathan, R. Ditchfield, M. D.
Newton, and J. A. Pople, Gaussian 70, Quantum Chemistry Program Exchange,
Program No. 237, 1970).
J. S. Binkley, R. A. Whiteside, P. C. Hariharan, R.
Seeger, J. A. Pople, W. J. Hehre, and M. D. Newton, Gaussian 76(Carnegie-Mellon
University, Pittsburgh, PA, 1976).
J. S. Binkley, R. A. Whiteside, R. Krishnan, R.
Seeger, D. J. Defrees, H. B. Schlegel, S. Topiol, L. R. Kahn, and J. A. Pople,
Gaussian 80 (Carnegie-Mellon Quantum Chemistry Publishing Unit, Pittsburgh, PA,
1980).
J. S. Binkley, M. J. Frisch, D. J. Defrees, R.
Krishnan, R. A. Whiteside, H. B. Schlegel, E. M. Fluder, and J. A. Pople,
Gaussian 82 (Carnegie-Mellon Quantum Chemistry Publishing Unit, Pittsburgh, PA,
1982).
M. J. Frisch, J. S. Binkley, H. B. Schlegel, K. Raghavachari,
C. F. Melius, R. L. Martin, J. J. P. Stewart, F. W. Bobrowicz, C. M. Rohlfing,
L. R. Kahn, D. J. Defrees, R. Seeger, R. A. Whiteside, D. J. Fox, E. M. Fluder,
and J. A. Pople, Gaussian 86 (Gaussian, Inc., Pittsburgh, PA, 1986).
M. J. Frisch, M. Head-Gordon, H. B. Schlegel, K.
Raghavachari, J. S. Binkley, C. Gonzalez, D. J. Defrees, D. J. Fox, R. A.
Whiteside, R. Seeger, C. F. Melius, J. Baker, L. R. Kahn, J. J. P. Stewart, E.
M. Fluder, S. Topiol, and J. A. Pople, Gaussian 88 (Gaussian, Inc., Pittsburgh,
PA, 1988).
M. J. Frisch, M. Head-Gordon, G. W. Trucks, J. B.
Foresman, K. Raghavachari, H. B. Schlegel, M. Robb, J. S. Binkley, C. Gonzalez,
D. J. Defrees, D. J. Fox, R. A. Whiteside, R. Seeger, C. F. Melius, J. Baker,
L. R. Kahn, J. J. P. Stewart, E. M. Fluder, S. Topiol, and J. A. Pople,
Gaussian 90 (Gaussian, Inc., Pittsburgh, PA, 1990).
M. J. Frisch, G. W. Trucks, M. Head-Gordon, P. M. W.
Gill, M. W. Wong, J. B. Foresman, B. G. Johnson, H. B. Schlegel, M. A. Robb, E.
S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C.
Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart,
and J. A. Pople, Gaussian 92 (Gaussian, Inc., Pittsburgh, PA, 1992).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W.
Gill, B. G. Johnson, M. W. Wong, J. B. Foresman, M. A. Robb, M. Head-Gordon, E.
S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C.
Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart,
and J. A. Pople, Gaussian 92/DFT (Gaussian, Inc., Pittsburgh, PA, 1993).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W.
Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson,
J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz,
J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe,
C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R.
Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J.
P. Stewart, M. Head-Gordon, C. Gonzalez, and J. A. Pople, Gaussian 94
(Gaussian, Inc., Pittsburgh, PA, 1995).
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E.
Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr.,
R. E. Stratmann, J. C. Burant, S. Dapprich, J. M.
Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, Ö. Farkas, J. Tomasi, V.
Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J.
Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, P. Salvador, J. J.
Dannenberg, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J.
Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P.
Piskorz, I. Komáromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M.
A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W.
Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle,
and J. A. Pople, Gaussian 98 (Gaussian, Inc., Pittsburgh, PA, 1998).
12. Т. Кларк. Компьютерная химия. — М.: Мир, 1990.-382с.
. Минкин В.И. Теория строения молекул 1997, 1997, 560 с.
. Цирельсон В.Г., Бобров М.Ф., Апостолова Е.С., Михайлюк А.И.
Лекции по квантовой химии. РХТУ, 1998. 350 с.
. В.И. Минкин, Б.Я. Симкин, Р.М. Миняев. Теория строения
молекул. Ростов-на-Дону «Феникс», 1998, 407 c .
. Абаренков И.В. Начала квантовой химии, 1989, 304 с.
17. http://www.gaussian.com/
Авторы:
Князев Сергей Петрович
Гордеев Евгений Георгиевич
Кирилин Алексей Дмитриевич
Описание:
Князев С. П., Гордеев Е. Г., Кирилин А. Д. Программный комплекс Gaussian 09: методы и приближения : учебно-методическое пособие / Князев С.П., Гордеев Е.Г., Кирилин А.Д.; М-во образования и науки Рос. Федерации, Моск. гос. акад. тонкой хим. технологии им. М.В. Ломоносова, Каф. химии и технологии элементоорган. соединений им. К.А. Андрианова. — Москва : МИТХТ, 2011. — 62 с. : ил. ; 21 см. — Библиогр.: с. 60-61 (5 назв.)
Рубрики:
Молекулы → Квантово-химические расчеты на компьютерах → Учебно-методические пособия для высших учебных заведений
Примечания:
Библиогр.: с. 60-61 (5 назв.)
Дата создания:
2021-05-09 21:14:58
Пожалуйста, помогите актуализировать информацию
Загрузить фотографию актуальной обложки книги
Дополнить или обновить информацию о книге
Купить
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Недоступно
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
-
Посмотреть
Реферат по теме Программный комплекс Gaussian 09: методы и приближения : учебно-методическое пособие
Помогите сайту стать лучше, ответьте на несколько вопросов про книгу:
Программный комплекс Gaussian 09: методы и приближения : учебно-методическое пособие
Опросы
В каком жанре книга?
Художественная литература
Словари, справочники, энциклопедии
Астрология, магия, эзотерика
Литература на иностранных языках
Содержание
- Объявление о покупке
- Книги этих же авторов
- Наличие в библиотеках
- Рецензии и отзывы
- Похожие книги
- Наличие в магазинах
- Информация от пользователей
- Книга находится в категориях
Реставрация Программный комплекс Gaussian 09: методы и приближения : учебно-методическое пособие
Мойка листов, чистка, отбеливание, устранение заломов, восстановление разрывов, следов от влаги,
травление насекомых, реставрация обложки и корешка, устранение укусов от собак и восстановление
заломов на картоне, восстановление после падений, восстановление тиснения и рисунков,
художественная покраска всех элементов обложки от мастеров Ленинской библиотеки.
Мелкий ремонт (удаление пятен, плесени) или реставрацию обложки, уголков, корешка, листов, переплета книги
Показать контакты
Объявление о покупке (разыскивается книга)
Подпишитесь на новые объявления
Наличие в библиотеках
Название и адрес
Режим работы
Контактная информация
Телефон
Централизованная система массовых библиотек г. Шымкента, ГУ
Туркестанская область, Шымкент городская администрация, Шымкент, Енбекшинский район, 18-й микрорайон м-н
18-й микрорайон, 2
Расположение на карте
Пн: 09:00-13:00 15:00-19:00
Вт: 09:00-13:00 15:00-19:00
Ср: 09:00-13:00 15:00-19:00
Чт: 09:00-13:00 15:00-19:00
Пт: 09:00-13:00 15:00-19:00
Название и адрес
Режим работы
Контактная информация
Телефон
Детская библиотека №8
Брянская область, Брянск городской округ, Брянск, Бежицкий район
Куйбышева, 19
Расположение на карте
сентябрь-май: пн-пт, вс 10:00-18:00; санитарный день: последний день месяца
Пн: 10:00-18:00
Вт: 10:00-18:00
Ср: 10:00-18:00
Чт: 10:00-18:00
Пт: 10:00-18:00
Название и адрес
Режим работы
Контактная информация
Телефон
Фундаментальная медицинская библиотека
Москва, Москва, Аэропорт район
Балтийская, 8
Расположение на карте
санитарный день: последний рабочий день месяца
Пн: 10:00-17:00
Вт: 10:00-17:00
Ср: 10:00-17:00
Чт: 10:00-17:00
Пт: 10:00-17:00
www.fbramn.ru
Название и адрес
Режим работы
Контактная информация
Телефон
санитарный день: последняя пт месяца
Вт: 12:00-22:00
Ср: 12:00-22:00
Чт: 12:00-22:00
Пт: 12:00-22:00
Сб: 12:00-22:00
Вс: 12:00-20:00
Вконтакте:
https://vk.com/biblioteka167
Инстаграм:
https://instagram.com/biblioteka167
Название и адрес
Режим работы
Контактная информация
Телефон
Центральная библиотека №136 им. Л.Н. Толстого
Москва, Москва, Нагатино-Садовники район
Коломенский проезд, 21
Расположение на карте
Вт: 10:00-21:00
Ср: 10:00-21:00
Чт: 10:00-21:00
Пт: 10:00-21:00
Сб: 10:00-21:00
Вс: 10:00-20:00
cbsuao.ru/
Вконтакте:
https://vk.com/bibliotekalvatolstogo
Facebook:
https://facebook.com/bibliotekalvatolstogo
Название и адрес
Режим работы
Контактная информация
Телефон
Межпоселенческая центральная библиотека им. И.И. Лажечникова
Московская область, Коломенский район, пос. Сергиевский
Центральная, 18
Расположение на карте
санитарный день: последняя пт месяца
Вт: 11:00-14:00 15:00-19:00
Ср: 11:00-14:00 15:00-19:00
Чт: 11:00-14:00 15:00-19:00
Пт: 11:00-14:00 15:00-19:00
Сб: 11:00-14:00 15:00-20:00
www.kolomna-regbibl.ru
Вконтакте:
https://vk.com/public71189606
Facebook:
https://facebook.com/groups/1801938529832472
Название и адрес
Режим работы
Контактная информация
Телефон
Центральная городская библиотека, МБУК, Информационно-библиотечный центр
Камчатский край, Петропавловск-Камчатский городской округ, Петропавловск-Камчатский
Индустриальная, 19
Расположение на карте
зимний период: пн-сб 11:00-18:00
Пн: 11:00-18:00
Вт: 11:00-18:00
Ср: 11:00-18:00
Чт: 11:00-18:00
Пт: 11:00-18:00
Вконтакте:
https://vk.com/kamlibpk
Инстаграм:
https://instagram.com/kamlibpk
Facebook:
https://facebook.com/kamlibpk
Одноклассники:
https://ok.ru/kamlibpk
Youtube:
https://youtube.com/channel/UCLXNmyAvFHE4TdhTCQdmSqg
Название и адрес
Режим работы
Контактная информация
Телефон
Никольская сельская библиотека
Тверская область, Калининский район, с. Никольское
Никольское пос, 13
Расположение на карте
Название и адрес
Режим работы
Контактная информация
Телефон
Библиотека №6, Калининский район
Санкт-Петербург, Санкт-Петербург, Калининский район, МО №23 «Северный»
Культуры проспект, 21 к1
Расположение на карте
зимний период: пн-пт 11:00-20:00; сб 11:00-18:00; санитарный день: последний день месяца
Пн: 11:00-20:00
Вт: 11:00-20:00
Ср: 11:00-20:00
Чт: 11:00-20:00
Пт: 11:00-20:00
Название и адрес
Режим работы
Контактная информация
Телефон
Краеведческий библиотечно-информационный центр им. М.А. Шолохова
Ростовская область, Ростов-на-Дону городской округ, Ростов-на-Дону, Железнодорожный район, Западный
Кулагина, 19
Расположение на карте
санитарный день: последняя ср месяца
Пн: 09:00-19:00
Вт: 09:00-19:00
Ср: 09:00-19:00
Чт: 09:00-19:00
Вс: 09:00-19:00
www.donlib.ru
Вконтакте:
https://vk.com/rostov_library
Наличие в библиотеках
Название и адрес
Режим работы
Контактная информация
Телефон
Централизованная система массовых библиотек г. Шымкента, ГУ
Туркестанская область, Шымкент городская администрация, Шымкент, Енбекшинский район, 18-й микрорайон м-н
18-й микрорайон, 2
Расположение на карте
Пн: 09:00-13:00 15:00-19:00
Вт: 09:00-13:00 15:00-19:00
Ср: 09:00-13:00 15:00-19:00
Чт: 09:00-13:00 15:00-19:00
Пт: 09:00-13:00 15:00-19:00
Название и адрес
Режим работы
Контактная информация
Телефон
Детская библиотека №8
Брянская область, Брянск городской округ, Брянск, Бежицкий район
Куйбышева, 19
Расположение на карте
сентябрь-май: пн-пт, вс 10:00-18:00; санитарный день: последний день месяца
Пн: 10:00-18:00
Вт: 10:00-18:00
Ср: 10:00-18:00
Чт: 10:00-18:00
Пт: 10:00-18:00
Название и адрес
Режим работы
Контактная информация
Телефон
Фундаментальная медицинская библиотека
Москва, Москва, Аэропорт район
Балтийская, 8
Расположение на карте
санитарный день: последний рабочий день месяца
Пн: 10:00-17:00
Вт: 10:00-17:00
Ср: 10:00-17:00
Чт: 10:00-17:00
Пт: 10:00-17:00
www.fbramn.ru
Название и адрес
Режим работы
Контактная информация
Телефон
санитарный день: последняя пт месяца
Вт: 12:00-22:00
Ср: 12:00-22:00
Чт: 12:00-22:00
Пт: 12:00-22:00
Сб: 12:00-22:00
Вс: 12:00-20:00
Вконтакте:
https://vk.com/biblioteka167
Инстаграм:
https://instagram.com/biblioteka167
Название и адрес
Режим работы
Контактная информация
Телефон
Центральная библиотека №136 им. Л.Н. Толстого
Москва, Москва, Нагатино-Садовники район
Коломенский проезд, 21
Расположение на карте
Вт: 10:00-21:00
Ср: 10:00-21:00
Чт: 10:00-21:00
Пт: 10:00-21:00
Сб: 10:00-21:00
Вс: 10:00-20:00
cbsuao.ru/
Вконтакте:
https://vk.com/bibliotekalvatolstogo
Facebook:
https://facebook.com/bibliotekalvatolstogo
Название и адрес
Режим работы
Контактная информация
Телефон
Межпоселенческая центральная библиотека им. И.И. Лажечникова
Московская область, Коломенский район, пос. Сергиевский
Центральная, 18
Расположение на карте
санитарный день: последняя пт месяца
Вт: 11:00-14:00 15:00-19:00
Ср: 11:00-14:00 15:00-19:00
Чт: 11:00-14:00 15:00-19:00
Пт: 11:00-14:00 15:00-19:00
Сб: 11:00-14:00 15:00-20:00
www.kolomna-regbibl.ru
Вконтакте:
https://vk.com/public71189606
Facebook:
https://facebook.com/groups/1801938529832472
Название и адрес
Режим работы
Контактная информация
Телефон
Центральная городская библиотека, МБУК, Информационно-библиотечный центр
Камчатский край, Петропавловск-Камчатский городской округ, Петропавловск-Камчатский
Индустриальная, 19
Расположение на карте
зимний период: пн-сб 11:00-18:00
Пн: 11:00-18:00
Вт: 11:00-18:00
Ср: 11:00-18:00
Чт: 11:00-18:00
Пт: 11:00-18:00
Вконтакте:
https://vk.com/kamlibpk
Инстаграм:
https://instagram.com/kamlibpk
Facebook:
https://facebook.com/kamlibpk
Одноклассники:
https://ok.ru/kamlibpk
Youtube:
https://youtube.com/channel/UCLXNmyAvFHE4TdhTCQdmSqg
Название и адрес
Режим работы
Контактная информация
Телефон
Никольская сельская библиотека
Тверская область, Калининский район, с. Никольское
Никольское пос, 13
Расположение на карте
Название и адрес
Режим работы
Контактная информация
Телефон
Библиотека №6, Калининский район
Санкт-Петербург, Санкт-Петербург, Калининский район, МО №23 «Северный»
Культуры проспект, 21 к1
Расположение на карте
зимний период: пн-пт 11:00-20:00; сб 11:00-18:00; санитарный день: последний день месяца
Пн: 11:00-20:00
Вт: 11:00-20:00
Ср: 11:00-20:00
Чт: 11:00-20:00
Пт: 11:00-20:00
Название и адрес
Режим работы
Контактная информация
Телефон
Краеведческий библиотечно-информационный центр им. М.А. Шолохова
Ростовская область, Ростов-на-Дону городской округ, Ростов-на-Дону, Железнодорожный район, Западный
Кулагина, 19
Расположение на карте
санитарный день: последняя ср месяца
Пн: 09:00-19:00
Вт: 09:00-19:00
Ср: 09:00-19:00
Чт: 09:00-19:00
Вс: 09:00-19:00
www.donlib.ru
Вконтакте:
https://vk.com/rostov_library
Информация от пользователей