Что такое последовательность инструкций в информатике

Опубликовано 19.10.2020 10:21

Что общего между программистом и художником, кроме творческого беспорядка на столе? Они оба создают интересные вещи, используя креативность и выходя за рамки привычного мышления. Главное отличие в том, что программист следует законам логики и разрабатывает точные алгоритмы создания произведения. Об этом мы сегодня и поговорим.

Где логика?

Логика – это наука о правильном мышлении. Или в нашем случае – о правильной постановке команд, которые приведут к нужному результату. 

Последовательность таких команд в виде инструкций, описывающих порядок действий, называется Алгоритмом. Набор инструкций, которые идут друг за другом по определённому алгоритму, называется Программой.

Наименьшая автономная часть программы – это инструкция (команда или набор команд). По-другому инструкции называют «оператор» или «statements». Один оператор выполняет конкретный программный код. Это главная часть любой программы. 

Пишите максимально подробные и логичные инструкции для компьютера, чтобы он понял команду именно так, как вам требуется. Если этого не сделать – нужного результата не выйдет.

По сути, инструкции и алгоритмы – это то, чему подчиняются все процессы в реальном мире. Чтобы наглядно показать, как всё это работает, приведем пример из жизни.

Разбираем «на пальцах»

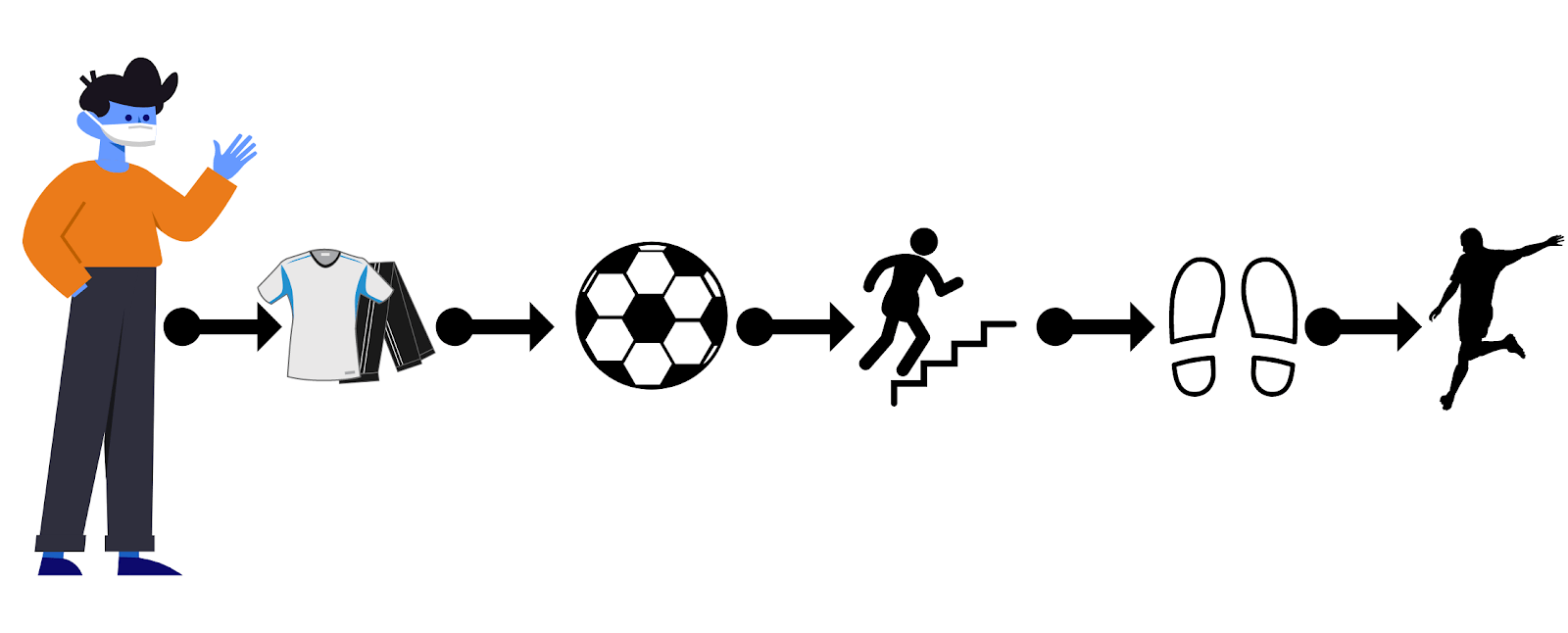
Вот Алексей. Он обычный парень, который любит играть в футбол. Нам необходимо прописать программу, симулирующую игру Лёши. Для этого мы прописываем конкретную инструкцию, которая состоит из таких команд:

1. Надеть спортивную одежду.

2. Взять мяч.

3. Выйти на улицу.

4. Поставить мяч на землю.

5. Ударить по мячу.

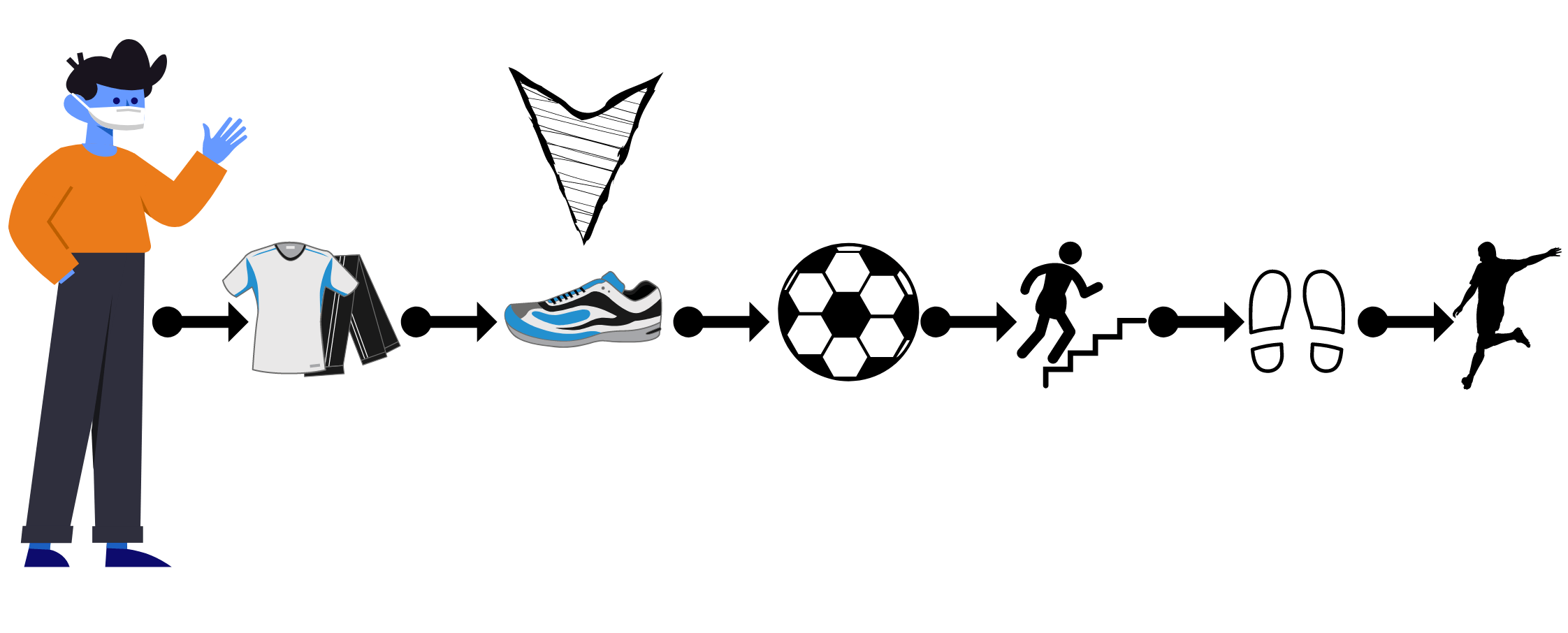
Запускаем игру и понимаем, что что-то идёт не так. Причина в том, что Алексей вышел играть в туфлях, а не в спортивной обуви, так как мы не учли в инструкции этот нюанс. 

Возвращаемся назад и дополняем:

1. Надеть спортивную одежду.

2. Надеть спортивную обувь.

3. Взять мяч.

4. Выйти на улицу.

5. Поставить мяч на землю.

6. Ударить по мячу.

Теперь игра идёт так, как мы задумали. 

Этот вариант примитивный. В настоящей программе инструкций будет гораздо больше. Каждое действие Алексея придётся прописывать подробно. Например, выход из дома: 

1. Открыть дверь.

2. Выйти.

3. Закрыть дверь.

4. Подойти к лифту.

5. Нажать на кнопку.

6. Зайти в лифт.

7. Нажать кнопку первого этажа.

8. Выйти из лифта и т. д.

Чем подробнее прописаны стейтменты, тем более качественно работает программа. 

Представьте количество команд, инструкций и сложность алгоритма в искусственном интеллекте или роботе. Сколько подробных инструкций предусматривает и прописывает программист, чтобы искусственный интеллект самостоятельно принимал решения, а робот ходил, разговаривал, отвечал и реагировал на действия.

Программа – живой организм, который постоянно развивается и изменяется. Актуализировать её придётся бесконечно: дописывать инструкции, расширять функционал, упрощать. При этом программа всё ещё не будет идеальной. Всегда есть что добавить или изменить.

В случае с Алексеем, дополнительно понадобилось бы прописать и то, что он идёт на выбранную спортивную площадку или стадион, зовёт с собой друзей и т. д.

Учитывайте тот факт, что ваша программа обязательно будет изменяться и дополняться. Тот, кто после вас займётся её поддержкой и развитием, должен понять вашу логику. Не слишком стремитесь к упрощению и минималистичности.

Виды алгоритмов

Последовательность команд и инструкций может быть разной. Но в основе лежат три вида алгоритмов: 

Линейный

Каждое действие выполняется последовательно друг за другом в строгом порядке. Когда выполнено одно, начинается другое. И так до последнего.

Циклический

По достижении определенного действия алгоритм возвращается на любое из предыдущих сколько угодно раз. Это делается с помощью циклов, которые мы обсудим на следующих уроках. В примере с футболистом цикличным алгоритм считался бы в том случае, если бы Алексей бесконечно бил по мячу.

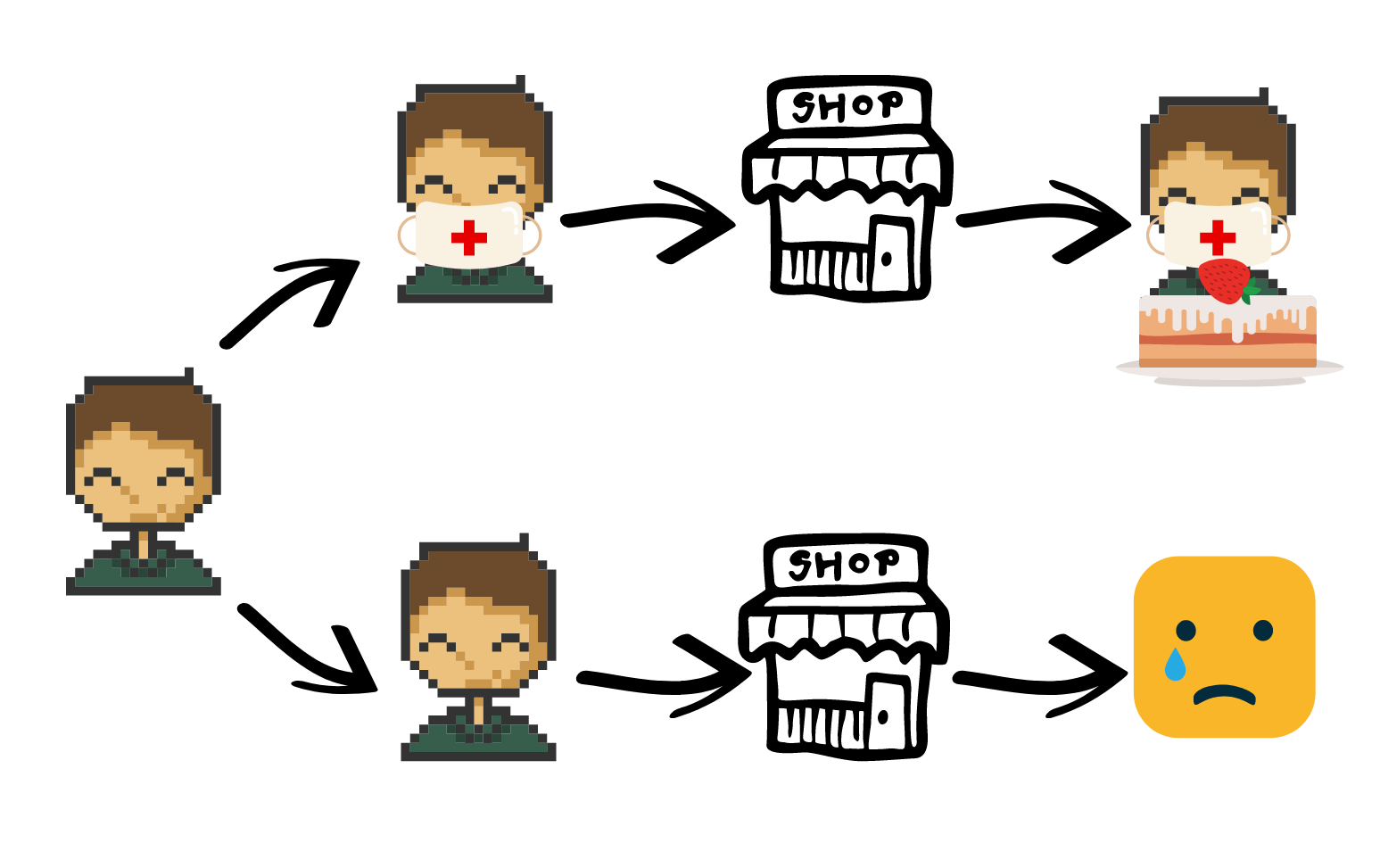
Ветвление

В одной из команд (или нескольких) прописывается разветвление. Доходя до него, необходимо выбрать на какую из ветвей пойти дальше. Представьте, что идёте по дороге и встречаете развилку. Вам необходимо выбрать путь налево или направо. Это и есть алгоритм ветвления.

В чистом виде эти алгоритмы встречаются лишь в простейших программах. Чаще всего они комбинируются между собой. Именно комбинируемый алгоритм – самый распространённый вид алгоритма. 

Каждая программа состоит из сложного набора инструкций, где есть и циклы, и ветвления, и прямые линии. Со стороны это похоже на большое дерево с множеством веток, которые растут в разные стороны.

Все алгоритмы выполняют конкретные логические задачи: сортировка, поиск, сравнение и т. д. В каждой из задач эффективными будут разные алгоритмические последовательности. Для сортировки одни, для поиска другие.

Для разработки подходящего алгоритма и потребуется креативность. Вы сами выбираете путь и способы достижения результата, вдохновляясь природными процессами, опираясь на собственные ощущения, и описываете их в программе. Вспомните об этом, когда кто-нибудь снова скажет, что программирование – это только математика

Домашнее задание

Напишите линейный, циклический или разветвленный алгоритм. Это должен быть порядок действий, список команд, конкретная инструкция. Программа должна упростить вашу жизнь, делать то, что сами вы делать не хотите.

Вопросы:

1. Алгоритм и его свойства

2. Форма записи алгоритмов

3. Базовые алгоритмические структуры

Алгоритм
и его свойства

В
математике для решения типовых задач
мы используем опреде­ленные
правила.
Обычно любые инструкции и правила
представляют со­бой
последовательность действий, которую
необходимо выполнить в оп­ределенном
порядке. Для решения задачи надо знать:

─ что дано,

─ что следует
получить и

─ какие действия,
и

─ в каком порядке
следует для этого выполнить.

Алгоритм
—
это точное предписание исполнителю
совершить ука-­
занную
последовательность действий для
получения решения задачи за
конечное
число шагов.

Приведенное
определение не является определением
в математиче­ском
смысле слова, а, скорее, описание
интуитивного понятия алгоритма,
раскрывающее
его сущность. Но для общего понимания
сущности алго­ритма
такого толкования оказывается, как
правило, достаточно.

Название
«алгоритм» произошло от латинской
формы имени вели­чайшего
среднеазиатского математика Мухаммеда
ибн Муса ал-Хорезми (Alhorithmi),
жившего в 783 -850 гг.
В своей книге «Об индийском счете»
он
изложил правила записи натуральных
чисел с помощью арабских цифр и
правила действий над ними «столбиком»,
знакомые теперь каждом школьнику.
В
XII
веке эта книга была переведена на латынь
и получила широкое
распространение в Европе.

Понятие
алгоритма является не только одним из
главных понятий математики,
но одним из главных понятий современной
пауки. Более того, с наступлением эры
информатики алгоритмы становятся одним
из важ­нейших
факторов цивилизации.

Свойства алгоритмов

К основным
свойствам алгоритмов относятся следующие
свойства:

1.
Понятность
для исполнителя, ─ исполнитель алгоритма
должен понимать,
как его выполнять. Иными словами, имея
алгоритм и произвольный
вариант исходных данных, исполнитель
должен знать, как надо действовать для
выполнения этого алгоритма.

2. Дискретность
(прерывность, раздельность) — алгоритм
должен представлять процесс решения
задачи как последовательное выполнение
простых (или ранее определенных) шагов
(этапов).

3. Определенность
— каждое правило алгоритма должно быть
четким, однозначным и не оставлять места
для произвола.

Благодаря этому
свойст­ву выполнение алгоритма носит
механический характер и не требует
ника­ких дополнительных указаний или
сведений о решаемой задаче.

4. Релевантность
(или конечность) состоит в том, что за
конечное число шагов алгоритм либо
должен приводит к решению задачи, либо
по­сле конечного числа шагов
останавливаться из-за невозможности
получить решение с выдачей соответствующего
сообщения, либо неограниченно продолжаться
в течение времени, отведенного для
исполнения алгоритма, с выдачей
промежуточных результатов.

5. Массовость
означает, что алгоритм решения задачи
разрабатывается в общем виде, т.е. он
должен быть применим для некоторого
класса задач, различающихся лишь
исходными данными. При этом исходные
данные могут выбираться из некоторой
области, которая называется областью
применимости алгоритма.

Правила
построения алгоритма

Чтобы
алгоритм выполнил свое предназначение,
eго
необходимо строить по определенным
правилам. В этом смысле нужно говорить
не о свойствах алгоритма, а о правилах
построения алгоритма, или о требова­ниях,
предъявляемых к алгоритму.

Первое
правило ─ при построении алгоритма,
прежде всего, необходимо задать множество
объектов,
с которыми будет работать алгоритм.
Формализованное (закодированное)
представление этих объектов носит
название данных. Алгоритм
приступает
к
работе
с некоторым набором данных, которые
называются входными, и в результате
своей работы выдает данные, которые
называются входными. Таким
образом, алгоритм преобразует входные
данные в выходные.

Это правило
позволяет сразу отделить алгоритмы от
«методов» и “способов”. Пока мы
не имеем формализованных входных данных,
мы не можем построить алгоритм.

Второе
правило ─ для работы алгоритма требуется
память.
В памяти размещаются входные данные, с
которыми алгоритм начинает работать,
промежуточные данные и выходные данные,
которые являются результа­том работы
алгоритма. Память является дискретной,
т.е. состоящей из от­дельных ячеек.
Поименованная ячейка памяти носит
название переменной. В теории алгоритмов
размеры памяти не ограничиваются, т. е.
считается, что мы можем предоставить
алгоритму любой необходимый для работы
объем памяти.

Третье
правило ─ дискретность. Алгоритм
строится из отдельных шагов
(действий, операций, команд). Множество
шагов, из которых составлен алгоритм,
конечно.

Четвертое
правило ─ детерменированность. После
каждого шага не­обходимо
указывать, какой шаг выполняется
следующим, либо давать ко­манду
остановки.

Пятое
правило ─ сходимость
(результативность).
Алгоритм
должен завершать
работу после конечного числа шагов. При
этом необходимо ука­зать,
что считать результатом работы алгоритма.

Итак,
алгоритм ─ неопределяемое понятие
теории алгоритмов. Алго­ритм
каждому определенному набору входных
данных ставит в соответст­вие
некоторый набор выходных данных, т. е.
вычисляет (реализует) функ­цию.
При рассмотрении конкретных вопросов
в теории алгоритмов всегда имеется
в виду какая-то конкретная модель
алгоритма.

Формы
записи алгоритма

Алгоритм,
как последовательность шагов или
инструкций, может быть
представлен в различных формах.

На
практике наиболее распространены
следующие формы
представления
алгоритмов:

1. словесная
   (запись
   на естественном языке);

2. графическая
   (изображения
   из графических символов);

3. псевдокоды
   (полуформализованные
   описания алгоритмов на ус­ловном
   алгоритмическом языке, включающие в
   себя как эле­менты
   языка программирования, так и фразы
   естественного языка,
   общепринятые математические обозначения
   и др.);
   

4. программная
   (тексты
   на языках программирования).

Словесная
форма записи алгоритмов

Словесный
способ записи алгоритмов представляет
собой описание последовательных
этапов обработки данных. Алгоритм
задается в произ­вольном
изложении на естественном языке.

Например.
Записать алгоритм нахождения наибольшего
общего делите­ля
(ИОД) двух натуральных чисел (алгоритм
Эвклида).

Алгоритм может
быть следующим:

1)
задать два числа;

2)
если числа равны, то взять любое т них
в качестве ответа и

остановиться,
в противном случае продолжить выполнение

алгоритма;

1. определить
   большее из чисел;

2. заменишь большее
   из чисел разностью большего и меньшего
   из чисел;

3. повторить алгоритм
   с шага 2.

Описанный
алгоритм, применим к любым натуральным
числам и должен приводить
к решению поставленной задачи.

Самостоятельно:
определить
с помощью этого алгоритма наибольший
общий делитель
чисел 125 и 75.

Словесный
способ не получил широкого распространения
из-за сле­дующих
недостатков:

1. Строго не
   формализуем;

2. Страдает
   многословностью записей;

3. Допускает
   неоднозначность толкования отдельных
   предписаний.

Графическая
форма записи алгоритмов

Графический
способ представления алгоритмов является
более ком­пактным
и наглядным по сравнению со словесным.
При
графическом представлении
алгоритм изображается в виде
последовательности связанных
между собой функциональных блоков,
каждый из которых соответствует
выполнению одного или нескольких
действий.

Такое
графическое представление называется
схемой
алгоритма или
блок-схемой.
В
блок-схеме каждому типу действий (вводу
исходных данных,
вычислению значений выражений, проверке
условий, управлению повторением
действий, окончанию обработки и т.п.)
соответствует геомет­рическая
фигура, представленная в виде блочного
символа.
Блочные
сим­волы
соединяются линиями
переходов,
определяющими
очередность вы­полнения
действий. В таблице 8.1 приведены наиболее
часто употреб­ляемые
блочные символы.

Таблица
7.1

Название символа	Обозначения и пример заполнения	Пояснения
Процесс		Вычислительное действие или последовательность действий
Решение		Проверка условий
Модификация		Начало цикла
Предопределенный процесс		Вычисления по подпрограмме, стандартной подпрограмме
Ввод-вывод		Ввод-вывод в общем виде
Пуск-остановка		Начало, конец алгоритма, вход и выход в подпрограмму
Документ		Вывод результатов на печать

Пояснения
к таблице 7.1.

1. Блок
   «процесс»
   применяется
   для обозначения действия или
   пос­ледовательности
   действий, изменяющих значение, форму
   пред­ставления
   или размещения данных. Для улучшения
   наглядности схемы
   несколько отдельных блоков обработки
   можно объединять
   в один блок. Представление
   отдельных операций достаточно
   свободно.

2. Блок
   «решение»
   используется
   для обозначения переходов управления
   по условию. В каждом блоке «решение»
   должны быть
   указаны вопрос, условие или сравнение,
   которые он опре­деляет.

3. Блок
   «модификация»
   используется
   для организации циклических
   конструкций. Внутри блока записывается
   параметр цикла, для
   которого указываются его начальное
   значение, граничное условие и шаг
   изменения значения параметра для
   каждого повторения.

4. Блок
   «предопределенный
   процесс»
   используется
   для указания обращений
   к вспомогательным алгоритмам, существующим
   автономно в виде некоторых самостоятельных
   модулей, и для об­ращений
   к библиотечным подпрограммам.

Псевдокод

Псевдокод
представляет собой систему обозначений
и правил, пред­назначенную
для единообразной записи алгоритмов.

Псевдокод
занимает промежуточное место между
естественным и формальным языками. С
одной стороны, он близок к обычному
естествен­ному
языку, поэтому алгоритмы могут па нем
записываться и читаться как обычный
текст. С другой стороны, в псевдокоде
используются некоторые формальные
конструкции и математическая символика,
что приближает запись алгоритма к
общепринятой математической записи.

В
псевдокоде не приняты строгие
синтаксические правила для запи­си
команд, присущие формальным языкам, что
облегчает запись алгоритма на
стадии его проектирования и дает
возможность использовать более ши­рокий
набор команд, рассчитанный па абстрактного
исполнителя.

Однако
в псевдокоде обычно имеются некоторые
конструкции, при­сущие
формальным языкам, что облегчает переход
от записи на псевдоко­де
к записи алгоритма на формальном языке.
В частности, в псевдокоде, так
же, как и в формальных языках, есть
служебные слова, смысл которых определен
раз и навсегда. Они выделяются в печатном
тексте жирным шрифтом,
а в рукописном тексте подчеркиваются.

Единого
или формального определения псевдокода
не существует, поэтому возможны
различные
псевдокоды,
отличающиеся набором слу­жебных
слов и основных (базовых) конструкций.

Примером
псевдокода является школьный
алгоритмический язык в русской
нотации (школьный АЯ), описанный в
учебнике А.Г. Кушниренко и
др. «Основы информатики и вычислительной
техники», 1991. Этот язык в дальнейшем
мы будем называть просто «алгоритмический
язык».

Программная
форма записи алгоритма

Программный
способ записи алгоритма представляет
собой напи­санный
на языке программирования C#
код программы.

Например:

//Ввод
чисел операндов

Console.Write(«Введите
первое число:»);

var
num1 = int.Parse(Console.ReadLine());

Console.Write(«Введите
второе число:»);

var
num2 = int.Parse(Console.ReadLine());

//Объявление
переменной типа bool

bool
znaj
= true;

//Зацикливание
меню

while
(znaj)

{

Console.WriteLine(«1)Сложение
+»);

Console.WriteLine(«2)Вычитание
-«);

Console.WriteLine(«3)Деление
:»);

Console.WriteLine(«4)Умножение
*»);

Console.WriteLine(«Если
хотите выйти из программы,то введите 0
и нажмите 2 раза Enter»);

Console.WriteLine(«Какие
действия вы хотите сделать с этими
числами»);

var
useranswer = int.Parse(Console.ReadLine());

//Задание
условия

switch
(useranswer)

{

//Выполнение
условия

case
0:

znaj =
false;

break;

case
1:

var
numplus = num1 + num2;

Console.WriteLine(«Сумма»
+ num1 + «+»
+ num2 + «=»
+ numplus);

Console.WriteLine();

break;

case
2:

var
numminus = num2 — num1;

Console.WriteLine(«Разность»
+ num2 + «-»
+ num1 + «=»
+ numminus);

Console.WriteLine();

break;

case
3:

var
numdivision = num2/num1;

Console.WriteLine(«Результат
деления чисел»
+ num2 + «/»
+ num1 + «=»
+ numdivision);

Console.WriteLine();

break;

case
4:

var
nummultiplaction = num1*num2;

Console.WriteLine(«Результат
умнохения чисел»
+ num1 + «*»
+ num2 + «=»
+ nummultiplaction);

Console.WriteLine();

break;

default:

Console.WriteLine(«Вы
ввели цифру или знак не отеченные в
условии»);

break;

}

}

Console.ReadKey();

Типы
базовых алгоритмических структур

В
общем случае блок-схема алгоритма имеет
сложную
структуру и, следовательно, может быть
выражена композицией
элементарных блок-схем, принято называть
базовыми.

Логическая
структура любого алгоритма может быть
представлена
комбинацией трех базовых

алгоритмических
структур:

1.
алгоритмы линейной структуры, которые
иногда называют следованием
(последовательностью)

2.
алгоритмы разветвляющейся структуры,
называемые ветвлением

3. алгоритмы
циклической структуры, называемые
циклами.

Характерной
особенностью базовых структур является
наличие в них одного
входа
и одного
выхода.

Линейная базовая
структура (“последовательность”)

Линейная
базовая структура – это алгоритм, в
котором блоки выполняются последовательно
друг за другом, в порядке, заданном
схемой.
Такой
порядок выполнения называется
естественным. Образуется последовательностью
действий, следующих одно за другим:

Таблица
7.2.

Процесс	Блок-схема
действие 1 действие 2 ………….. действие n

Пример:Вычислить
высоты треугольника со сторонами а, b
, с, используя формулы:

где

.

Для
решения любой нетривиальной задачи
существует несколько
алгоритмов, приводящих к получению
результата. Из возможных ал­горитмов
следует выбирать наилучший по некоторому
критерию. Чаще всего
в качестве критерия выбирается либо
оценка точности решения задачи,
либо затраты времени на ее решение, либо
некоторый инте­гральный
критерий, включающий оценки точности
и затраты времени.

При
решении данной задачи для исключения
повторений следует вычислять
высоты не по приведенным выше формулам
непосредственно, а
используя промежуточную переменную

тогда
h_a
= t/a, h_b
= t/b, h_c
= t/c.

При этом схема
алгоритма решения имеет вид, представленный
на рис. 8.1.

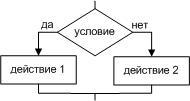
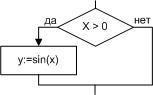
Базовая
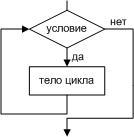
структура “ветвление”

Обеспечивает
в зависимости от результата проверки
условия (да
или
нет)
выбор одного из альтернативных путей
работы алгоритма. Каждый
из путей ведет к общему
выходу,
так что работа алгоритма будет продолжаться
независимо от того, какой путь будет
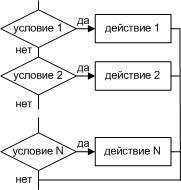
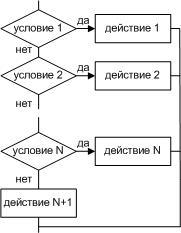
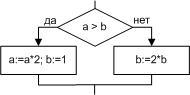
выбран. Структура
«ветвление» существует в четырех
основных вариантах:

1. если ─ то;

2. если ─ то ─ иначе;

3. выбор;

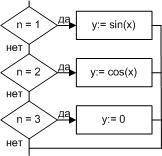
4. выбор ─ иначе.

Таблица
7.3

Выполняемые действия	Блок-схема
1. если─то
если условие то действие все
2. если─то─иначе
если условие то действие иначе действие 2 все
3. выбор
выбор при условие 1: действие 1 при условие 2: действие 2 …………….. при условие N: действие N все
4. выбор─иначе
выбор при условие 1: действие 1 при условие 2: действие 2 …………….. при условие N: действие N иначе действия N + 1 все

Примеры структуры
«ветвление»

Таблица
7.4

Выполняемые действия	Блок-схема
если x > 0 то y:= sin(x) все
если a>b то a:= 2*a; b:= 1 иначе b:= 2*b все
выбор при n = 1: y:= sin(x) при n = 2: y:= cos(x) при n = 3: y:= 0 все
выбор при a > 5; I:= I + 1 при a = 0; j:= j + 1 иначе I:= 10; j:= 0 все

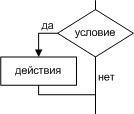
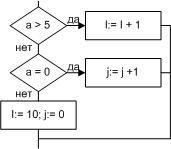
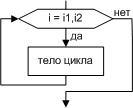
Базовая
структура “цикл”

Обеспечивает
многократное выполнение некоторой
совокупности действий, которая называется
телом цикла. Основные
разновидности циклов представлены в
таблице 8.5.

Таблица
7.5

Выполняемые действия	Блок-схема
Цикл типа пока. Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
пока условие тело тело цикла (последовательность действий)
Цикл типа для. Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.
для i от i1 до i2 тело цикла (последовательность действий)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Что такое алгоритм?! Часть первая

Терзаем вместе основной кирпичик программиста — Алгоритм.

Проблема

Текущее состояние в области программирования — это обучение ремеслу по большей части личной практикой или разборами примеров стороннего кода, с которым по каким-то причинам приходится сталкиваться.

В результате программированию учишься по наитию. Лишь немного в этом труде помогают сборники алгоритмов, прикладных техник и шаблонов проектирования. Общая совокупность предлагаемых ими рецептов выстраивается длинным списком, и его длина грозит каждому из прочитанных приемов быть позабытым (как была забыта 53-яя личная группа в «телеге» до введения разбиения по каталогам). Но даже тот прием, который остался в памяти, чаще всего просто является описанием прикладной задачи, в которой было успешно его использование.

Почему конкретный прием был успешен в задаче-образце? Будет ли он успешен в твоём проекте? Какие признаки проекта дают понять, что использование приёма уместно?

В личном опыте существования в профессии не раз отмечено, что каждый Junior борется с одинаковыми ветряными мельницами и постигает методы создания программ основываясь только на своих ошибках. Но ведь такие ошибки совершили уже очень многие. Почему до сих пор не создана система правил программирования, которая поможет обойти новоиспеченному кораблю-программисту подводные прибрежные камни? Ну, например, объяснение вреда использования метода «Copy-Paste» для развития кода. Если такие правила получится объяснить малым набором причин, их сформировавшим, то это объяснение обеспечит их запоминание и последующее использование в практике, тем самым поможет уклониться от бесчисленных грабель, разложенных тут и там.

Для компактного и полезного набора объяснений нужно:

• систематизировать методы работы с кодом;
• разобрать по группам приёмы работы с алгоритмами, которые являются главной целью написания любого кода;
• выделить простые признаки применения шаблонов проектирования;
• разработать универсальные правила и наборы эффективных способов построения сложных алгоритмов.

Если обобщить, то нужны алгоритмы для написания и развития алгоритмов.

Задуманная серия статей не претендует на полное решение указанной проблемы. Предпринимается небесспорная попытка сделать первый шаг на пути к этому решению. Этот шаг состоит в выделении структуры и свойств главного кирпичика программиста — Алгоритма.

Задача

Сформулируем основную задачу, которую хочется решить. Для этого сначала запишем операции над алгоритмами, которые программист выполняет в ходе написания своего проекта:

• методы синтеза макро-алгоритма из под-алгоритмов (последовательной, параллельной и смешанной группировкой);
• методы структурной трансформации макро-алгоритмов (оптимизационной, специализирующей, стыковочной…);
• методы сохранения и переноса алгоритмов;
• методы синтеза универсального алгоритма из сходных алгоритмов разных областей исполнения;
• методы специализации универсального алгоритма в новой области исполнения;
• методы формирования и развития комплексной системы совместно работающих алгоритмов;
• методы взаимодействия одновременно исполняющихся алгоритмов;
• и другие методы, полный список которых привести сложно, да и нет необходимости.

Рассмотрим существующие на текущий момент варианты значения слова «алгоритм» в поисках подсказок, о том как можно работать с алгоритмами.

Так, например, формулировка «конечная совокупность точно заданных правил решения произвольного класса задач» говорит что есть возможность как-то «точно задать правила» из них собрать «совокупность» и этой совокупностью «решить» некоторый «класс задач».

Сразу возникает масса вопросов к этому определению:

• Что такое правило?
• Как, кому и для кого это правило можно задать?
• Что есть объединение совокупностью?
• Каким образом правила соотносятся с задачей?
• Что формирует класс задачи?
• Определяется ли способ формирования совокупности правилами и задачами?
• …

Другая формулировка «набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи» говорит что есть «исполнитель», который может выполнять некоторые «действия», и при некотором «порядке» выполнения этих «действий» «решается задача». Вопросов не стало меньше:

• Какова структура набора?
• Какие есть варианты действий и исполнителей?
• Существуют ли минимально возможное действие, минимальный набор необходимых действий?
• Каким образом действия встроены в исполнителя?
• Какие есть способы создания копии исполнителя (например, если исполнитель — человек)?
• Как действия зависят друг от друга в упорядоченном выполнении?
• Что есть задача кроме того, что она выполняется последовательностью действий?
• Как задача соотносится с исполнителем и с действиями?
• Возможно ли использовать решение задачи в качестве действия?
• Какие возможны варианты указания порядка действий?
• Если воспроизведение патефоном записи звуков леса является алгоритмом, то какова структура этой задачи?
• Если репликация ДНК является алгоритмом, то каков её исполнитель?
• Если исполнителем является Машина Тьюринга, то как с её использованием решить механическую задачу, например, воспроизведение звука?

Перечислено много вопросов, но они мало помогают в поиске методов работы с алгоритмом. Поэтому поставим себе меньшую задачу, но тоже очень нам важную. Давайте попробуем сформулировать, что делает алгоритм способом решения наших задач, и какие процессы являются для него «действиями». Даже решение этой «маленькой» задачи оказывается очень объемным для одной статьи, поэтому будем его разбивать на части. И поэтому первую статью серии целиком посвятим только «Действию» и его признакам, которые опущены в указанных выше определениях алгоритма, но являются очень важными для ответов на все заданные вопросы.

Определение алгоритма

Рассмотрим определение алгоритма, говорящее, что он — приводящая к решению задачи последовательность действий. Как программисту мне приходится писать много кода. Этот код состоит из частей. Такими частями являются и функции, и классы, и модули. Когда я пишу текст функции — я занимаюсь написанием алгоритма.

Раньше алгоритм создавали в виде блок схем и полуавтоматически компилировали в машинные коды. Сейчас я избавлен от необходимости быть художником и компилятором для написания программы. Текст моей функции — это запись алгоритма в текстовом виде — его текстовая блок-схема. Здесь можно вспомнить Scratch, где используется визуальное создание блок-схемы алгоритма без написания текста. Способ записи алгоритма сейчас не так важен.

Важно, что в написании алгоритма функции я могу использовать вызовы других функции, которые я или другой программист уже написал до этого момента. Вспоминая фразу «последовательность действий, приводящая к решению задачи», можно отметить, что функции, написанные ранее, являются моими «действиями». То есть «действия» могут быть функциями. Если обобщать, то «действия» могут быть алгоритмами.

Если «действие = алгоритм», то определение можно попробовать переписать рекурсивно «алгоритм — это приводящая к решению задачи последовательность использования существующих алгоритмов». Рекурсивные определение не самое простое, что можно записать в словаре обычного человека. Но для программиста и математика эта форма знакома. Мы умеем с ней работать, и это даёт нам преимущество в рассмотрении разных задач, разбиваемых на подобные себе подзадачи. Так давайте воспользуемся этим преимуществом.

Чтобы разрешить рекурсию нам необходимо найти:

• терминальное условие выхода из рекурсии — минимальное неделимое «действие» (атомарный алгоритм), которое можно использовать в разработке алгоритма;
• способ перехода от текущего уровня рекурсии (набора «действий») к следующему уровню (алгоритму).

Действие

Для начала рассмотрим «действие» и попробуем найти причину, обеспечивающую возможность использования существующего «действия» для создания нового алгоритма.

Этой причиной является возможность повторного использования «действия» с получением тождественного результата. Только тогда разработанный с использованием этого «действия» алгоритм решения некоторой задачи будет одинаково решать эту задачу снова и снова. Мы нащупали важные законы нашего мира, в котором:

• существуют «действия», главным свойством которых является одинаковость результатов их исполнения в разные моменты времени и в разных местах,
• существует возможность создать такую схему использования нескольких «действий», которая сформирует из них новое «действие», которое мы назвали алгоритмом.

Какие признаки «действия» кроме повторимости делают возможным его использование в создании алгоритма? Что является терминальным неделимым «действием»? Чтобы ответить на этот вопрос стоит рассмотреть разные примеры «действий» из нашего опыта. Программисты встречали их много раз. Это и сложение, и умножение, и установка цвета пикселя на экране. Но мы знакомы с ними и вне программирования. Вся наука основывается на повторяемых явлениях.

Закон гравитации, описывающий повторяющееся явление падения яблока, тоже может стать действием. Ведь любое яблоко будет падать на землю? Значит этот процесс можно использовать в качестве «действия»! Например решая задачу прогнать Ньютона от яблони, на которую Вы случайно забрались ранее.

Рассмотрим, что происходит при выполнении «действия». Например, во время падения яблока с ветки яблони на землю. В этом процессе происходит несколько изменений. Если вспомнить школьную физику и рассмотреть ситуацию в системе отсчета, привязанной к Земле, то сила гравитации вызывает изменение скорости яблока, разгоняя его. При этом в процессе отмечается еще одно важное изменение — уменьшается расстояние между яблоком и Землей.

В рамках примера процесса «Земля-Яблоко» можно отметить у «действия» следующие признаки:

• наличие процесса изменения (расстояния и параметров движения объектов);
• наличие объектов, взаимодействие которых вызывает такие изменения;
• наличие локальности процесса, то есть существование значения расстояния между объектами, с превышением которого их взаимодействие перестает вызывать процесс изменения, что делает невозможным использование «действия» (Земля и гипотетическое яблоко, находящееся вне солнечной системы).

Рассмотрим с этими признаками разные области и процессы, выделяя в них примеры «действий» и контролируя особенности указанных признаков в описании структуры «действия».

Физические процессы

Для физических систем, процессы которых мы наблюдаем в нашем мире, характерные объекты и изменения опираются на фундаментальные взаимодействия и потому их достаточно просто выделить по аналогии с гравитационным взаимодействием Земли и яблока. Например, для системы из протона и электрона или системы двух протонов.

Отдельно от этих простых взаимодействий двух объектов стоят многокомпонентные процессы, например, ядерные реакции (по структуре «действия» близки к химическим процессам, рассматриваемым далее). Сложны и процессы описываемые суммарным взаимодействием большого числа элементов, например, «идеальный газ». Пока отложим их рассмотрение и сосредоточимся на самых простых примерах.

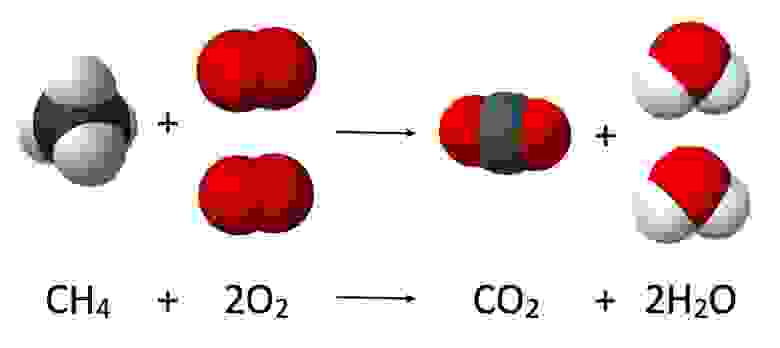
Химические процессы

Перейдем к следующей большой области — химическим процессам. Химические реакции (например, ) по признаку своей повторимости так же являются «действиями». Объектами в них являются атомы и молекулы. Для описания происходящих изменений необходимо немного преобразовать «физические» изменения. Так изменения параметров движения в совокупности дают нам изменение температуры в ходе химической реакции. А среди изменений расстояний между молекулами мы, игнорируя броуновское движение, можем выделить фиксацию расстояния в виде повторимого формирования и разрушения связей между частями взаимодействующих молекул. Локальность для химической реакции тоже существует — это отсутствие реакции при нахождении гидроксида натрия и соляной кислоты в разных пробирках и наличие реакции при соприкосновении веществ. Конечно, в «химической» области «действий» есть особенности не сводящиеся к молекулам, например, фотохимические реакции, где к объектам необходимо добавить фотоны. Самые простые процессы выбраны для рассмотрения намеренно.

Математические процессы

Следующей областью выберем «действия» из известных нам абстрактных алгоритмов. Самые яркие их представители — математические процессы. В этой области есть действительно «сложные случаи», но для этой статьи достаточно хорошо знакомых примеров. Рассмотрим в качестве «действия» достаточно элементарную операцию — сложение. А примером этого «действия» выберем сложение математиком двух целых чисел.

В ситуации с математиком можно выделить много объектов, но с точки зрения «действия» («сложение математиком двух целых чисел»), объекта всего три: это объект «математик», объект «первое число» и объект «второе число». В отличие от всех рассмотренных ранее объектов числа являются обозначениями, то есть виртуальными объектами. И их преобразование в алгоритме более сложно устроено нежели изменение расстояния и параметров движения объектов, как это было для «химических» действий. Подробности такого преобразования — это тема отдельной увлекательной статьи. А в рамках текущей рассмотрим древнего математика, который складывает числа, используя кучки камешков (рим. ‘calculi’), и более «современного» математика, использующего абак. Абстракции таких способов вычисления суммы не так далеко отошли от физических и химических процессов, поэтому структура процессов их «действий» полностью описывается изменениями расстояний и связей.

Интересно, что на примере древнего математика становится понятен смысл слова «сложить», которое отсылает нас к действию «класть» и к фразе «положить вместе».

Сложение и древний математик

Для математика, оперирующего камешками, сумма это «действие» со следующими характеристиками.

Исходные объекты:

• это сам «математик» (он взаимодействует со слагаемыми);
• лежащая отдельно кучка №1, содержащая и связывающая вместе камешки (подобно химическим связям), и обозначающая первое слагаемое;
• лежащая отдельно кучка камешков №2, обозначающая второе слагаемое.

Процессы:

• «математик» подходит к кучкам (физически изменяет расстояние между кучками и собой) и начинает с ними взаимодействие;
• «математик» объединяет две кучки (физически изменяет расстояние между двумя кучками или переносит все камешки одной кучки в другую, возможно, используя «действие» «Перенос по-одному» камешку)

Результирующие объекты:

• сформированная кучка камешков, обозначающая результат (сумму);
• «математик», отошедший от кучки результата и переставший на неё воздействовать.

Сложение и математик-абакист

У математика с абаком ситуация сложнее. Кучки разделены по значению на разрядные борозды.

Можно рассмотреть самый простой абак с двумя разрядами-бороздами. Пусть он будет десятичный. Тогда один камешек на борозде десятков соответствует десяти камешкам на борозде единиц. И 10 — это максимальное количество камешков на борозде единиц. По сравнению с действием первого математика меняется представление слагаемых. И в арсенале математика уже необходимы нескольких готовых «действий».

Действия:

• «Перенос по-одному» из борозды в борозду одинакового уровня (действие, позаимствованное у первого математика);
• «Перенос в десятки», которое необходимо выполнять, если борозда единиц полностью заполняется, тогда из неё убираются все камешки кроме одного, который переносится в борозду десятков.

Исходные объекты:

• это сам «математик» (он взаимодействует со слагаемыми);
• группа камешков №1, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих первое слагаемое;
• группа камешков №2, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих второе слагаемое;

Процессы:

• «математик» подходит к группам борозд (физически изменяет расстояние между ними и собой) и начинает с ними взаимодействие;
• «математик» объединяет камешки из двух борозд единиц (физически изменяет расстояние между камешками, разрушает связи со старой бороздой и создает связи с новой) с использованием действий «Перенос по-одному» и «Перенос в десятки»;
• «математик» объединяет камешки из двух борозд десятков с использованием действия «Перенос по-одному»

Результирующие объекты:

• сформированная группа камешков в двух бороздах (единиц и десятков), обозначающая результат (сумму);
• «математик», отошедший от группы камешков результата и переставший на них воздействовать.

Локальность в этих математических «действиях» описывается отсутствием взаимодействия двух слагаемых, находящихся далеко от математика, и запуском процессов сложения когда все три объекта сложения «близко». Повторяемое изменение в математическом «действии» выражается в изменении связей между камнями и удерживающими их локациями (кучками, бороздами).

Сложение и машина Тьюринга

Можно пойти чуть дальше и заменить математика в таких «действиях» на «управляющее устройство» машины Тьюринга. Тогда «ячейки ленты» машины Тьюринга будут содержать слагаемые.

При этом остаётся и признак локальности как возможность взаимодействия управляющего устройства только с текущей ячейкой ленты, и признак изменения параметров объектов, который можно описать как изменение состояния ячеек.

Подробное описание исходных и результирующих состояний объектов, а так же «действий» производящих эти изменения для сложения, исполняемого машиной Тьюринга, оставим за рамками этой статьи. Но упомянем, что перейдя к машине мы снижаем требования к исполнителю «действия», что является главным способом для создания формальных методов работы с алгоритмом. Можно поставить себе целью упрощение каждой составляющей алгоритма до состояния, когда её выполнение можно будет поручить компьютеру. Тогда в определении алгоритма не останется тёмных мест, и многочисленные вопросы, перечисленные в начале, найдут свои ответы. Пока формализован только исполнитель. Скажем спасибо за это Тьюрингу и вспомним про «действие», формализация которого уже на пороге.

Выводы

Соберём всё, что мы отметили рассматривая разные примеры «действия»:

• «действие» можно использовать для создания алгоритма;
• «действие» может быть элементарным;
• «действие» может быть реализовано алгоритмом;
• в «действии» обязательно участвует некоторый объект или группа объектов;
• для группы объектов «действие» происходит только тогда, когда эти объекты «достаточно близко»;
• в действии изменяются связи и параметры объектов (включая параметры их движения);
• «действие» всегда и обязательно должно быть повторимо.

Признак Повторимости помогает нам в создании наших алгоритмов. С его использованием мы из всех процессов выделяем те, что являются «действием» и на их основе создаём новые алгоритмы. Более того этот признак достаточно прост и на основе его формализации можно снизить требования к системе обнаруживающей и создающей «действия» и поручить это нашему компьютеру.

Следующая статья серии (Часть 2) будет посвящена рассмотрению способов, с использованием которых «действия» могут быть сгруппированы в алгоритм. Этих способов достаточно много и есть предпосылки, что их описание не получится уместить в одну статью. Напишем — увидим.

Спасибо Вам за внимание.

Отзывы

Буду очень благодарен за отзывы и предложения, так как они помогают мне скорректировать направление развития работы в области.

Отдельное волнение у меня есть по стилю и форматированию, используемым в статье (кавычки, абзацы, курсив). Напишите, пожалуйста, если у Вас есть замечания к ним. Можно личным сообщением.

Ссылки

• Главная страница и теория работы (GitLab GPL): Проект «Общая теория алгоритмов»
• Вводная статья работы «Разрабатываем теорию алгоритмов как проект с открытым исходным кодом». Пожалуйста, не судите строго эту наивную публикацию «сверх-идеи» устаревшей версии 2019 года.
• Статьи серии «Что такое алгоритм?!»
  • №1 «Действие» (текущая)
  • №2 «Жизнь»
  • №3 «Синтез алгоритма запоминанием»
  • №3.1 «Эволюция памяти»
  • №3.14 «Обучение»
  • №5 «Эволюция поведения»
  • №4 «Математика»
  • №4.0 «Физика»
  • №3.25 «Язык»
  • №5.0 «Философия»
  • №5.00 «Искусственный интеллект»
• Статьи в хабе «Программирование»:
  • Детская сказка программисту на ночь
  • Эволюция программного проекта и ООП
  • Как не понимать принципы развития архитектуры SOLID
• Все рисунки к статье (кроме заглавного) сформированы сообществом Wikipedia. Лицензия (Creative Commons Attribution-Share Alike 4.0 International)

Разгадываем загадку: что такое алгоритм в информатике?

Алгоритмы — основа всего, что связано с информатикой и программированием. Они представляют собой последовательность инструкций, которую компьютер

Алгоритмы — основа всего, что связано с информатикой и программированием. Они представляют собой последовательность инструкций, которую компьютер выполняет для решения определенной задачи. Но давайте разберем это подробнее! 😉

Как работает алгоритм?

Простыми словами, алгоритм — это как рецепт приготовления блюда. Имеются определенные ингредиенты и последовательность действий, которые нужно выполнить, чтобы получить конкретный результат. В случае алгоритма, «ингредиентами» могут быть данные, а «рецептом» — последовательность операций с этими данными.

Вот простой пример алгоритма для новичка:

1. Возьмите число (например, 5).
2. Добавьте к нему 2.
3. Результат умножьте на 3.

Результатом этого алгоритма будет число 21.

Зачем нужны алгоритмы в информатике?

Без алгоритмов компьютеры просто не смогли бы функционировать! 💻

Они используются во всех областях информатики, от базовых операций, таких как сортировка и поиск, до более сложных задач, включающих искусственный интеллект и машинное обучение.

Виды алгоритмов в информатике

Алгоритмы в информатике могут быть классифицированы по различным критериям, в том числе по сложности, по принципу работы, по области применения и т.д. Например, есть такие типы алгоритмов, как рекурсивные, итеративные, жадные, динамические и так далее.

Знание и понимание алгоритмов — важный шаг на пути становления профессионалом в области информатики. И помните, практика — лучший способ освоения нового материала! 🚀

Надеюсь, теперь вы понимаете, что такое алгоритмы в информатике. Продолжайте изучение и вскоре вы сможете создавать свои собственные алгоритмы!