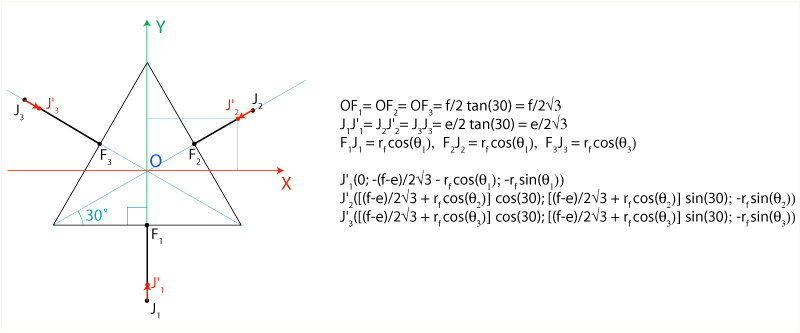В далёком 2009 году я загорелся идеей постройки собственного промышленного робота, который мог бы делать что-то полезное (а именно — сортировать мелкие детали на конвейере). Сразу скажу, что робота я построил (результат вы видите на заглавном фото), а заодно, в качестве побочного продукта, написал небольшую статью о кинематике дельта-роботов на форуме TrossenRobotics — американского продавца наборов из деталей для роботов. Они как раз проводили в то время какой-то конкурс для авторов. Конкурс я, разумеется, не выиграл, но статья на английском осталась. Несколько раз я порывался перевести её на родной язык, однако завершить начатое удалось только сейчас.
Если вы хотите построить свою модель дельта-робота, или просто разобраться, как можно вывести кинематические формулы для этого типа роботов (не выходя при этом за рамки школьной программы по алгебре и геометрии) — добро пожаловать под кат. Для тех, кто не очень любит теорию, в конце статьи приведены примеры готового кода на языке C.
Что такое дельта-робот
Дельта-робота (wiki) придумал в начале 1980-х швейцарский учёный Реймонд Клавель, ниже приведена иллюстрация из оригинального патента US4976582 на «Устройство для перемещения и позиционирования элемента в пространстве»:
Робот состоит из двух платформ: неподвижно закреплённого верхнего основания (1) и небольшой подвижной платформы (8), соединённых тремя рычагами. Каждый рычаг состоит из двух частей: верхнее плечо (4) жёстко соединено с двигателем (3), расположенным на верхнем основании, а нижнее представляет собой параллелограмм (5), в углах которого установлены т.н. универсальные шарниры (6, 7) (wiki), которые позволяют углам изменяться. Каждый параллелограмм соединён с верхним рычагом шарниром (16) таким образом, чтобы его верхняя сторона всегда оставалась перпендикулярной своему рычагу и параллельной плоскости верхнего основания. Благодаря этому подвижная платформа робота, прикреплённая к нижним сторонам параллелограммов также будет всегда параллельной верхнему основанию. Управлять положением платформы мы сможем, изменяя угол поворота верхних рычагов относительно основания робота при помощи двигателей.
В центре нижней платформы (8) крепится т.н. рабочий орган (в английском языке употребляют термин end effector) робота (9). Это может быть манипулятор, захватывающее устройство или, например, экструдер в случае 3D принтера. Дополнительно может использоваться ещё один двигатель (11), который обеспечивает вращение рабочего органа через штангу (14).
Главным преимуществом дельта-роботов является скорость: тяжёлые двигатели размещены на неподвижном основании, движутся только рычаги и нижняя платформа, которые стараются изготавливать из лёгких композитных материалов, уменьшая тем самым их инерцию. Вот, к примеру, статья на Geektimes с парой очень эффектных видеороликов.
Формулировка задачи
Чтобы построить своего собственного дельта-робота, необходимо научиться решать две задачи. В первой ситуации нам известна позиция, в которую мы хотим переместить манипулятор нашего робота (например, мы хотим схватить печенье, которое находится на конвейере в точке с координатами (x, y, z). Для этого нам требуется определить величины углов, на которые мы должны повернуть двигатели, связанные с рычагами робота, чтобы установить его в правильное положение для захвата. Процедура определения этих углов называется обратной (в некоторых русскоязычных источниках употребляется слово «инверсной») кинематической задачей.
Во второй ситуации нам известны углы, на которые повёрнуты управляющие моторы робота (если мы используем сервомоторы, то углы легко можно узнать, считав показания с датчиков углов поворота), и мы хотим найти положение платформы робота в пространстве (например, чтобы скорректировать его позицию). Это — прямая кинематическая задача.
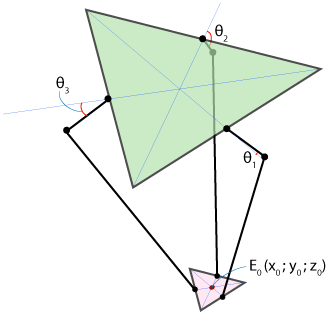
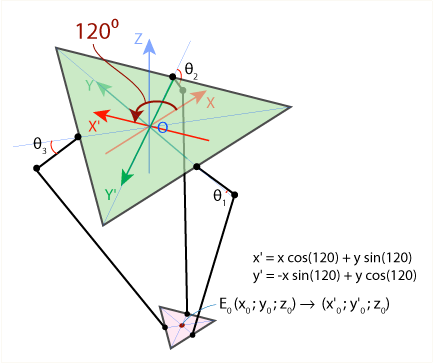
Формализуем обе задачи. И неподвижное основание робота, и его движущуюся платформу можно представить в виде равносторонних треугольников: на схеме ниже они закрашены зелёным и розовым цветами соответственно. Углы поворота рычагов робота относительно плоскости основания (они же — углы поворота моторов) обозначены как Ѳ1, Ѳ2 и Ѳ3, а координаты точки Е0, расположенной в центре подвижной платформы и в которой в реальной жизни будет закреплён манипулятор нашего робота — как (x0, y0, z0).
Получается, что мы должны придумать две функции:
- finverse(x0, y0, z0) → (Ѳ1, Ѳ2, Ѳ3) для решения обратной кинематической задачи и
- fforward(Ѳ1, Ѳ2, Ѳ3) → (x0, y0, z0) для решения прямой кинематической задачи.
Обратная кинематика
Зададим несколько ключевых параметров, которые определяются геометрическими размерами нашего робота:
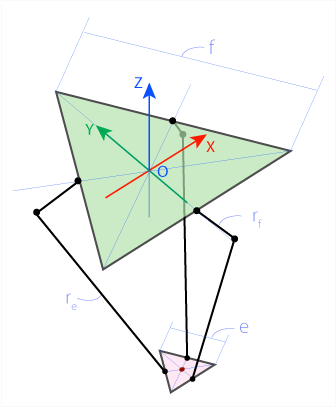
Обозначим длину стороны верхнего основания f, сторону нижней платформы e, длину верхнего плеча рычага rf и длину нижнего плеча (длинной стороны параллелограмма) re. Для вычислений выберем систему координат с точкой отсчёта, совпадающей с геометрическим центром верхнего треугольника. Ось Z направим вверх, таким образом, z-координата подвижной платформы всегда будет отрицательной.
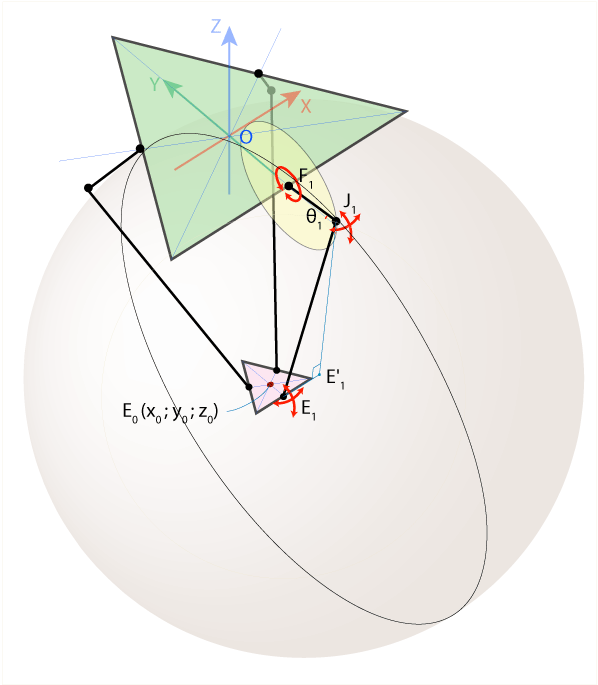
Конструкция робота подразумевает, что рычаг F1J1 (см. рисунок ниже) может вращаться лишь в плоскости YZ, описывая при этом окружность радиусом rf с центром в точке F1 (именно в этом месте он прикреплён к двигателю). В отличие от F1, в узлах J1 и E1 используются универсальные шарниры, благодаря которым плечо E1J1 может свободно вращаться относительно E1, описывая сферу радиусом re с центром в точке E1.
Пересечением этой сферы и плоскости YZ является окружность с центром в точке E’1 радиусом E’1J1, где точка E’1 находится как проекция точки E1 на плоскость YZ. Тогда точка J1 будет находиться на пересечении двух окружностей с центрами в точках E’1 и F1, причём радиусы этих окружностей мы можем определить. Тут есть небольшая тонкость: окружности пересекаются в двух точках, но нас интересует только одна из них — с меньшим значением координаты y, поскольку мы хотим, чтобы рычаги робота всегда торчали «локтями» наружу. Определив таким образом координаты точки J1, мы легко сможем найти угол интересующий нас угол Ѳ1.
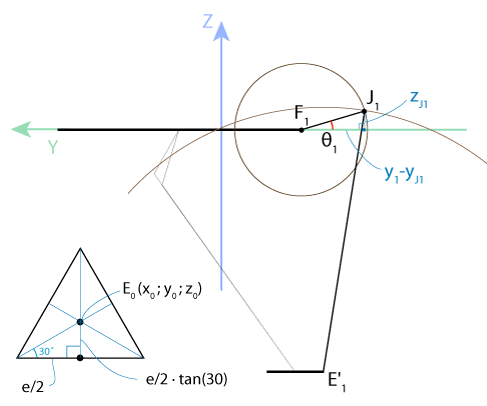
Для удобства восприятия ниже показана проекция нашей трёхмерной картинки на плоскость YZ:
Нижняя платформа является равносторонним треугольником, центром которого является точка E0(x0, y0, z0). Значит, расстояние
что даёт нам следующие координаты точки E1 и её проекции E’1 на плоскость YZ:
Расстояние E1E’1=x0, тогда, согласно теореме Пифагора,
Поскольку верхняя платформа также является равносторонним треугольником, то координаты у точки F1 будут
Чтобы найти координаты точки J1, являющейся пересечением двух окружностей, надо решить систему уравнений:
Координаты центров окружностей нам известны, если их подставить, получится следующее выражение:
Если раскрыть скобки и вычесть одно уравнение из другого, можно линейным образом выразить z-координату точки J1 через y-координату, после чего, подставив её во второе уравнение, получим обычное квадратное уравнение относительно y, из двух решений которого выберем наименьшее (об этом мы говорили выше). А получив таким образом координаты точки J1, найдём и угол
Все выражения получились достаточно простыми благодаря удачному выбору системы координат: плечо рычага F1J1 всегда движется в плоскости YZ, поэтому мы можем просто не учитывать координату x. Чтобы сохранить это преимущество при нахождении двух оставшихся углов Ѳ2 и Ѳ3, воспользуемся симметрией конструкции дельта-робота. Сначала повернём нашу систему координат на 120° против часовой стрелки в плоскости XY вокруг оси Z:
Мы получили новую систему координат X’Y’Z’, и в этой новой системе мы можем воспользоваться нашими готовыми формулами для нахождения угла Ѳ2. Единственная тонкость заключается в том, что мы должны предварительно пересчитать координаты точки E0 в новой системе отсчёта. Это легко сделать при помощи известной формулы (преобразования при повороте системы вокруг начала координат), показанной на рисунке выше. Для нахождения угла Ѳ3 необходимо будет также повернуть исходную систему отсчёта, но теперь уже по часовой стрелке. Этот приём очень удобно реализуется в виде программы: достаточно написать функцию для вычисления угла Ѳ в плоскости YZ, а затем вызвать её три раза для каждого из углов и систем отсчёта.
Прямая кинематика
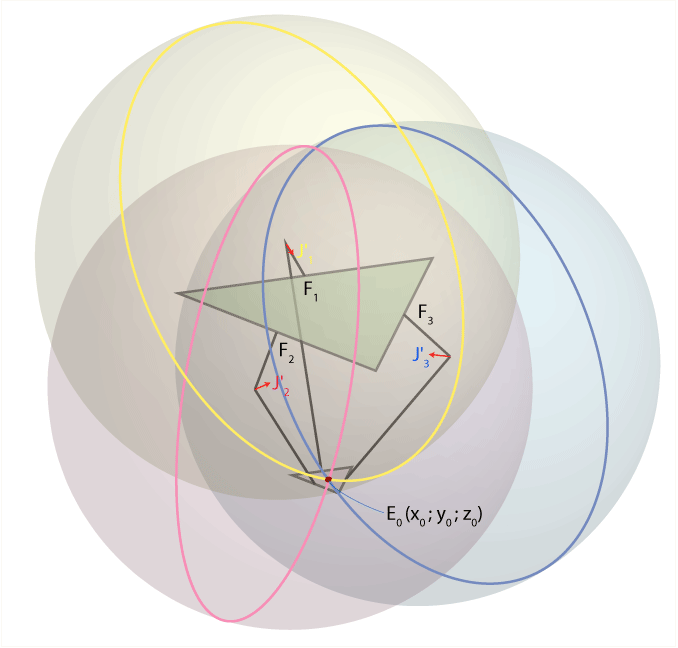
Попробуем решить обратную задачу: теперь нам известны углы Ѳ1, Ѳ2 и Ѳ3, и мы хотим найти координаты (x0, y0, z0) точки E0, расположенной в центре подвижной платформы нашего робота. Зная углы, мы легко можем найти координаты точек J1, J2 и J3 (см. рисунок ниже). Плечи рычагов J1E1, J2E2 и J3E3 могут свободно вращаться вокруг точек J1, J2 и J3 соответственно, образуя в пространстве три сферы с радиусами re.
Воспользуемся хитрым приёмом: сместим центры каждой из этих сфер из точек J1, J2, J3 в плоскости XY в направлении оси Z, используя вектора смещения E1E0, E2E0 и E3E0 соответственно (на рисунке они показаны в виде красных стрелочек). После этого преобразования окажется, что все три сферы пересекаются в точке E0, как показано на рисунке ниже:
Получается, что для определения координат (x0, y0, z0) точки E0 мы должны найти точку пересечения трёх сфер, радиусы и координаты центров которых нам известны. Иными словами, нам надо решить систему из трёх уравнений, описывающих трёхмерные сферы:
где (xi, yi, zi) — координаты центров сфер J’1, J’2 и J’3, которые можно найти следующим образом:
Ниже для сокращения записи я буду использовать в качестве координат точек J’1, J’2 и J’3 обозначения (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3) соответственно. Также хочу обратить внимание, что x1=0 (поскольку точка J’1 находится в плоскости YZ). Получаем следующую систему уравнений:
Введем обозначение
и, вычтя из верхнего уравнения второе и третье, а также из второго третье, получим:
Вычитая из первого уравнения второе (сократив, таким образом, y) и из второго третье (сократив x), сможем выразить x и y через z:
Теперь, подставив x и y, выраженные через z, в уравнение для первой окружности (с центром в точке J’1), получим:
Осталось решить это квадратное уравнение (стандартным образом, через дискриминант), чтобы найти z (мы помним, что надо выбирать наименьший из двух z!), а через него x и y.
Примеры исходного кода
Ниже приведены примеры функций для расчёта кинематики дельта-робота на языке С. Названия переменных соответствуют обозначениям, используемым в статье, углы theta1, theta2 и theta3 указываются в градусах.
// размеры робота
// (обозначения см. на схеме)
const float e = 115.0; // сторона подвижной платформы
const float f = 457.3; // сторона неподвижного основания
const float re = 232.0;
const float rf = 112.0;
// тригонометрические константы
const float sqrt3 = sqrt(3.0);
const float pi = 3.141592653; // PI
const float sin120 = sqrt3/2.0;
const float cos120 = -0.5;
const float tan60 = sqrt3;
const float sin30 = 0.5;
const float tan30 = 1/sqrt3;
// прямая кинематика: (theta1, theta2, theta3) -> (x0, y0, z0)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcForward(float theta1, float theta2, float theta3, float &x0, float &y0, float &z0) {
float t = (f-e)*tan30/2;
float dtr = pi/(float)180.0;
theta1 *= dtr;
theta2 *= dtr;
theta3 *= dtr;
float y1 = -(t + rf*cos(theta1));
float z1 = -rf*sin(theta1);
float y2 = (t + rf*cos(theta2))*sin30;
float x2 = y2*tan60;
float z2 = -rf*sin(theta2);
float y3 = (t + rf*cos(theta3))*sin30;
float x3 = -y3*tan60;
float z3 = -rf*sin(theta3);
float dnm = (y2-y1)*x3-(y3-y1)*x2;
float w1 = y1*y1 + z1*z1;
float w2 = x2*x2 + y2*y2 + z2*z2;
float w3 = x3*x3 + y3*y3 + z3*z3;
// x = (a1*z + b1)/dnm
float a1 = (z2-z1)*(y3-y1)-(z3-z1)*(y2-y1);
float b1 = -((w2-w1)*(y3-y1)-(w3-w1)*(y2-y1))/2.0;
// y = (a2*z + b2)/dnm;
float a2 = -(z2-z1)*x3+(z3-z1)*x2;
float b2 = ((w2-w1)*x3 - (w3-w1)*x2)/2.0;
// a*z^2 + b*z + c = 0
float a = a1*a1 + a2*a2 + dnm*dnm;
float b = 2*(a1*b1 + a2*(b2-y1*dnm) - z1*dnm*dnm);
float c = (b2-y1*dnm)*(b2-y1*dnm) + b1*b1 + dnm*dnm*(z1*z1 - re*re);
// дискриминант
float d = b*b - (float)4.0*a*c;
if (d < 0) return -1; // несуществующая позиция
z0 = -(float)0.5*(b+sqrt(d))/a;
x0 = (a1*z0 + b1)/dnm;
y0 = (a2*z0 + b2)/dnm;
return 0;
}
// обратная кинематика
// вспомогательная функция, расчет угла theta1 (в плоскости YZ)
int delta_calcAngleYZ(float x0, float y0, float z0, float &theta) {
float y1 = -0.5 * 0.57735 * f; // f/2 * tg 30
y0 -= 0.5 * 0.57735 * e; // сдвигаем центр к краю
// z = a + b*y
float a = (x0*x0 + y0*y0 + z0*z0 +rf*rf - re*re - y1*y1)/(2*z0);
float b = (y1-y0)/z0;
// дискриминант
float d = -(a+b*y1)*(a+b*y1)+rf*(b*b*rf+rf);
if (d < 0) return -1; // несуществующая точка
float yj = (y1 - a*b - sqrt(d))/(b*b + 1); // выбираем внешнюю точку
float zj = a + b*yj;
theta = 180.0*atan(-zj/(y1 - yj))/pi + ((yj>y1)?180.0:0.0);
return 0;
}
// обратная кинематика: (x0, y0, z0) -> (theta1, theta2, theta3)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcInverse(float x0, float y0, float z0, float &theta1, float &theta2, float &theta3) {
theta1 = theta2 = theta3 = 0;
int status = delta_calcAngleYZ(x0, y0, z0, theta1);
if (status == 0) status = delta_calcAngleYZ(x0*cos120 + y0*sin120, y0*cos120-x0*sin120, z0, theta2); // rotate coords to +120 deg
if (status == 0) status = delta_calcAngleYZ(x0*cos120 - y0*sin120, y0*cos120+x0*sin120, z0, theta3); // rotate coords to -120 deg
return status;
}
Используемая литература
Все ключевые идеи о кинематике дельта-робота я взял из работы проф. Paul Zsombor-Murray «Descriptive Geometric Kinematic Analysis of Clavel’s «Delta» Robot». Честно признаюсь, что моей математической подготовки не хватило, чтобы понять её до конца, поэтому многое пришлось выводить самому.
Заключение
Спасибо всем, кто прочитал эту статью до конца. Надеюсь, для кого-то она окажется полезной и вдохновит на создание своих вариантов дельта-робота.

Введение:
В данном уроке, двигаясь по шагам, мы соберём робот «Манипулятор».
Видео:
Для сборки нам понадобится крепеж:
| Наименование | Количество, шт. | |
|---|---|---|
| 1 | Гайка М3 | 10 |
| 2 | Винт М3х6 | 9 |
| 3 | Винт М3х8 | 10 |
| 4 | Винт М3х10 | 5 |
| 5 | Винт М3х12 | 7 |
| 6 | Винт М3х20 | 4 |
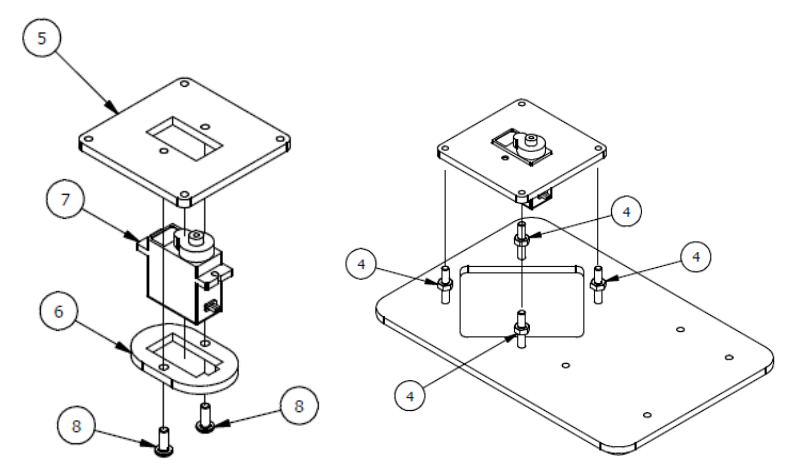
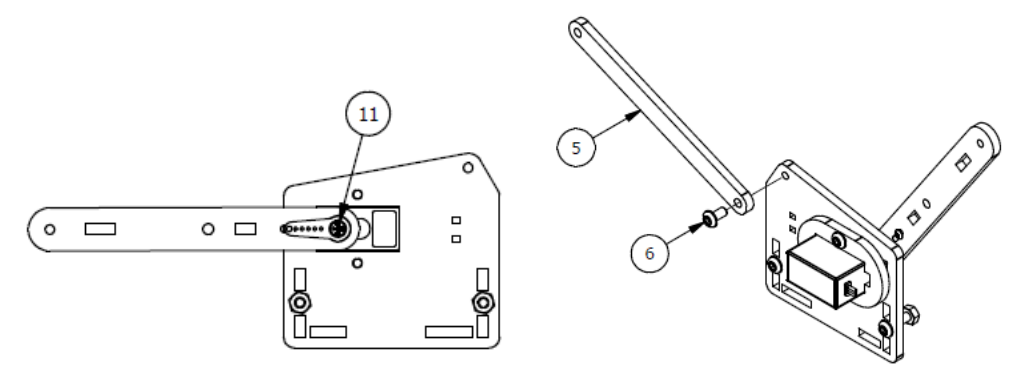
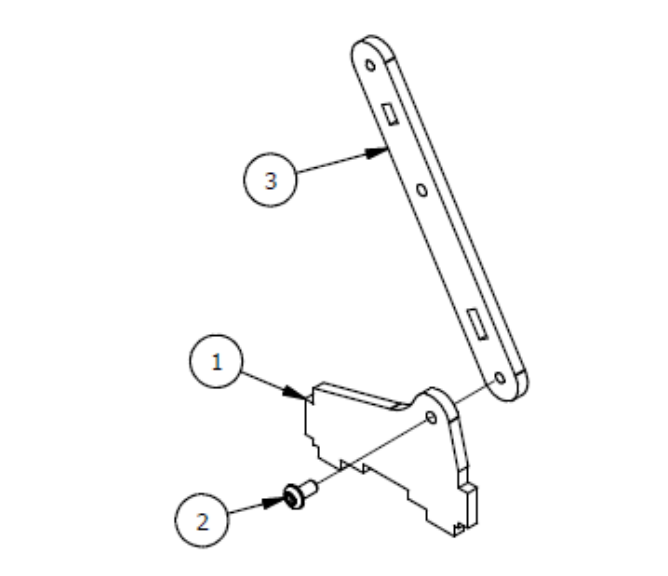
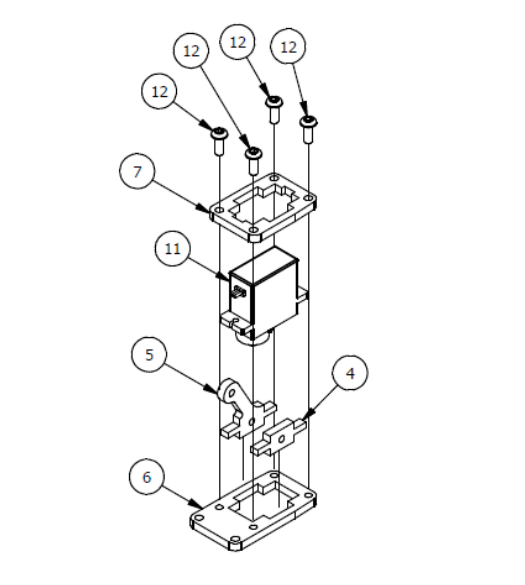
Шаг 1
Список деталей к Шагу 1
Если Вы используете для сборки Микросервопривод MG90S, необходимо отклеить с него наклейки!!! в противном случае он будет очень туго устанавливаться, в результате чего можете поломать крепеж!
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Основание |
| 3 | 4 | М3х20мм винт |
| 4 | 4 | М3 гайка |
| 5 | 1 | Опорная пластина |
| 6 | 1 | Крепление |
| 7 | 1 | Сервопривод |
| 8 | 2 | М3×8мм винт |
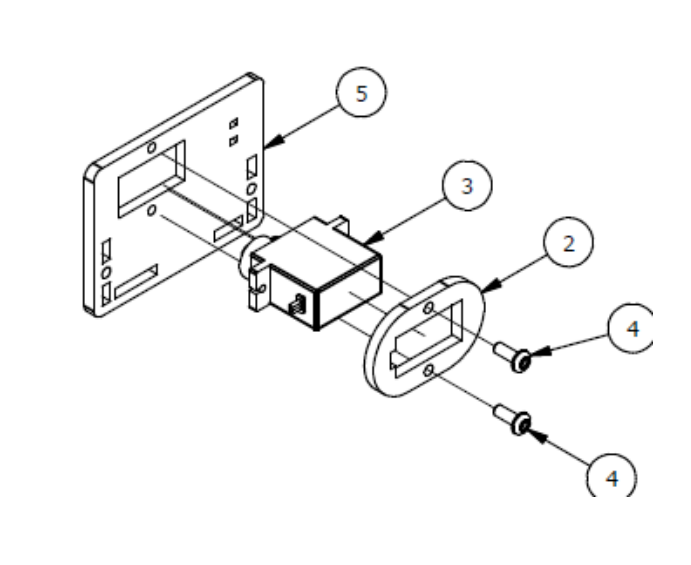
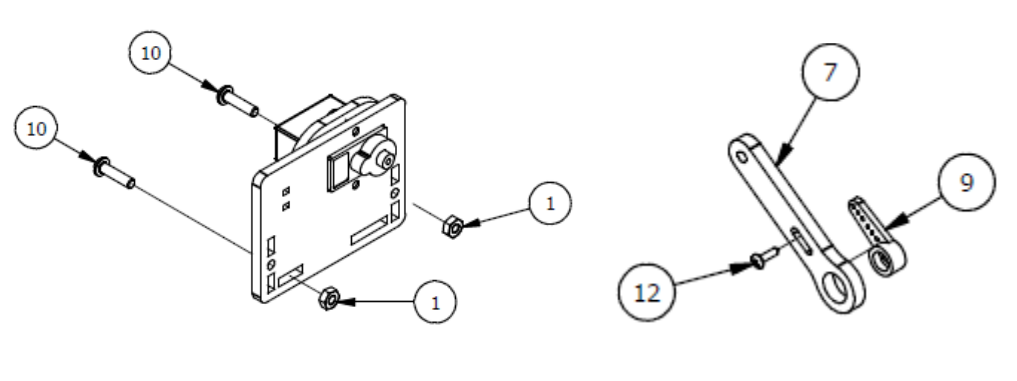
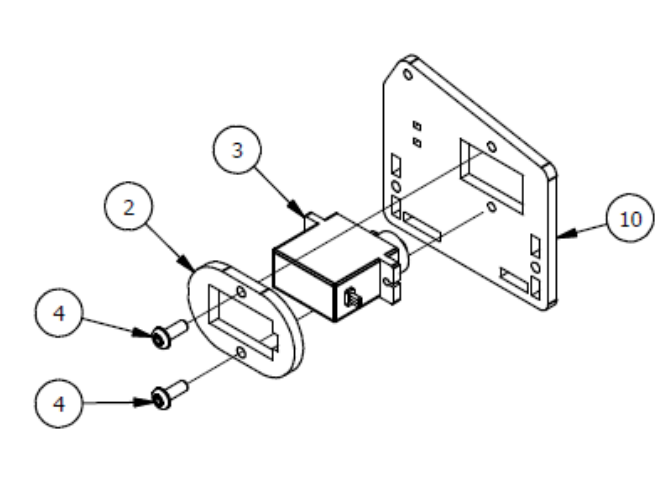
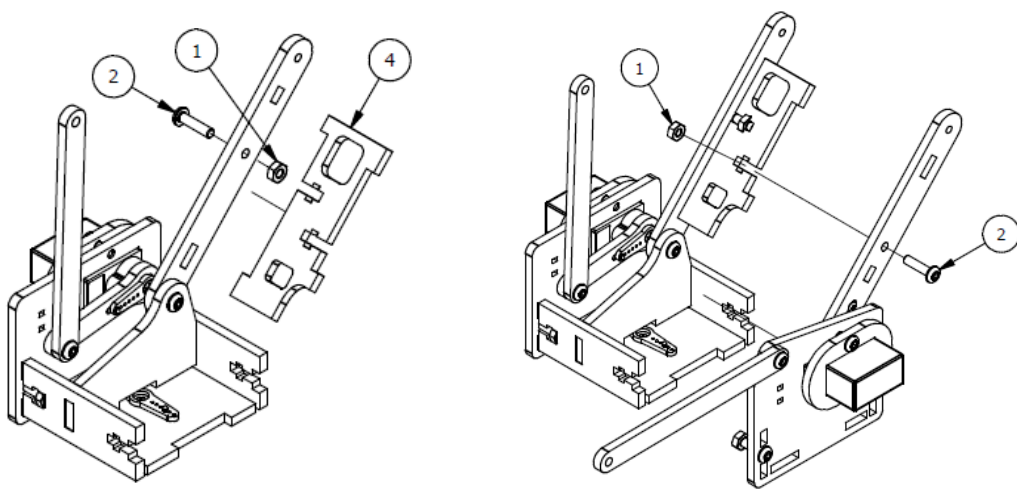
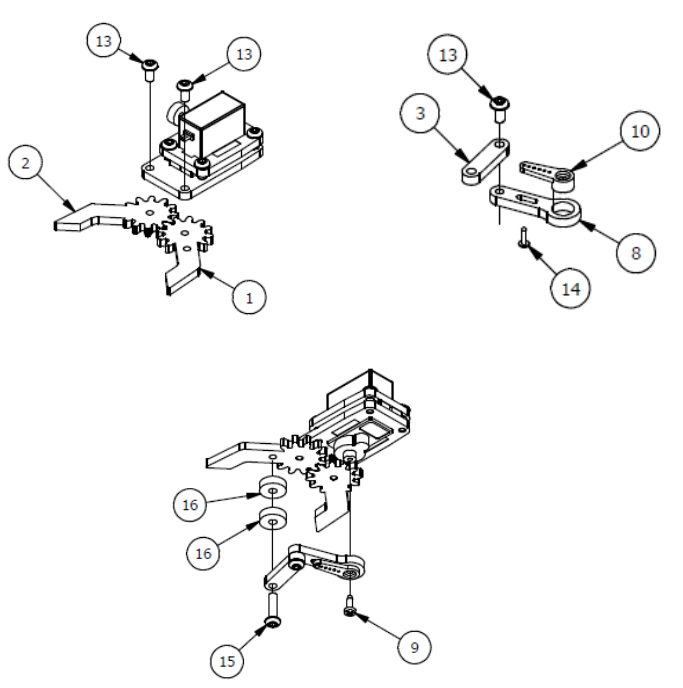
Шаг 2
Список деталей к Шагу 2
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 1 | Крепление |
| 3 | 1 | Сервопривод |
| 4 | 2 | М3х8 винт |
| 5 | 1 | Основа левой руки |
| 6 | 1 | Параллельное крепление |
| 7 | 1 | Рычаг руки |
| 8 | 1 | М3×6мм винт |
| 9 | 1 | Серво рычаг |
| 10 | 2 | М3х12мм винт |
| 11 | 1 | Осевой серверный винт |
| 12 | 1 | Фиксирующий серверный винт |
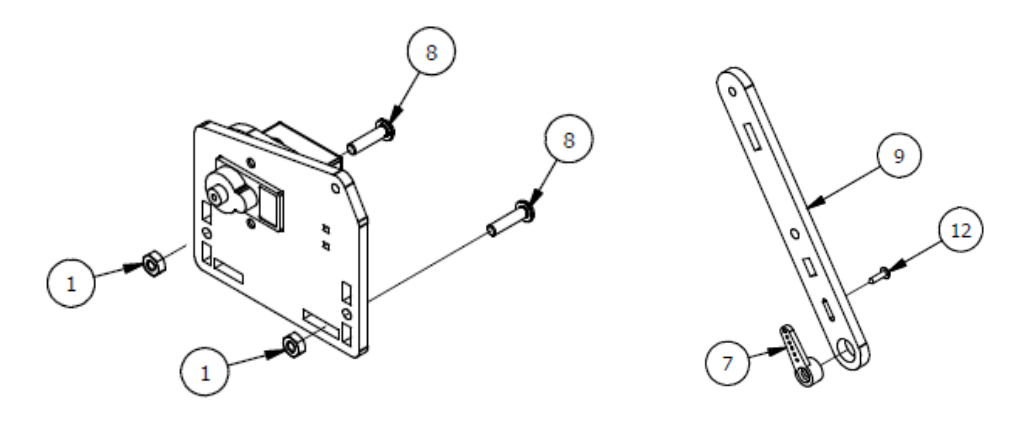
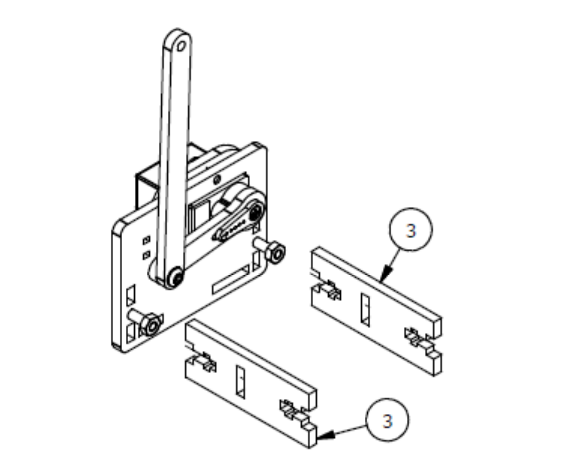
Шаг 3
Список деталей к Шагу 3
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 1 | Крепление |
| 3 | 1 | Сервопривод |
| 4 | 2 | М3х8 винт |
| 5 | 1 | Параллельное крепление |
| 6 | 1 | М3х6мм винт |
| 7 | 1 | Серво рычаг |
| 8 | 2 | М3×6мм винт |
| 9 | 1 | Рычаг правой руки |
| 10 | 1 | Основание правой руки |
| 11 | 1 | Осевой серверный винт |
| 12 | 1 | Фиксирующий серверный винт |
Шаг 4
Список деталей к Шагу 4
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Крепление вкладки левой руки |
| 2 | 1 | М3х6мм винт |
| 3 | 1 | Балка левой руки |
| 4 | 1 | Верхняя крышка |
| 5 | 1 | Двойной серво рычаг |
| 6 | 2 | Фиксирующий серверный винт. |
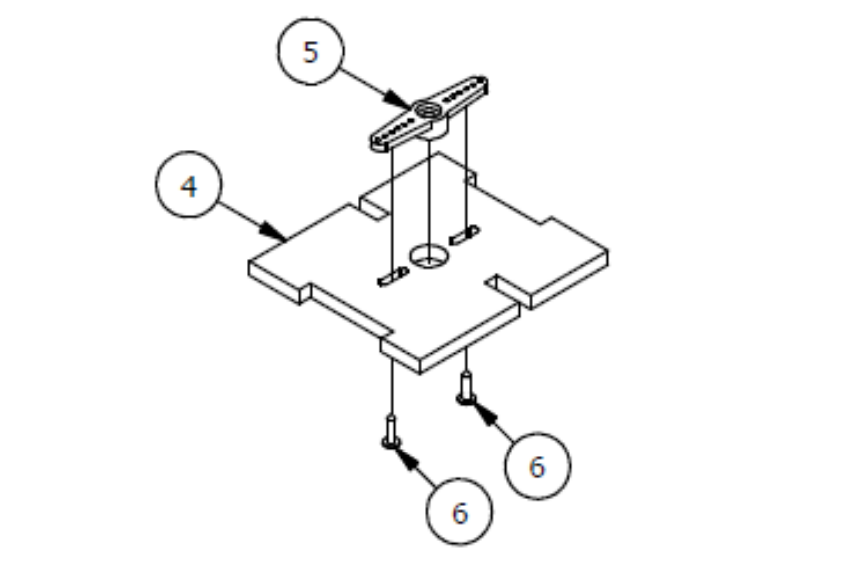
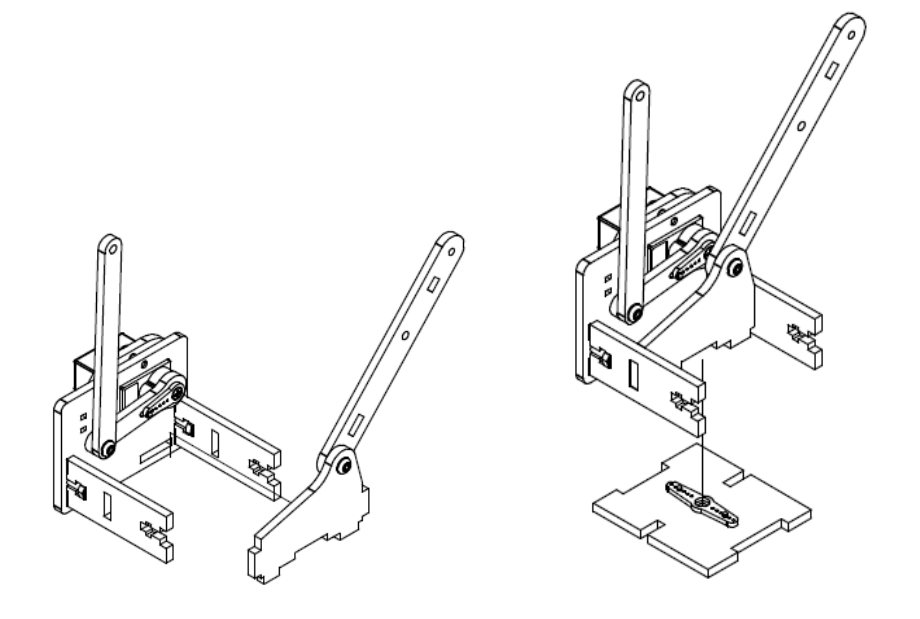
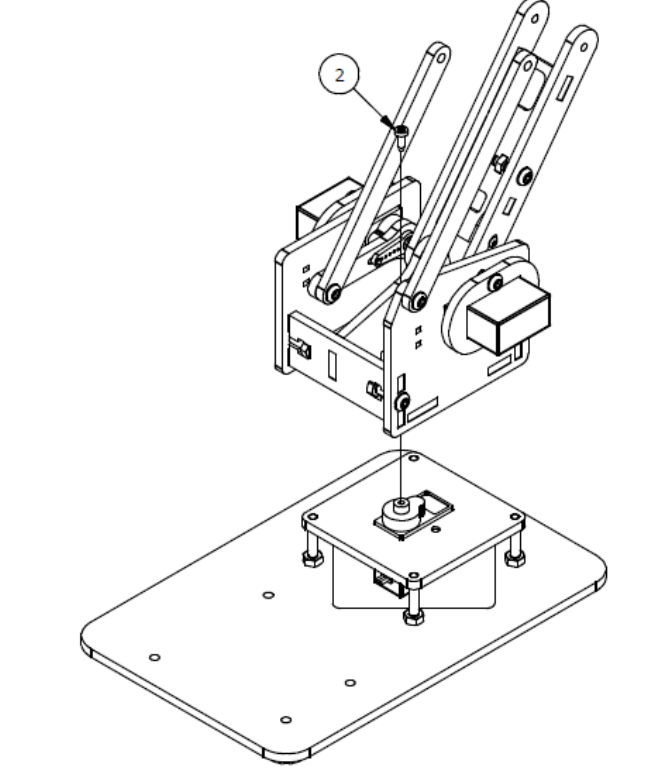
Шаг 5
Список деталей к Шагу 5
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 2 | М3х12мм винт |
| 3 | 1 | Траверса основания манипулятора |
| 4 | 1 | Соединительное ребро жесткости |
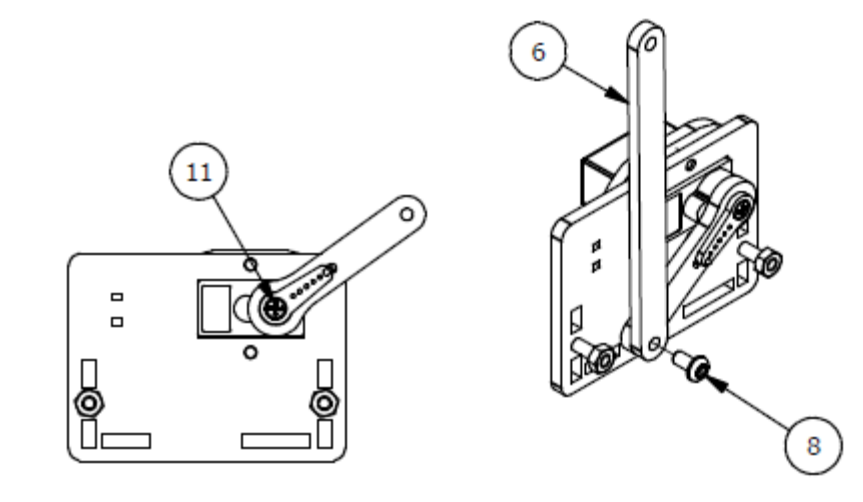
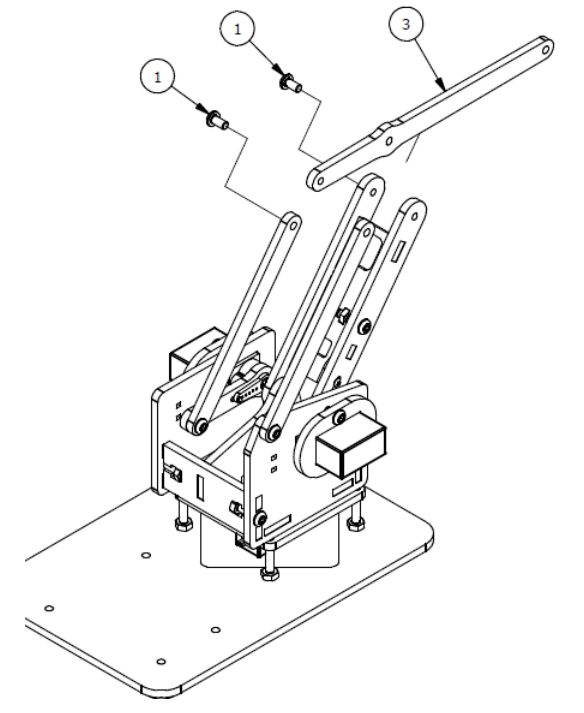
Шаг 6
Список деталей к Шагу 6
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3×6мм винт |
| 2 | 1 | Фиксирующий серверный винт |
| 3 | 1 | Балка левого запястья |
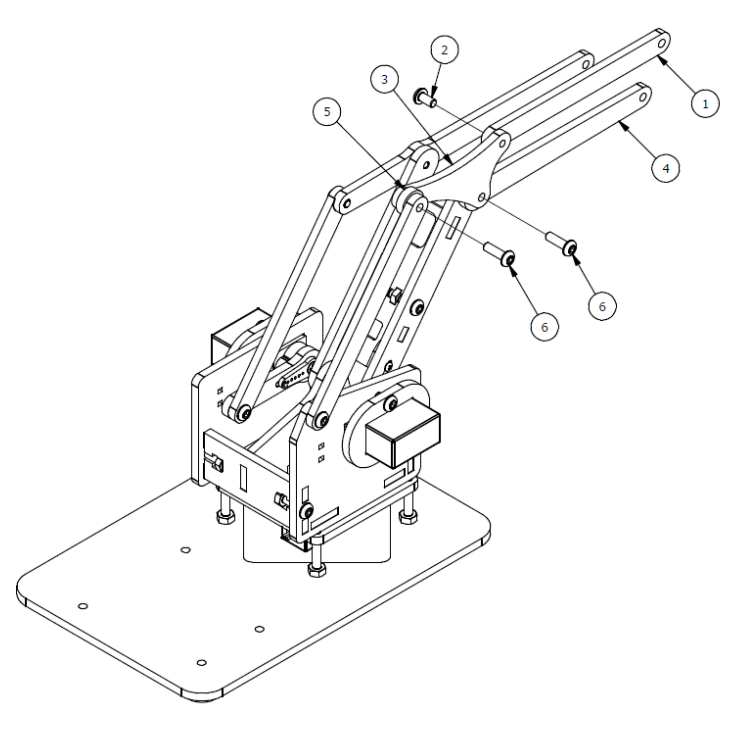
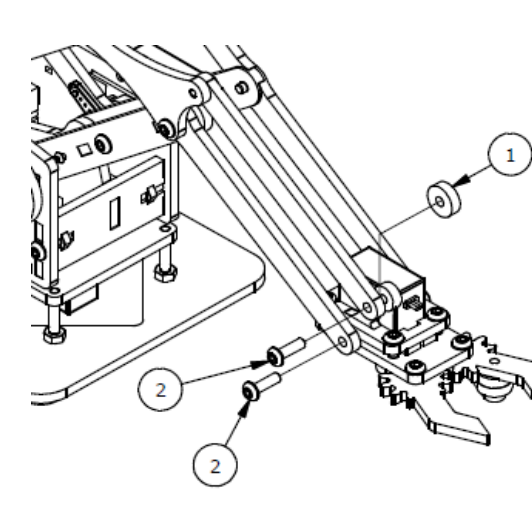
Шаг 7
Список деталей к Шагу 7
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Параллельная балка |
| 2 | 1 | М3х6мм винт |
| 3 | 1 | Коннектор |
| 4 | 1 | Балка правого запястья |
| 5 | 1 | Прокладка |
| 6 | 2 | M3x10 винт |
Шаг 8
Список деталей к Шагу 8
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Левый захват |
| 2 | 1 | Правый захват |
| 3 | 1 | Приводной рычаг |
| 4 | 1 | Левое крепление запястья |
| 5 | 1 | Правое крепление запястья |
| 6 | 1 | Нижнее крепление сервопривода |
| 7 | 1 | Верхнее крепление сервопривода. |
| 8 | 1 | Приводной рычаг |
| 9 | 1 | Осевой серверный винт. |
| 10 | 1 | Серво рычаг |
| 11 | 1 | Сервопривод |
| 12 | 4 | М3х8мм |
| 13 | 3 | М3х6мм |
| 14 | 1 | Фиксирующий серверный винт |
| 15 | 1 | М3х12мм винт |
| 16 | 2 | Прокладка |
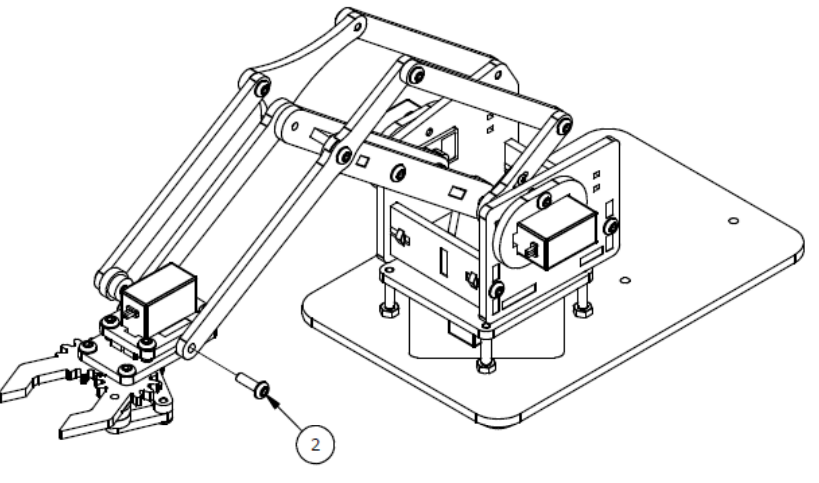
Шаг 9
Список деталей к Шагу 9
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Прокладка |
| 2 | 3 | М3х10мм винт |
Вы можете скачать данную инструкцию по ссылке: Сборка робота-манипулятора. Часть 1
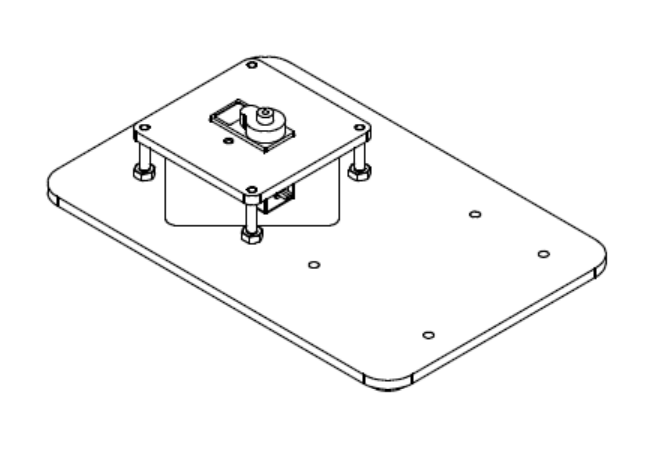
В собранном виде:

Учебный робот-манипулятор с угловой кинематикой предназначен для перемещения и ориентации объектов в пространстве со сферической системой координат и имитации технологических операций. Учебный робот-манипулятор реализован на основе интеллектуальных сервоприводов с последовательным коммуникационным интерфейсом управления, оснащенных трехконтурной системой управления с настраиваемыми параметрами регуляторов.
Конструкция манипуляционного робота выполнена из пластиковых элементов, усиленных металлическим каркасом. Блочно-модульный принцип конструкции позволяет модифицировать комплект за счет применения ресурсных комплектов и дополнительных аксессуаров. Например, в качестве рабочего органа манипулятора могут быть установлены схваты разных типов: угловой кинематики, плоско-параллельной, а также вакуумный захват.
Программируемый контроллер робота позволяет управлять кинематикой робот-манипулятора, одним из установленных на нем в данный момент рабочих органов, а также вспомогательными устройствами, установленными в макете производственной ячейки, собираемой на базе данных учебных манипуляторов. Управление возможно как за счет установления соединения между смарт-устройствами производственной ячейки посредством локальной сети, так и путем специализированного программного обеспечения для диспетчеризации и управления макетом производственной линии.
Программное обеспечение представляет собой серверное приложение для сбора, хранения и диагностики команд и сообщений, передаваемых между «смарт»-устройствами, учебными манипуляторами и удаленным облачным сервером. Программное обеспечение также предназначено для тестирования работоспособности системы управления макета производственной линии посредством имитации управляющих команд от сервера «Интернета вещей», а также логирования и верификации команд, поступающих от системы управления на устройства, входящие в макет производственной линии.
Программное обеспечение может быть оснащено дополнительными программными модулями для имитации оборудования, входящего в макет производственной линии (программные модули распространяются с пакетом обновлений ко всем изменениям конкурсных заданий). Программное обеспечение предоставляется отдельно в виде лицензии на учебное заведение.
В состав учебного робот-манипулятора входит: сервоприводы Dynamixel MX-106 — 1 шт, MX-64 — 1 шт, МХ-28 — 2 шт, АХ-18 — 2 шт; программируемый контроллер с интегрированным одноплатным микрокомпьютером с поддержкой интерфейсов Ethernet и WiFi для коммуникации со смарт устройствами; вычислительный «смарт»-контроллер и периферийная плата для реализации «смарт-устройств» и беспроводной коммуникации между ними; модуль технического зрения; модуль управления вакуумным захватом.
-
Contents
-
Table of Contents
-
Bookmarks
Quick Links
Robot Module
1303-D05A
Tool Module
1304-D57A
Tool Changer Safety Control Circuit
Manual 95575 Rev 05
July 1, 2013
648 Saratoga Road
Glenville, NY 12302 USA
Phone: 518 384 1000
Fax: 518 384 1200
Summary of Contents for Applied Robotics 1303-D05A
-
Page 1
Robot Module 1303-D05A Tool Module 1304-D57A Tool Changer Safety Control Circuit Manual 95575 Rev 05 July 1, 2013 648 Saratoga Road Glenville, NY 12302 USA Phone: 518 384 1000 Fax: 518 384 1200… -
Page 2
The information and drawings contained herein are the sole property of Applied Robotics Incorporated and shall not be divulged to any third party without the prior written consent of Applied Robotics Inc. The information in this document is subject to change without notice. Applied Robotics makes no warranty of any kind with regard to this user’s guide, including but not limited to, implied warranties or fitness… -
Page 3: Table Of Contents
1303-D05A & 1304-D57A Manual — 95575 Rev 05 Contents 1. Precautions ………………….. 4 2. System Description ……………….. 5 3. State Diagram ………………..6 4. Technical Specifications ………………7 5. Modules ………………….8 6. Installation ………………….9 6.1 Attachment to Tool Changer …………..9 6.2 Air Supply ………………..
-
Page 4: Precautions
1303-D05A & 1304-D57A Manual — 95575 Rev 05 1 Precautions READ MANUAL Do not start, operate or service machine until you read and understand operator’s manual. Failure to do so could result in serious injury. HAND CRUSH NOTICE Indicates the possibility for a crush force between components during coupling of the Robot and Tool adaptor.
-
Page 5: System Description
1303-D05A & 1304-D57A Manual — 95575 Rev 05 2 System Description Definitions Tool – A device that may be attached to a tool changer to perform a specific function Tool Changer – A device consisting of two adapters, one attached to a robot and one attached to a tool, that mechanically couple a robot to a tool, allowing a robot to use multiple tools.
-
Page 6: State Diagram
1303-D05A & 1304-D57A Manual — 95575 Rev 05 Diagnostic Coverage The diagnostic coverage monitors the status of the Tool Stand Present, Tool Present, and the Output Valve Spool Position through a set of normally open and normally closed contacts. In order for proper opera- tion of the system, all dual channel devices need to operate simultaneously.
-
Page 7: Technical Specifications
1303-D05A & 1304-D57A Manual — 95575 Rev 05 4 Technical Specifications Minimum Safety Classification Cat. 3 PLd EN ISO 13849-1 MTTFd 68 Years Mission Time 20a (20 years) Robot Side Dimensions 120mm x 118mm x 128mm Tool Side Dimensions 108mm x 59mm x 22mm…
-
Page 8: Modules
1303-D05A & 1304-D57A Manual — 95575 Rev 05 5 Modules 1303-D05A S.1-EM-R-V-ISO 13849-SCM 1304-D57A S.1-EM-T-V-ISO 13849-SCM…
-
Page 9: Installation
1303-D05A & 1304-D57A Manual — 95575 Rev 05 6 Installation 6.1 Attachment to Tool Changer With the Robot and Tool Adapter uncoupled and apart, install both the robot and tool side module on side one of the tool changer. 4 x ARI # 49798 SCR, SOC…
-
Page 10: Air Supply
1303-D05A & 1304-D57A Manual — 95575 Rev 05 6.2 Air Supply Connect the Air Supply to the 6mm air fitting show below: Upon supplying air to the Safety Control Module, the robot adaptor will be forced coupled. Make sure the tool adaptor is not within range of the robot side cams to cause an undesired couple.
-
Page 11
1303-D05A & 1304-D57A Manual — 95575 Rev 05 Power and Uncouple are supplied on two separate M12 connections J3 and J2, respectively. Connect the appro- priate cables to the connectors J3 and J2 as shown below: Make sure an uncouple signal is not being supplied by the cable you care connecting to J2. -
Page 12: Manual Uncouple
1303-D05A & 1304-D57A Manual — 95575 Rev 05 7 Manual Uncouple With all cables and air fittings properly installed the Safety Module is ready for operation. Please refer to the system description on Page 5 and State Diagram on page 6 for how the module functions. During initial pro- gramming or if an undesired or abnormal state is achieved, the two M5 screws may be removed from the face of the cover to manually actuate the valves to uncouple.
-
Page 13: Operational Guidelines
1303-D05A & 1304-D57A Manual — 95575 Rev 05 8.1 Operational Guidelines Review the guidelines below to understand how the Safety Control Module operates. Manual uncouple may be used in a case where a new tool is being installed and there is no tool stand pre- sent signal to interface with the Safety Control Module.
Содержание
- 1 Установка ПО
- 1.1 Загрузка и установка окружения
- 1.2 Скачивание необходимых пакетов
- 2 Описание кинематики манипулятора
- 2.1 Описание манипулятора
- 3 Структура системы управления
- 3.1 Модуль управления рукой манипулятора
- 3.2 Модуль управления схватом манипулятора
- 3.3 Модуль управления приводами манипулятора
- 4 Модель для симуляции
- 4.1 Структура пакета
- 4.2 Запуск модели в симуляции
- 4.3 Система топиков, нод и сервисов
Установка ПО
Загрузка и установка окружения
Для работы с пакетами управления манипулятором в среде ROS необходимо создать окружение. Для этого можно использовать виртуальную машину, порядок установки которой изложен по следующей ссылке. В случае, когда на персональном компьютере уже установлена Linux-система, то для корректной работы с пакетами управления манипулятором необходимо иметь систему Ubuntu 18.04 и ROS Melodic.
Скачивание необходимых пакетов
Для работы с манипулятором в системе ROS необходимо скачать специальные пакеты управления, позволяющие работать как с моделью для симуляции, так и с реальным роботом. Пакеты располагаются на GitHub. Скачать их можно либо через инструменты git (команда git clone {ссылка на скачиваемые файлы}) либо непосредственно с сайта.
В результате скачивания любым из представленных способов получены две папки (workspace). Одна из папок содержит пакеты для управления реальной моделью, вторая для работы с симуляцией. Полученные папки требуется расположить в следующем формате:
В данном случае папка robotic_arms_ws содержит пакеты для работы с реальным роботом, папка robotic_arms_ws_simulation — пакеты для работы с моделью для симуляции.
Описание кинематики манипулятора
Описание манипулятора
В качестве объекта управления используется манипулятор с угловой кинематикой компании Aplied Robotics.
Данный манипулятор представляет из себя устройство, в состав которого входят только вращательные подвижности. Всего подвижностей манипулятора пять — три переносные и две ориентирующие. Благодаря этому для однозначного задания положения схвата манипулятора в трехмерном пространстве достаточно указать три декартовы координаты центра системы координат схвата, а так же два угла ориентации её осей. Наличие только пяти степеней подвижности вносит некоторые ограничения в позиционировании схвата, так как для задания ориентации твердого тела в пространстве необходимо указать шесть параметров — три координаты положения и три угла ориентации. По этой причине схват манипулятора может не достигать некоторых положений.
На данной схеме изображены обобщенные координаты подвижностей манипулятора q1 — q5, звенья руки с индексами 0 — 4, а также схват 5. Под номером 0 обозначено условно неподвижное звено (стойка), которое является базовым. Все координаты, связанные с этим звеном, называются базовыми. За счет наличия пяти степеней подвижности, звенья манипулятора от 2 до 5 совершают плоское движение. Обобщенная координата q1 осуществляет вращения этой плоскости вокруг звена 1. Схват представляет из себя устройство, состоящее из сервомотора, двух пальцев, направляющей движения пальцев и дополнительных соединительных деталей.
Структура системы управления
Для структурирования системы управления удобно ее разделить на три основных модуля: модуль управления приводами, модуль управления рукой манипулятора, модуль управления схватом. Взаимосвязи между ними изображены на следующей схеме:
Модуль управления рукой манипулятора
Данный модуль реализует функционал по управлению рукой манипулятора. В нем производится решение прямой и обратной позиционной задачи кинематики, реализуется код по формированию и отображению траектории движения схвата, преобразование координат из показаний энкодеров приводов в радианы и обратно, а также реализует функционал, позволяющий в удобной форме задавать команду для движения схвата манипулятора, при этом контролируя достижение заданной точки.
Модуль управления схватом манипулятора
Модуль управления схватом манипулятора позволяет задавать команды по сжатию и отпусканию объектов, при этом реализуя обратную связь с информацией о том, находится ли деталь в схвате.
Модуль управления приводами манипулятора
Данный модуль реализован с помощью готовых библиотек по работе с сервомоторами Dynamixel. Он позволяет получать данные энкодеров, настраивать параметры ПИД регуляторов, получать значения с датчиков температур и тока сервомоторов, используя USB порт компьютера. Подключение манипулятора (цепи сервомоторов) к USB — порту ПК производится с помощью адаптера USB — DXL — AR и SMPS2Dynamixel, позволяющего обеспечить для сервомоторов отдельное 12V питание
Модель для симуляции
Структура пакета
Структура пакета управления моделью в симуляции имеет следующий вид:
Представленная структурная схема описывает подход к расположению различных модулей системы управления. Данная схема одинаков как для реального робота, так и для модели в симуляции за исключением пакета управления сервомоторами, который отсутствует для симуляции. В данной схеме выделены три основных блока: pc_image — пакет визуализации движения робота, nanopi_image — пакет управления роботом, arms_control_pkg — пакет запуска системы управления и визуализации.
Запуск модели в симуляции
Перед работой с пакетами управления необходимо произвести сборку проекта. Для этого, находясь в папке workspace требуется выполнить команду catkin_make.
Запуск модели в симуляции производится с помощью набора команд:
source devel/setup.bash
roslaunch arms_control_pkg angle_arm_control.launch
В результате выполнения команды запустится визуализация робота в среде RVIZ.
Для формирования задания манипулятору используются сервисы. Для задания команды необходимо открыть новый терминал в той же директории, из которой запускалась модель симуляции и выполнить команду source devel/setup.bash. Команда для задания желаемой точки и ориентации имеет следующий вид:
rosservice call /cmd_point “point: ‘{x} {y} {z} {pitch} {roll}’”
/cmd_point – имя сервиса для задания координаты рабочего инструмента в формате “{x} {y} {z} {pitch} {roll}”, где pitch – угол наклона схвата к горизонтали (вертикально вниз -1.57, вверх 0.70), roll – угол поворота схвата вокруг своей оси.
Для примера предложен набор достижимых точек: 350 0 350 0 0, -350 0 300 0 0, 250 0 110 -1 0, 150 150 150 -1 0, 150 150 100 -1.57 0 (в миллиметрах и радианах)
В качестве ответа сервис возвращает true, если все хорошо, false – если обратная задача кинематики не решается.
Для управления схватом манипулятора так же, как и в случае управления рукой, необходимо открыть новый терминал в той же директории и выполнить команду source devel/setup.bash. С помощью следующей команды производится вызов сервиса:
rosservice call /grippe_cmd “point: ‘расстояние между губками’”
Например ‘0.2’ – полностью открыт, ‘0’ – закрыт. Схват открывается и закрывается моментально.
Пример работы симуляции при следующем наборе управляющих точек: 240 150 300 0 0; -240 -150 200 -1 -1; 350 0 200 -0.5 1; 150 150 200 -0.5 1
-
240 150 300 0 0
-
-240 -150 200 -1 -1
-
350 0 200 -0.5 1
-
150 150 200 -0.5 1
Система топиков, нод и сервисов
В пакете симуляции управления манипулятором при его запуске доступны следующие топики
На рисунке представлен список всех топиков, работающих в системе ROS при запуске пакетов управления. Из них только топик /angle_robot/joint_states содержит полезную информацию, а именно текущие обобщенные координаты сочленений манипулятора.
Далее на рисунке представлен список нод, работающих в системе ROS при запуске модели для симуляции.
На рисунке изображены ноды /rosout и /rviz, которые являются системными. Далее нода /angle_robot/robot_state_publisher3 производит перемещение визуальной модели манипулятора, нода /main_to_point_control принимает поступающие команды, решает обратную задачу кинематики и отправляет полученные требуемые обобщенные координаты ноде /convert_and_publish,нода /convert_and_publish производит кинематическое моделирование движения робота.
На рисунке выше изображен граф взаимодействия нод в системе при запуске пакета симуляции.