Задания к § 15. Алгоритм как модель действий
- Можно ли назвать эти изображения текстовыми моделями устройств? — НЕТ
2. Заполни таблицу по образцу.
| Объект-оригинал | Модель объекта | Общие свойства объекта-оригинала и модели |
| Планета Земля | Глобус | Форма |
| Ребёнок | Кукла | Форма |
| Местность | Карта местности | Расположение объектов |
| Здание | Рисунок | Элементы, из которых состоит здание |
| Событие | Текст | Отношение |
| Явление природы | Макет | Вид |
| Процесс создания объекта | План действий | Алгоритм |
3. Отметь, какой вариант плана действий можно назвать алгоритмом решения задачи: «Петя купил 2 кг картошки и З кг моркови. Сколько стоила покупка?» — Вариант 2
Вариант N 1
1) Узнай стоимость картошки и моркови.
2) Определи стоимость покупки.
Вариант N 2+
1) Умножь стоимость одного килограмма картошки на 2.
2) Умножь стоимость одного килограмма моркови на З.
З) Найди сумму полученных произведений.
4. Вставь пропущенные слова.
| Свойство алгоритма | Описание свойства |
| Первое | Описание должно состоять из последовательности отдельных (дискретных) шагов (инструкций, команд). |
| Второе | Описание должно состоять из конечного числа отдельных инструкций |
| третье | Каждая инструкция должна быть понятна исполнителю. |
| четвёртое | Выполнение последовательности команд инструкций должно привести к ожидаемому результату |
| Пятое | Последовательность инструкций должна быть предназначена для решения не одной конкретной задачи, а может быть использована для решения целого класса задач |
5. Выбери (соедини стрелками) только то, что ты считаешь алгоритмом.
6. Отметь свойства алгоритма.
- Является понятным исполнителю +
- Имеет размер и цвет
- Имеет конечное число шагов +
- Может иметь бесконечное число шагов
- Исполнение инструкций приводит к ожидаемому результату +
- Позволяет решить только одну задачу
- Позволяет решить целый класс задач +
Используя список свойств алгоритма, сформулируй и запиши, что такое алгоритм:
Алгоритм является понятным исполнителю, который имеет конечное число инструкций, которое приведет к ожидаемому результату и позволит решить целый класс задач.
7. Ответь устно на вопросы.
- Чем отличается алгоритм от любого описания последовательности действий? Алгоритм имеет конечное число шагов, которое приведет к ожидаемому результату
- Что есть общего между алгоритмом и просто перечислением действий? Имеют шаги
- Можно ли назвать алгоритмом такой список действий?
- Прочитай.
-
- Запомни.
- Расскажи.
Да, данный алгоритм приведет к ожидаемому результату
- Можно ли сказать, что алгоритм всегда обладает свойством понятности исполнителю? Приведи пример. Да, алгоритм всегда должен быть понятен исполнителю.
8. Отметь общее свойство, которым обладают и алгоритм, и просто план действий.
- Предназначен для исполнения +
- Имеет всегда три шага (инструкции)
- Исполнение приводит к ожидаемому результату +
- Позволяет решить класс задач
- Позволяет решить только одну задачу
- Может иметь бесконечное число шагов
9. Зачеркни неверный алгоритм нахождения площади прямоугольника.
| 1) 2) З) | Измерь длину прямоугольника. Измерь ширину прямоугольника. Определи площадь как произведение длины на ширину. |
10. Реши задачу на перестановку чисел: расположи три числа 9, 5, 7 в порядке возрастания, используя алгоритм:
1) Сравни первое и второе числа; если первое больше второго, то поменяй их местами.
2) Сравни второе и третье числа; если второе больше третьего, то поменяй их местами.
З) Если теперь три числа расположены в порядке возрастания, то закончи выполнение действий; иначе вернись к пункту 1).
- 5,9,7
- 5,7,9
11. Отметь верные высказывания.
- Алгоритм — это подробный план последовательности действий, описывающий способ решения задачи.
- Описание последовательности действий может быть названо алгоритмом, если оно обладает необходимыми свойствами. +
- Алгоритм — это план-модель действий при решении класса задач. +
- План действий человека при уборке дома или при приготовлении пищи может быть алгоритмом. +
12. Составь алгоритм решения класса задач поиска площади прямоугольного пола в помещениях жилого дома. Используй план-схему квартиры:
- Измерить длину комнаты
- Измерить ширину комнаты
- Определи площадь как произведение длины на ширину
13. Заготовка для выполнения задания в учебнике (часть 2) на странице 27.
S = A*B = 20*10=30
Результат: площадь рабочей поверхности парты равна 30 cм2
Примечание: Цифры взяты рандомные, необходимо взять параметры своего стола.
Н. В. Матвеева, Е. Н. Челак Информатика Рабочая тетрадь для 4 класса. Ответы
Скачать материал
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Алгоритм как модель действий-часть 1.pptx

Скачать материал


- Сейчас обучается 29 человек из 15 регионов


- Сейчас обучается 35 человек из 25 регионов


- Сейчас обучается 341 человек из 65 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
В своей повседневной жизни мы постоянно сталкиваемся с выполнением различных действий. Часто мы составляем план для решения какой-то задачи. Чтобы решить задачу, надо знать, что для этого надо делать, как делать и в каком порядке.
-
2 слайд
Ты дружишь с математикой?
Рассмотрим пример простой математической задачи -
-
4 слайд
Есть два варианта плана действий для решения этой задачи:
Варианты № 1 и №2 — это различные описания порядка действий для решения задачи. -
5 слайд
Подумай, чем отличаются два варианта плана действий?
Вариант № 1 содержит неконкретные, нечеткие задания.
Вариант №2 — описание порядка действий четкое, ясное и понятное даже ученику 4 класса.
Таким образом, инструкции или команды для решения поставленной задачи должны быть понятными, конкретными, четкими, с описанием всех шагов. -
6 слайд
«Алгоритм — модель действий»
Подумай!
Как может называться тема нашего урока?Алгоритмом мы можем назвать описание порядка действий для решения поставленной задачи.
-
7 слайд
Алгоритм как модель действий
Прочитай и запомни:
Модель процесса решения задачи (подробный порядок действий) называется алгоритмом -
8 слайд
Подумай!
Что может называться алгоритмом?
Схема метро
Рецепт тортаИнструкция по пользованию телефоном
Расписание уроков
Таблица умножения
-
9 слайд
Молодец!
Раскрась бабочку!
Перейди к заданию Раскраска
Выбранный для просмотра документ Алгоритм как модель действий-часть 2.pptx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
Если твоя бабочка раскрашена, значит ты готов к дальнейшей работе!
Свойства алгоритма
-
2 слайд
Молодец !
Следуй далее
Алгоритмом мы можем называть только такое описание последовательности действий, которое обладает определенными свойствами.
Свойства алгоритма -
3 слайд
Свойства алгоритма
Отдельные (дискретные) шаги (команды, инструкции) в описании действий.
Конечное число шагов, инструкций.
Каждая инструкция понятна тому, кто будет выполнять.
Выполнение инструкций должно приводить к ожидаемому результату.
Предназначение инструкций для решения целого класса задач. -
4 слайд
1
1
2
1
3
4
5
Свойства алгоритма
1. Дискретность
2. Определенность
3. Понятность
4. Результативность
5. Массовость
Алгоритм должен состоять из
последовательности отдельных
(дискретных) шагов
(команд, инструкций).
3. Каждая команда (инструкция) должна быть понятна исполнителю, то есть тому, кто будет выполнять алгоритм.
2. Алгоритм должен состоять из
конечного числа инструкций, то есть их число должно быть точно определено.
4. Выполнение инструкций должно привести к ожидаемому результату.
5. Последовательность инструкций должна быть предназначена для решения не одной задачи, а целого класса однотипных задач. -
5 слайд
Молодец!
Ты хорошо поработал.
Проверь себя.
Перейди к выполнению теста!
Выбранный для просмотра документ РАСКРАСКА_тест.ppsx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
РАСКРАСКА
Ответь правильно на вопросы и бабочка будет раскрашена! -
2 слайд
Алгоритмом называется
Порядок действий для решения задачи
Краткое условие задачи -
3 слайд
«….Царь посылает за Андреем-стрелком.
— Сослужил ты мне две службы, сослужи третью: сходи туда — не знаю куда, принеси то — не знаю что.
Сослужишь — награжу по-царски, а не то мой меч — твоя голова с плеч.»Русская народная сказка
Подумай, является ли наказ царя алгоритмом для стрелка?
НЕТ
ДА -
4 слайд
Какое слово закодировано ребусом?
АЛЬБОМ
АЛГОРИТМ
АВТОМАТ -
5 слайд
Алгоритм – это …… действий для выполнения поставленной задачи
Какое слово пропущено?
ПОРЯДОК
ТАБЛИЦА -
6 слайд
В алгоритме «Вскипяти воду в чайнике» есть ошибка, найди её, правильно расставив действия:
Включи чайник.
Налей воды в чайник.
Дождись, пока вода закипит.
Завари чай в чашке.
Налей кипяток в чашку.
1, 3, 2, 4, 5
2, 1, 3, 4, 5
2, 1, 4, 3, 5 -
Выбранный для просмотра документ ТЕСТ.pptm

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
мин.
5
Время тестирования
Начать тестирование
4
Всего заданий
Введите фамилию и имя
Тест
по теме Алгоритм -
2 слайд
Далее
1
Задание
1 бал.
1
2
3
Продолжи предложение: Алгоритм – это …
Схема движения автобусов
Порядок действий для решения задачи
Инструкция пользования телефоном -
3 слайд
Далее
2
Задание
1 бал.
Выберите все правильные ответы!
1
2
3
4
5
Выберите свойства алгоритма
результативность
дискретность
непрерывность
понятность
неопределенность -
4 слайд
Итоги
4
Задание
1 бал.
Выберите все правильные ответы!
1
2
3
4
5
6
7
8
Расставь по порядку действия по приготовлению яблочного пирога (шарлотки)
2
8
3
7
1
4
5
6 -
5 слайд
Затрачено времени
Выход
Снова
бал.
Всего заданий
Ошибки в выборе ответов на задания:
Набранных баллов
Правильных ответов
Оценка
Подождите!
Идет обработка данных
Результаты
тестирования
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 221 608 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
4 из 5
- 03.02.2016
- 711
- 1
Рейтинг:
5 из 5
- 03.02.2016
- 10293
- 118
- 03.02.2016
- 1038
- 12
- 03.02.2016
- 610
- 1
- 03.02.2016
- 1252
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.
В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
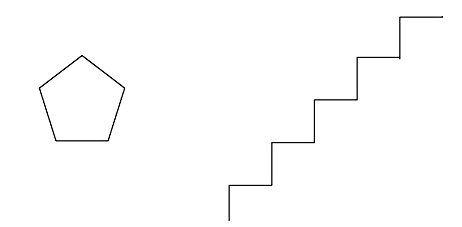
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:
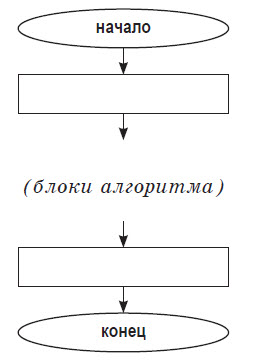
Общий вид блок–схемы алгоритма:
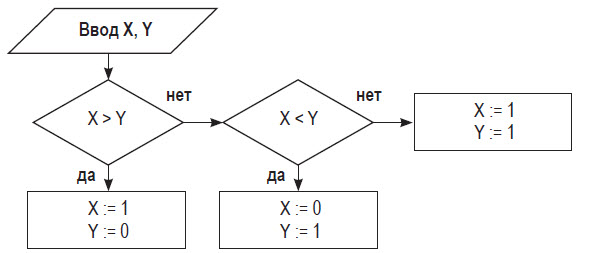
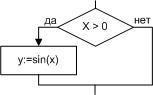
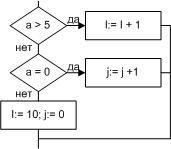
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
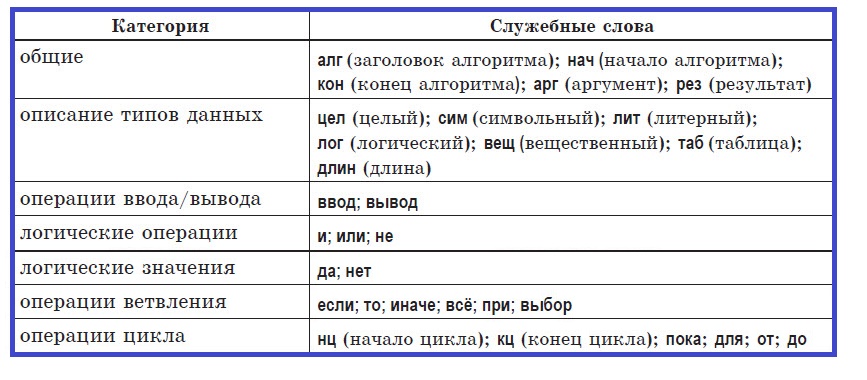
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:
В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:
В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:
На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.
Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.
Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».
Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.
Команды учебного алгоритмического языка
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:
ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).
Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:
Путь 200 м
Тот же результат был бы получен, если бы изменить строку вывода на
вывод «Путь «, v * t, » м»
Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».
Вернуться к Списку конспектов по информатике.
Вопросы:
1. Алгоритм и его свойства
2. Форма записи алгоритмов
3. Базовые алгоритмические структуры
Алгоритм
и его свойства
В
математике для решения типовых задач
мы используем определенные
правила.
Обычно любые инструкции и правила
представляют собой
последовательность действий, которую
необходимо выполнить в определенном
порядке. Для решения задачи надо знать:
─ что дано,
─ что следует
получить и
─ какие действия,
и
─ в каком порядке
следует для этого выполнить.
Алгоритм
—
это точное предписание исполнителю
совершить ука-
занную
последовательность действий для
получения решения задачи за
конечное
число шагов.
Приведенное
определение не является определением
в математическом
смысле слова, а, скорее, описание
интуитивного понятия алгоритма,
раскрывающее
его сущность. Но для общего понимания
сущности алгоритма
такого толкования оказывается, как
правило, достаточно.
Название
«алгоритм» произошло от латинской
формы имени величайшего
среднеазиатского математика Мухаммеда
ибн Муса ал-Хорезми (Alhorithmi),
жившего в 783 -850 гг.
В своей книге «Об индийском счете»
он
изложил правила записи натуральных
чисел с помощью арабских цифр и
правила действий над ними «столбиком»,
знакомые теперь каждом школьнику.
В
XII
веке эта книга была переведена на латынь
и получила широкое
распространение в Европе.
Понятие
алгоритма является не только одним из
главных понятий математики,
но одним из главных понятий современной
пауки. Более того, с наступлением эры
информатики алгоритмы становятся одним
из важнейших
факторов цивилизации.
Свойства алгоритмов
К основным
свойствам алгоритмов относятся следующие
свойства:
1.
Понятность
для исполнителя, ─ исполнитель алгоритма
должен понимать,
как его выполнять. Иными словами, имея
алгоритм и произвольный
вариант исходных данных, исполнитель
должен знать, как надо действовать для
выполнения этого алгоритма.
2. Дискретность
(прерывность, раздельность) — алгоритм
должен представлять процесс решения
задачи как последовательное выполнение
простых (или ранее определенных) шагов
(этапов).
3. Определенность
— каждое правило алгоритма должно быть
четким, однозначным и не оставлять места
для произвола.
Благодаря этому
свойству выполнение алгоритма носит
механический характер и не требует
никаких дополнительных указаний или
сведений о решаемой задаче.
4. Релевантность
(или конечность) состоит в том, что за
конечное число шагов алгоритм либо
должен приводит к решению задачи, либо
после конечного числа шагов
останавливаться из-за невозможности
получить решение с выдачей соответствующего
сообщения, либо неограниченно продолжаться
в течение времени, отведенного для
исполнения алгоритма, с выдачей
промежуточных результатов.
5. Массовость
означает, что алгоритм решения задачи
разрабатывается в общем виде, т.е. он
должен быть применим для некоторого
класса задач, различающихся лишь
исходными данными. При этом исходные
данные могут выбираться из некоторой
области, которая называется областью
применимости алгоритма.
Правила
построения алгоритма
Чтобы
алгоритм выполнил свое предназначение,
eго
необходимо строить по определенным
правилам. В этом смысле нужно говорить
не о свойствах алгоритма, а о правилах
построения алгоритма, или о требованиях,
предъявляемых к алгоритму.
Первое
правило ─ при построении алгоритма,
прежде всего, необходимо задать множество
объектов,
с которыми будет работать алгоритм.
Формализованное (закодированное)
представление этих объектов носит
название данных. Алгоритм
приступает
к
работе
с некоторым набором данных, которые
называются входными, и в результате
своей работы выдает данные, которые
называются входными. Таким
образом, алгоритм преобразует входные
данные в выходные.
Это правило
позволяет сразу отделить алгоритмы от
«методов» и “способов”. Пока мы
не имеем формализованных входных данных,
мы не можем построить алгоритм.
Второе
правило ─ для работы алгоритма требуется
память.
В памяти размещаются входные данные, с
которыми алгоритм начинает работать,
промежуточные данные и выходные данные,
которые являются результатом работы
алгоритма. Память является дискретной,
т.е. состоящей из отдельных ячеек.
Поименованная ячейка памяти носит
название переменной. В теории алгоритмов
размеры памяти не ограничиваются, т. е.
считается, что мы можем предоставить
алгоритму любой необходимый для работы
объем памяти.
Третье
правило ─ дискретность. Алгоритм
строится из отдельных шагов
(действий, операций, команд). Множество
шагов, из которых составлен алгоритм,
конечно.
Четвертое
правило ─ детерменированность. После
каждого шага необходимо
указывать, какой шаг выполняется
следующим, либо давать команду
остановки.
Пятое
правило ─ сходимость
(результативность).
Алгоритм
должен завершать
работу после конечного числа шагов. При
этом необходимо указать,
что считать результатом работы алгоритма.
Итак,
алгоритм ─ неопределяемое понятие
теории алгоритмов. Алгоритм
каждому определенному набору входных
данных ставит в соответствие
некоторый набор выходных данных, т. е.
вычисляет (реализует) функцию.
При рассмотрении конкретных вопросов
в теории алгоритмов всегда имеется
в виду какая-то конкретная модель
алгоритма.
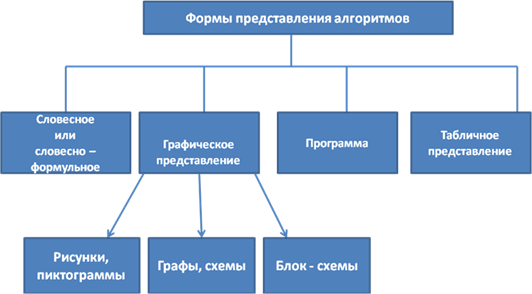
Формы
записи алгоритма
Алгоритм,
как последовательность шагов или
инструкций, может быть
представлен в различных формах.
На
практике наиболее распространены
следующие формы
представления
алгоритмов:
-
словесная
(запись
на естественном языке); -
графическая
(изображения
из графических символов); -
псевдокоды
(полуформализованные
описания алгоритмов на условном
алгоритмическом языке, включающие в
себя как элементы
языка программирования, так и фразы
естественного языка,
общепринятые математические обозначения
и др.);
-
программная
(тексты
на языках программирования).
Словесная
форма записи алгоритмов
Словесный
способ записи алгоритмов представляет
собой описание последовательных
этапов обработки данных. Алгоритм
задается в произвольном
изложении на естественном языке.
Например.
Записать алгоритм нахождения наибольшего
общего делителя
(ИОД) двух натуральных чисел (алгоритм
Эвклида).
Алгоритм может
быть следующим:
1)
задать два числа;
2)
если числа равны, то взять любое т них
в качестве ответа и
остановиться,
в противном случае продолжить выполнение
алгоритма;
-
определить
большее из чисел; -
заменишь большее
из чисел разностью большего и меньшего
из чисел; -
повторить алгоритм
с шага 2.
Описанный
алгоритм, применим к любым натуральным
числам и должен приводить
к решению поставленной задачи.
Самостоятельно:
определить
с помощью этого алгоритма наибольший
общий делитель
чисел 125 и 75.
Словесный
способ не получил широкого распространения
из-за следующих
недостатков:
-
Строго не
формализуем; -
Страдает
многословностью записей; -
Допускает
неоднозначность толкования отдельных
предписаний.
Графическая
форма записи алгоритмов
Графический
способ представления алгоритмов является
более компактным
и наглядным по сравнению со словесным.
При
графическом представлении
алгоритм изображается в виде
последовательности связанных
между собой функциональных блоков,
каждый из которых соответствует
выполнению одного или нескольких
действий.
Такое
графическое представление называется
схемой
алгоритма или
блок-схемой.
В
блок-схеме каждому типу действий (вводу
исходных данных,
вычислению значений выражений, проверке
условий, управлению повторением
действий, окончанию обработки и т.п.)
соответствует геометрическая
фигура, представленная в виде блочного
символа.
Блочные
символы
соединяются линиями
переходов,
определяющими
очередность выполнения
действий. В таблице 8.1 приведены наиболее
часто употребляемые
блочные символы.
Таблица
7.1
|
Название |
Обозначения |
Пояснения |
|
Процесс |
|
Вычислительное |
|
Решение |
|
Проверка |
|
Модификация |
|
Начало |
|
Предопределенный |
|
Вычисления |
|
Ввод-вывод |
|
Ввод-вывод |
|
Пуск-остановка |
|
Начало, |
|
Документ |
|
Вывод |
Пояснения
к таблице 7.1.
-
Блок
«процесс»
применяется
для обозначения действия или
последовательности
действий, изменяющих значение, форму
представления
или размещения данных. Для улучшения
наглядности схемы
несколько отдельных блоков обработки
можно объединять
в один блок. Представление
отдельных операций достаточно
свободно. -
Блок
«решение»
используется
для обозначения переходов управления
по условию. В каждом блоке «решение»
должны быть
указаны вопрос, условие или сравнение,
которые он определяет. -
Блок
«модификация»
используется
для организации циклических
конструкций. Внутри блока записывается
параметр цикла, для
которого указываются его начальное
значение, граничное условие и шаг
изменения значения параметра для
каждого повторения. -
Блок
«предопределенный
процесс»
используется
для указания обращений
к вспомогательным алгоритмам, существующим
автономно в виде некоторых самостоятельных
модулей, и для обращений
к библиотечным подпрограммам.
Псевдокод
Псевдокод
представляет собой систему обозначений
и правил, предназначенную
для единообразной записи алгоритмов.
Псевдокод
занимает промежуточное место между
естественным и формальным языками. С
одной стороны, он близок к обычному
естественному
языку, поэтому алгоритмы могут па нем
записываться и читаться как обычный
текст. С другой стороны, в псевдокоде
используются некоторые формальные
конструкции и математическая символика,
что приближает запись алгоритма к
общепринятой математической записи.
В
псевдокоде не приняты строгие
синтаксические правила для записи
команд, присущие формальным языкам, что
облегчает запись алгоритма на
стадии его проектирования и дает
возможность использовать более широкий
набор команд, рассчитанный па абстрактного
исполнителя.
Однако
в псевдокоде обычно имеются некоторые
конструкции, присущие
формальным языкам, что облегчает переход
от записи на псевдокоде
к записи алгоритма на формальном языке.
В частности, в псевдокоде, так
же, как и в формальных языках, есть
служебные слова, смысл которых определен
раз и навсегда. Они выделяются в печатном
тексте жирным шрифтом,
а в рукописном тексте подчеркиваются.
Единого
или формального определения псевдокода
не существует, поэтому возможны
различные
псевдокоды,
отличающиеся набором служебных
слов и основных (базовых) конструкций.
Примером
псевдокода является школьный
алгоритмический язык в русской
нотации (школьный АЯ), описанный в
учебнике А.Г. Кушниренко и
др. «Основы информатики и вычислительной
техники», 1991. Этот язык в дальнейшем
мы будем называть просто «алгоритмический
язык».
Программная
форма записи алгоритма
Программный
способ записи алгоритма представляет
собой написанный
на языке программирования C#
код программы.
Например:
//Ввод
чисел операндов
Console.Write(«Введите
первое число:»);
var
num1 = int.Parse(Console.ReadLine());
Console.Write(«Введите
второе число:»);
var
num2 = int.Parse(Console.ReadLine());
//Объявление
переменной типа bool
bool
znaj
= true;
//Зацикливание
меню
while
(znaj)
{
Console.WriteLine(«1)Сложение
+»);
Console.WriteLine(«2)Вычитание
-«);
Console.WriteLine(«3)Деление
:»);
Console.WriteLine(«4)Умножение
*»);
Console.WriteLine(«Если
хотите выйти из программы,то введите 0
и нажмите 2 раза Enter»);
Console.WriteLine(«Какие
действия вы хотите сделать с этими
числами»);
var
useranswer = int.Parse(Console.ReadLine());
//Задание
условия
switch
(useranswer)
{
//Выполнение
условия
case
0:
znaj =
false;
break;
case
1:
var
numplus = num1 + num2;
Console.WriteLine(«Сумма»
+ num1 + «+»
+ num2 + «=»
+ numplus);
Console.WriteLine();
break;
case
2:
var
numminus = num2 — num1;
Console.WriteLine(«Разность»
+ num2 + «-»
+ num1 + «=»
+ numminus);
Console.WriteLine();
break;
case
3:
var
numdivision = num2/num1;
Console.WriteLine(«Результат
деления чисел»
+ num2 + «/»
+ num1 + «=»
+ numdivision);
Console.WriteLine();
break;
case
4:
var
nummultiplaction = num1*num2;
Console.WriteLine(«Результат
умнохения чисел»
+ num1 + «*»
+ num2 + «=»
+ nummultiplaction);
Console.WriteLine();
break;
default:
Console.WriteLine(«Вы
ввели цифру или знак не отеченные в
условии»);
break;
}
}
Console.ReadKey();
Типы
базовых алгоритмических структур
В
общем случае блок-схема алгоритма имеет
сложную
структуру и, следовательно, может быть
выражена композицией
элементарных блок-схем, принято называть
базовыми.
Логическая
структура любого алгоритма может быть
представлена
комбинацией трех базовых
алгоритмических
структур:
1.
алгоритмы линейной структуры, которые
иногда называют следованием
(последовательностью)
2.
алгоритмы разветвляющейся структуры,
называемые ветвлением
3. алгоритмы
циклической структуры, называемые
циклами.
Характерной
особенностью базовых структур является
наличие в них одного
входа
и одного
выхода.
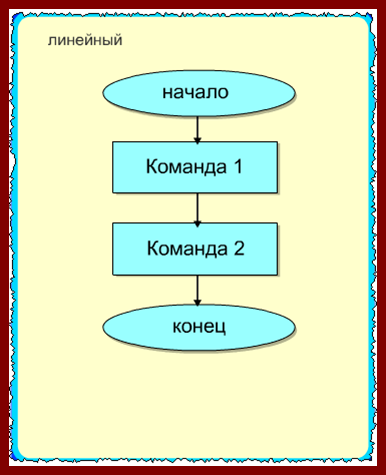
Линейная базовая
структура (“последовательность”)
Линейная
базовая структура – это алгоритм, в
котором блоки выполняются последовательно
друг за другом, в порядке, заданном
схемой.
Такой
порядок выполнения называется
естественным. Образуется последовательностью
действий, следующих одно за другим:
Таблица
7.2.
|
Процесс |
Блок-схема |
|
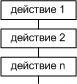
действие 1 действие 2 ………….. действие n |
|
Пример:Вычислить
высоты треугольника со сторонами а, b
, с, используя формулы:
где
.
Для
решения любой нетривиальной задачи
существует несколько
алгоритмов, приводящих к получению
результата. Из возможных алгоритмов
следует выбирать наилучший по некоторому
критерию. Чаще всего
в качестве критерия выбирается либо
оценка точности решения задачи,
либо затраты времени на ее решение, либо
некоторый интегральный
критерий, включающий оценки точности
и затраты времени.
При
решении данной задачи для исключения
повторений следует вычислять
высоты не по приведенным выше формулам
непосредственно, а
используя промежуточную переменную
тогда
ha
= t/a, hb
= t/b, hc
= t/c.
При этом схема
алгоритма решения имеет вид, представленный
на рис. 8.1.
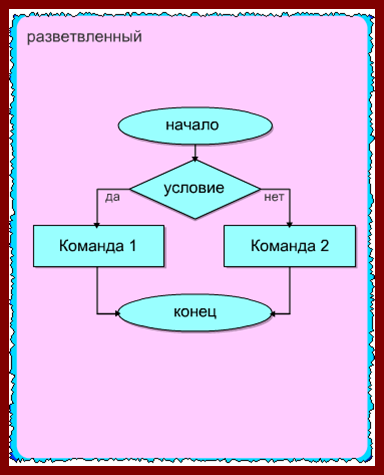
Базовая
структура “ветвление”
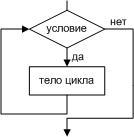
Обеспечивает
в зависимости от результата проверки
условия (да
или
нет)
выбор одного из альтернативных путей
работы алгоритма. Каждый
из путей ведет к общему
выходу,
так что работа алгоритма будет продолжаться
независимо от того, какой путь будет
выбран. Структура
«ветвление» существует в четырех
основных вариантах:
-
если ─ то;
-
если ─ то ─ иначе;
-
выбор;
-
выбор ─ иначе.
Таблица
7.3
|
Выполняемые |
Блок-схема |
|
1. |
|
|
если
то все |
|
|
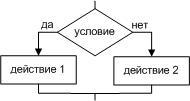
2. |
|
|
если
то иначе все |
|
|
3. |
|
|
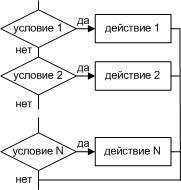
выбор
при
при ……………..
при все |
|
|
4. |
|
|
выбор
при
при ……………..
при иначе все |
|
Примеры структуры
«ветвление»
Таблица
7.4
|
Выполняемые |
Блок-схема |
|
если то все |
|
|
если то иначе все |
|
|
выбор при при при все |
|
|
выбор при при иначе все |
|
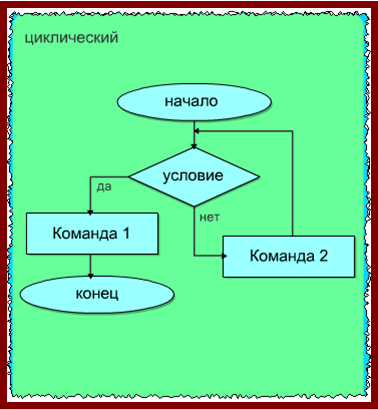
Базовая
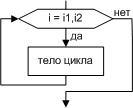
структура “цикл”
Обеспечивает
многократное выполнение некоторой
совокупности действий, которая называется
телом цикла. Основные
разновидности циклов представлены в
таблице 8.5.
Таблица
7.5
|
Выполняемые |
Блок-схема |
|
Цикл
Предписывает |
|
|
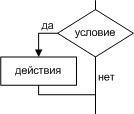
пока тело цикла
(последовательность |
|
|
Цикл
Предписывает |
|
|
для тело цикла
(последовательность |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье будет рассмотрено происхождение понятия «Алгоритм», а также то, какими свойствами обладают современные рациональные алгоритмы и какие задачи они решают. Дополнительное внимание будет уделено видам математических алгоритмов, которые могут быть представлены в виде циклов, разветвлений и линейных последовательностей.
Алгоритмом является определенная конечная последовательность инструкций, выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). Существует множество разнообразных вариантов этого определения, которые можно найти в учебной литературе (чаще всего, это математические книги, а также учебники по информатике и программированию). Основная мысль тут следующая: алгоритм — это некий замкнутый перечень действий, а также дискретный процесс, у которого есть входная и выходная точки. И результат исполнения (решение) достигается за счет пошагового выполнения конкретной последовательности (арифметической, логической и т. п.).
С какими значениями можно связать слово «алгоритм»:
— цикл;
— метод (способ);
— процесс;
— рецепт;
— инструкция.
Немного истории
Это сегодня данное понятие является фундаментальным как в информатике, так и в математике. Но сам термин появился очень давно — тогда, когда еще не было персональных компьютеров, смартфонов и прочей вычислительной техники.
Впервые термин Algorithm был широко озвучен в средние века — это произошло, когда ученые Европы узнали о методах вычислений, используемых математиком из Азии Мухаммедом аль-Хорезми. Как раз от его имени и образовалось слово «Алгоритм».
В течение следующих веков после того, как перевели его сочинения, возникло множество математических трудов, которые были посвящены искусству счета. Если посмотреть на описание алгоритма европейцами в те далекие годы, то можно увидеть следующее определение:
Еще несколько терминов
Поначалу алгоритмизация подразумевала выполнение вычислительных действий над десятичными числами. Спустя годы, этот термин стал использоваться при обозначении любой последовательности, позволяющей достигать конкретного результата. Но эти последовательности не являются абстрактными — они разрабатываются для определенного исполнителя:
— человека;
— механизма;
— компьютера;
— роботизированного устройства;
— языка программирования и т. п.
Такой исполнитель характеризуется способностью исполнять поставленные перед ним задачи в виде соответствующих команд. Это значит, что последовательность описывается на понятном для исполнителя языке, формируя программу.
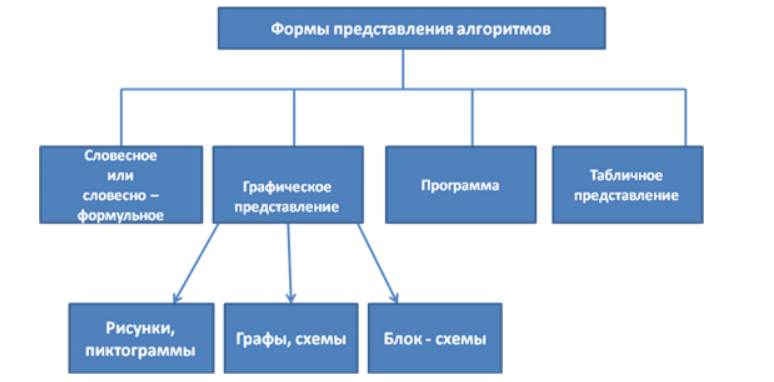
Способы представления алгоритмов бывают разные:
Подробнее о способах читайте здесь, а о блок-схемах — тут.
Основные свойства
Основные свойства следующие:
1. Массовость. Она же универсальность. Хороший и рациональный алгоритм может эффективно использоваться для разных наборов входных данных. Даже подставляя в абстрактную последовательность новые значения снова и снова, пользователь должен получать верный результат.
2. Дискретность. Другое название — разрывность. Здесь речь идет о структуре. Алгори тм считают дискретным, если он делится на шаги, то есть решить задачу — значит последовательно выполнить эти простые шаги или этапы, причем исполнение каждого шага занимает определенный временной отрезок. Такой алгоритм и будет дискретным.
3. Определенность. У этого свойства есть два синонима: точность и детерминированность. Важный момент — шаги должны быть строго определены, причем каждый, то есть разные толкования не допускаются. Строго определен и порядок выполнения этих этапов. Если все хорошо, при условии одинаковых исходных данных и той же самой цепочки команд (последовательности арифметических действий) результат будет одинаков для разных исполнителей.
4. Понятность, ясность. Уже выше было сказано, что последовательность описывается на понятном для исполнителя языке, то есть команды входят в систему понятий исполнителя.
5. Формальность. «Приказы не обсуждают, а выполняют» — говорит директор. Так и разработчик алгоритма — он формирует задачу исполнителю, к примеру, компьютеру, которому не важен смысл, — он просто выполняет соответствующие команды (задания) и получает результат. Зачем и почему — не его вопросы.
6. Завершаемость и результативность. При корректности входных данных рациональный алгоритм должен без проблем завершать свою работу за определенное и установленное разработчиком число шагов, то есть он не должен «зависать» и работать бесконечно. И завершение работы (решение алгоритма) будет сопровождаться получением конкретных результатов.
Виды алгоритмов: цикл, разветвление, линейная последовательность
Сегодня алгоритмов существует огромное множество. Если говорить вкратце, то можно выделить три основные группы:
— линейные;
— разветвляющиеся;
— циклические (они же циклы).
Следует рассмотреть эти группы подробнее, начиная с линейного алгоритма.
Линейность предполагает последовательное выполнение действий, то есть друг за другом. Вот как это может выглядеть на практике в виде блок-схемы:
Когда речь идет о разветвлении, подразумевается наличие хотя бы одного условия. Это условие проверяется по ходу работы. По итогу возможно разделение на несколько ветвей. Пример:
Отдельного упоминания заслуживает цикл, он же циклический алгоритм. При наличии цикла обеспечивается многократное повторение одной и той же операции. В цикле могут быть и вычисления, и перебор вариантов.
У цикла программы есть тело цикла (серия команд). И это тело цикла выполняется до тех пор, пока не будет удовлетворено конкретное условие.
Пример цикла на блок-схеме:
Источники:
- https://urok.1sept.ru/articles/631785;
- https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/sposoby-opisania-vidy-algoritmov;
- https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf.
Алгоритм и его свойства
Понятие алгоритма
Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение этого термина связано с математикой. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов.
Термин алгоритм происходит от имени средневекового персидского математика Мухаммеда Аль-Хорезми (787 – 850 гг.), который еще в IX в. (825 г.) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.
С 1747 г. вместо слова алгоризм стали употреблять алгорисмус, смысл которого состоял в комбинировании четырех операций арифметического исчисления – сложения, вычитания, умножения, деления.
К 1950 г. алгорисмус стал алгорифмом. Смысл алгорифма чаще всего связывался с алгорифмами Евклида – процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п.
Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Это определение не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения.
Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов).
Примеры алгоритмов
- Вычислить факториал числа n (произведение n натуральных чисел c=n!), который вычисляется по формуле c=1*2*3*4*…*n
Алгоритм:
- Полагаем c=1 и переходим к следующему пункту.
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем c=i*c и переходим к следующему пункту.
- Проверяем, равно ли i числу n. Если i=n, то вычисления прекращаем. Если i<n, то увеличиваем i на 1 и переходим к пункту 3.
- Найти наименьшее число M в последовательности из n чисел a1, a2,…, an (n?0) . Прежде чем записать словесный алгоритм данного примера, детально рассмотрим сам процесс поиска наименьшего числа. Первоначально в качестве числа M принимается число a1, т.е. полагаем M=a1, после чего M сравниваем с последующими числами последовательности, начиная с a2. Если M? a2, то M сравнивается a3; если M? a3 , то M сравнивается a4; и так до тех пор, пока найдется число ai < M. Тогда полагаем M= ai и продолжаем сравнение с M последующих чисел из последовательности, начиная с ai+1, до тех пор, пока не будут просмотрены все n чисел. В результате просмотра всех чисел M будет иметь значение, равное наименьшему числу последовательности (i – текущий номер числа).
Алгоритм:
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем M= ai и переходим к следующему пункту.
- Сравниваем i с n; если i< n, то переходим к пункту 4; если i= n, то процесс поиска останавливаем.
- Увеличиваем i на 1 и переходим к следующему пункту.
- Сравниваем ai с M. Если M? ai, то переходим к пункту 3; иначе (M >ai) переходим к пункту 2.
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами (первый алгоритм).
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям, называются логическими алгоритмами (второй алгоритм, поиск пути в лабиринте и др.).
Алгоритм – это понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий для достижения указанной цели или решения поставленной задачи (приводящую от исходных данных к искомому результату).
Свойства алгоритмов
Разработать алгоритм означает разбить задачу на определенную последовательность шагов. От разработчика алгоритма требуется знание особенностей и правил составления алгоритмов.
Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели. Разделение выполнения решения задачи на отдельные операции, выполняемые исполнителем по определенным командам – важное свойство алгоритмов, называемое дискретностью.
Алгоритм представляет собой последовательность команд (инструкций, директив), определяющих действия исполнителя (субъекта или управляемого объекта). Исполнитель, выполняя алгоритм, может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В этом случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и строго выполняет инструкции. Таким образом, возможность решения задачи, механически исполняя команды алгоритма в указанной последовательности, называется формальностью.
Всякий алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Для того чтобы алгоритм мог быть выполнен, нельзя включать в него команды, которые исполнитель не в состоянии выполнить. Нельзя повару поручать работу токаря, какая бы подробная инструкция ему не давалась. У каждого исполнителя имеется свой перечень команд, которые он может исполнить. Каждая команда алгоритма должна определять однозначно действие исполнителя. Такое свойство алгоритмов называется определенностью (или точностью) алгоритма.
Алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые он может выполнить. Это свойство алгоритма называется понятностью. Алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем, не предусмотренных алгоритмом.
Еще одно важное требование, предъявляемое к алгоритмам, – результативность (или конечность) алгоритма. Оно означает, что исполнение алгоритма должно закончиться за конечное число шагов.
Разработка алгоритмов – процесс творческий, требующий умственных усилий и затрат времени. Поэтому предпочтительно разрабатывать алгоритмы, обеспечивающие решения всего класса задач данного типа. Например, если составляется алгоритм решения кубического уравнения ax3 + bx2 + cx + d = 0, то он должен быть вариативен, т.е. обеспечивать возможность решения для любых допустимых исходных значений коэффициентов a, b, c, d. Про такой алгоритм говорят, что он отвечает требованию массовости.
Основные особенности и свойства алгоритмов:
- Наличие ввода исходных данных.
- Наличие вывода результата выполнения алгоритма, поскольку цель выполнения алгоритма – получение результата, имеющего вполне определенное отношение к исходным данным.
- Дискретность – разбивка алгоритма на элементарные команды, и выполнение очередной команды начинается после завершения предыдущей.
- Формальность – свойство, позволяющее любому исполнителю, способному воспринимать и выполнять отдельные указания алгоритма, правильно выполнить весь алгоритм.
- Определенность (точность) – однозначность предписанной последовательности действий, не допускающей ее двоякого толкования.
- Понятность – свойство, предусматривающее то, что алгоритм должен состоять только из тех команд, которые исполнитель может выполнить.
- Результативность (конечность) – исполнение алгоритма должно закончиться за конечное число шагов.
- Корректность – алгоритм должен задавать правильное решение задачи.
- Массовость – алгоритм разрабатывается для решения некоторого класса задач, различающихся исходными данными.
- Эффективность – алгоритм должен выполняться за разумное конечное время. При этом выбирается наиболее простой и короткий способ решения задачи при соблюдении всех ограничений и требований к алгоритму.
Свойства дискретности, формальности, точности, понятности и конечности являются необходимыми (иначе это не алгоритм). Свойство массовости не является необходимым свойством алгоритма, оно скорее определяет его качество.
Формы записи алгоритмов
Алгоритмы можно записывать по-разному. Форма записи, состав и количество операций алгоритма зависит от того, кто будет исполнителем этого алгоритма.
Способы описания алгоритма:
- Формульная запись
- Табличная запись
- Развернутая словесная
- На алгоритмическом языке
- Графический (в виде блок схемы)
- На языке программирования
-
- Формульная запись алгоритма производится с помощью простых математических, химических, физических формул.
Например:
S=V*t; V=S/t; t=S/V
-
- Табличная запись производится с помощью букв латинского алфавита и знака, который называется знаком присвоения :=.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | a:=5x |
| 2. | b:=a+3 |
| 3. | c:=4x |
| 4. | d:=c-7 |
| 5. | y:=b/d |
-
- Развернутое (словесное) описание алгоритма производится на любом национальном языке, единственным условием является соблюдение свойств алгоритма. Используется обычно для описания алгоритмов, предназначенных исполнителю – человеку. Команды записываются на обычном языке и выполняются по порядку. В командах могут использоваться формулы, специальные обозначения, но каждая команда должна быть понятна исполнителю. Естественный порядок команд может быть нарушен, в этом случае команды можно нумеровать и указывать команду, к которой требуется перейти.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | число 7 умножить на переменную x |
| 2. | из результата шага 1 вычесть число 4 |
| 3. | число 5 умножить на переменную x |
| 4. | к результату шага 3 прибавить число 3 |
| 5. | результат шага 2 разделить на результат шага 4 |
-
- Запись алгоритма на алгоритмическом языке записывается с помощью служебных слов, языка и формул (знаков присвоения).
Например: найти большее из трех чисел.
Алгоритм БИТ
- чтение a, b, c
- если a < b к 4
- y:=b; к 5
- y:=a
- если y > c к 7
- y:=c
- запись y
- конец
-
- Запись алгоритма в виде блок-схем (или графическая запись). Алгоритмы представляются в виде блок-схем. Существуют специальные стандарты для построения блок-схем, где определяются графические изображения блоков. Команды алгоритмов записываются внутри блоков на обычном языке или с использованием математических формул. Блоки соединяются по определенным правилам линиями связи, которые показывают порядок выполнения команд.
-
- На языке программирования. Если алгоритм разработан для решения задачи на ЭВМ, то для того, чтобы он мог выполниться исполнителем – ЭВМ, его необходимо записать на языке, понятном этому исполнителю. Для этого разработано множество языков программирования для решения задач разных классов. Запись алгоритма на языке программирования называется программой.
Контрольные вопросы
- Что такое алгоритм?
- Перечислите основные особенности алгоритмов.
- Назовите способы представления алгоритмов.
Цель урока: Формирования у учащихся правильного понимания алгоритмов, их свойств, видов и практических навыков составления алгоритмов.
Задачи урока:
Дидактические: Обеспечить условия:
- для изучения и закрепления основных понятия по теме;
- для усвоения, закрепления темы.
Воспитательные: Обеспечить условия:
- для воспитания чувства коллективизма и взаимопомощи, культуры общения;
- для критического отношения к своему труду, умение оценивать его.
Развивающие: Обеспечить условия:
- для развития мыслительной деятельности учащихся, умения анализировать, сравнивать, обобщать и делать выводы;
- для развития самостоятельности, логического изложения мыслей.
Демонстрационный материал к уроку:
- Мультимедийная презентация
- Портрет Мухаммеда Бен Муссы аль-Хорезми.
Ход урока
- Организационный момент. (2 мин.)
- Актуализация знаний. Постановка учебной задачи. (3 мин.)
- Изложение нового материала. (30 мин.)
- Закрепление нового материала (10 мин.)
Понятие алгоритма
Появление алгоритмов связывают с зарождением математики.
Более 1000 лет назад (825 г.)ученый из города Хорезма Абдулла (или Абу Ждафар) Мухаммед бен Мусса аль-Хорезми создал книгу по математике, в тором описал способы выполнения арифметических действий над многозначными числами.
Алгоритм – описание последовательности действий, исполнение которых приводит к решению поставленной задачи за конечное число шагов.
Алгоритм — понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящих от исходных данных к искомому результату.
Свойства алгоритма
- Дискретность
- Детерминированность
- Массовость
- Результативность
- Конечность
- Дискретность (от лат. Discretus–разделенный , прерывистый) – это свойство предполагает, что любой алгоритм должен состоять из последовательности шагов, следующих друг за другом.
- Детерминированность (от лат. Determinate – определенность, точность) — это свойство указывает, что любое действие в алгоритме должно быть строго и недвусмысленно определенно и описано для каждого случая.
- Массовость – это свойство подразумевает, что один и тот же алгоритм может применяться для решения целого класса задач, отличающихся исходными данными.
- Результативность (конечность) алгоритма — исполнение алгоритма должно закончиться за конечное число шагов.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример: Алгоритм «Зарядка»
- Потянитесь, лежа в постели.
- Сядьте на кровати, поставив ноги на пол.
- Нагнитесь вперед, пытаясь достать руками пальцы ног.
- Выгните спину дугой.
- Сосчитайте до 10.
- Вернитесь в исходное положение.
При словесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий.
Пусть, например, необходимо найти значение следующего выражения:
у=2а-(х+6).
Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:
- Ввести значения а и х.
- Сложить х и 6.
- Умножить а на 2.
- Вычесть из 2а сумму (х+6).
- Вывести у как результат вычисления выражения.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Виды алгоритма
Линейный алгоритм – это такой, в котором все операции выполняются
последовательно одна за другой.
Пример: Алгоритм посадки дерева.
- Выкопать в земле ямку;
- Опустить в ямку саженец;
- Засыпать ямку с саженцем землей;
- Полить саженец водой.
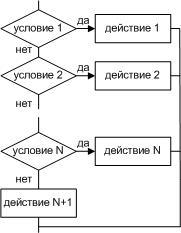
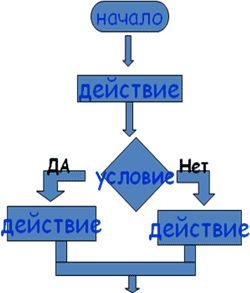
Разветвляющийся алгоритм – это алгоритм в котором выполняется либо одна, либо другая группа действий в зависимости от истинности или ложности условия.
Полная форма
Если <условие>, то <действие 1>, иначе <действие 2>
Неполная форма
Если <условие>, то <действия>
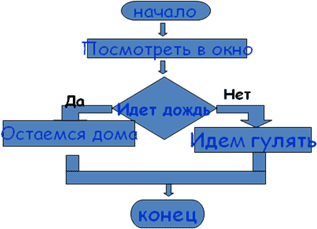
Пример: Если на улице дождь, то останемся дома, а если нет то идем гулять.
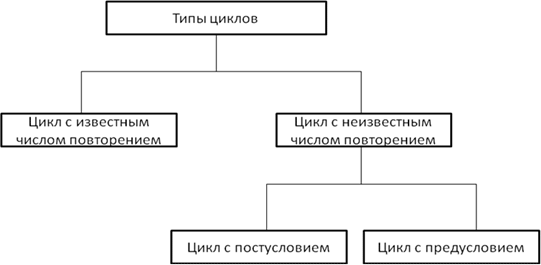
Циклический алгоритм – действия повторяются до тех пор, пока выполняется заданное условие.
Цикл с известным числом повторений
Цикл с известным числом повторений часто называют «циклом ДЛЯ»
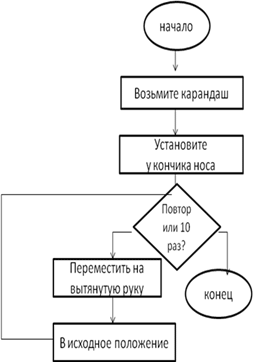
Пример: Алгоритм «Упражнение для глаз»
- Возьмите карандаш.
- Установите его в исходное положение у кончика носа
- Повторите 10 раз, следя за движение карандаша:
- Переместите карандаш на расстояние вытянутой руки;
- Верните карандаш в исходное положение
- Положите карандаш
- Конец алгоритма
Цикл с постусловием
Цикл с неизвестным числом повторений, в тором выход из цикла осуществляется при выполнении условия, принято называть «циклом с постусловием» или «циклом ПРИ»
Алгоритм «Пульс»
- Удобно положите левую руку ладонью вверх.
- Два пальца правой руки положите на запястье левой руки.
- Заметьте положение секундной стрелки
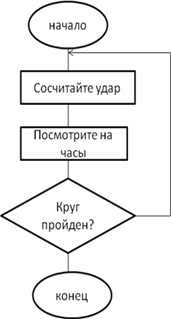
- Сосчитайте очередной удар
- Посмотрите на часы
- Если секундная стрелка прошла полный круг, то закончите действия, иначе перейдите к п.4
Конец алгоритма
Цикл с предусловием
Цикл с известным числом повторений, в котором цикл продолжается, пока выполняется условие, принято называть «циклом с предусловием» или «циклом ПОКА»
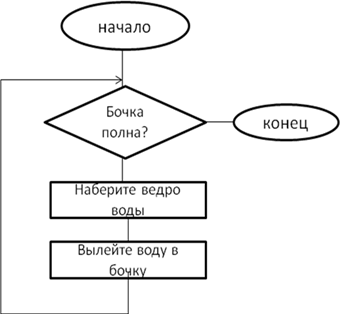
Алгоритм «Бочка»
- Подойдите к бочке
- Если бочка неполна (есть место для воды) , то перейдите к п.3, иначе конец алгоритма.
- Наберите ведро воды
- Вылейте ведро в бочку
- Перейдите к п.2.
Конец алгоритма
Задания для закрепление материала
- Последовательность действий ученика 6 класса Васи: «Если Павлик дома, будем решать задачи по математике. В противном случае следует позвонить Марине и вместе готовить доклад по биологии. Если же Марины нет дома, то надо сесть за сочинение.»
- Последовательность действий ученика 6 класса Васи: «Если Павлик дома, будем решать задачи по математике. В противном случае следует позвонить Марине и вместе готовить доклад по биологии. Если же Марины нет дома, то надо сесть за сочинение.»
- Составить блок-схему действий школьника, которому перед вечерней прогулкой следует выполнить домашнее задание по математике.
Алгоритм
– система формальных правил, четко и
однозначно определяющих процесс решения
поставленной задачи в виде конечной
последовательности действий или
операций.
Любой
алгоритм существует не сам по себе, а
предназначен для определенного
исполнителя (человека, робота, компьютера,
языка программирования и т. д.).
Совокупность команд, которые конкретный
исполнитель умеет выполнять, называется
системой
команд исполнителя
[2].
Рассмотрим свойства
алгоритма.
Дискретность.
Описываемый с помощью алгоритма процесс
должен быть разбит на последовательность
отдельных шагов, т. е. алгоритм должен
состоять из отдельных законченных
действий.
Определенность
(детерминированность). Это свойство
означает, что неоднозначность толкования
записи алгоритма недопустима, многократное
применение алгоритма к одним и тем же
исходным данным должно приводить к
одним результатам.
Результативность.
Алгоритм обязательно должен приводить
к определенному результату за конечное
число шагов и обеспечивать его выдачу
на устройство вывода информации (экран
монитора, принтер) или в файл. Для этого
в алгоритме должно быть предусмотрено
исключение недопустимых ситуаций
(деление на ноль, вычисление логарифма
нуля или отрицательного числа и т. п.).
Если решение задачи не существует, то
в качестве результата может быть
выведено сообщение об этом.
Последовательность
правил, повлекшая за собой процедуру
бесконечного выполения операций,
алгоритмом не является.
Массовость.
Обычно алгоритмы предназначены для
решения не одной конкретной задачи, а
некоторого класса задач данного типа.
В простейшем случае массовость
подразумевает возможность использования
различных исходных данных.
Формальность.
Эта особенность указывает на то, что
любой исполнитель, способный воспринимать
и выполнять инструкции алгоритма,
действует формально, т. е. отвлекается
от содержания поставленной задачи, не
вникает в ее смысл, а лишь строго
выполняет инструкции.
Эффективность.
Это свойство, которое позволяет решить
задачу за приемлемое время.
Различают следующие
виды алгоритмов:
линейный
– список команд (указаний), выполняемых
последовательно друг за другом;
разветвляющийся
– алгоритм, содержащий хотя бы одну
проверку условия, в результате которой
обеспечивается переход на один из
возможных вариантов решения;
циклический
– алгоритм, предусматривающий
многократное повторение одной и той
же последовательности действий.
Количество
повторений
обусловливается
исходными данными или условием задачи.
Любая
алгоритмическая конструкция может
содержать в себе другую конструкцию
того же или иного вида, т. е.
алгоритмические конструкции могут
быть вложенными.
2. Способы представления алгоритмов
Алгоритм,
составленный для некоторого исполнителя,
можно представить различными способами:
с помощью словесного или графического
описания, представленного на
алгоритмическом языке или языке
программирования.
Словесное
описание
отражает структуру алгоритма в
произвольной форме с помощью естественного
языка с требуемой пошаговой детализацией,
однако такая форма алгоритма громоздка
и не имеет наглядности, что делает ее
непригодной для реализации в математических
расчетах.
Алгоритмический
язык
в общем случае представляет собой
систему обозначений и правил для
единообразной и точной записи алгоритмов
и исполнения их. Примером такой системы
является псевдокод
– описание структуры алгоритма на
естественном, частично формализованном
языке. В псевдокоде применяются
формальные конструкции и математические
символы.
При записи алгоритма
с помощью псевдокода применяются
следующие служебные слова и символы:
АЛГ – АЛГоритм;
НАЧ – НАЧало
алгоритма;
КОН – КОНец
алгоритма;
НЦ – Начало
Цикла;
КЦ – Конец Цикла;
:=
– присвоить значение;
// – комментарий.
После
служебного слова АЛГ указывается
название алгоритма.
Каждая
команда записывается с новой строки.
В некоторых литературных источниках
серию команд, составляющих тело
какой-либо единой алгоритмической
конструкции, рекомендуется заключать
в операторные (фигурные) скобки.
Последовательность
записи алгоритма в псевдокоде:
АЛГ название
алгоритма
НАЧ
Команда 1
Команда 2
…………
КОН
Присвоить
значения переменным можно следующим
образом:
s
:= 5, x
:= 2 + y,
m
:= m
– n.
Такого рода запись означает, что сначала
выполняется действие над текущими
значениями переменных в правой части
от знака равенства, а затем полученный
результат присваивается переменной,
имя которой записано в левой части.
Например, в результате
операции k
:=
k
+
1 значение переменной k
будет увеличено на единицу.
Одним
из наиболее наглядных способов записи
алгоритма является изображение его в
виде графической
схемы. При
этом алгоритм представляется
последовательностью блоков (геометрических
фигур), выполняющих определенные
функции, и связей между ними, указывающих
порядок выполнения отдельных инструкций.
Конфигурация и размеры блоков в
графической схеме алгоритма (ГСА)
определяются стандартом [3]. Основное
направление линий связи между блоками
– сверху вниз и по часовой стрелке.
Линии связи в других направлениях
сопровождаются стрелками. Основные
элементы графических схем алгоритмов
приведены в табл. 1.
Таблица
1
Основные элементы
ГСА
|
Символ (блок) |
Обозначение |
Назначение |
|
Пуск, останов |
|
Начало (конец) |
|
Процесс |
|
Вычислительное |
|
Решение |
|
Проверка условия |
|
Модификация |
|
Цикл с параметром |
|
Ввод/вывод |
|
Ввод |
|
Предопределенный |
|
Вычисления |
|
Линия |
|
Связь между |
|
Соединитель |
|
Разрыв линии |
|
Комментарий |
|
Добавление |
Описание
алгоритма с помощью языка программирования
представляет собой программный
код
(программу).
Соседние файлы в папке Теория по информатике
- #
- #
- #
- #
- #
- #
АЛГОРИТМ КАК МОДЕЛЬ ДЕЙСТВИЙ
4 класс
Выполнил учитель
информатики
МКОУ СОШ № 14
Поселок Пятигорский
Ставропольский край
Громаков Станислав Иванович
Цель урока:
- Понять, какое описание последовательности действий может быть названо алгоритмом
- Какие бывают свойства у алгоритма
- Научиться отличать алгоритм от плана действий (описание последовательности действий)
Задача
- Лена купила 4 тетради по 20 рублей и 2 авторучки по 15 рублей. Сколько стоила ее покупка?
Решение:
1 вариант
Определи отдельно стоимость тетрадей и стоимость авторучек
Определи стоимость покупки
2 вариант
Умножь стоимость одной тетради на количество тетрадей
20х4=80 рублей – стоят 4 тетради
Умножь стоимость одной авторучки на количество авторучек
15х2=30 рублей – стоят 2 авторучки
Найди сумму полученных произведений
80+30=110 рублей – покупка Лены
Вариант №1 и вариант №2 – это различные описания последовательности действий.
Существенное отличие заключается в содержании шагов-инструкции.
Вариант №1 – неконкретный, нечеткий
Вариант №2 – конкретный и четкий
Какой же из этих вариантов АЛГОРИТМ?
Алгоритм — описание последовательности действий, которое обладает определенными свойствами
свойство
Описание свойства
Первое
Описание должно состоять из последовательности отдельных (дискретных) шагов (команд, инструкций). После выполнения одной команды можно приступить к выполнению следующей
Второе
Описание должно состоять из конечного числа инструкций, то есть их число должно быть точно определено
Третье
Каждая инструкция должна быть понятной исполнителю, то есть, кто будет ее выполнять.
Четвертое
Выполнение последовательности инструкций должно привести к ожидаемому результату
Пятое
Последовательность инструкций должна быть предназначена для решения не одной задачи, а для решения целого класса задач: найти площадь любого прямоугольника, а не только данного; найти стоимость любого количества тетрадей и авторучек и так далее.
ВАРИАНТ №2 –удовлетворяет всем пяти свойствам, значит эта последовательность алгоритм определения стоимости покупки предметов двух наименований
Алгоритм – последовательность инструкций для исполнителя,
обладающий свойствами:
- Состоит из отдельных инструкций
- Состоит из конечного числа инструкций
- Является понятной исполнителю
- Исполнение приводит к ожидаемому результату
- Позволяет решить не одну задачу, а целый класс подобных задач
Рассмотрим алгоритм определения площади прямоугольника
S
B
Математики нашли алгоритм
нахождения площади прямоугольника
A
- Измерь длину А прямоугольника
- Измерь ширину B прямоугольника
- Определи площадь S как произведение
длины A на ширину B
Этим алгоритмом пользуются все люди, когда хотят найти площадь
Земельного участка, жилую площадь дома, площади стен или
Прямоугольных окон, крыш при его строительстве или ремонте
Алгоритм – это модель процесса решения задач
Главное
- Алгоритм – это подробный план последовательности действий, описывающий решение задачи
- Последовательность шагов-инструкций может быть названа алгоритмом, если она обладает свойствами: число шагов известно и конечно, смысл инструкций понятен, ожидаемый результат известен, годится для решения целого класса задач
- Алгоритм – это модель процесса решения задач
Домашнее задание
§ 15 стр.21-27, рабочая тетрадь к § 15
ДАННЫЙ УРОК ПОДГОТОВЛЕН К УЧЕБНИКУ
4 КЛАСС ИНФОРМАТИКА
ФГОС
Н.В.Матвеева
Е.Н.Челак
Н.К.Конопатова
Л.П.Панкратова
Н.А.Нурова
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
Ежедневно человека окружают задачи. Которые он решает даже не задумываясь. На уровне подсознания.
Постоянная практика в решении задач доводит рефлексы человека до автоматизма.
Например:
Вы никогда, не задумывались как есть ложкой суп. А на самом деле в далеком детстве вы тренировались это делать не один десяток дней отрабатывая хватку неделями или даже месяцами.
А теперь можно вспомнить как человек который никогда не видел китайские палочки, неуклюже пытается ими управляться.
Конечно после определенной тренировки и решении некоторой последовательности задач у него получиться. И он разберется как неправильно держать палочки. Тем самым решив задачу поняв алгоритм действий.
По сути мы каждый раз решая задачу мы создаем алгоритм и далее просто следуем его правилам. Для достижения требуемого результата.
В широком смысле слово алгоритм обозначает следующее:
Алгоритм – это конечная последовательность указаний на языке понятном исполнителю, задающая процесс решения задач определенного типа и ведущая к получению результата, однозначно определяемого допустимыми исходными данными.
Исполнитель алгоритма:
Исполнитель – устройство или живое существо, выполняющее алгоритм соответственно, алгоритм должен состоять только из тех команд (инструкций), которые понятны исполнителю.
| Команды понятные роботу
|
Команды понятные собаке |
Команды понятные человеку
|
Так же существует термин универсальный исполнитель:
Универсальным исполнителем — называют исполнителя, для которого можно построить алгоритм, эквивалентный любому алгоритму для любого другого исполнителя.
Система команд такого исполнителя должна быть как можно проще — так его будет легче использовать в доказательствах.
В настоящее время универсальным исполнителем считается компьютер.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
1) Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
2) Если доказано, что алгоритма не существует, то задача неразрешима.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
Если доказано, что алгоритма не существует, то задача неразрешима.
В нашем случае, нам более интересен вопрос как объяснить решение задачи роботу собирающему автомобиль, чем как научить собаку давать лапу.
По своей сути любой робот это компьютер — который выполняет четкие указания заложенные в его программе. Решаемая им задача не основана на опыте который он приобрел сам, а основана на опыте программиста который решал ее.
Чтобы алгоритм заработал правильно и не давал сбоев, необходимо учитывать несколько факторов.
Необходимо соблюдать порядок выполнения алгоритма:
Фактор 1: Необходимо соблюдать порядок выполнения алгоритма
Фактор 2: При написании алгоритмов необходимо проверять обладает ли алгоритм обязательными свойствами
Фактор 1
Порядок выполнения алгоритма:
1) Действия в алгоритме выполняются в порядке их записи
2) Нельзя менять местами никакие из действий алгоритма
3) Нельзя не закончив одного действия переходить к следующему
4) Если возможны несколько вариантов полученного результата в действии то необходимо учитывать все возможные ситуации.
Исполнитель алгоритма обычно выполняет следующие действия:
1) Алгоритм получает на вход данные (в дискретном виде – цифры или буквы);
2) Алгоритм обрабатывает полученные данные по шагам, вычисляя на каждом шаге промежуточные данные. Этот процесс может быть конечным и бесконечным.
а) Если процесс работы алгоритма окончен, то результат работы алгоритма — данные, вычисленные на последнем шаге.
б) Если процесс работы алгоритма бесконечен (зациклился), то результат его работы — неопределённы. Для таких алгоритмов можно предусмотреть вывод промежуточной информации.
Фактор 2:
Свойства алгоритма
1) Дискретность и упорядоченность — (Любое действие делиться на более простые пока будет невозможно разделить действия на более простые). Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом.
Пример задачи:
Прийти на занятие. Что может быть проще ?
Если разбить задачу на более простые действие то получиться следующее:
1) Войти в колледж
2) Найти расписание
3) Найти пару в расписании
3.1) Узнать какой сегодня день (Вдруг выходной)
3.2) Вспомнить свой номер группы (самое сложное)
3.3) Узнать текущее время (Вдруг уже все закончилось)
3.4) Узнать номер кабинета (главное вспомнить цифры)
4) Дойти до кабинета
4.1) Определиться с направлением движения
4.2) Пройти нужное расстояние
5) Зайти внутрь
6) Занять свободное место (если есть)
2) Детерминированность (однозначная определенность).— Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат.
Если каждый студент одной группы проделает последовательность действий из задачи. Прийти на занятие, подставив одинаковые исходные данные, то все студенты придут на занятие в одну и туже аудиторию.
3) Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Наш алгоритм может работать для каждого занятия текущего дня или всего времени обучения для любого студента любой группы.
Так как он учитывает нужные для этого входные параметры такие как:
дата, время и номер группы.
4) Результативность (или конечность). — Это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
При решении любой задачи нужно определиться с точкой начала (моментом начала задачи) и конечным результатом ( моментом когда цель будет достигнута)
Иначе любой алгоритм можно раздуть до невероятного размера что снизит скорость решения задачи в разы, либо, вовсе не позволит ее решить.
5) Формальность ( определённость ) — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Поэтому при проектировании алгоритмов нам необходимо досконально понимать и предсказывать все ситуации которые могут возникнуть при решении задачи.
Задания к § 15. Алгоритм как модель действий
- Можно ли назвать эти изображения текстовыми моделями устройств? — НЕТ
2. Заполни таблицу по образцу.
| Объект-оригинал | Модель объекта | Общие свойства объекта-оригинала и модели |
| Планета Земля | Глобус | Форма |
| Ребёнок | Кукла | Форма |
| Местность | Карта местности | Расположение объектов |
| Здание | Рисунок | Элементы, из которых состоит здание |
| Событие | Текст | Отношение |
| Явление природы | Макет | Вид |
| Процесс создания объекта | План действий | Алгоритм |
3. Отметь, какой вариант плана действий можно назвать алгоритмом решения задачи: «Петя купил 2 кг картошки и З кг моркови. Сколько стоила покупка?» — Вариант 2
Вариант N 1
1) Узнай стоимость картошки и моркови.
2) Определи стоимость покупки.
Вариант N 2+
1) Умножь стоимость одного килограмма картошки на 2.
2) Умножь стоимость одного килограмма моркови на З.
З) Найди сумму полученных произведений.
4. Вставь пропущенные слова.
| Свойство алгоритма | Описание свойства |
| Первое | Описание должно состоять из последовательности отдельных (дискретных) шагов (инструкций, команд). |
| Второе | Описание должно состоять из конечного числа отдельных инструкций |
| третье | Каждая инструкция должна быть понятна исполнителю. |
| четвёртое | Выполнение последовательности команд инструкций должно привести к ожидаемому результату |
| Пятое | Последовательность инструкций должна быть предназначена для решения не одной конкретной задачи, а может быть использована для решения целого класса задач |
5. Выбери (соедини стрелками) только то, что ты считаешь алгоритмом.
6. Отметь свойства алгоритма.
- Является понятным исполнителю +
- Имеет размер и цвет
- Имеет конечное число шагов +
- Может иметь бесконечное число шагов
- Исполнение инструкций приводит к ожидаемому результату +
- Позволяет решить только одну задачу
- Позволяет решить целый класс задач +
Используя список свойств алгоритма, сформулируй и запиши, что такое алгоритм:
Алгоритм является понятным исполнителю, который имеет конечное число инструкций, которое приведет к ожидаемому результату и позволит решить целый класс задач.
7. Ответь устно на вопросы.
- Чем отличается алгоритм от любого описания последовательности действий? Алгоритм имеет конечное число шагов, которое приведет к ожидаемому результату
- Что есть общего между алгоритмом и просто перечислением действий? Имеют шаги
- Можно ли назвать алгоритмом такой список действий?
- Прочитай.
-
- Запомни.
- Расскажи.
Да, данный алгоритм приведет к ожидаемому результату
- Можно ли сказать, что алгоритм всегда обладает свойством понятности исполнителю? Приведи пример. Да, алгоритм всегда должен быть понятен исполнителю.
8. Отметь общее свойство, которым обладают и алгоритм, и просто план действий.
- Предназначен для исполнения +
- Имеет всегда три шага (инструкции)
- Исполнение приводит к ожидаемому результату +
- Позволяет решить класс задач
- Позволяет решить только одну задачу
- Может иметь бесконечное число шагов
9. Зачеркни неверный алгоритм нахождения площади прямоугольника.
| 1) 2) З) | Измерь длину прямоугольника. Измерь ширину прямоугольника. Определи площадь как произведение длины на ширину. |
10. Реши задачу на перестановку чисел: расположи три числа 9, 5, 7 в порядке возрастания, используя алгоритм:
1) Сравни первое и второе числа; если первое больше второго, то поменяй их местами.
2) Сравни второе и третье числа; если второе больше третьего, то поменяй их местами.
З) Если теперь три числа расположены в порядке возрастания, то закончи выполнение действий; иначе вернись к пункту 1).
- 5,9,7
- 5,7,9
11. Отметь верные высказывания.
- Алгоритм — это подробный план последовательности действий, описывающий способ решения задачи.
- Описание последовательности действий может быть названо алгоритмом, если оно обладает необходимыми свойствами. +
- Алгоритм — это план-модель действий при решении класса задач. +
- План действий человека при уборке дома или при приготовлении пищи может быть алгоритмом. +
12. Составь алгоритм решения класса задач поиска площади прямоугольного пола в помещениях жилого дома. Используй план-схему квартиры:
- Измерить длину комнаты
- Измерить ширину комнаты
- Определи площадь как произведение длины на ширину
13. Заготовка для выполнения задания в учебнике (часть 2) на странице 27.
S = A*B = 20*10=30
Результат: площадь рабочей поверхности парты равна 30 cм2
Примечание: Цифры взяты рандомные, необходимо взять параметры своего стола.
Н. В. Матвеева, Е. Н. Челак Информатика Рабочая тетрадь для 4 класса. Ответы
Скачать материал
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Алгоритм как модель действий-часть 1.pptx

Скачать материал


- Сейчас обучается 29 человек из 15 регионов


- Сейчас обучается 35 человек из 25 регионов


- Сейчас обучается 341 человек из 65 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
В своей повседневной жизни мы постоянно сталкиваемся с выполнением различных действий. Часто мы составляем план для решения какой-то задачи. Чтобы решить задачу, надо знать, что для этого надо делать, как делать и в каком порядке.
-
2 слайд
Ты дружишь с математикой?
Рассмотрим пример простой математической задачи -
-
4 слайд
Есть два варианта плана действий для решения этой задачи:
Варианты № 1 и №2 — это различные описания порядка действий для решения задачи. -
5 слайд
Подумай, чем отличаются два варианта плана действий?
Вариант № 1 содержит неконкретные, нечеткие задания.
Вариант №2 — описание порядка действий четкое, ясное и понятное даже ученику 4 класса.
Таким образом, инструкции или команды для решения поставленной задачи должны быть понятными, конкретными, четкими, с описанием всех шагов. -
6 слайд
«Алгоритм — модель действий»
Подумай!
Как может называться тема нашего урока?Алгоритмом мы можем назвать описание порядка действий для решения поставленной задачи.
-
7 слайд
Алгоритм как модель действий
Прочитай и запомни:
Модель процесса решения задачи (подробный порядок действий) называется алгоритмом -
8 слайд
Подумай!
Что может называться алгоритмом?
Схема метро
Рецепт тортаИнструкция по пользованию телефоном
Расписание уроков
Таблица умножения
-
9 слайд
Молодец!
Раскрась бабочку!
Перейди к заданию Раскраска
Выбранный для просмотра документ Алгоритм как модель действий-часть 2.pptx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
Если твоя бабочка раскрашена, значит ты готов к дальнейшей работе!
Свойства алгоритма
-
2 слайд
Молодец !
Следуй далее
Алгоритмом мы можем называть только такое описание последовательности действий, которое обладает определенными свойствами.
Свойства алгоритма -
3 слайд
Свойства алгоритма
Отдельные (дискретные) шаги (команды, инструкции) в описании действий.
Конечное число шагов, инструкций.
Каждая инструкция понятна тому, кто будет выполнять.
Выполнение инструкций должно приводить к ожидаемому результату.
Предназначение инструкций для решения целого класса задач. -
4 слайд
1
1
2
1
3
4
5
Свойства алгоритма
1. Дискретность
2. Определенность
3. Понятность
4. Результативность
5. Массовость
Алгоритм должен состоять из
последовательности отдельных
(дискретных) шагов
(команд, инструкций).
3. Каждая команда (инструкция) должна быть понятна исполнителю, то есть тому, кто будет выполнять алгоритм.
2. Алгоритм должен состоять из
конечного числа инструкций, то есть их число должно быть точно определено.
4. Выполнение инструкций должно привести к ожидаемому результату.
5. Последовательность инструкций должна быть предназначена для решения не одной задачи, а целого класса однотипных задач. -
5 слайд
Молодец!
Ты хорошо поработал.
Проверь себя.
Перейди к выполнению теста!
Выбранный для просмотра документ РАСКРАСКА_тест.ppsx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
РАСКРАСКА
Ответь правильно на вопросы и бабочка будет раскрашена! -
2 слайд
Алгоритмом называется
Порядок действий для решения задачи
Краткое условие задачи -
3 слайд
«….Царь посылает за Андреем-стрелком.
— Сослужил ты мне две службы, сослужи третью: сходи туда — не знаю куда, принеси то — не знаю что.
Сослужишь — награжу по-царски, а не то мой меч — твоя голова с плеч.»Русская народная сказка
Подумай, является ли наказ царя алгоритмом для стрелка?
НЕТ
ДА -
4 слайд
Какое слово закодировано ребусом?
АЛЬБОМ
АЛГОРИТМ
АВТОМАТ -
5 слайд
Алгоритм – это …… действий для выполнения поставленной задачи
Какое слово пропущено?
ПОРЯДОК
ТАБЛИЦА -
6 слайд
В алгоритме «Вскипяти воду в чайнике» есть ошибка, найди её, правильно расставив действия:
Включи чайник.
Налей воды в чайник.
Дождись, пока вода закипит.
Завари чай в чашке.
Налей кипяток в чашку.
1, 3, 2, 4, 5
2, 1, 3, 4, 5
2, 1, 4, 3, 5 -
Выбранный для просмотра документ ТЕСТ.pptm

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
мин.
5
Время тестирования
Начать тестирование
4
Всего заданий
Введите фамилию и имя
Тест
по теме Алгоритм -
2 слайд
Далее
1
Задание
1 бал.
1
2
3
Продолжи предложение: Алгоритм – это …
Схема движения автобусов
Порядок действий для решения задачи
Инструкция пользования телефоном -
3 слайд
Далее
2
Задание
1 бал.
Выберите все правильные ответы!
1
2
3
4
5
Выберите свойства алгоритма
результативность
дискретность
непрерывность
понятность
неопределенность -
4 слайд
Итоги
4
Задание
1 бал.
Выберите все правильные ответы!
1
2
3
4
5
6
7
8
Расставь по порядку действия по приготовлению яблочного пирога (шарлотки)
2
8
3
7
1
4
5
6 -
5 слайд
Затрачено времени
Выход
Снова
бал.
Всего заданий
Ошибки в выборе ответов на задания:
Набранных баллов
Правильных ответов
Оценка
Подождите!
Идет обработка данных
Результаты
тестирования
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 221 608 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
4 из 5
- 03.02.2016
- 711
- 1
Рейтинг:
5 из 5
- 03.02.2016
- 10293
- 118
- 03.02.2016
- 1038
- 12
- 03.02.2016
- 610
- 1
- 03.02.2016
- 1252
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.
В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:
Общий вид блок–схемы алгоритма:
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:
В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:
В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:
На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.
Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.
Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».
Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.
Команды учебного алгоритмического языка
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:
ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).
Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:
Путь 200 м
Тот же результат был бы получен, если бы изменить строку вывода на
вывод «Путь «, v * t, » м»
Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».
Вернуться к Списку конспектов по информатике.
Вопросы:
1. Алгоритм и его свойства
2. Форма записи алгоритмов
3. Базовые алгоритмические структуры
Алгоритм
и его свойства
В
математике для решения типовых задач
мы используем определенные
правила.
Обычно любые инструкции и правила
представляют собой
последовательность действий, которую
необходимо выполнить в определенном
порядке. Для решения задачи надо знать:
─ что дано,
─ что следует
получить и
─ какие действия,
и
─ в каком порядке
следует для этого выполнить.
Алгоритм
—
это точное предписание исполнителю
совершить ука-
занную
последовательность действий для
получения решения задачи за
конечное
число шагов.
Приведенное
определение не является определением
в математическом
смысле слова, а, скорее, описание
интуитивного понятия алгоритма,
раскрывающее
его сущность. Но для общего понимания
сущности алгоритма
такого толкования оказывается, как
правило, достаточно.
Название
«алгоритм» произошло от латинской
формы имени величайшего
среднеазиатского математика Мухаммеда
ибн Муса ал-Хорезми (Alhorithmi),
жившего в 783 -850 гг.
В своей книге «Об индийском счете»
он
изложил правила записи натуральных
чисел с помощью арабских цифр и
правила действий над ними «столбиком»,
знакомые теперь каждом школьнику.
В
XII
веке эта книга была переведена на латынь
и получила широкое
распространение в Европе.
Понятие
алгоритма является не только одним из
главных понятий математики,
но одним из главных понятий современной
пауки. Более того, с наступлением эры
информатики алгоритмы становятся одним
из важнейших
факторов цивилизации.
Свойства алгоритмов
К основным
свойствам алгоритмов относятся следующие
свойства:
1.
Понятность
для исполнителя, ─ исполнитель алгоритма
должен понимать,
как его выполнять. Иными словами, имея
алгоритм и произвольный
вариант исходных данных, исполнитель
должен знать, как надо действовать для
выполнения этого алгоритма.
2. Дискретность
(прерывность, раздельность) — алгоритм
должен представлять процесс решения
задачи как последовательное выполнение
простых (или ранее определенных) шагов
(этапов).
3. Определенность
— каждое правило алгоритма должно быть
четким, однозначным и не оставлять места
для произвола.
Благодаря этому
свойству выполнение алгоритма носит
механический характер и не требует
никаких дополнительных указаний или
сведений о решаемой задаче.
4. Релевантность
(или конечность) состоит в том, что за
конечное число шагов алгоритм либо
должен приводит к решению задачи, либо
после конечного числа шагов
останавливаться из-за невозможности
получить решение с выдачей соответствующего
сообщения, либо неограниченно продолжаться
в течение времени, отведенного для
исполнения алгоритма, с выдачей
промежуточных результатов.
5. Массовость
означает, что алгоритм решения задачи
разрабатывается в общем виде, т.е. он
должен быть применим для некоторого
класса задач, различающихся лишь
исходными данными. При этом исходные
данные могут выбираться из некоторой
области, которая называется областью
применимости алгоритма.
Правила
построения алгоритма
Чтобы
алгоритм выполнил свое предназначение,
eго
необходимо строить по определенным
правилам. В этом смысле нужно говорить
не о свойствах алгоритма, а о правилах
построения алгоритма, или о требованиях,
предъявляемых к алгоритму.
Первое
правило ─ при построении алгоритма,
прежде всего, необходимо задать множество
объектов,
с которыми будет работать алгоритм.
Формализованное (закодированное)
представление этих объектов носит
название данных. Алгоритм
приступает
к
работе
с некоторым набором данных, которые
называются входными, и в результате
своей работы выдает данные, которые
называются входными. Таким
образом, алгоритм преобразует входные
данные в выходные.
Это правило
позволяет сразу отделить алгоритмы от
«методов» и “способов”. Пока мы
не имеем формализованных входных данных,
мы не можем построить алгоритм.
Второе
правило ─ для работы алгоритма требуется
память.
В памяти размещаются входные данные, с
которыми алгоритм начинает работать,
промежуточные данные и выходные данные,
которые являются результатом работы
алгоритма. Память является дискретной,
т.е. состоящей из отдельных ячеек.
Поименованная ячейка памяти носит
название переменной. В теории алгоритмов
размеры памяти не ограничиваются, т. е.
считается, что мы можем предоставить
алгоритму любой необходимый для работы
объем памяти.
Третье
правило ─ дискретность. Алгоритм
строится из отдельных шагов
(действий, операций, команд). Множество
шагов, из которых составлен алгоритм,
конечно.
Четвертое
правило ─ детерменированность. После
каждого шага необходимо
указывать, какой шаг выполняется
следующим, либо давать команду
остановки.
Пятое
правило ─ сходимость
(результативность).
Алгоритм
должен завершать
работу после конечного числа шагов. При
этом необходимо указать,
что считать результатом работы алгоритма.
Итак,
алгоритм ─ неопределяемое понятие
теории алгоритмов. Алгоритм
каждому определенному набору входных
данных ставит в соответствие
некоторый набор выходных данных, т. е.
вычисляет (реализует) функцию.
При рассмотрении конкретных вопросов
в теории алгоритмов всегда имеется
в виду какая-то конкретная модель
алгоритма.
Формы
записи алгоритма
Алгоритм,
как последовательность шагов или
инструкций, может быть
представлен в различных формах.
На
практике наиболее распространены
следующие формы
представления
алгоритмов:
-
словесная
(запись
на естественном языке); -
графическая
(изображения
из графических символов); -
псевдокоды
(полуформализованные
описания алгоритмов на условном
алгоритмическом языке, включающие в
себя как элементы
языка программирования, так и фразы
естественного языка,
общепринятые математические обозначения
и др.);
-
программная
(тексты
на языках программирования).
Словесная
форма записи алгоритмов
Словесный
способ записи алгоритмов представляет
собой описание последовательных
этапов обработки данных. Алгоритм
задается в произвольном
изложении на естественном языке.
Например.
Записать алгоритм нахождения наибольшего
общего делителя
(ИОД) двух натуральных чисел (алгоритм
Эвклида).
Алгоритм может
быть следующим:
1)
задать два числа;
2)
если числа равны, то взять любое т них
в качестве ответа и
остановиться,
в противном случае продолжить выполнение
алгоритма;
-
определить
большее из чисел; -
заменишь большее
из чисел разностью большего и меньшего
из чисел; -
повторить алгоритм
с шага 2.
Описанный
алгоритм, применим к любым натуральным
числам и должен приводить
к решению поставленной задачи.
Самостоятельно:
определить
с помощью этого алгоритма наибольший
общий делитель
чисел 125 и 75.
Словесный
способ не получил широкого распространения
из-за следующих
недостатков:
-
Строго не
формализуем; -
Страдает
многословностью записей; -
Допускает
неоднозначность толкования отдельных
предписаний.
Графическая
форма записи алгоритмов
Графический
способ представления алгоритмов является
более компактным
и наглядным по сравнению со словесным.
При
графическом представлении
алгоритм изображается в виде
последовательности связанных
между собой функциональных блоков,
каждый из которых соответствует
выполнению одного или нескольких
действий.
Такое
графическое представление называется
схемой
алгоритма или
блок-схемой.
В
блок-схеме каждому типу действий (вводу
исходных данных,
вычислению значений выражений, проверке
условий, управлению повторением
действий, окончанию обработки и т.п.)
соответствует геометрическая
фигура, представленная в виде блочного
символа.
Блочные
символы
соединяются линиями
переходов,
определяющими
очередность выполнения
действий. В таблице 8.1 приведены наиболее
часто употребляемые
блочные символы.
Таблица
7.1
|
Название |
Обозначения |
Пояснения |
|
Процесс |
|
Вычислительное |
|
Решение |
|
Проверка |
|
Модификация |
|
Начало |
|
Предопределенный |
|
Вычисления |
|
Ввод-вывод |
|
Ввод-вывод |
|
Пуск-остановка |
|
Начало, |
|
Документ |
|
Вывод |
Пояснения
к таблице 7.1.
-
Блок
«процесс»
применяется
для обозначения действия или
последовательности
действий, изменяющих значение, форму
представления
или размещения данных. Для улучшения
наглядности схемы
несколько отдельных блоков обработки
можно объединять
в один блок. Представление
отдельных операций достаточно
свободно. -
Блок
«решение»
используется
для обозначения переходов управления
по условию. В каждом блоке «решение»
должны быть
указаны вопрос, условие или сравнение,
которые он определяет. -
Блок
«модификация»
используется
для организации циклических
конструкций. Внутри блока записывается
параметр цикла, для
которого указываются его начальное
значение, граничное условие и шаг
изменения значения параметра для
каждого повторения. -
Блок
«предопределенный
процесс»
используется
для указания обращений
к вспомогательным алгоритмам, существующим
автономно в виде некоторых самостоятельных
модулей, и для обращений
к библиотечным подпрограммам.
Псевдокод
Псевдокод
представляет собой систему обозначений
и правил, предназначенную
для единообразной записи алгоритмов.
Псевдокод
занимает промежуточное место между
естественным и формальным языками. С
одной стороны, он близок к обычному
естественному
языку, поэтому алгоритмы могут па нем
записываться и читаться как обычный
текст. С другой стороны, в псевдокоде
используются некоторые формальные
конструкции и математическая символика,
что приближает запись алгоритма к
общепринятой математической записи.
В
псевдокоде не приняты строгие
синтаксические правила для записи
команд, присущие формальным языкам, что
облегчает запись алгоритма на
стадии его проектирования и дает
возможность использовать более широкий
набор команд, рассчитанный па абстрактного
исполнителя.
Однако
в псевдокоде обычно имеются некоторые
конструкции, присущие
формальным языкам, что облегчает переход
от записи на псевдокоде
к записи алгоритма на формальном языке.
В частности, в псевдокоде, так
же, как и в формальных языках, есть
служебные слова, смысл которых определен
раз и навсегда. Они выделяются в печатном
тексте жирным шрифтом,
а в рукописном тексте подчеркиваются.
Единого
или формального определения псевдокода
не существует, поэтому возможны
различные
псевдокоды,
отличающиеся набором служебных
слов и основных (базовых) конструкций.
Примером
псевдокода является школьный
алгоритмический язык в русской
нотации (школьный АЯ), описанный в
учебнике А.Г. Кушниренко и
др. «Основы информатики и вычислительной
техники», 1991. Этот язык в дальнейшем
мы будем называть просто «алгоритмический
язык».
Программная
форма записи алгоритма
Программный
способ записи алгоритма представляет
собой написанный
на языке программирования C#
код программы.
Например:
//Ввод
чисел операндов
Console.Write(«Введите
первое число:»);
var
num1 = int.Parse(Console.ReadLine());
Console.Write(«Введите
второе число:»);
var
num2 = int.Parse(Console.ReadLine());
//Объявление
переменной типа bool
bool
znaj
= true;
//Зацикливание
меню
while
(znaj)
{
Console.WriteLine(«1)Сложение
+»);
Console.WriteLine(«2)Вычитание
-«);
Console.WriteLine(«3)Деление
:»);
Console.WriteLine(«4)Умножение
*»);
Console.WriteLine(«Если
хотите выйти из программы,то введите 0
и нажмите 2 раза Enter»);
Console.WriteLine(«Какие
действия вы хотите сделать с этими
числами»);
var
useranswer = int.Parse(Console.ReadLine());
//Задание
условия
switch
(useranswer)
{
//Выполнение
условия
case
0:
znaj =
false;
break;
case
1:
var
numplus = num1 + num2;
Console.WriteLine(«Сумма»
+ num1 + «+»
+ num2 + «=»
+ numplus);
Console.WriteLine();
break;
case
2:
var
numminus = num2 — num1;
Console.WriteLine(«Разность»
+ num2 + «-»
+ num1 + «=»
+ numminus);
Console.WriteLine();
break;
case
3:
var
numdivision = num2/num1;
Console.WriteLine(«Результат
деления чисел»
+ num2 + «/»
+ num1 + «=»
+ numdivision);
Console.WriteLine();
break;
case
4:
var
nummultiplaction = num1*num2;
Console.WriteLine(«Результат
умнохения чисел»
+ num1 + «*»
+ num2 + «=»
+ nummultiplaction);
Console.WriteLine();
break;
default:
Console.WriteLine(«Вы
ввели цифру или знак не отеченные в
условии»);
break;
}
}
Console.ReadKey();
Типы
базовых алгоритмических структур
В
общем случае блок-схема алгоритма имеет
сложную
структуру и, следовательно, может быть
выражена композицией
элементарных блок-схем, принято называть
базовыми.
Логическая
структура любого алгоритма может быть
представлена
комбинацией трех базовых
алгоритмических
структур:
1.
алгоритмы линейной структуры, которые
иногда называют следованием
(последовательностью)
2.
алгоритмы разветвляющейся структуры,
называемые ветвлением
3. алгоритмы
циклической структуры, называемые
циклами.
Характерной
особенностью базовых структур является
наличие в них одного
входа
и одного
выхода.
Линейная базовая
структура (“последовательность”)
Линейная
базовая структура – это алгоритм, в
котором блоки выполняются последовательно
друг за другом, в порядке, заданном
схемой.
Такой
порядок выполнения называется
естественным. Образуется последовательностью
действий, следующих одно за другим:
Таблица
7.2.
|
Процесс |
Блок-схема |
|
действие 1 действие 2 ………….. действие n |
|
Пример:Вычислить
высоты треугольника со сторонами а, b
, с, используя формулы:
где
.
Для
решения любой нетривиальной задачи
существует несколько
алгоритмов, приводящих к получению
результата. Из возможных алгоритмов
следует выбирать наилучший по некоторому
критерию. Чаще всего
в качестве критерия выбирается либо
оценка точности решения задачи,
либо затраты времени на ее решение, либо
некоторый интегральный
критерий, включающий оценки точности
и затраты времени.
При
решении данной задачи для исключения
повторений следует вычислять
высоты не по приведенным выше формулам
непосредственно, а
используя промежуточную переменную
тогда
ha
= t/a, hb
= t/b, hc
= t/c.
При этом схема
алгоритма решения имеет вид, представленный
на рис. 8.1.
Базовая
структура “ветвление”
Обеспечивает
в зависимости от результата проверки
условия (да
или
нет)
выбор одного из альтернативных путей
работы алгоритма. Каждый
из путей ведет к общему
выходу,
так что работа алгоритма будет продолжаться
независимо от того, какой путь будет
выбран. Структура
«ветвление» существует в четырех
основных вариантах:
-
если ─ то;
-
если ─ то ─ иначе;
-
выбор;
-
выбор ─ иначе.
Таблица
7.3
|
Выполняемые |
Блок-схема |
|
1. |
|
|
если то все |
|
|
2. |
|
|
если то иначе все |
|
|
3. |
|
|
выбор при при …………….. при все |
|
|
4. |
|
|
выбор при при …………….. при иначе все |
|
Примеры структуры
«ветвление»
Таблица
7.4
|
Выполняемые |
Блок-схема |
|
если то все |
|
|
если то иначе все |
|
|
выбор при при при все |
|
|
выбор при при иначе все |
|
Базовая
структура “цикл”
Обеспечивает
многократное выполнение некоторой
совокупности действий, которая называется
телом цикла. Основные
разновидности циклов представлены в
таблице 8.5.
Таблица
7.5
|
Выполняемые |
Блок-схема |
|
Цикл Предписывает |
|
|
пока тело цикла (последовательность |
|
|
Цикл Предписывает |
|
|
для тело цикла (последовательность |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье будет рассмотрено происхождение понятия «Алгоритм», а также то, какими свойствами обладают современные рациональные алгоритмы и какие задачи они решают. Дополнительное внимание будет уделено видам математических алгоритмов, которые могут быть представлены в виде циклов, разветвлений и линейных последовательностей.
Алгоритмом является определенная конечная последовательность инструкций, выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). Существует множество разнообразных вариантов этого определения, которые можно найти в учебной литературе (чаще всего, это математические книги, а также учебники по информатике и программированию). Основная мысль тут следующая: алгоритм — это некий замкнутый перечень действий, а также дискретный процесс, у которого есть входная и выходная точки. И результат исполнения (решение) достигается за счет пошагового выполнения конкретной последовательности (арифметической, логической и т. п.).
С какими значениями можно связать слово «алгоритм»:
— цикл;
— метод (способ);
— процесс;
— рецепт;
— инструкция.
Немного истории
Это сегодня данное понятие является фундаментальным как в информатике, так и в математике. Но сам термин появился очень давно — тогда, когда еще не было персональных компьютеров, смартфонов и прочей вычислительной техники.
Впервые термин Algorithm был широко озвучен в средние века — это произошло, когда ученые Европы узнали о методах вычислений, используемых математиком из Азии Мухаммедом аль-Хорезми. Как раз от его имени и образовалось слово «Алгоритм».
В течение следующих веков после того, как перевели его сочинения, возникло множество математических трудов, которые были посвящены искусству счета. Если посмотреть на описание алгоритма европейцами в те далекие годы, то можно увидеть следующее определение:
Еще несколько терминов
Поначалу алгоритмизация подразумевала выполнение вычислительных действий над десятичными числами. Спустя годы, этот термин стал использоваться при обозначении любой последовательности, позволяющей достигать конкретного результата. Но эти последовательности не являются абстрактными — они разрабатываются для определенного исполнителя:
— человека;
— механизма;
— компьютера;
— роботизированного устройства;
— языка программирования и т. п.
Такой исполнитель характеризуется способностью исполнять поставленные перед ним задачи в виде соответствующих команд. Это значит, что последовательность описывается на понятном для исполнителя языке, формируя программу.
Способы представления алгоритмов бывают разные:
Подробнее о способах читайте здесь, а о блок-схемах — тут.
Основные свойства
Основные свойства следующие:
1. Массовость. Она же универсальность. Хороший и рациональный алгоритм может эффективно использоваться для разных наборов входных данных. Даже подставляя в абстрактную последовательность новые значения снова и снова, пользователь должен получать верный результат.
2. Дискретность. Другое название — разрывность. Здесь речь идет о структуре. Алгори тм считают дискретным, если он делится на шаги, то есть решить задачу — значит последовательно выполнить эти простые шаги или этапы, причем исполнение каждого шага занимает определенный временной отрезок. Такой алгоритм и будет дискретным.
3. Определенность. У этого свойства есть два синонима: точность и детерминированность. Важный момент — шаги должны быть строго определены, причем каждый, то есть разные толкования не допускаются. Строго определен и порядок выполнения этих этапов. Если все хорошо, при условии одинаковых исходных данных и той же самой цепочки команд (последовательности арифметических действий) результат будет одинаков для разных исполнителей.
4. Понятность, ясность. Уже выше было сказано, что последовательность описывается на понятном для исполнителя языке, то есть команды входят в систему понятий исполнителя.
5. Формальность. «Приказы не обсуждают, а выполняют» — говорит директор. Так и разработчик алгоритма — он формирует задачу исполнителю, к примеру, компьютеру, которому не важен смысл, — он просто выполняет соответствующие команды (задания) и получает результат. Зачем и почему — не его вопросы.
6. Завершаемость и результативность. При корректности входных данных рациональный алгоритм должен без проблем завершать свою работу за определенное и установленное разработчиком число шагов, то есть он не должен «зависать» и работать бесконечно. И завершение работы (решение алгоритма) будет сопровождаться получением конкретных результатов.
Виды алгоритмов: цикл, разветвление, линейная последовательность
Сегодня алгоритмов существует огромное множество. Если говорить вкратце, то можно выделить три основные группы:
— линейные;
— разветвляющиеся;
— циклические (они же циклы).
Следует рассмотреть эти группы подробнее, начиная с линейного алгоритма.
Линейность предполагает последовательное выполнение действий, то есть друг за другом. Вот как это может выглядеть на практике в виде блок-схемы:
Когда речь идет о разветвлении, подразумевается наличие хотя бы одного условия. Это условие проверяется по ходу работы. По итогу возможно разделение на несколько ветвей. Пример:
Отдельного упоминания заслуживает цикл, он же циклический алгоритм. При наличии цикла обеспечивается многократное повторение одной и той же операции. В цикле могут быть и вычисления, и перебор вариантов.
У цикла программы есть тело цикла (серия команд). И это тело цикла выполняется до тех пор, пока не будет удовлетворено конкретное условие.
Пример цикла на блок-схеме:
Источники:
- https://urok.1sept.ru/articles/631785;
- https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/sposoby-opisania-vidy-algoritmov;
- https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf.
Алгоритм и его свойства
Понятие алгоритма
Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение этого термина связано с математикой. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов.
Термин алгоритм происходит от имени средневекового персидского математика Мухаммеда Аль-Хорезми (787 – 850 гг.), который еще в IX в. (825 г.) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.
С 1747 г. вместо слова алгоризм стали употреблять алгорисмус, смысл которого состоял в комбинировании четырех операций арифметического исчисления – сложения, вычитания, умножения, деления.
К 1950 г. алгорисмус стал алгорифмом. Смысл алгорифма чаще всего связывался с алгорифмами Евклида – процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п.
Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Это определение не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения.
Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов).
Примеры алгоритмов
- Вычислить факториал числа n (произведение n натуральных чисел c=n!), который вычисляется по формуле c=1*2*3*4*…*n
Алгоритм:
- Полагаем c=1 и переходим к следующему пункту.
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем c=i*c и переходим к следующему пункту.
- Проверяем, равно ли i числу n. Если i=n, то вычисления прекращаем. Если i<n, то увеличиваем i на 1 и переходим к пункту 3.
- Найти наименьшее число M в последовательности из n чисел a1, a2,…, an (n?0) . Прежде чем записать словесный алгоритм данного примера, детально рассмотрим сам процесс поиска наименьшего числа. Первоначально в качестве числа M принимается число a1, т.е. полагаем M=a1, после чего M сравниваем с последующими числами последовательности, начиная с a2. Если M? a2, то M сравнивается a3; если M? a3 , то M сравнивается a4; и так до тех пор, пока найдется число ai < M. Тогда полагаем M= ai и продолжаем сравнение с M последующих чисел из последовательности, начиная с ai+1, до тех пор, пока не будут просмотрены все n чисел. В результате просмотра всех чисел M будет иметь значение, равное наименьшему числу последовательности (i – текущий номер числа).
Алгоритм:
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем M= ai и переходим к следующему пункту.
- Сравниваем i с n; если i< n, то переходим к пункту 4; если i= n, то процесс поиска останавливаем.
- Увеличиваем i на 1 и переходим к следующему пункту.
- Сравниваем ai с M. Если M? ai, то переходим к пункту 3; иначе (M >ai) переходим к пункту 2.
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами (первый алгоритм).
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям, называются логическими алгоритмами (второй алгоритм, поиск пути в лабиринте и др.).
Алгоритм – это понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий для достижения указанной цели или решения поставленной задачи (приводящую от исходных данных к искомому результату).
Свойства алгоритмов
Разработать алгоритм означает разбить задачу на определенную последовательность шагов. От разработчика алгоритма требуется знание особенностей и правил составления алгоритмов.
Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели. Разделение выполнения решения задачи на отдельные операции, выполняемые исполнителем по определенным командам – важное свойство алгоритмов, называемое дискретностью.
Алгоритм представляет собой последовательность команд (инструкций, директив), определяющих действия исполнителя (субъекта или управляемого объекта). Исполнитель, выполняя алгоритм, может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В этом случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и строго выполняет инструкции. Таким образом, возможность решения задачи, механически исполняя команды алгоритма в указанной последовательности, называется формальностью.
Всякий алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Для того чтобы алгоритм мог быть выполнен, нельзя включать в него команды, которые исполнитель не в состоянии выполнить. Нельзя повару поручать работу токаря, какая бы подробная инструкция ему не давалась. У каждого исполнителя имеется свой перечень команд, которые он может исполнить. Каждая команда алгоритма должна определять однозначно действие исполнителя. Такое свойство алгоритмов называется определенностью (или точностью) алгоритма.
Алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые он может выполнить. Это свойство алгоритма называется понятностью. Алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем, не предусмотренных алгоритмом.
Еще одно важное требование, предъявляемое к алгоритмам, – результативность (или конечность) алгоритма. Оно означает, что исполнение алгоритма должно закончиться за конечное число шагов.
Разработка алгоритмов – процесс творческий, требующий умственных усилий и затрат времени. Поэтому предпочтительно разрабатывать алгоритмы, обеспечивающие решения всего класса задач данного типа. Например, если составляется алгоритм решения кубического уравнения ax3 + bx2 + cx + d = 0, то он должен быть вариативен, т.е. обеспечивать возможность решения для любых допустимых исходных значений коэффициентов a, b, c, d. Про такой алгоритм говорят, что он отвечает требованию массовости.
Основные особенности и свойства алгоритмов:
- Наличие ввода исходных данных.
- Наличие вывода результата выполнения алгоритма, поскольку цель выполнения алгоритма – получение результата, имеющего вполне определенное отношение к исходным данным.
- Дискретность – разбивка алгоритма на элементарные команды, и выполнение очередной команды начинается после завершения предыдущей.
- Формальность – свойство, позволяющее любому исполнителю, способному воспринимать и выполнять отдельные указания алгоритма, правильно выполнить весь алгоритм.
- Определенность (точность) – однозначность предписанной последовательности действий, не допускающей ее двоякого толкования.
- Понятность – свойство, предусматривающее то, что алгоритм должен состоять только из тех команд, которые исполнитель может выполнить.
- Результативность (конечность) – исполнение алгоритма должно закончиться за конечное число шагов.
- Корректность – алгоритм должен задавать правильное решение задачи.
- Массовость – алгоритм разрабатывается для решения некоторого класса задач, различающихся исходными данными.
- Эффективность – алгоритм должен выполняться за разумное конечное время. При этом выбирается наиболее простой и короткий способ решения задачи при соблюдении всех ограничений и требований к алгоритму.
Свойства дискретности, формальности, точности, понятности и конечности являются необходимыми (иначе это не алгоритм). Свойство массовости не является необходимым свойством алгоритма, оно скорее определяет его качество.
Формы записи алгоритмов
Алгоритмы можно записывать по-разному. Форма записи, состав и количество операций алгоритма зависит от того, кто будет исполнителем этого алгоритма.
Способы описания алгоритма:
- Формульная запись
- Табличная запись
- Развернутая словесная
- На алгоритмическом языке
- Графический (в виде блок схемы)
- На языке программирования
-
- Формульная запись алгоритма производится с помощью простых математических, химических, физических формул.
Например:
S=V*t; V=S/t; t=S/V
-
- Табличная запись производится с помощью букв латинского алфавита и знака, который называется знаком присвоения :=.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | a:=5x |
| 2. | b:=a+3 |
| 3. | c:=4x |
| 4. | d:=c-7 |
| 5. | y:=b/d |
-
- Развернутое (словесное) описание алгоритма производится на любом национальном языке, единственным условием является соблюдение свойств алгоритма. Используется обычно для описания алгоритмов, предназначенных исполнителю – человеку. Команды записываются на обычном языке и выполняются по порядку. В командах могут использоваться формулы, специальные обозначения, но каждая команда должна быть понятна исполнителю. Естественный порядок команд может быть нарушен, в этом случае команды можно нумеровать и указывать команду, к которой требуется перейти.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | число 7 умножить на переменную x |
| 2. | из результата шага 1 вычесть число 4 |
| 3. | число 5 умножить на переменную x |
| 4. | к результату шага 3 прибавить число 3 |
| 5. | результат шага 2 разделить на результат шага 4 |
-
- Запись алгоритма на алгоритмическом языке записывается с помощью служебных слов, языка и формул (знаков присвоения).
Например: найти большее из трех чисел.
Алгоритм БИТ
- чтение a, b, c
- если a < b к 4
- y:=b; к 5
- y:=a
- если y > c к 7
- y:=c
- запись y
- конец
-
- Запись алгоритма в виде блок-схем (или графическая запись). Алгоритмы представляются в виде блок-схем. Существуют специальные стандарты для построения блок-схем, где определяются графические изображения блоков. Команды алгоритмов записываются внутри блоков на обычном языке или с использованием математических формул. Блоки соединяются по определенным правилам линиями связи, которые показывают порядок выполнения команд.
-
- На языке программирования. Если алгоритм разработан для решения задачи на ЭВМ, то для того, чтобы он мог выполниться исполнителем – ЭВМ, его необходимо записать на языке, понятном этому исполнителю. Для этого разработано множество языков программирования для решения задач разных классов. Запись алгоритма на языке программирования называется программой.
Контрольные вопросы
- Что такое алгоритм?
- Перечислите основные особенности алгоритмов.
- Назовите способы представления алгоритмов.
Цель урока: Формирования у учащихся правильного понимания алгоритмов, их свойств, видов и практических навыков составления алгоритмов.
Задачи урока:
Дидактические: Обеспечить условия:
- для изучения и закрепления основных понятия по теме;
- для усвоения, закрепления темы.
Воспитательные: Обеспечить условия:
- для воспитания чувства коллективизма и взаимопомощи, культуры общения;
- для критического отношения к своему труду, умение оценивать его.
Развивающие: Обеспечить условия:
- для развития мыслительной деятельности учащихся, умения анализировать, сравнивать, обобщать и делать выводы;
- для развития самостоятельности, логического изложения мыслей.
Демонстрационный материал к уроку:
- Мультимедийная презентация
- Портрет Мухаммеда Бен Муссы аль-Хорезми.
Ход урока
- Организационный момент. (2 мин.)
- Актуализация знаний. Постановка учебной задачи. (3 мин.)
- Изложение нового материала. (30 мин.)
- Закрепление нового материала (10 мин.)
Понятие алгоритма
Появление алгоритмов связывают с зарождением математики.
Более 1000 лет назад (825 г.)ученый из города Хорезма Абдулла (или Абу Ждафар) Мухаммед бен Мусса аль-Хорезми создал книгу по математике, в тором описал способы выполнения арифметических действий над многозначными числами.
Алгоритм – описание последовательности действий, исполнение которых приводит к решению поставленной задачи за конечное число шагов.
Алгоритм — понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящих от исходных данных к искомому результату.
Свойства алгоритма
- Дискретность
- Детерминированность
- Массовость
- Результативность
- Конечность
- Дискретность (от лат. Discretus–разделенный , прерывистый) – это свойство предполагает, что любой алгоритм должен состоять из последовательности шагов, следующих друг за другом.
- Детерминированность (от лат. Determinate – определенность, точность) — это свойство указывает, что любое действие в алгоритме должно быть строго и недвусмысленно определенно и описано для каждого случая.
- Массовость – это свойство подразумевает, что один и тот же алгоритм может применяться для решения целого класса задач, отличающихся исходными данными.
- Результативность (конечность) алгоритма — исполнение алгоритма должно закончиться за конечное число шагов.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример: Алгоритм «Зарядка»
- Потянитесь, лежа в постели.
- Сядьте на кровати, поставив ноги на пол.
- Нагнитесь вперед, пытаясь достать руками пальцы ног.
- Выгните спину дугой.
- Сосчитайте до 10.
- Вернитесь в исходное положение.
При словесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий.
Пусть, например, необходимо найти значение следующего выражения:
у=2а-(х+6).
Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:
- Ввести значения а и х.
- Сложить х и 6.
- Умножить а на 2.
- Вычесть из 2а сумму (х+6).
- Вывести у как результат вычисления выражения.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

Виды алгоритма
Линейный алгоритм – это такой, в котором все операции выполняются
последовательно одна за другой.
Пример: Алгоритм посадки дерева.
- Выкопать в земле ямку;
- Опустить в ямку саженец;
- Засыпать ямку с саженцем землей;
- Полить саженец водой.
Разветвляющийся алгоритм – это алгоритм в котором выполняется либо одна, либо другая группа действий в зависимости от истинности или ложности условия.
Полная форма
Если <условие>, то <действие 1>, иначе <действие 2>
Неполная форма
Если <условие>, то <действия>
Пример: Если на улице дождь, то останемся дома, а если нет то идем гулять.
Циклический алгоритм – действия повторяются до тех пор, пока выполняется заданное условие.
Цикл с известным числом повторений
Цикл с известным числом повторений часто называют «циклом ДЛЯ»
Пример: Алгоритм «Упражнение для глаз»
- Возьмите карандаш.
- Установите его в исходное положение у кончика носа
- Повторите 10 раз, следя за движение карандаша:
- Переместите карандаш на расстояние вытянутой руки;
- Верните карандаш в исходное положение
- Положите карандаш
- Конец алгоритма
Цикл с постусловием
Цикл с неизвестным числом повторений, в тором выход из цикла осуществляется при выполнении условия, принято называть «циклом с постусловием» или «циклом ПРИ»
Алгоритм «Пульс»
- Удобно положите левую руку ладонью вверх.
- Два пальца правой руки положите на запястье левой руки.
- Заметьте положение секундной стрелки
- Сосчитайте очередной удар
- Посмотрите на часы
- Если секундная стрелка прошла полный круг, то закончите действия, иначе перейдите к п.4
Конец алгоритма
Цикл с предусловием
Цикл с известным числом повторений, в котором цикл продолжается, пока выполняется условие, принято называть «циклом с предусловием» или «циклом ПОКА»
Алгоритм «Бочка»
- Подойдите к бочке
- Если бочка неполна (есть место для воды) , то перейдите к п.3, иначе конец алгоритма.
- Наберите ведро воды
- Вылейте ведро в бочку
- Перейдите к п.2.
Конец алгоритма
Задания для закрепление материала
- Последовательность действий ученика 6 класса Васи: «Если Павлик дома, будем решать задачи по математике. В противном случае следует позвонить Марине и вместе готовить доклад по биологии. Если же Марины нет дома, то надо сесть за сочинение.»
- Последовательность действий ученика 6 класса Васи: «Если Павлик дома, будем решать задачи по математике. В противном случае следует позвонить Марине и вместе готовить доклад по биологии. Если же Марины нет дома, то надо сесть за сочинение.»
- Составить блок-схему действий школьника, которому перед вечерней прогулкой следует выполнить домашнее задание по математике.
Алгоритм
– система формальных правил, четко и
однозначно определяющих процесс решения
поставленной задачи в виде конечной
последовательности действий или
операций.
Любой
алгоритм существует не сам по себе, а
предназначен для определенного
исполнителя (человека, робота, компьютера,
языка программирования и т. д.).
Совокупность команд, которые конкретный
исполнитель умеет выполнять, называется
системой
команд исполнителя
[2].
Рассмотрим свойства
алгоритма.
Дискретность.
Описываемый с помощью алгоритма процесс
должен быть разбит на последовательность
отдельных шагов, т. е. алгоритм должен
состоять из отдельных законченных
действий.
Определенность
(детерминированность). Это свойство
означает, что неоднозначность толкования
записи алгоритма недопустима, многократное
применение алгоритма к одним и тем же
исходным данным должно приводить к
одним результатам.
Результативность.
Алгоритм обязательно должен приводить
к определенному результату за конечное
число шагов и обеспечивать его выдачу
на устройство вывода информации (экран
монитора, принтер) или в файл. Для этого
в алгоритме должно быть предусмотрено
исключение недопустимых ситуаций
(деление на ноль, вычисление логарифма
нуля или отрицательного числа и т. п.).
Если решение задачи не существует, то
в качестве результата может быть
выведено сообщение об этом.
Последовательность
правил, повлекшая за собой процедуру
бесконечного выполения операций,
алгоритмом не является.
Массовость.
Обычно алгоритмы предназначены для
решения не одной конкретной задачи, а
некоторого класса задач данного типа.
В простейшем случае массовость
подразумевает возможность использования
различных исходных данных.
Формальность.
Эта особенность указывает на то, что
любой исполнитель, способный воспринимать
и выполнять инструкции алгоритма,
действует формально, т. е. отвлекается
от содержания поставленной задачи, не
вникает в ее смысл, а лишь строго
выполняет инструкции.
Эффективность.
Это свойство, которое позволяет решить
задачу за приемлемое время.
Различают следующие
виды алгоритмов:
линейный
– список команд (указаний), выполняемых
последовательно друг за другом;
разветвляющийся
– алгоритм, содержащий хотя бы одну
проверку условия, в результате которой
обеспечивается переход на один из
возможных вариантов решения;
циклический
– алгоритм, предусматривающий
многократное повторение одной и той
же последовательности действий.
Количество
повторений
обусловливается
исходными данными или условием задачи.
Любая
алгоритмическая конструкция может
содержать в себе другую конструкцию
того же или иного вида, т. е.
алгоритмические конструкции могут
быть вложенными.
2. Способы представления алгоритмов
Алгоритм,
составленный для некоторого исполнителя,
можно представить различными способами:
с помощью словесного или графического
описания, представленного на
алгоритмическом языке или языке
программирования.
Словесное
описание
отражает структуру алгоритма в
произвольной форме с помощью естественного
языка с требуемой пошаговой детализацией,
однако такая форма алгоритма громоздка
и не имеет наглядности, что делает ее
непригодной для реализации в математических
расчетах.
Алгоритмический
язык
в общем случае представляет собой
систему обозначений и правил для
единообразной и точной записи алгоритмов
и исполнения их. Примером такой системы
является псевдокод
– описание структуры алгоритма на
естественном, частично формализованном
языке. В псевдокоде применяются
формальные конструкции и математические
символы.
При записи алгоритма
с помощью псевдокода применяются
следующие служебные слова и символы:
АЛГ – АЛГоритм;
НАЧ – НАЧало
алгоритма;
КОН – КОНец
алгоритма;
НЦ – Начало
Цикла;
КЦ – Конец Цикла;
:=
– присвоить значение;
// – комментарий.
После
служебного слова АЛГ указывается
название алгоритма.
Каждая
команда записывается с новой строки.
В некоторых литературных источниках
серию команд, составляющих тело
какой-либо единой алгоритмической
конструкции, рекомендуется заключать
в операторные (фигурные) скобки.
Последовательность
записи алгоритма в псевдокоде:
АЛГ название
алгоритма
НАЧ
Команда 1
Команда 2
…………
КОН
Присвоить
значения переменным можно следующим
образом:
s
:= 5, x
:= 2 + y,
m
:= m
– n.
Такого рода запись означает, что сначала
выполняется действие над текущими
значениями переменных в правой части
от знака равенства, а затем полученный
результат присваивается переменной,
имя которой записано в левой части.
Например, в результате
операции k
:=
k
+
1 значение переменной k
будет увеличено на единицу.
Одним
из наиболее наглядных способов записи
алгоритма является изображение его в
виде графической
схемы. При
этом алгоритм представляется
последовательностью блоков (геометрических
фигур), выполняющих определенные
функции, и связей между ними, указывающих
порядок выполнения отдельных инструкций.
Конфигурация и размеры блоков в
графической схеме алгоритма (ГСА)
определяются стандартом [3]. Основное
направление линий связи между блоками
– сверху вниз и по часовой стрелке.
Линии связи в других направлениях
сопровождаются стрелками. Основные
элементы графических схем алгоритмов
приведены в табл. 1.
Таблица
1
Основные элементы
ГСА
|
Символ (блок) |
Обозначение |
Назначение |
|
Пуск, останов |
|
Начало (конец) |
|
Процесс |
|
Вычислительное |
|
Решение |
|
Проверка условия |
|
Модификация |
|
Цикл с параметром |
|
Ввод/вывод |
|
Ввод |
|
Предопределенный |
|
Вычисления |
|
Линия |
|
Связь между |
|
Соединитель |
|
Разрыв линии |
|
Комментарий |
|
Добавление |
Описание
алгоритма с помощью языка программирования
представляет собой программный
код
(программу).
Соседние файлы в папке Теория по информатике
- #
- #
- #
- #
- #
- #
АЛГОРИТМ КАК МОДЕЛЬ ДЕЙСТВИЙ
4 класс
Выполнил учитель
информатики
МКОУ СОШ № 14
Поселок Пятигорский
Ставропольский край
Громаков Станислав Иванович
Цель урока:
- Понять, какое описание последовательности действий может быть названо алгоритмом
- Какие бывают свойства у алгоритма
- Научиться отличать алгоритм от плана действий (описание последовательности действий)
Задача
- Лена купила 4 тетради по 20 рублей и 2 авторучки по 15 рублей. Сколько стоила ее покупка?
Решение:
1 вариант
Определи отдельно стоимость тетрадей и стоимость авторучек
Определи стоимость покупки
2 вариант
Умножь стоимость одной тетради на количество тетрадей
20х4=80 рублей – стоят 4 тетради
Умножь стоимость одной авторучки на количество авторучек
15х2=30 рублей – стоят 2 авторучки
Найди сумму полученных произведений
80+30=110 рублей – покупка Лены
Вариант №1 и вариант №2 – это различные описания последовательности действий.
Существенное отличие заключается в содержании шагов-инструкции.
Вариант №1 – неконкретный, нечеткий
Вариант №2 – конкретный и четкий
Какой же из этих вариантов АЛГОРИТМ?
Алгоритм — описание последовательности действий, которое обладает определенными свойствами
свойство
Описание свойства
Первое
Описание должно состоять из последовательности отдельных (дискретных) шагов (команд, инструкций). После выполнения одной команды можно приступить к выполнению следующей
Второе
Описание должно состоять из конечного числа инструкций, то есть их число должно быть точно определено
Третье
Каждая инструкция должна быть понятной исполнителю, то есть, кто будет ее выполнять.
Четвертое
Выполнение последовательности инструкций должно привести к ожидаемому результату
Пятое
Последовательность инструкций должна быть предназначена для решения не одной задачи, а для решения целого класса задач: найти площадь любого прямоугольника, а не только данного; найти стоимость любого количества тетрадей и авторучек и так далее.
ВАРИАНТ №2 –удовлетворяет всем пяти свойствам, значит эта последовательность алгоритм определения стоимости покупки предметов двух наименований
Алгоритм – последовательность инструкций для исполнителя,
обладающий свойствами:
- Состоит из отдельных инструкций
- Состоит из конечного числа инструкций
- Является понятной исполнителю
- Исполнение приводит к ожидаемому результату
- Позволяет решить не одну задачу, а целый класс подобных задач
Рассмотрим алгоритм определения площади прямоугольника
S
B
Математики нашли алгоритм
нахождения площади прямоугольника
A
- Измерь длину А прямоугольника
- Измерь ширину B прямоугольника
- Определи площадь S как произведение
длины A на ширину B
Этим алгоритмом пользуются все люди, когда хотят найти площадь
Земельного участка, жилую площадь дома, площади стен или
Прямоугольных окон, крыш при его строительстве или ремонте
Алгоритм – это модель процесса решения задач
Главное
- Алгоритм – это подробный план последовательности действий, описывающий решение задачи
- Последовательность шагов-инструкций может быть названа алгоритмом, если она обладает свойствами: число шагов известно и конечно, смысл инструкций понятен, ожидаемый результат известен, годится для решения целого класса задач
- Алгоритм – это модель процесса решения задач
Домашнее задание
§ 15 стр.21-27, рабочая тетрадь к § 15
ДАННЫЙ УРОК ПОДГОТОВЛЕН К УЧЕБНИКУ
4 КЛАСС ИНФОРМАТИКА
ФГОС
Н.В.Матвеева
Е.Н.Челак
Н.К.Конопатова
Л.П.Панкратова
Н.А.Нурова
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
Ежедневно человека окружают задачи. Которые он решает даже не задумываясь. На уровне подсознания.
Постоянная практика в решении задач доводит рефлексы человека до автоматизма.
Например:
Вы никогда, не задумывались как есть ложкой суп. А на самом деле в далеком детстве вы тренировались это делать не один десяток дней отрабатывая хватку неделями или даже месяцами.
АЛГОРИТМ КАК МОДЕЛЬ ДЕЙСТВИЙ
4 класс
Выполнил учитель
информатики
МКОУ СОШ № 14
Поселок Пятигорский
Ставропольский край
Громаков Станислав Иванович
Цель урока:
- Понять, какое описание последовательности действий может быть названо алгоритмом
- Какие бывают свойства у алгоритма
- Научиться отличать алгоритм от плана действий (описание последовательности действий)
Задача
- Лена купила 4 тетради по 20 рублей и 2 авторучки по 15 рублей. Сколько стоила ее покупка?
Решение:
1 вариант
Определи отдельно стоимость тетрадей и стоимость авторучек
Определи стоимость покупки
2 вариант
Умножь стоимость одной тетради на количество тетрадей
20х4=80 рублей – стоят 4 тетради
Умножь стоимость одной авторучки на количество авторучек
15х2=30 рублей – стоят 2 авторучки
Найди сумму полученных произведений
80+30=110 рублей – покупка Лены
Вариант №1 и вариант №2 – это различные описания последовательности действий.
Существенное отличие заключается в содержании шагов-инструкции.
Вариант №1 – неконкретный, нечеткий
Вариант №2 – конкретный и четкий
Какой же из этих вариантов АЛГОРИТМ?
Алгоритм — описание последовательности действий, которое обладает определенными свойствами
свойство
Описание свойства
Первое
Описание должно состоять из последовательности отдельных (дискретных) шагов (команд, инструкций). После выполнения одной команды можно приступить к выполнению следующей
Второе
Описание должно состоять из конечного числа инструкций, то есть их число должно быть точно определено
Третье
Каждая инструкция должна быть понятной исполнителю, то есть, кто будет ее выполнять.
Четвертое
Выполнение последовательности инструкций должно привести к ожидаемому результату
Пятое
Последовательность инструкций должна быть предназначена для решения не одной задачи, а для решения целого класса задач: найти площадь любого прямоугольника, а не только данного; найти стоимость любого количества тетрадей и авторучек и так далее.
ВАРИАНТ №2 –удовлетворяет всем пяти свойствам, значит эта последовательность алгоритм определения стоимости покупки предметов двух наименований
Алгоритм – последовательность инструкций для исполнителя,
обладающий свойствами:
- Состоит из отдельных инструкций
- Состоит из конечного числа инструкций
- Является понятной исполнителю
- Исполнение приводит к ожидаемому результату
- Позволяет решить не одну задачу, а целый класс подобных задач
Рассмотрим алгоритм определения площади прямоугольника
S
B
Математики нашли алгоритм
нахождения площади прямоугольника
A
- Измерь длину А прямоугольника
- Измерь ширину B прямоугольника
- Определи площадь S как произведение
длины A на ширину B
Этим алгоритмом пользуются все люди, когда хотят найти площадь
Земельного участка, жилую площадь дома, площади стен или
Прямоугольных окон, крыш при его строительстве или ремонте
Алгоритм – это модель процесса решения задач
Главное
- Алгоритм – это подробный план последовательности действий, описывающий решение задачи
- Последовательность шагов-инструкций может быть названа алгоритмом, если она обладает свойствами: число шагов известно и конечно, смысл инструкций понятен, ожидаемый результат известен, годится для решения целого класса задач
- Алгоритм – это модель процесса решения задач
Домашнее задание
§ 15 стр.21-27, рабочая тетрадь к § 15
ДАННЫЙ УРОК ПОДГОТОВЛЕН К УЧЕБНИКУ
4 КЛАСС ИНФОРМАТИКА
ФГОС
Н.В.Матвеева
Е.Н.Челак
Н.К.Конопатова
Л.П.Панкратова
Н.А.Нурова
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
Ежедневно человека окружают задачи. Которые он решает даже не задумываясь. На уровне подсознания.
Постоянная практика в решении задач доводит рефлексы человека до автоматизма.
Например:
Вы никогда, не задумывались как есть ложкой суп. А на самом деле в далеком детстве вы тренировались это делать не один десяток дней отрабатывая хватку неделями или даже месяцами.
А теперь можно вспомнить как человек который никогда не видел китайские палочки, неуклюже пытается ими управляться.
Конечно после определенной тренировки и решении некоторой последовательности задач у него получиться. И он разберется как неправильно держать палочки. Тем самым решив задачу поняв алгоритм действий.
По сути мы каждый раз решая задачу мы создаем алгоритм и далее просто следуем его правилам. Для достижения требуемого результата.
В широком смысле слово алгоритм обозначает следующее:
Алгоритм – это конечная последовательность указаний на языке понятном исполнителю, задающая процесс решения задач определенного типа и ведущая к получению результата, однозначно определяемого допустимыми исходными данными.
Исполнитель алгоритма:
Исполнитель – устройство или живое существо, выполняющее алгоритм соответственно, алгоритм должен состоять только из тех команд (инструкций), которые понятны исполнителю.
| Команды понятные роботу
|
Команды понятные собаке |
Команды понятные человеку
|
Так же существует термин универсальный исполнитель:
Универсальным исполнителем — называют исполнителя, для которого можно построить алгоритм, эквивалентный любому алгоритму для любого другого исполнителя.
Система команд такого исполнителя должна быть как можно проще — так его будет легче использовать в доказательствах.
В настоящее время универсальным исполнителем считается компьютер.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
1) Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
2) Если доказано, что алгоритма не существует, то задача неразрешима.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
Если доказано, что алгоритма не существует, то задача неразрешима.
В нашем случае, нам более интересен вопрос как объяснить решение задачи роботу собирающему автомобиль, чем как научить собаку давать лапу.
По своей сути любой робот это компьютер — который выполняет четкие указания заложенные в его программе. Решаемая им задача не основана на опыте который он приобрел сам, а основана на опыте программиста который решал ее.
Чтобы алгоритм заработал правильно и не давал сбоев, необходимо учитывать несколько факторов.
Необходимо соблюдать порядок выполнения алгоритма:
Фактор 1: Необходимо соблюдать порядок выполнения алгоритма
Фактор 2: При написании алгоритмов необходимо проверять обладает ли алгоритм обязательными свойствами
Фактор 1
Порядок выполнения алгоритма:
1) Действия в алгоритме выполняются в порядке их записи
2) Нельзя менять местами никакие из действий алгоритма
3) Нельзя не закончив одного действия переходить к следующему
4) Если возможны несколько вариантов полученного результата в действии то необходимо учитывать все возможные ситуации.
Исполнитель алгоритма обычно выполняет следующие действия:
1) Алгоритм получает на вход данные (в дискретном виде – цифры или буквы);
2) Алгоритм обрабатывает полученные данные по шагам, вычисляя на каждом шаге промежуточные данные. Этот процесс может быть конечным и бесконечным.
а) Если процесс работы алгоритма окончен, то результат работы алгоритма — данные, вычисленные на последнем шаге.
б) Если процесс работы алгоритма бесконечен (зациклился), то результат его работы — неопределённы. Для таких алгоритмов можно предусмотреть вывод промежуточной информации.
Фактор 2:
Свойства алгоритма
1) Дискретность и упорядоченность — (Любое действие делиться на более простые пока будет невозможно разделить действия на более простые). Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом.
Пример задачи:
Прийти на занятие. Что может быть проще ?
Если разбить задачу на более простые действие то получиться следующее:
1) Войти в колледж
2) Найти расписание
3) Найти пару в расписании
3.1) Узнать какой сегодня день (Вдруг выходной)
3.2) Вспомнить свой номер группы (самое сложное)
3.3) Узнать текущее время (Вдруг уже все закончилось)
3.4) Узнать номер кабинета (главное вспомнить цифры)
4) Дойти до кабинета
4.1) Определиться с направлением движения
4.2) Пройти нужное расстояние
5) Зайти внутрь
6) Занять свободное место (если есть)
Система команд такого исполнителя должна быть как можно проще — так его будет легче использовать в доказательствах.
В настоящее время универсальным исполнителем считается компьютер.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
1) Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
2) Если доказано, что алгоритма не существует, то задача неразрешима.
Такого исполнителя можно использовать для доказательства разрешимости или неразрешимости задач.
Если удается построить алгоритм решения задачи для универсального исполнителя, то задача разрешима.
Если доказано, что алгоритма не существует, то задача неразрешима.
В нашем случае, нам более интересен вопрос как объяснить решение задачи роботу собирающему автомобиль, чем как научить собаку давать лапу.
По своей сути любой робот это компьютер — который выполняет четкие указания заложенные в его программе. Решаемая им задача не основана на опыте который он приобрел сам, а основана на опыте программиста который решал ее.
Чтобы алгоритм заработал правильно и не давал сбоев, необходимо учитывать несколько факторов.
Необходимо соблюдать порядок выполнения алгоритма:
Фактор 1: Необходимо соблюдать порядок выполнения алгоритма
Фактор 2: При написании алгоритмов необходимо проверять обладает ли алгоритм обязательными свойствами
Фактор 1
Порядок выполнения алгоритма:
1) Действия в алгоритме выполняются в порядке их записи
2) Нельзя менять местами никакие из действий алгоритма
3) Нельзя не закончив одного действия переходить к следующему
4) Если возможны несколько вариантов полученного результата в действии то необходимо учитывать все возможные ситуации.
Исполнитель алгоритма обычно выполняет следующие действия:
1) Алгоритм получает на вход данные (в дискретном виде – цифры или буквы);
2) Алгоритм обрабатывает полученные данные по шагам, вычисляя на каждом шаге промежуточные данные. Этот процесс может быть конечным и бесконечным.
а) Если процесс работы алгоритма окончен, то результат работы алгоритма — данные, вычисленные на последнем шаге.
б) Если процесс работы алгоритма бесконечен (зациклился), то результат его работы — неопределённы. Для таких алгоритмов можно предусмотреть вывод промежуточной информации.
Фактор 2:
Свойства алгоритма
1) Дискретность и упорядоченность — (Любое действие делиться на более простые пока будет невозможно разделить действия на более простые). Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом.
Пример задачи:
Прийти на занятие. Что может быть проще ?
Если разбить задачу на более простые действие то получиться следующее:
1) Войти в колледж
2) Найти расписание
3) Найти пару в расписании
3.1) Узнать какой сегодня день (Вдруг выходной)
3.2) Вспомнить свой номер группы (самое сложное)
3.3) Узнать текущее время (Вдруг уже все закончилось)
3.4) Узнать номер кабинета (главное вспомнить цифры)
4) Дойти до кабинета
4.1) Определиться с направлением движения
4.2) Пройти нужное расстояние
5) Зайти внутрь
6) Занять свободное место (если есть)
2) Детерминированность (однозначная определенность).— Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат.
Если каждый студент одной группы проделает последовательность действий из задачи. Прийти на занятие, подставив одинаковые исходные данные, то все студенты придут на занятие в одну и туже аудиторию.
3) Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Наш алгоритм может работать для каждого занятия текущего дня или всего времени обучения для любого студента любой группы.
Так как он учитывает нужные для этого входные параметры такие как:
дата, время и номер группы.
4) Результативность (или конечность). — Это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
При решении любой задачи нужно определиться с точкой начала (моментом начала задачи) и конечным результатом ( моментом когда цель будет достигнута)
Иначе любой алгоритм можно раздуть до невероятного размера что снизит скорость решения задачи в разы, либо, вовсе не позволит ее решить.
5) Формальность ( определённость ) — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Поэтому при проектировании алгоритмов нам необходимо досконально понимать и предсказывать все ситуации которые могут возникнуть при решении задачи.
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
Часть 1. Основы языка Паскаль
Первая часть пособия предназначена для изучения базовых
приемов программирования. Она последовательно знакомит читателя с азами программистского
искусства, начиная с простейших расчетов, состоящих из нескольких формул, и заканчивая
применением циклов и массивов.
1. Алгоритм и программа
Написанию программы всегда предшествует разработка некоторого
плана (алгоритма) решения задачи. Кратко опишем основные понятия теоретической
информатики, связанные с алгоритмами.
1.1. Алгоритм
Алгоритм — это
однозначно определенная последовательность действий, записанная на понятном исполнителю
алгоритмическом языке и определяющая процесс перехода от исходных данных
к результату.
В этом определении уже указаны основные свойства алгоритма.
Во-первых, алгоритм состоит из конечного набора инструкций или шагов, во-вторых,
каждый шаг трактуется исполнителем единственным образом, что позволяет гарантированно
получить решение для некоторого набора входных данных, в-третьих, алгоритм всегда
сводится к некоторому преобразованию исходных данных в результат или результаты.
В этом смысле формулы для решения квадратного уравнения или даже четко составленную
инструкцию по варке кофе можно считать алгоритмами, выполнимыми исполнителем-человеком.
Для машины, разумеется, требуется более четкая формализация задачи, чем для человека,
понимать естественный язык компьютеры пока неспособны, отсюда необходимость учета
при составлении алгоритма ограниченного набора инструкций ЭВМ.
1.2. Свойства алгоритма
Перечислим
выделенные в п. 1.1 свойства алгоритма.
·
Дискретность — алгоритм состоит из отдельных инструкций (шагов).
·
Однозначность — каждый шаг понимается исполнителем единственным
образом.
·
Массовость — алгоритм работает при меняющихся в некоторых пределах
входных данных.
·
Результативность — за конечное число шагов достигается некоторый результат.
1.3. Формы записи алгоритма
Принято выделять 2 основных формы записи алгоритма.
Графическая форма
записи (блок-схема) характерна тем, что отдельные шаги алгоритма изображаются
геометрическими фигурами, а последовательность выполнения шагов — связями
между этими фигурами. На рис. 1.1 указаны основные элементы блок-схем.
4) Результативность (или конечность). — Это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
При решении любой задачи нужно определиться с точкой начала (моментом начала задачи) и конечным результатом ( моментом когда цель будет достигнута)
Иначе любой алгоритм можно раздуть до невероятного размера что снизит скорость решения задачи в разы, либо, вовсе не позволит ее решить.
5) Формальность ( определённость ) — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Поэтому при проектировании алгоритмов нам необходимо досконально понимать и предсказывать все ситуации которые могут возникнуть при решении задачи.
Фамилия, имя, класс_____________________________________________________________________
- Назовите свойства алгоритма.
1.Алгоритм должен состоять из последовательности ______________________________________________.
2.Алгоритм должен состоять _______________________________________________отдельных инструкций.
3.Каждая инструкция должна быть ______________________________________________________________.
4.Выполнение последовательности команд-инструкций должно привести к ___________________________
____________________________________________________________________________________________.
5.Последовательность инструкций должна быть предназначена для решения __________________________
____________________________________________________________________________________________.
- Поставьте в соответствие начало и конец высказывания
Задания к § 15. Алгоритм как модель действий
- Можно ли назвать эти изображения текстовыми моделями устройств? — НЕТ
2. Заполни таблицу по образцу.
| Объект-оригинал | Модель объекта | Общие свойства объекта-оригинала и модели |
| Планета Земля | Глобус | Форма |
| Ребёнок | Кукла | Форма |
| Местность | Карта местности | Расположение объектов |
| Здание | Рисунок | Элементы, из которых состоит здание |
| Событие | Текст | Отношение |
| Явление природы | Макет | Вид |
| Процесс создания объекта | План действий | Алгоритм |
3. Отметь, какой вариант плана действий можно назвать алгоритмом решения задачи: «Петя купил 2 кг картошки и З кг моркови. Сколько стоила покупка?» — Вариант 2
Вариант N 1
1) Узнай стоимость картошки и моркови.
2) Определи стоимость покупки.
Вариант N 2+
1) Умножь стоимость одного килограмма картошки на 2.
2) Умножь стоимость одного килограмма моркови на З.
З) Найди сумму полученных произведений.
4. Вставь пропущенные слова.
| Свойство алгоритма | Описание свойства |
| Первое | Описание должно состоять из последовательности отдельных (дискретных) шагов (инструкций, команд). |
| Второе | Описание должно состоять из конечного числа отдельных инструкций |
| третье | Каждая инструкция должна быть понятна исполнителю. |
| четвёртое | Выполнение последовательности команд инструкций должно привести к ожидаемому результату |
| Пятое | Последовательность инструкций должна быть предназначена для решения не одной конкретной задачи, а может быть использована для решения целого класса задач |
5. Выбери (соедини стрелками) только то, что ты считаешь алгоритмом.
6. Отметь свойства алгоритма.
- Является понятным исполнителю +
- Имеет размер и цвет
- Имеет конечное число шагов +
- Может иметь бесконечное число шагов
- Исполнение инструкций приводит к ожидаемому результату +
- Позволяет решить только одну задачу
- Позволяет решить целый класс задач +
Используя список свойств алгоритма, сформулируй и запиши, что такое алгоритм:
Алгоритм является понятным исполнителю, который имеет конечное число инструкций, которое приведет к ожидаемому результату и позволит решить целый класс задач.
7. Ответь устно на вопросы.
- Чем отличается алгоритм от любого описания последовательности действий? Алгоритм имеет конечное число шагов, которое приведет к ожидаемому результату
- Что есть общего между алгоритмом и просто перечислением действий? Имеют шаги
- Можно ли назвать алгоритмом такой список действий?
- Прочитай.
-
- Запомни.
- Расскажи.
Да, данный алгоритм приведет к ожидаемому результату
- Можно ли сказать, что алгоритм всегда обладает свойством понятности исполнителю? Приведи пример. Да, алгоритм всегда должен быть понятен исполнителю.
8. Отметь общее свойство, которым обладают и алгоритм, и просто план действий.
- Предназначен для исполнения +
- Имеет всегда три шага (инструкции)
- Исполнение приводит к ожидаемому результату +
- Позволяет решить класс задач
- Позволяет решить только одну задачу
- Может иметь бесконечное число шагов
9. Зачеркни неверный алгоритм нахождения площади прямоугольника.
| 1) 2) З) | Измерь длину прямоугольника. Измерь ширину прямоугольника. Определи площадь как произведение длины на ширину. |
10. Реши задачу на перестановку чисел: расположи три числа 9, 5, 7 в порядке возрастания, используя алгоритм:
1) Сравни первое и второе числа; если первое больше второго, то поменяй их местами.
2) Сравни второе и третье числа; если второе больше третьего, то поменяй их местами.
З) Если теперь три числа расположены в порядке возрастания, то закончи выполнение действий; иначе вернись к пункту 1).
- 5,9,7
- 5,7,9
11. Отметь верные высказывания.
- Алгоритм — это подробный план последовательности действий, описывающий способ решения задачи.
- Описание последовательности действий может быть названо алгоритмом, если оно обладает необходимыми свойствами. +
- Алгоритм — это план-модель действий при решении класса задач. +
- План действий человека при уборке дома или при приготовлении пищи может быть алгоритмом. +
12. Составь алгоритм решения класса задач поиска площади прямоугольного пола в помещениях жилого дома. Используй план-схему квартиры:
- Измерить длину комнаты
- Измерить ширину комнаты
- Определи площадь как произведение длины на ширину
13. Заготовка для выполнения задания в учебнике (часть 2) на странице 27.
S = A*B = 20*10=30
Результат: площадь рабочей поверхности парты равна 30 cм2
Примечание: Цифры взяты рандомные, необходимо взять параметры своего стола.
Н. В. Матвеева, Е. Н. Челак Информатика Рабочая тетрадь для 4 класса. Ответы
АЛГОРИТМ КАК МОДЕЛЬ ДЕЙСТВИЙ
4 класс
Выполнил учитель
информатики
МКОУ СОШ № 14
Поселок Пятигорский
Ставропольский край
Громаков Станислав Иванович
Цель урока:
- Понять, какое описание последовательности действий может быть названо алгоритмом
- Какие бывают свойства у алгоритма
- Научиться отличать алгоритм от плана действий (описание последовательности действий)
Задача
- Лена купила 4 тетради по 20 рублей и 2 авторучки по 15 рублей. Сколько стоила ее покупка?
Решение:
1 вариант
Определи отдельно стоимость тетрадей и стоимость авторучек
Определи стоимость покупки
2 вариант
Умножь стоимость одной тетради на количество тетрадей
20х4=80 рублей – стоят 4 тетради
Умножь стоимость одной авторучки на количество авторучек
15х2=30 рублей – стоят 2 авторучки
Найди сумму полученных произведений
80+30=110 рублей – покупка Лены
Вариант №1 и вариант №2 – это различные описания последовательности действий.
Существенное отличие заключается в содержании шагов-инструкции.
Вариант №1 – неконкретный, нечеткий
Вариант №2 – конкретный и четкий
Какой же из этих вариантов АЛГОРИТМ?
Алгоритм — описание последовательности действий, которое обладает определенными свойствами
свойство
Описание свойства
Первое
Описание должно состоять из последовательности отдельных (дискретных) шагов (команд, инструкций). После выполнения одной команды можно приступить к выполнению следующей
Второе
Описание должно состоять из конечного числа инструкций, то есть их число должно быть точно определено
Третье
Каждая инструкция должна быть понятной исполнителю, то есть, кто будет ее выполнять.
Четвертое
Выполнение последовательности инструкций должно привести к ожидаемому результату
Пятое
Последовательность инструкций должна быть предназначена для решения не одной задачи, а для решения целого класса задач: найти площадь любого прямоугольника, а не только данного; найти стоимость любого количества тетрадей и авторучек и так далее.
ВАРИАНТ №2 –удовлетворяет всем пяти свойствам, значит эта последовательность алгоритм определения стоимости покупки предметов двух наименований
Алгоритм – последовательность инструкций для исполнителя,
обладающий свойствами:
- Состоит из отдельных инструкций
- Состоит из конечного числа инструкций
- Является понятной исполнителю
- Исполнение приводит к ожидаемому результату
- Позволяет решить не одну задачу, а целый класс подобных задач
Рассмотрим алгоритм определения площади прямоугольника
S
B
Математики нашли алгоритм
нахождения площади прямоугольника
A
- Измерь длину А прямоугольника
- Измерь ширину B прямоугольника
- Определи площадь S как произведение
длины A на ширину B
Этим алгоритмом пользуются все люди, когда хотят найти площадь
Земельного участка, жилую площадь дома, площади стен или
Прямоугольных окон, крыш при его строительстве или ремонте
Алгоритм – это модель процесса решения задач
Главное
- Алгоритм – это подробный план последовательности действий, описывающий решение задачи
- Последовательность шагов-инструкций может быть названа алгоритмом, если она обладает свойствами: число шагов известно и конечно, смысл инструкций понятен, ожидаемый результат известен, годится для решения целого класса задач
- Алгоритм – это модель процесса решения задач
Домашнее задание
§ 15 стр.21-27, рабочая тетрадь к § 15
ДАННЫЙ УРОК ПОДГОТОВЛЕН К УЧЕБНИКУ
4 КЛАСС ИНФОРМАТИКА
ФГОС
Н.В.Матвеева
Е.Н.Челак
Н.К.Конопатова
Л.П.Панкратова
Н.А.Нурова